Control of reaction-diffusion equations on time-evolving manifolds

Abstract

Among the main actors of organism development there are morphogens, which are signaling molecules diffusing in the developing organism and acting on cells to produce local responses. Growth is thus determined by the distribution of such signal. Meanwhile, the diffusion of the signal is itself affected by the changes in shape and size of the organism. In other words, there is a complete coupling between the diffusion of the signal and the change of the shapes.

In this paper, we introduce a mathematical model to investigate such coupling. The shape is given by a manifold, that varies in time as the result of a deformation given by a transport equation. The signal is represented by a density, diffusing on the manifold via a diffusion equation. We show the non-commutativity of the transport and diffusion evolution by introducing a new concept of Lie bracket between the diffusion and the transport operator. We also provide numerical simulations showing this phenomenon.

INTRODUCTION

Modeling growth of living organism attracted the interest of many investigators both in the field of Developmental Biology and the Applied Mathematics (see [4], [7], [11], [12], [16]). Developmental biologists have shown that development is primarily induced by morphogens, which act on the organism as signals by triggering signaling pathways and provoking a response resulting in cell growth or differentiation [21]. Several modeling approaches have been explored from the mathematical point of view. From a microscopic standpoint (see [11]), tissues are considered as a collection of cells, and discrete models such as cellular automata are used. We instead adopt a macroscopic standpoint, where the relevant quantity is the density of the signal on a manifold. As a specific example, in certain fruit flies species such as Drosophila melanogaster, a morphogen called Gurken is responsible for initiating the EGFR signalling pathway, resulting in the specification of cells that eventually form structures called dorsal appendages on the drosphila eggshell [9], [21]. Interestingly Gurken diffuses in a thin space, called perivitelline space, which can be modeled by an evolving surface. This leads naturally to model the growing organism by coupling a growing surface with a signal diffusing on it, see [15]. Because of the biological motivation, this framework was called Developmental Partial Differential Equations. In this paper we consider a general model, where the boundary of the organism is described by a Riemannian manifold, that evolves with respect to time due to the growth induced by the signal on it. In turn the evolution (for instance, heat diffusion) of the signal on the manifold is affected by the shape of the manifold. Indeed, intrinsic heat diffusion is described by the heat equation with the Laplace-Beltrami operator. Our aim is to investigate the coupling between growth and diffusion. There is a wide literature of studies for PDEs on manifolds, see for instance [17], [19], or Turing Patterns on evolving manifolds, see for instance [2], [5]. However the coupling of PDE and time-evolving manifold was apparently newly introduced in [15].

As a first step to understand what shapes of the manifold can be attained from an initial configuration, we explore the non-commutativity of the growth (manifold change in time) and the diffusion operator (on the manifold itself). A newly defined concept of Lie bracket between the diffusion (2nd order operator) and growth (1st order operator) is able to capture such non-commutativity and thus provide new shapes towards which the manifold may evolve. As in classical geometric control theory [1], [3], [18], the concept of Lie bracket may indeed enclose all the needed information to capture the controlled dynamics. Moreover, such bracket can be understood as a new available direction for the growth of the organism.

The paper is structured as follows. We begin by introducing the general model, or Developmental Partial Differential Equation describing the coupling of growth and diffusion on a Riemannian manifold. We then prove existence and uniqueness of the solution to the DPDE by introducing a numerical scheme that discretizes time and solves diffusion and growth independently on each time interval. We prove that the limit of the scheme is the solution to the DPDE. We then use the scheme to define a new kind of Lie bracket between the diffusion and the growth operators. By computing the bracket explicitly, we show that it is not zero. Numerical simulations confirm the analytical computation of the bracket.

I. DESCRIPTION OF MORPHOGENESIS

In this section, we describe a simplified model for morphogenesis, i.e. for the development of the shape of a living body. The shape of an organism is described by its boundary, represented by a time-varying manifold ℳ_t embedded in an Euclidean space ℝ^d with the dimension d being fixed (naturally d = 3 in real examples). On such manifold, a growth signal is represented by a probability measure μ_t ∈ ℘(ℳ_t). Here ℘(ℳ_t) is the space of probability measures on ℳ_t, endowed with the Wasserstein distance W_p (see more details in Section I-A). Using the embedding of ℳ_t into the ambient space ℝ^d, we can consider μ_t as a probability measure on ℝ^d.

The organism development is determined by a growth vector field v[μ_t] given by the current shape of the organism and by the signal, with v[·] : ℘_c(ℝ^d) → Lip(ℝ^d) ∪ ℒ^∞(ℝ^d). The signal μ_t on ℳ_t diffuses following the heat equation intrinsically defined on ℳ_t. Indeed, since ℳ_t inherits the Riemannian structure of the ambient space ℝ^d, we can define an intrinsic Laplacian, called the Laplace-Beltrami operator. We denote with Δ_t the Laplace-Beltrami operator on ℳ_t. These two phenomena (growth and diffusion) can be summarized by describing the evolution of the signal μ_t via the following transport-diffusion Partial Differential Equation :

$${\partial }_t{\mu }_t+\nabla ·(v[{\mu }_t]{\mu }_t)={\mathrm{\Delta }}_t{\mu }_t,$$ (1)

where the manifold ℳ_t is the support of μ_t at each time. Since μ_t are measures in ℝ^d, such equation needs to be interpreted in the weak sense, i.e. for all f ∈ C^∞(ℝ^d) it holds

$${\partial }_t{\int }_{{ℝ}^d}fd{\mu }_t-{\int }_{{ℝ}^d}(\nabla f·\nabla v[{\mu }_t])d{\mu }_t={\int }_{{ℝ}^d}{\mathrm{\Delta }}_{t}fd{\mu }_t.$$ (2)

We will provide in Section I-B existence and uniqueness results for such equation.

Remark 1

Notice that the developed theory can be adapted to include reaction terms of the type h[μ_t] on the right-hand side of (1) by using the generalized Wasserstein distance, see [14].

A. Transport equation and Wasserstein distance

In this section, we recall the definition of the Wasserstein distance and its connection with nonlinear transport equation, i.e. equation (1) with no diffusion. Let us first recall the definition of the Wasserstein distance (see [20]). Recall that, for every probability measure μ and measurable map ϕ, the push-forward ϕ#μ is defined by ϕ#μ(A) = μ(ϕ⁻¹(A)).

Definition 2

Fix p ≥ 1. Given two probability measures μ and ν in ℝ^d, the p-Wasserstein distance between μ and ν is given by:

$${\mathcal{W}}_p(\mu ,\nu ):=\underset{\pi \in \mathrm{\Pi }(\mu ,\nu )}{min}{\left({\int }_{{ℝ}^d\times {ℝ}^d}{\mid x-y\mid }^{p}d\pi (x,y)\right)}^{1/p}$$

where Π(μ, ν) is the set of transference plans from μ to ν, i.e. of the probability measures on ℝ^d × ℝ^d with marginals μ, ν, respectively. In other words P_x#π = μ and P_y#π = ν (where P_x, respectively P_y denote the projection on the first, respectively second, component of (x, y).)

The transference plans in Π(μ, ν) can be seen as methods to transport μ to ν and the term ∫_ℝ^d×ℝ^d|x − y|^pdπ(x, y) can be interpreted as a cost (as p-power of the distance) to move the mass of μ onto the mass of ν via the plan π. Hence, the Wasserstein distance is the minimal cost to move one mass over the other. For a complete introduction to the topic of Wasserstein distances we refer the reader to [20].

Let us now consider the Cauchy problem

$$\{\begin{array}{l}{\partial }_t{\mu }_t+\nabla ·(v[{\mu }_t]{\mu }_t)=0,\hfill \\ \mu (t=0)={\mu }_0.\hfill \end{array}$$ (3)

We assume that v is a uniformly Lipschitz operator with respect to the Wasserstein distance on ℘(ℝ^d) and the Euclidean distance in ℝ^d, i.e. that there exists a constant L such that

$$\Vert v[\mu ](t,x)-v[\nu ](t,y)\Vert \le L{W}_p(\mu ,\nu )+L\Vert x-y\Vert$$ (4)

for all t ∈ ℝ, μ, ν ∈ ℘(ℝ^d) and x, y ∈ ℝ^d × ℝ^d. We have the following key result ([13]):

Theorem 3

Let v satisfy (4), then there exists a unique solution to (3).

B. Existence of a solution to (1)

In this section, we prove existence of a solution for (1), by providing a numerical scheme approximating such solution. Fix a final time T ∈ ℝ and an initial measure μ₀. For a given discretization parameter n ∈ ℕ, we define a sequence of curves ( ${\mu }_s^n$) via the following scheme:

SCHEME 𝕊.

In the definition of 𝕊, we distinguish t_n and τ_n for better description and approximation of the two phenomena of deformation and heat diffusion. We now prove existence of a solution to (1) with the following lemma.

Lemma 4

There exists a subsequence of (μⁿ) converging to a measure μ^*, providing a solution of (1).

Proof

We will prove that each μⁿ is Hölder as function of time with values in the space of probability measures (endowed with the Wasserstein distance), in order to use the Arzelà–Ascoli theorem. The proof will be performed for p = 2 thus we drop the subscript p and simply write 𝒲. Let ι ∈ {0, …, 2ⁿ−1}, t ∈ (0, t_n) and define $\sigma :={\varphi }_{l{t}_n}^t\#{\mu }^n(l{t}_n)$. Then by the triangular inequality,

$$\begin{gathered} \mathcal{W}({\mu }^n(l{t}_n+t),{\mu }^n(l{t}_n))=\mathcal{W}(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,{\mu }^n(l{t}_n)) \\ \le \mathcal{W}(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )+\mathcal{W}(\sigma ,{\mu }^n(l{t}_n)). \end{gathered}$$ (5)

For the first term, we use the evolution variational inequality given in [8]:

$$\frac{d}{dt}\frac{1}{2}{\mathcal{W}}^2(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )\le H(\sigma )-H(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma )-\frac{K}{2}{\mathcal{W}}^2(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )$$

where H(ρ) denotes the relative entropy of ρ and K the lower bound of the Ricci curvature of ℳ. By recalling that the heat equation is the gradient flow for the relative entropy H, it holds H(e^Διt_n+ttσ) ≤ H(σ). Also observe that the relative entropy is bounded on a compact manifold, see e.g. [8, Lemma 4.1]. Finally, observe that the Ricci curvature K is bounded from below on a compact manifold too. Hence we obtain:

$$\frac{d}{dt}{\mathcal{W}}^2(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )\le C-K{\mathcal{W}}^2(e^{{\mathrm{\Delta }}_{l{t}_n+t}t}\sigma ,\sigma )$$ (6)

where C is independent of n and, by Gronwall’s inequality:

$${\mathcal{W}}^2(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )\le -\frac{C}{K}(e^{-Kt}-1)=Ct+o(t)\le 2Ct$$

for t small enough. Finally, for some C > 0 it holds:

$$\mathcal{W}(e^{{\mathrm{\Delta }}_{l{t}_n+t^t}}\sigma ,\sigma )\le C\sqrt{t}.$$

The second term of (5) was estimated in [13]: $\mathcal{W}({\varphi }_{l{t}_n}^t\#{\mu }^n(l{t}_n),{\mu }^n(l{t}_n))\le Lt$ where L is the Lipschitz constant of V [μ_s]. Notice that L does not depend on μⁿ nor on t. Summing the two terms we obtain:

$$\mathcal{W}({\mu }^n(l{t}_n+t),{\mu }^n(l{t}_n))\le Lt+C\sqrt{t}.$$

Iteratively and by the triangular inequality, we get: $\mathcal{W}({\mu }^n(t),{\mu }^n(s))\le L\mid t-s\mid +C\sqrt{\mid t-s\mid }$ for any s, t ∈ [0, T]. Hence the sequence (μⁿ) satisfies a uniform Hölder condition of order $\frac{1}{2}$. The sequence is also equibounded, since μ₀ is fixed. Then, according to the Arzelà–Ascoli theorem, there exists a subsequence of (μⁿ) that converges uniformly to a curve μ^*. Using the same methods as [13][Sec 3.3], one can prove that μ^* is a solution to (1).

II. DEFINITION OF LIE BRACKET

Here onward, for simplicity we assume that the growth vector field v does not depend on μ_t. This is a suitable approximation since the Lie bracket we are going to define is a local object (as the original Lie bracket).

A. Reduction to a time-varying Riemannian structure onℳ₀

In this section, we transform the problem (1) on a time-varying manifold ℳ_t into a problem defined on the fixed manifold ℳ⁰ with a time-varying Riemannian structure. We use this transformation to prove uniqueness of the solution to (1) with v not depending on μ_t.

Given v not depending on μ_t, the definition of ℳ_t is given by ℳ_t = ϕ^t(ℳ₀), where ϕ^t is the flow of v. Endow ℳ_t with the Riemannian structure given by its embedding in ℝ^d. For each time t, the flow ϕ^t is a diffeomorphism between ℳ₀ and ℳ_t, hence we can endow M₀ with a Riemannian structure induced by the one on ℳ_t. Applying this technique at each time, we have defined a time-varying Riemannian structure < ., . >_t on the fixed manifold ℳ₀. We denote with ${\mathrm{\Delta }}_t^{\prime }$ the corresponding Laplace-Beltrami operator onℳ₀. We are now ready to prove uniqueness of solution to (1).

Theorem 5

Let v be a Lipschitz vector field on ℝ^d, independent of μ. Then, there exists a unique solution to (1).

Proof

Let μ_t any solution to (1), define the measure ν_t := ϕ^−t#μ_t, i.e. the pull-back of μ_t via the flow ϕ^t generated by v. The transformation defined above permits to prove that ν_t is a measure on ℳ₀ and it satisfies the following heat equation on ℳ₀:

$$\partial {\nu }_t={\mathrm{\Delta }}_t^{\prime }{\nu }_t.$$

Observe now that such equation admits a unique solution, see e.g. [10]. Moreover, uniqueness of ν_t implies uniqueness of μ_t.

B. First-order Taylor expansion of the Laplace-Beltrami operator

In this section, we describe the evolution of the Laplace-Beltrami operator Δ_t by computing its first-order Taylor expansion at time t = 0. By applying the transformation described in Section II-A, we consider the Laplace-Beltrami operator as being defined on the fixed manifold ℳ₀, with time-varying Riemannian structure < .,. >_t on it. For simplicity of notation, we denote ℳ:=ℳ₀.

We now compute the Riemannian structure < ., . >_t on ℳ. The definition of the push-forward implies

$$<w_1,w_2{>}_t=<{\varphi }_t\#w_1,{\varphi }_t\#w_2{>}_E,$$ (7)

where < .,. >_E is the standard Riemannian metric in ℝ^d (i.e. the standard scalar product.) It holds

$${\varphi }_t\#w=w+\mathit{tJv}·w+o(t),$$

where J is the Jacobian with respect to the Euclidean structure of ℝ^d and · represents the linear action of the linear operator Jv on w. This implies

$$<w_1,w_2{>}_t=<w_1,w_2{>}_E+t(<Jv·w_1,w_2{>}_E+<Jv·w_2,w_1{>}_E)+o(t).$$

Since vectors w₁, w₂ belong to T_xℳ, we will denote with J_ℳv the restriction of Jv to T_xℳ by projection, i.e.

$$J_{\mathcal{M}}v:\{\begin{array}{ccc}{T}_x\mathcal{M}& \to & T_x\mathcal{M}\\ w& \mapsto & {(Jv·w)}_{\mathcal{M}},\end{array}$$

where z_ℳ is the component of the vector z ∈ T_xℝ^d on the subspace T_xℳ. Observe that we are using here the Riemannian structure of ℝ^d to define projections.

We now compute the Laplace-Beltrami operator ${\mathrm{\Delta }}_t^{\prime }$ intrinsically defined on the manifold ℳ with the Riemannian structure < .,. >_t. We are interested in describing such operator as a function of t. Recalling that the Laplace-Beltrami operator is the divergence of the gradient, we aim at describing div^t and grad^t as a function of time. In particular, we aim at computing first-order development of such operators with respect to time. We first study the gradient grad^t f for a function f ∈ C^∞(ℳ), via its intrinsic definition. For all w ∈ T_xℳ it holds

$$<{\text{grad}}^t(f),w{>}_t={\mathcal{L}}_{w}f.$$

In particular this identity holds at time t = 0 holds for grad⁰. Writing grad^t f = grad⁰ f + tB₁, for a vector field B₁ to be found, we get

$$\begin{gathered} <{\text{grad}}^0(f)+t{B}_1+\mathit{tJv}·{\text{grad}}^0(f)+o(t),w+tJv·w+o(t){>}_E \\ ={\mathcal{L}}_{w}ft(<B_1,w{>}_E+<Jv·{\text{grad}}^0(f),w{>}_E+<{\text{grad}}^{0}f,Jv·w{>}_E)+o(t)=0. \end{gathered}$$

We then have B₁ = −(Jv · grad⁰(f))_ℳ − B where (Jv · grad⁰(f))_ℳ is the component of Jv · grad⁰(f) on the tangent space of ℳ, and B(f, v) is intrinsically defined by the following rule: for all w ∈ T_xℳ it holds

$$<B(f,v),w{>}_E=<{\text{grad}}^0(f),Jv·w{>}_E.$$ (8)

Summing up, we have

$${\text{grad}}^t(f)={\text{grad}}^0(f)-t{(Jv·{\text{grad}}^0(f))}_{\mathcal{M}}-tB(f,v)+o(t)$$

with B(f, v) defined by (8).

We now study the divergence div^t(X) for a vector field X ∈ Vec (ℳ). Denoting by vol_t the volume form of the Riemannian manifold, it holds

$${\text{div}}^t(X){\text{vol}}_t={\mathcal{L}}_X{\text{vol}}_t.$$ (9)

Observe that ${\text{vol}}_t=\sqrt{\mid g^t\mid }d{X}_1\wedge d{X}_2\wedge \dots \wedge d{X}_m$ for any base X₁, …, X_m of the Riemannian manifold (M,< ., . >_t ). We choose an orthonormal basis for (M,< ., . >₀) and study the evolution of vol_t. Since g⁰ = Id and |Id + tA| = 1 + tTr (A) + o(t), we have

$$\mid g^t\mid =1+2t\sum _{i=1}^m<Jv·X_i,X_i{>}_E=1+2t\text{Tr}{(Jv)}_{\mathcal{M}},$$

where the operator Jv is restricted to the tangent space of ℳ. Then $\sqrt{{\mid g\mid }^t}=1+t\text{Tr}{(Jv)}_{\mathcal{M}}$. Writing div^t(X) = div⁰X + tf + o(t) for a function f to be found, we get

$$(({\text{div}}^0(X)+tf)(1+t\text{Tr}{(Jv)}_{\mathcal{M}})+o(t)){\text{vol}}_0=({\mathcal{L}}_X(1+t\text{Tr}{(Jv)}_{\mathcal{M}})){\text{vol}}_0+(1+t\text{Tr}{(Jv)}_{\mathcal{M}}){\mathcal{L}}_X{\text{vol}}_0.$$

From (9) applied for t = 0 we have ℒ_Xvol₀ = div⁰(X)vol₀, thus

$${\text{div}}^t(X)={\text{div}}^0(X)+t{\mathcal{L}}_X\text{Tr}{(Jv)}_{\mathcal{M}}.$$ (10)

Observe that this formula is intrinsic, since the trace of the linear operator Jv does not depend on the chosen orthonormal frame.

We now compute the Laplace-Beltrami operator ${\mathrm{\Delta }}_t^{\prime }$. Since ${\mathrm{\Delta }}_t^{\prime }f={\text{div}}^t({\text{grad}}^t(f))$ by definition, and observing that it holds L_grad⁰(f)Tr (Jv)_ℳ =< grad⁰(f), grad⁰(Tr (Jv)_ℳ) >_E, we have

$${\mathrm{\Delta }}_t^{\prime }(f)={\mathrm{\Delta }}_0(f)+t(<{\text{grad}}^0(f),{\text{grad}}^0(\text{Tr}{(Jv)}_{\mathcal{M}}){>}_E-{\text{div}}^0(B(f,v)+{(Jv·{\text{grad}}^0(f))}_{\mathcal{M}}))+o(t).$$ (11)

C. Non commutativity of the heat and growth evolutions

In this section, we show non-commutativity of the growth and diffusion terms in the dynamics (1), which describes morphogenesis. For sake of clarity, let us recall how non-commutativity works in the finite dimensional case, and, more specifically for switching systems. Consider two vector fields X₀,X₁ and the system

$$\{\begin{array}{l}\stackrel{.}{x}=X_{u(t)}\hfill \\ x(0)=x_0.\hfill \end{array}$$

where u ∈ {0, 1}. For every measurable switching function u : [0, T] → {0, 1} the solution at time T, denoted by x(T, u), is unique. The set of points reachable with these trajectories is not limited to the directions given by X₀ and X₁. A classical result in control theory, the Orbit theorem, (roughly) states that the set of attainable configurations is related to the Lie bracket [X₀,X₁] (and to other higher order brackets), and in particular that one can choose good switching functions to drive the system along a direction arbitrarily close to the vector field [X₀,X₁]. See e.g. [3], [18], [1]. Lie brackets are a powerful tool for finite-dimensional control systems. In infinite dimension, they are less easy to define. However, in some cases, they can still be used to study the controllability of PDEs, as shown in [6].

For this reason, we study in this article the bracket between the “heat vector field” and the “transport vector field”. Indeed, one can consider the solution of an heat equation as a continuous (and even differentiable) curve in P₂(X) endowed with the Wasserstein distance. The, the time derivative of this curve in a point μ_t (that is clearly the Laplacian Δ_tμ_t) can be considered as a vector field, that we call the heat vector field. Similarly, we define the transport vector field as the derivative of the solution of the transport equation in a point.

By borrowing the notation from Lie brackets of vector fields, we define

$$[\mathrm{\Delta },v]\mu :=\underset{t,\tau \to 0}{lim}\frac{{\varphi }_{-t}\#(e^{\tau {\mathrm{\Delta }}_t}({\varphi }_t\#\mu ))-e^{\tau {\mathrm{\Delta }}_0}\mu }{t\tau },$$ (12)

where ϕ_t is flow generated by the vector field v, and e^{τΔ _t} is the semigroup generated by Δ_t at time τ. Then, for any test function $f\in C_c^{\infty }(M)$, one can write (12) as follows:

$$\begin{gathered} ([\mathrm{\Delta },v]\mu )(f)=\underset{t,\tau \to 0}{lim}{\int }_{\mathcal{M}}\frac{f}{t\tau }d\left({\varphi }_{-t}\#(e^{\tau {\mathrm{\Delta }}_t}({\varphi }_t\#\mu ))-e^{\tau {\mathrm{\Delta }}^0}\mu \right) \\ =\underset{t,\tau \to 0}{lim}{\int }_{\mathcal{M}}\frac{f}{t\tau }d\left(e^{\tau {\mathrm{\Delta }}_t^{\prime }}\mu -e^{\tau {\mathrm{\Delta }}_0}\mu \right) \\ =\underset{t\to 0}{lim}{\int }_{\mathcal{M}}\frac{f}{t}d({\mathrm{\Delta }}_t^{\prime }\mu -{\mathrm{\Delta }}_0\mu )=\underset{t\to 0}{lim}{\int }_{\mathcal{M}}({\mathrm{\Delta }}_t^{\prime }-{\mathrm{\Delta }}_0)\frac{f}{t}d\mu \\ ={\int }_{\mathcal{M}}<{\text{grad}}^0(f),{\text{grad}}^0(\text{Tr}{(Jv)}_{\mathcal{M}}){>}_E-{\text{div}}^0(B(f,v)+{(Jv·{\text{grad}}^0(f))}_{\mathcal{M}})d\mu , \end{gathered}$$ (13)

where we used ∫ f dΔμ = ∫ Δf dμ, which is the definition of the Laplace-Beltrami operator as an operator on the space of measures. Then, (13) is the intrinsic formula for the bracket (12), indeed the operator B is intrinsically defined by (8).

III. SIMULATIONS

We now compute the bracket [Δ, v] for two examples on a time-varying manifold ℳ_t with v independent on μ. We will also compare the analytic computation using formula (13) and the numerical simulations with the scheme 𝕊 defined in Section I-B.

We consider the unit circle ℳ₀ = S¹ in ℝ² parametrized by an angle θ as the initial manifold, and the vector field v = (x−1, 2y). It is easy to verify that at time t the unit circle is transported to an ellipse of equation: ${(\frac{x-x_c}{e^t})}^2+{(\frac{y}{e^{2t}})}^2=1$ where x_c = 1− e^t (see Fig. 1). We consider the Euclidean metric on ℝ², i.e. Riemannian structure given by the orthonormal frame ∂_x, ∂_y at each point. The corresponding Riemannian structure on M_t is given by ∂_θ = −y∂_x + x∂_y. This implies

Fig. 1.

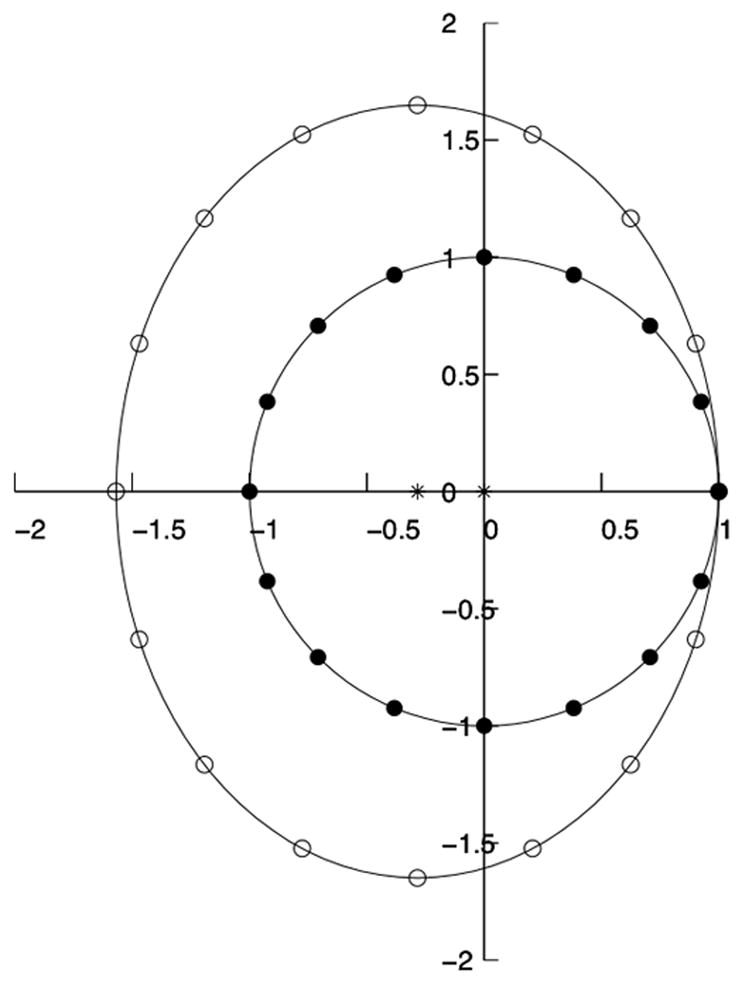
Transport of the unit sphere (black dots) by the vector field v(x, y) := (x−1, 2y). At t = 0.25, the resulting ellipse (white dots) is centered at (1 − e^0.25, 0).

$$(J_{M}v)·{\delta }_{\theta }={\left(\begin{array}{c}-y\\ 2x\end{array}\right)}_M=(1+x^2){\partial }_{\theta },$$

thus Tr (J_Mv) = 1 + cos². Since the initial data is the Riemannian volume form, the divergence theorem implies

$$\begin{gathered} ([\mathrm{\Delta },v]\mu )(f)={\int }_M<\frac{\partial f}{\partial \theta }{\partial }_{\theta },\frac{\partial (1+{cos}^2(\theta ))}{\partial \theta }{\partial }_{\theta }{>}_{E}d\theta \\ ={\int }_M-f\frac{{\partial }^2{cos}^2(\theta )}{\partial {\theta }^2}d\theta ={\int }_{M}2fcos(2\theta )d\theta . \end{gathered}$$

As a first exmple, we consider an initial constant signal ${\mu }_0(\theta )=\frac{1}{2\pi }$. We then have [Δ, v]μ₀ = 2cos(2θ)μ₀. As a second exemple, for a more complicated initial data μ₀ = (1+cos(θ))dθ, the second term in (13) is no longer 0. First, notice that:

$$<{\text{grad}}^0(f),{\text{grad}}^0(\text{Tr}{(Jv)}_M)>=<\frac{\partial f}{\partial \theta }{\partial }_{\theta },\frac{\partial (1+{cos}^2(\theta ))}{\partial \theta }{\partial }_{\theta }>=\frac{\partial f}{\partial \theta }(-2cos\theta sin\theta ).$$ (14)

Secondly, we calculate the term B(f, v) knowing that 〈B(f, v), w)〉_E = 〈grad⁰(f), Jv · w〉_E. Taking a vector w = (w_x, w_y)^T, we write:

$$\begin{gathered} B_x{w}_x+B_y{w}_y={\langle {\text{grad}}^0(f),Jv·w\rangle }_E \\ ={\langle \left(\begin{array}{c}{\partial }_{x}f\\ {\partial }_{y}f\end{array}\right),\left(\begin{array}{c}{w}_x\\ 2w_y\end{array}\right)\rangle }_E={\partial }_{x}f{w}_x+2{\partial }_{y}f{w}_y. \end{gathered}$$ (15)

Hence we have :

$$B_{\theta }=\langle \left(\begin{array}{c}{\partial }_{x}f\\ 2{\partial }_{y}f\end{array}\right),\left(\begin{array}{c}-y\\ xf\end{array}\right)\rangle =(1+{cos}^2\theta ){\partial }_{\theta }f.$$

Similarly,

$${(Jv·{\text{grad}}_0(f))}_M=\langle \left(\begin{array}{c}{\partial }_{x}f\\ 2{\partial }_{y}f\end{array}\right),{\partial }_{\theta }\rangle {\partial }_{\theta }=(1+{cos}^2\theta ){\partial }_{\theta }f{\partial }_{\theta }.$$

So

$$\begin{gathered} {\text{div}}^0{(B(f,v)+Jv·{\text{grad}}^0(f))}_M=2{\partial }_{\theta }((1+{cos}^2\theta ){\partial }_{\theta }f) \\ =2(1+{cos}^2\theta ){\partial }_{\theta }^{2}f-4cos\theta sin\theta {\partial }_{\theta }f. \end{gathered}$$

Then, a direct computation shows

$$([\mathrm{\Delta },v]\mu )(f)={\int }_{\mathcal{M}}f(12{cos}^3\theta +4{cos}^2\theta -6cos\theta -2)d\theta .$$

In order to study the bracket [v, Δ], we use two schemes 𝕊 and 𝕊̃ that discretize the diffusion-growth problem described above. We define 𝕊̃ similarly to 𝕊 (defined in Section I-B), but inverting steps 1 and 2. Hence 𝕊 does a series of growth and diffusion operations on the function μ₀ starting with growth, while 𝕊̃ does the same starting with diffusion. Figure 2 shows the first two iterations of each scheme, starting from the same function μ₀ (renamed x₀ and y₀ for notation convenience), and denoting respectively by x_n and y_n the solutions after each iteration of 𝕊 and 𝕊̃. We first apply this scheme to the initial signal given by the constant function μ₀(θ) = 0.1. To numerically compute the lie bracket, we apply the schemes 𝕊 and 𝕊̃ to μ₀ and compute the numerical expression of the bracket given by [Δ, v]_num = lim_ε→0(y₁ −x₁)/ε² (where x₁ and y₁ respectively correspond to the first iterations of 𝕊 and 𝕊̃).

Fig. 2.

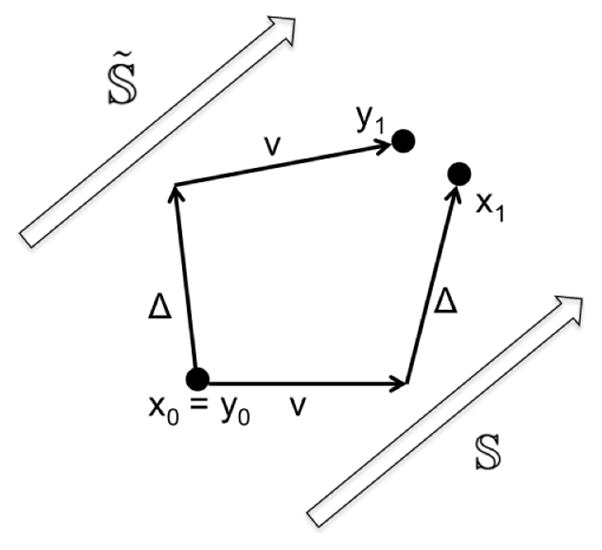
One iteration of the schemes 𝕊 and 𝕊̃ starting from the same point x₀ = y₀.

Figure 3 shows the convergence of the bracket when the time step T = t+τ tends to 0: The bracket converges to the theoretical value [Δ, v]_theo(μ₀) = 0.2 cos(θ).

Fig. 3.

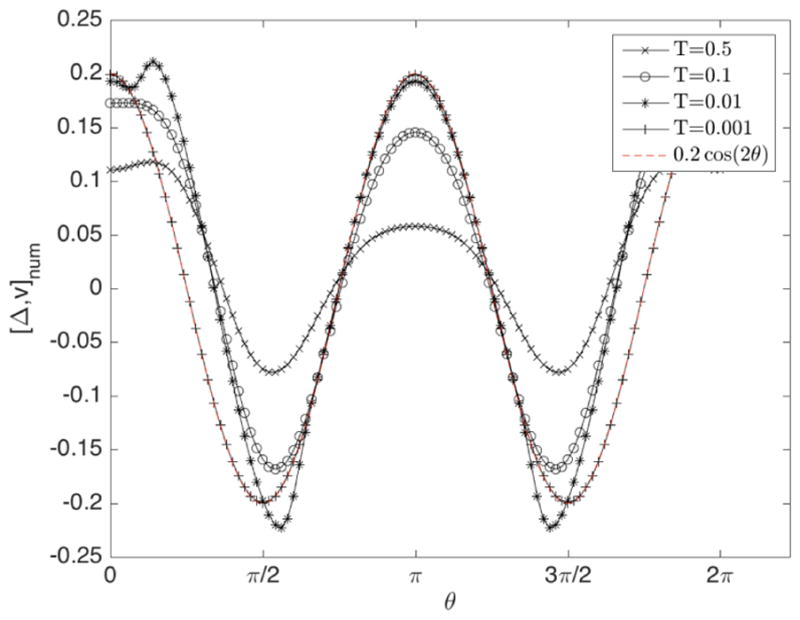
Convergence of the bracket to the theoretical one for the initial signal μ₀(θ) = 0.1dθ.

Figure 4 shows the convergence of the bracket for the initial signal μ₀(θ) = 0.1(cos(θ) + 1)dθ. The bracket converges to the theoretical value [Δ, v]_theo(μ₀) = 12 cos³ θ + 4cos² θ − 6 cos θ − 2.

Fig. 4.

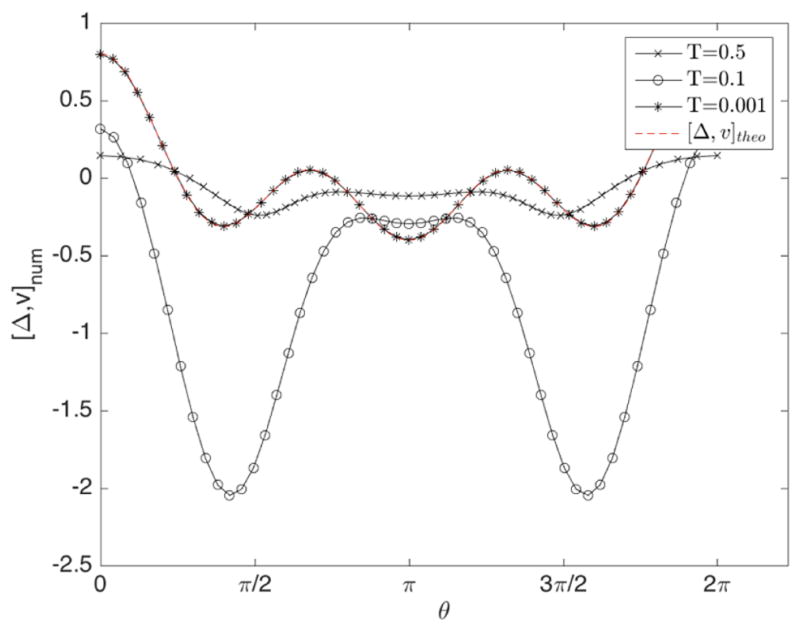
Convergence of the bracket for the initial signal μ₀(θ) = 0.1(cos(θ) + 1)dθ.

CONCLUSION

In this paper, we described morphogenesis of organisms by evolution of a manifold, representing their boundary. The presence of morphogens, that are signals stimulating deformations, is modeled by the presence of a growth signal evolving on the manifold.

We showed that the resulting dynamics can be described by the reaction-diffusion Partial Differential Equation (1), whose solution in the sense of measures is supported on the evolving manifold. The existence of solutions is achieved using the framework of Wasserstein distances. In such equation, the interplay between the growth and diffusion can be described by a new concept of Lie bracket between the transport term and the Laplace-Beltrami diffusion operator. The two operators are of different nature, but they can be both applied to measures on the ambient space. This allows a precise definition of such Lie bracket and its explicit expression is given (13). Then via numerical simulations we verified the effect of the non-commutativity of the diffusion and growth and the found expression for the bracket.

Future work will be devoted to develop a complete theory for PDEs on time-evolving manifolds and numerically study the shapes achievable by appropriate control mechanisms.