Optimizing Neural Information Capacity through Discretization

Abstract

Discretization in neural circuits occurs on many levels, from the generation of action potentials and dendritic integration, to neuropeptide signaling and processing of signals from multiple neurons, to behavioral decisions. It is clear that discretization when implemented properly can convey many benefits. However, the optimal solutions depend on both the level of noise and how it impacts a particular computation. This Perspective discusses how current physiological data could potentially be integrated into one theoretical framework based on maximizing information. Key experiments for testing that framework are discussed.

Biological systems are notorious for the complexity of their organization as reflected by the heterogeneity of circuit elements at all levels, from proteins to cell types. Can this complexity be systematized and understood? I believe the answer is yes, and will outline here a potential roadmap for doing so. The theory is based on three ingredients: (1) the fact that arbitrary complex functions can be implemented by combinations of linear and nonlinear logistic operations (Cybenko, 1989; Kolmogorov, 1957) (Fig.1A), (2) the need to maximize information transfer, and (3) metabolic constraints. Traditionally, classification of cell types in the nervous system has focused on differences in the stimulus patterns that trigger their responses, i.e. the linear part of the computation. However, as I discuss below, nonlinear aspects of the computation are also likely to account for a significant fraction of biological diversity. This is because to accurately approximate a nonlinear function with threshold-like devices, one generally needs to use multiple thresholds. Elements with different thresholds would then correspond to different types of ion channels, cell types, or brain areas that, at their respective levels of organization, can be understood as working together to represent a single nonlinear function across the whole range of inputs. A theoretical understanding of how to effectively combine different threshold-like elements to encode inputs with different statistics and under different metabolic constrains would likely go a long way towards developing a systematic description of biological complexity.

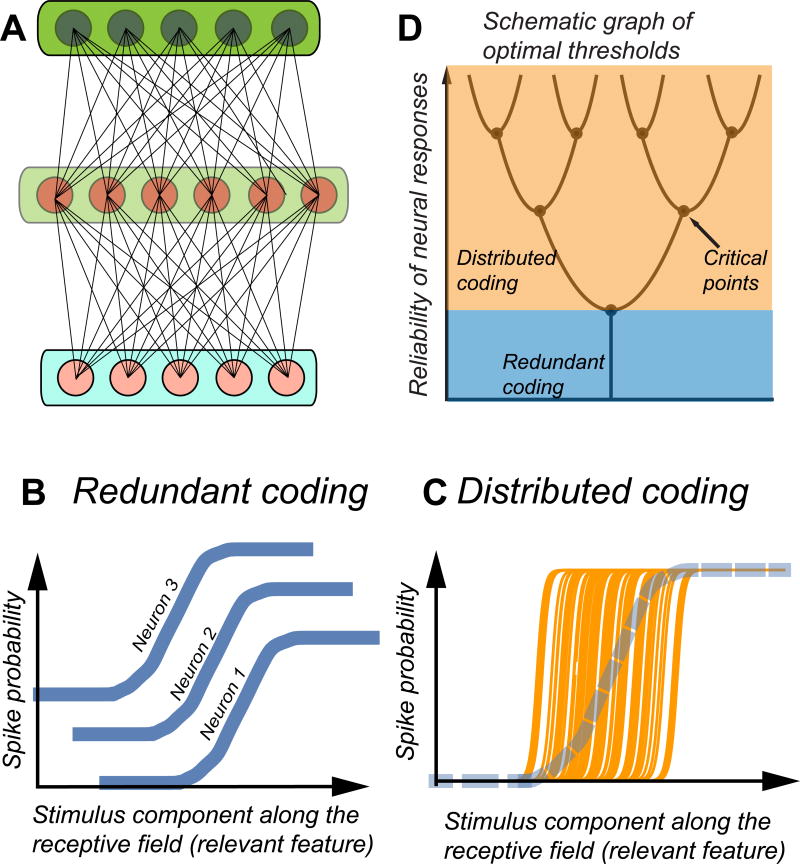
Figure 1. Approximating optimal nonlinear transformations with threshold-like computations.

(A) Networks with three or more layers serve as “universal functional approximations”, meaning that they can compute any desired function of input variables provided the intermediate layer has a sufficient number of units. Deep networks can reduce the size of the intermediate layer while still approximating complex functions of inputs. (B)A logistic function, a necessary ingredient for achieving flexible computations, can be approximated by averaging over large number of identical low-precision devices. (C) An alternative is to use many high-precision threshold devices while staggering their thresholds to match the input distribution. (D) Graph of optimal thresholds showing their successive splitting with increased precision of individual neurons.

Several theoretical groups have analyzed precisely this problem over the past 20 years (Brinkman et al., 2016; Brunel and Nadal, 1998; Ganguli and Simoncelli, 2014; Gjorgjieva et al., 2014; Harper and McAlpine, 2004; Kastner et al., 2015; McDonnell et al., 2006; Nikitin et al., 2009; Pitkow and Meister, 2012; Sharpee, 2014; Wei and Stocker, 2016). For the sake of specificity, our initial discussion will be for the case where discretization occurs at the level of single neurons, with neurons acting as threshold-like devices processing the same analogue inputs. Later, we will generalize to other levels of organization, as well as incorporate dynamics in neural responses beyond simple thresholds. The first theoretical observation is that optimal configurations depend on the level of reliability or noise in individual neurons. Noise is defined here as the variability of neural responses to the same input. In example of Fig. 1B, the probability to observe a spike in small time-bins takes fractional numbers much different from either 0 or 1 because the same stimulus elicits a spike only on a fraction of trials. Example nonlinearities in Fig. 1C correspond to higher-precision neurons, with smaller effective noise, because the range of inputs where the neural response is uncertain is smaller. For the purposes of discussion below, it will suffice to consider an effective noise that represents cumulative effects of noise from the afferent circuitry and the spike generation process; the reader may find detailed treatments of the impact of different types of noise in a recent study (Brinkman et al., 2016).

Logistic-like nonlinearities, a key aspect of performing diverse computations, can be built from neural responses in two ways. The first approach is based on averaging neural responses across multiple neurons and/or across multiple time intervals. This strategy corresponds to redundant coding (Fig. 1B). Each neuron has the same threshold and similar response characteristics, and therefore functionally the neurons can be characterized as belonging to one class. Even though the individual neurons are noisy, the noise is reduced through the averaging process, assuming there is no need to perform the measurement quickly. A second approach for building flexible nonlinearities is to average responses of neurons with different thresholds. Such staggered thresholds, as shown in Figure 1C, provide another way to approximate the logistic function. This strategy corresponds to distributed coding. This strategy becomes especially useful when there is a mismatch between the shape of the desired nonlinearity and the shape of the response function for the individual neurons. We are beginning to work with what potentially might be different cell types, because if neurons consistently respond to inputs from different ranges, then they make different contributions to the neural code. In the biological system, the differences in functional properties will likely be reflected also in anatomical differences in neural wiring. For example, higher threshold sensitivity neurons might receive a stronger input from an inhibitory neuron compared to neurons encoding the same input feature at lower threshold sensitivities.

Which of the two coding schemes – redundant or distributed – is better? The answer depends on the reliability of individual neurons. When this reliability is low, redundant coding based on a single neuronal type provides more information about the stimulus compared to distributed coding using staggered thresholds (Kastner et al., 2015; McDonnell et al., 2006; Nikitin et al., 2009; Sharpee, 2014). When the reliability increases beyond a certain threshold, a distributed coding based on multiple thresholds, and therefore multiple neuronal types, transmits more information (Figure 1D). Clearly, neuronal types are defined not just by differences in thresholds but also by the type of stimulus features that trigger their responses. For example, parvocelullar and magnocellular neurons in the retina differ in their sensitivity to low and high spatial and temporal frequencies. Much of the previous research on neuronal cell types in sensory systems has focused on differences in the preferred stimulus features (Balasubramanian and Sterling, 2009; Sterling, 1983). The present discussion expands this framework by taking into account differences in nonlinearities, even for neurons encoding the same stimulus features. Obtaining a full treatment that describes both the optimal distribution relevant stimulus features and the number of different staggered thresholds to encode them is an open problem for future research.

What determines the critical noise level below which it is optimal to use staggered thresholds? How many different thresholds (i.e. different neuronal types) might one expect to observe in a given population? The specific answers to these questions are not fully known at present. However, we do know that the number of different thresholds can vary depending on the number of neurons in the population, and by the amount and type of noise that affects responses of individual neurons. It also depends upon metabolic constraints, such as the average spike rate across the population or its maximum. Considering the case where all neurons have the same noise level, we know that in the limit of very large noise, it will be optimal for all neurons to have the same threshold (Kastner et al., 2015; McDonnell et al., 2006; Nikitin et al., 2009; Sharpee, 2014). In the opposite limit of very small noise, the threshold distribution should match the input distribution. In this way, the population input-output function will match the cumulative distribution of inputs, echoing the early result by Laughlin (Laughlin, 1981). Solutions for intermediate noise levels have been worked out for small neuronal populations (McDonnell et al., 2006). For sizable neuronal populations, such as up to 1000 neurons, there are numerical results on optimal thresholds distributions (Harper and McAlpine, 2004; McDonnell et al., 2006; McDonnell et al., 2012). However, numerical simulations for large populations have been reported to be affected by local minima yielding unstable and changing results with decreasing noise level (McDonnell et al., 2012). Analyses for the case where neuronal noise differs across neurons have been limited to a two-neuron circuit (Kastner et al., 2015).

The available theoretical results have yielded quantitative explanations for the experimental observation on the number and properties of neuronal sub-types in the retina, long a canonical test bed for theories of cell type specialization (Balasubramanian and Sterling, 2009; Borghuis et al., 2008; Garrigan et al., 2010; Ratliff et al., 2010; Sterling, 1983). A case in point is a recent experimental observation of adapting and sensitizing cell types of retinal ganglion cells (RGCs) that encode the same temporal modulations of light intensities within their receptive fields, but with different thresholds (Kastner and Baccus, 2011). The adapting cells had consistently higher thresholds than the sensitizing cells (Kastner and Baccus, 2011). Both of these cell types were Off neurons, meaning that their response was keyed primarily to decrements in light intensity. The analogous On cell type that encoded similar temporal fluctuations of light intensity but in the positive direction did not split into the adapting and sensitizing cells sub-types. We know that adapting and sensitizing Off-cells form separate sub-types because their receptive fields form separate overlapping mosaics (Kastner and Baccus, 2011). Thus, the question arises as to why would Off neurons split into two subtypes whereas the corresponding On neurons do not? It turns out that Off neurons have smaller noise levels than the On neurons (Kastner and Baccus, 2011). Importantly, the noise value for Off neurons falls below the critical value obtained theoretically for the splitting of a two-neuron pathway into separate channels. The noise for On neurons was above that critical value. In a two-neuron system, the critical noise value can be determined exactly for a given expected evoked firing rate for two neurons across the input distribution. Taking this value from experimental measurements of the average evoked spike rate yields a parameter-free prediction for the critical noise value (Kastner et al., 2015). This value fell right in between the values for Off and On neurons, thus explaining why Off neurons split into sub-types whereas On neurons did not. Further, a theoretical analysis of optimal thresholds for neurons with different noise levels indicated that neurons with lower noise should have smaller thresholds (Kastner et al., 2015). Experimentally, the two types of Off neurons have slightly (but statistically significantly) different thresholds, a difference that was maintained across a range of visual contrasts (Kastner and Baccus, 2011). In agreement with theoretical results, adapting Off neurons had higher noise values than the sensitizing cells. This is consistent with theoretical predictions because adapting cell also have higher thresholds than the sensitizing cells. Overall, the theory of cell type specialization appears to have passed its first tests when applied to a set of three sub-types of retinal ganglion cells. From here, expanding the framework to describe multidimensional input signals and different metabolic constraints (Borghuis et al., 2008; Fitzgerald and Sharpee, 2009; Ganguli and Simoncelli, 2014; Garrigan et al., 2010; Tkacik et al., 2010) may allow to systematize our understanding of how neuronal types from different species relate to each to each other, for example in the retina. Other sensory systems where information maximization could account for coordinated encoding include olfactory receptor neurons in the fly (Asahina et al., 2009) and chemosensory neurons in C. elegans (Chalasani et al., 2007). Both systems use staggered thresholds to encode a wide dynamic range of inputs.

Why might these results potentially generalize to different levels of biological organization? The reason is that an information theoretic analysis is not specific to neurons encoding their input signals. It could just as easily be applied to the distribution of neuropeptides encoded by their receptors, or the distribution or intracellular voltages that are encoded into sequences of spikes by a set of voltage-activated ion channels. Let us first consider the case of neuropeptide signaling. The number of receptors for tachykinin peptides, which includes substance P and represent one of the largest families of neuropeptides, differs across species and among closely related receptors: e.g. drosophila has one receptor for natalisin (NTL), a peptide regulating fecundity, whereas the silkworm has two NTL receptors (Jiang et al., 2013). The fly receptor has an intermediate activation threshold for NTL11 compared to the thresholds of the two moth receptors for the same ligand (Jiang et al., 2013). One could speculate that such differences in signaling between the fly and moth receptors could conform to predictions based on information theory, provided moth receptors have sharper activation functions (equivalent to having smaller effective noise) compared to those of the fly, cf. Fig. 2B. This theoretical prediction remains to be tested. If confirmed, it could serve as a starting point for a systematic characterization of neuropeptide signaling based on information theory and discretization of the input range to approximate nonlinear transformations.

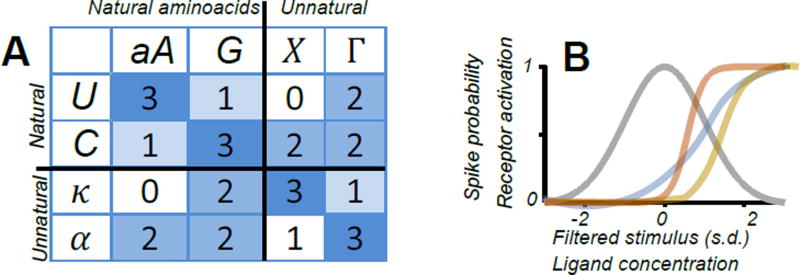
Figure 2.

Examples of discrete symmetry breaking in biology. (A) Two mutually exclusive genetic codes: with similar binding profiles. The top 2×2 matrix corresponds to standard base pairing, and the bottom right 2×2 matrix is an alternative code with notations from (Piccirilli et al., 1990). Binding affinities are denoted by color and approximate binding strengths based on the model from (Wagner, 2005). The two codes are mutually exclusive because of strong mixed binding (off-diagonal blocks). (B) Optimal encoding based on two (or more) distinct thresholds (orange and yellow curves here) requires sharper activation functions compared to encoding based on a single type of nonlinearity (blue). Further, the activation function (orange) whose threshold is closer to the peak of the input distribution (gray) should be sharper than the activation function with a larger (further removed from the peak) threshold (yellow). The theoretical approach can be applied to encoding by neurons or intracellular receptors.

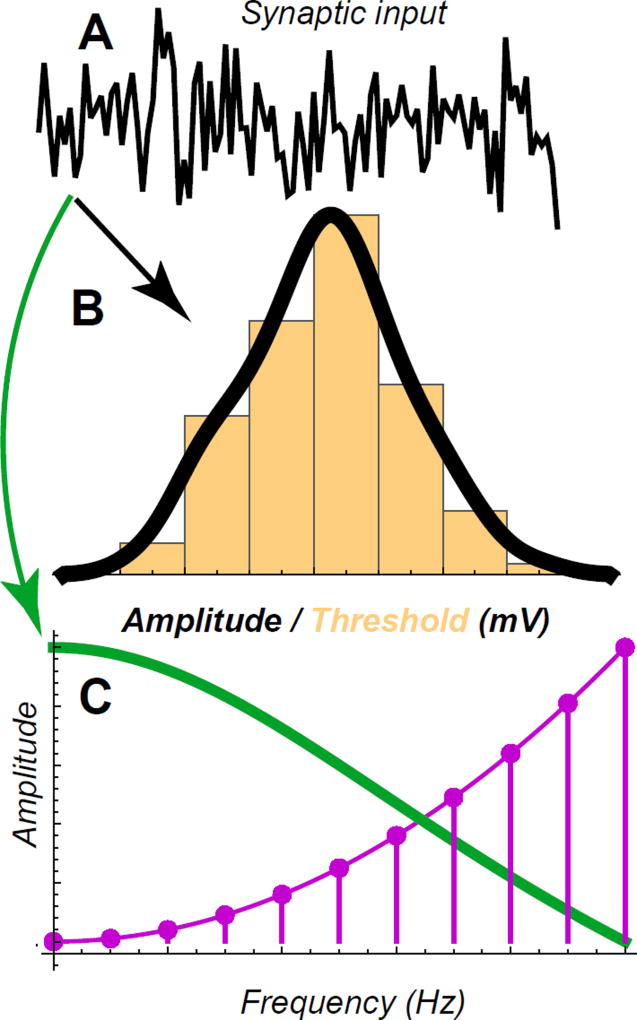
With increased number of elements, discretization arguments can be applied sequentially to ultimately produce an almost continuous representation of functional types (McDonnell et al., 2012), cf. Fig. 1D. Initially, large populations of low-precision threshold device encode the input range with a single threshold. As the precision of individual elements increases, they can specialize to encode different input ranges. Finally, in the limit of very high precision, when each threshold-like operation has a sharp activation function, the distribution of thresholds across the population should approximate the distribution of inputs (Laughlin, 1981). I’ll argue that this theoretical argument could help systematize, for instance, the diversity in the number and types of ion channels. Within each major ion channel type, such as voltage-activated Na or Ca ion channels, multiple sub-types exist that differ in their activation thresholds, inactivation dynamics, and responses to neuromodulator (Stuart et al., 2008). The distribution of these ion channel varies across the cell surface, and in particular along the dendritic tree, in a manner that depends on neuronal type and developmental stage (Stuart et al., 2008). Overall, the diversity of ion channel composition is overwhelming. Further, we know that while some of this variability is important to neural computation, some is likely not (Schulz et al., 2006). Without a systematic theoretical framework, the number of necessary measurements could vastly exceed any feasible experimental effort. In this situation, one could start with the broad hypothesis that the observed variability reflects the need to encode inputs with different statistics, and that input statistics differ across synapses and/or developmental time points. For a given type of neuron or synapse, one could record typical intra-cellular voltage traces. These time-varying signals can be analyzed in terms their amplitude distributions (Figure 3B) and power spectra (Figure 3C). To a first approximation, one may suppose that the distribution of threshold activation for the Na channels should be matched to the amplitude distribution, as schematized in Figures 1B, 2B, and 3B. Similarly, different inactivation time constants should be matched to the power spectra of the input dynamics as follows. Each of the ion channels has band-passed characteristics. The total filtering characteristics of all channels (weighted by their relative densities) should match the inverse of the input Fourier spectra (within the operating range) in order to maximize the mutual information (Atick and Redlich, 1990; Atick and Redlich, 1992; Sharpee et al., 2006). The dual view of action potentials encoding input signals according to thresholds based on their amplitude and temporal filtering is broadly consistent with the dual analogue-digital encoding that has been reported for spike trains (Alle and Geiger, 2006; Shu et al., 2006).

Figure 3.

Predictions that relate the distribution of ion channel type and density to the statistics of presynaptic inputs. (A) Schematic representation of the synaptic inputs. (B) The amplitude of synaptic inputs should be matched by the distribution of thresholds for Na channels and their density. (C) The Fourier spectra should be matched to the inactivation dynamics of ion channels present at the synapse.

It is important to point out that these arguments, when applied at a given level of organization, primarily follow the ‘reductionist’ approach: We are finding optimal building blocks for the neural circuit, such as types of ion channels or neurons, in an approach advocated by (Getting, 1989). At the same time, the information maximization framework (or optimization of other objectives as discussed below) also provides a prescription for how the outputs from one level of organization should be combined at the next stage of processing. For example, we know when it is sufficient to just sum the outputs of neurons (if they have same noise characteristics) or when one should pay attention to the combinatorial aspects of the neural code (if noise parameters differ across neurons). Further, knowing how many functional building blocks one expects to find at the next stage of processing and how they work together can help to identify them and bridge across levels of organization. Successful theories that bridge across levels of organization in physics illustrate that the ‘independent components’ at one level of organization could look nothing like the sum of components from more microscopic levels. For example, collective quasi-particles in a two-dimensional sea of electrons, each of which has a charge 1 e, could have fractional charges such as 1/3, 2/5 and other values that depend on the strength of the magnetic field that confines electrons to two dimensions (Laughlin, 1983; Stormer, 1999).

Taking the latest example more broadly, why would lessons from physics be relevant to biology? One could think of two reasons: a more conceptual one and a more practical one. At a conceptual level, discoveries in physics have illustrated that “The behavior of large and complex aggregates of elementary particles, it turns out, is not to be understood in terms of a simple extrapolation of the properties of a few particles. Instead, at each level of complexity entirely new properties appear” (Anderson, 1972). This statement, written primarily about physical systems (although Anderson also discussed examples from psychology), seems very relevant to the present-day challenges that face brain research. For example, we presume that consciousness derives from the collective action of neurons. Yet, it surely seems qualitatively different and independent from the presence or absence of spikes from a particular neuron or even entire brain regions (as evidenced by lesion studies and stroke patients). At the same time, the answer in fact might not be too complicated as to be fully out of our reach (Shadlen and Kiani, 2013). A relevant example from physics is that although solutions at a larger level of organization cannot decomposed into individual building blocks operating at the lower level, they are in a sense self-similar, meaning that they share certain functional characteristics but with different parameters. Following up on the example above regarding quasi-particles with fractional charge, one observes that the behavior of these quasi-particles within the electron “liquid” follows many of the same rules as ordinary electrons at the lower level of organization do. In the case of neuroscience, one observes that certain “canonical” operations such as a summation followed by logistic nonlinearities occur at different stages of sensory systems (Pagan and Rust, 2014; Pagan et al., 2016) and different levels of organization. Examples include the decisions of whether to generate a spike or not, whether to generate a dendritic spike, or at the behavioral level, whether to ‘engage’ in certain behaviors (Shadlen and Kiani, 2013). Further, as Shadlen and Kiani have suggested, one can think of consciousness as a series of these binary ‘decisions to engage’ (Shadlen and Kiani, 2013). Notice that the very notion of a “decision” implies a nonlinear threshold-like operation. Thus, the theory of neuronal types that was discussed above in the case of sensory circuits is likely to apply to decision-making circuits of the brain that operate on more abstract quantities.

A more practical argument for the relevance lessons from physics to biology is that physics offers (arguably) the only known and widely successful theory bridging across scales, namely – the theory of phase transitions, also known as the theory of “broken symmetries.” The term broken symmetries refers to the fact that large systems can spontaneously assume one of several available configurations and are too large to switch to the other possible configuration (Anderson, 1972). The observations of broken symmetries have been noted in biology at many scales of organization. For example, most natural amino-acids are left-handed. Similarly, most natural sugars are ‘right-handed’, even though biochemical synthesis typically would generate both left- and right-handed molecules in equal proportions unless special catalysts are included (Anderson, 1972). The initial choice of chirality for amino-acids and DNA was likely purely random (Meierhenrich, 2008). Further, even the choice of base pairs for the genetic code plausibly represents one of two biochemically equivalent possibilities that some argue was the result of a random choice (Piccirilli et al., 1990; Wagner, 2005), a symmetry breaking between two approximately equivalent biochemical possibilities (Figure 2A).

In the context of neural systems, the language of the theory of “broken symmetries” applies directly to the specialization of function discussed in the beginning of this article. The broken symmetry is the exchange symmetry between neurons: initially equivalent neurons are assigned different functional roles, forming different neuronal types. When responses of individual neurons have low precision (Figure 1B), all neurons play identical roles in representing stimuli. When the reliability increases (Figure1C), different neurons take over specific parts of the input dynamics range. The choice of which particular neuron shifts its thresholds up or down is arbitrary. However, once neurons select separate thresholds, the spikes from those neurons represent different signals from the environment. The symmetry has been broken. There is no reason why these arguments cannot be applied at different levels of organization, as discussed above for ion channels, dendritic spikes, or activation thresholds for different brain areas.

Importantly, these considerations based on symmetry lead to quantitative and experimentally testable predictions on the properties of neural circuits. A given change in symmetry across the transition is associated with specific scaling properties for systems operating close to the transition (Stanley, 1971). For sensory neurons, the theoretical predictions specify how different parameters of neural response functions should vary relative to each other within the neural population that jointly represents input stimuli. The specific predictions are that one should observe power-law scale-free relationships between variations in thresholds and noise levels across the neural population. The scaling exponents for these power-laws can be predicted quantitatively with no adjustable parameters using the theory of phase transitions in physics. When evaluated on retinal cell types, scaling exponents not only matched theoretical predictions, but also were consistent with scaling exponents observed in physical systems undergoing the same type of symmetry breaking (Kastner et al., 2015).

Scale-free power law dynamics have also been observed in cortical slices (Friedman et al., 2012; Shew et al., 2009; Shew et al., 2011) and in whole-brain activity (Plenz et al., 2014; Yu et al., 2013), but remain a matter of debate (Beggs and Timme, 2012). The controversy stems from the fact that experimental constraints only make it possible to observe power law behavior within a limited range. In these circumstances what is needed is a theoretical model that can explain why one would expect to observe a power law behavior at the level of whole-brain activity (Stumpf and Porter, 2012). In this regard, recall that information theoretic arguments can be applied at different levels of organization and different kinds of inputs. In the retina, we saw that coordination between different threshold-like mechanisms that maximizes information transmission generates scale-free and power law behavior scaling between neuronal parameters across the population. Such parametric power-laws are likely to generate power law dynamics as well. Further, there is every reason to believe that a similar coordination takes place between other threshold-like operations that process more complex signals that are neither purely sensory nor motor. This then provides a tentative mechanism for observations of scale-free brain activity.

In conclusion, it is important to note that although much of the previous discussion was built on information as the optimization function, the key features are reproduced with different optimization functions, such as Fisher information (Harper and McAlpine, 2004). Further, stepping back form specific formulations, one could argue, with good reasons, that the task of the nervous system is not to represent stimuli as accurately as possible given the metabolic constraints, but rather to make decisions and perform concrete tasks (Shadlen and Kiani, 2013). This concern can be addressed by considering the mutual information not about full stimuli but about only certain aspects of the stimulus pertinent to a given decision, i.e. focusing on the so-called relevant stimuli. Determining these relevant stimuli for a given task is a major open problem in its own right. For example, relevant stimulus features, especially at object-level representation, strongly depend on the task (Borji and Itti, 2014). Thus, the need to switch quickly between features that need “to be paid attention to” on a moment-by-moment basis necessitates the use of top-down signals. These top-down changes would work in addition to automatic adaptive changes driven by changes in the input statistics (Wark et al., 2007). Correspondingly, top-down signals and attentional modulation strongly impact an animal’s performance. Recent studies have begun to formalize the impact of attention from the perspective of efficient coding (Borji and Itti, 2014). Further studies are needed to make the leap between strategies that provide the most information about the current stimuli to those that maximize information about the future state of the environment. An analysis of the neural code in the retina shows tuning to features that carry information about stimuli in the immediate future (Palmer et al., 2015). Finding the right time horizon to work with, and how to make long-term predictions, is a major open problem with a wide range of applications in both neuroscience and artificial intelligence.