Efficient Bayesian hierarchical functional data analysis with basis function approximations using Gaussian-Wishart processes

Summary

Functional data are defined as realizations of random functions (mostly smooth functions) varying over a continuum, which are usually collected on discretized grids with measurement errors. In order to accurately smooth noisy functional observations and deal with the issue of high-dimensional observation grids, we propose a novel Bayesian method based on the Bayesian hierarchical model with a Gaussian-Wishart process prior and basis function representations. We first derive an induced model for the basis-function coefficients of the functional data, and then use this model to conduct posterior inference through Markov chain Monte Carlo methods. Compared to the standard Bayesian inference that suffers serious computational burden and instability in analyzing high-dimensional functional data, our method greatly improves the computational scalability and stability, while inheriting the advantage of simultaneously smoothing raw observations and estimating the mean-covariance functions in a nonparametric way. In addition, our method can naturally handle functional data observed on random or uncommon grids. Simulation and real studies demonstrate that our method produces similar results to those obtainable by the standard Bayesian inference with low-dimensional common grids, while efficiently smoothing and estimating functional data with random and high-dimensional observation grids when the standard Bayesian inference fails. In conclusion, our method can efficiently smooth and estimate high-dimensional functional data, providing one way to resolve the curse of dimensionality for Bayesian functional data analysis with Gaussian-Wishart processes.

1. Introduction

Functional data — defined as realizations of random functions varying over a continuum (Ramsay and Silverman, 2005) — include a variety of data types such as longitudinal data, spatial-temporal data, and image data. Because functional data are generally collected on discretized grids with measurement errors, constructing functions from noisy discrete observations (referred to as smoothing) is an essential step for follow-up analysis (Ramsay and Dalzell, 1991; Ramsay and Silverman, 2005). However, the smoothing step has been neglected by most of the existing functional data analysis (FDA) methods, which integrate functional representations in the analysis models. For examples, functional data and effects are represented by basis functions in functional linear regression models (Cardot et al., 2003; Hall et al., 2007; Zhu et al., 2011), functional additive models (Scheipl et al., 2015; Fan et al., 2015), functional principle components analysis (Crainiceanu and Goldsmith, 2010; Zhu et al., 2014), and nonparametric functional regression models (Ferraty and Vieu, 2006; Gromenko and Kokoszka, 2013); as well as represented by Gaussian processes (GP) in Bayesian nonparametric models (Gibbs, 1998; Shi et al., 2007; Banerjee et al., 2008; Kaufman and Sain, 2010; Shi and Choi, 2011).

On the other hand, most of the existing smoothing methods process one functional sample at a time, such as cubic smoothing splines (CSS) and kernel smoothing (Green and Silverman, 1993; Ramsay and Silverman, 2005). Consequently, when multiple functional observations are sampled from the same distribution, these methods of individual smoothing lead to less accurate results, by ignoring the shared mean-covariance functions. Alternatively, Yang et al. (2016) proposed a Bayesian hierarchical model (BHM) with Gaussian-Wishart processes for simultaneously and nonparametrically smoothing multiple functional observations and estimating mean-covariance functions, which is shown to be comparable with the frequentist method — Principle Analysis by Conditional Expectation (PACE) proposed by Yao et al. (2005b).

BHM assumes a general measurement error model for the observed functional data {Y_i(t); t ∈ $\mathcal{T}$, i = 1,⋯, n},

$$\begin{array}{l}{Y}_i\left(t\right)=Z_i\left(t\right)+{\epsilon }_i\left(t\right);Z_i(\cdot )\sim GP\left({\mu }_Z(\cdot ),{\displaystyle {\sum }_Z\left(\cdot ,\cdot \right)}\right),{\epsilon }_i(\cdot )\sim N\left(0,{\sigma }_{\epsilon }^2\right);{\sigma }_{\epsilon }^2\sim IG\left(a_{\epsilon },b_{\epsilon }\right),\\ {\mu }_Z(\cdot )|{\displaystyle {\sum }_Z\left(\cdot ,\cdot \right)}\sim GP\left({\mu }_0(\cdot ),\frac{1}{c}{\displaystyle {\sum }_Z\left(\cdot ,\cdot \right)}\right),{\displaystyle {\sum }_Z\left(\cdot ,\cdot \right)\sim \mathit{IWP}\left(\delta ,{\sigma }_s^{2}A\left(\cdot ,\cdot \right)\right);{\sigma }_s^2\sim IG\left(a_s,b_s\right);}\end{array}$$ (1)

where {Z_i(t)} denotes the true functional data following the same GP distribution, IG denotes the Inverse-Gamma prior, IWP denotes the Inverse-Wishart process (IWP) prior (Dawid, 1981) for the covariance function, and (μ₀(·), c, δ, A(·,·), a_ε, b_ε, a_s, b_s) are hyper-prior parameters to be determined. The IWP prior enables the BHM to analyze both stationary and nonstationary functional data with nonparametric covariance models. In addition, ${\sigma }_s^2$ provides the flexibility of estimating the scale of the covariance structure (A(·,·)) in the IWP prior from the data. Because of the hierarchical representation of Z_i(t) in (1), the proposed hierarchical model (1) can also be viewed as a generalization of the spatial random-effect GP regression model considered in Quick et al. (2013).

However, just like the other GP based models, the BHM suffers serious computational burden and instability when functional data are observed on high-dimensional or random grids. To address this computational issue of GP based models, existing reduce-rank methods focus on kriging with partial data (Cressie and Johannesson, 2008; Banerjee et al., 2008), implementing direct low-rank approximations for the covariance matrix (Rasmussen and Williams, 2006; Quiñonero Candela et al., 2007; Banerjee et al., 2013), and using predictive processes (Sang and Huang, 2012; Finley et al., 2015). Although these reduce-rank methods can be applied to the standard GP regression models (Shi et al., 2007; Banerjee et al., 2008; Kaufman and Sain, 2010) that only model group-level GPs with parametric covariance functions, they will greatly increase the complexity in BHM for handling signal-specific posterior GPs, mean GP, and the IWP prior. For example, the corrected predictive process methods (Sang and Huang, 2012; Finley et al., 2015) need to handle different residual processes for all functional observations, mean GP, and the IWP prior. Moreover, these low-rank methods require fairly large rank to perform well for high-dimensional data, which results in high computational cost (Datta, Banerjee, Finley, and Gelfand, 2016). Stein (2014) further theoretically (using Kullback-Leibler divergence) proved that the low rank approximation performs poorly under particular settings.

Here, we propose a novel Bayesian framework with Approximations by Basis Functions for the original BHM method, referred to as BABF, which is computationally efficient and stable for analyzing high-dimensional functional data. Basically, we approximate the underlying true functional data {Z_i(t)} with basis functions, and derive an induced Bayesian hierarchical model for the basis-function coefficients from the assumptions of BHM (1). Then we conduct posterior inference for functional signals {Z_i(t)} and mean-covariance functions (μ_Z(·), Σ_Z(·,·)), by Markov chain Monte Carlo (MCMC) under the induced model of basis-function coefficients, namely by MCMC in the basis-function space with a reduced rank. As a result, our BABF method not only improves the computational scalability over the original BHM, but also inherits the advantage of modeling the functional data and mean-covariance functions in a flexible nonparametric manner. In addition, because of basis function approximations, BABF can naturally handle functional data observed on random or uncommon grids.

Thus, our basis function approximation approach has two-fold advantages: (i) Compared to the alternative reduce-rank approaches, it is easier to apply to Bayesian hierarchical GP methods that model individual levels of GPs (e.g., BHM). (ii) It induces a nonparametric Bayesian model with a Gaussian-Wishart prior for the basis-function coefficients, which is different from modeling the basis-function coefficients as independent variables as in the standard functional linear regression models (Cardot et al., 2003; Hall et al., 2007; Zhu et al., 2011) and functional additive models (Scheipl et al., 2015; Fan et al., 2015), and also different from directly modeling the basis-function coefficients in semiparametric forms as in Baladandayuthapani et al. (2008).

By simulation studies with both stationary and nonstationary functional data, we demonstrate that BABF produces accurate smoothing results and mean-covariance estimates. Specifically, when functional data are observed on low-dimensional common grids, BABF generates similar results to those obtainable by BHM. When functional data are observed on high-dimensional or random grids, BHM fails because of computational issues, while BABF efficiently produces smoothed signal estimates with smaller root mean square errors (RMSEs) than the alternative methods (aforementioned CSS and PACE).

Furthermore, using a real application with the sleeping energy expenditure (SEE) measurements of 106 children and adolescents (44 obese cases, 62 controls) over 405 time points (Lee et al., 2016), we show that BABF captures better periodic patterns of the measurements, producing more reasonable estimates for the functional signals and mean-covariance functions. Moreover, compared to the raw data and smoothed data by CSS and PACE, the smoothed data by BABF lead to better classification results for the SEE data.

This paper is organized as follows: We provide the details of the BABF method and the corresponding posterior inference procedure in Section 2. We present simulation and real studies in Sections 3 and 4, respectively. Then we conclude with a discussion in Section 5.

2. BABF method

Because BHM (Yang et al., 2016) conducts MCMC on the pooled observation grid for handling uncommon grids, it has computational complexity O(np³m) with n samples, p pooled-grid points, and m MCMC iterations. To resolve the computational bottleneck issue for smoothing functional data with large pooled-grid dimension p by BHM, we propose our BABF method by approximating functional data with basis functions under the same model assumptions in (1).

2.1 Approximation by basis functions

First, we approximate the GP evaluations {Z_i(τ)} by a system of basis functions (e.g., cubic B-splines), with a working grid based on data density, $\mathit{\tau }={({\tau }_1,{\tau }_2,\cdots ,{\tau }_L)}^T\subset \mathcal{T}$, L ≪ p. Let B(·) = [b₁(·), b₂(·),⋯, b_K(·)] denote K selected basis functions with coefficients ζ_i = (ζ_i1, ζ_i2, ⋯ ζ_iK)^T, then

$$Z_i\left(\mathit{\tau }\right)={\displaystyle \sum _{k=1}^K{\zeta }_{ik}{b}_k\left(\mathit{\tau }\right)=\mathit{B}\left(\mathit{\tau }\right)}{\mathit{\zeta }}_{\mathit{i}}.$$ (2)

Assuming K = L, we can write ζ_i = B(τ)⁻¹Z_i(τ) as a linear transformation of Z_i(τ). Note that even if B(τ) is singular or non-square, ζ_i can still be written as a linear transformation of Z_i(τ) with the generalized inverse (James, 1978) of B(τ). Consequently, the true signals {Z_i(t_i)} can be approximated by {B(t_i)ζ_i} with given {ζ_i}.

Next, we derive the induced Bayesian hierarchical model for the basis-function coefficients {ζ_i}. Because ζ_i is a linear transformation of Z_i(τ) that follows a multivariate normal distribution MN(μ_Z(τ), Σ_Z(τ, τ)) under the assumptions in (1), the induced model for ζ_i is

$${\mathit{\zeta }}_{\mathit{i}}\sim MN\left({\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right);{\mathit{\mu }}_{\mathit{\zeta }}=\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_Z\left(\mathit{\tau }\right);{\mathbf{\sum }}_{\mathit{\zeta }}=\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\sum }_Z\left(\mathit{\tau },\mathit{\tau }\right)\mathit{B}{\left(\mathit{\tau }\right)}^{-T}.$$ (3)

Further, from the assumed priors of (μ_Z(·), Σ_Z(·,·)) in (1), the following priors of (μ_ζ, Σ_ζ) are also induced:

$${\mathit{\mu }}_{\mathit{\zeta }}|{\mathbf{\sum }}_{\mathit{\zeta }}\sim MN\left(\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_0\left(\mathit{\tau }\right),c{\mathbf{\sum }}_{\mathit{\zeta }}\right);$$ (4)

$${\mathbf{\sum }}_{\mathit{\zeta }}\sim IW\left(\delta ,{\sigma }_s^2\mathit{B}{\left(\mathit{\tau }\right)}^{-1}A\left(\mathit{\tau },\mathit{\tau }\right)\mathit{B}{\left(\mathit{\tau }\right)}^{-T}\right).$$ (5)

Then, we can estimate ({Z_i(·)}, μ_Z(·), Σ_Z(·,·)) by a Gibbs-Sampler (Geman and Geman, 1984) with computation complexity O(nK³m) under the above induced model of {ζ_i}. Details of the Gibbs-Sampler (MCMC) are provided in Section 2.3.3. We take the corresponding averages of the posterior MCMC samples as our Bayesian estimates, whose uncertainties can easily be quantified by the MCMC credible intervals.

2.2 Hyper-prior and basis-function selections

Before describing the MCMC sampling procedure, we first discuss the issues of selecting hyper-priors, basis functions, and the working grid for the BABF method.

To set hyper-priors, we use the same data-driven strategy as BHM (Yang et al., 2016). Specifically, we set μ₀(·) as the smoothed sample mean, and c = 1, δ = 5 for uninformative priors of the mean-covariance functions. We set A(·,·) as a Matérn covariance function (Matérn, 1960) for stationary data, or as a smooth covariance estimate for nonstationary data (e.g., PACE estimate, smoothed empirical estimate). A heuristic Bayesian approach is used for setting the values of (a_ε, b_ε, a_s, b_s), by matching hyper-prior moments with the empirical estimates.

Although the induced model makes BABF robust with respect to the selected basis functions and working grid, appropriately selected basis functions and working grid will help improve the performance of BABF. The general strategies of selecting basis functions for interpolating over the working grid apply here, e.g., selecting Fourier series for periodic data, B-splines for GP data, and wavelets for signal data. Our choice of B-splines is widely used by GP regression methods (Rasmussen and Williams (2006); Shi et al. (2007)). For constructing the basis functions of B-splines, the optimal knot sequence for best interpolation at the working grid τ can be obtained using the method developed by Gaffney and Powell (1976); Micchelli et al. (1976); de Boor (1977), and implemented by the Matlab function optknt. The working grid τ can be chosen to represent data densities over the domain, such as given by the $(\frac{1}{L+1},\dots ,\frac{L}{L+1})$ percentiles of the pooled observation grid. As for the dimension L of the working grid, one may try a few values with a small testing data set, and then select the optimal one with the smallest RMSE of the signal estimates.

BABF inherits the advantage of nonparametrically smoothing without the necessity of tuning smoothing parameters, where the amount of smoothness in the posterior estimates is determined by the data and the IWP prior of the covariance function.

2.3 Posterior inference

For BHM (1), the joint posterior distribution of $(\mathit{Z},{\mu }_Z,{\sum }_Z,{\sigma }_{\epsilon }^2,{\sigma }_s^2)$ is

$$\begin{array}{c}f\left(\mathit{Z},{\mu }_Z,{\sum }_Z,{\sigma }_{\epsilon }^2,{\sigma }_s^2|\mathit{Y}\right)\propto f\left(\mathit{Y}|\mathit{Z},{\sigma }_{\epsilon }^2\right)f\left(\mathit{Z}|{\mu }_Z,{\sum }_Z|\right)f\left({\mu }_Z|{\sum }_Z\right)f\left({\sum }_Z|{\sigma }_s^2\right)f\left({\sigma }_{\epsilon }^2\right)f\left({\sigma }_s^2\right),\\ \mathit{Z}=\left\{Z_1\left({\mathit{t}}_i\right),\cdots ,Z_n\left({\mathit{t}}_n\right)\right\},\mathit{Y}=\left\{Y_1\left({\mathit{t}}_i\right),\cdots ,Y_n\left({\mathit{t}}_n\right)\right\}.\end{array}$$ (6)

Equivalently, because of ζ_i = B(τ)⁻¹Z_i(τ), the joint posterior distribution of $(\mathit{\zeta },{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }},{\sigma }_{\epsilon }^2,{\sigma }_s^2)$ is

$$\begin{array}{c}f\left(\mathit{\zeta },{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }},{\sigma }_{\epsilon }^2,{\sigma }_s^2|\mathit{Y}\right)\propto f\left(\mathit{Y}|\mathit{\zeta },{\sigma }_{\epsilon }^2\right)f\left(\mathit{\zeta }|{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right)f\left({\mathit{\mu }}_{\mathit{\zeta }}|{\mathbf{\sum }}_{\mathit{\zeta }}\right)f\left({\mathbf{\sum }}_{\mathit{\zeta }}|{\sigma }_s^2\right)f\left({\sigma }_{\epsilon }^2\right)\left({\sigma }_s^2\right),\\ \mathit{\zeta }=\left\{{\mathit{\zeta }}_1,\cdots ,{\mathit{\zeta }}_n\right\},{\mathit{\mu }}_{\mathit{\zeta }}=\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_Z\left(\mathit{\tau }\right),{\sum }_{\zeta }=\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\sum }_Z\left(\mathit{\tau },\mathit{\tau }\right)\mathit{B}{\left(\mathit{\tau }\right)}^{-T}.\end{array}$$ (7)

2.3.1 Full conditional distribution of ζ_i

From (7), we can see that

$$f\left(\mathit{\zeta }|\mathit{Y},{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right)\propto f\left(\mathit{Y}|\mathit{\zeta },{\sigma }_{\epsilon }^2\right)f\left(\mathit{\zeta }|{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right).$$

Then the full conditional posterior distribution of ζ_i is derived as

$$\begin{array}{c}{\mathit{\zeta }}_{\mathit{i}}|\left(Y_i\left({\mathit{t}}_{\mathit{i}}\right),{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right)\sim MN\left[{\mathit{m}}_{{\mathit{\zeta }}_{\mathit{i}}|{\mathit{Y}}_{\mathit{i}}},{\mathit{V}}_{{\mathit{\zeta }}_{\mathit{i}}|{\mathit{Y}}_{\mathit{i}}}\right];\\ {\mathit{V}}_{{\mathit{\zeta }}_{\mathit{i}}|{\mathit{Y}}_{\mathit{i}}}={\left(\frac{\mathit{B}{\left({\mathit{t}}_{\mathit{i}}\right)}^T\mathit{B}\left({\mathit{t}}_{\mathit{i}}\right)}{{\sigma }_{\epsilon }^2}+{\mathbf{\sum }}_{\mathit{\zeta }}^{-1}\right)}^{-1},{\mathit{m}}_{{\mathit{\zeta }}_{\mathit{i}}|{\mathit{Y}}_{\mathit{i}}}={\mathit{V}}_{{\mathit{\zeta }}_{\mathit{i}}|{\mathit{Y}}_{\mathit{i}}}\left(\frac{\mathit{B}{\left({\mathit{t}}_{\mathit{i}}\right)}^T{Y}_i\left({\mathit{t}}_{\mathit{i}}\right)}{{\sigma }_{\epsilon }^2}+{\mathbf{\sum }}_{\mathit{\zeta }}^{-1}{\mathit{\mu }}_{\mathit{\zeta }}\right).\end{array}$$ (8)

2.3.2 Full conditional distribution for μ_ζ, Σ_ζ

Conditioning on {ζ_i}, the posterior distribution of (μ_ζ, Σ_ζ) is

$$f\left({\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}|{\mathit{\zeta }}_1,\cdots ,{\mathit{\zeta }}_n\right)\propto {\displaystyle \prod _{i=1}^{n}f\left({\mathit{\zeta }}_i|{\mathit{\mu }}_{\mathit{\zeta }},{\mathbf{\sum }}_{\mathit{\zeta }}\right)f\left({\mathit{\mu }}_{\mathit{\zeta }}|{\mathbf{\sum }}_{\mathit{\zeta }}\right)f\left({\mathbf{\sum }}_{\mathit{\zeta }}\right)},$$

where f(μ_ζ|Σ_ζ) and f(Σ_ζ) are given by (4), (5). Therefore,

$$\begin{array}{l}{\mathit{\mu }}_{\mathit{\zeta }}|\left({\mathit{\zeta }}_1,\dots ,{\mathit{\zeta }}_{\mathit{n}},{\mathbf{\sum }}_{\mathit{\zeta }}\right)\sim MN\left(\frac{1}{n+c}\left({\displaystyle {\sum }_{i=1}^n{\mathit{\zeta }}_{\mathit{i}}+c\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_0\left(\mathit{\tau }\right)}\right),\frac{1}{n+c}{\mathbf{\sum }}_{\mathit{\zeta }}\right);\\ \end{array}$$ (9)

$$\begin{array}{c}{\mathbf{\sum }}_{\mathit{\zeta }}|\left({\mathit{\zeta }}_1,\dots ,{\mathit{\zeta }}_{\mathit{n}},{\mathit{\mu }}_{\mathit{\zeta }}\right)\sim IW\left(\stackrel{\sim }{{\delta }_{\zeta }},\stackrel{\sim }{{\Psi }_{\mathit{\zeta }}}\right),\\ \stackrel{\sim }{{\delta }_{\zeta }}=n+1+\delta ,\stackrel{\sim }{{\Psi }_{\mathit{\zeta }}}={\displaystyle {\sum }_{i=1}^n({\mathit{\zeta }}_{\mathit{i}}-{\mathit{\mu }}_{\mathit{\zeta }})}{\left({\mathit{\zeta }}_{\mathit{i}}-{\mathit{\mu }}_{\mathit{\zeta }}\right)}^T+\\ c\left({\mathit{\mu }}_{\mathit{\zeta }}-\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_0\left(\mathit{\tau }\right)\right){\left({\mathit{\mu }}_{\mathit{\zeta }}-\mathit{B}{\left(\mathit{\tau }\right)}^{-1}{\mu }_0\left(\mathit{\tau }\right)\right)}^T+{\sigma }_s^2\mathit{B}{\left(\mathit{\tau }\right)}^{-1}A\left(\mathit{\tau },\mathit{\tau }\right)\mathit{B}{\left(\mathit{\tau }\right)}^{-T}.\end{array}$$ (10)

2.3.3 MCMC procedure

We design the following Gibbs-Sampler algorithm for MCMC, which ensures computational convenience and posterior convergence.

Step 0: Set hyper-priors (Section 2.2) and initial parameter values. Initial values for $\left({\mu }_Z\right(\mathit{\tau }),{\sum }_Z(\mathit{\tau },\mathit{\tau }),{\sigma }_{\epsilon }^2)$ can be set as empirical estimates, which will induce the initial values for (μ_ζ, Σ_ζ) by (3).

Step 1: Conditioning on observed data Y and $({\mathit{\mu }}_{\mathit{\zeta }},{\sum }_{\mathit{\zeta }},{\sigma }_{\epsilon }^2)$, sample {ζ_i} from (8).

Step 2: Conditioning on ζ, update μ_ζ and Σ_ζ respectively from (9) and (10).

Step 3: Conditioning on ({ζ_i}, μ_ζ, Σ_ζ), approximate {Z_i(t_i), μ_Z(t_i), Σ_Z(t_i, t_i), Σ_Z(τ, t_i), Σ_Z(t_i, τ), Σ_Z(τ, τ)} by

$$\begin{array}{c}{Z}_i\left({\mathit{t}}_{\mathit{i}}\right)=\mathit{B}\left({\mathit{t}}_{\mathit{i}}\right){\mathit{\zeta }}_{\mathit{i}},{\mu }_Z\left({\mathit{t}}_{\mathit{i}}\right)=B\left({\mathit{t}}_{\mathit{i}}\right){\mathit{\mu }}_{\mathit{\zeta }},{\sum }_Z\left({\mathit{t}}_{\mathit{i}},{\mathit{t}}_{\mathit{i}}\right)=\mathit{B}\left({\mathit{t}}_{\mathit{i}}\right){\mathbf{\sum }}_{\mathit{\zeta }}\mathit{B}{\left({\mathit{t}}_{\mathit{i}}\right)}^T,\\ {\sum }_Z{\left(\mathit{\tau },{\mathit{t}}_{\mathit{i}}\right)}^T={\displaystyle {\sum }_Z\left({\mathit{t}}_{\mathit{i}},\mathit{\tau }\right)}=\mathit{B}\left({\mathit{t}}_{\mathit{i}}\right){\mathbf{\sum }}_{\mathit{\zeta }}\mathit{B}{\left(\mathit{\tau }\right)}^T,{\sum }_Z\left(\mathit{\tau },\mathit{\tau }\right)=\mathit{B}\left(\mathit{\tau }\right){\mathbf{\sum }}_{\mathit{\zeta }}\mathit{B}{\left(\mathit{\tau }\right)}^T.\end{array}$$

Step 4: Conditioning on Z and Y, update ${\sigma }_{\epsilon }^2$ by

$$IG\left(a_{\epsilon }+\frac{1}{2}{\displaystyle \sum _{i=1}^n{p}_i},b_{\epsilon }+\frac{1}{2}{\displaystyle \sum _{i=1}^n\left(Y_i{\left({\mathit{t}}_{\mathit{i}}\right)-Z_i\left({\mathit{t}}_{\mathit{i}}\right))}^T\left(Y_i({\mathit{t}}_{\mathit{i}}\right)-Z_i\left({\mathit{t}}_{\mathit{i}}\right)\right)}\right),$$

which is derived from

$$f\left({\sigma }_{\epsilon }^2|Y_1\left({\mathit{t}}_1\right),Z_1\left({\mathit{t}}_1\right),\cdots ,Y_n\left({\mathit{t}}_n\right),Z_n\left({\mathit{t}}_{\mathit{n}}\right)\right)\propto {\displaystyle \prod _{i=1}^{n}f\left(Y_i\left({\mathit{t}}_{\mathit{i}}\right)|Z_i\left({\mathit{t}}_{\mathit{i}}\right),{\sigma }_{\epsilon }^2\right)f\left({\sigma }_{\epsilon }^2\right).}$$

Step 5: Given Σ_τ = Σ_Z(τ, τ), update ${\sigma }_s^2$ by

$${\sigma }_s^2|{\mathbf{\sum }}_{\mathit{\tau }}\sim G\left(a_s+\frac{\left(\delta +K-1\right)K}{2},b_s+\frac{1}{2}\mathit{trace}\left(\mathit{A}\left(\mathit{\tau },\mathit{\tau }\right){\mathbf{\sum }}_{\tau }^{-1}\right)\right),$$

which is derived from

$$f\left({\sigma }_s^2|{\mathbf{\sum }}_{\mathit{\tau }}\right)\propto f\left({\mathbf{\sum }}_{\mathit{\tau }}|{\sigma }_s^2\right)f\left({\sigma }_s^2\right).$$

Generally, the posterior samples will pass the convergence diagnosis by potential scale reduction factor (PSRF) (Gelman and Rubin, 1992), with a fairly large number of MCMC iterations (e.g., 12,000 in our numerical studies).

3. Simulation studies

In the following simulation studies, we compared the BABF method with CSS (Green and Silverman, 1993), PACE (Yao et al., 2005a), Bayesian functional principle component analysis (BFPCA) (Crainiceanu and Goldsmith, 2010), standard Bayesian GP regression (BGP) (Gibbs, 1998), and BHM (Yang et al., 2016). We considered scenarios with stationary and nonstationary functional data, common and random observation grids, Gaussian and non-Gaussian data. Because both BFPCA and BGP are developed for common-grid scenarios, BHM has computational issues with a high-dimensional pooled-grid (the case with random grids), and BHM is known to be comparable with PACE (Yang et al., 2016); we compared all methods in the common-grid scenarios, but only compared BABF with CSS and PACE in the random-grid scenarios.

Because simulation data were evenly distributed over the domain, we selected an equally spaced working grid with size L = 20 for BABF. CSS was applied to each functional observation independently with the smoothing parameter selected by general cross-validation (GCV). For BFPCA, we used the covariance estimate by PACE, and selected the number of principle functions subject to capture 99.99% data variance. For BGP, we assumed the Matérn model for the covariance function with stationary data, while fixing the covariance at the PACE estimate with nonstationary data. All MCMC samples consisted of 2, 000 burn-ins and 10, 000 posterior samples, and passed the convergence diagnoses by PSRF (Gelman and Rubin, 1992).

3.1 Studies with common grids

We generated 30 stationary functional curves (true signals) on the common equally-spaced-grid with 40 points over $\mathcal{T}=\left(0,\pi /2\right)$, denoted by Z, from

$$GP(\mu \left(t\right)=3\sin \left(4t\right),\sum \left(s,t\right)=5{\mathit{Matern}}_{\mathit{cor}}\left(\left|s-t\right|;\rho =0.5,\nu =3.5\right)).$$ (11)

Here, Matern_cor denotes the Matérn covariance function given by

$${\mathit{Matern}}_{\mathit{cor}}\left(d;\rho ,\nu \right)=\frac{1}{\mathrm{\Gamma }\left(\nu \right)2^{\nu -1}}{\left(\sqrt{2\nu }\frac{d}{\rho }\right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }\frac{d}{\rho }\right),d⩾0,\nu >0,$$

where ρ is the scale parameter, ν is the order of smoothness, Γ(·) is the gamma function, and K_ν(·) is the modified Bessel function of the second kind. The noise terms {ε_ij} were generated from $N\left(0,{\sigma }_{\epsilon }=\sqrt{5}/2\right)$, such that the signal to noise ratio (SNR) was 2 (resulting in a relatively high volume of noise in the simulated data). The observed noisy functional data curves were given by Y = Z + ε.

Similarly, we generated 30 nonstationary functional curves on the same equally-spaced-grid with size L = 40, from a nonstationary $\text{GP}\stackrel{\sim }{X}\left(t\right)=h\left(t\right)X\left(s\left(t\right)\right)$ (i.e., a nonlinear transformation of a stationary GP), where X(·) denotes the GP in (11) and h(t) = t + 1/2, s(t) = t^2/3. Noisy observation data were obtained by adding noises from $N\left(0,{\sigma }_{\epsilon }=\sqrt{5}/2\right)$ to the generated nonstationary GP data (true signals).

We repeated the simulations 100 times, and calculated the RMSEs of the estimates of signals {Z_i(t)}, mean function μ_Z(t), covariance surface Σ_Z(t, t), and residual variance ${\sigma }_{\epsilon }^2$ (t denotes the common observation grid). The average RMSEs (with standard deviations among these 100 simulations) for stationary and nonstationary data are shown in Table 1, where the CSS estimates of (μ_Z, Σ_Z) are sample estimates with pre-smoothed signals by CSS, and average RMSEs are omitted if the parameters are not directly estimated by the corresponding methods, such as $({\mu }_Z,{\sum }_Z,{\sigma }_{\epsilon }^2)$ for BFPCA, ${\sigma }_{\epsilon }^2$ for CSS.

Table 1.

Simulation results with common grids: average RMSEs and corresponding standard deviations (in parentheses) of {Z_i(t)}, μ(t), Σ_Z(t, t), and ${\sigma }_{\epsilon }^2$ produced by CSS, PACE, BFPCA, BGP, BHM, and BABF. Average RMSEs are omitted if the corresponding parameters are not directly estimated. Two best results are bold for each parameter.

	CSS	PACE	BFPCA	BGP	BHM	BABF
Stationary
{Zi(t)}	0.4808	0.4553	0.5657	0.4020	0.4067	0.4073
	(0.0213)	(0.0268)	(0.0550)	(0.0219)	(0.0207)	(0.0204)
μ(t)	0.4757	0.4194	–	0.3982	0.3961	0.3961
	(0.1347)	(0.1593)	–	(0.1527)	(0.1538)	(0.1535)
Σ(t, t)	1.0017	1.0375	–	1.0988	0.9601	0.9590
	(0.3079)	(0.2850)	–	(0.4934)	(0.2902)	(0.2913)
${\sigma }_{\epsilon }^2$	–	0.0764	–	0.0460	0.0491	0.0483
	–	(0.0516)	–	(0.0327)	(0.0357)	(0.0352)
Nonstationary
{Zi(t)}	1.0271	0.5185	0.6314	0.5183	0.5759	0.5133
	(0.00463)	(0.0255)	(0.0632)	(0.0265)	(0.0227)	(0.0227)
μ(t)	0.9446	0.5782	–	0.5387	0.5530	0.5356
	(0.1509)	(0.2095)	–	(0.2090)	(0.2038)	(0.2094)
Σ(t, t)	1.9635	1.9751	–	1.9733	2.0296	1.9768
	(0.8386)	(0.8160)	–	(0.6831)	(0.6891)	(0.7835)
${\sigma }_{\epsilon }^2$	–	0.0810	–	0.1472	0.2432	0.0692
	–	(0.0541)	–	(0.0879)	(0.0644)	(0.0492)

Table 1 shows that BGP produces the best estimates for the signals and residual variance (with the lowest RMSEs), while BHM and BABF give the second best estimates for the signals and residual variance, as well as the best estimates for the mean-covariance functions. With nonstationary data of common grids, BGP and PACE produce the best covariance estimates, while BABF produces closely accurate covariance estimates, as well as the best estimates for the signals, mean function, and residual variance. Because of stable computations with nonstationary data, our BABF method produces better estimates than BHM. In addition, the CSS and BFPCA methods produce the least accurate estimates (with the highest RMSEs) for both stationary and nonstationary data, which demonstrates the advantage of simultaneously smoothing and estimating functional data as in BGP, BHM, and BABF.

Figure 1 (a, b, c, d) shows that all three Bayesian methods produce similarly accurate estimates for the functional signals and mean function of common grids. With nonstationary data, our BABF method produces the best signal estimates (Figure 1(b)). As for the functional covariance estimates (Web Figure 1), the parametric estimate by BGP is a Matérn function because of the assumed true Matérn model, but with underestimated diagonal variances. Practically, a wrong covariance model is usually assumed in BGP, which is likely to produce estimates with large errors and wrong structures. In contrast, the nonparametric methods such as BHM and BABF are more flexible and applicable for estimating the covariance function of real data.

Figure 1.

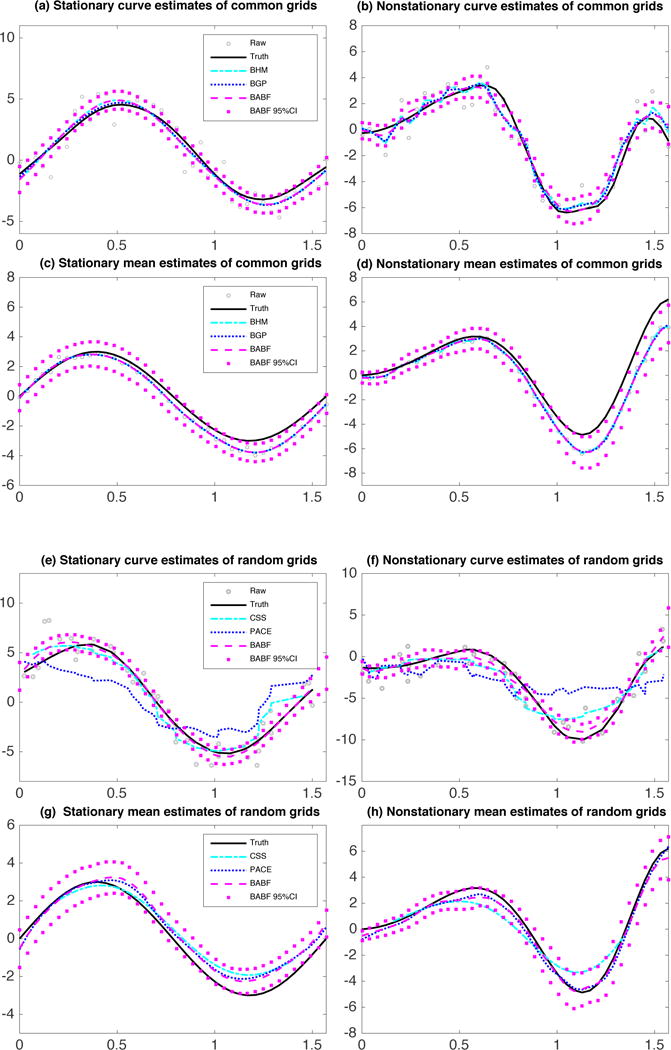
Example smoothed functional data of common grids in (a, b), mean estimates of common grids in (c, d), example smoothed functional data of random grids in (e, f), and mean estimates of random grids in (g, h), along with 95% pointwise CIs by BABF.

In addition, we examined the coverage probabilities of the 95% pointwise credible intervals (CI) generated by BGP, BHM, and BABF, for the functional signals and mean-covariance functions (Web Table 1). For functional signals, BGP results in the highest coverage probability with stationary data (0.9483 vs. 0.9217, 0.9208), but the lowest coverage probability with nonstationary data (0.8350 vs. 0.9450, 0.8742). All methods have similar coverage probabilities for the functional mean (~ 0.7), where the relatively low coverage probabilities are due to the narrow 95% confidence intervals. As for the covariance, the coverage probability by BGP is significantly lower than the ones by BHM and BABF for both stationary (0.000 vs. 0.7869, 0.7869) and nonstationary data (0.3819 vs. 0.9913, 0.9938), because BGP underestimates the diagonal variances.

In summary, with common grids, GP based Bayesian regression methods (BGP, BHM, and BABF) produce better smoothing and estimation results, compared to estimating mean-covariance functions using the pre-smoothed functional data by CSS. Moreover, the results by BABF are at least similar to the ones by BHM, and better with nonstationary data.

3.2 Studies with random grids

For this set of simulations, we generated 30 true functional curves from the stationary and non-stationary GPs as in Section 3.1, with observational grids (L = 40) that were randomly (uniformly) generated over $\mathcal{T}=\left(0,\pi /2\right)$. Raw functional data were then obtained by adding noises from $N\left(0,\sqrt{5}/2\right)$ to the true signals. We compared our BABF method (using an equally spaced working grid ${\mathit{\tau }}_{1\times 20}\subset \mathcal{T}$) with CSS and PACE, by 100 simulations.

Table 2 presents the average RMSEs of the signals, residual variance, and mean-covariance functions (evaluated on the equally-spaced grid over $\mathcal{T}$ with length 40), along with the standard deviations from 100 simulations in the parentheses. It is shown that our BABF method (with lowest RMSEs) performs consistently better than CSS and PACE for signal and mean estimates, with both stationary and nonstationary data of random grids.

Table 2.

Simulation results with random grids: average RMSEs and corresponding standard deviations (in parentheses) of {Z_i(t)}, μ(t), Σ_z (t, t), and ${\sigma }_{\epsilon }^2$ by CSS, PACE, and BABF. Average RMSEs are omitted if the corresponding parameters are not directly estimated. Best results are bold for each parameter.

	Stationary			Nonstationary
	CSS	PACE	BABF	CSS	PACE	BABF
{Zi(t)}	0.4839	1.4141	0.4079	1.0137	2.6300	0.6832
	(0.0229)	(0.1424)	(0.0219)	(0.0511)	(0.2876)	(0.0576)
μ(t)	0.4229	0.4196	0.3690	0.9905	0.6157	0.5920
	(0.1471)	(0.1290)	(0.1302)	(0.1888)	(0.2160)	(0.2138)
Σ(t, t)	1.0445	1.4089	1.0054	1.6403	2.4120	2.2090
	0.4313	(0.3502)	(0.3286)	(0.6086)	(0.6497)	(0.4506)
${\sigma }_{\epsilon }^2$	–	0.1900	0.0509	–	0.4007	0.2209
	–	(0.1818)	(0.0387)	–	(0.2960)	(0.1189)

Figure 1 (e, f) shows that BABF produces the best signal estimates in the random-grid scenarios. This is because CSS smooths functional samples independently; PACE only uses limited information per pooled-grid point; while BABF borrows strength across all observations through basis function approximations. For both stationary and nonstationary functional data, PACE and BABF give closely accurate mean estimates, while CSS gives the least accurate mean estimate (Figure 1 (g, h)). In addition, PACE produces the roughest covariance estimate (Web Figure 2), for only using limited information on the pooled-grid points. The BABF coverage probability of the covariance is 0.9506 for stationary data and 0.8550 for nonstationary data, showing the good performance of our BABF method.

In summary, with random grids, our BABF method produces the best signal and mean estimates, compared to CSS and PACE. Although the sample covariance estimate using the pre-smoothed data generated by CSS has the lowest RMSE for nonstationary data, the analogous estimate using the more accurately smoothed data generated by BABF will have at least similar RMSE.

3.3 Studies about robustness

To test the robustness of our BABF method for handling non-Gaussian data, we further simulated stationary functional data from a non-Gaussian process, 0.2(X(t)²−1)+X(t), which is a modified Hermite polynomial transformation of the GP X(t) in (11). We simulated functional data with n = 30, random grids (p = 40) over $\mathcal{T}=\left(0,\tau /2\right)$, and noises from $N\left(0,\sqrt{5}/2\right)$. Compared to CSS, our BABF method has RMSE 0.4278 vs. 0.7092 for the signal estimates, 0.1271 vs. 0.4992 for the functional mean estimate, and 0.4417 vs. 0.8886 for the functional covariance estimate. These results demonstrate that our BABF method is robust for analyzing non-Gaussian functional data. In addition, we note that it is crucial to select a correct prior structure, A(·,·) in (1), of the covariance function. In general, we suggest using the Matérn model for stationary data and a smoothed covariance estimate by PACE for nonstationary data.

3.4 Goodness-of-fit diagnostics

In addition to model fitting, we considered goodness-of-fit diagnosis of the proposed BABF method. Specifically, we applied the goodness-of-fit diagnosis method using pivotal discrepancy measures (PDMs) (Yuan and Johnson, 2012) on the residuals, ε_i(t) = Y_i(t)−Z_i(t), in the Bayesian hierarchical model (1) on which BABF is based. Following the method proposed by Yuan and Johnson (2012), we constructed PDMs using standardized residuals from the posterior samples in MCMC. The PDM follows a chi-squared distribution under the null hypothesis that the residuals follow the $N\left(0,{\sigma }_{\epsilon }^2\right)$ distribution (i.e., global goodness-of-fit for the Bayesian hierarchical model). In all simulation studies, the p-values of testing the null hypothesis of global goodness-of-fit for the Bayesian hierarchical model are greater than 0.25, providing no evidence of lack-of-fit.

4. Application on real data

We analyzed a functional dataset from an obesity study with children and adolescents (Lee et al., 2016), by the Children’s Nutrition Research Center (CNRC) at Baylor College of Medicine. This study estimated the energy expenditure (EE in unit kcal) of 106 children and adolescents (44 obese cases, 62 nonobese controls) during 24 hours with a series of scheduled physical activities and a sleeping period (12:00am–7:00am), by using the CNRC room respiration calorimeters (Moon et al., 1995). We only analyzed the sleeping energy expenditure (SEE) data measured at 405 time points during the sleeping period. This real SEE data set provides a good example of high-dimensional common grids. The goal of this study was to discover different data patterns between obese cases and controls, providing insights about obesity diagnosis.

We applied CSS, PACE, and BABF on this SEE functional data. Specifically, CSS was applied independently per sample with a smoothing parameter selected by GCV; PACE was applied with common grid [1 : 405]; and BABF was applied with the equally spaced working grid over [1 : 405] with size L = 30. Both PACE and BABF were applied separately for the functional data of obese and nonobese groups. Figure 2 (a, b) shows that CSS produces the roughest signal estimates, leading to the roughest mean-covariance estimates (Figures 2 (c, d); Web Figures 3 and 4). Both PACE and BABF produce smoothed signal estimates and mean-covariance estimates. The mean estimate by BABF has better periodic patterns than the one by PACE (Figures 5 (c, d)), and the BABF estimates of the correlations between two apart time points are less than the PACE estimates (Web Figure 4).

Figure 2.

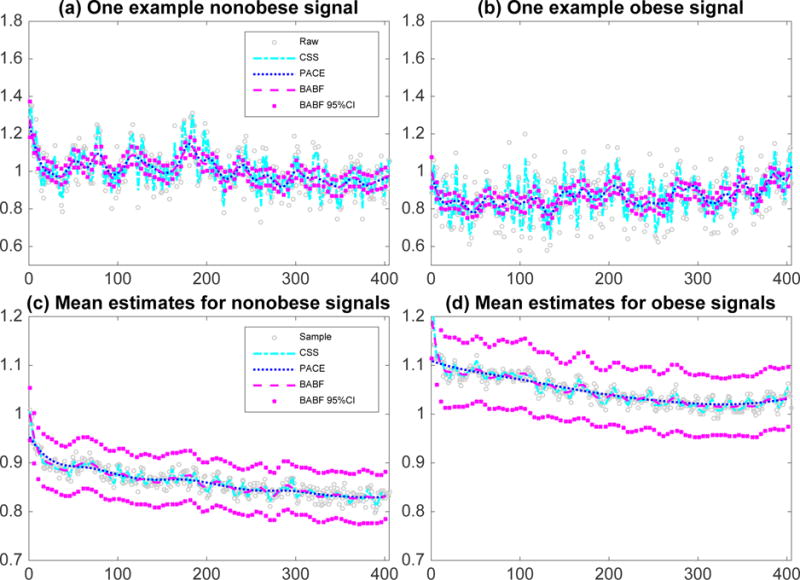
Example smoothed functional data in (a, b) and mean estimates in (c, d), along with 95% pointwise CIs by BABF, for the real SEE data.

Further, we applied the goodness-of-fit test (Yuan and Johnson, 2012) to the residuals from the BABF method (one test per functional sample). Although the residual means are consistently close to 0, the p-values for 52% functional curves are less than 0.05/n, suggesting evidences of lack-of-fit with Bonferroni correction (Bonferroni, 1936) for multiple testing. This is because the residual variances of this real data are no longer the same across all observations. To address the issue of lack-of-fit for this SEE data, we need to assume sample-specific residual variances in the Bayesian hierarchical model (1), which is beyond the scope of this paper but will be part of our future research.

Despite the lack-of-fit issue for this real data application by BABF, the smoothed data are still improved over the raw data and the smoothed data by alternative methods for follow-up analyses. Using the classification analysis as an example, we next illustrate the advantage of using the smoothed data by BABF for follow-up analyses. Considering the SEE data of obese and nonobese children as two classes, we used the leave-one-out cross-validation (LOOCV) approach to evaluate the classification results for using the raw data, and the smoothed data by CSS, PACE, and BABF. Basically, for each sample curve, we trained a SVM model (Cortes and Vapnik, 1995) using the other sample curves, and then predicted if the test sample was an obese case. The error rate (the proportion of misclassification out of 106 samples) is 48.11% for using the raw data, 40.57% for using the smoothed data by CSS, and 36.79% for using the smoothed data by PACE, and 33.02% for using the smoothed data by BABF. The smoothed data by our BABF method lead to the smallest error rate. Thus, we believe using the smoothed data by BABF will be useful for follow-up analyses.

5. Discussion

In this paper, we propose a computationally efficient Bayesian method (BABF) for smoothing and estimating mean-covariance functions of high-dimensional functional data, improving upon the previous BHM method by Yang et al. (2016). Our BABF method projects the original functional data onto the space of selected basis functions with reduced rank, and then conducts posterior inference through MCMC of the basis-function coefficients. As a result, BABF method not only retains the same advantages as BHM, such as simultaneously and nonparametrically smoothing and estimating mean-covariance functions, but also provides additional computational advantages of scalability, efficiency, and stability.

With n functional observations, a pooled observation grid of length p, and m MCMC iterations, BABF reduces the computational complexity from O(np³m) to O(nK³m), and the memory usage from O(p²m) to O(K²m), by MCMC in the basis-function space with reduced rank K ≪ p. For examples, using a 3.2 GHz Intel Core i5 processor, BABF only costs about 3 minutes for n = 30, K = 20, and m = 12, 000, and about 9 minutes for n = 44, K = 30, and m = 12, 000. Although BABF (with 12, 000 MCMC iterations) takes about 4× longer time than PACE, BABF provides complementary credible intervals to quantify the uncertainties of the posterior estimates, as well as basis function representations for the nonparametric estimates of functional signals and mean-covariance functions. Moreover, BABF produces more accurate results than PACE for functional data observed on random grids.

Both simulation and real studies demonstrate that BABF performs similarly to BHM and other Bayesian GP regression methods with functional data observed on low-dimensional common grids, and that BABF outperforms the alternative methods (e.g., CSS and PACE) with functional data observed on random grids or high-dimensional common grids. In addition, the real application shows that the classification analysis using the smoothed data by BABF produces the most accurate results.

For now, BABF assumes the same mean-covariance functions and residual variance for functional data, both of which are not true for most of the real data. Despite the model inadequacy, the smoothed data by BABF are still useful for follow-up analyses as shown in the real application of SEE data. To make the method more flexible for real data analysis, one might assume group-specific mean-covariance functions and sample-specific residual variances. This is beyond the scope of this paper and will be part of our future research.

In conclusion, BABF greatly improves computational scalability and decreases the memory usage required by the standard MCMC procedure used in BHM, while efficiently smoothing functional data and estimating mean-covariance functions in a nonparametric way. By implementing MCMC with the induced model of basis-function coefficients, BABF provides one solution for the computational bottleneck of general Bayesian GP regression methods, especially for analyzing high-dimensional functional data (e.g., spatial-temporal data) with Gaussian-Wishart processes. It is noteworthy to see that BABF coincides with the idea of using least squares with basis functions as linear regressors, as mentioned by Stein (2014), which provides an alternative approach from the scalable (dynamic) nearest neighbor GP models by constructing a sparsity-inducing prior for the covariance function (Datta, Banerjee, Finley, and Gelfand, 2016; Datta, Banerjee, Finley, Hamm, and Schaap, 2016).