Characterizing Residue-Bilayer Interactions Using Gramicidin A as a Scaffold and Tryptophan Substitutions as Probes

Abstract

Previous experiments have shown that the lifetime of a gramicidin A dimer channel (which forms from two non-conducting monomers) in a lipid bilayer is modulated by mutations of the tryptophan (Trp) residues at the bilayer-water interface. We explore this further using extensive molecular dynamics simulations of various gA dimer and monomer mutants at the Trp positions in phosphatidylcholine bilayers with different tail lengths. gA interactions with the surrounding bilayer are strongly modulated by mutating these Trp residues. There are three principal effects: eliminating residue hydrogen bonding ability (i.e., reducing the channel-monolayer coupling strength) reduces the extent of the bilayer deformation caused by the assembled dimeric channel; a residue’s size and geometry affects its orientation, leading to different hydrogen bonding partners; and increasing a residue’s hydrophobicity increases the depth of gA monomer insertion relative to the bilayer center, thereby increasing the lipid bending frustration.

Graphical Abstract

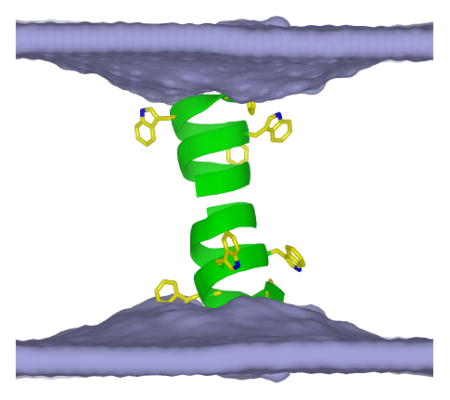
INTRODUCTION

Membrane proteins often have “aromatic belts,” rich in Trp and Tyr residues, at the bilayer-water interface (see Pogozheva et al.¹ for a review). These regions are important in determining protein folding,^2–4 interfacial anchoring,^5–9 and function.^10–15 Gramicidin A (gA) channels have been important tools in establishing these principles. Previous molecular dynamics (MD) studies on gA suggested that the bilayer deformation profiles at the two ends of a pore-forming, asymmetric monomer are quite different, i.e., the Trp-rich N-terminus deforms the adjacent lipids more than the hydrophobic C-terminus (Figure S1 from Kim et al.¹⁶). To explore the effects of gA residues at the bilayer-water interface on the adjacent lipids and channel itself, we performed extensive all-atom MD simulations of gA dimers and monomers where the four Trp residues per monomer have been substituted with other residues.

gA^Trp channels (i.e., wild-type gA; monomer sequence of of formyl-VGALAVVVW⁹LW¹¹LW¹³LW¹⁵-ethanolamide, where D-amino acids are underlined) form by transmembrane dimerization of two anti-parallel β-helical monomers (Figure 1A),⁵ which are anchored to the bilayer interface by the amphipathic Trp residues.^2,3,5 The monomer↔dimer equilibrium is described by:^3,11,17,18

Figure 1.

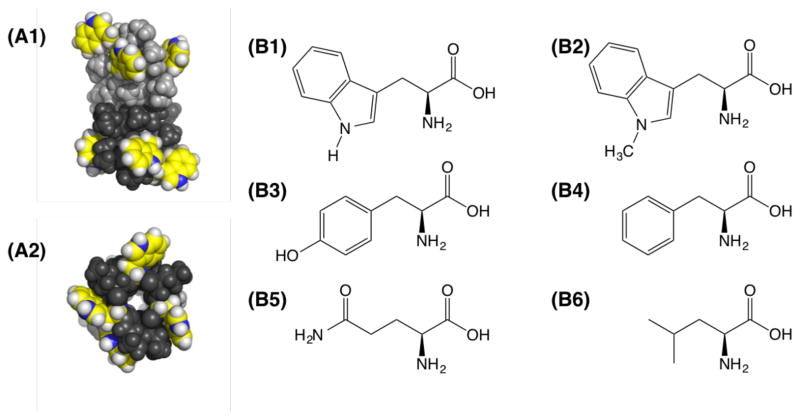
Positions of the Trp residues in gramicidin A channels and the side chain structures examined here. (A1) Side and (A2) top views of equilibrated gA^Trp (initial PDB: 1JNO).²² The Trp locations are shown in yellow with the indole nitrogen in blue. Experimental data are available for (B1) tryptophan, (B2) 1-methyltryptophan, (B3) tyrosine, and (B4) phenylalanine. The simulations in this article also use (B5) glutamine, (B6) leucine, and the alchemical 1-methyltryptophan without charges.

$$\frac{[\mathrm{D}]}{{[\mathrm{M}]}^2}=\frac{k_1}{k_{-1}}=exp\left\{-\frac{\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}+\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}}{k_{\mathrm{B}}T}\right\}$$ (1)

where M and D denote the non-conducting monomers and conducting dimers, k₁ and k₋₁ are the association and dissociation rate constants, respectively, k_B is Boltzmann’s constant, and T the temperature in Kelvin. $\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}$ encompasses the energy associated with inter-monomer hydrogen bonds formed by formyl-V¹GALA⁵ at the dimer interface. Although the transition state is not well characterized, we assume that $\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}$ is independent of the mutations studied here because N-terminal modifications have minimal effects on the energetics of subunit dimerization at the C-termini (where the monomers are linked).¹⁰ If $\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}$ is assumed to be constant for all mutants, differences in mean channel lifetime must be attributed to changes in $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$, the bilayer deformation energy associated with the formation of dimeric channels.

For uncorrelated events, such as channel monomerization/dimerization, that occur at an average rate, there is a distribution of channel lifetimes that can be described by a mean channel lifetime, τ (for a review, see Lundbæk et al.¹⁹). Table 1 summarizes published experimental mean channel lifetimes for gA channels where the four Trp residues of gA^Trp were mutated to: i) 1-methyltryptophan (gA^mTrp); ii) tyrosine (gA^Tyr); or iii) phenylalanine (gA^Phe); see Figure 1 for more information on these mutations. Appendix I provides a detailed theoretical treatment relating experimental mean channel lifetimes with the bilayer deformation energetics ( $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$) assuming that $\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}$ (gA monomer-monomer association energetics) is constant across all mutations. It is shown here that the variations in channel lifetime imply that residue-specific interactions at the bilayer-water interface alter $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$. It is also apparent that lipid type affects channel lifetime.^11,17,20 As within the rest of this manuscript, results should be compared between structurally related residues (e.g., Trp and mTrp; Tyr and Phe) because residue size/geometry affects the mean channel lifetime in nontrivial ways.²¹

Table 1.

Mean lifetimes (τ) of channels (in ms) formed by gA^Trp and analogues in dC_18:1 (1,2-di-oleoyl-phosphatidylcholine, DOPC), 4ME dC_16:0 (1,2-di-phytanoyl-phosphatidylcholine, DPhPC), dC_18:2 (1,2-di-linoleoyl-phosphatidylcholine, DLoPC).^†

Mutant	dC18:1#	4ME dC16:0 #	dC18:2&
Lipid
gATrp	600 ± 140	570 ± 57	3100 ± 150
gAmTrp	–	2200 ± 220	–
gATyr	110 ± 15	80 ± 8	520 ± 140
gAPhe	670 ± 100	330 ± 30	3400 ± 760

^†Experimental conditions: 1.0 M CsCl, ±200 mV, and 25 ± 1 °C.

^#From Table 2 of Girshman et al.¹⁷

^&From Table 2 of Fonseca et al.,¹¹ (gA^mTrp data from Table 3 of Sun et al.³)

MD simulations were performed on channels where experimental mean channel lifetimes are available (gA^Trp, gA^mTrp, gA^Tyr, gA^Phe), as well as: i) an alchemical 1-methyltryptophan without side-chain charges (gA^nc-mTrp); ii) glutamine (gA^Gln); and iii) leucine (gA^Leu). The set of gA^Trp, gA^mTrp, and gA^nc-mTrp were selected to study the roles of the indole hydrogen bond donor site (which is eliminated in mTrp) and the Trp/mTrp side chain dipole (which is nearly identical for mTrp and Trp,³ but absent in nc-mTrp). Similarly, the Tyr/Phe and Gln/Leu pairs are structurally related, but differ in their side chain dipoles and ability to form hydrogen bonds. The influence of Trp mutations is described in terms of i) the structure and dynamics of gA bilayer-spanning dimers (the root mean squared deviations (RMSD) and fluctuations (RMSF), gA tilt, hydrogen bonding and interaction patterns, and Trp and mutant residues’ side chain orientations); ii) bilayer hydrophobic thickness (and its decomposition) profiles as a function of radial distance from the channel; and iii) the relationships between lipid traces, the per area free energy of bending with respect to curvature, monomer z-positioning, and the channel-monolayer interfacial slope.

METHODS

System setup

All systems were built, minimized, and partially equilibrated using the Membrane Builder module^23,24 of CHARMM-GUI (www.charmm-gui.org).²⁵ The dimer gA^Trp structure (PDB:1JNO) was used for the gA^Trp simulations as well as the scaffold for Trp mutations.²² The topology and parameter information for gA^mTrp, not available in the standard CHARMM force field,^26–29 was obtained from the GAAMP gateway (http://gaamp.lcrc.anl.gov).³⁰ See Table 2 and Table S1 for system information.

Table 2.

Lipid type and channel combinations used in this study.^†

Mutant	dC18:1	dC20:1	dC22:1
Lipid
gATrp	Y	Y	Y
gAmTrp	Y	Y	Y
gAnc-mTrp	Y	Y	Y
gATyr	Y	–	Y
gAPhe	Y	–	Y
gAGln	Y	–	–
gALeu	Y	–	–

^†Phosphatidylcholine (PC) lipids were used and are denoted by their tail type, e.g., dC_18:1 (1,2-di-oleoyl-PC, DOPC), dC_20:1 (1,2-di-eicosenoyl-PC), and dC_22:1 (1,2-di-erucoyl-PC). “Y” denotes simulations were performed for this combination; “–” denotes that no simulations were performed.

The first set of simulations contained 90 dC_18:1 lipids per leaflet and 0.15 M KCl. Three independent replicas for each mutation were simulated for 220 ns using NAMD³¹ in the isothermal-isobaric (NPT) ensemble. Constant temperature was maintained at 303.15 K using Langevin dynamics with a collision frequency of 1 ps⁻¹. Constant pressure was maintained at 1 atm by a Nosé-Hoover Langevin piston^32,33 with a piston period of 50 fs and a piston decay of 25 fs. The CHARMM all-atom protein force field²⁶ including dCMAP^27,28 was used with the C36 lipid force field²⁹ and TIP3P water model³⁴. The SHAKE algorithm³⁵ was used with a 2-fs time step. Electrostatic interactions were calculated using the particle-mesh Ewald method³⁶ (mesh size ~1 Å, ϰ = 0.34 Å⁻¹, and sixth-order B-spline interpolation), and van der Waals interactions were switched off between 10–12 Å by a force-switching function.³⁷

The second set of simulations were performed with 90 dC_20:1 or dC_22:1 lipids per leaflet. The gA^Trp data were previously published,³⁸ and gA^mTrp, gA^nc-mTrp, gA^Tyr, and gA^Phe simulations were performed with the following conditions: i) harmonic RMSD restraints on the dimer and monomers, ii) xy positional restraints to keep monomers at maximum separation, iii) 1 fs time step, and iv) constant temperature of 310.15 K. The other simulation parameters are the same as in the above simulations with dC_18:1. Three replicas of monomer-containing and dimer-containing systems were run for 100–170 ns each.

Constructing lipid traces

To better understand the lipid conformational changes imposed by the channel, average lipid traces were calculated.³⁸ The trace is a radial property, which assuming cylindrical symmetry, describes the average position of lipid as function of distance (r) from the center of the channel. Briefly, a histogram in r (bin width of 0.06 Å) is formed based on the coordinates of the head group through sn-2 tail atoms of all lipids. For each radial bin, there is a density, ρ_i(r), and an average height, z_i, for each atom type i. A value r₀ is calculated for the first trace (i.e., lipids closest to the channel), such that:

$${\int }_0^{r_0}{\rho }_i(r)\mathrm{d}r=n,$$ (2)

where n is a user-defined, targeted number of atom type i (e.g., n = 3.5, which is same value used in Sodt et al.³⁸). The space between traces is based on n, so traces are spaced closer at large r compared to traces near the channel (i.e., the number of lipids per bin goes as 2π(r_b − r_b−1), where b is some arbitrary bin). Once r₀ is known, the weighted average radial position, 〈r_i〉, and weighted average height, 〈z_i〉, of atom type i between 0 and r₀ are known:

$$n^{-1}{\int }_0^{r_0}{\rho }_i(r)\{r,z_i(r)\}\mathrm{d}r=\{\langle r_i\rangle ,\langle z_i\rangle \}.$$ (3)

The first radial trace is constructed with these {〈r_i〉, 〈z_i〉} pairs by connecting them as they are chemically from the head group through the sn-2 lipid tail. For the next n lipids (i.e., the second trace), r₀ is used as a lower limit and Equation 2 defines the next upper limit. This process is repeated until enough traces have been constructed to provide a clear view of the lipid bending and tilt as a function of r. These traces should not be confused with radial lipid shells, which have been previously defined by Voronoi tessellations.²⁰ Although the spacing between traces (dependent on n) presented herein is arbitrary, the traces could be formed by shell. However, the radial extent of lipid shells is large enough to wash out some details associated with the finely binned traces.

Also note that traces do not reach z = 0 because each atom position in the trace is based on the average, and not the most likely position. Figure S2, produced from simulations of lipid-only dC_22:1 (data from Sodt et al.³⁸), demonstrates why the traces do not reach z = 0. Although the lipid terminal carbon atoms are mostly positioned around z = 0 Å, there are shoulders on the probability distributions (where the terminal carbon atoms approach the head groups due to tail entropy). These shoulders raise the weighted average position of the terminal carbon atoms to z ≈ 3.5 Å. This matches well with the z-position where the traces end when the lipids are in the effective bulk (e.g., see Figure 6; it is assumed that lipids at large r behave similarly to how they would in a lipid-only system).

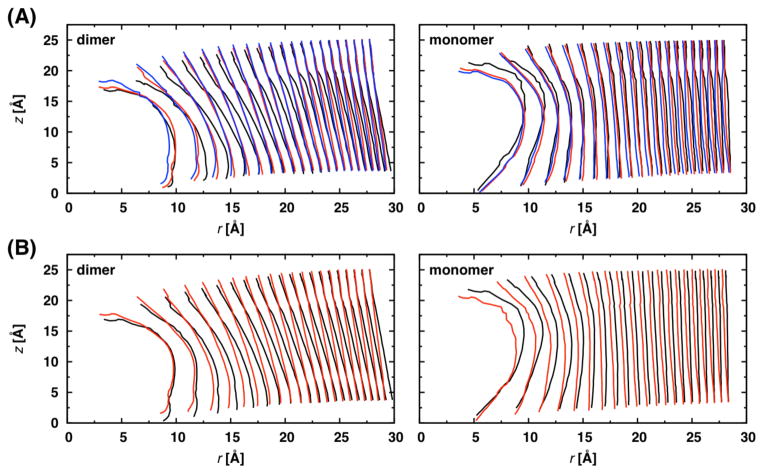
Figure 6.

dC_22:1 lipid traces around dimers and monomers: (A) gA^Trp (black), gA^mTrp (red), and gA^nc-mTrp (blue); (B) gA^Tyr (black) and gA^Phe (red). The x-axis is extended relative to the y-axis to make the differences between the traces clearer.

Lipid per-area free energy change with respect to curvature, F̄′(0)

Traces provide insight into the leaflet bending frustration, but the frustration can be quantified by the leaflet per-area free energy change with respect to curvature (at zero curvature), F̄′(0), which is calculated by:^38–42

$${\overline{F}}^{\prime }(0)={\frac{d\overline{F}}{d{R}^{-1}}|}_{R^{-1}=0}=-{\int }_0^{\infty }z[p_{\mathrm{L}}(z)-p_{\mathrm{N}}(z)]\mathrm{d}z,$$ (5)

where F̄ is the per-area Helfrich bending energy,⁴³ R⁻¹ is leaflet curvature at the pivotal plane, and the integrand describes the pressure within the leaflet (where p_L(z) and p_N(z) are the lateral and normal components of the pressure tensor, respectively). Because the leaflets are constrained to be planar by hydrophobic interactions and periodic boundary conditions, F̄′(0) is evaluated at R⁻¹ = 0. As defined, F̄′(0) = 0 means that there is no bending frustration, and the magnitude of F̄′(0) provides information about the bending frustration within a leaflet. By convention, a positive F̄′(0) indicates a leaflet would bend toward its head groups if it was unconstrained (i.e., a negative curvature).

In bilayers that are thicker than the dimeric channel, the bending frustration includes three contributions. First, the lipids considered in this study have negative intrinsic curvature, so forcing these lipids to be in a planar bilayer creates leaflet frustration. Second, inserting a gA monomer into a leaflet could alleviate or exacerbate the leaflet frustration (being a physical contribution to the leaflet frustration, F̄′_m(0)). Last, inserting a dimer introduces a physical contribution from the two monomers and a contribution from the dimerization event itself, F̄′_d(0). By simulating independent monomers (one per leaflet) and independent dimers (one per bilayer) at the same channel/lipid ratio, we can calculate leaflet F̄′_m(0) and F̄′_d(0), respectively. The difference between these values, ΔF̄′(0) = F̄′_d(0) − F̄′_m(0), is the leaflet bending frustration due to dimerization. ΔF̄′(0) can be used to understand differences in mean channel lifetime (i.e., the more bending frustration as a result of dimerization, the shorter the lifetime).

RESULTS AND DISCUSSION

In this section, gA^Trp and mutant channels are first considered in dC_18:1 lipid bilayers (Table 2). The results in the following subsection demonstrate channel stability on our simulation timescale and describe residue orientation (χ₁-χ₂ distributions) as a function of size and geometry. The remaining subsections provide insight into the bilayer compression and bending contributions to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ and how these results relate to experimental mean channel lifetimes. Bilayer hydrophobic thickness profiles are presented and decomposed to describe how bilayer deformations primarily depend on a residue’s ability to form hydrogen bonds to adjacent lipids and secondarily on the residue’s hydrophobicity. These hydrophobic thickness profiles provide information on the compression contribution to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$. Finally, using simulations of a subset of channel mutants in dC_20:1 and dC_22:1 bilayers, lipid traces and the per area free energy of bending with respect to curvature are discussed and related to the channel-monolayer interfacial slope.

gA channel dynamics are affected by mutation

Before considering the channel-induced bilayer deformations, we describe the mutant channel characteristics. In dC_18:1 bilayers, all channels were stable for the duration of the simulations, as evident from the per-residue root-mean-square fluctuations (RMSF: Figure S3) and root-mean-square deviations (RMSD) with respect to the minimized initial structure (Figure S4). As expected (e.g., Ingólfsson et al.²⁷), there are variations in the RMSF at the N-termini of all channels (particularly in gA^Gln and gA^Leu) as well as some transient structural variations (evident from the increases in RMSD) in the mutants. Channel tilt is also affected by the mutations (see Figure S5 and Table S2 for the tilt distributions and average tilt angles, respectively). Channels with residues that can form hydrogen bonds with the bilayer have smaller tilt angles than their counterpart residues that cannot form hydrogen bonds, implying that these interactions are important for positioning/anchoring of the channels in the bilayer. Comparing gA^mTrp and gA^nc-mTrp further suggests that the side chain dipole helps orient/stabilize the channel.

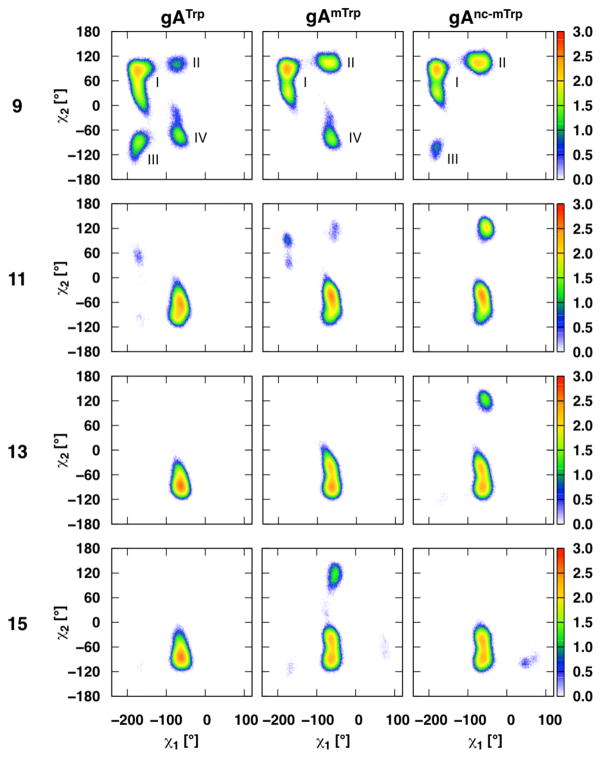
Although channel tilt is affected by the mutations, related residues (Trp, mTrp, and nc-mTrp; Tyr and Phe; Gln and Leu) have nearly identical major χ₁-χ₂ populations (some minor populations differ among related residues). For example, although Trp, mTrp, and nc-mTrp have different hydrophobicity and ability to form hydrogen bonds, their χ₁-χ₂ population distributions are nearly identical (Figure 2, in agreement with Sun et al.³). Tyr and Phe also have very similar χ₁–χ₂ distributions, as do Gln and Leu (Figure S6 and S7, respectively). These distributions suggest that residue size and geometry affect preferred rotamer states more than hydrophobicity or hydrogen bond formation. These preferred states determine how the residue will interact with its environment, thereby partially determining the residue’s hydrogen bonding partners.

Figure 2.

Trp, mTrp, and nc-mTrp χ₁-χ₂ dihedral angles in dC_18:1. χ₁ is the dihedral of the backbone N, Cα, Cβ, and Cγ atoms. χ₂ is the dihedral of the Cα, Cβ, Cγ, and Cδ atoms (Cδ is double bonded to Cγ and bonded to indole N). The color scheme for the heat plots is shown on the right with log{count/bin} and 1° bin widths in both dimensions.

dC_18:1 lipid slippage is affected by channel mutation

Previous MD simulations have shown that lipids tend to slip over the top of the channel, which releases some of the bilayer’s frustration caused by hydrophobic adaptation to the channel.^{16,20,38,44,45} The number of lipids that slip over the top of the channel is linked to the strength of the interactions between the channel and the adjacent lipids. This channel-bilayer coupling was explored using two complementary methods: radial distribution functions (Figure S8) and lipid contacts with the channel (Figure S9).

The radial distribution functions show that lipid acyl chains remain outside of r ≈ 8–10 Å (the approximate channel radius). Channels with residues capable of forming hydrogen bonds (Trp, Tyr, Gln) have low choline densities near r = 0 Å. Residues that cannot form hydrogen bonds (mTrp, nc-mTrp, Phe, and Leu) have higher densities near r = 0 Å, demonstrating that the extent of lipid slippage depends on polar interactions between the channel and the adjacent lipids (Table S3). Next, we quantified the lipid components (acyl chain, carbonyl, phosphate, or choline) and water that were within 4 Å of any channel side chain heavy atom (Figure S9). All residues that can form hydrogen bonds (Trp, Tyr, and Gln) have more contact with the carbonyl and phosphate groups, as well as the choline (because the lipids are more restricted in z due to hydrogen bonding), as compared to residues that cannot form hydrogen bonds. Residues that cannot form hydrogen bonds have higher contact incidence with the lipid tails because of lipid slippage (causing these more hydrophobic residues to be buried in lipid tails).

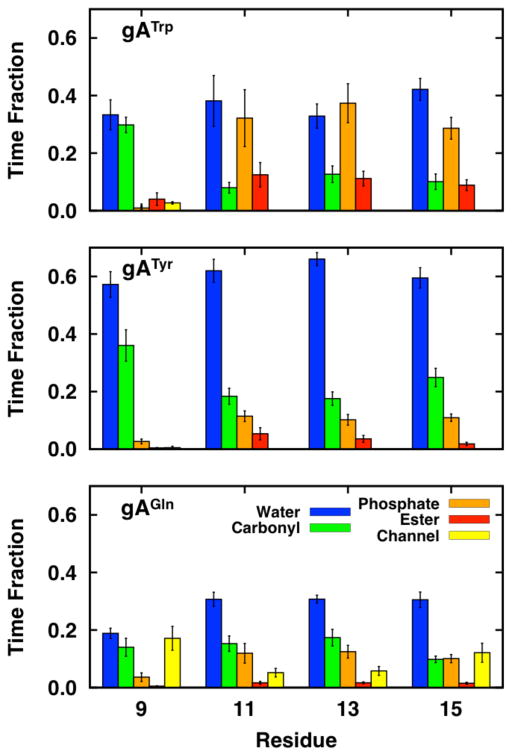
The observation that different residues prefer to be close to different lipid chemical features is corroborated by the frequency of hydrogen bond formation for gA^Trp, gA^Tyr, and gA^Gln channels in dC_18:1 (Figure 3). The average fraction of time that a given residue formed hydrogen bonds was decomposed into the contributions from the lipid carbonyl, lipid phosphate, water, and channel backbone. Trp interacts preferentially with lipid and Tyr with water. Gln stands out by its interactions with the channel backbone, as all Gln residues form occasional hydrogen bonds to backbone oxygen of adjacent residues (its flexibility is also reflected in its preferred rotamer plots; Figure S7). The Gln9 and Gln15 side chains furthermore form two relatively strong reciprocal hydrogen bonds with each other (N–H···O=C and vice versa). These hydrogen bond frequency distributions demonstrate that residues do indeed prefer different chemical features in the environment. Intuitively, these interactions influence the channel and surrounding bilayer conformations.

Figure 3.

Fraction of time that gA^Trp, gA^Tyr, and gA^Gln form hydrogen bonds to dC_18:1. A hydrogen bond is defined as a donor and acceptor pair within 2.4 Å of each other (with no angular cutoff). The fractions do not sum to unity because the residues do not form hydrogen bonds at all times.

Adjacent lipid compression is a function of interfacial residues

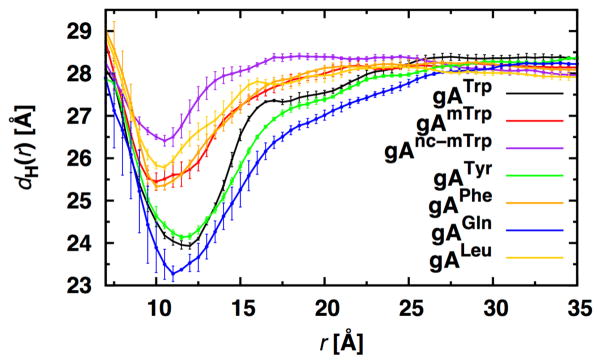
Radial bilayer hydrophobic thickness profiles, d_H(r), determined from the average z locations of the C22 and C32 lipid tail carbon atoms (i.e., the carbon atoms bonded to the lipid carbonyl group), provide insight into the bilayer deformation (i.e., the compression contribution to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$) caused by the channel. The profiles for gA^Trp, gA^Tyr, and gA^Gln are similar to each other and distinct from the profiles around channels that cannot form hydrogen bonds with lipids, demonstrating that lipids are constrained to match residues that can form hydrogen bonds, as compared to residues that cannot form hydrogen bonds. This is evident by deeper minima at the edge of the channel (r ≈ 10–12 Å) for gA^Trp, gA^Tyr, and gA^Gln compared to gA^mTrp, gA^nc-mTrp, gA^Phe, and gA^Leu (i.e., the steep increase in d_H(r) at r < 10 Å arises because lipids slip over the top of the channel; Figure 4).

Figure 4.

Radial hydrophobic thickness profiles of dC_18:1 bilayers with different embedded gA analogues.

The difference in the depths of minima for related residues (Trp, mTrp, and nc-mTrp; Tyr and Phe; Gln and Leu) reflects the different leaflet frustration due to these residues. As discussed previously,^20,38 the main energetic contribution of the deformation energy adjacent to the channel is lipid compression (curvature frustration to be discussed later in this article). Hydrogen bond formation appears to be the major factor in determining channel-lipid coupling (e.g., compare the Trp and mTrp profiles and minima), but hydrophobicity also plays a role in the deformation (e.g., compare mTrp and nc-mTrp profiles and minima). Trp causes a larger deformation compared to mTrp, and correspondingly the gA^Trp channel’s mean channel lifetime is substantially shorter than the gA^mTrp channels. The same is true for gA^Tyr and gA^Phe, where gA^Tyr channels produce a larger deformation and have a comparatively shorter lifetime than gA^Phe channels.

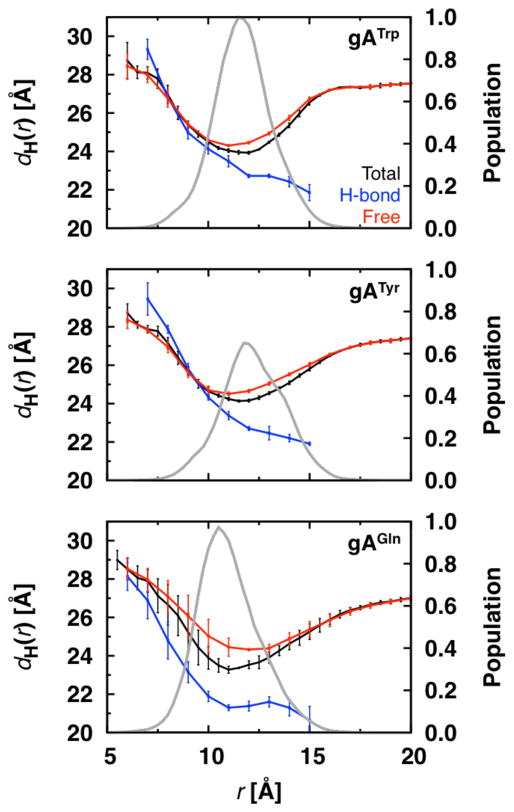
Because the ability to form hydrogen bonds appears to be the key factor in deforming the bilayer adjacent to the channel, we decomposed d_H(r) into contributions from lipids whether they form hydrogen bonds with Trp, Tyr, or Gln. A lipid forming hydrogen bonds with a target residue is placed in the appropriate radial bin for the “H-bond” group; otherwise, it is placed in the “Free” group (Figure 5).

Figure 5.

Decomposition of the radial hydrophobic thickness profiles for gA^Trp, gA^Tyr, and gA^Gln channels in dC_18:1. The total hydrophobic thickness profiles from Figure 4 are decomposed into profiles from lipids that form hydrogen bonds to the channel (H-bond) and lipids that do not form hydrogen bonds with the channel (Free). Grey lines show the radial distributions of lipids that form hydrogen bonds to the channel (plots are normalized to the peak of the gA^Trp distribution).

The profiles for the H-bond lipids (blue curves) are similar in that d(r) ≈ 23 Å at r ≈ 10–12 Å, close to the canonical hydrophobic length of gA^Trp channels^46–48. Because the channel and lipids are able to tilt, channel-lipid hydrogen bonds can be formed at large radial distances, as shown in the frequency distribution for hydrogen bond formation (in grey). If the channel or lipids do tilt to form hydrogen bonds, the bilayers appear to be thinner, which is the case at larger r (blue curves). The “Free” lipids have a biphasic thickness profile, with a minimum at the edge of the channel, which most likely due to the hydrophobic matching requirement (to the channel, to the H-bond lipids, or to both).

With access to atomistic details, the differences in the hydrophobic thickness profile minima can be attributed to hydrogen bonding between gA channels and surrounding bilayers. As shown explicitly in Appendix I, effective channel hydrophobic lengths can be used to explain differences in mean channel lifetimes. That is, an effectively “longer” channel would have a longer lifetime in thick bilayers. Ideally, the differences in hydrophobic thickness minima near the channel could be directly related to the channel’s effective hydrophobic length, and therefore, the channel lifetime. Based on the lifetimes of gA^Tyr and gA^Phe in dC^18:1 (Table 1), one would predict ~3 Å difference in effective channel length. Figure 4, however, shows a smaller difference in apparent hydrophobic length between gA^Tyr and gA^Phe (~1.25 Å), suggesting energetic contributions other than simple compression may be involved. One such contribution could be the bilayer curvature frustration (i.e., the second major contributor to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ along with compression frustration).

dC_20:1 and dC_22:1 bilayers are affected by channel mutation

To gain energetic insight into the curvature frustration due to hydrophobic mismatch and interfacial residue influence, we calculated the per area free energy change with respect to curvature, F̄′(0) (see Methods for more details). To increase the signal-to-noise ratio associated with these calculations, the simulations for F̄′ 0 calculations were carried out in dC_20:1 and dC_22:1. As noted in the Methods, an RMSD restraint was placed on all channel backbones to eliminate structural changes that are possible at large channel-bilayer hydrophobic mismatch,^2,17,49 but the RMSD restraint applied in this study has little effect on the Trp χ₁-χ₂ dynamics (Figure S10).

Lipid traces were calculated for both gA dimers and monomers (see Methods), and the results in dC_22:1 are shown in Figure 6; the traces were similar in dC_20:1 (results not shown). All traces near the dimers have a similar shape, but there appears to be some lipid tilt at large r (i.e., the traces around the gA^Trp dimers are tilted relative to those around the gA^mTrp dimers). There are also changes in the traces adjacent to the monomers, but these differences are not propagated as far in r. Some lipid tails curl underneath the monomers to form basket-like assemblies as has been reported for other interfacial peptides.⁴¹

While the lipid traces provide a useful representation of lipid distortion caused by the peptide, more quantitative information regarding the curvature frustration is obtained by calculating F̄′(0) (Table 3). In particular, ΔF̄′(0) describes the leaflet curvature frustration due to the dimerization event, and is therefore directly related to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$. Table 3 lists F̄′_m(0), F̄′_d(0), and ΔF̄′(0) for gA^Trp, gA^mTrp and gA^nc-mTrp in dC_20:1 and dC_22:1; estimates for gA^Trp are from previous work,³⁸ and results for gA^Tyr and gA^Phe in dC_22:1 are included.

Table 3.

Leaflet curvature frustration F̄′(0) (in kcal/mol/Å) for gA^Trp, gA^mTrp, gA^nc-mTrp, gA^Tyr, and gA^Phe monomers and dimers in dC_20:1 and dC_22:1.^†

		gATrp	gAmTrp	gAnc-mTrp	gATyr	gAPhe
dC20:1	F̄′m(0)	0.0786 ± 0.0037	0.0838 ± 0.0018	0.0865 ± 0.0025	–	–
	F̄′d(0)	0.0927 ± 0.0031	0.0919 ± 0.0017	0.0927 ± 0.0018	–	–
	ΔF̄′(0)	0.0141 ± 0.0048	0.0081 ± 0.0024	0.0062 ± 0.0031	–	–
dC22:1	F̄′m(0)	0.0685 ± 0.0017	0.0765 ± 0.0025	0.0830 ± 0.0026	0.0622 ± 0.0024	0.0716 ± 0.0024
	F̄′d(0)	0.1169 ± 0.0046	0.1104 ± 0.0021	0.1099 ± 0.0020	0.1081 ± 0.0023	0.1035 ± 0.0025
	ΔF̄′(0)	0.0484 ± 0.0049	0.0340 ± 0.0032	0.0269 ± 0.0033	0.0459 ± 0.0033	0.0319 ± 0.0035

^†The F̄′(0) are 0.0578 ± 0.0046 kcal/mol/Å and 0.0558 ± 0.0030 kcal/mol/Å for pure dC_20:1 and pure dC_22:1, respectively.³⁸

ΔF̄′(0) varies for structurally related residues as: gA^Trp > gA^mTrp > gA^nc-mTrp and gA^Tyr > gA^Phe in dC_22:1 (and gA^Trp > gA^mTrp ≈ gA^nc-mTrp in dC_20:1). As expected, ΔF̄′(0) is larger in dC_22:1 than in dC_20:1 for all channels due to hydrophobic matching considerations.³⁸ In either membrane environment, removing an interfacial residue’s ability to form hydrogen bonds reduces the leaflet curvature frustration. In dC_22:1, the curvature frustration gA^Trp > gA^mTrp > gA^nc-mTrp indicates that hydrogen bond formation and hydrophobic interactions are important. Within a residue family (Trp, mTrp, and nc-mTrp; Tyr and Phe), we observe that monolayer curvature frustration is linked to channel lifetime. It is energetically more costly for gA^Trp channels to remain dimers than gA^mTrp dimers; the same is true for gA^Tyr and gA^Phe channels, which agrees with the experimental mean channel lifetimes (Table 1).

A few possibly interfering effects are represented by F̄′(0). These effects are: the change in real surface curvature by dimerization indicated by the contact slope; the introduction of lipid-channel interactions that contribute to lateral stress; and the “wedge effect” where space is created to relieve the entropic strain of lipid tails, also altering the lateral stress. The wedge effect and contact slope are discussed herein, relating how system properties correlate to the expected change in F̄′(0). However, we recognize the possibility that mutations themselves affect the value of F̄′(0) by influencing the lateral stress profile. Since the effect is present in both monomer and dimer values, this is approximately canceled when taking the difference between the two, ΔF̄′(0). Nevertheless, these considerations complicate assigning the change in frustration completely to a particular mechanism. Therefore, when we interpret the monomer values directly in the “wedge effect” section below, there are unknown contributions to the lateral forces due to the mutations.

The “wedge effect” on ΔF̄′(0)

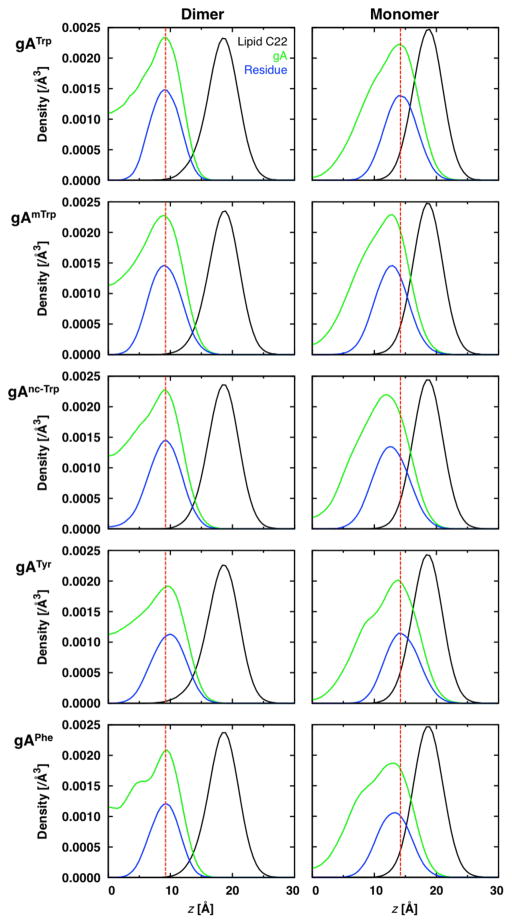
The wedge effect is expected to impact ΔF̄′(0) through the monomer F̄′(0) value because for monomers lipids can extend their tails under the sub-unit so that it acts as a wedge. It has previously shown that the location of rod-like amphipathic peptides along the z-axis influences F̄′(0),^40,41,50,51 and this study extends the treatment to gA monomers. To study this, we constructed symmetrized z-density plots to correlate gA’s preferred positioning in the bilayer with F̄′(0) (Figure 7 for dC_22:1 and Figure S11 for dC_20:1). Here, a gA monomer can be thought of as a wedge, whose position relative to the lipid pivotal plane (approximately the lipid C22 atom) affects the preferred bending of the lipid leaflet (see Figure 8). The monomers studied here have high density below the pivotal plane, and thereby induce negative curvature frustration (i.e., a more positive F̄′_m(0) compared to the lipid-only value); the insertion depth correlates to the value of F̄′_m(0). For example, gA^Trp monomers frustrate the leaflets less than gA^mTrp monomers (Table 3 and Figures 7 & 8).

Figure 7.

Heavy-atom z-density plots for the lipid C22 atom (black), entire channel (green), and the channel’s interfacial residues (blue) in dC_22:1. Dotted red lines are shown to accentuate the entire channel peak shifts relative to gA^Trp. Data is plotted in 0.5 Å bins. Systems were centered by shifting the bilayer’s center of mass to z = 0 Å.

Figure 8.

Illustration of (A) gA^Trp and (B) gA^mTrp monomers in a leaflet in which there is a large channel-bilayer hydrophobic mismatch (e.g., dC_22:1). The monolayer pivotal plane is represented by the black dotted line, the approximate average interfacial residue z-position is the red dotted line, the bilayer center (i.e., z = 0) is the solid line, and the lipid head groups are circles. gA^Trp resides closer to the lipid head groups and has more density above the pivotal plane, whereas gA^mTrp has more density below the plane. When there is more gA density below the pivotal plane, the lipids will more strongly prefer to bend toward the head groups. The extent of the bending will be constrained by the opposing leaflet because the two leaflets are coupled by hydrophobic constraints, but a curvature frustration will be produced. The magnitude of frustration will depend on the position of the monomer in its leaflet. Note that this, too, is an approximation because if the intrinsic curvature in the upper leaflet were sufficiently high it would also affect the lower leaflet; also see Phillips et al.⁵²

The monomer z-positions vary with side chain preference for the interface relative to the bilayer core, which can be evaluated using a suitable free energy scale.⁵³ For example, Tyr prefers the interface over the bilayer core,⁵⁴ as evident by the large amount of hydrogen bonding to water (Figure 3). Trp similarly prefers to be at the interface, whereas mTrp and nc-mTrp prefer to be deeper in the core. Therefore, gA^mTrp, gA^nc-mTrp, and gA^Phe monomers are shifted closer to z = 0, as compared to gA^Trp and gA^Tyr monomers. Hydrophobicity affects monomer position in the bilayer, which affects the leaflet bending frustration.

Contact slope effect on ΔF̄′(0)

As shown previously, the slope at the gA^Trp-lipid interface is correlated with the bending frustration of the lipid monolayer.³⁸ In this section, the interfacial slope is tied to the coupling between a channel and the surrounding lipids. We assume that the residues at the bilayer-water interface determine the channel-monolayer coupling. Changes in coupling strength affect the lipid monolayer contact slope, which can be observed directly from simulation, or through a surface model, inferred from F̄′(0).

As a validation of this assumption, consider the curvature frustration of the Helfrich Hamiltonian (F̄′(0)) due to a monolayer meeting a cylindrically symmetric inclusion with slope h′(r₀):

$${\overline{F}}^{\prime }{(0)}_{2\mathrm{D}}=k_{\mathrm{c},\mathrm{m}}{A}^{-1}\left(2\pi r_0{h}^{\prime }(r_0)\right)$$ (4)

where 2D indicates this is the curvature-only two-dimensional surface model (see Sodt et al.³⁸ and Ring⁵⁵ for more information and the derivation of the connection between slope and total curvature). The monolayer bending modulus is k_c,m, A is the modeled area, and r₀ is the radius of the channel.

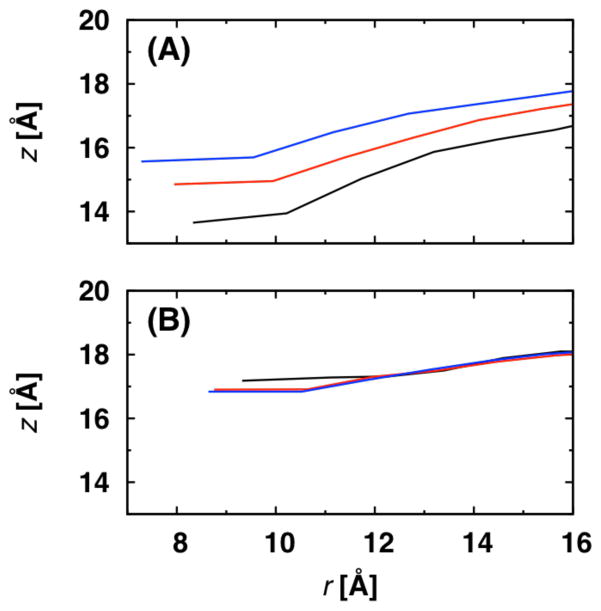
As shown in Sodt et al.,³⁸ an estimate for h′(r₀) can be obtained from the C22 lipid atom (the first carbon below the carbonyl of the sn-2 chain) locations in the lipid traces, which eliminates the artifact in h′(r₀) from lipids slipping over the top of gA.⁵⁶ Lipid C22 atom positions are shown in Figure 9, which is developed from the traces in Figure 6A. For this discussion, h′(r₀) is defined as the change in lipid thickness as a function of radius, and is calculated from the beginning of the trace (r ≈ 8 Å) to r ≈ 15 Å, which is considered to be the radial extent of the first lipid shell.

Figure 9.

The C22 atom surface constructed from the dC_22:1 lipid traces in Figure 6A around gA^Trp (black), gA^mTrp (red), and gA^nc-mTrp (blue): (A) dimers and (B) monomers.

The value of h′(r₀) near the channel appears to relax slowly, particularly for gA^nc-mTrp, presumably due to the complex environment of the channel-monolayer interface. Vales of h′(r₀) are 0.39 ± 0.03 (gA^Trp), 0.32 ± 0.01 (gA^mTrp), and 0.23 ± 0.05 (gA^nc-mTrp). The h′(r₀) near the monomer are much closer to zero, which further validates the assumption that gA monomers do not strongly deform their monolayer, which is necessary for the theory discussed in this study.

Using Equation 4, F̄′(0)_2D was calculated and compared to ΔF̄′(0) from Table 3 (comparison shown in Table 4). These values are comparable because the method of calculating ΔF̄′(0) from the all-atom simulations cancels out extraneous interactions between gA and the bilayer that might affect curvature stress. With this consideration, they both theoretically are models of the deformation energy due to dimerization. The value of k_c,m is defined as a linear interpolation between bilayer (k_c,b = 2k_c,m) values for dC_18:1 (k_c,b = 17.0 kcal/mol) and dC_24:1 (k_c,b = 31.7 kcal/mol) taken from Venable et al.⁵⁷ This results in k_c,m ≈ 13.5 kcal/mol for dC_22:1. The value of r₀ is empirically defined to be 10 Å.

Table 4.

Comparison between F̄′(0)_2D calculated from simulation values of h′(r₀) and ΔF̄′(0) from simulation.

	F̄′(0)2D	ΔF̄′(0)
gAnc-mTrp	0.030 ± 0.007	0.0269 ± 0.0033
gAmTrp	0.042 ± 0.002	0.0340 ± 0.0032
gATrp	0.052 ± 0.005	0.0484 ± 0.0049

Plotting F̄′(0)_2D against ΔF̄′(0) provides a slope of 1.14 ± 0.52. That is, there is good correlation between the two theories. Although there is high statistical uncertainty in obtaining F̄′(0)_2D and ΔF̄′(0), the statistics allow some statements to be made. First, it reiterates that mutations of residues at the bilayer-water interface have profound effects on lipid bending energetics (i.e., these interfacial residues play a role in curvature generation). Moreover, it puts the effect into quantitative terms that models of complex bilayers, employing the Helfrich Hamiltonian, can use to model how the membrane affects channel function. In other words, if the coupling strength increases, h′(r₀) increases and thus the lipid bending frustration in a particular functional state (here, the dimer) increases. Therefore, the value of F̄′(0) not only describes the lipid bending frustration, but it also gives insight into the deformation itself and how it couples to the state of the inclusion.

CONCLUSIONS

This manuscript describes the effects of mutating the Trp residues of gA dimers and monomers in chemically similar lipid types (dC_18:1, dC_20:1, and dC_22:1) and relates these results to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$, the energy associated with deforming the bilayer when dimeric gramicidin channels form, which in turn is related to experimental mean channel lifetimes. Before describing the bilayer energetics, we first demonstrated that the dimer backbone structure (RMSD) and dynamics (RMSF) are mostly unchanged by mutation in dC_18:1 bilayers on a typical MD timescale (~200 ns). Additionally, on a dimer, a residue at a particular location (9, 11, 13, 15) has its orientation determined by its size and geometry, as evidenced in χ₁-χ₂ plots.

While a residue’s size/geometry determines its orientation in the bilayer, a residue’s ability to form hydrogen bonds has direct correlation to the bilayer deformation caused by the channel. Trp, Tyr, and Gln perturb dC_18:1 bilayers similarly, while mTrp, Phe, and Leu perturb the bilayer less than their counterparts that can form hydrogen bonds with lipids. Hydrophobicity impacts bilayer deformations as well, but does not seem to have as large of effects as the ability to hydrogen bonds. The hydrophobic nc-mTrp, for example, perturbs the bilayer less than mTrp (Figure 4), but the difference between the radial thickness profiles for nc-mTrp and mTrp is less than the difference between mTrp and Trp. Indeed, decomposition of the radial thickness profiles (Figure 5) demonstrates that residue-lipid hydrogen bonds play a key role in the overall deformation. Because a channel’s lifetime is determined by the transition energy for channel dissociation, which is related to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$, we attribute residue-lipid hydrogen bond formation to the differences between gA^Trp/gA^mTrp and gA^Tyr/gA^Phe lifetimes.

Overall, there was a distinct trend in the leaflet curvature frustration due to dimerization, ΔF̄′(0). gA analogues with residues that can form hydrogen bonds produced more bilayer leaflet frustration more than those that cannot; residue hydrophobicity also is important for determining curvature frustration (gA^mTrp compared with gA^nc-mTrp). As was the case with compression contributions, curvature frustration also contributes to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$. Indeed, within a residue family (Trp and mTrp; Tyr and Phe), the ΔF̄′(0) correlate well with experimental channel lifetimes. The value of ΔF̄′(0) is innately tied to the interfacial monolayer slope at the channel-monolayer interface, with the slope itself dependent on the channel-monolayer coupling strength.

Although F̄′_d(0) was similar, within error, for all mutant dimers, F̄′_m(0) differs among the mutant monomers due to lipid conformational differences near the channel (including basket-formations), which can be understood by considering residue hydrophobicity. gA monomers with hydrophobic residues (nc-mTrp > Phe ≈ mTrp) embed deeper in their leaflet compared to Trp and Tyr. The more monomer density there was below the lipid pivotal plane, the more curvature frustration was induced (supported by z-density plots; Figures 7 & 8).

The results here were obtained on a simple channel, but the overall effects of mutations at the bilayer-water interface should apply generally to other membrane proteins. A mutation involving a change in residue size/geometry, ability to form hydrogen bonds with lipids, and/or hydrophobicity could change the protein’s orientation, adjacent bilayer deformation, and/or preferred positioning relative to the bilayer core.

APPENDIX I

Experimental Discussion

The bilayer free energy change due to a channel-caused deformation can be approximated as:^20,58

$$\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}(u_0)=H{(d_0-l)}^2=H{(2u_0)}^2$$ (A1)

where u₀ is the bilayer deformation equal to the difference in thickness between the unperturbed (d₀) lipid bulk and effective channel length (l). H is the phenomenological spring coefficient that describes the bilayer “stiffness.”

Though $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ denotes the free energy of the gramicidin monomer↔dimer equilibrium, we focus here only on the channel lifetimes, not the rates of appearance because side chain mutations that remove the ability of Trp and Tyr to form hydrogen bonds also promote other, non-channel conformers,^2,3 which complicates any analysis of the rates of appearance. Therefore, we focus on the sequence-dependent contributions to $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ to describe differences in mean channel lifetimes.

Working from transition state theory, the dissociation rate (and therefore, the channel lifetime, τ) is related to the transition free energy ΔG^‡ (specifically, the activation energy due to a dimer reaching the dissociation transition state):

$$k_{-1}=\frac{1}{\tau }=\frac{1}{{\tau }_0}{e}^{-\frac{\mathrm{\Delta }{G}^{‡}}{k_{\mathrm{B}}T}}$$ (A2)

where 1/τ₀ the frequency factor for the reaction. ΔG^‡ contains contributions from $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ and $\mathrm{\Delta }{G}_{\text{protein}}^{\mathrm{M}\to \mathrm{D}}$, which is discussed in the Introduction. Lundbæk et al.⁵⁹ provide an analysis of the relation between changes in $\mathrm{\Delta }{G}_{\text{bilayer}}^{\mathrm{M}\to \mathrm{D}}$ and changes in ΔG^‡.

When the channel reaches the transition state during dissociation, the inter-monomer separation has increased by δ (generally accepted to be ~1.6 Å), which is associated with the initial steps of breaking the inter-monomer hydrogen bonds:

$$\mathrm{\Delta }{G}^{‡}\propto \mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bilayer}}^0=H({(2u_0-\delta )}^2-{(2u_0)}^2)=H(4u_0-\delta )\delta$$ (A3)

where $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bilayer}}^0$ describes the bilayer energy difference when the channel is fully associated and when it is at δ separation. Combining Equations A2 and A3, and taking the derivative with respect to u₀:⁵⁸

$$\frac{\mathrm{d}\left(ln(k_{-1})\right)}{\mathrm{d}{u}_0}=\frac{\mathrm{d}\left(-ln(\tau )\right)}{\mathrm{d}{u}_0}=\frac{4H\delta }{RT}$$ (A4)

Equation A4 relates the channel lifetime to the bilayer deformation, bilayer stiffness and inter-monomer separation at the transition state. From Equation A4 we can equate the effective channel lengths of two channel types to their mean lifetimes:

$$\frac{-[ln({\tau }_2)-ln({\tau }_1)]}{\frac{1}{2}[(d_0-l_2)-(d_0-l_1)]}=\frac{4H\delta }{RT}$$ (A5)

which can be rearranged to:

$$l_2-l_1=\frac{RT}{2H\delta }[ln({\tau }_2)-ln({\tau }_1)]$$ (A6)

Equation A6 states how the difference between the effectives lengths of two channels is related to the difference in lifetimes of the two channels. Therefore, using the previously published lifetimes in Table 1, the difference in effective channel lengths can be estimated. In dC_18:1:

$$l_{\text{Phe}}-l_{\text{Tyr}}=\frac{RT}{2H\delta }[ln(0.670)-ln(0.110)]\approx 3Å$$ (A7)

where Hδ is defined to be 784 J/(mol·Å).²⁰ That is, gA^Phe has a longer effective hydrophobic length than gA^Tyr.