Skip to main content
PMC home page
Molecular Pharmacology logoLink to Molecular Pharmacology
. 2017 Nov;92(5):556–563. doi: 10.1124/mol.117.109595

The Actions of Drug Combinations on the GABAA Receptor Manifest as Curvilinear Isoboles of Additivity

Daniel J Shin 1, Allison L Germann 1, Joe Henry Steinbach 1, Gustav Akk 1,✉
PMCID: PMC5635521  PMID: 28790148

Abstract

Drug interactions are often analyzed in terms of isobolograms. In the isobologram, the line connecting the axial points corresponding to the concentrations of two different drugs that produce an effect of the same magnitude is termed an isobole of additivity. Although the isobole of additivity can be a straight line in some special cases, previous work has proposed that it is curvilinear when the two drugs differ in their maximal effects or Hill slopes. Modulators of transmitter-gated ion channels have a wide range of maximal effects as well as Hill slopes, suggesting that the isoboles for drug actions on ion channel function are not linear. In this study, we have conducted an analysis of direct activation and potentiation of the human α1β2γ2L GABAA receptor to demonstrate that: 1) curvilinear isoboles of additivity are predicted by a concerted transition model where the binding of each GABAergic drug additively and independently reduces the free energy of the open receptor compared with the closed receptor; and 2) experimental data for receptor activation using the agonist pair of GABA and propofol or potentiation of responses to a low concentration of GABA by the drug pair of alfaxalone and propofol agree very well with predictions. The approach assuming independent energetic contributions from GABAergic drugs enables, at least for the drug combinations tested, a straightforward method to accurately predict functional responses to any combination of concentrations.

Introduction

Administration of two (or more) drugs that produce similar physiologic effects can be a powerful way to lower drug dosage requirements while maintaining the intended functional effect (Hendrickx et al., 2008). Characterization of the effectiveness of drug combinations is often conducted using isobolographic analysis (Loewe, 1953; Foucquier and Guedj, 2015; Tallarida, 2016). In classic two-drug isobolograms, the doses of the two drugs that separately produce a functional effect of the same magnitude are plotted as axial points on a two-dimensional Cartesian graph. The two points, with coordinates of (x, 0) and (0, y), are connected with a line known as the isobole of additivity, which corresponds to additive dose pairs and separates subadditive (antagonistic) from superadditive (synergistic) dose combinations (Loewe, 1953; Geary, 2013).

It has been shown that the isobole of additivity is linear when the two drugs exhibit a constant effect ratio (i.e., the concentration-response curves for the two drugs are superimposable by a shift along the abscissa; Grabovsky and Tallarida, 2004; Geary, 2013; Tallarida, 2016). This, however, is not the case for many ion channel modulators, which often differ in their maximal effects or numbers of interaction sites. In these cases, the isoboles can be curvilinear (Grabovsky and Tallarida, 2004) and may not even be uniquely defined (Tallarida, 2006; Geary, 2013), making classic isobolographic analysis an unreliable approach to defining synergy.

Here, we have conducted an isobolographic analysis of direct activation and potentiation of the α1β2γ2L GABAA receptor by pairs of GABAergic drugs. We employed GABA and propofol, separately and in combination, to activate receptors. To examine potentiation, we activated receptors with a low concentration of GABA, and potentiated with propofol and the steroid alfaxalone, separately and in combination. We predicted the isoboles using a coagonist concerted transition model (Monod et al., 1965; Forman, 2012). In this model, each agonist independently contributes to the energy stabilizing the open-channel state, with no interactions between agonists (Forman, 2012). The predicted isoboles have strongly curvilinear shapes. The results from electrophysiological experiments confirm the predictions.

Materials and Methods

Receptors, Expression, and Two-Electrode Voltage Clamp.

The experiments were conducted on human α1β2γ2L GABAA receptors. The cDNAs were subcloned into the pcDNA3 vector in the T7 orientation, and linearized by digestion with XbaI (NEB Laboratories, Ipswich, MA). The complementary RNAs were produced using mMessage mMachine (Ambion, Austin, TX).

The receptors were expressed in Xenopus laevis oocytes. Oocyte harvests were performed in accordance with the Guide for the Care and Use of Laboratory Animals as adopted and promulgated by the National Institutes of Health. The protocol was approved by the Animal Studies Committee of Washington University in St. Louis (Approval 20140150). Oocytes are a widely used expression system that enables functional studies of receptors of defined composition to provide specific and reliable pharmacological information.

Oocytes were injected with a total of 7 ng of complementary RNA in a final volume of 20 nl of distilled H2O at a ratio of 1:1:5 (α:β:γ). After injection, the oocytes were incubated in ND96 buffer with supplements (96 mM NaCl, 2 mM KCl, 1.8 mM CaCl2, 1 mM MgCl2, 2.5 mM Na pyruvate, 100 U/ml penicillin, 100 μg/ml streptomycin, 50 μg/ml gentamycin, and 5 mM HEPES, pH 7.4) at 16°C, and used in electrophysiological recordings within 24–48 h.

All experiments were conducted using standard two-electrode voltage clamp. The oocytes were clamped at −60 mV. The RC-1Z chamber (Warner Instruments, Hamden, CT) was perfused continuously with a bath solution (92.5 mM NaCl, 2.5 mM KCl, 1 mM MgCl2, 10 mM HEPES, pH 7.4). Solutions were gravity applied from 30-ml glass syringes. Current responses were amplified with an OC-725C amplifier (Warner Instruments), filtered at 40 Hz, digitized with a Digidata 1200 series digitizer (Molecular Devices, Sunnyvale, CA) at a 100 Hz sampling rate, and stored using pClamp (Molecular Devices). The traces were subsequently analyzed with Clampfit (Molecular Devices) to determine the maximal amplitude of current response. Concentration-response relationships for activation were determined by exposing an oocyte to increasing concentrations of GABA or propofol. The durations of drug applications were typically 20–40 s, which was aimed at reaching the peak response without unnecessary further exposure to the drug. Each drug application was followed by a 2–3 min washout in bath solution.

The Concerted Transition Model: Data Analysis and Predicted Isobolograms.

Functional characterization of receptor activity was conducted in the Monod-Wyman-Changeux (MWC) allosteric model framework (Monod et al., 1965; Karlin, 1967; Chang and Weiss, 1999; Forman, 2012). MWC analysis uses open probability (Po) rather than raw amplitude values as the dependent variable. The conversion of raw concentration-response data and response amplitudes into units of Po was accomplished by matching the relative peak responses against a scale ranging from an estimated Po (Poest) of 0–1. The term Poest rather than Po is used to describe experimental data due to potential errors that are associated with this approach. The major source of potential error is an underestimated true peak amplitude in response to saturating GABA and propofol due to, for example, fast desensitization.

A current level corresponding to a Poest value of 1 was determined by activating the receptors with a saturating concentration (1 mM) of GABA in the presence of 50 μM propofol. From this approach, the Poest of α1β2γ2L receptors in the presence of saturating GABA is 0.83 ± 0.03 (mean ± S.E.M.; n = 5 cells), which is in agreement with previous single-channel and whole-cell studies (Steinbach and Akk, 2001; Lema and Auerbach, 2006; Keramidas and Harrison, 2010; Ruesch et al., 2012; Hernandez et al., 2017).

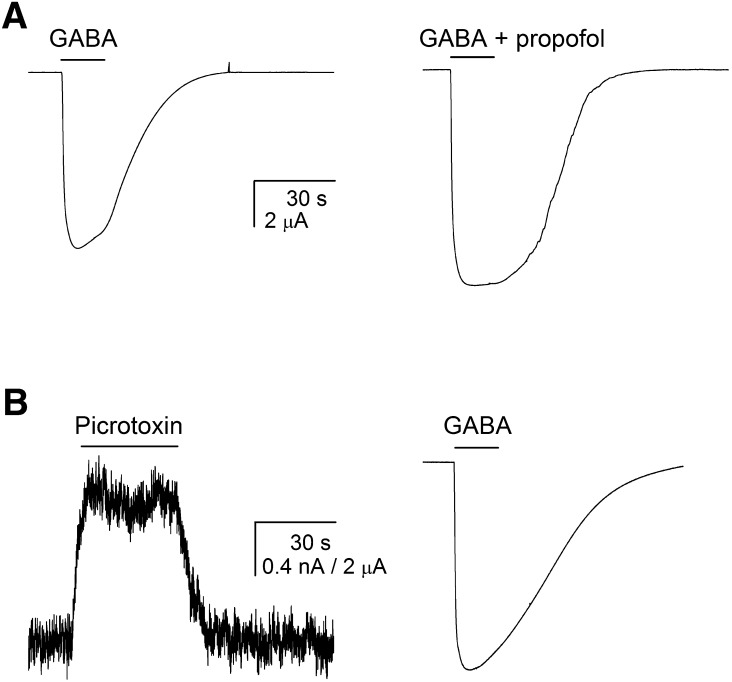
Spontaneous activity (i.e., current in the absence of an agonist) was determined by exposing the receptors to the channel blocker picrotoxin. The Po of spontaneously active receptors (Po, spont) was calculated by comparing the amplitude of the response to 300 μM picrotoxin, which is expected to produce a current level with Poest of 0, and the peak response to saturating GABA that produces a response with Poest of 0.83. Using this approach, we estimate that the Po, spont value of the human α1β2γ2L receptor is 0.00012 ± 0.00001 (n = 5). This value is in the range of previous estimates for Po, spont (Chang and Weiss, 1999; Ruesch et al., 2012; Ziemba and Forman, 2016). Sample traces are shown in Fig. 1.

Fig. 1.

Fig. 1.

Open in a new tab

Determination of receptor Po. (A) The Po for α1β2γ2L GABAA receptors activated by saturating GABA was determined by comparing peak responses to 1 mM GABA (left trace) and to 1 mM GABA + 50 μM propofol (right trace). The combination of GABA + propofol is expected to generate a response with a Po value indistinguishable from 1 (Ruesch et al., 2012). Both traces are from the same cell. (B) The Po value of receptors in the absence of agonist (i.e., Po, spont) was determined by comparing the effect of 300 μM picrotoxin on holding current (left trace) to the peak response to saturating GABA (right trace). Exposure to 300 μM picrotoxin is expected to result in a current level with a Po value of 0, whereas the peak response to saturating GABA has a Poest value of 0.83. Both traces are from the same cell.

In the MWC formalism, the probability of being open is given by the following equation (Chang and Weiss, 1999; Ruesch et al., 2012):

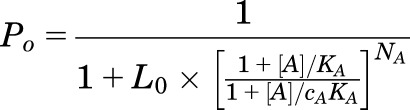graphic file with name mol.117.109595eq1.jpg (1)

where [A] is the concentration of agonist A, KA is the closed receptor equilibrium dissociation constant for the agonist, and NA corresponds to the number of agonist binding sites (constrained to 2 for GABA, 5 for propofol). cA is a measure of gating efficacy, expressed as the ratio of the open receptor dissociation constant to the closed receptor dissociation constant. L0 is the gating equilibrium constant for unliganded receptors, which is calculated as the ratio of the fraction of receptors with closed channels to the fraction with open channels. From Po, spont data, we calculate an L0 of 8409 ± 610 (n = 5). Throughout the analysis, L0 was constrained to 9000. The concentration-response relationship for Poest was fitted with eq. 1 using constrained values for L0 and NA to provide estimates for KA and cA.

When two agonists (A and B) that do not bind to the same site are present at the same time, the state function of the receptor is as follows:

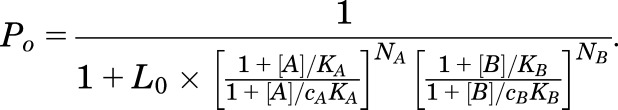graphic file with name mol.117.109595eq2.jpg (2)

Inspection of eq. 2 indicates that the effect of agonist B on activation by agonist A can be expressed through a new parameter L*, as follows:

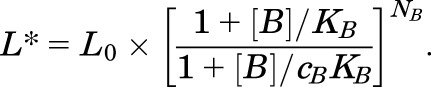graphic file with name mol.117.109595eq3.jpg (3)

In essence, the presence of drug B changes the level of basal gating.

Binding and gating parameters for alfaxalone were determined from Poest data obtained in experiments where receptors activated by 5 μM GABA were potentiated by alfaxalone. This approach was necessary because alfaxalone is such an inefficacious agonist that the direct approach employing eq. 1 was unreliable due to the small responses in direct activation by the steroid. The parameters for activation by alfaxalone were then determined by fitting a modified version of eq. 1, as follows:

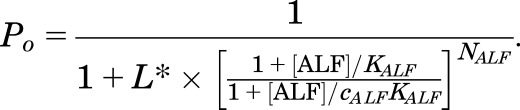graphic file with name mol.117.109595eq4.jpg (4)

The value for L* was directly determined from the response to 5 µM GABA alone, according to (1 − Po, 5 μM GABA)/Po, 5 μM GABA (L* = 16.25; Po, 5 μM GABA = 0.058). The number of binding sites for alfaxalone (NALF) was held at 2 (Hosie et al., 2006; Bracamontes et al., 2011).

Using eq. 1, we first calculated the concentrations of GABA or propofol alone that would produce a Po value of 0.5. We then calculated the concentrations of propofol necessary to elicit this response when combined with arbitrarily selected GABA concentrations of 2, 5, 10, 15, or 20 μM. In each case, a value for L* was calculated for a specific concentration of GABA, then the concentration of propofol required to produce Po = 0.5 estimated using eqs. 2 and 3.

Effects of two potentiating drugs were predicted in a similar fashion. We measured the response to 5 µM GABA alone, then calculated the concentrations of alfaxalone and propofol that separately would potentiate the response to GABA to Po = 0.5. We then predicted the concentrations of propofol that when combined with alfaxalone at concentrations of 0.2, 0.5, 1, or 1.5 μM would potentiate the response to 5 µM GABA to a Po value of 0.5.

These calculations resulted in highly curvilinear isoboles of additivity. To test the predicted isobolograms experimentally, we exposed oocytes to the drugs separately or in combination at the predicted concentrations, as well as to the combination of 1 mM GABA + 50 µM propofol to estimate the response corresponding to Poest = 1.

Curve fitting was performed using Origin version 7.5 (Originlab Corp., Northampton, MA). Pairwise statistical comparison was conducted using Student’s t test. Statistical analyses were performed using Excel (Microsoft, Redmond, WA) or Stata/IC (StataCorp LP, College Station, TX). Curve-fitting results are shown as the best-fit parameter ± S.E.

Results

GABAA Receptor Activation by GABA, Propofol, or Combinations of GABA and Propofol.

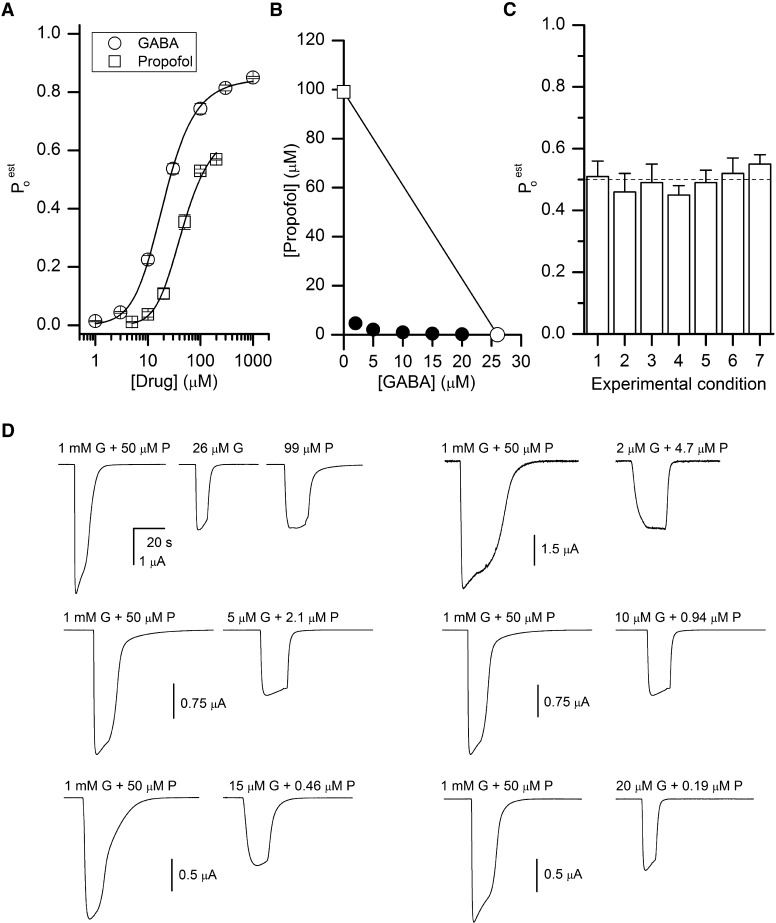
Human α1β2γ2L GABAA receptors were expressed in oocytes and exposed to 1–1000 μM GABA or 5–500 μM propofol. The raw current responses were converted to units of Po. For that, the concentration-response data were normalized to the peak response obtained from the same set of cells in the presence of 1 mM GABA + 50 μM propofol. This drug combination elicits a current response that is >10% larger than the response to 1 mM GABA alone and that we have assigned a Poest value of 1. Curve fitting was performed on data pooled from at least five cells under each condition using eq. 1. The gating equilibrium constant for unliganded receptors (L0) was held at 9000 (see Materials and Methods). For receptors activated by GABA, we estimate a KGABA (affinity of the receptor to GABA when the channel is closed) value of 35 ± 2 μM and a cGABA (ratio of the affinity of the receptor to GABA when the channel is open to that when the channel is closed) value of 0.0045 ± 0.0001. The number of binding sites for GABA was held at 2 (Amin and Weiss, 1993; Baumann et al., 2003). For propofol, we estimate a KProp (affinity of the receptor to propofol when the channel is closed) value of 19 ± 2 μM and cProp (ratio of the affinity of the receptor to propofol when the channel is open to that when the channel is closed) of 0.139 ± 0.003 when the number of binding sites is fixed at 5. The actual number of propofol binding sites is not well established. Photolabeling studies have indicated that there are two classes of sites with two copies of each class of sites per ternary receptor, giving a total of at least four sites (Yip et al., 2013; Jayakar et al., 2014). Previous functional studies have proposed two to five sites per receptor (Ruesch et al., 2012; Eaton et al., 2016; Maldifassi et al., 2016; Nourmahnad et al., 2016;). The data and fits are shown in Fig. 2A. From the K and c values, we calculate that the concentration of GABA that would produce a response with a Po value of 0.5 is 26 μM, and the concentration of propofol that would produce a Po response of 0.5 is 99 μM (open symbols in Fig. 2B).

Fig. 2.

Fig. 2.

Open in a new tab

Activation of the α1β2γ2L GABAA receptor by GABA, propofol, or combinations of GABA and propofol. (A) Concentration-response relationships for activation by GABA or propofol. The data show mean ± S.E.M. from seven (GABA) or five (propofol) cells. The Poest value was determined as described in Materials and Methods. The curves were generated by fitting pooled data to eq. 1. The best-fit parameters are KGABA = 35 μM and cGABA = 0.0045 for GABA (R2 of the fit 0.9997), and KProp = 19 μM and cProp = 0.139 for propofol (R2 = 0.9956). (B) An isobologram for receptor activation by GABA or propofol, calculated to produce a response with a Po value of 0.5. The two axial points (open symbols) are connected with a straight line. The filled circles show GABA and propofol concentration combinations predicted to produce responses with a Po value of 0.5. (C) Summary of electrophysiological recordings. The graph shows response ratios (mean ± S.E.M. from five to nine cells) vs. 1 mM GABA + 50 μM propofol for 1) 26 μM GABA (0.51 ± 0.05; P = 0.9 for comparison with the expected ratio of 0.50), 2) 99 μM propofol (0.46 ± 0.06; P = 0.52), 3) 2 μM GABA + 4.7 μM propofol (0.49 ± 0.06; P = 0.9), 4) 5 μM GABA + 2.1 μM propofol (0.45 ± 0.03; P = 0.20), 5) 10 μM GABA + 0.94 μM propofol (0.49 ± 0.04; P = 0.76), 6) 15 μM GABA + 0.46 μM propofol (0.52 ± 0.05; P = 0.67), or 7) 20 μM GABA + 0.19 μM propofol (0.55 ± 0.03; P = 0.20). The dashed line shows the expected response of 0.5. (D) Sample current traces showing responses to 1 mM GABA (G) + 50 μM propofol (P) expected to produce a Po value of 1, and 26 μM GABA, 99 μM propofol, or various combinations of GABA + propofol expected to produce a Po value of 0.5. The traces in each set are from the same cell.

We tested the sensitivity of the fitting results to the imposed value of L0. The KGABA and KProp values were minimally affected when L0 varied between 1000 and 50,000. An increase in L0 was associated with a decrease in fitted c values, reflecting the larger energetic contribution by the ligand required to offset the increased standard enthalpy, ΔH, of the gating equilibrium. However, manipulations in imposed L0 did not affect the calculated agonist concentrations eliciting responses with a Po value of 0.5, which were 24–26 μM and 97–101 μM, respectively, for GABA and propofol.

We then calculated the concentrations of GABA and propofol in mixtures of the two agonists that are predicted to produce a response with a Po value of 0.5. We chose values for GABA of 2, 5, 10, 15, and 20 μM and then used eq. 2 to determine the concentrations of propofol that, when combined with the particular concentration of GABA, would generate a response with a Po value of 0.5. These value are 4.65, 2.1, 0.94, 0.46, and 0.19 μM propofol, respectively. In the isobologram graph (filled circles in Fig. 2B), the predicted pairs fall on a highly curvilinear plot.

To examine the agreement between the predictions and experimental data, we exposed oocytes expressing α1β2γ2L receptors to the drug mixtures predicted to generate a response with a Po value of 0.5. As can be seen in Fig. 2C and Table 1, the mean responses are indistinguishable from the predicted value of 0.5. Sample current traces are shown in Fig. 2D.

TABLE 1.

Summary of data for activation by GABA, propofol, and combinations of the two agonists

The first column shows the concentrations of GABA and/or propofol (Prop) applied while the second identifies the data sets shown in Figs. 2C and 4A. The column headed ∆Po gives the mean ± S.E.M. (number of cells) for the measured Po produced by that agonist or combination of agonists, expressed as the difference from the basal Po value (0.00012). P vs. ∆Po predicted gives the P value (one-sample t test) for the difference between the measured and predicted differences (in each case, the predicted response is 0.49988). The column headed ∆Sum gives the arithmetic sum of the predicted responses to the given concentrations of agonists applied separately (e.g., Po of 2 µM GABA applied alone plus Po of 4.65 µM propofol applied alone) in terms of the difference from the basal Po value. The final column (P to ∆Sum) gives the P value for the difference between the measured response and the predicted sum.

Agonists Used Set ∆Po P vs. ∆Po Predicted ∆Sum P vs. ∆Sum
26 μM GABA 1 0.51 ± 0.05 (5) 0.9 0.50 0.9
99 μM Prop 2 0.46 ± 0.06 (5) 0.5 0.50 0.5
2 μM GABA + 4.65 μM Prop 3 0.49 ± 0.06 (6) 0.9 0.02 0.001
5 μM GABA + 2.1 μM Prop 4 0.45 ± 0.03 (5) 0.2 0.08 <0.001
10 μM GABA + 0.94 μM Prop 5 0.49 ± 0.04 (7) 0.8 0.22 <0.001
15 μM GABA + 0.46 μM Prop 6 0.52 ± 0.05 (7) 0.7 0.34 0.01
20 μM GABA + 0.19 μM Prop 7 0.55 ± 0.03 (7) 0.2 0.42 0.006
Open in a new tab

Potentiation of GABA-Activated Receptors by Alfaxalone, Propofol, or Combinations of Alfaxalone and Propofol.

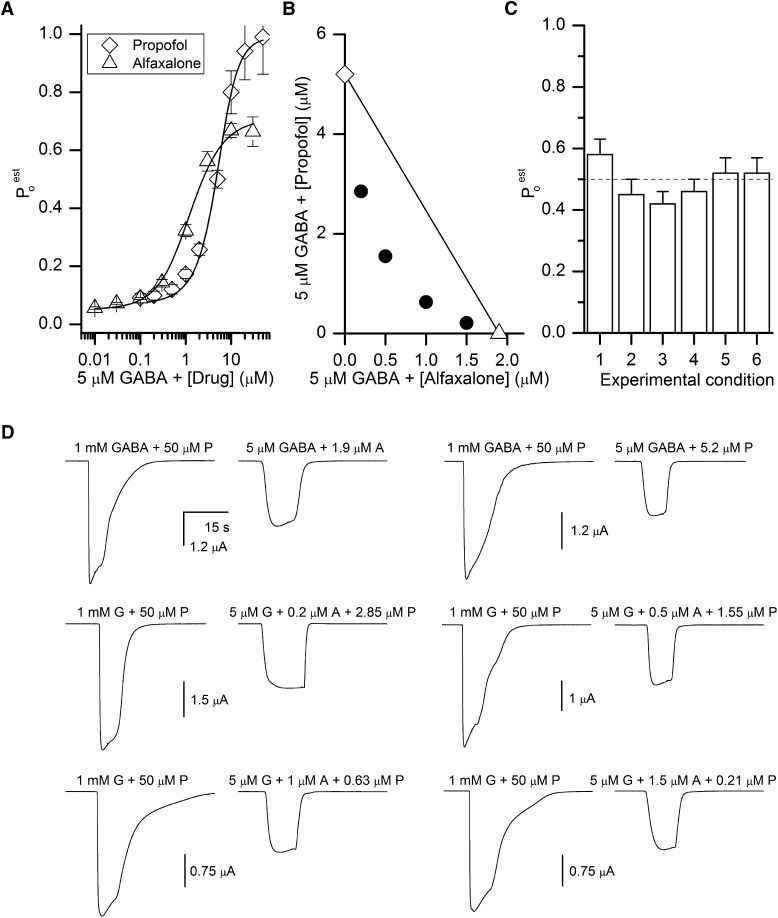
We next examined potentiation of the α1β2γ2L receptor. The receptors were activated by 5 μM GABA in the presence of alfaxalone, propofol, or combinations of alfaxalone and propofol. The raw current responses were converted to units of Po as described above. We calculated the value for L* from the response to 5 μM GABA alone as 16.25 and assumed that there are two binding sites for alfaxalone (Hosie et al., 2006; Bracamontes et al., 2011). Employing eqs. 2–4, we estimate a KALF value of 1.75 ± 0.20 μM and a cALF value of 0.147 ± 0.005 for alfaxalone, and a KProp value of 21.0 ± 5.8 μM and a cProp value of 0.21 ± 0.03 for propofol. The concentration-response data are shown in Fig. 2A. The affinity and efficacy estimates for propofol are similar to those obtained in direct activation experiments, confirming the independent, additive actions of GABA and propofol. Alfaxalone is a weak activator of the α1β2γ2L receptors; determination of KALF and cALF from direct activation experiments was not technically feasible due to the low maximal Po value (<0.004 at 10 μM).

From the K and c estimates, we calculated the concentrations of alfaxalone, propofol, and several combinations of alfaxalone and propofol that when combined with 5 μM GABA are expected to generate peak responses with a Po value of 0.5. We estimated that 5 μM GABA coapplied with 1.9 μM alfaxalone or 5.2 μM propofol will produce responses with a Po value of 0.5 (open symbols in Fig. 3B). Similarly, we predicted that drug combinations of 5 μM GABA + 0.2 μM alfaxalone + 2.85 μM propofol, 5 μM GABA + 0.5 μM alfaxalone + 1.55 μM propofol, 5 μM GABA + 1 μM alfaxalone + 0.63 μM propofol, and 5 μM GABA + 1.5 μM alfaxalone + 0.21 μM propofol will generate responses with Po of 0.5 (filled circles in Fig. 3B). While the predicted isobole is curvilinear, it is interesting to note that the degree of curvature of the isobologram in Fig. 3B is less than in Fig. 2B. Our simulations show that the curvature is strongly affected by the value of L0 or L* (L0 = 9000 for the activation data in Fig. 2, while L* = 16.25 for the potentiation data in Fig. 3).

Fig. 3.

Fig. 3.

Open in a new tab

Potentiation of GABA-activated receptors by alfaxalone, propofol, or combinations of alfaxalone and propofol. (A) Concentration-response relationships for potentiation of receptors activated by 5 μM GABA by propofol or alfaxalone. The data show the mean ± S.E.M. from five cells. Poest was determined as described in Materials and Methods. The curves were generated by fitting pooled data to eq. 3 with a modified L0 (L*) reflecting basal activity in the presence of 5 μM GABA. The best-fit parameters are KProp = 21 μM and cProp = 0.21 for propofol (R2 = 0.9966), and KALF = 1.75 μM and cALF = 0.147 for alfaxalone (R2 = 0.9955). (B) An isobologram for potentiation of GABA-activated receptors by alfaxalone or propofol, calculated to produce a response with a Po value of 0.5. The two axial points (open symbols) are connected with a straight line. The filled circles show alfaxalone and propofol concentration combinations predicted to produce responses with a Po of 0.5. (C) Summary of electrophysiological recordings. The graph shows response ratios (mean ± S.E.M. from six cells) vs. 1 mM GABA + 50 μM propofol for 1) 5 μM GABA + 1.9 μM alfaxalone (0.58 ± 0.05; P = 0.18 for comparison with the expected ratio of 0.50), 2) GABA + 5.2 μM propofol (0.45 ± 0.05; P = 0.41), 3) GABA + 0.2 μM alfaxalone + 2.85 μM propofol (0.42 ± 0.04; P = 0.09), 4) GABA + 0.5 μM alfaxalone + 1.55 μM propofol (0.46 ± 0.04; P = 0.42), 5) 5 μM GABA + 1 μM alfaxalone + 0.63 μM propofol (0.52 ± 0.05; P = 0.7), and 6) 5 μM GABA + 1.5 μM alfaxalone + 0.21 μM propofol (0.52 ± 0.05; P = 0.7). The dashed line shows the expected response of 0.5. (D) Sample current traces showing responses to 1 mM GABA (G) + 50 μM propofol (P) expected to produce a Po value of 1, and 5 μM GABA + 1.9 μM alfaxalone (A), 5 μM GABA + 5.2 μM propofol, or various combinations of 5 μM GABA + alfaxalone + propofol expected to produce a Po value of 0.5. The traces in each set are from the same cell.

To verify these predictions, we compared peak amplitudes from oocytes expressing α1β2γ2L receptors exposed to the test drug mixtures and to the control response (1 mM GABA + 50 μM propofol) with a Poest of 1. As can be seen in Fig. 3C the relative responses are indistinguishable from the predicted ratio of 0.5. Sample current traces are shown in Fig. 3D.

Discussion

In this study, we conducted an isobolographic analysis of the human α1β2γ2L GABAA receptor to determine the concentrations of several GABAergic agents that, alone or in combination, produce a response with a Po value of 0.5. The analysis was conducted in two experimental settings. We first studied the direct activation of the receptor by GABA, propofol, and combinations of GABA and propofol. In the second setting, we examined the potentiation of GABA-activated receptors by the steroid alfaxalone, propofol, and combinations of alfaxalone and propofol.

Deviation from a linear isobole of additivity is often interpreted as superadditivity or subadditivity of drug interactions (Loewe, 1953; Tallarida, 2016). We show here that simple addition of stabilization energy in a coagonist concerted transition model predicts strongly curvilinear isoboles, deep in the region classically assigned to synergistic interactions. The predicted deflection from linearity is confirmed by experimental data.

The classic method for constructing an isobole of additivity is to transform the concentration of drug A into an equivalent concentration of drug B (denoted as B′), then to calculate the predicted effect of the combination of drugs by expressing the effect of the combination of A + B as B′ + B using the empirical concentration-effect relationship for drug B (Grabovsky and Tallarida, 2004). One potential problem with this approach is that the direction of transformation (i.e., A to B′ or B to A′) can influence the curvature of isoboles when the two drugs have different Hill slopes (Lorenzo and Sanchez-Marin, 2006).

We calculated the isobole of additivity using an equation that describes a single concentration-effect relationship for all agonists (albeit with unique parameter values for each agent). Our approach relies on having a single relationship describing the activation of the receptor by multiple agonists, rather than utilizing empirical concentration-effect relationships for each agonist. The effect of each agonist is to change the relative free energies of the closed and open states in a fashion quantitatively described by the model. This approach assumes independent energetic contributions by all agonists (i.e., no interactions between agonists). Responses to any concentration of an agonist or a combination of multiple agonists can be predicted, once the affinity (K) and efficacy (c) values for the compounds are known. Furthermore, to predict an isobologram, K and c for just one of the agonists needs to be known. For the second agonist, only its functional response at the concentration of interest needs to be determined because that determines the value for L*. Our results apply to the agonist pair of GABA and propofol, and to the triple combination of GABA + alfaxalone + propofol. It remains to be determined whether these findings apply to other GABAergic drugs, particularly for combinations involving volatile anesthetics (Sebel et al., 2006; Jenkins et al., 2008).

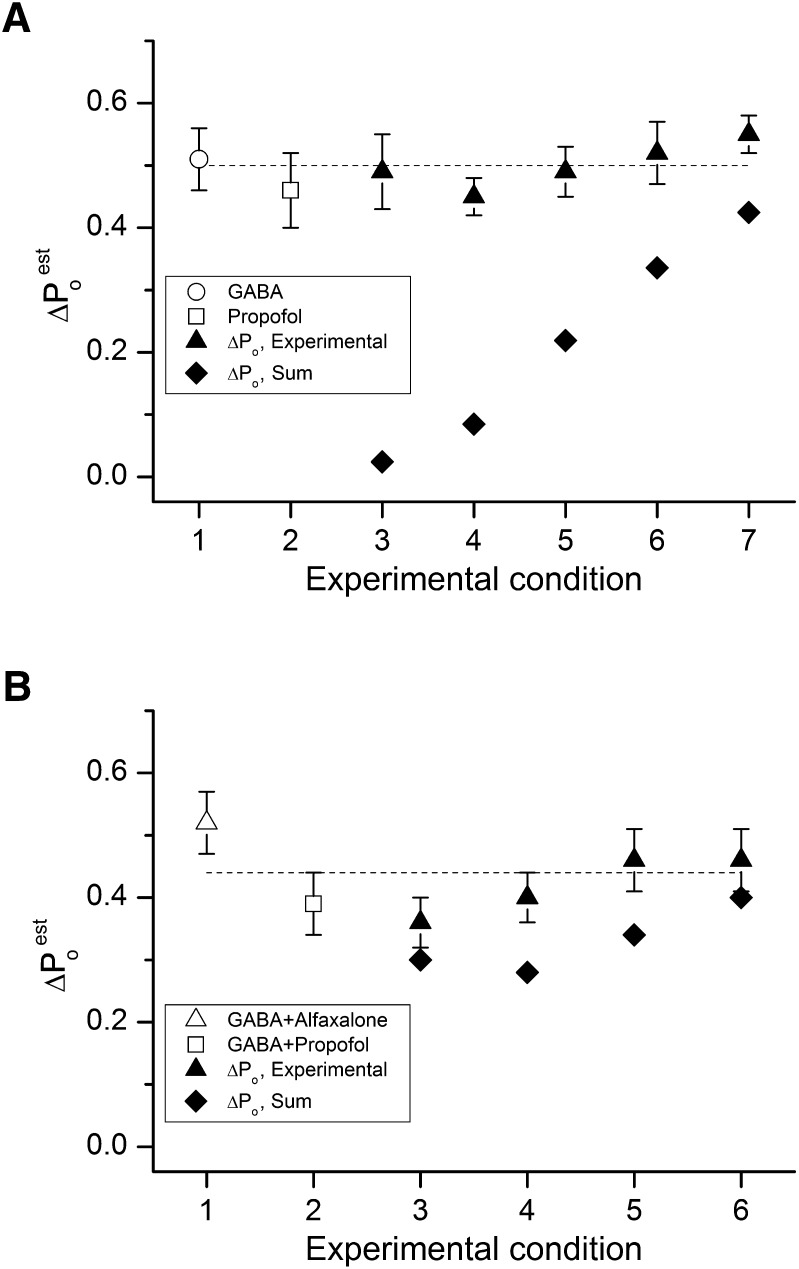
Figure 4 and Tables 1 and 2 summarize the experimental observations in terms of the effects of the combinations of agents compared with the sum of the individual effects of the agents. The effects are expressed as the net change (ΔPo) from the baseline or background activation present (no agent for data in Fig. 4A and Table 1, or 5 µM GABA in Fig. 4B and Table 2). As can be seen for the activation by GABA, propofol, and combinations, the combinations produce a larger effect than the sum of the effects of GABA and propofol. It is interesting that the same model for activation may result in situations for which the effect of the combination is not significantly different from the sum of the individual effects. This situation arises when the basal level of activity of the receptor is relatively high, as can occur when a combination of drugs is used to potentiate the response to a low concentration of GABA (Fig. 4B).

Fig. 4.

Fig. 4.

Open in a new tab

Summary of the data. (A) Calculated and experimentally determined Po responses for GABA, propofol, and GABA + propofol: 1) 26 μM GABA, 2) 99 μM propofol, 3) 2 μM GABA + 4.7 μM propofol, 4) 5 μM GABA + 2.1 μM propofol, 5) 10 μM GABA + 0.94 μM propofol, 6) 15 μM GABA + 0.46 μM propofol, and 7) 20 μM GABA + 0.19 μM propofol. The graph shows the effects of agonists and agonist combinations on receptor Po (∆Po calculated as experimentally determined Po − basal ∆Po of 0.00012). The symbols show the effect on receptor Po for GABA alone (open circle), propofol alone (open square), and for combinations of GABA + propofol (filled triangles). The filled diamonds give the arithmetic sums of ∆Po for predicted responses to the given concentrations of agonists applied separately. (B) Calculated and experimentally determined Po responses for GABA in combination with alfaxalone, propofol, and alfaxalone + propofol: 1) 5 μM GABA + 1.9 μM alfaxalone, 2) GABA + 5.2 μM propofol, 3) GABA + 0.2 μM alfaxalone + 2.85 μM propofol, 4) GABA + 0.5 μM alfaxalone + 1.55 μM propofol, 5) 5 μM GABA + 1 μM alfaxalone + 0.63 μM propofol, and 6) 5 μM GABA + 1.5 μM alfaxalone + 0.21 μM propofol. The symbols show Po values for GABA + alfaxalone (open triangle), GABA + propofol (open square), and for combinations of GABA + alfaxalone + propofol (filled triangles). The filled diamonds give the arithmetic sums of ∆Po for predicted potentiating effects of each potentiator in the combination applied separately.

TABLE 2.

Summary of data for potentiation of GABA-activated receptors by alfaxalone, propofol, and combinations

The first column shows the concentrations of GABA and of alfaxalone (ALF) and/or propofol (Prop) applied, whereas the second column identifies the data sets shown in Figs. 3C and 4B. The column headed ∆Po gives the mean ± S.E.M. (number of cells) for the measured Po value produced by that potentiator or combination of potentiators, expressed as the difference from the background Po value in the presence of 5 μM GABA (0.058). P vs. ∆Po predicted gives the P value (one-sample t test) for the difference between the measured and predicted differences (in each case the predicted response is 0.442). The column headed ∆Sum gives the arithmetic sum of the predicted responses to the given concentration of potentiator or combinations of potentiators applied separately (e.g., 0.2 µM alfaxalone applied alone plus 2.85 µM propofol applied alone) in terms of the difference from the basal Po value (0.058). The final column (P to ∆Sum) gives the P value for the difference between the measured response and the predicted sum.

Drugs Used Set ∆Po P vs. ∆Po Predicted ∆Sum P vs. ∆Sum
5 µM GABA + 1.9 µM ALF 1 0.52 ± 0.05 (6) 0.2 0.44 0.2
5 µM GABA + 5.2 µM Prop 2 0.39 ± 0.05 (6) 0.9 0.44 0.4
5 µM GABA + 0.2 µM ALF + 2.85 µM Prop 3 0.36 ± 0.04 (6) 0.6 0.30 0.2
5 µM GABA + 0.5 µM ALF + 1.55 µM Prop 4 0.40 ± 0.04 (6) 0.7 0.28 0.04
5 µM GABA + 1 µM ALF + 0.63 µM Prop 5 0.46 ± 0.05 (6) 0.2 0.34 0.05
5 µM GABA + 1.5 µM ALF + 0.21 µM Prop 6 0.46 ± 0.05 (6) 0.2 0.40 0.2
Open in a new tab

Isobolographic analysis is widely used to describe the effects of combinations of GABAergic drugs. Deviation from a linear isobole of additivity, typically interpreted as synergy, has been observed in the modulation of GABA-activated α1β2γ2L receptors by the combination of propofol and flurazepam (Reynolds and Maitra, 1996), the enhancement of [3H]diazepam binding to cerebrocortical synaptoneurosomes by the combination of GABA and pentobarbital, the enhancement of [3H]muscimol binding by pentobarbital and diazepam (DeLorey et al., 1993), and the production of loss-of-righting in rats by combinations of barbiturates and benzodiazepines (DeLorey et al., 1993). Superadditive anxiolytic effects have been found for certain concentration combinations of triazolam and pregnanolone and for clonazepam and ganaxalone in the elevated zero maze assay (Gunter et al., 2016). In patients, the combination of midazolam and propofol apparently synergistically produces a loss of response to command (McClune et al., 1992; Minto et al., 2000). Drug effects and interactions at the whole-organism level can depend on a variety of confounding factors, including ceiling effects or amplication cascades, and compensatory actions. The present study investigated a model system with a single target (the α1β2γ2L GABAA receptor) and an easily measured endpoint (a response with a Po value of 0.5) to provide insight into a single step in the possible clinical effects of drugs acting on the GABAA receptor.

Abbreviations

cALF

ratio of the affinity of the receptor to alfaxalone when the channel is open to that when the channel is closed

cGABA

ratio of the affinity of the receptor to GABA when the channel is open to that when the channel is closed

cProp

ratio of the affinity of the receptor to propofol when the channel is open to that when the channel is closed

KALF

affinity of the receptor to alfaxalone when the channel is closed

KGABA

affinity of the receptor to GABA when the channel is closed

KProp

affinity of the receptor to propofol when the channel is closed

L0

gating equilibrium constant for unliganded receptors

MWC

Monod-Wyman-Changeux

Po

open probability

Poest

estimated open probability

Authorship Contributions

Participated in research design: Steinbach, Akk.

Conducted experiments: Shin, Germann.

Performed data analysis: Shin, Germann, Steinbach, Akk.

Wrote or contributed to the writing of the manuscript: Shin, Germann, Steinbach, Akk.

Footnotes

This work was supported by the National Institutes of Health National Institute of General Medical Sciences [Grant R01GM108580]; and funds from the Taylor Family Institute for Innovative Psychiatric Research.

References

  1. Amin J, Weiss DS. (1993) GABAA receptor needs two homologous domains of the beta-subunit for activation by GABA but not by pentobarbital. Nature 366:565–569. [DOI] [PubMed] [Google Scholar]
  2. Baumann SW, Baur R, Sigel E. (2003) Individual properties of the two functional agonist sites in GABA(A) receptors. J Neurosci 23:11158–11166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bracamontes J, McCollum M, Esch C, Li P, Ann J, Steinbach JH, Akk G. (2011) Occupation of either site for the neurosteroid allopregnanolone potentiates the opening of the GABAA receptor induced from either transmitter binding site. Mol Pharmacol 80:79–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chang Y, Weiss DS. (1999) Allosteric activation mechanism of the alpha 1 beta 2 gamma 2 gamma-aminobutyric acid type A receptor revealed by mutation of the conserved M2 leucine. Biophys J 77:2542–2551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. DeLorey TM, Kissin I, Brown P, Brown GB. (1993) Barbiturate-benzodiazepine interactions at the gamma-aminobutyric acidA receptor in rat cerebral cortical synaptoneurosomes. Anesth Analg 77:598–605. [DOI] [PubMed] [Google Scholar]
  6. Eaton MM, Germann AL, Arora R, Cao LQ, Gao X, Shin DJ, Wu A, Chiara DC, Cohen JB, Steinbach JH, et al. (2016) Multiple non-equivalent interfaces mediate direct activation of GABAA receptors by propofol. Curr Neuropharmacol 14:772–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Forman SA. (2012) Monod-Wyman-Changeux allosteric mechanisms of action and the pharmacology of etomidate. Curr Opin Anaesthesiol 25:411–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Foucquier J, Guedj M. (2015) Analysis of drug combinations: current methodological landscape. Pharmacol Res Perspect 3:e00149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Geary N. (2013) Understanding synergy. Am J Physiol Endocrinol Metab 304:E237–E253. [DOI] [PubMed] [Google Scholar]
  10. Grabovsky Y, Tallarida RJ. (2004) Isobolographic analysis for combinations of a full and partial agonist: curved isoboles. J Pharmacol Exp Ther 310:981–986. [DOI] [PubMed] [Google Scholar]
  11. Gunter BW, Jones SA, Paul IA, Platt DM, Rowlett JK. (2016) Benzodiazepine and neuroactive steroid combinations in rats: anxiolytic-like and discriminative stimulus effects. Psychopharmacology (Berl) 233:3237–3247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hendrickx JF, Eger EI, II, Sonner JM, Shafer SL. (2008) Is synergy the rule? A review of anesthetic interactions producing hypnosis and immobility. Anesth Analg 107:494–506. [DOI] [PubMed] [Google Scholar]
  13. Hernandez CC, Kong W, Hu N, Zhang Y, Shen W, Jackson L, Liu X, Jiang Y, Macdonald RL. (2017) Altered channel conductance states and gating of GABAA receptors by a pore mutation linked to dravet syndrome. eNeuro 4:1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hosie AM, Wilkins ME, da Silva HM, Smart TG. (2006) Endogenous neurosteroids regulate GABAA receptors through two discrete transmembrane sites. Nature 444:486–489. [DOI] [PubMed] [Google Scholar]
  15. Jayakar SS, Zhou X, Chiara DC, Dostalova Z, Savechenkov PY, Bruzik KS, Dailey WP, Miller KW, Eckenhoff RG, Cohen JB. (2014) Multiple propofol-binding sites in a γ-aminobutyric acid type A receptor (GABAAR) identified using a photoreactive propofol analog. J Biol Chem 289:27456–27468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Jenkins A, Lobo IA, Gong D, Trudell JR, Solt K, Harris RA, Eger EI., II (2008) General anesthetics have additive actions on three ligand gated ion channels. Anesth Analg 107:486–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Karlin A. (1967) On the application of “a plausible model” of allosteric proteins to the receptor for acetylcholine. J Theor Biol 16:306–320. [DOI] [PubMed] [Google Scholar]
  18. Keramidas A, Harrison NL. (2010) The activation mechanism of alpha1beta2gamma2S and alpha3beta3gamma2S GABAA receptors. J Gen Physiol 135:59–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lema GM, Auerbach A. (2006) Modes and models of GABA(A) receptor gating. J Physiol 572:183–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Loewe S. (1953) The problem of synergism and antagonism of combined drugs. Arzneimittelforschung 3:285–290. [PubMed] [Google Scholar]
  21. Lorenzo JI, Sánchez-Marín P. (2006) Comments on “Isobolographic analysis for combinations of a full and partial agonist: curved isoboles”. J Pharmacol Exp Ther 316:476–478. [DOI] [PubMed] [Google Scholar]
  22. Maldifassi MC, Baur R, Sigel E. (2016) Functional sites involved in modulation of the GABAA receptor channel by the intravenous anesthetics propofol, etomidate and pentobarbital. Neuropharmacology 105:207–214. [DOI] [PubMed] [Google Scholar]
  23. McClune S, McKay AC, Wright PM, Patterson CC, Clarke RS. (1992) Synergistic interaction between midazolam and propofol. Br J Anaesth 69:240–245. [DOI] [PubMed] [Google Scholar]
  24. Minto CF, Schnider TW, Short TG, Gregg KM, Gentilini A, Shafer SL. (2000) Response surface model for anesthetic drug interactions. Anesthesiology 92:1603–1616. [DOI] [PubMed] [Google Scholar]
  25. Monod J, Wyman J, Changeux JP. (1965) On the nature of allosteric transitions: a plausible model. J Mol Biol 12:88–118. [DOI] [PubMed] [Google Scholar]
  26. Nourmahnad A, Stern AT, Hotta M, Stewart DS, Ziemba AM, Szabo A, Forman SA. (2016) Tryptophan and cysteine mutations in M1 helices of α1b3γ2L γ-aminobutyric acid type A receptors indicate distinct intersubunit sites for four intravenous anesthetics and one orphan site. Anesthesiology 125:1144–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Reynolds JN, Maitra R. (1996) Propofol and flurazepam act synergistically to potentiate GABAA receptor activation in human recombinant receptors. Eur J Pharmacol 314:151–156. [DOI] [PubMed] [Google Scholar]
  28. Ruesch D, Neumann E, Wulf H, Forman SA. (2012) An allosteric coagonist model for propofol effects on α1β2γ2L γ-aminobutyric acid type A receptors. Anesthesiology 116:47–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sebel LE, Richardson JE, Singh SP, Bell SV, Jenkins A. (2006) Additive effects of sevoflurane and propofol on gamma-aminobutyric acid receptor function. Anesthesiology 104:1176–1183. [DOI] [PubMed] [Google Scholar]
  30. Steinbach JH, Akk G. (2001) Modulation of GABA(A) receptor channel gating by pentobarbital. J Physiol 537:715–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Tallarida RJ. (2006) An overview of drug combination analysis with isobolograms. J Pharmacol Exp Ther 319:1–7. [DOI] [PubMed] [Google Scholar]
  32. Tallarida RJ. (2016) Drug combinations: tests and analysis with isoboles. Curr Protoc Pharmacol 72:9 19 11–9 19 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Yip GM, Chen ZW, Edge CJ, Smith EH, Dickinson R, Hohenester E, Townsend RR, Fuchs K, Sieghart W, Evers AS, et al. (2013) A propofol binding site on mammalian GABAA receptors identified by photolabeling. Nat Chem Biol 9:715–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ziemba AM, Forman SA. (2016) Correction for inhibition leads to an allosteric co-agonist model for pentobarbital modulation and activation of α1β3γ2L GABAA receptors. PLoS One 11:e0154031. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Molecular Pharmacology are provided here courtesy of American Society for Pharmacology and Experimental Therapeutics

RESOURCES