Ancestral Genome Reconstruction on Whole Genome Level

Abstract

Comparative genomics, evolutionary biology, and cancer researches require tools to elucidate the evolutionary trajectories and reconstruct the ancestral genomes. Various methods have been developed to infer the genome content and gene ordering of ancestral genomes by using such genomic structural variants. There are mainly two kinds of computational approaches in the ancestral genome reconstruction study. Distance/event-based approaches employ genome evolutionary models and reconstruct the ancestral genomes that minimize the total distance or events over the edges of the given phylogeny. The homology/adjacency-based approaches search for the conserved gene adjacencies and genome structures, and assemble these regions into ancestral genomes along the internal node of the given phylogeny. We review the principles and algorithms of these approaches that can reconstruct the ancestral genomes on the whole genome level. We talk about their advantages and limitations of these approaches in dealing with various genome datasets, evolutionary events, and reconstruction problems. We also talk about the improvements and developments of these approaches in the subsequent researches. We select four most famous and powerful approaches from both distance/event-based and homology/adjacency-based categories to analyze and compare their performances in dealing with different kinds of datasets and evolutionary events. Based on our experiment, GASTS has the best performance in solving the problems with equal genome contents that only have genome rearrangement events. PMAG++ achieves the best performance in solving the problems with unequal genome contents that have all possible complicated evolutionary events.

1. INTRODUCTION

Ancestral reconstruction was used to infer the ancestral states and biological characteristics based on the analyses of encoding genes or genome segments in molecular level [1-4]. Afterwards, this study was extended to explore the genomic structures of ancestral genes and genomes [5, 6]. Recently, the availability of fully sequenced and well-annotated whole genome data allowed researchers to reconstruct ancestral genomes using gene orders on the whole genome level. Ancestral reconstruction from gene orders and karyotypes was first studied by Dobzhansky and Sturtevant in the Drosophila chromosomes in 1938 [7]. However, the computational methods were first developed in 1990s [8, 9], later they were widely explored in reconstruction of ancestral genomes and phylogenies in the next two decades.

Reconstructing ancestral genomes on the whole-genome level offers opportunities to explore the genome features and ancestral characters of the organisms that extinct millions of years ago. It can also be used to study the evolutionary procedures and trajectories of the modern species. Nevertheless, it is hard to determine the timings and the intermediate steps of the evolutionary events just based on the information researchers currently have. Even for the simplest case, the median genome problem: given three genomes, constructing the intermediate ancestral genome that minimizes the sum of total pairwise distances to the other three genomes has been proven to be NP-complete [10, 11]. To solve the ancestral reconstruction problems, researchers have developed a few evolutionary models to simulate the gene order evolutions and solve the ancestral reconstruction problems, such as breakpoints distance [12], rearrangement distance [13], universal double-cut-and-join (DCJ) [14], single-cut-or-join (SCJ) [15] and the existence or likelihood of adjacencies [16-18].

There are mainly two kinds of computational approaches in the ancestral genome reconstruction study. Distance/event-based approaches usually employ genome evolutionary models and search for the exact ancestral genomes that minimizes the total distance or events over all edges of the given phylogeny. BPAnalysis [9], GRAPPA [19] and MGR [13] are the pioneering studies of distance/event-based approaches. They reconstruct the ancestral genomes by finding the local median genomes. These methods have already encountered challenges in handling current complicated genome data due to their simplified model and NP-hard complexity. Recent distance/event-based approaches include MGRA2 [11, 20], GASTS [21] and PATHGROUPS [22], which use more advanced and efficient graph-based algorithms to find the median genomes. Homology/adjacency-based approaches view the genomes as a set of gene adjacencies or genome segments, and assemble these conserved adjacencies and genome regions into ancestral genomes along the internal node of the given phylogeny. Homology/adjacency-based approaches are explored more frequently in recent years, such as PMAG [17], InferCARS [23], proCARS [24], ANGES [25] and Gapped Adjacency [26].

Distance/event-based approaches are computationally costly and time-consuming since they usually need to solve the problems of NP-hard complexity. Homology/adjacency-based approaches are fast, and have lower error rates since the adjacencies in the ancestral genome are derived from the shared common information of children genomes. Distance/event-based approaches usually have higher probabilities of correct adjacencies but also have higher error rates, because they need to reconstruct the ancestral genomes that minimize distances and fill the missing adjacencies [47].

Each ancestral reconstruction always starts with a phylogeny. Phylogeny is an evolutionary tree that indicates the evolutionary relationships and classifications of the taxon, which is based on the analysis of their morphological and genetic characters. Current ancestral reconstruction approaches either assume there already exists a phylogeny to represent the evolutionary relationships of given species, and employ it as a guide tree to reconstruct the ancestral genome, which is known as the small phylogeny problem (SPP). Or they may first build the most appropriate phylogeny from the input data and then use it to reconstruct the ancestral genome, which is known as the big phylogeny problem (BPP). Only a few of the approaches can handle the big phylogeny problem and reconstruct phylogeny and ancestral genome using the same input data, such as GRAPPA [27], MGR [13], MGRA2 [11], SCJ [15], MLGO [18] and GASTS [21].

Gene orders represent the gene permutations of a genome, and can reflect the genome level evolutionary events such as genome rearrangements, deletions, insertions and duplications. Compared to the sequence data, gene order data has several inherent advantages. Gene order variations are considered rare evolutionary events when compared with the nucleotide level mutation. It can help researchers build accurate evolutionary models and simulate the evolutionary history across different species. Gene order can represent the gene content, direction, and their relative positions, such as {1, -2, -3, 4…. n}. Each distinct integer represents a homologous gene or conserved genome region across different species. The sign (+/−) of the gene order indicates the strand or direction of each gene or region. So genomes can be represented by a permutation of signed integers that corresponds to gene orders with orientations. Adjacency is used to represent the relative position among genes orders. For instance, two adjacent genes, 1 and 2, form an adjacency if they are next to each other, and 1 is followed by 2, or equivalently –2 is followed by –1. The breakpoint of the genome is defined as an adjacency that is missing in one genome but exists in one or more other genomes. The ordering of genome segments or genes can be changed by the genome level evolutionary events.

2. DISTANCE/EVENT-BASED ANCESTRAL RECONSTRUCTION APPROACHES

2.1. Ancestral Reconstruction Approaches Based on Local Optimal Solutions

2.1.1. BPAnalysis

Before BPAnalysis there was no effective algorithm to measure the genomic distance for more than two genomes. In 1997, Blanchette and Sankoff first defined the “breakpoint”: if two genes were adjacent in genome A but not in genome B [9]. They also used the “breakpoint distance” (number of breakpoints between two genomes) to measure the genomic distance without any assumptions of the evolutionary mechanisms [9]. They developed a few heuristics for reconstructing the ancestral genomes by minimizing the total breakpoint distance summed along the each edge of a fixed phylogeny. BPAnalysis reduced the median genome problem to a travel salesman problem, and it iteratively labeled the internal nodes with median genome for the entire phylogeny. Since this method labeled the internal node iteratively, initialization of the set of genomes was critical to its performance. The simulation experiments showed that a better initialization could help to output a better solution.

BPAnalysis was the pioneering study of automated ancestral genome reconstruction and it brought this study area to a new era. However, the integrative labeling procedure was very computationally intensive and time-consuming, since each iteration was solving one NP-hard TSP problem. Most of the solutions were discarded since they did not bring any improvement. The computational complexity of this algorithm grew exponentially with each additional genome. For a dataset with 13 genomes of 105 gene segments, it might need 200 years to obtain the solution [27]. Although the procedure remained a heuristic and each internal node was labeled accurately, the tree labeling might still not the optimal unless there were only three leaves [27].

2.1.2. GRAPPA

GRAPPA was a new implementation and improvement of the BPAnalysis [27]. Compared to BPAnalysis [9], GRAPPA made a few changes in low-level algorithms, data structures and coding strategies. GRAPPA was more cache-sensitive, and obtained significant improvements in speed, quality, and robustness. GRAPPA employed an efficient tree generation method that could generate a preorder encoding of tree, and then produced the topology from this encoding. This method could generate the next tree in amortized constant time. Instead of solving the median problem for each internal node, GRAPPA only needed to resolve the median problem for the nodes that had at least one of relabeled neighbors in the last pass. The GRAPPA scored the tree incrementally after each relabeling if the label had changed, which also took a constant time. GRAPPA used two approximate solvers to solve the TSP problem from the Concorde library-the chained and the simple versions of famous Lin-Kernighan heuristic [28]. It also used another exact TSP solver, which only considered nontrivial edges and treated the others as an undifferentiated pool.

GRAPPA presented a novel implementation of breakpoint analysis and improved the BPAnalysis by 2 to 3 orders of magnitude. It could handle a much larger dataset that couldn’t be resolved by the BPAnalysis [27]. However, GRAPPA still employed a simplified evolutionary model and could only deal with a limit type of genome rearrangement events.

2.1.3. MGR

Due to the facts that BPAnalysis was not robust enough when adapting to the multi-chromosomal genomes [9], and the breakpoint median was hardly corresponding to the ancestral median. Bourque et al. developed the MGR approach in 2002, an ancestral reconstruction method based on the reversal distance and multiple rearrangement scenarios. MGR could be applied to both unichromosomal and multi-chromosomal genomes [13] and had significant improvements in the analyses of pairwise genome rearrangements [29].

MGR was successfully applied to reconstructing the phylogeny and ancestral gene orders for the human-mouse cat dataset [13]. On the other hand, the MGR approach was still limited to handling the small genome dataset and low-resolution data with only a few hundred syntenic blocks [21]. MGR required the input genome datasets to have equal gene content and unique genome markers. Furthermore, it was hard to make the distinction between the reliable and unreliable rearrangements [20]. In 2008, Sankoff et al. introduced the DCJ model to the MRG and applied it to a mammalian dataset with seven species. This improved version of MGR could process more complicated evolutionary events such as reciprocal translocation, transposition and block interchange [30].

2.1.4. SCJ

The Single-Cut-or-Join (SCJ) approach was based on a novel rearrangement distance between multi-chromosomal genomes, which modeled the most fundamental rearrangement operations, cutting and joining adjacencies [15]. The cutting operation cut one old adjacency and created two telomeres. The joining operation linked two telomeres into a new adjacency. So that the SCJ model could simulate the genome rearrangements events by deleting old adjacencies and bring new adjacencies into the genome adjacency set, which was similar to the breakpoint model [39]. SCJ could only handle the genome rearrangement events since it was still based on the genome rearrangement distance. SCJ applied the Fitch’s algorithm and used a parsimony strategy to reconstruct the ancestral genome in a polynomial time with a very low false positive rate.

SCJ could output very conservative genome reconstructions. However, it could not recover the phylogeny and ancestral genome very accurately. Only 60 percent to 95 percent of the phylogeny splits and 50 percent to 85 percent of the ancestral adjacencies could be recovered. SCJ had been applied to simulated datasets and the real biological datasets of the Campanulaceae and Protostomes groups. It could reconstruct phylogenetic trees with good quality compared to the accepted species trees [15]. In 2016, Luhmann et al. introduced the adjacency weights to the SCJ model and designed an algorithm based on the Sankoff-Rousseau dynamic programming algorithm [40]. Their study on both the mammalian and bacterial datasets showed that their algorithm had a significant impact in reducing the fragmentation of ancestral gene orders and obtained more robust ancestral genome structures [41].

2.2. Ancestral Reconstruction Approaches Based on Global Optimal Solutions

2.2.1. MGRA and MGRA2

MGRA was developed upon the multiple breakpoint graphs, which made it suitable for ancestral reconstructions of multi-chromosomal genomes [20]. It used the cycles or paths in the breakpoint graphs as guidance to reconstruct the ancestral genomes. MGRA turned the genomes P₁...P_k into genome graphs and marked them in unique colors. The breakpoint graph G (P₁...P_k) was the superposition of these individual genome graphs and constructed by “gluing” the labeled vertices in the genome graph. MRGA let X be the common ancestral genome of genomes and let t be the transformation as a collection of paths in T. Each internal node on path T was an internal genome of this node. Recovering t could be achieved by reconstructing the internal genomes of T. MGRA restored a reverse transformation of t and eventually recovered t and the ancestral genomes [20].

The MGRA was conceptually simpler and less time-consuming than the MGR and had a better performance in dealing with the semi-independent rearrangement and breakpoint re-use. MGRA could solve the big phylogeny problem and reconstruct the rearrangement-based phylogenetic tree, even if the phylogeny was unknown. MGRA was further adapted to study the rearrangement history of seven mammalian genomes and achieved a good performance [20]. However, MGRA was also restricted to the genome dataset with the equal genome content and unique genes. In 2016, Alekseyev et al. improved the MGRA algorithm to the MGRA2. MGRA2 could handle more kinds of complicated genome evolutionary events, including insertion, deletion, and duplications [11]. MGRA2 was also applied to both simulated datasets and real mammalian genome dataset, which showed very good performance [11].

2.2.2. GASTS

Generalized Adequate Subtree Tree Scoring (GASTS) was a tree-scoring approach based on generalized adequate sub-graphs [21]. GASTS could be used to solve the big phylogeny problems. It sorted for a fixed phylogenetic tree that minimized the overall sum of the pairwise DCJ distances between input genomes and the ancestral genomes. GASTS used two different styles of phylogenetic inference to obtain an accurate tree-scoring algorithm in turn: the brute force search and the incremental construction. It also utilized a novel algorithm to solve the median genome problem, which merged the inversion medians with Xu’s extensions into capped multiple breakpoint graphs [31]. GASTS either detected a capped adequate sub-graph and divided the current problem into sub-problems in a divide-and-conquer way, or added adjacencies into the median genome in a polynomial number of ways, according to the criterion that matched the adequate sub-graphs. It could merge the circular chromosomes with linear chromosomes with a greedy algorithm to minimize the incremental increase of median scores.

GASTS solved a problem that subsumed from the median problems, so that it was equally NP-Hard. However, GASTS scaled linearly instead of exponentially with the expected length of the tree and the genome size involved. So that it could run magnitude faster and handle high-resolution data. GASTS maintained a very high speed and accuracy for phylogenetic tree reconstruction up to 100 taxa and up to 10,000 syntenic blocks for each genome. For real biological vertebrate data, GASTS could handle the genome datasets with equal contents and over 2000 syntenic blocks [21].

GASTS overcame the crucial initialization issue of the BPAnalysis and GRAPPA, which was the good performance could only be achieved by appropriate initial assignment. Nevertheless, GASTS could only handle the simplified genome datasets with equal genome content and unique syntenic blocks; it could not take account of the gene duplication, gene loss, and gain events. And it couldn‘t output the intermediate ancestral genomes of the ancestral reconstruction process.

2.2.3. PATHGROUPS

PATHGROUPS was a data structure enabling rapid heuristic solutions for ancestral reconstruction based on the genome rearrangement distance [22, 32]. Using PATHGOURPS, researchers could employ a look-ahead based generic greedy algorithm to reconstruct the ancestral genomes in linear time. Each branch distance in the given phylogeny was corresponding to a breakpoint graph. There were two kinds of edges in the breakpoint graph. The blue edges in the breakpoint graph were determined by the given genome information. The red edges in the breakpoint graph were corresponding to the reconstructed ancestral genome, which was identical in all of the breakpoint graphs. A PATHGROUP was a set of these paths, which started with the same vertex; each path was from a partial breakpoint graph that currently being constructed. This algorithm set an entire set of PATHGROUPs for each internal node. The PATHGROUP that connected with two given nodes would be processed first, and then built all of the three paths and combine the PATHGROUPs one by one. The red edge would be changed to the blue edge after it was added to the path in the corresponding PATHGROUP for the ancestral genomes that connected to it. The edges were accumulated in their PATHGROUPs and form cycles, which could be corresponding to the fragment of reconstructed ancestral genomes.

This greedy algorithm updated the data structure during the running time and then chose the priority scheme in the next step. Even though this algorithm could not find the exact solution, it was fast enough to obtain a reasonably accurate solution for the large-scale instances. PATHGROUPS required a given phylogeny to reconstruct the ancestral genomes. And the phylogeny information had to be hard-coded into the program. It could only resolve the problems for equal content genome dataset with simplified evolutionary events [22, 32].

3. HOMOLOGY/ADJACENCY-BASED ANCESTRAL RECONSTRUCTION APPROACHES

3.1. Ancestral Reconstruction Using Contiguous Ancestral Regions (CARs)

3.1.1. InferCARs and InferCARsPro

InferCARs was a Fitch parsimony-based computational heuristic algorithm that predicted the permutations and orientations of conserved segments and orthologous blocks [23]. This algorithm output the ancestral genomes in the form of “contiguous ancestral regions” (CARs), which were large genome segments. This algorithm was built on graph theory, and it introduced to the graph edges to represent the reliability of the adjacencies. InferCARs first sorted the edges by weight and added edges to the vertex-disjoint paths, which were representing the CARs. Secondly, it searched for a set of paths that could cover all nodes in the graph to maximize the total edge weights in the paths.

InferCARs could output the intermediate ancestral genomes during the reconstruction, so that researchers could estimate the breakages on each evolutionary lineage. This algorithm discarded all of the conserved segments or orthologous blocks that shorter than 50 kb, so that the highest resolution was only 50 kb. The output of inferCARs was contiguous chromosome segments, so there was no guarantee to assemble the CARs into mature chromosomes. The local parsimony-based algorithm might ignore many true adjacencies that should exist in the ancestral genome.

In 2010, Ma et al. further introduced a probabilistic model to replace the parsimony model that used in inferCARs and developed the InferCARsPro approach [16]. InferCARsPro predicted the posterior probability of the adjacency of the ancestral genomes based on an extended Jukes-Cantor model for breakpoints. InferCARsPro used a neutral model to calculate the adjacencies variations. However, the biased model was now already been applied for ancestral genome reconstruction [33, 34]. InferCARsPro required a given phylogeny with known branch lengths to reconstruct the ancestral genome, which was hard to satisfy when it was applied to real genome dataset [16, 33]. Both InferCARs and InferCARsPro could only resolve the small phylogeny problems since it needed to assume that there was already a known phylogeny for input genomes. Although they were both applied to reconstruct the ancestral genomes for mammal genome datasets with four species and two out-groups, these two approaches still cannot deal with complicated evolutionary events including insertion, deletion and duplication [11, 16, 23].

In 2008 Ma et al. proposed a heuristic ancestral reconstruction approach DUPCAR, which put the genome rearrangements and gene duplication in a unified framework. DUPCAR was based on their previous CARs method and incorporated gene duplication events into the ancestral gene order predictions. The DUPCAR approach reconstructed the chromosome X of a placental mammal dataset and ancestral genomes of Paramecium tetraurelia [35].

3.1.2. ProCARs

ProCARs was a homology/adjacency-based approach that used a progressive approach to detect and assemble ancestral adjacencies into CARs. It firstly iteratively identified a set of potential ancestral adjacencies based on the current set of CARs. Next, it used a 2-phase procedure to compute new adjacent blocks to concatenate current CARs progressively. This algorithm started with a given phylogeny and a set of non-duplicated syntenic block seeds, which were obtained from the multiple sequence alignments [36, 37]. In each step, a set of CARs was first detected, and then a subset of non-conflicting adjacencies were selected and added to the current CARs. The proCARs approach finally output a set of concatenated CARs as the ancestral genome. These CARs had the maximum number of adjacencies and the minimum total homoplasy cost. The proCARS approach had been used to reconstruction of the Boreoeutherian ancestral genome from the dataset with ten mammals and two birds species.

ProCARs was a parameter-free method. Even though it still required a given phylogeny for ancestral reconstruction, it didn’t need the branch lengths of the phylogeny. The reconstructed ancestor was a set of completely resolved CARs with the information of rearrangement events that occurred. However, ProCARs could only consider the genomes with equal genome content and non-duplicated blocks. It did not allow insertion and deletion event either. In the ancestral reconstruction of real genome dataset, proCARs initiated the CARs set with 100kb syntenic blocks, so that the highest resolution was only 100kb, which was even lower than the InferCARs and InferCARsPro [24].

3.1.3. Gapped Adjacency

Gapped Adjacency was a homology/adjacency-based ancestral genome reconstruction algorithm, which used a flexible model to handle different kinds of genome level evolutionary events, including rearrangements, gene insertions, and losses and duplication [26]. Gapped Adjacency introduced a cutoff threshold t and constant value MAXa among contiguous ancestral regions, and reconnected the neighboring regions by considering gapped adjacencies. This algorithm iterated in a two-step procedure, which determined the genome content and multiplicity for each ancestral node in the first step. It increased the value from 1 to the constant MAXa and computed the adjacency scores, which allowed different number of gaps between adjacencies until reached the maximum setting. In the second step, it constructed a complete undirected graph Q. In this graph, the vertices were the two ends for each CARs, and the edges were then weighted according to the a-adjacency scores in step one. The ancestral reconstruction problem was converted to finding the heaviest Hamiltonian cycle through Q, where the edges with weight under threshold t were excluded to discard the less reliable adjacencies. Then it used the heuristic TSP solver Chained Lin-Khernigan (http://www.math.uwater loo.ca/tsp/concorde/index.html) to solve this problem and output the ancestral genome with gene ordering [26].

The TSP solver used in this algorithm ensured a completely assembled genome with a low error rate. The threshold t ensured that the final output won’t be only one single long chromosome that concatenation all genes. The Gapped Adjacency could only deal with the small phylogeny problem, so an existing phylogeny should be provided for reconstructing the ancestral genome. Gapped Adjacency was tested in the simulated datasets with WGD and non-WGD events. Their reconstructed ancestral genome remarkably reduced the number of CARs, and still kept a very low error rate. In the testing of simulated and real biological datasets (yeasts and cereal genome), it reduced the final number of CARs and output reasonable number of large segments.

3.1.4. ANGES

ANGES was a Python program that reconstructed the ‘Contiguous Ancestral regions’ (CARs) by comparing the organizations of modern genomes [25]. This approach was inspired by techniques of computing the physical maps of current genomes [38]. ANGES had a similar two-step procedure with Gapped Adjacency [26], which was establishing the genome content in the first step and determining the gene ordering in the second step. ANGES first detected genomic markers with similar organizations of each pair of genomes in given phylogeny, and it then derived the ‘Ancestral Contiguous Sets’ (ACS) with a given weight by the occurrence in the extant genomes. Next, ANGES linked these genomic makers into linear or circular segments, which could be referred to the ‘Contiguous Ancestral regions’ (CARS) [23]. ANGES used a greedy heuristic algorithm [23] and branch-and-bound [39] algorithm to compute the subset of CARs from the modern genomes and utilized a PQ-tree or the related PC-tree to represent the ancestral genomes. ANGES could reconstruct ancestral genome maps for multi-chromosomal linear genomes and unichromosomal circular genomes. It also could handle whole genome duplication, insertion and deletion events in the ancestral reconstructing. However, it still needed a given phylogeny as reference tree and could only deal with the small phylogeny problems. ANGES had been tested on simulated datasets, Boreoeutherian and yeast genome datasets. These ancestral reconstructions had discarded less than 5% of ACS, and maintained very low level of conflicting signals.

3.2. Ancestral Reconstruction Using Gene Adjacencies

3.2.1. EMRAE

In 2007, Zhao and Bourque developed the EMRAE algorithm to recover the ancestral rearrangement events based on a fixed phylogenetic tree [40]. EMRAE was a homology/adjacency-based algorithm and relied on the shared adjacencies across genomes in the phylogeny. The initial version of EMRAE could only deal with simplified rearrangement events in unichromosomal genomes. In 2009, they further improved this algorithm to handle more complicated genome rearrangement events, such as translocations, fusions, and fission for muti-chromosomal genomes. This algorithm first searched for the conserved adjacencies that existed in extent genomes. Then it used the distinctive signatures in the conserved adjacencies to track back the rearrangement events based on a parsimony assumption [40]. This algorithm was tested on simulated datasets and showed to have comparable sensitivity and higher specificity than the MGR algorithm [13]. EMRAE also processed same mammalian genome data that used in InferCARs [23], and predicted 1109 rearrangement events including 831 inversions, 15 translocations, 237 transpositions, and 26 fusions/fissions. The improved version of EMRAE could handle more complicated rearrangements events and breakpoint reuse of muti-chromosomal genomes, however, it still couldn't handle the duplication, insertion, and deletion events [40, 41].

3.2.2. PMAG/PMAG++

PMAG was designed to reconstruct the ancestral genome based on a probabilistic framework and flexible evolutionary model. PMAG used Bayes’ theorem and a novel transition evolutionary model to compute the adjacency variations along the edge of the given phylogeny. It first encoded genome content and gene adjacencies into binary strings and then calculated the conditional probability for each observed adjacency [42]. Next, PMAG assembled the gene adjacencies into ancestral genomes with maximum overall probability by converting this problem into an instance of Traveling Salesman Problem (TSP) [33, 17]. It employed the Chained-Lin-Kernighan heuristic TSP solver Linkern (http://www.math.uwaterloo.ca/tsp/index.html) to reconstruct the ancestral genomes. The initial version of PMAG could only handle the genome rearrangement insertion, and deletion. In the newest version, PMAG++ was improved to deal with the duplication and whole genome duplication events [43-45].

The reconstructed ancestral genomes were directly from the outputs of TSP solver, which could successfully link the gene adjacencies into completed mature chromosomes. These reconstruction results were very similar to the output of Gapped Adjacency. However, the Gapped Adjacency needed additional parameter and procedures to determine the chromosome number. PMAG also required a given phylogeny to reconstruct the ancestral genomes. Later PMAG was integrated with a gene order based phylogeny reconstruction approach [46], and set up a new ancestral reconstruction pipeline MLGO [18]. MLGO can handle big phylogeny problems and reconstruct the ancestral genomes even though the phylogeny is unknown. PMAG/PMAG++ could deal with the genome dataset with very high resolution (up to one gene), which was higher than all other current approaches.

4. DISCUSSION

Currently, most of the computational ancestral reconstruction approaches can only handle the genome datasets with equal contents with unique genome markers. And most of them can only handle the genome rearrangement event, which is only a fraction of the complicated evolutionary events in real life evolution. To deal with the complicated evolutionary event including insertion, deletion, duplication and whole-genome duplication, a few improvements have previously been studied [11, 26, 47]. Whole genome duplication is a special case in the evolution that results in doubling all the chromosomes of a genome, which is shown in the evolutionary history across the whole eukaryote domain [26]. It is further found to occur in the evolution of the Saccharomyces family and cancer cells [48, 49]. Ancestral reconstruction problems will become even more difficult and challenging when considering these complicated events mentioned above [26, 33]. In this paper, MGRA2 is the only distance/event-based approach reported can handle all kinds of evolutionary events [11]. For homology/adjacency-based approaches, only PMAG++, Gapped Adjacency and ANGES are reported can handle all kinds genome level evolutionary events. These approaches have the potential to be applied to solve real life ancestral reconstruction problems.

To explore the performance of these ancestral reconstruction approaches, we select four most famous and powerful approaches from both distance/event-based and homology/adjacency-based categories. We analyze and compare their performance on simulated datasets and evaluate their outputs. For the distance/event-based approaches, we select MGRA2 and GASTS. MGRA2 is the only distance/event-based approach that could deal with all kinds of evolutionary events [11]. GASTS is famous for its speed and accuracy for small-scale datasets, but it could only handle the problems with equal genome content [21]. For the homology/adjacency-based approaches, we select the PMAG++ and Gapped Adjacency. These two approaches are more powerful than the ANGES since they could deal with the high-resolution data. We also try to run InferCARsPro on the same datasets. However, it cannot output any solutions for all of the testing datasets after running 48 hours.

To make the simulated data more approximate to the real genome data, we provide a few simulated genome datasets in different genome sizes and evolutionary complexities (with different kinds of evolutionary events and rates). Each genome in the dataset has a total gene number n, n ∈ {1000, 2000, 3000, 4000}. Each genome may have different evolutionary rates r, r ∈ {0.5, 1, 2} with 50% relative fluctuation. So that the total number of evolutionary events between any two generations is in the interval of [,]. We also group each genome datasets with 20 genomes. And each genome has 5 chromosomes. For each genome dataset, the ancestral reconstruction approaches need to reconstruct 19 ancestral genomes, including 1 root ancestor and 18 internal ancestors. To make these experiments statistically reliable, for each particular setting, it simulates 10 independent datasets with distinct phylogenies. We record the average running time for each experiment and analysis the overall average accuracy from 10 independent experiments. The accuracy is calculated by the function:

A=

and represent the gene adjacencies or gene content in the true and reconstructed ancestral genomes. This experiment adapts a set of different evolutionary events in the simulated datasets, including genome rearrangements, insertion and deletion. Since GASTS and all other distance/event-based approaches could only deal with the genome rearrangements in equal content dataset, we conduct two separate experiments to evaluate the performance: reconstruction for equal content genome datasets with only genome rearrangement, and reconstruction for unequal genome content datasets with a combination of genome rearrangement, insertion and deletion.

4.1. Experiments on Equal Content Genome Datasets

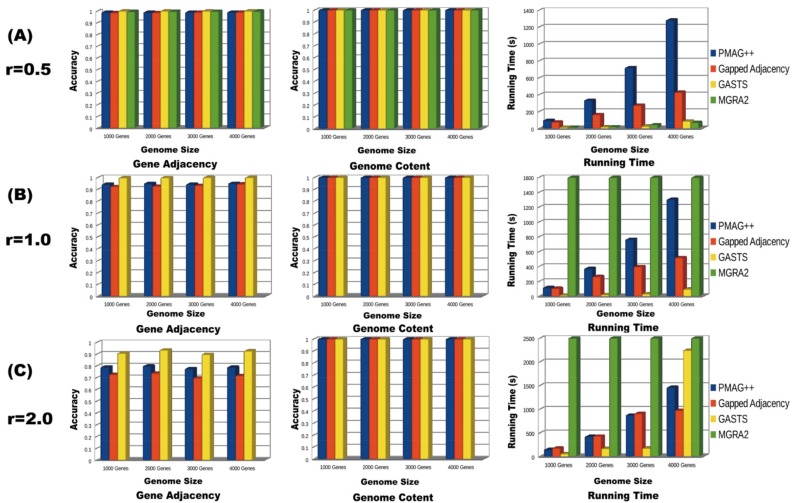
As shown in (Fig. 1), we present the results analyses on gene adjacency and genome content reconstruction for equal genome content datasets. 80% of the genome rearrangement events are set to inversions. And 20% are set to translocations. As shown in (Fig. 1A), when the evolutionary rate r is small (0.5), the homology/adjacency-based approaches PMAG++ and Gapped Adjacency can reach very high accuracy (almost 1) in gene adjacency reconstruction. For the distance/event-based approach, GASTS and MGRA2 have achieved a little bit higher accuracy (also almost 1) than the homology/adjacency-based approaches. MGRA2 has a lower accuracy than GASTS. All of these four methods could recover 100% of the genome content. In this case, distance/event-based approaches require less running time than the homology/adjacency-based approaches. For all four methods, as the genome size gets larger, the running time gets longer and the accuracy tends to be a bit lower but not much. (Fig. 1B) shows that as the revolutionary rate gets higher (r=1), the gene adjacency accuracies of PMAG++, Gapped Adjacency and GASTS get lower, but still preserve high accuracies that larger than 0.9. However, the MGRA2 could not give any output after running for 48 hours for all of the genome datasets with an evolutionary rate r larger than 1. GASTS achieve the highest accuracy and the shortest running time of these four approaches. When the evolutionary rate is set to 2, (Fig. 1C) shows that GASTS still keeps the highest accuracy (around 0.9), PMAG++ achieves the second highest accuracy (around 0.8), and Gapped Adjacency has the lowest accuracy (around 0.7). MGRA2 does not give any output. As the genome size getting larger, the running time of GASTS increases much faster than the homology /adjacency-based approaches.

Fig. (1).

Results analyses and comparisons of different approaches on equal content genome datasets. (The legend of MGRA2 is missing in Fig. B and C, because it cannot give any output after running 48 hours.)

In this experiment, none of these four approaches misses any genome content in the ancestral reconstruction. For the distance/event-based approaches, GASTS could grantee a sound performance in recovering the gene adjacencies. It can solve the ancestral reconstruction problems in very short time when the evolutionary rate is low. The homology/adjacency-based approaches need a few hundred seconds to solve the same problems. However, as the evolutionary rate getting higher, GASTS needs much more time than the homology/adjacency-based approaches to output the solutions for the large-scale datasets. Since it needs to solve much more difficult median problems with NP-complete complexity [21]. MGRA2 could only deal with the genome dataset with a low evolutionary rate. It could not give any output after running for 48 hours for the genome dataset with a high evolutionary rate. The homology/adjacency-based approaches PMAG++ and Gapped Adjacency could keep very high accuracy while the evolutionary rates are low. As the evolutionary rate increases, the performances for all methods decrease. The PMAG++ always has higher accuracy than the Gapped Adjacency in all cases. It is also important to notice that the gene number in the genome dataset has little influence on the performance of accuracies for the ancestral reconstruction.

4.2. Experiments on Unequal Content Genome Datasets

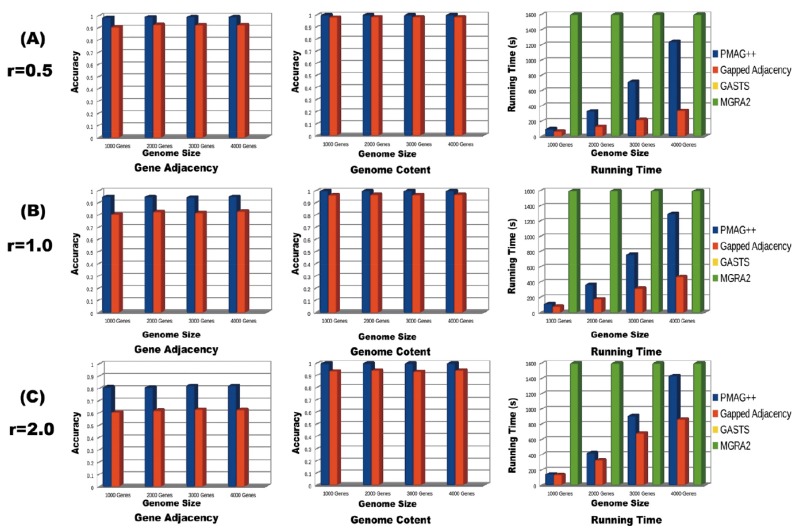
In order to compare the performances in unequal content genome datasets with more complicated genome evolutionary events. We set up evolutionary events between any two generations with 80% inversions, 10% translocations, 5% insertions and 5% deletions. The settings for the evolutionary rates and genome sizes are the same. (Fig. 2) presents the results analyses and comparisons for these four approaches. For the distance/event-based approaches, GASTS could not handle these complicated evolutionary events. MGRA2 was reported being capable of handling this kind of problem [11], but it could not give any output after running for 48 hours for any of these datasets. Only the homology/adjacency-based approaches could solve these problems and reconstruct the ancestral genomes. As it shown in (Fig. 2A), PMAG++ preserve very high gene adjacency accuracy (almost 1) for all four datasets with different genome size, while the accuracy of Gapped Adjacency is always about 10% lower (around 0.9). Both the PMAG++ and Gapped Adjacency could reconstruct the genome contents with very high accuracy. The PMAG++ preserves a higher accuracy (almost 1) than Gapped Adjacency (around 0.95) in the genome content reconstruction. The Gapped Adjacency requires less running time than PMAG++. (Fig. 2B) shows, when the evolutionary rate reaches 1, the PMAG++ could still keep a high accuracy (around 0.95), while the Gapped Adjacency could only reach the accuracy of 0.8. In the genome content and running time comparison, they have the similar result with (Fig. 2A). (Fig. 2C) shows the performance of these approaches under high evolutionary rate r=2. In this experiment, PMAG can still grantee a sound gene adjacency accuracy of 0.8 for all four genome datasets. However, the Gapped Adjacency can only reach the accuracy of 0.6. PMAG++ also maintains higher accuracy (> 0.95) than Gapped Adjacency (around 0.9) in the genome content reconstruction.

Fig. (2).

Results analyses and comparisons of different approaches on unequal content genome datasets. (The legend of MGRA2 is missing in this figure, because it cannot give any output after running 48 hours. The legend of GASTS is missing in this figure, because it cannot handle this datasets.)

Compared with the three experiments above, PMAG++ outperforms Gapped Adjacency in reconstructing the ancestral genome adjacency and genome content. PMAG++ preserves consistently better performance than the Gapped Adjacency in all cases. As the evolutionary rate getting higher, the accuracy gets lower, but PMAG++ could still keep a high accuracy even the evolutionary rate is high. Both PMAG++ and Gapped Adjacency can maintain very high accuracy in reconstructing the genome content. Both of them only require hundreds of seconds to get the solutions for the small-scale or large-scale dataset. The genome size of the testing dataset also has little influence on the performance of accuracy for gene adjacency and genome content, but it did affect the running time. Gapped Adjacency requires less running time than the PMAG++ in all experiments. MGAR2 cannot give any output after running for 48 hours for all experiments.

4.3. Improvement of Current Approaches

Recently the “intermediate genomes” approach is proposed, which is more likely a combined algorithm that could universally improve the current ancestral reconstruction methods. It searches for all possible adjacencies of intermediate genomes in a parsimonious path between two genomes. It also uses the restriction that all internal nodes must be in the intermediate genomes, to improve the current gene adjacency sets and find the ancestral genome. This algorithm uses an ancestral reconstruction approaches (such as SCJ and inferCARs) as extra information to search for the possible set of “intermediate ancestral genomes”, which is also called the “adjacency guide G”. The “adjacencies guide G” is used as a guide and call another function Guided-IG to build a set of adjacencies of the ancestral genome by calling the function Guided-IG-C. The Guide-IG-C function calls itself recursively in turn when an adjacency is applied in a component. It keeps running and finishing the ancestral genome reconstruction until no new adjacency being returned for homology/adjacency-based approaches, or until all adjacencies are in the same color, and one with more common adjacencies with the input genomes is returned for distance-base approaches [47]. This approach could improve the performance of homology/adjacency-based approaches with slightly increasing in wrong adjacencies. It also can improve distance/event-based approaches in almost all measurements [50].

CONCLUSION

This paper reviews the most recent and popular ancestral reconstruction approaches on the whole genome level. These approaches are either based on the evolutionary distance/ events among genomes, or the similarities of homologies /adjacencies of genomes. We review the advantages and limitations of these approaches in dealing with different datasets, evolutionary event and reconstruction problems. We also talk about the improvement and development of these approaches. Only a few of these approaches can deal with big phylogeny problem and reconstruct the phylogeny and ancestral genomes using the same input dataset, even if the phylogeny is unknown. These approaches include GRAPPA, MGR, MGRA MGRA2, MLGO, GASTS, and SCJ. Only Gapped Adjacency, PMAG++, MGRA2 and ANGES can handle unequal content genome datasets and all kinds of genome level evolutionary events. This paper selects two distance/event-based and two homology/adjacency-based approaches, analyzes and compares their performance in dealing with different datasets with different evolutionary events and complexities. GASTS achieves the best performance in solving the problems with equal genome contents, but it needs much more time when the evolutionary rate and genome size get larger. PMAG++ achieves the best performance in solving the problems with complicated evolutionary events with unequal genome contents, but the accuracy will get lower when the evolutionary rate gets higher. It is also important to notice that the intermediate genomes method could universally improve the performances for both distance/event-based and homology/adjacency-based approaches.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.