Abstract
The goal of this review article is to provide a conceptual based summary of how heritability estimates for complex traits such as obesity are determined and to explore the future directions of research in the heritability field. The target audience are researchers who use heritability data rather than those conducting heritability studies. The article provides an introduction to key concepts critical to understanding heritability studies including: i) definitions of heritability: broad sense versus narrow sense heritability; ii) how data for heritability studies are collected: twin, adoption, family and population-based studies; and iii) analytical techniques: path analysis, structural equations and mixed or regressive models of complex segregation analysis. For each section, a discussion of how the different definitions and methodologies influence heritability estimates is provided. The general limitations of heritability studies are discussed including the issue of “missing heritability” in which heritability estimates are significantly higher than the variance explained by known genetic variants. Potential causes of missing heritability include restriction of many genetic association studies to single nucleotide polymorphisms, gene by gene interactions, epigenetics, and gene by environment interactions. Innovative strategies of accounting for missing heritability including modeling techniques and improved software are discussed.
Keywords: Heritability, Complex traits, Twin studies, Family studies, Path analysis, Missing heritability
1. INTRODUCTION
The nature versus nurture debate of disease causation has been occurring since the mid-1800s. As the understanding of genetic and environmental influences has improved it has become clear that both nature and nurture play important roles in most complex diseases. Heritability is the quantification of the overall phenotypic variation that is attributable to genetic factors [1-4]. Applications of heritability estimates include defining the upper and lower boundaries for the ability of genetics to predict disease, determining disease risk in family members, providing the justification for further genetic studies, allowing for the comparison of the genetic origins of the same trait across different populations and the same trait within a population across time, and indirectly providing insights into the mechanisms of action of genes [2, 5]. However, there are inherent limitations of heritability studies that can decrease the accuracy and reliability of estimates that need to be understood by those who use them. The intended audience of this review are users of heritability data, rather than those conducting heritability studies with the goal of providing a conceptually based summary of how heritability estimates are determined including the limitations of each technique and the future directions of research in the heritability field.
1.1. Definitions of Heritability
Heritability estimates discriminate between genetic and environmental contributors to phenotypic variance which are categorized into four categories A, C, D, and E [4, 6]. The sources of genetic variance include:
A: Additive genetic influences which are calculated as the sum of the effect of each allele at all loci which influence the phenotype
-
D: Non-additive genetic influences which include the interaction between alleles at the same locus (dominance) or at different loci (epistasis)
The sources of environmental variance include:
C: Shared environmental factors which are influences common to members of a family such as socioeconomic status
E: Unique environmental influences such as differences in parental treatment, prenatal environment, and life events
There are two different definitions for heritability commonly described in the literature. Narrow-sense heritability (h2) refers only to the additive genetic component (A) and represents the degree to which genes transmitted by parents determine the phenotype of their children [5]. Broad sense heritability (H2) is the ratio of total genetic variance (A and D) divided by the total phenotypic variance. It explains the amount of phenotypic variation attributable to genetics, including gene x gene interactions and dominant effects [3, 5]. In practice, heritability is estimated in a variety of ways. As an illustration, a systematic review of heritability studies of body mass index (BMI) finding a total nine different definitions of heritability from 32 studies [7]. Many papers fail to distinguish between the types of heritability leading to poor reporting of heritability estimate methodology in individual papers and the inappropriate combination of estimates in meta-analyses [3].
2. CLASSICAL STUDY DESIGNS FOR HERITABILITY– TWIN, ADOPTION, AND FAMILY STUDY DESIGNS
2.1. Types of Data for Classical Heritability Studies
Three main sources of data are used for heritability studies; monozygotic (MZ) and dizygotic (DZ) twins, adoption studies, and family studies. For each data source, an example of a commonly used heritability formula is included to clarify the assumptions made about relationships between relatives.
2.1.1. Twin Studies
Twin studies are a frequently used method to determine heritability taking advantage of the nearly 100% shared genetic data of monozygotic (MZ) twin pairs. Because MZ pairs do not differ from one another genetically (A and D) and also have the same shared environmental factors (C), any differences in phenotypic traits can be attributed to unique environmental influences (E). Dizygotic twins (DZ), like other sibling pairs only share 50% of their genetic data and are assumed to have the same shared environment (C) [4, 6]. Assuming that the unique environment (E) equally contributes to the development of the phentoype of interest in MZ and DZ pairs, it is possible to estimate the variance contributed by both additive and non-additive genetic effects (H2) by comparing the phenotypic correlation in MZ and DZ pairs [6]. Falconer’s Formula is applied which subtracts the phenotypic correlation in DZ pairs from the phenotypic correlation in MZ pairs and multiplies the result by two [H2= 2(rMZ – rDZ)] [4, 8, 9]. To simplify, because MZ pairs share 100% of their DNA, any phenotypic differences between twin pairs must be because of their unique environment (E). Furthermore, both MZ and DZ twin pairs are expected to have the same shared environment (C). The application of the formula also assumes that the unique environment (E) contributes to phenotypic variance equally in MZ and DZ pairs. If the environment has the same effect in DZ and MZ twins, the additional phenotypic correlation between DZ and MZ pairs must be because of genetic factors. Subtracting the DZ phenotypic correlation from the MZ phenotypic correlation provides an estimate of the variance contributed by genetics when 50% of DNA is shared. Therefore, the result must be multipled by two to estimate the effect for 100% shared DNA. The resulting estimate is a measure of broad sense hertiability.
Limitations of twin studies include that the application of the formula assumes that gene-environment correlations and interactions are minimal and that the amount of variance explained by shared environmental factors is identical in MZ and DZ pairs [4]. A limitation of heritability estimates derived from twin studies is the potential for unmeasured gene by environment interactions to contribute to phenotypic variance [10]. Modeling techniques discussed in the next section can take into account known gene by environment interactions, however challenges in understanding the interactions limit their utility [2, 4, 5]. Similarly, the evidence indicates that it is likely that MZ twins have a greater shared environment compared to DZ twins, but the effect on heritability estimates is modest [11]. Twin studies also do not take the effect of epigenetics into account. DNA methylation patterns are significantly more different in pairs of DZ twins compared to MZ twins [12]. Making these assumptions increases the risk that heritability estimates are artificially inflated by incorrectly attributing the contribution of environmental factors to genetics [10].
2.1.2. Adoption Studies
In 1979, the interest in twins expanded to include twins who have been reared apart. Adoption studies of MZ pairs improve upon normal twin studies because there is no shared environment (C) therefore bypassing the potentially incorrect assumption that the shared environment explains the same amount of variance in MZ and DZ twins [4]. The variance explained by unique environmental influences can be safely assumed to be equal in the separated twins. In this unique situation, the intra-pair correlations are estimates of the amount of the variance explained by genetic factors alone and this provides a broad sense heritability estimate (H2). The formula used to determine heritability in adoption studies is the phenotypic correlation divided by the genotypic correlation [5]. Though adoption studies are considered the best estimate of heritability, the results should still be cautiously interpreted. If twins are not separated until later in childhood, the shared environment factor should not be assumed to be zero. Additionally, the biological parents, adoptive parents, and twins themselves may not be representative of the general population which could limit the generalizability of findings from adoption studies [4, 5, 13].
2.1.3. Family Studies
Family studies are also used to determine the heritability of phenotypes. Compared to twin and adoption studies, it is often easier to recruit participants for family studies because of the increase in the number of people meeting eligibility criteria. Genotypic data can be collected using either genetic marker data or more frequently, estimates of the expected genetic relatedness based upon the relationship between the two individuals. For example, full siblings and parent-child units are expected to share 50% of their genetic material while first cousins are only expected to share 12.5% [5]. For binary outcomes such as a disease trait being present or absent, a 2 by 2 contingency table showing the concordance and discordance of the disease status in relatives can be created. The formula provides the intraclass correlation coefficient (t). N11 is the number of relatives concordant for having the disease, N00 is the number of relatives concordant for not having the disease, and both N01 and N10 are the numbers of relative pairs discordant for the disease. Dividing t by the coefficient of correlation for the expected genetic relatedness of the individuals (for example 0.5 for full siblings) provides a narrow sense heritability estimate (h2) [5]. For quantitative characteristics such as BMI, heritability can be estimated by the slope of the regression line which approximates the heritability of a trait when the mean phenotypic value of the parents is used. If data from only one parent is available, heritability is estimated as two times the value of the slope of the regression line [2].
Classical family study designs are limited by only being applicable to family members with the same relationship, for example pairs of siblings, or parent-offspring combinations as well as the risk of confounding of genetic and environmental effects because the formula ignores non-additive genetic effects (D) and shared environmental factors (C), particularly in full siblings [5]. If family studies only include only one parent, the parent of origin effect in which the expression of the phenotype is dependent on whether the genes are from the mother or father cannot be investigated. To minimize confounding of shared environmental effects, other more distant familial relations can be tested, however this decreases the power [14]. Additionally, the underlying assumptions of the genetic relationships between relatives are flawed. Offspring tend to inherit long segments of DNA from each parent resulting in deviations from the expected 50% of DNA coming from each parent [1, 15]. Different combinations of DNA segments from each parent in sibling pairs results in between 37 and 62% shared genetic information [15].
Expanding upon the work done in natural populations such as animals where pedigrees may not be known and genetic markers are used to determine relatedness [16], Visscher et al. (2006) developed a method that compares whole genomes of relatives to determine genetic relatedness and then correlates the genetic relatedness with the phenotype of interest to provide an estimate of heritability free of environmental causes as only within and not between family differences are necessary. Interestingly, when this technique was used to estimate the heritability of height, the estimate provided (H2 = 0.80) is very similar to the results from twin studies [15]. While the genetic marker method seems equivalent to twin studies in theory, it is more feasible as large numbers of family members are easier to come by than large numbers of twins. However, the cost of genotyping all participants may not be worth the added benefits [15].
2.2. Modeling Techniques Used for Heritability Estimates Using Twin and Family Designs - Path Analysis, Structural Equations, POINTER and REGRESS
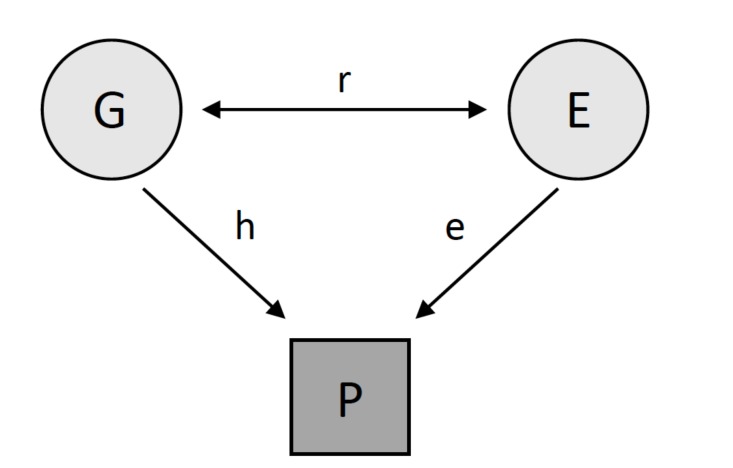
Path analysis diagrams (Fig. 1) are a method of schematically showing the covariance between measured and unmeasured variables by connecting variables with single or double headed arrows showing the direction of relationships [4]. The models displayed by path analysis can be used to create structural equation models (SEM), a class of mixed liner models, which estimate narrow sense heritability (h2) by maximizing the goodness-of-fit function between observed and predicted covariance matrices, typically using maximum-likelihood methods. In the context of heritability, SEM allows for the association between latent traits including shared and unique genetic shared environmental variables and the phenotype to be measured while factoring in the genetic covariance [1, 4, 5]. In SEM, the shared environmental factors are confounded with non-additive genetic effects unless adopted twins have been included in the study due to an inability to measure each variable independently. Heritability is calculated as a2 / (a2 + c2 + e2) where a2 is the amount of variance in phenotype explained by additive genetic effects, c2 is the amount of variance in phenotype explained by shared environmental influences, and e2 is the amount of variance in the phenotype explained by unique environmental factors. In some cases, d2 may be substituted for c2 dependent on which appears to be the stronger driver of the correlation between family members [1, 4, 5]. SEM offers a significant advantage over formulas because they are able to take multi-variable data into account such as sex, allowing for the combination of different types of familial relationships to be included within the same model, are able to test the goodness of fit of a model, allow for different models to be compared, provide estimates of measurement error, investigate the genetic overlap between disorders [4, 5], as well as allowing for gene by environment interactions to be investigated [6]. Despite the many advantages of SEM, issues can arise when including too many variables in the model, particularly with a small sample size, and the constraint of the variance values to certain parameters can cause bias increasing heritability estimates [5].
Fig. (1).
G represents genetic effects, E represents environment effects, and P represents the phenotype of interest. R is the correlation between genetics and the environment, h is the narrow-sense heritability estimate and e is the effect of the environment.
Mixed and regressive models of complex segregation analysis, as implemented in the computer programs POINTER or REGRESS, have been developed to estimate heritability in presence of a major disease-causing gene [17-20]. However, the validity of these approaches has been questioned, as the claims for major loci controlling complex traits such as insulin secretion or abdominal body fat have not been validated by subsequent gene identification studies [21, 22].
2.3. Summary and Limitations of Twin, Adoption and Family Designs
Twin, adoption and family study designs for heritability share several similarities. A summary of statistical methods can be found in (Table 1). Each design assumes that there are
Table 1.
Comparison of statistical methods used to assess heritability estimates for human complex traits.
| Method of Assessing Heritability |
Type of
Participants |
Statistical Methods | Strengths | Limitations | ||
|---|---|---|---|---|---|---|
| Twin studies | Monozygotic and dizygotic twins | Falconers formula is used to provide a broad sense heritability estimate. This formula assumes that the higher degree of correlation in MZ twins compared to DZ twins is attributable entirely to genetics. Falconers formula: H2= 2(rMZ – rDZ) Where H2 is broad sense heritability, rMZ is the correlation in monozygotic twins and rDZ is the correlation in dizygotic twins for the same phenotype. |
Conceptually simple Can be calculated without advanced statistical programs Does not require genotyping |
Assumes gene-environment correlations and interaction are minimal Assumes variance explained by shared environmental factors is identical in monozygotic and dizygotic pairs Could result in over estimation of heritability |
||
| Adoption studies | Monozygotic twins raised separately | Adoption studies are used to estimate broad sense heritability. The formula assumes that all phenotypic correlation is due only to genetic factors as there is no shared environment and the unique environmental influences should be equal. H2= rphenotype /rgenotype Where H2 is broad sense heritability, rphenotype is the correlation in the phenotype of monozygotic twins and rgenotype is the genetic correlation in MZ twins (which equals 1). |
Considered the best estimate of heritability due to most number of underlying assumptions being true | Difficult to find a sufficient sample size Need to have twins that were separated early in life Biological parents, adopted twins, and adoptive parents may have characteristics that cannot be generalizable to the average person |
||
| Family Studies | Family dyads with a known degree of relatedness | An estimate of narrow sense heritability is calculated by comparing the agreement of the phenotype in family pairs by the expected correlation based on genetic relatedness using the formula: Where t is the intraclass correlation coefficient, N11 is the number of relatives concordant for having the disease, N00 is the number of relatives concordant for not having the disease, and both N01 and N10 are the numbers of relative pairs discordant for the disease. Dividing t by the coefficient of correlation for the expected genetic relatedness of the individuals (for example 0.5 for full siblings) |
Compared to twin studies, easier to find a sufficient sample size | All relatives must have the same relationship Risk of confounding of genetic and environmental effects because the formula ignores non-additive genetic effects and shared environmental factors Underlying assumptions about genetic relationships are often flawed due to long segments of DNA being inherited |
||
| Method of Assessing Heritability |
Type of Participants |
Statistical Methods | Strengths | Limitations | ||
| Structural Equation Modeling | Twin or family data | Estimates narrow sense heritability by creating linear regression models and maximizing the goodness-of-fit function between observed and predicted covariance matrices. h2 = a2 / (a2 + c2 + e2) c2 can be replaced with d2 if non-additive genetic effects are a bigger driver of the relationship of the phenotype in pairs of twins |
Allows the use of multi-variable data so family members with different relationships can be included Can investigate gene x environment interactions Can adjust for sex and other potential confounders or effect modifiers Genetic testing is not required |
Like classical family study designs, the assumptions of the underlying genetic relationships between individuals may not be true. Small sample size limits how many variables can be included in the model Can only include either shared environmental influences or non-additive genetic effects in model |
||
| Genome-wide association studies | Data from unrelated individuals | Genome wide association studies look at the association using linear or logistic regression between individual single nucleotide polymorphisms and the genotype of interest in a large number of people. Narrow sense heritability can be calculated by summing the variance in the phenotype explained by each individual SNP. However, this method is not commonly used to estimate heritability due to the number of SNPs not yet identified for any given phenotype. | Can use unrelated individuals Linear and logistic regression models allow the inclusion of covariates |
To date, the sample size requirements to detect gene by gene interactions and gene by environment interactions have been a limiting factor. Requires genotyping of all individuals included in the study. SNPs often have small effect sizes and are difficult to detect. |
||
| Genome-wide complex trait analyses | Data from unrelated individuals | Genome-wide complex trait analyses includes all SNPs simultaneously in a mixed linear regression model which provides a higher estimate of heritability compared to genome-wide association studies. | Includes more SNPs than genome-wide association studies and therefore provides estimates of heritability that are closer to those derived from classic twin and family designs. | Same limitations as for genome-wide association studies. | ||
four contributors to the observed phenotype, additive genetic influences, non-additive genetic influences, shared environmental factors, and unique environmental influences. Each design also assumes the degree of relatedness amongst participants based on the theory that offspring receive exactly 50% of their genes from each parent, which has been proven to be incorrect. Using these assumptions, different formulas are used to calculated heritability. Falconer’s formula is applied to twin studies which provides an estimate of broad sense heritability (H2) by comparing the correlation of the phenotype in monozygotic twins to dizygotic twins. The assumption is that any differences in monozygotic twins and dizygotic twins must be due to genetic differences. Adoption studies similarly provide an estimate of broad sense heritability (H2) by assessing the correlation in phenotype between pairs of monozygotic twins using the assumption that the correlation is solely due to genetic effects as there is no shared environment. Family studies on the other hand calculate narrow sense heritability using more complex formulas taking the degree of relatedness into consideration. In addition to basic heritability formulas, twin, adoption, and family studies can all be assessed using SEM to model the observed relationship between the phenotype in different relatives and the underlying latent constructs of genetic and environmental effects.
Twin, adoption, and family studies are a simple method of understanding the genetic contribution to disease and are limited in their utility. They make assumptions about the degree of genetic relatedness, have relatively rigid study designs and inflexibility for analyses and can only inform researchers about the extent to which genetics contribute to phenotypic variances but not provide any insight about the underlying genetic architecture of the disease. Regardless of the design used, an overarching challenge with classical heritability estimates is that they are population specific. All components of the model, additive genetic effects (A), non-additive genetic factors (D), shared environment (C), and unique environment (E) are specific to the population of study. If the contribution of just one of these four factors of disease risk is altered between populations the resulting heritability estimate will also change. Another limitation of all three study designs is that the participants for these studies are rarely randomly selected and the population from which they came is not well defined. Often, participants in genetic studies are recruited based on their phenotype and family members are then invited to participate in the study. These family members may undergo additional testing for the phenotype. If this occurs, the prevalence of the phenotype will likely appear to be higher in the family members than in the general population which can result in an increase in the heritability estimate 5. Several techniques exist to correct heritability estimates for ascertainment bias when the study participants are selected based on the phenotype. The two most common methods are briefly described. Hopper and Mathews method adjusts the heritability estimate based on the specific mean and total variance of the genetic and environmental components for each individual family grouping. Elston and Sobel proposed that the same correction be applied to all family groupings whenever the family is selected based on a certain threshold of the phenotypic trait [23].
The problems of the study designs and population specific estimates is clear when looking at the evidence of the heritability of body mass index (BMI), a measure of obesity calculated as kilograms of weight divided by meters squared of height (kg/m2). A meta-analysis of 88 independent twin studies (n=140,525) estimated the heritability to be 0.75 (95% confidence interval 0.74 to 0.76),with substantial between study heterogeneity (I2 = 86.1%, p<0.001) and individual study estimates ranging from 0.47 to 0.90. Data from 27 family studies (n=42,968) provided an estimate of 0.46 (95% confidence interval 0.40 to 0.52) with a between study heterogeneity of 90.4% (p<0.001) and individual study estimates ranging from 0.24 to 0.81 [24]. Due to small sample sizes, the confidence intervals of heritability estimates from twins reared apart studies overlap, but range from 0.39 to 0.60 [13]. A study by Stunkard et al. (1990) is of particular interest. In addition to a twin adoption study which estimated heritability to be 0.70 (95% confidence interval 0.52 to 0.88) in men and 0.66 (95% confidence interval 0.52 to 0.75) in women, they also used a classic twin design with MZ (n=154) and DZ (n=208) pairs to provide a heritability estimate of 0.82 (95% confidence interval 0.66 to 0.98) for males and 0.78 (95% confidence interval from 0.64 to 0.92) for females. Applying a model using maximum-likelihood estimations yielded heritability estimates of 0.74 for males and 0.69 for females. If the assumption that adoption studies provide the best available estimates for heritability is true, then such modeling strategies appear to provide more accurate estimates in comparison to the classic twin design [25].
3. NOVEL METHODS FOR ESTIMATING HERITABILITY
3.1. Genome-wide Association Studies
With the wide-spread availability of cost-effective whole-genome SNP arrays, the focus has shifted from classic heritability studies which estimate the genetic similarity between individuals by assessing their degree of relatedness, to using data at the single nucleotide polymorphism level to assess the genetic similarity between individuals through the use of genome-wide-association studies (GWAS) Briefly, GWAS is an approach which analyzes a complete set of DNA and looks for associations between specific makers and a phenotypic trait. A significant advantage of the GWAS approach is that unrelated individuals can be used for analyses offering greater flexibility in study design and recruitment. For complex diseases, the association between any given SNP and the phenotype is small and difficult to detect [10, 26]. Consequently, a limited number of SNPs have been identified for any specific trait and the variance in the phenotype explained by those SNPs is much lower than what is found using classic heritability studies [24, 27]. In traditional GWAS analyses which uses logistic or linear regression models to predict the phenotype using each SNP of interest in a separate model, only SNPs meeting the requirements for a genome-wide association p < 5 × 10-8 [28] are used as predictor variables. However, it has been found that the inclusion of SNPs that meet a minimum threshold for association with the phenotype of interest, but do not necessarily meet the requirements for a genome-wide association can improve the accuracy of disease risk prediction, particularly when used in conjunction with novel technology such as machine learning algorithms which allow for models to take advantage of interactions between genetic markers. This technique was applied to GWAS data for Type 1 Diabetes which significantly improved the predictive value of the model compared to only using confirmed SNPs in regression models [29].
3.2. Genome-wide Complex Trait Analysis
Software programs such as GCTA (genome-wide complex trait analysis) have since been developed to facilitate the use of GWAS data and circumvent the issue of undetected SNPs with small effect sizes. GCTA can estimate the amount of the phenotype explained by genetic factors without needing to know all the genetic variants associated with the genotype [30, 31]. Like GWAS, GCTA analyses can include unrelated individuals, but improves upon the single SNP model by including all SNPs simultaneously in a mixed linear model including both random and fixed effects. Fixed effects include variable such as sex and age and the total genetic effects for the whole genome or a single chromosome is included as a random effect [32]. Applying this type of analysis method to human height increased the estimate of the variance explained be genetic factors from approximately 5% to 84%, which is much closer to the 0.80 estimate provided by classic heritability studies [31].
4. MISSING HERITABILITY
One of the challenges in understanding the genetics of complex traits is the discrepancy between heritability estimates calculated using the classical designs and the amount of variance explained by known genetic variants identified through genome wide association studies (GWAS) [10, 30]. Using obesity as an example, even the most conservative heritability estimates indicate that over 20% of the variation in obesity is explained by genetics, whereas the single nucleotide polymorphisms (SNPs) identified by GWAS only account for approximately 2.7% of obesity risk [24, 27]. GCTA has also been used to estimate the percentage variance in BMI explained by genetic factors in both children and adults. In adults, the variance explained was estimated to be 27% [33] and in children it was estimated to be 37% [34] suggesting a significant improvement over standard GWAS association studies. The discrepancy between the percentages of variability in the phenotype explained by twin, adoption and family designs compared to GWAS or GCTA can largely be attributed to the method of estimation. The classic study designs provide higher estimates of heritability because the calculations capture all genetic effects, both additive and non-additive, by comparing the individuals with a known degree of relatedness and consequently an assumed percentage of genetic similarities. In contrast, the variability in GWAS only includes additive genetic effects from previously identified SNPs using conservative statistical thresholds (P < 5 x 10-8). GCTA includes more genetic information that GWAS by including markers from an entire chromosome or genome, but still only includes additive effects and a restricted number of SNPs while excluding other types of genetic variations (e.g. rare mutations, CNVs). The concern with including a limited number of SNPs in estimating variability can be explained by the infinitesimal model which states that an infinite number of unlinked loci each with an infinitesimal effect produce the phenotypic trait [35]. This appears to be true in complex diseases such as obesity. To date, there have been around 140 SNPs found to be associated with BMI / obesity, [36] but like most complex diseases, the effects of individual SNPs are quite small, typically with odds ratios of less than 1.5 and often as small as 1.1 [10, 26].
The infinitesimal model assumes that the SNPs contributing to the phenotype are unlinked. In practice, SNPS for complex diseases are commonly in linkage disequilibrium which has caused further problems in gene identification efforts. Examples of the challenges posed by linkage disequilibrium include the potential that alleles tested in GWAS may not be the true risk alleles and instead alleles in linkage disequilibrium with risk alleles, decreasing the measurable effect size [27-39]. Similarly, common SNPs in linkage disequilibrium with a rare variant may also lead to the detection of false associations [40]. Already small effect sizes become harder to detect when corrections for multiple testing are made. The significance level for a genome wide association is p < 5 × 10-8 [28]. Low minor allele frequencies can further impede gene identification efforts [30, 31]. Rare variants with very low allele frequencies not included in GWAS could also have large effect sizes [8, 37, 39].
The current perspective on missing heritability largely focuses on genetic risk variants that have not been discovered. However, as shown by Zuk et al., 2012 through different models, some of the “missing heritability” for complex diseases may instead be termed “phantom heritability”. Phantom heritability occurs when gene x gene and gene x environment interactions contribute to heritability estimates based on twin/family studies, but are not included in the estimates of heritability based on known risk variants [41]. GWAS are limited in detecting gene x gene interactions, also called epistasis, without additional advanced mathematical modeling. Geneticists are also poorly equipped to study gene by environment interactions. Environmental factors can refer to both external environmental factors such as socioeconomic factors and medication use as well as individual factors such as lifestyle choices [42]. Both gene by gene and gene by environment interactions are difficult to study because of small effect sizes. Additionally, because interaction analyses require a greater number of individual tests than investigating the effects of single SNPs, more stringent p-values are required after adjusting for multiple testing [43].
Another challenging component of heritability to study is epigenetics. Epigenetics refers to modifications in gene expression that are unrelated to changes in DNA typically referring to modifications of the histones which the nucleotides are wrapped around, methylation of the cytosine residue in DNA and microRNA-mediated post-transcriptional gene silencing [44]. Genetic variants that are present in one generation result in epigenetic modifications that affect phenotypes in subsequent generations, thereby decoupling the conventional relations between genotype and phenotype, and perhaps, contributing to 'missing heritability'. Under some conditions, these transgenerational genetic effects can be as frequent and strong as conventional inheritance, and can persist for multiple generations [45]. Epigenetic changes are often influenced by environmental factors and can be reversed making measurement of epigenetics problematic [39]. In the context of heritability it is known that epigenetic changes can be passed on to the next generation like normal genetic mutations but with a notable exception, the epigenetic transmission may be spontaneously reversed. The magnitude of the effect of epigenetic changes on disease risk is not yet known, nor is it understood how frequently transgenerational epigenetic changes take place and how permanent these changes are in subsequent generations [44].
Further complicating our understanding of the role of epigenetics in the context of heritability is disentangling transgenerational epigenetic changes from epigenetic changes that happen in utero in response to maternal experiences [46]. Given our limited understanding of epigenetics, it is difficult to determine the contribution of epigenetics to missing heritability. True transgenerational epigenetic effects would be likely to increase heritability estimates, while non-transgenerational epigenetic effects may inflate heritability estimates if they cluster in families, or decrease heritability estimates if they do not [47]. The last commonly cited explanation for missing heritability is that traditional GWAS have focused on single nucleotide polymorphisms. There are other important components of the genome including small insertions and deletions, copy number variants, inversions and translocations, and chromosomal abnormalities which contribute to variations in the genome [48]. Despite the development of techniques to help explain the “missing heritability”, there is still the need to consider that family and twin studies of heritability are prone to overestimate the variance explained by genetic factors.
CONCLUSION AND PERSPECTIVES
There are many useful study designs to estimate the variance of a phenotype explained by genetics. Twin, adoption, and family studies are classic heritability designs that regardless of the formulas or models applied, attempt to partition the genetic and environmental effects based on assumptions of the genetic relatedness between individuals. In the post-GWAS era, the focus has shifted towards gene identification and estimating the variation of a phenotype explained by genetics by combining the individual additive effects of known associated SNPs. At this point in time, the variance explained by SNPs is very small relative to the heritability estimates provided by classic designs with the difference being termed “missing heritability”. It is clear that a great deal of the missing heritability puzzle is explained by the multiple SNPs associated with complex diseases, other types of genetic variations (e.g. copy number variants), the effect of epigenetics, and challenges in identifying gene by gene and gene by environment interactions. However, the strong likelihood of confounding factors for environment and genetic effects present in classic heritability studies may potentially be causing artificially inflated heritability estimates and cannot be discounted as contributing to missing heritability. The availability of whole-genome information in large populations coupled to the development of integrative methods that deal with different types of gene variations, gene by gene and gene by environment interactions may ultimately precise the contribution of genetics to the variation of complex traits [49]. Until gene identification methods for complex diseases improve, classic heritability studies provide the best approximation of the contribution of genetics to phenotypes. However, the users of heritability data must be aware of the limitations of the study designs and not be over zealous in their interpretation of the results.
AUTHORS’ CONTRIBUTIONS
Both authors contributed to the conception and production of the manuscript and approved the final version.
ACKNOWLEDGEMENTS
David Meyre is supported by a Tier 2 Canada Research Chair in Genetics of Obesity.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
REFERENCES
- 1.Vinkhuyzen A.A., Wrap N.R., Yang J., Goddard M.E., Visscher P.M. Estimation and partioning of heritability in human populations using whole genome analysis methods. Annu. Rev. Genet. 2014;47:75–95. doi: 10.1146/annurev-genet-111212-133258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Visscher P.M., Hill W.G., Wray N.R. Heritability in the genomics era -concepts and misconceptions. Nat. Rev. Genet. 2008;9(4):255–266. doi: 10.1038/nrg2322. [DOI] [PubMed] [Google Scholar]
- 3.Wray N.R., Visscher P.M. Estimating trait heritability. New Educator. 2008;1(1):29. [Google Scholar]
- 4.Rijsdijk F.V., Sham P.C. Analytic approaches to twin data using structural equation models. Brief. Bioinform. 2002;3(2):119–134. doi: 10.1093/bib/3.2.119. [DOI] [PubMed] [Google Scholar]
- 5.Tenesa A., Haley C.S. The heritability of human disease: estimation, uses and abuses. Natl. Rev. 2013;14(2):139–149. doi: 10.1038/nrg3377. [DOI] [PubMed] [Google Scholar]
- 6.Boomsma D., Busjahn A., Peltonen L. Classical twin studies and beyond. Nat. Rev. Genet. 2002;3(11):872–882. doi: 10.1038/nrg932. [DOI] [PubMed] [Google Scholar]
- 7.Min J., Chiu D.T., Wang Y. Variation in the heritability of body mass index based on diverse twin studies: a systematic review. Obes. Rev. 2013;14(11):871–882. doi: 10.1111/obr.12065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sham P.C., Cherny S.S., Purcell S. Application of genome-wide SNP data for uncovering pairwise relationships and quantitative trait loci. Genetica. 2009;136(2):237–243. doi: 10.1007/s10709-008-9349-4. [DOI] [PubMed] [Google Scholar]
- 9.Falconer D.S. Introduction to Quantitative Genetics. New York: Ronald Press Co; 1960. [Google Scholar]
- 10.Manolio T.A., Collins F.S., Cox N.J., Goldstein D.B., Hindorff L.A., Hunter D.J., McCarthy M.I., Ramos E.M., Cardon L.R., Chakravarti A., Cho J.H., Guttmacher A.E., Kong A., Kruglyak L., Mardis E., Rotimi C.N., Slatkin M., Valle D., Whittemore A.S., Boehnke M., Clark A.G., Eichler E.E., Gibson G., Haines J.L., Mackay T.F., McCarroll S.A., Visscher P.M. Finding the missing heritability of complex diseases. Nature. 2009;461(7265):747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Felson J. What can we learn from twin studies? A comprehensive evaluation of the equal environments assumption. Soc. Sci. Res. 2014;43:184–199. doi: 10.1016/j.ssresearch.2013.10.004. [DOI] [PubMed] [Google Scholar]
- 12.Kaminsky Z.A., Tang T., Wang S-C., Ptak C., Oh G.H., Wong A.H., Feldcamp L.A., Virtanen C., Halfvarson J., Tysk C., et al. DNA methylation profiles in monozygotic and dizygotic twins. Nat. Genet. 2009;41(2):240–245. doi: 10.1038/ng.286. [DOI] [PubMed] [Google Scholar]
- 13.Maes H.H., Neale M.C., Eaves L.J. Genetics and environmental factors in relative body weight and huma adiposity. Behav. Genet. 1997;27(4):325–351. doi: 10.1023/a:1025635913927. [DOI] [PubMed] [Google Scholar]
- 14.Ødegård J., Meuwissen T.H. Estimation of heritability from limited family data using genome-wide identity-by-descent sharing. Genet. Sel. Evol. 2012;44(16) doi: 10.1186/1297-9686-44-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Visscher P.M., Medland S.E., Ferreira M.A., Morley K.I., Zhu G., Cornes B.K., Montgomery G.W., Martin N.G. Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genet. 2006;2(3):e41. doi: 10.1371/journal.pgen.0020041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bérénos C., Ellis P.A., Pilkington J.G., Pemberton J.M. Estimating quantitative genetic parameters in wild populations: a comparison of pedigree and genomic approaches. Mol. Ecol. 2014;23:3434–3451. doi: 10.1111/mec.12827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lalouel J.M., Morton N.E. Complex segregation analysis with pointers. Hum. Hered. 1981;31(5):312–321. doi: 10.1159/000153231. [DOI] [PubMed] [Google Scholar]
- 18.Lalouel J.M., Yee S. POINTER: a computer program for complex segregation analysis with pointers. Honolulu: 1980. [Google Scholar]
- 19.Bonney G.E. On the statistical determination of major gene mechanisms in continuous human traits: regressive models. Am. J. Med. Genet. 1984;18:731–749. doi: 10.1002/ajmg.1320180420. [DOI] [PubMed] [Google Scholar]
- 20.Bonney G.E. Regressive logistic models for familial disease and other binary traits. Biometrics. 1986;42(3):611–625. [PubMed] [Google Scholar]
- 21.Iselius L., Lindsten J., Morton N., Efendic S., Cerasi E., Luft R. Evidence for an autosomal recessive gene regulating the persistence of the insulin response to glucose in man. Clin. Genet. 1982;22(4):180–194. doi: 10.1111/j.1399-0004.1982.tb01432.x. [DOI] [PubMed] [Google Scholar]
- 22.Bouchard C. Genetic determinants of regional fat distribution. Hum. Reprod. 1997;12(S1):1–5. doi: 10.1093/humrep/12.suppl_1.1. [DOI] [PubMed] [Google Scholar]
- 23.De Andrade M., Amos C.I. Ascertainment issues in variance components models. Genet. Epidemiol. 2000;19(4):333–344. doi: 10.1002/1098-2272(200012)19:4<333::AID-GEPI5>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 24.Elks C.E., den Hoed M., Zhao J.H., Sharp S.J., Wareham N.J., Loos R.J., Ong K.K. Variability in the heritability of body mass index: a systematic review and meta-regression. Front. Endocrinol. 2012;28(3) doi: 10.3389/fendo.2012.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stunkard A.J., Harris J.R., Pedersen N.L., McClearn G.E. The body mass index of twins who have been reared apart. N. Engl. J. Med. 1990;322:1483–1487. doi: 10.1056/NEJM199005243222102. [DOI] [PubMed] [Google Scholar]
- 26.Wray N.R., Goddard M.E., Visscher P.M. Prediction of individual genetic risk of complex disease. Curr. Opin. Genet. Dev. 2008;18(3):257–263. doi: 10.1016/j.gde.2008.07.006. [DOI] [PubMed] [Google Scholar]
- 27.Locke A.E., Kahali B., Berndt S.I., Justice A.E., Pers T.H., Day F.R., Powell C., Vedantam S., Buchkovich M.L., Yang J., Croteau-Chonka D.C., Esko T., Fall T., Ferreira T., Gustafsson S., Kutalik Z., Luan J., Mägi R., Randall J.C., Winkler T.W., Wood A.R., Workalemahu T., Faul J.D., Smith J.A., Zhao H.J., Zhao W., Chen J., Fehrmann R., Hedman Å.K., Karjalainen J., Schmidt E.M., Absher D., Amin N., Anderson D., Beekman M., Bolton J.L, Bragg-Gresham J.L, Buyske S, Demirkan A, Deng G, Ehret G.B, Feenstra B, Feitosa M.F, Fischer K, Goel A, Gong J, Jackson A.U, Kanoni S, Kleber M.E, Kristiansson K, Lim U, Lotay V, Mangino M, Mateo Leach I, Medina-Gomez C, Medland S.E, Nalls M.A, Palmer C.D, Pasko D, Pechlivanis S, Peters M.J, Prokopenko I, Shungin D, Stančáková A, Strawbridge R.J, Ju Sung Y, Tanaka T, Teumer A, Trompet S, van der Laan S.W, van Setten J, Van Vliet-Ostaptchouk J.V, Wang Z, Yengo L, Zhang W, Isaacs A, Albrecht E, Ärnlöv J, Arscott G.M, Attwood A.P, Bandinelli S, Barrett A, Bas I.N, Bellis C, Bennett A.J, Berne C, Blagieva R, Blüher M, Böhringer S, Bonnycastle L.L, Böttcher Y, Boyd H.A, Bruinenberg M, Caspersen I.H, Ida Chen Y.D, Clarke R, Daw E.W, de Craen A.J, Delgado G, Dimitriou M, Doney A.S, Eklund N, Estrada K, Eury E, Folkersen L, Fraser R.M, Garcia M.E, Geller F, Giedraitis V, Gigante B, Go A.S, Golay A, Goodall A.H, Gordon S.D, Gorski M, Grabe H.J, Grallert H, Grammer T.B, Gräßler J, Grönberg H, Groves C.J, Gusto G, Haessler J, Hall P, Haller T, Hallmans G, Hartman C.A, Hassinen M, Hayward C, Heard-Costa N.L, Helmer Q, Hengstenberg C, Holmen O, Hottenga J.J, James A.L, Jeff J.M, Johansson Å, Jolley J, Juliusdottir T, Kinnunen L, Koenig W, Koskenvuo M, Kratzer W, Laitinen J, Lamina C, Leander K, Lee N.R, Lichtner P, Lind L, Lindström J, Sin Lo K, Lobbens S, Lorbeer R, Lu Y, Mach F, Magnusson P.K, Mahajan A, McArdle W.L, McLachlan S, Menni C, Merger S, Mihailov E, Milani L, Moayyeri A, Monda K.L, Morken M.A, Mulas A, Müller G, Müller-Nurasyid M, Musk A.W, Nagaraja R, Nöthen M.M, Nolte I.M, Pilz S, Rayner N.W, Renstrom F, Rettig R, Ried J.S, Ripke S, Robertson N.R, Rose L.M, Sanna S, Scharnagl H, Scholtens S, Schumacher F.R, Scott W.R, Seufferlein T, Shi J, Vernon Smith A, Smolonska J, Stanton A.V, Steinthorsdottir V, Stirrups K, Stringham H.M, Sundström J, Swertz M.A, Swift A.J, Syvänen A.C, Tan S.T, Tayo B.O, Thorand B, Thorleifsson G, Tyrer J.P, Uh H.W, Vandenput L, Verhulst F.C, Vermeulen S.H, Verweij N, Vonk J.M, Waite L.L, Warren H.R, Waterworth D, Weedon M.N, Wilkens L.R, Willenborg C, Wilsgaard T, Wojczynski M.K, Wong A, Wright A.F, Zhang Q, Brennan E.P, Choi M, Dastani Z, Drong A.W, Eriksson P, Franco-Cereceda A, Gådin J.R, Gharavi A.G, Goddard M.E, Handsaker R.E, Huang J, Karpe F, Kathiresan S, Keildson S, Kiryluk K, Kubo M, Lee J.Y, Liang L, Lifton R.P, Ma B, McCarroll S.A, McKnight A.J, Min J.L, Moffatt M.F, Montgomery G.W, Murabito J.M, Nicholson G, Nyholt D.R, Okada Y, Perry J.R, Dorajoo R, Reinmaa E, Salem R.M, Sandholm N, Scott R.A, Stolk L, Takahashi A, Tanaka T, Van’t Hooft F.M, Vinkhuyzen A.A, Westra H.J, Zheng W, Zondervan K.T, Heath A.C, Arveiler D, Bakker S.J, Beilby J, Bergman R.N, Blangero J, Bovet P, Campbell H, Caulfield M.J, Cesana G, Chakravarti A, Chasman D.I, Chines P.S, Collins F.S, Crawford D.C, Cupples L.A, Cusi D, Danesh J, de Faire U, den Ruijter H.M, Dominiczak A.F, Erbel R, Erdmann J, Eriksson J.G, Farrall M, Felix S.B, Ferrannini E, Ferrières J, Ford I, Forouhi N.G, Forrester T, Franco O.H, Gansevoort R.T, Gejman P.V, Gieger C, Gottesman O, Gudnason V, Gyllensten U, Hall A.S, Harris T.B, Hattersley A.T, Hicks A.A, Hindorff L.A, Hingorani A.D, Hofman A, Homuth G, Hovingh G.K, Humphries S.E, Hunt S.C, Hyppönen E, Illig T, Jacobs K.B, Jarvelin M.R, Jöckel K.H, Johansen B, Jousilahti P, Jukema J.W, Jula A.M, Kaprio J, Kastelein J.J, Keinanen-Kiukaanniemi S.M, Kiemeney L.A, Knekt P, Kooner J.S, Kooperberg C, Kovacs P, Kraja A.T, Kumari M, Kuusisto J, Lakka T.A, Langenberg C, Le Marchand L, Lehtimäki T, Lyssenko V, Männistö S, Marette A, Matise T.C, McKenzie C.A, McKnight B, Moll F.L, Morris A.D, Morris A.P, Murray J.C, Nelis M, Ohlsson C, Oldehinkel A.J, Ong K.K, Madden P.A, Pasterkamp G, Peden J.F, Peters A, Postma D.S, Pramstaller P.P, Price J.F, Qi L, Raitakari O.T, Rankinen T, Rao D.C, Rice T.K, Ridker P.M, Rioux J.D, Ritchie M.D, Rudan I, Salomaa V, Samani N.J, Saramies J, Sarzynski M.A, Schunkert H, Schwarz P.E, Sever P, Shuldiner A.R, Sinisalo J, Stolk R.P, Strauch K, Tönjes A, Trégouët D.A, Tremblay A, Tremoli E, Virtamo J, Vohl M.C, Völker U, Waeber G, Willemsen G, Witteman J.C, Zillikens M.C, Adair L.S, Amouyel P, Asselbergs F.W, Assimes T.L, Bochud M, Boehm B.O, Boerwinkle E, Bornstein S.R, Bottinger E.P, Bouchard C, Cauchi S, Chambers J.C, Chanock S.J, Cooper R.S, de Bakker P.I, Dedoussis G, Ferrucci L, Franks P.W, Froguel P, Groop L.C, Haiman C.A, Hamsten A, Hui J, Hunter D.J, Hveem K, Kaplan R.C, Kivimaki M, Kuh D, Laakso M, Liu Y, Martin N.G, März W, Melbye M, Metspalu A, Moebus S, Munroe P.B, Njølstad I, Oostra B.A, Palmer C.N, Pedersen N.L, Perola M, Pérusse L, Peters U, Power C, Quertermous T, Rauramaa R, Rivadeneira F, Saaristo T.E, Saleheen D, Sattar N, Schadt E.E, Schlessinger D, Slagboom P.E, Snieder H, Spector T.D, Thorsteinsdottir U, Stumvoll M, Tuomilehto J, Uitterlinden A.G, Uusitupa M, van der Harst P, Walker M, Wallaschofski H, Wareham N.J, Watkins H, Weir D.R, Wichmann H.E, Wilson J.F, Zanen P, Borecki I.B, Deloukas P, Fox C.S, Heid I.M, O’Connell J.R, Strachan D.P, Stefansson K, van Duijn C.M, Abecasis G.R, Franke L, Frayling T.M, McCarthy M.I, Visscher P.M, Scherag A, Willer C.J, Boehnke M, Mohlke K.L, Lindgren C.M, Beckmann J.S, Barroso I, North K.E, Ingelsson E, Hirschhorn J.N, Loos R.J, Speliotes E.K. Genetic studies of body mass index yield new insights for obesity biology. Nature. 2015;518(7538):197–206. doi: 10.1038/nature14177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dudbridge F., Gusnanto A. Estimation of significance thresholds for genomewide association scans. Genet. Epidemiol. 2008;32(3):227–234. doi: 10.1002/gepi.20297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wei Z., Wang K., Qu H-Q., Zhang H., Bradfield J., Kim C., Frackleton E., Hou C., Glessner J.T., Chiavacci R., Stanley C., Monos D., Grant S.F., Polychronakos C., Hakonarson H. From disease association to risk assessment: an optimistic view from genome-wide association studies on type 1 diabetes. PLoS Genet. 2009;5(10):e1000678. doi: 10.1371/journal.pgen.1000678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Golan D., Rosset S. Accurate estimation of heritability in genome wide studies using random effects models. Bioinformatics. 2011;27(13):i317–i323. doi: 10.1093/bioinformatics/btr219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W., Goddard M.E., Visscher P.M. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42(7):565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yang J., Lee S.H., Goddard M.E., Visscher P.M. GCTA: A tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 2011;88(1):76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yang J., Bakshi A., Zhu Z., Hemani G., Vinkhuyzen A.A., Lee S.H., Robinson M.R., Perry J.R., Nolte I.M., van Vliet-Ostaptchouk J.V., Snieder H., Esko T., Milani L., Mägi R., Metspalu A., Hamsten A., Magnusson P.K., Pedersen N.L., Ingelsson E., Soranzo N., Keller M.C., Wray N.R., Goddard M.E., Visscher P.M. LifeLines Cohort Study.; Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet. 2015;47(10):1114–1120. doi: 10.1038/ng.3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Llewellyn C.H., Trzaskowski M., Plomin R., Wardle J. Finding the missing heritability in pediatric obesity: the contribution of genome-wide complex trait analysis. Int. J. Obes. 2013;37(11):1506–1509. doi: 10.1038/ijo.2013.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fisher R.A., Thomson J.A. The correlation between relatives on the supposition of Mendelian inheritance. Proc. R. Soc. Edinb. 1918;52:399–433. [Google Scholar]
- 36.Pigeyre M., Yazdi F.T., Meyre D. Recent progress in genetics, epigenetics and metagenomics unveils the pathophysiology of human obesity. Clin. Sci. 2016;130(12):943–986. doi: 10.1042/CS20160136. [DOI] [PubMed] [Google Scholar]
- 37.Gibson G. Rare and common variants: twenty arguments. Nat. Rev. Genet. 2012;13(2):135–145. doi: 10.1038/nrg3118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wray N.R., Goddard M.E., Visscher P.M. Prediction of individual genetic risk of complex disease. Curr. Opin. Genet. Dev. 2008;18(3):257–263. doi: 10.1016/j.gde.2008.07.006. [DOI] [PubMed] [Google Scholar]
- 39.Marian A.J. Elements of “missing heritability.”. Curr. Opin. Cardiol. 2012;27(3):197–201. doi: 10.1097/HCO.0b013e328352707d. [DOI] [PubMed] [Google Scholar]
- 40.Koch L. Insights into missing heritability. Nat. Rev. Genet. 2014;15:218. doi: 10.1038/nrg3713. [DOI] [PubMed] [Google Scholar]
- 41.Zuk O., Hechter E., Sunyaev S.R., Lander E.S. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA. 2012;109(4):1193–1198. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Simon P.H., Sylvestre M-P., Tremblay J., Hamet P. Key Considerations and methods in the dtudy of gene-environment interactions. Am. J. Hypertens. 2016;29(8):891–899. doi: 10.1093/ajh/hpw021. [DOI] [PubMed] [Google Scholar]
- 43.Reddon H., Gueant J., Meyre D. The importance of gene-environment interactions in human obesity. Clin. Sci. 2016;130(18):1571–1597. doi: 10.1042/CS20160221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Slatkin M. Epigenetic Inheritance and the Missing Heritability Problem. Genetics. 2009;182:845–850. doi: 10.1534/genetics.109.102798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nelson V.R., Nadeau J. Transgenerational genetic effects. Epigenomics. 2010;2(6):797–806. doi: 10.2217/epi.10.57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zaitlen N., Kraft P. Heritability in the genome-wide association era. Hum. Genet. 2012;131(10):1655–1664. doi: 10.1007/s00439-012-1199-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Martos S., Tang W., Wang Z. Elusive inheritance: Transgenerational effects and epigenetic inheritance in human environmental disease. Prog. Biophys. Mol. Biol. 2015;118(1-2):44–54. doi: 10.1016/j.pbiomolbio.2015.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sadee W., Hartmann K., Sweryn M., Pietrzak M., Handelman S.K., Rempala G.A. Missing heritability of common disease and treatments outside the protien-coding exome. Hum. Genet. 2014;133(10):1199–1215. doi: 10.1007/s00439-014-1476-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Alyass A., Turcotte M., Meyre D. From big data analysis to personalized medicine for all: challenges and opportunities. BMC Med. Genomics. 2015;8(33) doi: 10.1186/s12920-015-0108-y. [DOI] [PMC free article] [PubMed] [Google Scholar]