In Vivo Brain Rosette Spectroscopic Imaging (RSI) with LASER Excitation, Constant Gradient Strength Readout, and Automated LCModel Quantification for all Voxels

Abstract

Purpose

To optimize the Rosette trajectories for high-sensitivity in vivo brain spectroscopic imaging and reduced gradient demands.

Methods

Using LASER localization, a rosette based sampling scheme for in vivo brain spectroscopic imaging data on a 3 Tesla (T) system is described. The two-dimensional (2D) and 3D rosette spectroscopic imaging (RSI) data were acquired using 20 × 20 in-plane resolution (8 × 8 mm²), and 1 (2D) −18 mm (1.1 cc) or 12 (3D) −8 mm partitions (0.5 cc voxels). The performance of the RSI acquisition was compared with a conventional spectroscopic imaging (SI) sequence using LASER localization and 2D or 3D elliptical phase encoding (ePE). Quantification of the entire RSI data set was performed using an LCModel based pipeline.

Results

The RSI acquisitions took 32 s for the 2D scan, and as short as 5 min for the 3D 20 × 20 × 12 scan, using a maximum gradient strength G_max = 5.8 mT/m and slew-rate S_max = 45 mT/m/ms. The Bland-Altman agreement between RSI and ePE CSI, characterized by the 95% confidence interval for their difference (RSI-ePE), is within 13% of the mean (RSI+ePE)/2. Compared with the 3D ePE at the same nominal resolution, the effective RSI voxel size was three times smaller while the measured signal-to-noise ratio sensitivity, after normalization for differences in effective size, was 43% greater.

Conclusion

3D LASER-RSI is a fast, high-sensitivity spectroscopic imaging sequence, which can acquire medium-to-high resolution SI data in clinically acceptable scan times (5–10 min), with reduced stress on the gradient system.

INTRODUCTION

MR Spectroscopy (MRS) has been shown to be a valuable noninvasive tool in the study of neurological diseases (1). Single voxel (SV) MRS can be useful when the disease isfocal and the region of interest (ROI) is known before the study or the pathology is homogeneous. However, for disorders such as epilepsy and traumatic brain injury, where the site of injury is potentially unknown, or in brain tumors where the primary lesion may be very large and heterogeneous, obtaining spectral information for multiple spatial locations is preferable. MR spectroscopic imaging (MRSI) or chemical shift imaging [CSI, (2)], traditionally using only phase encoding (PE), enables collection of spatial and spectral information. Unfortunately, total data acquisition times using conventional PE methods, including methods sampling only a portion of the k-space (e.g. elliptical encoding), are lengthy, due to the acquisition of a single k-space position per repetition time (TR).

More efficient sampling methods have been developed that simultaneously collect spectral information and spatial information in one (3–7) or two dimensions (8–11), within a single TR. The k-space locations are sampled at regular time intervals; typically, at least once every spectral dwell time. Although multiple encoding steps/shots are usually needed to fully sample the entire k–t space, these approaches significantly decrease the acquisition time, by one to two orders of magnitude, in comparison to conventional CSI acquisitions. While a relatively high receiver bandwidth (BW) is used (e.g., for a 10 μs sampling rate, BW = 100 kHz), the sensitivity ( $\mathit{tSNR}=\mathit{SNR}/\sqrt{t_{\mathit{ACQ}}}$, also referred to as signal-to-noise ratio [SNR] efficiency) is similar to that of a conventional phase encoded CSI of the same duration (9,12,13). The spectral response function for these acquisitions is approximately the same as for CSI (10).

Even faster acquisitions have been demonstrated, using readout gradients and stochastic sampling schemes (14–17). In contrast to the fully sampled k–t space methods, for the stochastic methods, the k-space locations are purposefully sampled at irregular/random time intervals. The stochastic techniques, however, have a significantly lower sensitivity compared with the fully encoded techniques (18) and, therefore, may not be appropriate for lower concentration brain metabolites.

Rosette trajectories have been demonstrated for both stochastic (15,16) and high sensitivity full k–t space sampling (10,19,20) and shown to provide similar encoding speed to spiral spectroscopic imaging (SSI) or echo-planar SI (EPSI) techniques. Rosette trajectories are appealing for their smoothly varying gradient waveforms and because the data are collected and used over the entire signal decay window. This is in contrast to spiral-out only SSI or flyback EPSI implementations that have gaps in readout, or conventional EPSI techniques when data along the ramp are not used in reconstruction. Additionally, the rosettes can achieve a greater spectral width (SW) than EPSI or SSI, under the equivalent gradient strength and slew rate constraints. At 3 Tesla (T) and above, SSI and EPSI typically require the readout trajectories to be interleaved temporally or methods like cyclical spectral unwrapping based on prior knowledge of in vivo spectral patterns to be used to achieve a sufficient SW of ~10 ppm (21,22). In comparison to rosette trajectories, constant sampling density spirals need a higher slew rate near the center of k-space and EPSI acquisitions require high slew rates when readout trajectory changes direction. For example, for a SSI 30 × 30 acquisition matrix, field of view of 16 cm, SW = 1200 Hz, three temporal interleaves, the maximum readout gradient strength and slew rate are G_max = 12.8 mT/m and S_max = 127 mT/m/ms (22). The equivalent RSI acquisition, without interleaving, can be achieved with gradient and slew rates as low as G_max = 8.3 mT/m and S_max = 31 mT/m/ms, while the use of three temporal interleaves can reduce gradient demands to G_max = 2.8 mT/m and S_max = 3.5 mT/m/ms – more than a 30-fold decrease in required slew rate. To decrease gradient demands for a constant density spiral acquisition, the readout gradient speed can be reduced and/or the constant sampling density portion of the trajectory can be started further away from the center of k-space. However, a lower spiral readout gradient (and thus longer readout “leaves”) requires an increased number of temporal interleaves to reach the targeted SW and, when these trajectories start twisting further away from k = 0, a higher number of spiral interleaves in (k_x, k_y) space are needed (23). More importantly, for the latter case, the k-space region with constant sampling density would decrease, reducing the overall sampling uniformity (η, also referred to as sampling efficiency) and, therefore, decreasing sensitivity.

The design of the rosette trajectories is very flexible and can be easily tailored to the performance of the gradient system. At medium to higher spatial resolutions, SNR typically becomes limiting for MRSI data, such that additional averaging is required (5,22). Alternatively, the time associated with signal averaging can be “traded” for lower peak gradient and slew rates to acquire a single fully sampled k–t space, with no or minimal increase in total acquisition time. In addition, minimizing physical stress on the gradient system, effects due to eddy currents (24), gradient induced frequency drifts (25) and acoustic levels are reduced, leading to potential improvements in spectral quality and patient compliance. The purpose of this study was to optimize the RSI acquisition with LASER excitation for in vivo brain ¹H spectroscopic imaging at 3T, in clinically feasible scanning times.

METHODS

Rosette Trajectory Design Considerations

Rosette trajectories (15,26), oscillate in the radial direction with an angular frequency ω₁ = 2π · f₁, while rotating in (k_x, k_y) plane with angular oscillation frequency ω₂ = 2π · f₂, such that:

$$\overrightarrow{k}(t)=k_{max}·sin({\mathrm{\omega }}_1·t)·e^{i·{\mathrm{\omega }}_2·t}$$ [1]

where k_max = N_x/(2 · fov) is the highest spatial frequency sampled, ω₁ = π · SW/n_TI; SW is the spectral width of the acquisition; n_TI is the number of time interleaves. ω₂ can take any value between 0 and ${\mathrm{\omega }}_2^{max}$, where ${\mathrm{\omega }}_2^{max}$ is limited either by maximum gradient, slew rate or by the Nyquist constraint along the readout trajectory, γ · G_max ·FOV + SW ≤ 1/dt (10). G_max, dt and γ = 42.57 MHz/T are the maximum gradient strength along the trajectory, complex data sampling rate, and the ¹H gyromagnetic ratio, respectively. The maximum and minimum gradient and slew rate along the trajectory are given by:

$$\begin{array}{l}{G}_{max}=k_{max}·max\left({\mathrm{\omega }}_1,{\mathrm{\omega }}_2\right)/\mathrm{\gamma };\\ G_{min}=k_{max}·min\left({\mathrm{\omega }}_1,{\mathrm{\omega }}_2\right)/\mathrm{\gamma }\end{array}$$ [2]

$$S_{max}=k_{max}·\left({\mathrm{\omega }}_1^2+{\mathrm{\omega }}_2^2\right)/\mathrm{\gamma };{\mathrm{S}}_{min}=k_{max}·2·{\mathrm{\omega }}_1·{\mathrm{\omega }}_2/\mathrm{\gamma }.$$ [3]

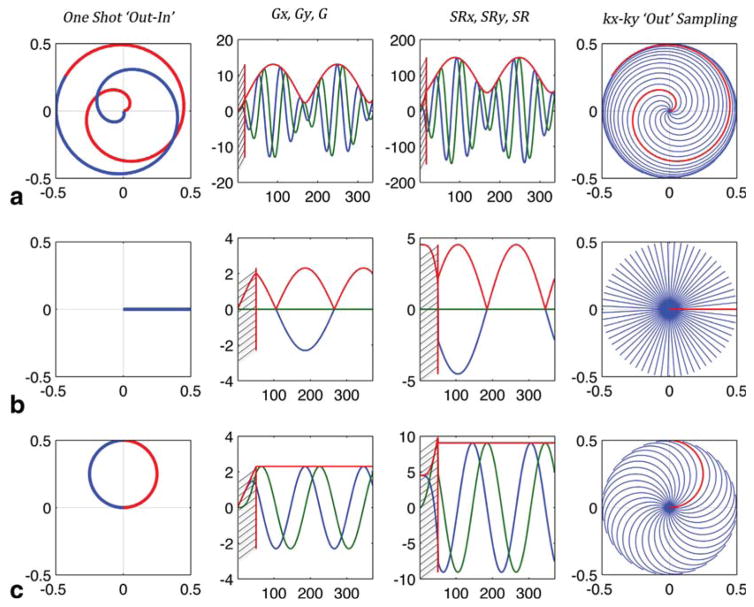
The rosette trajectory (examples shown in Figure 1) will have the maximum twist and cover more of the (k_x, k_y) space when ${\mathrm{\omega }}_2={\mathrm{\omega }}_2^{max}$ (Fig. 1a) and will look like a projection imaging (PI) spike in (k_x, k_y) space when ω₂ = 0 (Fig. 1b). The latter case (ω₂ = 0) is similar to the PREP (projection reconstruction echo planar) acquisition (3,4) with the difference that the rosette trajectory natively returns to the center of k-space when reaching k = k_max, without wasting up to 17% of the readout time (12). In addition, the sampling uniformity for RSI (η_RSI = 0.90) is higher than for PREP (η_PI = 0.87). Both factors contribute to a higher sensitivity for RSI (10). For ω₂, any value in between 0 and ${\mathrm{\omega }}_2^{max}$ can be chosen. ${\mathrm{\omega }}_2={\mathrm{\omega }}_2^{max}$ (Fig. 1a) corresponds to the fewest number of excitations needed to cover (k_x, k_y) space for an RSI experiment, and fastest acquisition; albeit imposing the highest demands on gradient performance. ω₂ = 0 requires more acquisitions but minimizes gradient performance requirements. Regardless of the value of ω₂, as long as an appropriate minimal number of acquisitions are used, the sampling efficiency factor, and, therefore, the sensitivity, remains constant at their maximal value of η_RSI = 0.90 (9,10) (η ≤ 1 with η_CSI = 1 for conventional phase encoded -PE or ePE- CSI).

FIG. 1.

Examples of rosette trajectory design for S_max = 150 mT/m/ms, G_max = 21 mT/m, dt = 10 ms, N_x = 20, FOV = 20 cm, SW = 625 Hz. (a) The fastest coverage as in Schirda et al (10), with slew rate reaching maximum value allowed by the gradient system and ${\mathrm{\omega }}_2={\mathrm{\omega }}_2^{max}$. (b) The lowest slew rate and ω₂ = 0, with rosette trajectories appearing PI/PREP-like. (c) Corresponds to the balanced approached proposed and used in this study, ω₂ = ω₁, with trajectories looking like circles sampling periodically k = 0. Left column shows a one-shot trajectory from k = 0 to k_max (“Out”, red) and back to k = 0 (“In”, blue). Second left and second right columns show the gradient readout waveforms and slew rate functions, respectively, for the x-axis (blue), y-axis (green) and strength/magnitude (red). The most right column depicts the (k_x, k_y) coverage with the “Out” portion of the trajectories, in one temporal slice, in half the spectral dwell time Δt_δ/2, where Δt_δ = 1/SW. Hashed regions on the gradient and slew rate plots represent transitional, gradient ramp-up regions at the beginning of the readout for each shot (10).

In Figure 1, rosette trajectories and corresponding gradient and slew rate functions, for a FOV = 20 cm and N_x = 20, are shown for fastest k-space coverage/maximum twist - ${\mathrm{\omega }}_2={\mathrm{\omega }}_2^{max}$ (required N_sh = 11, Figure 1a), for slowest k-space coverage ω₂ = 0 (PI/PREP-like trajectories N_sh = 63, Figure 1b) and for ω₂ = ω₁ (N_sh = 32, Figure 1c). For the fastest acquisition the number of shots required to cover k–t space is almost six-fold lower than the PREP-like acquisition. Because some averaging would be needed to obtain adequate SNR, the total acquisition time, independent of ω₂ values, would be similar, substantially less than the difference suggested by N_sh, with acquisitions using lower ω₂’s putting fewer demands on the gradient system.

Although the maximum slew rate along the trajectory doubles when ω₂ = ω₁ compared with ω₂ = 0, the maximum slew rate remains reasonably small for typical matrix sizes used for in vivo ¹H brain acquisitions (Fig. 2). In addition, the maximum peak gradients for acquisitions with ω₂ = ω₁ and ω₂ = 0 are equivalent. However, unlike the ω₂ = 0 case, when ω₂ = ω₁ the gradient strength is constant for the entire readout trajectory. When the receive bandwidth needed FBW = γ · G_max · FOV + SW is less than the receiver bandwidth 1/dt, a low-pass filter applied postacquisition, with bandwidth equal to FBW < 1/dt, is used to reduce the noise introduced by the receiver. This filtering is more efficient for all data points collected on an FID when G = G_max is constant.

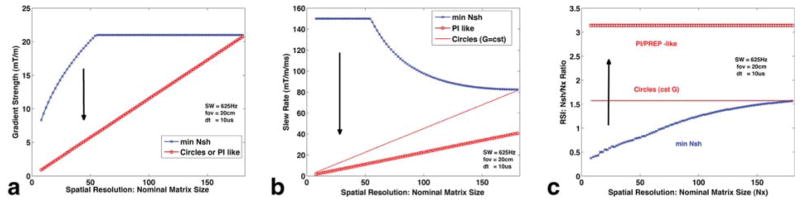
FIG. 2.

Change in peak gradient (a)/slew-rate (b) strength and the number of needed spatial interleaved shots (c), as a function of spatial resolution (Nx). Blue corresponds to the fastest acquisition [Schirda et al (10)], which pushes the gradient system the most, with least amount of spatially interleaved shots. Red circles correspond to a PI/PREP-like acquisition (trajectory depicted in Fig 1b), with the lowest demands on the gradient system and the most amount of shots needed to cover (k_x, k_y), π · N_x The solid red line corresponds to a circle-like acquisition (depicted in Fig 1c), with same gradient strength (a), but twice the slew rate of the PI/PREP-like acquisition (b). However, for typical brain SI acquisitions (N_X < 64), the slew rate needed for circle-like trajectories is still substantially lower than for the fastest acquisition (b) and the number of excitations needed is twice as low as for the PI-like acquisition, π · N_x/2 (c).

Using the formula in Schirda et al (10) to determine the number of shots required to cover a 2D partition/slice:

$$N_{sh}\left(\frac{{\mathrm{\omega }}_2}{{\mathrm{\omega }}_1}\le 1\right)=\frac{\mathrm{\pi }·N_x}{\sqrt{1+3·{\mathrm{\omega }}_2^2/{\mathrm{\omega }}_1^2}};N_{sh}\left(\frac{{\mathrm{\omega }}_2}{{\mathrm{\omega }}_1}>1\right)=\frac{\mathrm{\pi }·N_x}{\sqrt{3+{\mathrm{\omega }}_2^2/{\mathrm{\omega }}_1^2}}$$ [4]

when ω₂ = ω₁, the number of shots (rounding to closest integer) is:

$$N_{sh}=\mathrm{\pi }·N_x/2.$$ [5]

For ω₂ = ω₁ and ω₁ = π · SW/n_TI, the gradient strength and slew rate are constant along the readout trajectory and, using Eqs. [2] and [3], given by:

$$\begin{array}{l}G=G_{max}=(\mathrm{\pi }/\mathrm{\gamma })·k_{max}·SW/n_{TI}\\ \mathrm{S}=S_{max}=(2·{\mathrm{\pi }}^2/\mathrm{\gamma })·k_{max}·S{W}^2/n_{TI}^2.\end{array}$$ [6]

Data Acquisition and Reconstruction

Data were collected using a 32-channel head coil on a Siemens (Erlangen, Germany) 3T Tim Trio scanner and a head-and-neck coil (using the 12-channels for the head part) on a Siemens molecular MR system (mMR, also known as MR/PET). The scanners are capable of up to 40 mT/m peak gradient and 170 mT/m/ms peak slew rate. A 2.7 liter spherical MRS BRAINO phantom (manufactured by GE Medical Systems) was used, with metabolite concentrations described in Maril and Lenkinski (27). The in vivo brain data were collected in three healthy controls (HC) and two glioblastoma (GBM) patients. For all MRS scans (RSI, PE, ePE, three-dimensional [3D], and 2D), LASER excitation based on GOIA-W (4,16) pulses [duration/bandwidth/amplitude = 3.5 ms/20 kHz/820 Hz, (28)] was used with an echo time TE = 45 ms to localize a volume of interest (VOI).

The 2D acquisitions used a FOV = 16 cm (anterior–posterior [AP] and right–left [RL] directions) and a 20 × 20 matrix (N_x = 20) and slice thickness of 18 mm. In the phantom, two conventional, fully encoded PE scans were collected to assess scanner SNR variability. The data from these scans were also processed using only the k-space locations corresponding to an elliptical, ePE, 2D acquisition with the same nominal resolution. For these 2D PE scans and for the 2D RSI, a water reference was also acquired. Typical VOI was 100 × 80 mm² (AP-RL) and slice thickness was 18 mm (head–foot HF). The number of shots/excitations estimated as needed for the 2D acquisition was (Eq. [5]) N_sh = π · N_x/2 = 32. Because Eq. [4] (and, therefore, Eq. [5]) is a slight overestimate (10), we also tested acquisitions with 24 shots (~25% less), 28 shots (~12% less), and also with 36 shots (~12% more), with corresponding decreases/increases in SNR based on total acquisition duration, but no aliasing artifacts present.

The 3D scans were collected with FOV = 16 × 16 × 9.6 cm³ (AP-RL-HF), matrix 20 × 20 × 12, for a nominal isotropic resolution of 8 mm and voxel size of 0.5 cc; for RSI, conventional encoding was used in the z-direction with N_z = 12. For the 3D scans, typical VOI was 100 × 80 × 48 mm³ (AP-RL-HF). The number of shots/excitations estimated for the 3D acquisition was (Eq. [5]) 12 × 32 = 384 shots.

The acquisition spectral dwell time for all MRS scans was chosen to be 800 μs, for a spectral width SW = 1250 Hz (10.10 ppm). Using the ω₂ = ω₁ for the rosette trajectory, the gradient strength and slew rate were G_max = 5.8 mT/m and S_max = 45 mT/m/ms. The acquisition readout was T_read = 320 ms and complex data sampling rate was 10 μs. The repetition time for the phantom scans was TR = 1 s and for the participants varied from TR = 1 s to TR = 1.5 s with acquisition times of less than 1 min for the 2D-RSI and 5 to 10 min for the 3DRSI.

The readout k-space trajectory was calculated as the integral of the gradient waveform designed to be played on the scanner. RSI data were reconstructed for each channel using 3D gridding (simultaneously on kx, ky and time axis), on a two-fold oversampled grid, with a Kaiser-Bessel kernel with a window W = 4 (29). Post-gridding density compensation was applied. Zero-padding was used to interpolate to a 32 × 32 × 16 reconstructed matrix; thus, 16 × 16 × 8 = 2048 to 22 × 16 × 8 = 2816 reconstructed voxels were within excited VOI when FOV = 80 mm (AP) and FOV = 110 mm (AP), respectively. For in vivo data, spatial filtering was applied with a 2D full Hamming filter in the xy-direction (disk shape) and a 1D full Hamming filter in the z-direction. For phantom data, no spatial filtering was applied (unless explicitly stated), to enable comparison between acquisition sequences. Data from the individual channels were recombined using two methods. Method 1, the first free induction decay (FID) point, as described in Brown (30), was used when spatial filtering was not applied to the reconstructed data. The channel-combined time domain data for all voxels within VOI were then passed to LCModel (31) (http://www.s-provencher.com/pages/lcmodel.shtml), for automatic quantification. Method 2, as described in Maril and Lenkinski (27), in which data for each individual channel are zero and first order phase corrected with LCModel, before recombination, was used for the higher SNR Hamming filtered data. Spectra were processed in the range 4.0–0.2 ppm. Programs to read the LCmodel results for all voxels (phase-corrected spectra, baseline, fit, concentrations and Crammer-Rao lower bounds (CRLB) for all metabolites, etc.) were developed, to enable statistical analysis across all spectra acquired, generate images of the quantified metabolites and estimation errors (CRLB) maps.

Comparison: RSI and Elliptical Phase Encoded (PE) CSI

Bland-Altman Analysis

Agreement between the rosette- and elliptical phase-encoding sequences was analyzed using the NAA resonance area normalized to the sum of the resonance areas of all the resonances in the spectrum, NAA/Sum. This was done for the phantom data as in (22), by using the Bland-Altman method (32), to plot the difference between the two measurements against their mean. Voxels with a CRLB less than 20% for tNAA (total N-acetylaspartate: NAA+NAAG), tCr (total Creatine: Cr+PCr), tCho (total Choline: PCho+GPC), Inositol (Ins+Gly) and Glx (Glutamate/Glutamine: Glu+Gln) were included in comparison.

RSI-CSI Correlation Coefficient r = RSI*CSI: Scalar Product of the RSI and CSI Spectra

To assess the agreement between the RSI and ePE acquisitions, we calculated for each voxel a correlation coefficient r = RSI*ePE, the scalar/dot product of the LCModel calculated, phase-corrected and baseline-subtracted, normalized RSI and ePE spectra. Here, r = 1 equates to identical spectral information for the two acquisitions. This calculation was performed for the 3D phantom acquisitions and the 2D-RSI and 2D-ePE scans acquired in a GBM patient.

Normalized SNR Efficiency Comparison

The SNR for tNAA, tCr, tCho, Ins, and Glx, was calculated using the LCModel phase- and baseline-corrected spectra, by taking the ratio of the peak intensity for each metabolite, divided by the standard deviation of the noise in a metabolite free region (0.5–0.2 ppm).

For the 2D acquisitions, the sensitivity of RSI, PE, and ePE was measured and compared using only the unfiltered reconstructions. For the 3D acquisitions, the RSI and ePE sensitivities are compared, for the unfiltered reconstructions and also for reconstructions with a Hamming filter. All voxels which had CRLB<20% for all five metabolites considered (tNAA, tCr, tCho, Ins, Glx), for both RSI and ePE, were included in analysis.

The relative sensitivity of the RSI method, with respect to the phase encoded one, when no filtering/windowing is applied, is (10)

$${\mathrm{\Omega }}_{\mathit{RSI}/PE}=\frac{{\mathit{tSNR}}_{\mathit{RSI}}}{{\mathit{tSNR}}_{PE}}={\mathrm{\eta }}_{\mathit{RSI}}·\frac{V_{PE}^{\mathit{Kspace}}}{V_{PE}^{\mathit{Kspace}}}·\sqrt{\frac{T_{\mathit{RSI}}^{\mathit{read}}}{T_{PE}^{\mathit{read}}}}.$$ [7]

$V_{PE}^{\mathit{Kspace}}/V_{\mathit{RSI}}^{\mathit{Kspace}}$ is the k-space volume sampled by the PE/RSI acquisition. While there are time savings advantages and an increase in SNR efficiency associated with sampling a smaller k-space volume, this results in an increase in the effective voxel size. Therefore, the SNR efficiency normalized to the effective voxel size is a more appropriate and objective tool to compare the performance of two techniques. The effective resolution, or full-volume at half maximum (FVHM), is calculated by integrating all the simulated voxels with signal greater than half of the maximum signal in the simulated 3Dpoint spread function (PSF) (34,35). The normalized SNR efficiency is: nSNR = tSNR_meas/FVHM, where ${\mathit{tSNR}}_{\mathit{meas}}={\mathit{SNR}}_{\mathit{meas}}/\sqrt{t_{\mathit{ACQ}}}$ is the measured sensitivity. The relative sensitivity Ω_RSI/PE (Eq. [7]) is used to compare the normalized sensitivities of the RSI and PE/ePE acquisitions:

$$\frac{{\mathit{nSNR}}_{\mathit{RSI}}}{{\mathit{nSNR}}_{PE}}={\mathrm{\Omega }}_{\mathit{RSI}/PE}·\frac{{\mathit{FVHM}}_{PE}}{{\mathit{FVHM}}_{\mathit{RSI}}}.$$ [8]

PSF for RSI, PE, and ePE (Simulations)

The PSF for the 2D and 3D RSI, PE and ePE sampling schemes were simulated with the same parameters as for the phantom and in vivo acquisitions, a 20 × 20 × 12 matrix with FOV = 16 × 16 × 9.6 cm³.

In Vivo Brain Studies

For in vivo 3D RSI scans, the volume of interest (VOI) was selected based on the size of the brain so as to avoid scalp lipid contamination, ranging from 80–100 mm × 80 mm × 48 mm, AP-RL-HF direction. Because a 20 × 20 × 12 elliptical PE acquisition would require almost 30 min to acquire with TR = 1 s (and almost 90 min for the 3D PE), no 3D PE/ePE scans were collected in any of the participants. However, for one HC and one GBM patient, a 2D RSI and 2D ePE acquisitions were collected, for a direct comparison of in vivo data. A T1- weighted 1 mm isotropic MPRAGE (Magnetization Prepared Rapid Acquisition Gradient Echo) image was collected for each participant.

RESULTS

Agreement between RSI and Elliptical PE Techniques

Phantom Data (3D Acquisition)

Bland-Altman plots comparing the 3D RSI and ePE techniques for the phantom data, are shown in Figure 3. For the unfiltered reconstruction, N_voxels = 2725 (97% of 2816 voxels within VOI had CRLB < 20% for all five metabolites) and the confidence interval for the limits of agreement was 13% of the mean 0.24 (Fig. 3a). When RSI and ePE data are reconstructed with a Hamming filter, the SNR improves and the LCmodel estimation accuracy increases, with 100% of the voxels (N_voxels = 2816) having CRLB < 20% for all five metabolites considered. The data agreement between the two sequences, as calculated with the Bland-Altman analysis, further improves, with the confidence interval for the limits of agreements improving to 6% of the mean (also 0.24, Figure 3b). The average (SD) scalar product RSI*ePE was 0.958 (±0.036) for the nonwindowed reconstruction and 0.978 (±0.017) for the Hamming filtered one.

FIG. 3.

Bland-Altman plots indicating the limits of agreement between 3D RSI and 3D elliptical phase-encoding (ePE) measurements of NAA/Sum: Agreement for nonwindowed reconstructed data (N = 2725 voxels included in analysis) (a) and data reconstructed with a spatial Hamming filter applied (N = 2816) (b).

In Vivo Data (2D Acquisition)

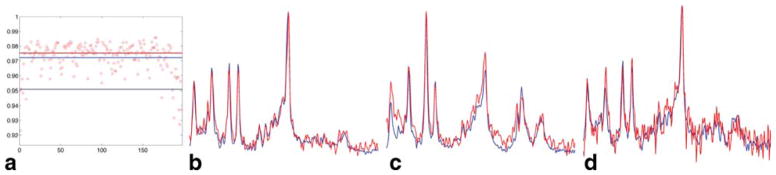
For one GBM patient for which a 2D acquisition was done with both rosette trajectories and ePE, N = 197 voxels (out of 288 voxels in the VOI) had CRLB < 20% and the average (SD) scalar product between RSI and ePE spectra for these voxels was 0.972 (±0.011) (Fig. 4).

FIG. 4.

Scalar product r = RSI*ePE comparison in one GBM patient, for all voxels (N = 197/288, a) with CRLB < 20% (for tNAA, tCr, tCho, Ins, Glx). The horizontal red/superior blue/inferior blue lines in (a) correspond to median/mean/(mean-2*SD) values. The RSI*ePE values are in the range 0.923–0.986, with 5% of the voxels (N = 10/197) showing an agreement less than 0.951 (mean-2*SD). RSI (red) and ePE (blue) spectra, corresponding to the highest/median/(mean-2*SD) = 0.986/0.975/0.951 (b/c/d). The 2D RSI and ePE data were acquired in 32 s and 4:13 min:s, respectively.

Normalized SNR Efficiency Comparison (Phantom Data)

2D RSI versus PE versus ePE

The average difference in SNR for the two PE scans, normalized to its average, for the five metabolites considered, was found to be 6%; for the two ePE scans (data extracted from the fully sampled PE scans) was 4%. The relative sensitivity (Ω) between the RSI, PE, and ePE sequences, along with the FVHM and normalized sensitivity ratios are shown in Table 1. The relative RSI/PE sensitivity Ω_RSI/PE = 1.15 for the reconstruction using Method 2 with ECC (eddy current correction), is in agreement with that reported previously using simulations (10). For the 2D acquisitions, a value of Ω_ePE/PE = 4/π = 1.27 is expected and Ω_RSI/ePE = η_RSI = 0.9 (Eq. [6]), if the k-space area covered by ePE was that of a disk, $K_{max}^2$. However, because of the relatively low spatial resolution (small N_x) and due to the discrete sampling (Fig. 5a), the k-space area covered by ePE is different than the value given by the analytical expression for the disk area. The relative ePE/PE sensitivity can be expressed as ${\mathrm{\Omega }}_{\mathit{ePE}/PE}=N_{PE}^{\mathit{Kspace}}/N_{\mathit{ePE}}^{\mathit{Kspace}}$, where $N_{PE}^{\mathit{Kspace}}=400$ and $N_{\mathit{ePE}}^{\mathit{Kspace}}=253$ are the number of sampled k-space points for the PE acquisition and ePE, respectively for the Siemens PE/ePE implementation of a 20 × 20 CSI acquisition. Therefore, Ω_ePE/PE = 1.58 and Ω_RSI/ePE = Ω_RSI/PE/Ω_ePE/PE = 1.15/1.58 = 0.73. Method 2 w/ECC results matches the predicted values the best. Method 1 and Method 2 (without ECC) also produced results close to predicted values, within the scanner SNR variability.

Table 1.

2D Acquisition, RSI, PE, and ePE Relative Sensitivity (Ω) Comparison of Experimental Phantom Data

		ePE/PE	RSI/PE	RSI/ePE
Ω	Method 1	1.52	1.18	0.77
	Method 2	1.53	1.16	0.76
	Method 2 w/ECC	1.57	1.15	0.73
FVHM Ratio		1.64	1.07	0.65
nSNR Ratio		0.96	1.07	1.12

^aData are for the two-channel recombination methods used (see “Data acquisition and reconstruction” section, under Methods). In addition, data for each channel was processed with Method 2 and eddy current correction (ECC) was performed before recombination (Method 2 w/ECC). The relative normalized sensitivity (nSNR Ratio) is calculated (Eq. [8]) using the FVHM ratio shown and the relative sensitivity (Ω) measured with Method 2 w/ECC.

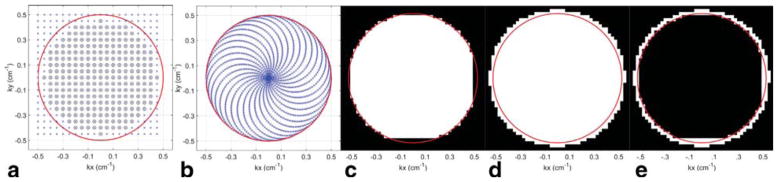
FIG. 5.

Phase encoded (PE, ePE) and RSI (kx,ky) sampling and effect of reconstruction settings for RSI on PSF: PE (blue x) and ePE (black o) (kx,ky) sampling (a); RSI (kx,ky) sampling for the outgoing trajectory segments (b); (kx,ky) grid PSF data following gridding with a Kaiser-Bessel W = 2 kernel, when no zero-padding is used (c); (kx,ky) grid PSF data following gridding with a Kaiser-Bessel W = 4 kernel, and with zero-padding (d). e: Difference between (d) and (c). The extra (kx,ky) grid coverage shown results in a sharper PSF for (d) versus (c), with 7% lower FWHM and 13% smaller FVHM, for Nx = 20 selected. As the sampled matrix size Nx increases, the relative improvement in PSF achieved through gridding and zero-padding will decrease. Red circle in (a–e) represents the edge of the (kx,ky) disk sampled by the rosette trajectories.

3D RSI versus ePE

Results for the 3D RSI vs ePE sensitivity and FVHM comparison for the five resonances are given in Table 2. Using the average measured relative sensitivity for the five metabolites, the RSI to ePE normalized sensitivity ratio for the unfiltered reconstruction is ((0.48+0.48+0.48+0.49+0.51)/5)/0.34 = 1.43. If a Hamming spatial filter is used, the RSI normalized sensitivity was found to be more than twice (2.08) that of ePE.

Table 2.

3D Acquisition RSI vs. ePE: BRAINO Phantom Sensitivity Comparison^a

		No Spatial filter			With Hamming
		RSI	ePE	RSI/ePE	RSI	ePE	RSI/ePE
FVHM (cm3)		0.5465	1.5955	0.34	1.5968	3.4957	0.46
tSNR (min−1/2)	tNAA	28.14 (3.37%)	58.13 (2.23%)	0.48	90.54 (2.22%)	95.07 (2.08%)	0.95
	tCr	22.56 (3.65%)	46.96 (2.47%)	0.48	73.94 (2.36%)	77.60 (2.21%)	0.95
	tCho	21.55 (5.95%)	45.32 (4.44%)	0.48	71.05 (4.13%)	74.91 (4.01%)	0.95
	Ins	12.57 (6.16%)	25.39 (4.55%)	0.49	40.78 (3.86%)	42.03 (3.80%)	0.97
	Glx	8.72 (8.27%)	17.22 (5.01%)	0.51	28.09 (5.14%)	28.29 (4.67%)	0.99

^aAverage mean sensitivity tSNR = SNR/√Taq in min^−1/2 for all voxels with LCModel Crammer Rao lower bounds CRLB<20%, for the five metabolites listed. Without spatial filtering, for the RSI sequence, 96% of voxels in VOI had CRLB<20% for all five metabolites; the 4% of voxels which did not qualify were all on the edges of VOI. When the spatial Hamming filter was used, 100% of the voxels within VOI had CRLB<20% for all five metabolites. In parentheses, the average CRLB for all voxels included in analysis is shown, for that specific metabolite, sequence and processing. Hamming filter applied for ePE sampling was 3D spherical/ellipsoidal and it goes to zero (0.08) at the edge of the k-space sampled; for RSI, it was a product of a 2D filter covering a disk in XY-dir and a 1D filter in Z-dir. The metabolites analyzed are (LCModel sums used): tNAA (total N-acetyl-aspartate: NAA+NAAG), tCr (total Creatine: Cr+PCr), tCho (total Choline: PCho+GPC), Inositol (Ins+Gly), Glx (Glutamate/Glutamine: Glu+Gln).

PSF Comparison for RSI, PE, and ePE

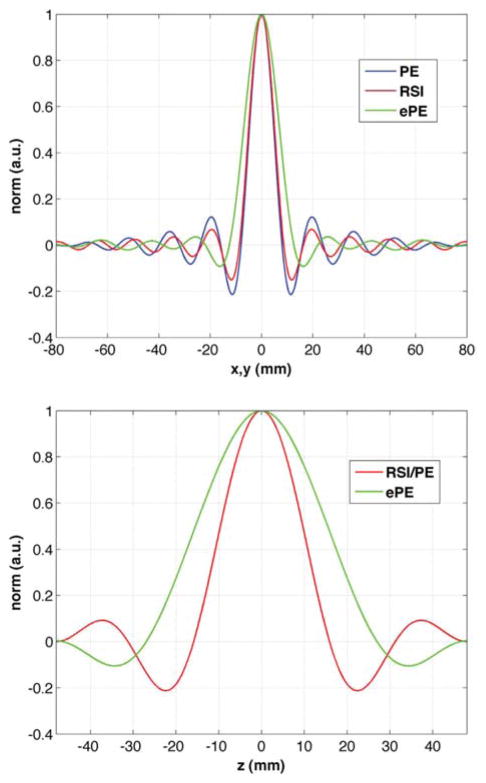
The simulated PSF in the x- and z-direction are compared for the three sampling schemes in Figure 6. The RSI full-width at half maximum (FWHM) in x-direction is less than 5% wider than for PE and, the PSF in z-direction is virtually identical to the PE sequence (same z-FWHM). The ePE sequence has a PSF FWHM 46% and 60% wider than the PE sequence in the x- and z- directions, respectively.

FIG. 6.

Comparison of the simulated x- (top) and z-direction (bottom) PSF for nominal 8mm isotropic 3D RSI (red), PE (blue) and ePE (green) sequences, with nominal matrix size 20 × 20 × 12 and field-of-view 16 × 16 × 9.6 cm³ (AP-RL-HF). The PSF for RSI (and ePE) is the same in any direction in the xy-plane, due to the k-space circular support, while the PSF for PE is not. The PE spatial resolution for a nonwindowed, zero-padded reconstruction is anisotropic, exhibiting angular dependence (46).

In Vivo Data

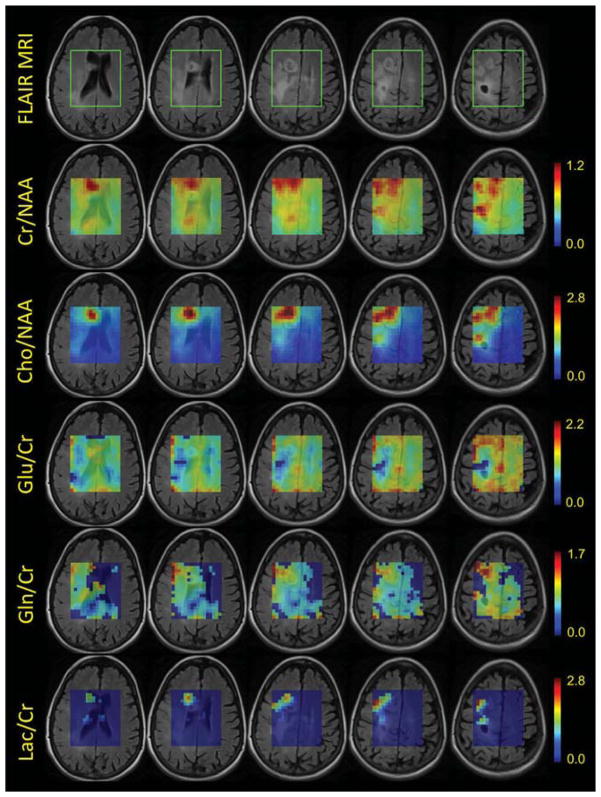
Fused anatomical FLAIR images and 3D RSI metabolite ratio maps for the five most superior of the eight reconstructed SI slices in the excited VOI, are shown in Figure 7, for one GBM patient. Examples of spectra for the same patient are shown in Figure 8, overlaid on top of the MPRAGE image. The data are from a 55-year-old female with a history of fibrillary astrocytoma enrolled in a vaccine study treating low-grade gliomas. The presence of higher content of glutamine (Gln) in the patient, in and around the tumor regions, enables accurate quantification (CRLB<20%) for both glutamate (Glu) and Gln, rather than only for the sum (Glx). This is also the case for lactate (Lac), as seen in Figure 7. The 3D RSI acquisitions for the five participants yielded an average of 1670 ± 250 voxels/participant with CRLB<20% for tNAA, tCr, tCho, Ins, and Glx.

FIG. 7.

Fused FLAIR images and metabolite ratio maps for the 8-min, 8-mm isotropic resolution, 3D RSI acquisition, from a 55-year-old female with a history of fibrillary astrocytoma. 12 partitions were encoded with 32 excitations each and a TR = 1250 ms was used. From left to right, slices 4 through 8 (out of the reconstructed eight for the excited VOI, with slice 1 at the lowest excited location) are shown. Most right column, slice number 8, with the “black hole” on the FLAIR image, corresponds to the highest brain location excited with LASER. The area enclosed in the green box shown on the FLAIR images, represents the excited LASER region. Maps for Creatine/NAA (Cr/NAA), Choline/NAA, Glutamate/Cr (Glu/Cr), Glutamine/Cr (Gln/Cr), and Lactate/Cr (Lac/Cr) are shown. Metabolite ratios values for all voxels are the ones calculated by LCModel. For the Glu/Cr, Gln/Cr, and Lac/Cr maps, a mask was applied: only voxels with reasonably good quantification accuracy (CRLB < 20%) are shown; otherwise, when CRLB > 20%, the displayed ratio was set to zero. Decreased Glu/Cr and increased Gln/Cr can be seen in and around the tumor regions visible on the FLAIR. Increased/strong Lactate signal in the tumor areas results in improved quantification accuracy (CRLB < 20%) – these areas are visible in the Lac/Cr maps in the bottom row.

FIG. 8.

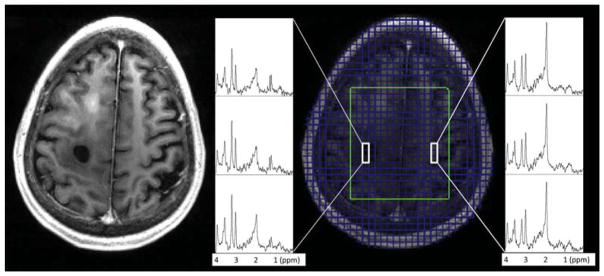
Examples of the 3D RSI spectra for SI slice number 8 (highest excited location), for the same GBM patient shown in Figure 7, overlaid here on top of the T1-weighted images. The anatomical image shown is the average of six 1 mm-MPRAGE slices corresponding to the reconstructed SI slice position. Green box – excited LASER VOI. Example spectra displayed correspond to “black hole” ROI (tumor region) and normal appearing tissue. Decreased NAA and increased Choline and Lactate can be seen in the spectra within and around the lesion.

DISCUSSION

In this study, we demonstrated that rosette spectroscopic imaging is a fast, high sensitivity acquisition technique, capable of medium to high resolution in vivo brain ¹H SI at high field (3T), in clinically feasible times, and with reduced demands on the scanner gradient system. The 2D RSI data with 1.1 cc voxels were collected in as little as 32 s while the 3D 8-mm isotropic data sets (0.5 cc voxels) were acquired in 5 to 10 min, with a maximum gradient G_max = 5.8 mT/m and a maximum slew-rate S_max = 45 mT/m/ms. The RSI technique provided virtually the same spectral information as the phase encoding method; this was demonstrated using the Bland-Altman analysis and by investigating the scalar product of the RSI and PE/ePE spectra in each voxel, across all voxels inside the excited VOI. Elliptical phase encoding provides for faster acquisitions than the fully encoded one; however, it does so at the expense of a wider PSF, larger FWHM and bigger effective voxel size; thus, decreased effective resolution. While we did not collect a fully phase encoded 20 × 20 × 12 acquisition, we simulated its PSF and found FVWM = 0.51 cm³. RSI’s effective voxel size (Table 2) is less than 7% larger and the x- FWHM is less than 5% wider than for the fully encoded PE scan for the 20 × 20 acquisition matrix used (Figure 5 and Figure 6), while an order of magnitude faster acquisition sequence than both the PE and ePE sequences.

For the RSI acquisition presented in this study, i.e., ω₂ = ω₁ and constant strength gradient and slew rate readout, the trajectories in k-space appear as circles, somewhat similar to another technique previously presented (11). The main difference between the two methods is that, unlike the SI method which uses circles concentric with the center of k-space for readout, each RSI circle/trajectory starts at the center of k-space (and samples it periodically), which can make the RSI technique more robust to motion. In addition, for the same N_x and SW, the demands on the gradient system for RSI are overall somewhat lower and the same for all shots, as opposed to the concentric circle method. This is due to the fact that for concentric circles, the trajectories with the larger radii require higher gradient strength and slew rates, with the most peripheral circle needing twice the gradient strength and twice the slew rate used for RSI with ω₂ = ω₁.

When compared with echo-planar or spiral SI, which achieve sampling density efficiencies of 1 and up to 0.97, the RSI technique has a lower sampling efficiency of 0.90. However, RSI can achieve similar encoding speeds for the same spatial resolution and spectral bandwidth, while using a much lower gradient readout strength and/or slew rate. Because rosette trajectories simultaneously encode one spectral and two spatial dimensions, they can be faster than EPSI which encodes the spectral and one spatial dimension at the same time. Consider the EPSI 50 × 50 × 18 acquisition covering a FOV = 280×280×180 mm³, achieving an in-plane resolution (IPR) of 5.6 mm, which was used previously (21,36,37). Using the acquisition parameters provided (21), an RSI technique with FOV = 200×200×180 mm³ and a 36 × 36 × 18 acquisition matrix, if designed for fastest acquisition (10), would achieve the same 5.6 mm resolution and the same SW = 833 Hz using just 32 shots/partition, if maximum slew rate is set at 150 mT/m/ms (lower than EPSI’s peak 200 mT/m/ms used for the 100 μs gradient ramps), and the peak gradient strength along the trajectory would be just under 17 mT/m. The total number of encoding steps 32 shots/slice × 18 slices = 576 shots represents only 64% of the acquisition time needed by the EPSI’s 50 shots/slice × 18 slices = 900 encoding steps. Using ω₂ = ω₁, RSI would require 56 shots/partition for the same spatial and spectral coverage, and the scan time would be ~12% greater than for EPSI. However, in this case, the gradient strength and slew rate would be constant along the readout trajectory and equal to 5.5 mT/m and 29 mT/m/ms, respectively. Furthermore, as already mentioned, a 15–25% decrease in the number of spatially interleaved rosette shots (and equivalent decrease in acquisition time) is possible with no adverse aliasing effects. Cyclical spectral unwrapping could also be used to double the effective SW of the RSI acquisition, similar to that described for an EPSI acquisition (21).

Finally, SSI is the most similar to RSI, because spirals also simultaneously encode one spectral and two spatial dimensions, covering a disk in (k_x, k_y)-space and, like rosette trajectories, the center of k-space is periodically sampled. For either spirals or rosettes, because readout trajectories start at k = 0, the phase for the 1^st point should be the same for all shots in a given partition (and temporal interleave). This enables easy identification and correction for motion (38,39), when it is mild. Implementing a navigator for real time motion correction and shim updating (40), is another option to deal with more severe movement. Both spiral and rosette acquisitions have similar flexibility in designing their trajectories. Variable sampling density spirals to increase imaging resolution without significant increase in acquisition time (41), to reduce truncation artifacts (42), or to obtain a desirable PSF for the SSI acquisition (43) have been demonstrated. The sampling uniformity factor η_SSI varies for these trajectories between 0.81 and 0.97, with the highest value corresponding to the constant sampling density spirals (41,44); this latter type is desirable for ¹H brain SSI, because it provides the highest sensitivity. However, if SSI is used in a “spiral-out” implementation (trajectories leave k = 0 to k_max, and a rewinder is used to bring them back to k = 0), compared with a “out-in” implementation (where a spiral readout is also used from k_max to k = 0), up to 15% of the readout duration would be unused (22), reducing the benefit of constant sampling density. The relative sensitivity of SSI to RSI is: ${\mathrm{\Omega }}_{\mathit{SSI}/\mathit{RSI}}={\mathrm{\eta }}_{\mathit{SSI}}/{\mathrm{\eta }}_{\mathit{RSI}}·\sqrt{T_{\mathit{SSI}}^{\mathit{read}}/T_{\mathit{RSI}}^{\mathit{read}}}=.97/.9·\sqrt{0.85}=0.99$. Therefore, to fully realize its SNR potential, constant sampling density SSI would benefit from being used in an “out-and-in” implementation. However, unlike rosette trajectories which have the innate property of rewinding toward k = 0 because the gradient radial component becomes null when k = k_max, for spirals this is not the case and careful implementation is necessary in rewinding them (9,44). Constant sampling density spirals cover k–t space somewhat more quickly than the rosette trajectories, with fewer spatial angular interleaves needed; but they typically require more temporal interleaves and, at medium-to-higher resolutions, averaging is necessary. Consider the 22 × 22 × 12 SSI protocol previously demonstrated (22) for a nominal 7.3 mm isotropic resolution (0.39 cm³) and SW = 1200 Hz. The protocol fully acquires k–t space in 2:24 min:s (for TR = 1 s), using six angular interleaves (N_sh = 6), two temporal interleaves (n_TI = 2), for a total of N_sh · n_TI · N_z = 144 encoding steps, with maximum gradient and slew rate of 12.8 mT/m and 127 mT/m/ms. However, two to four signal averages are needed to increase SNR, for a scan time of 4:48 to 9:36 min:s, similar to the acquisition times used in our RSI implementation. Furthermore, the RSI acquisition uses a gradient readout strength less than half and a slew rate almost one-third of the one for SSI. Finally, compared with the effective SSI voxel size of 0.66 cm³, which is 69% bigger than the nominal voxel size of 0.39 cm³, RSI achieves an effective voxel size of 0.55 cm³ (Table 2), which is only 7% larger than the nominal resolution of 0.51 cm³ (8-mm isotropic).

One sequence limitation—as for other studies using LASER, PRESS, or STEAM excitation—is the limited brain coverage; while superior sensitivity with very small CSDE (chemical shift displacement error) is achieved for the LASER excitation (22,28), no metabolite information is collected for cortical regions closer to the scalp. For patients with pathology in those regions, an excitation scheme using an inversion recovery pulse for lipid nulling could be used, for example, even if the sensitivity decreases compared with the LASER excitation. The decrease in SNR could be mitigated by using a higher magnetic field scanner (e.g., 7T) or/and a PTX (parallel transmit) system (45), with rosette trajectories’ capability of achieving higher spectral bandwidth than other fast sampling schemes, making them a perfect candidate in meeting the challenge of higher SW needed for higher B₀ field strengths.

In conclusion, RSI is a fast, high sensitivity technique, which is suitable for in vivo brain spectroscopic imaging at high B₀ fields, capable of data acquisition with reduced demands on the scanner gradient system; the lower stress on the gradient system results in decreased acoustic noise/vibrations and, therefore, reduced patient discomfort and increased compliance. Automatic data processing is necessary for fast MRSI techniques due to the large number of spectra generated and we have developed programs that, in conjunction with LCModel software, form a complete pipeline to process and quantify spectral data for all voxels acquired.