Poly(ethylene glycol)s in Semidilute Regime: Radius of Gyration in the Bulk and Partitioning into a Nanopore

Abstract

Using two approaches, small-angle neutron scattering (SANS) from bulk solutions and nanopore conductance-fluctuation analysis, we studied structural and dynamic features of poly(ethylene glycol) (PEG) water/salt solutions in the dilute and semidilute regimes. SANS measurements on PEG 3400 at the zero-average contrast yielded the single chain radius of gyration (R_g) over 1–30 wt %. We observed a small but statistically reliable decrease in R_g with increasing PEG concentration: at 30 wt % the chain contracts by a factor of 0.94. Analyzing conductance fluctuations of the α-hemolysin nanopore in the mixtures of PEG 200 with PEG 3400, we demonstrated that polymer partitioning into the nanopore is mostly due to PEG 200. Specifically, for a 1:1 wt/wt mixture the smaller polymer dominates to the extent that only about 1/25 of the nanopore volume is taken by the larger polymer. These findings advance our conceptual and quantitative understanding of nanopore polymer partitioning; they also support the main assumptions of the recent “polymers-pushing-polymers” model.

Graphical Abstract

INTRODUCTION

Understanding polymer partitioning into nanoscale cavities of different nature is important for many technological applications that include, but are not limited to, analytical chromatography, separation techniques, and purification methods. It is also critical in the qualitative interpretation and quantitative analysis of molecular interactions and biological regulation in the crowded cellular environment. This necessitates model studies with polymer solutions explored in both dilute and semidilute regimes.

Some of the early experimental investigations on polymer confinement were conducted using Vycor glass as a nanoporous medium.^1–3 Small-angle neutron scattering (SANS) was used to determine the structure of solution phase polymers within the confined matrix and in the bulk. While the results were insightful, certain caveats were discovered with using Vycor.³ For example, polymer adsorption to the pore walls has to be considered and may require chemical treatment to passivate the Vycor surface. Also, random pore geometries complicate the analysis. It was realized that having better defined pore geometries would greatly improve these experiments and serve to more robustly test and develop theoretical approaches.

During the past 30 years it became clear that certain biological channels provide well-defined nanopores for studying both polymer partitioning^4–14 and its osmotic action.^15–17 In addition, it was shown that conductance fluctuation analysis of single nanopores allows one to study the dynamic side of polymer partitioning, which offers advantages over ensemble techniques. To the best of our knowledge, the first experiments on polymer-induced noise in the nanopore current were reported for alamethicin channels interacting with differently sized poly(ethylene glycol)s (PEGs)¹⁸ and then further advanced and extended to other biological nanopores.^6,19–21 Highly water-soluble and “soft” PEGs proved to be most popular in partitioning studies. In particular, it was demonstrated that under appropriate conditions PEG-induced single-molecular events¹⁰ can be perfectly time-resolved²² and used for PEG dispersion analysis at the submonomeric resolution.^23–25 An interesting latest development in this single-molecule technique relates to the unexpected temperature dependence of the lifetime of a single polymer molecule trapped by the α-hemolysin (aHL) nanopore.²⁶ It turned out that the temperature effect can be opposite for PEGs of different molecular weights. For the relatively small PEGs (molecular weight <2000) the time was found to exponentially decrease with temperature, while increasing for the larger PEGs (molecular weight 2000 and higher).

Recently,²⁷ polymer partitioning from semidilute solutions of PEG mixtures was studied with a number of membrane-spanning β-barrel channels of different origin: the voltage-dependent anion channel (VDAC) from outer mitochondrial membrane, bacterial porin OmpC, and channel-forming toxin aHL. PEGs of molecular weight 200 (PEG 200) and 3400 (PEG 3400), and their mixtures in different proportions, were used. The results for the mixtures were rationalized within the earlier formulated “polymers-pushing-polymers” model of nanopore partitioning,²⁸ which is based on the assumptions that the larger component of the polymer mixture, being preferentially excluded from the cavity, pushes the smaller component into the cavity, thus representing forced polymer redistribution between the bulk and the channel. Here we study polymer mixtures by using two different methods—SANS and nanopore conductance fluctuation analysis—to quantify the larger polymer parameters in the bulk and the degree of its partitioning in the pore, respectively. We show that the reduction of the PEG 3400 characteristic size with its increasing concentration in the bulk is statistically significant but small. We also demonstrate that partitioning of the larger polymer in the nanopore is negligible, below 4%, if its relative weight fraction is kept smaller than 1/2, in excellent agreement with the major assumptions of the recent study.²⁷

EXPERIMENTAL SECTION

Materials

The synthesis of perdeuterated PEG of MW 3900 (dPEG 3900) was achieved using a custom-made glass reactor with constrictions and break-seal techniques under high-vacuum conditions. Potassium 2-(tetrahydropyranyloxy)ethanol was used as the initiator and tetrahydrofuran as the solvent. Details of the synthesis and characterization of the dPEG are similar to previously reported.²⁹ Deuterium oxide (Cambridge Isotope Laboratories, 99.9% D) was used without further purification. Staphylococcus aureus aHL, PEGs of MW 200 and 3400, KCl, and HEPES for nanopore experiments were purchased from Sigma, and diphytanoylphosphatidylcholine was from Avanti Polar Lipids. The buffered KCl solutions containing various wt % of PEG 200, PEG 3400, and their mixtures were prepared in double-distilled water.

Small-Angle Neutron Scattering

SANS experiments were performed on the extended Q-range small-angle neutron scattering (EQ-SANS, BL-6) beamline at the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory (ORNL). In 60 Hz operation mode, a 2.5 m sample-to-detector distance with 2.5–6.46 Å wavelength band was used³⁰ to obtain the relevant wave-vector transfer, Q = 4π sin(θ)/ λ, where 2θ is the scattering angle. Samples were loaded into 1 mm path-length circular-shaped quartz cuvettes (Hellma USA, Plainville, NY), and SANS measurements were performed at 25 °C. Data reduction followed standard procedures using MantidPlot.³¹ The measured scattering intensity was corrected for the detector sensitivity and scattering contribution from the solvent and empty cells and then placed on absolute scale using a calibrated standard.³²

PEG solutions for SANS were prepared in 5 mM HEPES (pH 7), 1 M KCl buffer, consistent with the single-channel experiments. The SANS zero-average contrast (ZAC) condition³³ was used to obtain the single PEG chain conformation over the entire concentration series. Here the scattering intensity, I(Q), can be described by

$$I(Q)=[f_{\mathrm{D}}\mathrm{\Delta }{{\rho }_{\mathrm{D}}}^2+(1-f_{\mathrm{D}})\mathrm{\Delta }{{\rho }_{\mathrm{H}}}^2]S_1(Q)+{[f_{\mathrm{D}}\mathrm{\Delta }{\rho }_{\mathrm{D}}+(1-f_{\mathrm{D}})\mathrm{\Delta }{\rho }_{\mathrm{H}}]}^2{S}_2(Q)$$ (1)

where f_D is the fraction dPEG, Δρ_D is the dPEG contrast with H₂O/ D₂O solvent, Δρ_H is the hydrogenated PEG (hPEG) contrast with H₂O/D₂O solvent, S₁(Q) is the intrachain scattering, and S₂(Q) is the interchain scattering. To nullify the S₂(Q) contribution, the second term in eq 1 was set to 0 by choosing f_D = 0.5 (1:1 hPEG 3400:dPEG 3900) and then solving for the appropriate D₂O percentage (= 63.3% D₂O). Both hPEG and dPEG have a similar degree of polymerization (DP ~ 80), which is important for the ZAC method. PEG concentrations are reported as total wt % PEG (hPEG 3400 + dPEG 3900) for the ZAC experiments. SANS curves were fit to the Debye model for Gaussian polymer chains

$$I(Q)=I(0)\frac{2({\mathrm{e}}^{-x}+x-1)}{x^2}$$ (2)

where the scattering intensity, I(Q), is described by the zero-angle scattering intensity, I(0), and x = Q²R_g², where R_g is the radius of gyration.

Nanopore Experiments

Bilayer lipid membranes were prepared from diphytanoylphosphatidylcholine/pentane solution using the lipid monolayer-opposition technique on a circular aperture in a Teflon partition separating two compartments of an experimental cell.²⁰ PEGs and their mixtures were added to 1 M KCl aqueous solutions. Single membrane-spanning nanopores were formed by adding 25 μg/mL stock aHL solution directly to one of the compartments. Ion current measurements were performed with an Axopatch 200B amplifier (Molecular Devices, Eugene, OR) at room temperature (~24 °C). A pair of Ag/AgCl electrodes in 15% agarose/2 M KCl bridges was used to apply transmembrane voltages and to record ion currents. A positive potential of 100 mV was applied from the side opposite to aHL addition. The output signal of the amplifier was filtered by the amplifier built-in 10 kHz Bessel filter and in-line low-pass eight-pole Butterworth filter (Model 9002; Frequency Devices, Ottawa, IL) at 15 kHz and directly saved into computer memory with a sampling frequency of 50 kHz. Amplitude and fluctuation analyses were performed using ClampFit 10.2 (Molecular Devices) and Origin 9.1 software (OriginLab, Northampton, MA).

Viscosity

The kinematic viscosity, ν, of PEG 200/PEG 3400 mixtures in 5 mM HEPES (pH 7), 1 M KCl buffer was measured in duplicate or triplicate using Cannon–Fenske viscometers. Using density, ρ, measurements with a standard balance, the dynamic viscosity η (= νρ) was then calculated.

RESULTS AND DISCUSSION

SANS: Chain Contraction in the Semidilute Regime

We first used SANS from bulk PEG solutions to evaluate polymer chain contraction with increasing polymer concentration. To accomplish this, we took advantage of the zero-average contrast (ZAC) condition for SANS,³³ where an optical theta condition is reached to cancel out intermolecular scattering contributions and yield only the single chain scattering independent of the PEG concentration. This method also was used in previous SANS studies on polymer structure in Vycor.^1–3 We achieved the ZAC condition for PEG by using 1:1 hPEG 3400:dPEG 3900 and 63.3% D₂O (see Experimental Section) to unambiguously determine the single polymer chain conformation over the full concentration range measured. Importantly, the same buffered salt solution was used for SANS and the nanopore polymer partitioning experiments. The SANS curves and fits to the scattering as expected from a random coil (solid lines) are shown in Figure 1A for the PEG concentration series, from 1 to 30 wt %. As a control, the I(0) values obtained from the random coil fits were normalized by I(0) at c = 1 wt %, I(0,c)/I(0,1 wt %), to compare with the wt % concentration. The direct correlation demonstrated in Figure 1B verifies that S₂(Q) in eq 1 has no contribution with only single chain scattering detected. Since hPEG 3400 and dPEG 3900 have a similar DP, we simply refer to this 1:1 mixture as “PEG 3400” below.

Figure 1.

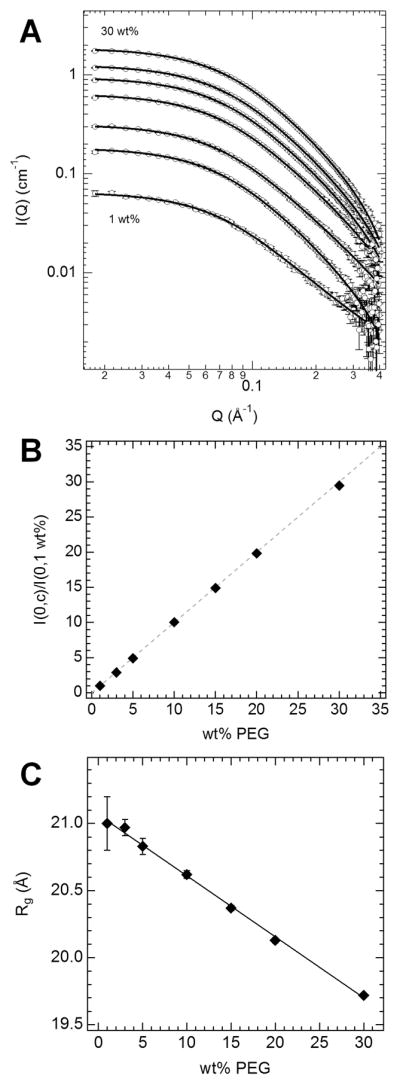
(A) SANS curves on 1:1 hPEG 3400:dPEG 3900 in 63.3% D₂O buffer. The total PEG concentration was varied as 1, 3, 5, 10, 15, 20, and 30 wt % (with the lowest and highest wt % indicated). SANS curves were fit to the Debye equation (solid lines). (B) Normalized I(0) vs wt % PEG (solid diamonds) compared to the direct wt % vs wt % PEG correlation (dashed line). (C) PEG 3400 single chain radius of gyration R_g vs wt % determined using SANS at the ZAC point. A linear fit to the data (solid line) yields the equation R_g (Å) = 21.07–0.046 (wt %).

Figure 1C shows that the PEG 3400 R_g slightly decreases with increasing polymer concentration. A linear fit to the data provided the size extrapolated to infinite dilution, R_g,0 = 21.0 Å, which matches the value at 1 wt %. As the semidilute regime is approached, R_g decreases to 19.7 Å at 30 wt %. The SANS results here provide two main observations. First, they demonstrate that even at 1 M KCl bulk polymer behavior does not change significantly, as the polymer size at infinite dilution is close to the expected value based on its length and persistence length.³⁴ This seems to be an important finding, as interactions between PEG and salt are well documented.³⁵ Second, the decrease in polymer size with increasing polymer concentration, though statistically significant, is small at ~1.3 Å. The R_g ratio between 30 and 1 wt % is about 0.94.

Previous SANS measurements³⁶ on hydrogenated PEG 3400 in D₂O found a similar dilute solution R_g but with a more pronounced decrease in the “apparent” R_g with increasing polymer concentration. Going from ~3 to 16 wt %, the reported R_g decreased by more than 10 Å. As the authors of ref 36 discuss, the reason for the stronger effect is that the measured “apparent” R_g is also influenced by the onset of interpolymer interactions (S₂(Q) in eq 1), causing the measured R_g value to appear to decrease with increasing concentration. However, it is difficult to separate out the individual PEG chain R_g since interpolymer scattering contributions can become dominant. The “apparent” R_g values in this previous SANS study therefore are informing on a characteristic correlation length within the PEG solutions. By using ZAC to nullify the S₂(Q) contribution in our SANS measurements, we show that the single PEG chain R_g does decrease, but the concentration effect is more subtle. This slight decrease in the size of individual PEG chains can be partially attributed to a decrease in water activity, which reduces the solvent quality for the PEG to favor a more compact conformation. A similar effect is observed upon raising the temperature, where PEG 3400 collapses in size due to decreased solubility.²⁶

Nanopore Fluctuation Analysis: Predominant Small-Chain Partitioning into the Nanopore

One of the main assumptions of the polymers-pushing-polymers model used for the analysis of the forced PEG partitioning into nanopores²⁷ was that in a mixture of smaller and larger polymers, namely, PEG 200 and PEG 3400, it is predominantly the smaller polymer that fills the pore, up to the larger polymer weight fraction of 0.5. We now show that fluctuation analysis of pore conductance in the presence of polymer mixtures allows one to check this assumption experimentally. To achieve this goal, we use single transmembrane channels or water-filled pores formed by α-hemolysin³⁷ in planar lipid bilayers.

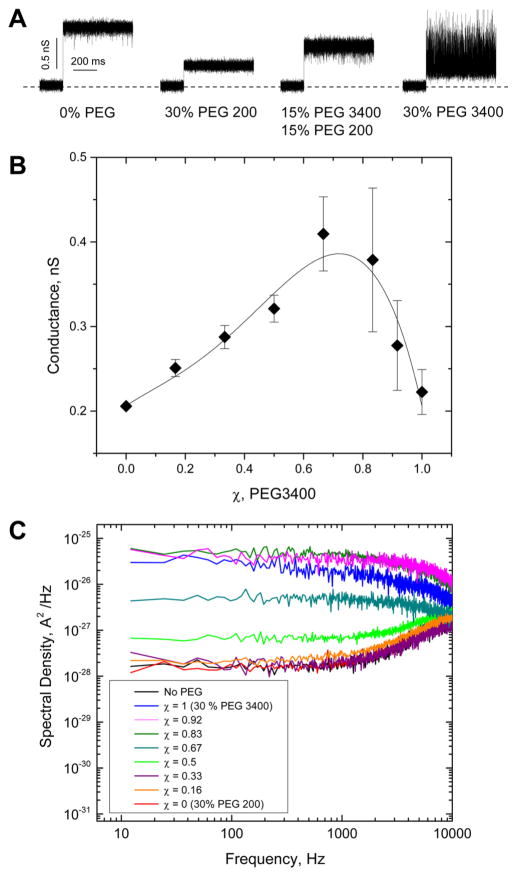
Figure 2A displays samples of the currents through the channels before and after addition of different PEG mixtures. It shows two effects of PEG on the current: PEG addition to the membrane-bathing 1 M KCl aqueous solution reduces pore conductance and changes the noise in the ion current. Both effects depend on the composition of the polymer mixture.

Figure 2.

(A) Traces of ionic currents through single aHL nanopores in lipid bilayers at different compositions of the polymer mixtures. The events of spontaneous assembly of nanopores are manifested as upward jumps in the current. Addition of polymers decreases the current due to their partitioning into the pore. It is also seen that the increasing concentration of PEG 3400 promotes excess fluctuations. Dashed line denotes zero current. Applied voltage was 100 mV. All traces were filtered by a low-pass filter with 10 kHz cutoff frequency. (B) Average conductance of the nanopore in the presence of 30 wt % PEG as a function of the relative fraction χ of PEG 3400. As PEG 3400 fraction grows from χ = 0, corresponding to pure PEG 200, to about χ = 2/3, the conductance increases, reporting on a reduced polymer partitioning into the pore. Further increase in PEG 3400 content decreases conductance increasing partitioning. (C) Power spectral densities of ion current noise in the polymer-free and polymer-containing solutions of different relative fractions χ of PEG 3400.

Figure 2B gives the relative channel conductance in PEG 200/PEG 3400 mixtures of different composition, in which the total monomeric concentration of PEG is held constant at the 30 wt % level at a varying relative fraction χ of PEG 3400 in the mixture, defined as χ = [PEG 3400]/([PEG 3400] + [PEG 200]), where square brackets stand for the weight concentration. Surprisingly, channel conductance displays a non-monotonic dependence on the relative fraction of PEG 3400. It first increases with the increasing fraction of the larger PEG in the mixture, but then, after this fraction reaches about 2/3 (corresponds to 20 wt % of PEG 3400), it starts to decrease. Using the language of conductance-derived partitioning,²⁷ this can be interpreted in the following way. Substitution of smaller PEG 200 by larger PEG 3400 first leads to a decrease in partitioning which is manifested by an increase in the conductance of the pore due the reduced pore occupancy by polymer. This is an expected behavior because of the extra entropic penalty of moving larger polymer into the nanopore; but then, surprisingly, with the fraction of the larger polymer increasing, the partitioning increases again.

Figure 2C shows the results of the spectral analysis of fluctuations in the currents through the α-hemolysin nanopore in the polymer-free solutions and in the presence of the PEG 200/PEG 3400 mixtures of different small vs large polymer proportions. It is immediately seen that while for the solutions enriched with PEG 200 the noise is barely different from that of the nanopore in the absence of polymers, for the ones enriched with PEG 3400 the polymer-induced noise is quite significant. The larger polymer induces a lot of current fluctuations while the smaller one does not.

Visual examination of the data suggests that at the relative fraction of PEG 3400 not greater than χ = 1/2 (corresponding to 15 wt % PEG 3400 in the bulk) the contribution of PEG 3400 to the partitioning is negligible. Indeed, the low-frequency spectral density of current fluctuations at this relative fraction is more than 2 orders of magnitude lower than it is in pure PEG 3400 solutions, χ = 1. Assuming that this spectral parameter reports on the presence of PEG 3400 in the nanopore, one may conclude that this larger polymer is practically excluded from the pore at χ = 1/2.

To obtain quantitative estimates, we need to use the available analytical approaches. One of them, deemed to be most appropriate in our case, is based on the diffusion model of channel-facilitated transport.³⁸ For the fluctuations, which are induced by equilibrium exchange of nonconductive particles between the pore and the bulk, it gives the following expression for the spectral density of current noise S_I( f) as a function of frequency f:

$$S_I(f)=\langle N\rangle {(\mathrm{\Delta }G)}^2{V}^{2}S(f)$$ (3)

where 〈N〉 is the average number of particles in the pore, ΔG is the reduction in pore conductance due to entering of one particle, V is the applied voltage, and S(f) is the spectral density obtained from the normalized correlation function of the number of particles in the pore C(t):

$$S(f)=4{\int }_0^{\infty }C(t)cos(2\pi ft)\mathrm{d}t$$ (4)

Solutions for C(t) demonstrate that the spectral density may have a quite complex frequency behavior,³⁹ which is determined by many parameters of the pore and pore/particle interactions. However, for the low-frequency spectral limit, S(0), and particle diffusional dynamics in a cylindrical pore, the expression is simplified to³⁸

$$S(0)=\frac{L^2}{3D}\left(1+\frac{3\pi }{2}\frac{Da}{D_{\mathrm{b}}L}\right)$$ (5)

where L is the channel length, a is the channel radius, D is the particle diffusivity in the channel, and D_b is the particle diffusivity in the bulk. Because for the pore in question L ≫ a³⁷ and D_b ≫ D,²⁰ the last term in the brackets can be omitted, and we obtain the following:

$$S_I(0)=\langle N\rangle \frac{L^2}{3D}{(\mathrm{\Delta }G)}^2{V}^2$$ (6)

It is convenient to introduce the normalized fluctuation spectra by the following expression:

$$S_{\text{rel}}(f)\equiv \frac{S_I(f)}{{\langle G\rangle }^2{V}^2}$$ (7)

where 〈G〉 is the average conductance of the nanopore. As a result, we have a simple expression:

$$S_{\text{rel}}(0)=\langle N\rangle \frac{L^2}{3D}{\left(\frac{\mathrm{\Delta }G}{\langle G\rangle }\right)}^2$$ (8)

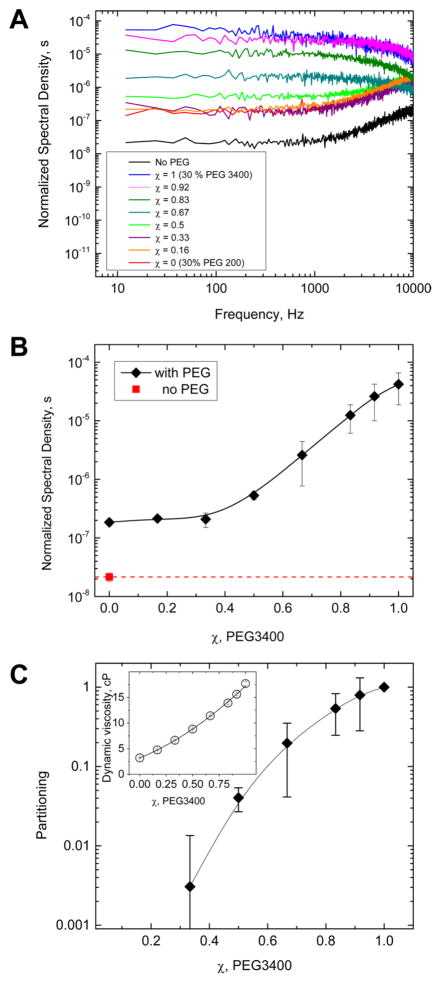
Experimentally obtained spectra transformed according to eq 7 are shown in Figure 3A. The values of S_rel(0), defined as an average of the normalized spectra in Figure 3A over the 10–300 Hz range, are given in Figure 3B.

Figure 3.

(A) Power spectral densities of Figure 2C normalized by pore average conductance according to eq 7. The normalization demonstrates that the relative conductance fluctuations are increased by polymer presence for all mixtures. (B) Low-frequency spectral density, S(0)_χ, as a function of polymer mixture composition characterized by the relative fraction of PEG 3400, χ. Pores in contact with solutions of the increasing PEG 3400 content display increasing noise intensities at χ > 1/3. (C) PEG 3400 partition coefficient as a function of mixture composition calculated according to eq 11 using dynamic viscosity data shown in the inset.

Now, these data and eq 8 allow us to quantify the relative population of PEG 3400 in the nanopore. Indeed, assuming that ΔG/〈G〉, the normalized change in conductance due to the entrance of one PEG 3400 molecule, does not change much for the studied mixtures and that the intrachannel diffusion coefficient scales with the mixture composition similarly to its bulk counterpart and is inversely proportional to viscosity, we can estimate the average number of PEG 3400 molecules in the pore. Their average number, 〈N(χ)〉, as a function of polymer composition in the bulk, χ, can be expressed through their average number in pure PEG 3400 solutions (χ = 1), 〈N(1)〉, as

$$\frac{\langle N(\chi )\rangle }{\langle N(1)\rangle }\simeq \frac{S_{\text{rel}}{(0)}_{\chi }}{S_{\text{rel}}{(0)}_{\chi =1}}\frac{{\eta }_{\mathrm{p}}(1)}{{\eta }_{\mathrm{p}}(\chi )}$$ (9)

where S_rel(0)_χ and S_rel(0) _χ=1 are the low-frequency spectral densities of PEG 3400-induced fluctuations at the PEG 3400 relative fraction χ and χ = 1, respectively, and η_p(1)/η_p(χ) is the ratio of mixture viscosities in the pore at PEG 3400 relative fraction in the bulk indicated as arguments. As it is suggested by the conductance data in Figure 2B, PEG 3400 practically equipartitions at χ = 1, so that its content-dependent partitioning coefficient can be defined as p(χ) = 〈N(χ)〉/ 〈N(1)〉.

According to eq 9, in order to obtain the partition coefficient from the noise data, we need to know the intrapore viscosity ratio. We deduce the intrapore viscosity from the data on bulk dynamic viscosity measurements. These are shown in Figure 3C inset and approximated by the solid line

$$\eta (\chi )=3.20+8.31\chi +5.72{\chi }^{1.96}$$ (10)

drawn through the data points, assuming that the solution viscosity in the pore is proportional to the solution dynamic viscosity, eq 10, with the larger polymer relative fraction corrected for partitioning, η_p(p(χ)) ∝ η (p(χ)). As a result, on the basis of eq 9, we arrive at

$$p(\chi )=\frac{S_{\text{rel}}{(0)}_{\chi }}{S_{\text{rel}}{(0)}_{\chi =1}}\frac{\eta (1)}{\eta (p(\chi ))}$$ (11)

Solving eq 11 numerically, we obtain the values of p(χ) shown in Figure 3C. The figure demonstrates that partitioning of PEG 3400 is highly composition-dependent. Indeed, at χ = 0.5 (1:1 PEG 3400:PEG 200 solutions) it is only about 4 × 10^–2 relative to its value in pure PEG 3400 solutions (χ = 1) and at χ = 0.33 PEG 3400 partitioning drops to a fraction of one percent. Partitioning increases sharply, reaching unity at χ = 1 where only the larger polymer is in solution. Here PEG 3400 is pushed into the nanopore due to high solution nonideality; in the dilute regime its partitioning is negligible.²⁷ Interestingly, in the case of the PEG 200/PEG 3400 mixture, the increase in viscosity produced by PEG 3400 relative fraction increase from χ = 0.5 to χ = 1 (corresponding to PEG 3400 concentration of 15 and 30%, respectively) is about a factor of 2 (Figure 3 inset and eq 10). This is significantly smaller than the viscosity change for pure PEG 3400 solutions at these two concentrations interpolated from the data published previously.⁴⁰

CONCLUSIONS

Structural parameters in the bulk and dynamic partitioning into a nanopore of PEG 3400 water solutions in the presence of PEG 200 and 1 M potassium chloride salt were studied by SANS from bulk solutions and by analysis of nanopore conductance fluctuations, respectively. It was demonstrated that at the increasing fraction of PEG 3400 in the PEG 3400/ PEG 200 mixtures with the total monomeric concentration of PEG kept constant at 30 wt %, partitioning of the larger polymer into the α-hemolysin nanopore change. Increasing PEG 3400 concentration also leads to a decrease in the characteristic chain size. However, conclusions from both our analysis of the structural features and dynamic partitioning are in excellent accord with the major assumptions of the recently formulated polymers-pushing-polymers approach.^27,28 Indeed, the R_g of PEG 3400 reduces from 21.0 Å (extrapolated to infinite dilution) to 19.7 Å as the polymer concentration increases from 1 to 30 wt %. This is a statistically reliable (Figure 1C) but small effect.

Partitioning of PEG 3400 grows rapidly with χ but is estimated as negligible, specifically, p(χ) ≤ 4 × 10^–2, for the fraction of this polymer in the mixture as large as χ = 0.5 (Figure 3C). This level of partitioning means that in comparison to χ = 1 only 4% of the polymer-accessible volume of the pore is taken up by PEG 3400; the rest of the volume is filled by the smaller PEG 200. Taking into account the 17-fold difference in their molecular weight, we conclude that the ratio of the average number of small polymer molecules in the pore to that of the large ones exceeds 400 at this and smaller PEG 3400 relative fractions. With the increasing PEG 3400 fraction, the partitioning of this larger polymer starts to dominate. Quite unexpectedly, due to a significant nonideality at χ = 1, this large polymer fills the α-hemolysis pore to nearly the same degree as pure PEG 200 at its 30% concentration (Figure 2B). This means that polymer–polymer repulsive interactions overcome the cost of its confinement by the pore.^11,41

We believe that these findings are important for understanding and quantifying polymer behavior in the bulk and polymer partitioning into nanopores in dilute and semidilute regimes.