Multiple- vs Non- or Single-Imputation based Fuzzy Clustering for Incomplete Longitudinal Behavioral Intervention Data

Abstract

Disentangling patients’ behavioral variations is a critical step for better understanding an intervention’s effects on individual outcomes. Missing data commonly exist in longitudinal behavioral intervention studies. Multiple imputation (MI) has been well studied for missing data analyses in the statistical field, however, has not yet been scrutinized for clustering or unsupervised learning, which are important techniques for explaining the heterogeneity of treatment effects. Built upon previous work on MI fuzzy clustering, this paper theoretically, empirically and numerically demonstrate how MI-based approach can reduce the uncertainty of clustering accuracy in comparison to non-and single-imputation based clustering approach. This paper advances our understanding of the utility and strength of multiple-imputation (MI) based fuzzy clustering approach to processing incomplete longitudinal behavioral intervention data.

I. Introduction

Behavioral interventions (e.g., physician advice; individual, group, or telephone counseling; self-help, including Internet use, and emerging use of wearable biosensors) [1]–[16] are commonly used to facilitate substance use treatments. Many such interventions have multiple components and are implemented over time, e.g., [17]–[32]. Over the course of an intervention, patients display complex and varying behaviors such as relapsing or dropping out for various psychological, social and environmental reasons, e.g., [33]–[41]. Their variations in engaging with or responding to interventions may contribute to different outcomes. Failure to appreciate these variations within, not only those between treatment and control groups, can ultimately lead to inappropriate and ineffective interventions, e.g., [38]–[42]. Thus, disentangling patients’ behavioral variations, is a critical step for better understanding an intervention’s effects on individual outcomes. However, capturing these variations poses significant computational and analytical challenges. Methods have been called for to address the variations in intervention effects for improving the design, conduct, and analyses of patient-oriented research [43]. Missing data also commonly exist in such complex longitudinal data, aggravating these methodological challenges. For these reasons, we propose an innovative trajectory pattern-recognition approach to tackle incomplete longitudinal behavioral intervention data, built upon our methods studied for observational studies and our previous work on fuzzy clustering and missing data in longitudinal studies [44]–[52].

Multiple imputation (MI) has been well studied for statistical analyses [53], [54] but has not yet been scrutinized for clustering [55], [56]. One of major reasons is that we do not know how much the uncertainty of imputed data will affect the clustering accuracy. To answer this question, we need to compare the MI approach with single- (SI) and non-imputation (NI) based clustering approaches, which are commonly adopted in current pattern recognition areas. Although no single clustering approach can handle every type of data problem, our proposed MI-based Fuzzy clustering [48] was especially designed for longitudinal behavior related data that are typically non-normal, high dimensional, contain missing values, and of different types (i.e., continuous, ordinal and nominal). MI-Fuzzy was developed primarily because no other clustering technique overcomes all eight disadvantages for processing such data: 1) Cannot handle missing data directly; relies on list-wise/pair-wise deletion or single imputation; 2) Lack (available, tractable, replicable, or easy-to-use) validation indices or integrated validating processes; 3) Require statistical or prior distribution assumptions; 4) Require (manually) complicated parameter settings and repeated adjustment of model constraints and starting values of parameters in the clustering process; 5) Computationally intensive or malfunction for high-dimensional and longitudinal data with relatively large portions of missing values or increased number of clusters; 6) Results are (sometimes) not replicable (even using the same data set); 7) No graphic visualization of clusters from high-dimensional data or longitudinal data trajectories; 8) Unclear utility in behavior-related data.

For example, probabilistic clustering, including Gaussian Mixture models [57] and Hidden Markov Model-based Bayesian clustering [58]–[61] are commonly used for clustering. For such models, we must specify underlying statistical distributions (Gaussian) or prior distributions (Bayesian approach). The expectation-maximum (EM) algorithm for the Gaussian model is iterative and requires specifying initial values of parameters and adjusting parameters during modeling. EM often converges to a local maximum or does not converge at all; also, it can be computationally very slow when there are multi-modal distributions or mixture of Gaussians (e.g., potential clusters) and large proportions, say greater than 20%, of missing values with high-dimensional data and many clusters. Bayesian clustering is also computationally intensive and requires parameter adjustment and setting model constraints. Bayesian clustering has been developed and tested for large datasets (e.g., gene data) but its utility beyond gene analyses is unclear. If the observed data are generated by the assumed distributions, these probabilistic clustering models should be robust. However, high-dimensional behavioral intervention data typically have multi-modal distributions and their exact (joint) distributions are a priori unknown.

Neural networks models [62], [63] are mostly used for supervised learning (e.g., classification where the group labels of each subject are previously known). The well-known neural networks model for unsupervised learning (clustering where the group labels of each subject are a priori unknown) is called Kohonen’s Self Organizing Map (SOM). The SOM architecture consists of an input layer and a Kohonen layer. The number of neurons (nodes) in the input layer corresponds to the number of attributes. Each input to the Kohonen layer is modified by a weight, which multiplies with the input value. SOM initializes weights by assigning them random values. The Kohonen layer represents potential clusters. Hidden layers can also be added between the input and Kohonen layers to fit nonlinear data; however the number of neurons on this layer is arbitrary, and different settings lead to different results even for the same data. SOM has been applied in areas such as imaging, speech and voice recognition. Its validation indices or procedures are unclear. SOM itself cannot handle missing values. Its utility in behavioral intervention studies is unknown.

Hierarchical clustering [62], [64] has two major forms: Agglomerative (bottom-up) and Divisive (top-down). Agglomerative clustering starts with an every individual in his own cluster; at every step it merges the closest pair of clusters. Divisive clustering starts with all subjects in one cluster and split this cluster into smaller pieces. We will focus on agglomerative, as divisive clustering is much less used in applications [62], [64]. No matter what form, the disadvantages of hierarchical clustering are well-known: its inability to incorporate information about the shape and size of clusters, and its static nature (data are committed to a cluster once and cannot be moved to another cluster later [40]). It assumes the data have a hierarchical or nested structure which is implausible for, say, distinct components of behavioral interventions. Although it works in some areas, this model performed poorly in our preliminary prenatal tobacco exposure studies, yielding unreliable and trivial clusters (e.g., many small clusters with few individuals in each). With a pre-specified number of clusters, its clustering accuracy and inconsistency rates were the poorest in comparison to MI-Fuzzy and K-means. Partition-based clustering [62], [64] also comes in two flavors: hard (crisp) clustering that partitions the data set into mutually exclusive subsets, and fuzzy clustering that allows subjects to belong to several subsets but with different degrees of membership (see Section Innovation). The best-known hard clustering model is K-Means. It was designed to cluster numerical data into clusters in which each cluster has a center called mean. Although K-Means has been widely applied with appealing computational efficiency, it cannot handle missing values. Our preliminary analyses indicate that it has lower accuracy and higher inconsistency rates than MI-based fuzzy-clustering for pregnant smoking behavioral data.

Based on our prior research for longitudinal behavior intervention data, we will theoretically comparing MI- to SI- and NI-based fuzzy clustering approaches. In addition to our theoretical demonstration, we will use two real datasets. Table I are the notations of symbols used in this paper.

Table I.

Notations

Symbols	Notations
Xobs, Xmis	Observed data and missing values
X	Dataset consists of Xobs and Xmis
M	Number of imputations
N	Number of cases in data X
N′	Number of cases in data X with missingness
ncontrol	Number of mislabeled control group members
nintervention	Number of mislabeled intervention group members
𝔍	Clustering accuracy
𝔍NI	Non-imputation clustering accuracy
𝔍SI-mean	Mean-imputation clustering accuracy
𝔍SI-regression	Regression-imputation clustering accuracy
𝔍SI-hotdeck	Hot deck-imputation clustering accuracy
𝔍MI	Multiple-imputation clustering accuracy
P, P′	Observed and unobserved attributes of X
CT	Termination clustering number
U	Fuzzy degree of cluster membership
V	Cluster centroids
n′	Number of patients with observed first attribute
r	Percentage of missing values
μ	Mean value
d	dimension of data X
k	Number of clusters

The rest of this paper is organized as follows: Section II introduces MI-based Fuzzy clustering. Section III theoretically compares and demonstrates MI-, SI- and NI-based fuzzy clustering approaches. Section IV presents numerical results under three missing data mechanisms. Section V concludes the paper.

II. Multiple Imputation Based Fuzzy Clustering

To compare the three missing data imputation approaches, two longitudinal behavioral intervention datasets will be used as examples to demonstrate our MI-based approach: TDTA [65], [66] and QuitPrimo (QP) [67]. TDTA data were collected from a culturally-adapted smoking cessation intervention for Korean Americans. Intervention attributes in MI-Fuzzy were based on data availability and/or selected to maximize information that depicts individual response variations resulting from their psychological factors and engagement with the intervention. All designed intervention components and time for cessation counseling were included at the beginning. The three components were (a) cognitive behavioral therapy, (b) cultural adaptation, and (c) nicotine replacement therapy. The first two components described smokers’ psychological reactions to the culturally adapted cognitive behavioral therapy, which were measured by scores on Perceived Risks and Benefits of Quitting Smoking, Perceived Family and Peer Norm for Quitting, and Self-efficacy in Quitting scales. Each scale has four repeated measures collected at four follow-ups: 1, 3, 6, and 12 months from the quit day, total 20 intervention attributes (5 subscales×4 times). The last component “Nicotine Replacement Therapy” was measured by the number of nicotine patches returned after use (1 attribute) and the counseling time was measured in the unit of minutes (1 attribute). In all, 22 intervention attributes were initially used for MI-Fuzzy clustering. The percentage of missingness of TDTA data ranges from 9% to 18% on each of tested intervention attribute; and 65% participants have all values, 34% have more than 5 values on intervention attributes.

QP is a two-arm longitudinal web trial used to assist in the smoking cessation of a general smoker population. The data were collected via an online referral portal with 1320 individuals. The intervention arm was engaged with three components which the control arm cannot see. The first intervention component describes how often smokers communicate with a tobacco treatment specialist in a secure form. The second one measures how often the smokers are engaged or encouraged by experts. The third main component describes how many times smokers view messages and dialogue from peers and ex-smokers through a resource website. Each smoker has six monthly measures for each component for six months (total 18 attributes).

MI-Fuzzy is the first clustering model to date that employs a full theoretical integration of (a) multiple imputation (MI), (b) fuzzy clustering, and (c) comprehensive validation [48], [49]. It simultaneously copes with real-world situations where patients have membership in multiple clusters, handles high-dimensional longitudinal intervention data with missing values (e.g. multiple repeatedly-measured correlated constructs), and validates response patterns.

Our MI process was described in detail elsewhere and implemented in Matlab [68]. Briefly, we assume intervention data follow an arbitrary missing pattern, where other missing patterns such as monotone patterns are special cases [69]. Imputed datasets were generated using the Markov Chain Monte Carlo (MCMC) method with multiple chains, non-informative Jeffreys prior of the Bayesian approach, and 500 burn-in iterations. Before the MCMC process, an expectation-maximization (EM) procedure is conducted to train the parameters of the data. At each MCMC iteration, an I-step is conducted to fill the data by random draws from the model according to the trained parameters, followed by a P-step to update the parameters in the new completed data. The I-step and P-step are conducted iteratively until the Markov Chains stabilized.

The fuzzy clustering aims to minimize an objective function

$$\begin{array}{l}{f}_m(X,U,V)=\sum _{k=1}^c\sum _{i=1}^n{(u_{ik})}^w{\Vert x_i-v_k\Vert }^2\\ \text{subject}\text{to}\sum _{k=1}^c{u}_{ik}=1,\forall i,\end{array}$$ (1)

where X is the dataset, V is the cluster centroids, k is the k-th cluster, w is parameter of U is a vector of u_ik where 0 ≤ u_ik ≤ 1, ∀ i, k denotes the fuzzy degree of membership for subjects i, (i = 1, 2, . . . , n) in the respective cluster k. In MI-Fuzzy, we minimized this fuzzy objective function (e.g., we minimized the intra-cluster variance) for each imputed data set,

$$f_m(X,U,V)=\sum _{k=1}^c\sum _{i=1}^n{(u_{ik})}^w{\Vert x_i-v_k\Vert }^2+\sum _{i=1}^n\lambda \left(\sum _{k=1}^c{u}_{ik}-1\right),$$ (2)

where λ is a weight and λ ≥ 0.

Intervention data have a unique feature that can be used to evaluate clustering accuracy. For example, MI-Fuzzy can be evaluated based on the intervention clustering accuracy rate (𝔍) for treatment data where we know the labels with certainty (for example, who is in the control vs. intervention group), but not whether there will be different clusters (subgroups) within the intervention group due to behavioral variations. This rate is calculated as the average clustering accuracy rates across M imputed datasets:

$$\mathfrak{J}=\frac{1}{M}\sum _{i=1}^M(N-n_{\mathit{control}}-n_{\mathit{intervention}})/N,$$ (3)

where N is the total sample size, n_control is the number of mislabeled control group members and n_intervention is the number of mislabeled intervention group members. The larger the rate the more accurate the clustering.

Given a termination clustering number (CT), $CT=\sqrt{N/2}$, where N is the sample size, the MI-Fuzzy algorithm searched for the optimal number of clusters through a comprehensive validation procedure [48], [49], [51].

III. MI- VS. SI- AND NI- FUZZY CLUSTERING

For statistical analyses, MI-based parameter estimation were shown more reliable than single imputation approach (e.g., mean, regression, and hot deck) which can introduce bias or lose precision. However, for clustering, MI-based approach has not yet been theoretically demonstrated better than other imputations, although intuitively would improve the uncertainty of clustering accuracy. Below we showed our theoretical demonstration.

1) MI vs Non-imputation (NI) Clustering

Lemma 1. MI- achieves higher clustering accuracy rate than NI-based Fuzzy Clustering

Proof

Let X denote the N * d data matrix, where n denotes the number of patients who belong to k clusters and d the number of attributes. Let X_mis denote the missing part of X, and X_obs denotes the observed part with N′ patients, N′ < N, who also belong to these k clusters. Assume the n patients are clustered into the k clusters with accuracy 𝔍. With NI-fuzzy clustering, (N − N′) patients are not clustered due to their missing values on d. Then the clustering accuracy for NI is

$${\mathfrak{J}}_{NI}=\mathfrak{J}\times N^{\prime }/N,$$ (4)

For MI, X_mis are multiply-imputed, therefore, N patients are clustered. Suppose N^MI (0 < N^MI ≤ N − N′) patients with X_mis is correctly clustered, then the accuracy is,

$${\mathfrak{J}}_{MI}=\mathfrak{J}(N^{\prime }+N^{MI})/N.$$ (5)

Therefore, 𝔍_MI > 𝔍_NI. Thus, the MI-based achieves higher accuracy than NI-based fuzzy clustering.

2) MI vs Single Impution (SI) Clustering

The most commonly used single imputation methods include mean, regression and hot-deck imputation [70], which are used for demonstration in comparison to MI based clustering hereafter.

Lemma 2. MI-based approach reduces the uncertainty of clustering accuracy for incomplete longitudinal data compared to SI-based fuzzy clustering

Proof

1) Mean based SI

The missing values are filled by the means of the observed values. The variance of data is underestimated after mean imputation. For clustering, the patients close to each other are more likely to be classified into the same cluster. Since the missing values are filled by the same value (the mean), the patients with these means become closer to each other, and likely to be classified into the same cluster.

For a completed d-dimensional data X with n patients, suppose X contains k clusters where each cluster has N/k patients. Let r be the percentage of missingness, then each cluster has rN/k patients with missing values. The missing values are imputed by the mean SI before clustering. Then patients with imputed values (μ) are likely to be clustered in the same cluster and the mean SI-based clustering accuracy is expressed as

$${\mathfrak{J}}_{SI-\mathit{mean}}=1-rN(k-1)/k,$$ (6)

where rN(k − 1)/k is the number of mistakenly clustered patients.

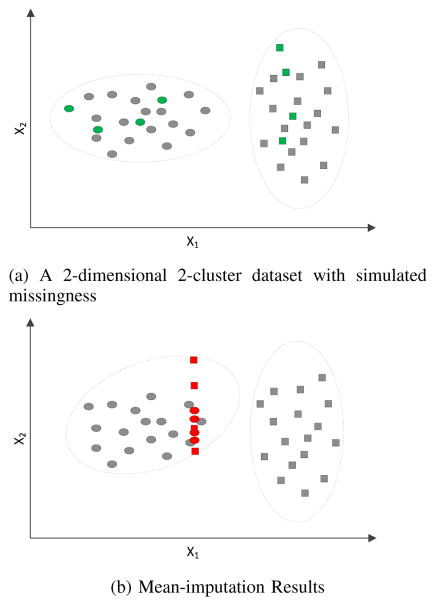
Figure 1a demonstrates a scenario where the mean-imputation reduces the clustering accuracy 𝔍. The scatter plot shows a two-dimentional X represented by (x_i1, x_i2), where k = 2. The missing values of x_i1 are marked by green circles in the 1st cluster and by green squares in the 2nd cluster. The patient i with missing values are denoted by

Fig. 1.

An illustration of mean-imputation

$$X_i-\mathit{mis}=\{(x_{i1-\mathit{mis}},x_{i2})\}.$$ (7)

By conducting one-time mean-imputation, all the missing values are filled by x_1μ (marked by red circles/squares), then the patients are represented by

$$X_{SI-\mathit{mean}}=\{(x_{i\mu },x_{i2})\},$$ (8)

where $x_{i\mu }=\frac{1}{n^{\prime }}{\displaystyle \sum _{i=1}^{n^{\prime }}}{x}_{i1}$ and n′ is the number of observed x_i1 from all patients.

This one-time imputed values are the same and treated as if they are observed values and then used for clustering. As demonstrated in Figure 1b, 50% of the patients with missing values can be mistakenly clustered into the 1st cluster marked by circles.

2) Regression based SI clustering

A regression model can be learned from X_obs and the learned model with estimated coefficient is used to impute missing values of a variable based on other variables. For illustrative purposes, the regression co-efficient β̂ can be learned based on observed two-dimensional data, e.g.,

$$x_{i2}=\widehat{\beta }{x}_{i1}+\epsilon ,$$ (9)

then

$$x_{i2-\mathit{mis}}=\widehat{\beta }{x}_{i1}.$$ (10)

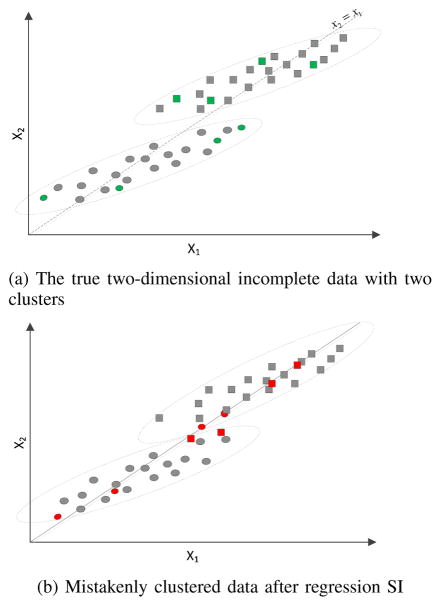
Figure 2a demonstrates a scenario 𝔍_SI-reg where the regression SI reduces the clustering accuracy. With the same notation, the patient i with missing values on the second variable are denoted by

Fig. 2.

Clustering accuracy of single regression imputation

$$X_{i-\mathit{mis}}=\{(x_{i1},x_{i2-\mathit{mis}})\}.$$ (11)

The missing values are imputed only once by this regression SI (marked by red circles/squares), and more likely to fit perfectly along the regression line since the imputed data do not have an error term included in their estimation,

$$X_{SI-\mathit{regression}}=\left\{(x_{i1},\widehat{\beta }{x}_{i1})\right\}.$$ (12)

Again, this one-time imputed values with errors are treated as if they are actual observed values and used for clustering. In the worst case, all cases with missing values can be mistakenly clustered, as shown in Figure 2b.

3) Hot-deck SI clustering

This type of SI first sorts a dataset according to any variables, and fill the missing values by using the observed values immediately prior to them and repeat this process until all missing values are imputed. If the selected variable that used to order the data does not have a significant role in clustering patients, the imputed data could be fully messed up after sorting and the likelihood of clustering the patients with missing values to their corresponding clusters is small.

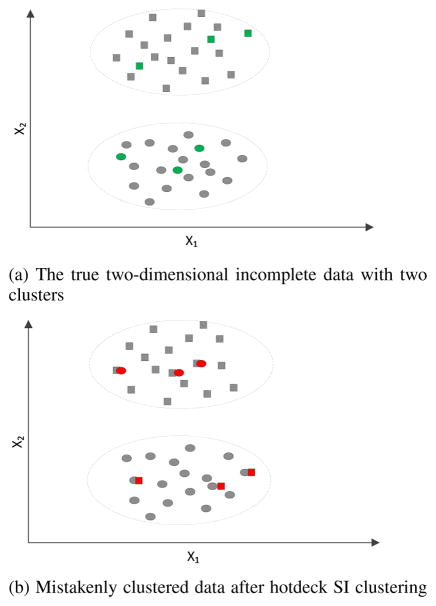
Figure 3a shows how hot-deck SI reduces the clustering accuracy. Similarly, for a two-dimensional data X, represented by (x1, x2), where k = 2. The missing values of x₁ are marked by green or circles squares in these two clusters, respectively. By conducting the hot-deck SI, the data are sorted by x₁, and the missing values are filled by the observed x₁ values just prior to them (marked by red circles/squares),

Fig. 3.

Clustering accuracy of single hotdeck imputation

$$X_{SI-\mathit{hotdeck}}=\{(x_{i1},x_{j2})\},$$ (13)

where j is the index of the case just before the i-th cases ordered according to x₂. As shown in Figure 3b, the cases with missing values could be completely misplaced in different clusters using this imputation.

Overall, the 𝔍_SI can be computed as,

$${\mathfrak{J}}_{SI}=(N-n_{\mathit{control}}-n_{\mathit{intervention}})/N.$$ (14)

Although SI-derived data have the appearance of completeness, it can mislead the clustering results because SI again does not account for the imputation uncertainty and clustering accuracy from such data is uncertain.

4) MI-clustering

Unlike SI methods, the uncertainty of clustering accuracy is accounted by computing the average of clustering accuracy from clustering each of multiply imputed datasets generated from the stochastic processes. The variance of 𝔍_MI aforementioned above is computed as,

$$var\left({\mathfrak{J}}_{MI}\right)=\frac{1}{M-1}\sum _{i=1}^M{\left(\widehat{\mathfrak{J}}-\overline{\mathfrak{J}}\right)}^2,$$ (15)

where M is the number of imputations which can be estimated given the expected relative efficiency and the missing information of parameter estimates of attributes [71]. As shown in Table II, given our expected relative efficiency of 0.98 and missing information for TDTA (20%) and QP (10%), we chose 10 imputations for each.

Table II.

RE vs. r and M

M	r=10%	r=20%	r=30%	r=50%
3	0.968	0.938	0.910	0.857
5	0.980	0.962	0.934	0.910
10	0.990	0.980	0.971	0.952
20	0.995	0.990	0.985	0.976

The confidence interval of 𝔍_MI could be estimated as:

$${\mathfrak{J}}_{MI}\pm 1.96\times \sqrt{var({\mathfrak{J}}_{MI})/N}.$$ (16)

For example, given two dimensions, x₁ and x₂,

$$\begin{array}{l}\begin{array}{cc}{x}_1& x_2\end{array}\\ \left|\begin{array}{cc}3& 6\\ 5& ·\\ 6& 12\end{array}\right|\end{array}$$

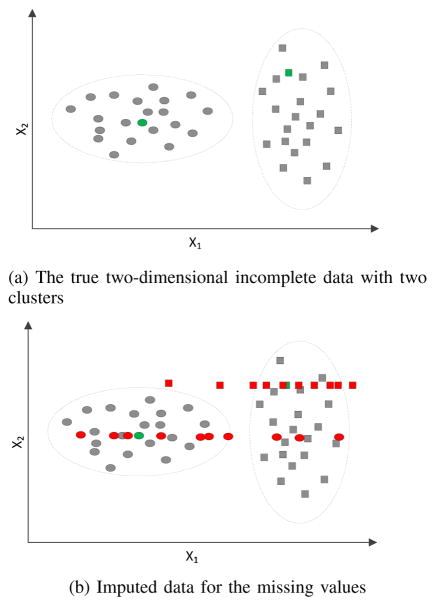
and assume the true value for the missing value is 4, the mean SI would fill the missing value as 9, regression SI will estimate 10 (x₂ = 2 × x₁), and hotdeck sorts x₂ and gives 12. Then these values will treated as “true”. Differently, MI can estimate the missing value 10 times to account for the imputation uncertainty and thus, for clustering, it can reduce the uncertainty of clustering accuracy. As shown in Figure 4a, two patients marked green in each cluster have missing values on x₁ or x₂. Assuming missing values are imputed 10 times, based on the clustering results from the ten imputed datasets, the two patients would still stay in their own clusters, even if the ten impute values can differ widely, as shown in Figure 4(b). Thus, the imputation uncertainty is accounted in MI process and the consequent uncertainty of 𝔍_MI is reduced.

Fig. 4.

Clustering accuracy of multiple imputation

Overall, our theoretical demonstration indicates MI-based clustering is superior to NI- and SI-clustering because it accounts for the uncertainty of imputation and clustering accuracy for incomplete data.

IV. NUMERICAL ANALYSES

This section evaluates the performance of MI-based fuzzy clustering in comparison to SI- and NI-clustering using TDTA and QP data. In addition, we simulated data using the parameters from these two behavioral intervention studies. Specifically, we evaluated these three imputation-based clustering approaches under three missing data mechanisms. We also varied the percentage of missingness to evaluate the clustering performance based on the same validation index, called overlap over septation validation (OOS [51]) and clustering accuracy.

A. The Missing Mechanisms

In statistical theories, the three missing data mechanisms are termed as missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR) [72], [73]. Using incomplete TDTA and QP data as an example, let X be the complete data without missing values, X = X_obs ∪ X_mis, X_mis are the missing values on observed attributes P in the incomplete data X; and P′ are unobserved attributes. For example, for QP web trial study, we have longitudinal zero-inflated count data, then zero-inflated Poisson (ZIP) models are considered for data simulation under the generalized linear mixed model (GLMM) framework while the typical GLMM were used to generate data using parameters from TDTA.

1. Missing Complete At Random (MCAR): we simulated data assuming X_mis are missing independently of both observed attributes P and unobserved P′.

2. Missing At Random (MAR): Data were simulated assuming X_mis are missing independently of unobserved P′.

3. Missing Not At Random (MNAR): Data were simulated assuming X_mis relate to unobserved attributes P′. MNAR occurs when the condition of MAR is violated.

B. Performance Evaluation Using TDTA and QuitPrimo

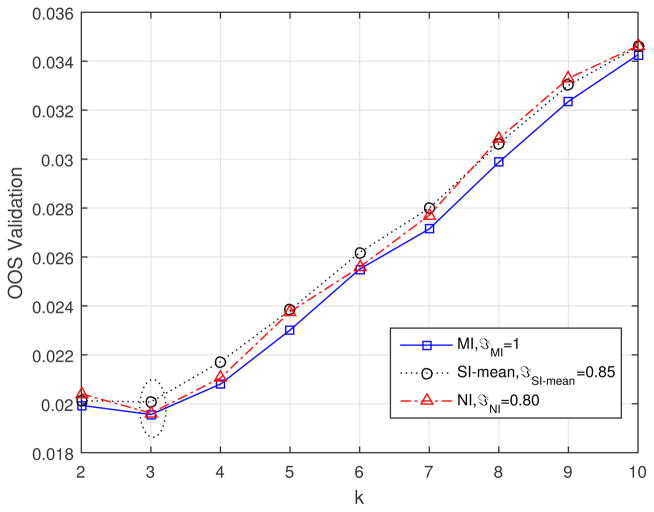
As shown in Figure 5, for TDTA, MI-based fuzzy clustering identified the optimal number of clusters as three, because the validation index reaches the lowest value, with clustering accuracy of 100%. SI-based clustering identified 3 clusters with accuracy of 85% and NI-based identified 3 clusters with accuracy of 80%.

Fig. 5.

Performance of MI-, SI- and NI-clustering on TDTA data

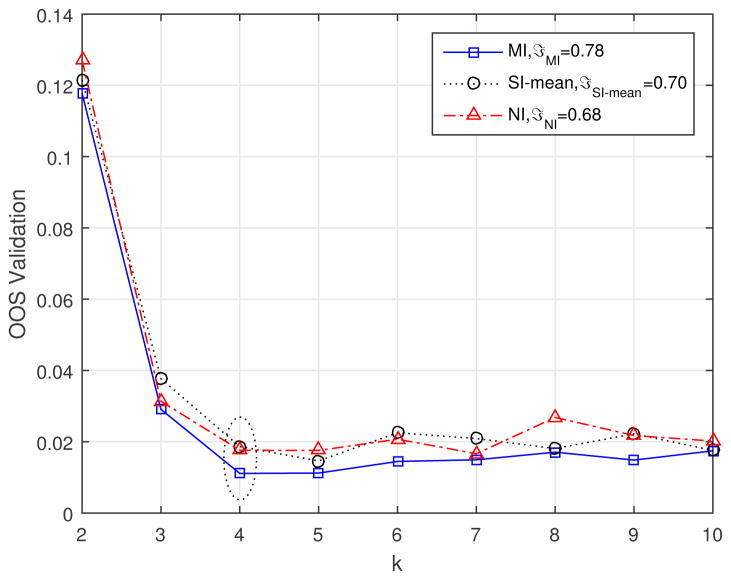
For QP, MI Fuzzy identified 4 clusters with with clustering accuracy of 78%, as shown in Figure 6. SI-based clustering identified 5 clusters with accuracy of 70% and NI-based identified 4 clusters with accuracy of 68%.

Fig. 6.

Performance of MI-, SI- and NI-clustering on QP data

As demonstrated in the theoretical section, SI- and NI-based approach do not account for the uncertainty of imputation and treated the imputed values as if they are observed for clustering. Therefore, their clustering results could be misleading, and the uncertainty of clustering accuracy is also not counted. Even if they identified the same clusters as MI-, the results could be due to chance.

We also evaluated the three imputation clustering approaches using simulation, where we primarily focus on their performance with a medium percentage of missingness (10%–15%) for each missing mechanism. We set the sample size n at 1000 and the dimension d at 20.

C. Performance under MCAR

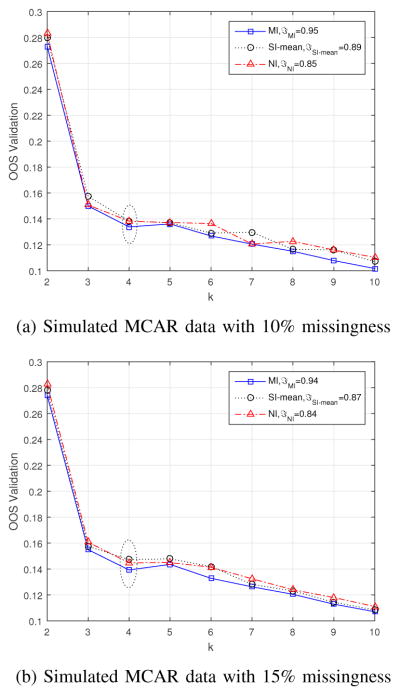
As shown in Figure 7, for MCAR, MI-based fuzzy clustering identified the correct number of clusters, 4, and achieves 95% and 94% accuracy for 10% and 15% missingness, respectively. SI-based fuzzy clustering identified 4 clusters, with accuracy of 89% and 87% for 10% and 15% missingness, respectively. NI-based fuzzy clustering identified 4 clusters, with accuracy of 85% and 84% for 10% and 15% missingness, respectively.

Fig. 7.

MI- vs. SI- and NI-clustering under MCAR

D. Performance under MAR

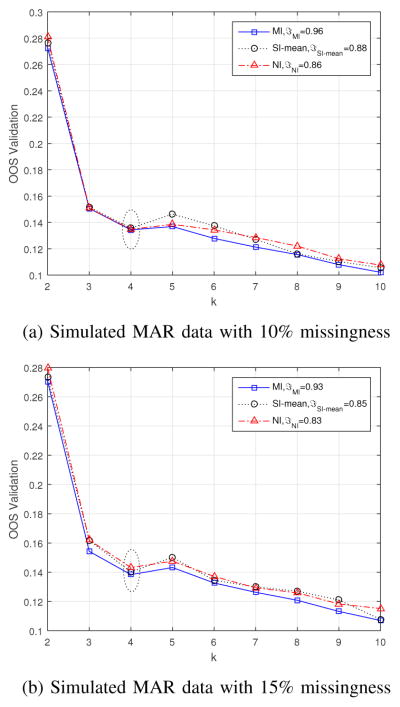
As shown in Figure 8, for MAR, MI-based fuzzy clustering identified the correct number of clusters, 4, and achieves the accuracy of 96% and 93% for 10% and 15% missingness, respectively. SI-based fuzzy clustering identified 4 clusters, with accuracy of 88% and 85% for 10% and 15% missingness, respectively. NI-based fuzzy clustering identified 4 clusters, with accuracy of 86% and 83% for 10% and 15% missingness, respectively.

Fig. 8.

MI- vs. SI- and NI-clustering under MAR

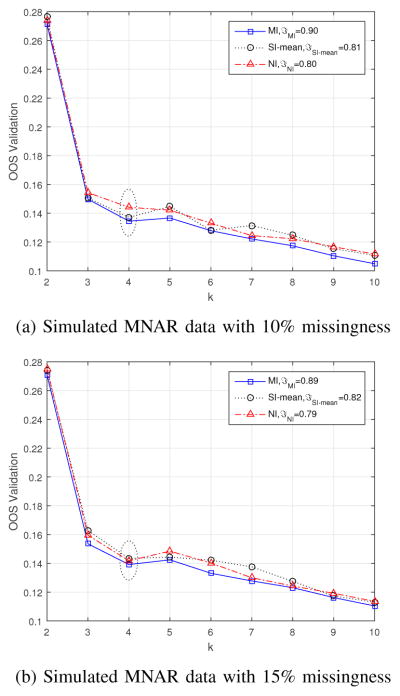
E. Performance under MNAR

As shown in Figure 9, for MNAR, MI-based fuzzy clustering identified the correct number of clusters, 4, and achieves the accuracy of 90% and 89% for 10% and 15% missingness, respectively. SI-based fuzzy clustering identified 4 clusters, with accuracy of 81% and 82% for 10% and 15% missingness, respectively. NI-based fuzzy clustering identified 4 clusters, with accuracy of 80% and 79% for 10% and 15% missingness, respectively.

Fig. 9.

MI- vs. SI- and NI-clustering under MNAR

Overall, under three mechanisms, MI-based clustering performance are similar and seems invariant to different missing data mechanisms. This invariant property of MIFuzzy may attribute to the fact that the actual MIFuzzy algorithm does not learn the ”concepts” of missing mechanisms but is somewhat sensitive to the real numbers such as the percentage of missingness. With the increase of the percentage of missingness, MI-based clustering accuracy decreased but still achieved at least 93% across the three mechanisms. Although SI and NI identified the same number of clusters, as discussed in the theoretical section, it is likely due to chance and their clustering accuracy is lower and misleading, as they cannot account for the imputation uncertainty and therefore the accuracy is uncertain.

V. Conclusion

Reliable and more accurate trajectory pattern recognition approaches will help capture patients’ variations in engaging with or responding to behavioral interventions. Explaining these observed variations within and between treatment and control groups can ultimately lead to appropriate and effective interventions adaptive to patients with at-risk patterns. This paper advances our understanding of the utility and strength of multiple-imputation (MI) based fuzzy clustering approach to processing incomplete longitudinal behavioral intervention data. Specifically, this paper theoretically, empirically and numerically demonstrated how MI-based approach can reduce the uncertainty of clustering accuracy in comparison to non-and single-imputation based clustering approach. Our future research will further evaluate MI-based approach under a large percentage of missingness and focus on visualization-aided validation to further expand the MI-based clustering approaches.