Characterizing the dynamics of mental representations: the temporal generalization method

Abstract

Parsing a cognitive task into a sequence of operations is a central problem in cognitive neuroscience. We argue that a major advance is now possible owing to the application of pattern classifiers to time-resolved recordings of brain activity [electroencephalography (EEG), magnetoencephalography (MEG), or intracranial recordings]. By testing at which moment a specific mental content becomes decodable in brain activity, we can characterize the time course of cognitive codes. Most importantly, the manner in which the trained classifiers generalize across time, and from one experimental condition to another, sheds light on the temporal organization of information-processing stages. A repertoire of canonical dynamical patterns is observed across various experiments and brain regions. This method thus provides a novel way to understand how mental representations are manipulated and transformed.

Understanding the organization of processing stages: from behavior to neuroimaging

Understanding how mental representations unfold in time during the performance of a task is a central goal for cognitive psychology. Donders [1] first suggested that mental operations could be dissected by comparing the subjects’ response times in different experimental conditions. This ‘mental chronometry’ was later enriched with several methodological inventions, including the additive-factors method [2] and the psychological refractory period method [3]. Although these behavioral techniques can provide considerable information on the temporal organization of cognitive computations, they remain fraught with ambiguities. For instance, they cannot fully separate serial from parallel processes [4] or processes organized into a discrete series of steps from those operating as a continuous flow or ‘cascade’ of overlapping stages [5].

More recently, the advent of brain-imaging techniques has provided unprecedented access into the content and the dynamics of mental representations. EEG, MEG, local field potentials, and neuronal recordings can provide a fine-grained dissection of the sequence of brain activations (e.g., see [6,7]). Here we show how the analysis of these time-resolved signals can be enhanced through the use of multivariate pattern analysis (MVPA), also known informally as ‘decoding’. We argue that temporal decoding methods offer a vast and largely untapped potential for the determination of how mental representations unfold over time.

Decoding fMRI data identifies the localization and structure of mental representations

MVPA was first introduced to brain imaging in order to refine the analysis of functional MRI (fMRI). Temporal resolution aside, fMRI is an efficient tool to isolate and localize the brain mechanisms underlying specific mental representations. Initially, fMRI was primarily used with binary contrasts that revealed major differences in regional brain activity (e.g., faces versus non-faces in the fusiform cortex [8]). MVPA, however, led to a considerable refinement of such inferences because it proved able to resolve, inside an area, the fine-grained patterns of brain activity that contain detailed information about the stimulus or the ongoing behavior (for reviews, see [9–11]).

Using MVPA, subtle details of mental representations can be decoded from fMRI activity patterns. It is now possible to decode low-level visual features such as orientation [12–15] or color [16] and determine how their cortical representation is changed, tuned, or suppressed according to subjects’ goals [13] and prior knowledge [14]. Using distributed activity over the ventral visual pathway, it is possible to reconstruct which static images [17–21], moving objects [22], or movies [23] that the subject is watching. The identification of these mental contents is not limited to sensory information; in the absence of any stimulus, mental objects can still be decoded, for instance during mental imagery [24,25], working memory [25,26], or even dreams [27]. More recently, MPVA has also been used to decode non-visual representations, including auditory [28,29], mnemonic [30], numerical [31], and executive information [32,33]. Although this approach has provided unprecedented details about the structure and brain correlates of various mental representations [11], its temporal resolution remains largely inadequate to describe the way they are dynamically constructed, transformed, and manipulated (although some slow processes can be tracked with fMRI; e.g., [12,13,25]).

Decoding time-resolved signals identifies when mental representations are activated

MVPA applied to fMRI signals does not reveal much about the dynamics with which mental representations are activated. Here we focus specifically on the less explored question of what MVPA may bring to our understanding of the dynamics of information processing in the brain.

Methodologically, MVPA readily applies to EEG, MEG, or intracranial recording data (e.g., multiunit neuronal recordings, local field potentials) where time can be considered as an additional dimension besides the spatial information provided by the multiple sensors. To obtain time-course information, a series of classifiers can be trained, each using as an input a specific time slice of the original data (Box 1). The output is a curve representing decoding performance as a function of time that specifies when a certain piece of information becomes explicitly encoded in brain activity. Multiple such classifiers can be trained to decode distinct features of the trial, thus dissecting a trial into a series of overlapping stages. Recently, for instance, in a simple response-time task, we decoded successively the location of the stimulus, the subject’s required response, his actual motor response (which differed on error trials), and whether the brain detected whether the response was correct or erroneous [34].

Box 1. Methodological issues in decoding from time-resolved brain-imaging data.

The ability of MVPA to extract information from a complex multidimensional dataset has rendered this statistical technique indispensable to the neuroimaging community [11]. By concentrating the information distributed in several data points, MVPA increases the signal-to-noise ratio and facilitates single-trial decoding. These advantages are particularly useful when signals present a high interindividual variability that prevents spatial averaging. MVPA simplifies such complex datasets by presenting the results in an information space of direct relevance [11,70] in which data from multiple subjects can readily be averaged.

Here we specifically emphasize the usefulness of MVPA applied to time-resolved intracranial, MEG, and EEG recordings. MVPA projects such multidimensional data into a smaller-dimensionality space whose axes are the cognitive codes of interest (e.g., stimulus features, subject response). The output axes are shared across individuals, but the projection is optimized for each subject and each time point. In MEG, for example, this approach allows maximizing the spatial resolution of the signals without necessarily addressing the difficult issue of source localization.

In fMRI, MVPA is often used in combination with a searchlight method [71,72], which comprises sliding a small spatial window over the data to detect which segments contain decodable information. By analogy, with time-resolved signals, a sliding time window can be used to detect periods of optimal decodability. Furthermore, this approach can be extended by testing whether a classifier is able to generalize to other moments in time. Not only can decoding determine when and for how long a given piece of information is explicitly present in brain activity, but with generalization it becomes able to characterize whether this information recurs in time, and when.

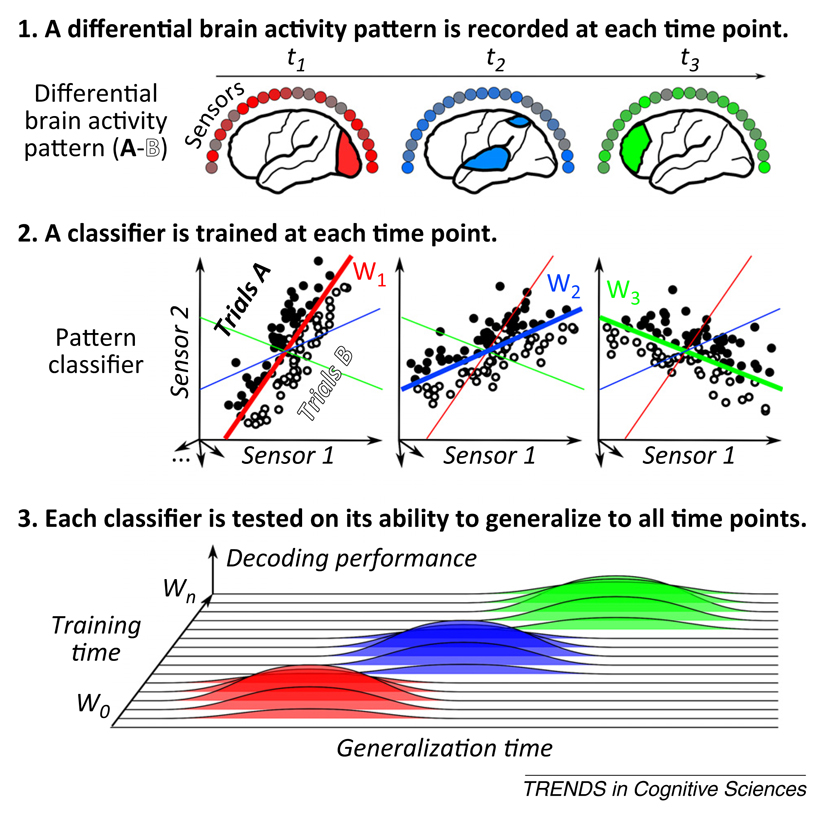
When applied systematically, the method yields a full temporal generalization matrix where classifiers are trained and tested at all available time points (Figure I.). Various methods can be used to build such a matrix, including support vector machines (SVMs) (e.g., [57,61]), linear discriminant analyses (e.g., [35,43]), or even simple linear regression (e.g., [58,59,73]) (see [36] for empirical comparisons). To avoid data over-fitting, MVPA must be nested inside a cross-validation loop, such that performance is measured only on novel left-out data samples (for both diagonal and off-diagonal time points). To evaluate classifier performance, ‘criterion-free’ estimates should be preferred over mean accuracy, because the latter may lead to systematic biases during generalization (i.e., all trials may be classified in the same category). When dealing with a two-class problem, we favor using the area under the curve (AUC), a sensitive, nonparametric criterion-free measure of generalization.

Figure I.

The principles underlying temporal decoding and temporal generalization. Multivariate pattern analysis (MVPA) applied to time-resolved signals allows tracking mental representations across time by detecting and comparing the patterns of neural activity recorded across time. Specifically, at each time point t, a multivariate pattern classifier w(t) is trained to identify the linear combination of measurements [e.g., weights of electroencephalography (EEG) electrodes, magnetoencephalography (MEG) sensors, individual neurons] that best discriminates two or more experimental conditions (e.g., A and B). This combination may vary with time as the underlying pattern of activity changes. Classifier performance is assessed not only at the time used for training [e.g., classifier w(t₁) is tested at t₁, w(t₂) is tested at t₂,…, hereafter referred to as ‘diagonal decoding’], but also on data from other time samples [e.g., classifier w(t₁) is tested at all times t₁, t₂, t₃,…, hereafter referred to as ‘off-diagonal decoding’]. The outcome is a ‘temporal generalization matrix’ representing the decoding performance of each classifier at each time point. By convention, we depict this matrix with training time on the y-axis and generalization time on the x-axis. With this convention, horizontal ‘slices’ through the matrix show the time course of activation of the brain systems identified by a given classifier.

Even scalp EEG recordings contain a lot of information sufficient to discriminate various processing stages. Low-level attributes such as the position [35,36] and the size [36] of a visual stimulus, as well as the orientation of large visual gratings [37–39], can be reconstructed from EEG and MEG signals. Higher processing stages of perceptual decision making, related to either the objective stimulus or its subjective report, can be similarly tracked [35,40–43]. EEG even permits decoding the covert production of imagined syllables [44]. Motor [45], auditory [46], conceptual and semantic information [47–49], and even music samples [50] have also been decoded from EEG and MEG recordings.

These studies typically decode information from raw sensor data in the time domain. The expansion of brain signals through a time–frequency transform may reveal additional information spread over both frequency and time [44,51,52].

Contrary to what is generally assumed, these studies suggest that the spatial resolution of EEG and MEG may suffice to decode and track various different mental representations. Furthermore, two approaches can be used to provide a more accurate understanding of the spatial origin of the decoded signals. First, source reconstruction analyses may provide an approximate location of the neural generators underlying scalp recordings [53]. Following source reconstruction, decoding may then be restricted to specific regions of interest, thus clarifying which brain regions contain decodable information. Second, intracranial recordings can now be acquired from dozens or even hundreds of different cortical and subcortical sites. When applied to intracranial data, decoding can reveal a rich temporal dynamics of fine-grained codes. For example, in the olfactory bulb of the zebra fish, decoding identified a sequence of neuronal responses to odors, revealing that ambiguous mixtures of odors are initially coded continuously and become categorically represented later in time [54]. In humans, decoding has been used to show that perceived phonemes are categorically represented in the posterior superior temporal gyrus, with a peak as early as 110 ms following sound onset [55]. Similarly, the production of spoken syllables can be deciphered from the sensorimotor somatotopic cortex, with sequential activation of distinct codes for the initial consonant and the subsequent vowel [56].

Overall, applying decoding techniques to successive time points can identify when, and for how long, a specific piece of information is represented in the brain. The next question we may ask is: how does the underlying neural code evolve in time?

Generalization across time reveals how mental representations are dynamically transformed

The decoding approach detailed above can be extended to ask whether the neural code that supports above-chance decoding is stable or is dynamically evolving (see Figure I in Box 1). The principle is simple: instead of applying a different classifier at each time point, the classifier trained at time t can be tested on its ability to generalize to time t’. Generalization implies that the neural code that was identified at time t recurred at time t’.

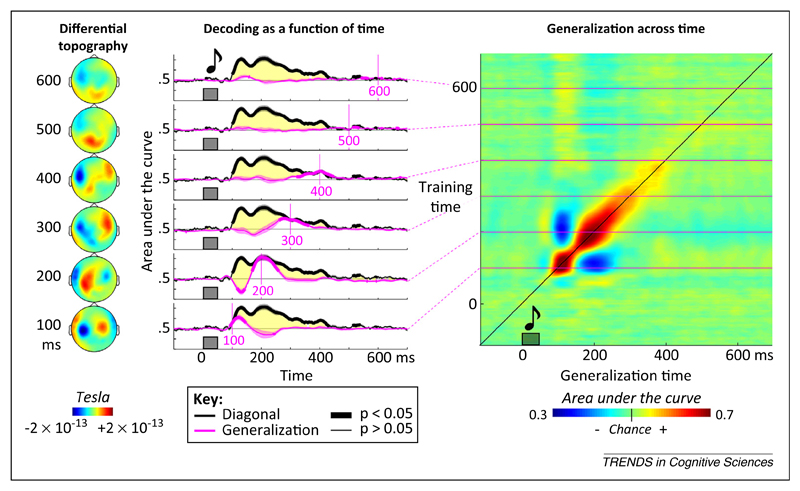
Systematically adopting this approach leads to a temporal generalization matrix in which each row corresponds to the time at which the classifier was trained and each column to the time at which it was tested. For instance, when we applied this method to the decoding of novel versus habitual sounds [57], we found that mismatch signals, classically assigned to a single ‘mismatch response’, actually correspond to an extended sequence of distinct brain activation patterns (Figure 1). Although sound novelty can be decoded over a long time window, each of the classifiers is time specific and does not generalize over a long time period. All of this information is apparent in the temporal generalization matrix, which takes a diagonal form.

Figure 1.

Example of generalization across time. In an auditory mismatch magnetoencephalography (MEG) experiment, subjects were presented with four identical sounds followed by either the same sound or a different sound (thus generating a mismatch response). Classifiers were trained to determine, at each time point, whether the sound was repeated or deviant. Decoding performance was assessed by the area under the curve, a nonparametric measure of effect size derived from signal-detection theory. Between approximately 100 and 400 ms after sound onset, decoding was above chance (thick black lines). However, each classifier generalized over a transient time period only, as indicated by the diagonal generalization matrix and the fact that diagonal performance (thick black line) was systematically superior to off-diagonal temporal generalization (six pink lines, each indicating a classifier trained at the indicated time). The changing topographies on the left confirm that the differences in magnetic field evolve over time. These findings suggest that the same stimulus (an unexpected sound) elicits a series of distinct patterns of brain activity over time. Adapted from [57].

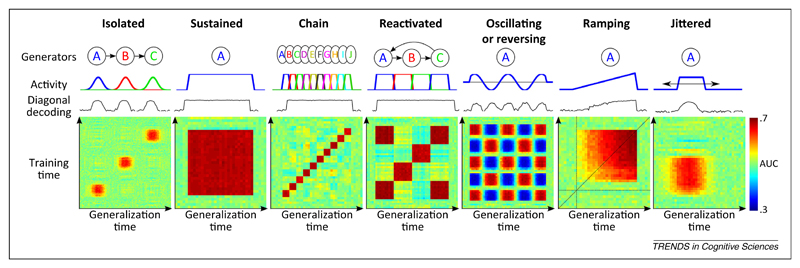
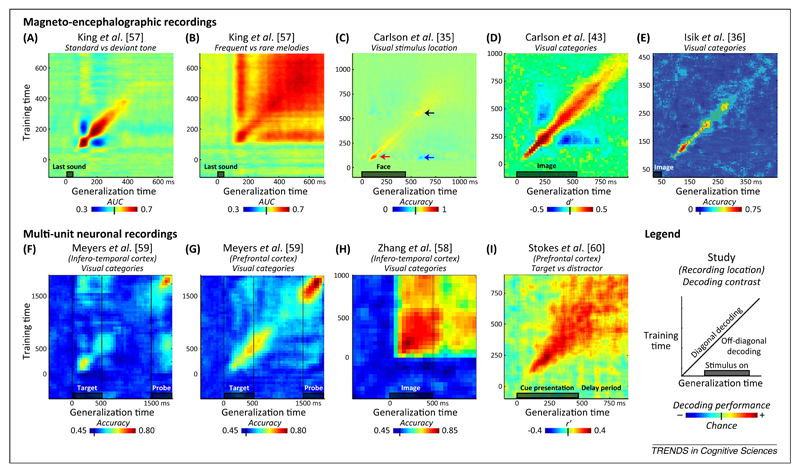
The simulations presented in Figure 2 exemplify how the temporal generalization method may distinguish fundamentally different dynamics of brain activity to which traditional sliding-window classifiers can be blind. So far, this method has been used only sporadically in the literature. The few available examples suggest that the diagonal pattern, indicative of a series of processing stages, is only one of several canonical dynamics modes of brain activity (Figure 3). For instance, when we analyze a slightly different response to auditory novelty – the late brain response to frequent versus rare auditory melodies [57] – we find that it obeys a strikingly different dynamics from the mismatch response, with a square generalization matrix indicating a stable neural code (compare Figure 3A and B). A similar square matrix was observed for categories of visual pictures in the inferotemporal cortex during a simple attention task [58]. Interestingly, other experiments [59,60] find that the same area, as well as the prefrontal cortex, may switch to a diagonal pattern during a delayed match-to-sample task (Figure 3F–I). These examples suggest that, in different contexts, either a stable activity pattern or a time-changing code is used by the brain to bridge across a long temporal delay.

Figure 2.

Generalization across time: principles and possibilities. The temporal generalization matrix (see Figure I in Box 1) contains detailed information about the underlying brain processes. For illustration, we simulated seven different temporal structures. For each one, the generators (neural generators A, B, C, and so on), their time course, the diagonal decoding performance summarized with the area under the curve (AUC), and the full temporal generalization matrix are displayed. Isolated: Three simulated brain regions are differentially activated at three distinct times, leading to three isolated patterns of above-chance decoding performance. Sustained: Analysis of a single process maintained over time leads to a square-shaped decoding performance. Chain: Decoding a chain of distinct generators leads to a diagonal-shaped decoding performance, because each component generalizes over a brief amount of time only. Reactivated: A given generator reactivates at a later time, leading to transient off-diagonal generalization. Note that the maintained, chain, and reactivated conditions are indistinguishable from their diagonal performance, but are easily separated by their temporal generalization matrices. Oscillating: An oscillatory or reversing component leads to transient below-change performance. Ramping: Slowly increasing activity leads to a subtle asymmetry; temporal generalization is higher when the classifier is trained with high signal-to-noise data and tested with noisier signals than in the converse condition. Jittered: Temporal jitter in activation onset smoothes the generalization matrix both horizontally and vertically.

Figure 3.

Examples of empirical findings. Temporal generalization has been empirically tested on both noninvasive magnetoencephalography (MEG) data [35,36,43,57] and invasive multiunit neuronal recordings [58–60] using different decoding categories [e.g., decoding auditory regularities (A,B), decoding the position of a visual stimulus (C)], different types of classifier (e.g., support vector machine, linear discriminant analysis), different decoding performance metric [e.g., accuracy, area under the curve (AUC)], and different chance levels. The temporal generalization matrices are reproduced from each of these nine studies (A–I). The results illustrate some of the major dynamic structures postulated in Figure 2: diagonal chain (e.g., A,C,D,E,G), reactivation at the time of a second stimulus (F,G) or at stimulus offset (C), sustained activity (B,H), or transition from diagonal to sustained (I). Reversing brain patterns are visible as below-chance generalization performance (below-chance patches in panels A, C, and D). Interestingly, across studies the same brain region (e.g., the inferotemporal cortex) seems capable of generating very distinct dynamics (compare panels F and H). Furthermore, similar types of stimulus can lead to very different types of dynamics (compare panels A and B).

Other types of dynamics undoubtedly exist. For instance, the neural code may oscillate as a function of time. Fuentemilla and collaborators [52] trained a multivariate pattern classifier during the presentation of indoor or outdoor stimuli. When testing during the delay period of a working-memory task, they obtained above-chance performance that, interestingly, oscillated at the theta rhythm (4–8 Hz), indicating that a working-memory code recurred cyclically.

Other temporal generalization data suggest that neural codes may reverse over time. For example, Carlson et al. trained a classifier to decode the position of a visual stimulus [35]. They showed that, after training a classifier at the onset of the image, the classifier led to below-chance predictions at the time of stimulus offset, suggesting that the neural activity pattern recurred with a reversed polarity. Similar off-diagonal below-chance generalization has been observed by others [35,43,57,61]. Understanding when and why such reversals occur is an interesting question for future research.

Generalization across conditions reveals how information processing is changed

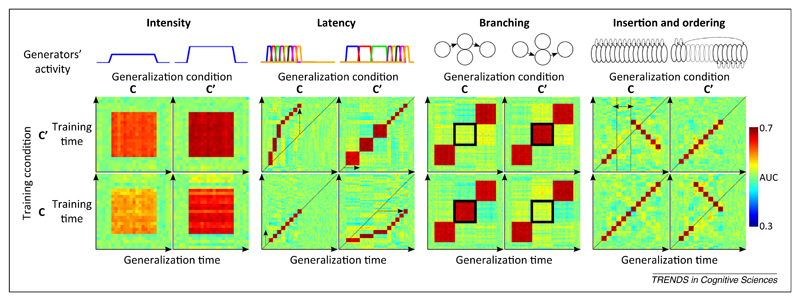
We just showed that the temporal generalization matrix provides detailed information about the sequence of processing stages engaged in a particular task. If we change the experimental conditions, however, some of these processing stages may remain unaffected whereas others may be accelerated, slowed, deleted, or inserted. Can decoding also illuminate such reorganizations? If a classifier is trained in one condition and tested on its ability to generalize to another, the resulting temporal generalization matrix may indicate how information processing has changed (see simulations in Figure 4). For instance, an acceleration of some stages would be perceptible as a displacement of the generalization window outside the diagonal. The method can identify at what time, and for how long, the acceleration occurred. Other changes, such as the deletion or insertion of processing stages or their temporal reordering, can be similarly characterized (Figure 4).

Figure 4.

Generalization across time and experimental conditions: principle and possibilities. When data are available from two experimental conditions (C and C’), the classifiers can be trained in one condition and tested on their ability to generalize to the other. The resulting pattern of generalization across time and conditions provides diagnostic information about the organization of brain processes. The four simulations, using similar principles to the ones detailed in Figure 2, indicate how changes in activation intensity, latency, branching, or ordering each lead to a distinct cross-condition generalization matrix. Note that a change of signal intensity leads to asymmetric generalizations across conditions because it can be more efficient to train a decoder with relatively high signal-to-noise ratio (SNR) data and generalize it to low SNR data rather than vice versa. Changes in the speed of information processing (latency) and in the selection (branching) and order of processing stages can be tracked by comparing the temporal generalization matrices across conditions.

Although the proposed method has rarely been used empirically, it offers great potential for revealing the changing dynamics of processing stages. Indeed, neurophysiological studies indicate that complex temporal reorganization of brain activity may occur. A striking example is provided by the decoding of an animal’s spatial location from multiunit neuronal recordings. Capitalizing on the earlier demonstration that rat location could be accurately decoded from hippocampal place-cell activity [62], Louie and Wilson [63] identified a sequence of place-cell firing that reproducibly tagged the animal’s movement through a circular track. They then showed that the same sequence was replayed during rapid eye-movement (REM) sleep, at approximately the same speed or slower (also see [64]). Subsequently, Lee and Wilson [65] showed that place-cell activity, which could be used to detect the location and direction of animal movement, was also replayed at 20 times-faster speed during slow-wave sleep, while the animal was, of course, immobile. Accelerated replay was also observed in the awake state [66]. Recently, Pfeiffer and Foster [67] found that fast replay of place-cell activity also occurred when the animal was searching for a goal. When decoded, the neuronal activity unfolded into a goal-directed trajectory that anticipated, at an accelerated pace, the subsequent movement of the rat on the same trial. Place-cell firing may also recur in reverse order [68], perhaps reflecting a form of goal-based problem solved by means–ends analysis. Those examples prove that temporal accelerations and reversals do occur in brain activity and invite a search for their occurrence in other cognitive domains (e.g., bird song [69]) using the temporal generalization matrix as a telling signature.

Concluding remarks

Since Donders and Sternberg, brain algorithms have been dissected by manipulating experimental factors such as attention, expectation, or instructions that selectively accelerate, slow, remove, insert, or reorder specific processing stages. Behavioral methods of mental chronometry, however, provide only indirect information about such reorganizations. Here we summarized several ideas and empirical studies that suggest that MVPA can provide considerable information about the fine temporal organization of information-processing stages. In the past decade, MVPA has been primarily used to analyze brain-imaging data at a fine spatial scale and to characterize the structure of mental representations [11]. Here we suggest that applying MPVA across space, time, and experimental conditions can reveal not only the time at which information becomes decodable, but also the dynamics with which the underlying representations are processed. Characterizing the building blocks of cognitive processes in time, rather than solely in space, presents many challenges and open issues (Boxes 2 and 3) for which we hope that the temporal generalization method may prove useful.

Box 2. Does the brain operate as a decoder of its own signals?

MVPA is a powerful method. Could it also be considered a useful metaphor for some brain operations? Consider the problem of identifying a face from retinal inputs. The primary visual area contains all the information needed to identify a flashed face, yet this information is ‘entangled’ in a complex manifold of firing rates [74,75]. A central goal of cognitive neuroscience is thus to understand how the hierarchy of brain areas in the ventral visual stream ‘disentangles’ visual information to make it explicitly coded in the firing rate of a neuronal population – that is, easily decodable by other regions.

For inferotemporal neurons, learning to become sensitive to a specific face may comprise learning a classification function that, given the input firing rates, separates instances of this face from any other stimulus. Similarly, training on a psychophysical experiment may imply that the prefrontal and parietal areas learn to weigh evidence from the relevant sensory neurons and disregard uninformative cells. Each brain area may thus be confronted with a multivariate classification problem similar to that of the neuroscientist attempting to sift through a pile of recorded data.

Asking whether a brain area acts as a decoder of its afferent inputs begs the question of what type of decoding algorithm it uses. First, is the brain confronted with issues of over-fitting and, if so, does it use regularization or penalization schemes, as some pattern-classification algorithms do (e.g., SVM [76])? Does it reject outlier data? Does it suffer from a ‘curse of dimensionality’ and, if so, does the pyramidal neuron’s limited dendritic span provide a solution by drastically reducing the data under consideration?

Second, does the brain use linear or nonlinear decoders? Some theories suggest that once the information is properly encoded in stochastic firing rates, a linear combination of spiking inputs suffices to approximate complex Bayesian operations [77]. Furthermore, the spontaneous fMRI activity in the extrastriate cortex has been modeled as a linear combination of the signals from the primary visual cortex (V1) and secondary visual cortex (V2) [78], thus revealing the structure of corticocortical projections. Recently, the activity of single neurons in the inferotemporal cortex [79,80] or medial–superior temporal cortex [81] has also been modeled as a weighted sum of individual responses to simple lines or local motion at predefined locations. In this case, however, the addition of nonlinear terms improved the model significantly for many neurons. An interesting suggestion is that nonlinearities may enter at only the input and output stages, thus leaving the learning problem itself essentially linear [81]. Such a nonlinear input and output transformation may have the advantage of providing increased selectivity for feature combinations by changing the summation of inputs into a product [79–81].

Understanding which classification algorithm, if any, applies inside the brain is an important goal for learning theory. Ultimately, MVPA should aim to decipher precisely those signals that the brain uses for its internal computations. MVPA should not use exceedingly powerful nonlinear algorithms; otherwise, even abstract information could be decoded from V1. Rather, MVPA should aim to attain the same performance as subjects’ brain and behavior (e.g., [75,82]) and fail on exactly the same trials [83].

Box 3. Outstanding questions.

• What factors make certain cerebral operations appear as ‘diagonal’ and others as ‘square’ in temporal generalization matrices?

• What other dynamical patterns may appear in brain activity? Does the brain rely on a limited repertoire of canonical dynamical patterns that recur in different types of computation?

• Does each brain region possess a characteristic repertoire of dynamical patterns (e.g., serial flow in the ventral stream, evidence accumulation in the parietal cortex, all-or-none maintenance in the prefrontal cortex)?

• Is there a systematic correspondence between dynamical patterns at the single-neuron and macroscopic (ECOG, EEG, and MEG) levels?

• Does sensory processing comprise a discrete series of stages (as suggested by the labels of EEG components: e.g., P1, N1, P2) or does it involve a continuous cascade of events?

• Why do we often see a reversal of generalization, leading classifiers to perform below chance level when tested away from their initial training time?

• How do experimental factors such as expectation, task relevance, or task difficulty affect the dynamics of neuronal encoding and decoding? Do they systematically modulate, delay, or reorganize brain activity?