Summary
The human brain exhibits fundamental limitations in multitasking. When subjects engage in a primary task, their ability to respond to a second stimulus is degraded. Two competing models of multitasking have been proposed: either cognitive resources are shared between tasks, or they are allocated to each task serially. Using a novel combination of magneto-encephalography and multivariate pattern analyses, we obtained a precise spatio-temporal decomposition of the brain processes at work during multitasking. We discovered that each task relies on a sequence of brain processes. These sequences can operate in parallel for several hundred milliseconds but beyond ~500 ms, they repel each other: processes evoked by the first task are shortened, while processes of the second task are either lengthened or postponed. These results contradict the resource-sharing model and further demonstrate that the serial model is incomplete. We therefore propose a new theoretical framework for the computational architecture underlying multitasking.
Introduction
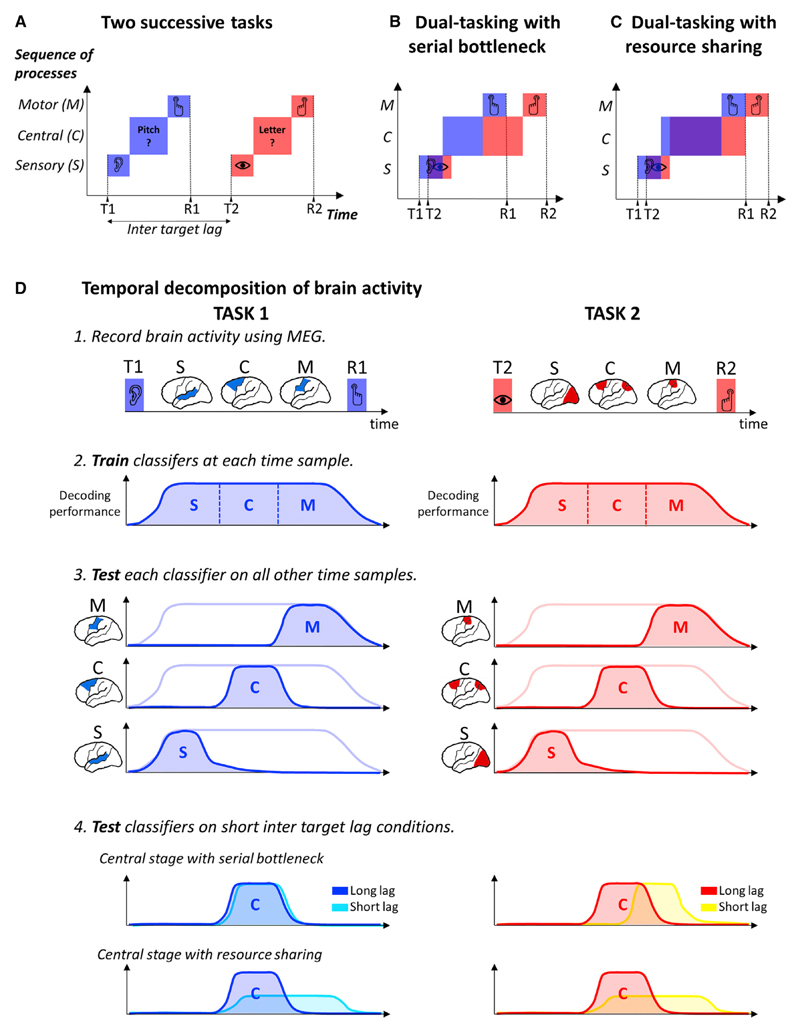
However alert we may be, we can hardly focus on more than one task at any one time. The process by which the human brain selects relevant information from the environment has fundamental temporal constraints, dramatically illustrated in dual-task settings: when subjects focus on a task, this engagement impairs their ability to initiate the motor response to another stimulus (the psychological refractory period) (Pashler, 1994) or even to detect it (the attentional blink) (Raymond et al., 1992). Current models of dual-task interference agree that (1) performing a task involves at least three stages (sensory, central decision, and motor processing; Figure 1A), (2) sensory and motor stages can operate in parallel with other operations, but (3) the central stage has limited capacities. A key point of disagreement between models regards the central stage: the serial bottleneck model hypothesizes that the central stage is serial; that is, it processes only one task at a time (Pashler, 1994; Sigman and Dehaene, 2005) (Figure 1B). By contrast, the resource-sharing model proposes that the central stage can process multiple tasks in parallel but possesses limited resources that therefore have to be shared between tasks (Kahneman, 1973; Tombu and Jolicoeur, 2003). As the delay between tasks 1 and 2 shortens, the period during which resources are shared increases, therefore slowing down both tasks’ processing (Figure 1C).
Figure 1. Resource-Sharing and Bottleneck Models of Dual-Task Interference.
(A) Schematic representations of non-conflicting tasks. Task 1 (blue) and Task 2 (red) are divided in sensory (S), central (C), and motor stages (M).
(B) Serial bottleneck model: the central stage dedicates its full resources to one task at a time and thus performs them one after the other.
(C) Resource-sharing model: tasks are performed in parallel but with reduced effectiveness.
(D) Schematic representation of the decoding analyses. The brain activity is recorded using MEG while subjects perform a dual task. Each task induces a sequence of patterns of brain activity from the stimulus onset to the motor response, here schematized by three hypothetical stages, S, C, and M. At each time sample, a classifier is trained to separate the conditions of interest. Each classifier can be tested on its ability to generalize to other time samples to reveal the dynamics of the successive patterns of brain activity. The classifiers trained at a long inter-target lag were also tested on their ability to generalize to short inter-target lag conditions. The effects of lag on the dynamics of the sequence of brain processes could then be examined and compared to the predictions of the models.
To understand how the human brain handles multi-task situations, we investigated three critical predictions that disentangle the resource sharing and the serial bottleneck models. First, the resource-sharing model suggests that Task 1 processing is prolonged during dual tasking, while the bottleneck model predicts that it remains unchanged. Second, resource-sharing models propose that the central stages of Task 1 and 2 are performed in parallel, while bottleneck models propose that they are performed one after the other. Third, if capacities are shared, the amplitude of brain activations associated with central stages should decrease for both tasks during task overlap. By contrast, according to the bottleneck model, activation amplitude for the task that is currently processed should be similar within or outside the interference period.
Testing these predictions is challenging as it requires simultaneously monitoring, at the whole-brain level, each of the cognitive processing stages of the two tasks, from stimulus presentation to motor response. Recent developments in magnetoencephalography (MEG) combined with multivariate pattern analysis (MVPA) may provide a first approximation of this ideal recording setup, by isolating and tracking within each subject the neural patterns specific to each processing stage. MVPA can be applied to MEG signals by fitting a different classifier on every time sample separately (Figure 1D). The resulting time course reveals whether two experimental conditions can be separated based on the succession of brain responses they elicit and how this information evolves across time. An important aspect of this technique is that each classifier trained at time t (thereafter referred to as “training time”) can also be tested on its ability to discriminate conditions at other time points t’ (“testing time”). Such temporal generalization (Figure 1D) is a good way to reveal the onset and the duration of a given pattern of brain activity, and how it varies with experimental conditions (King and Dehaene, 2014). Here, we apply this tool to the decomposition of dual-task processes. We first identify a series of classifiers that decode the successive steps of each task outside the interference period (i.e., at a long inter-target lag). We then apply the same classifiers to experimental recordings obtained while the same tasks were executed during the interference period. In this way, we discover which brain processes are selectively shortened, delayed, reduced, or abolished during dual tasking.
Results
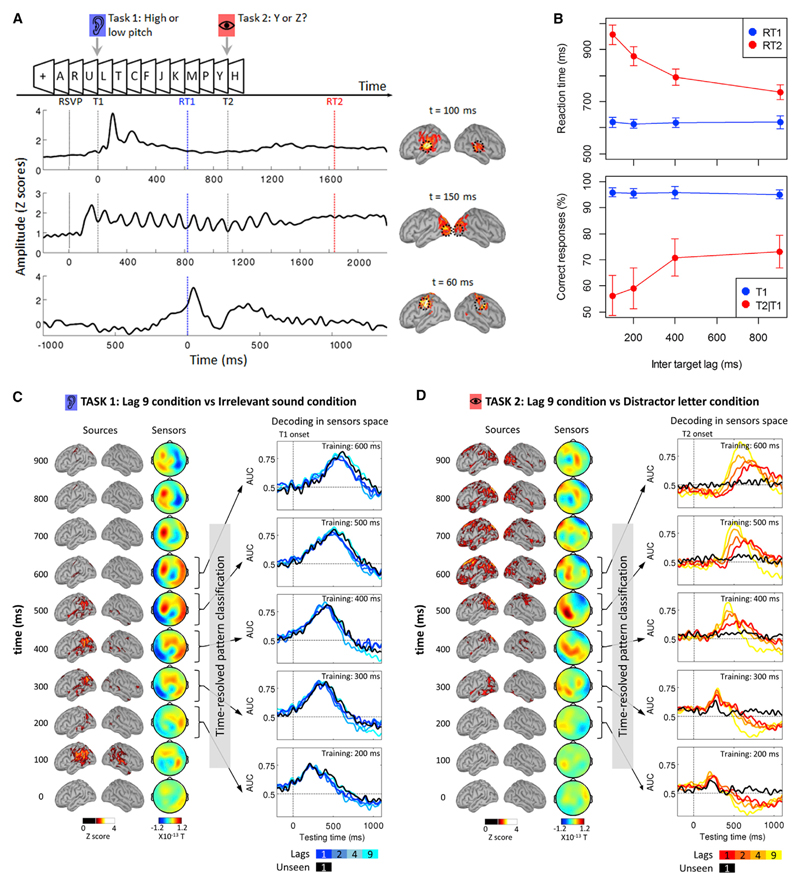
We applied this method to MEG recordings from a previously published dual-task experiment (Marti et al., 2012) aimed at investigating the neural mechanisms common to the attentional blink and to the psychological refractory period. During the main dual-task runs, ten subjects had to discriminate, as fast as possible, one of two target sounds (Task 1), and then one of two target letters (Task 2) embedded in a series of random letters (10/s, see Figure 2A). The sound (T1) was separated from the target letter (T2) by 1, 2, 4, or 9 letters, thereafter called “Lags 1, 2, 4, and 9,” respectively, where each lag lasts for 100 ms. In a fifth condition, T2 was replaced by a distractor letter (“Distractor letter” condition). Finally, participants performed a separate control condition, during which they were instructed to ignore the sound (“Irrelevant sound” condition) (details about stimuli and experimental procedures can be found in the Supplemental Information). All analyses were performed on trials in which the response to the auditory T1 was first and accurate (>95% of the trials). Hence, RT1 always refers to the response time to the auditory task and RT2 always refers to the response time to the visual task.
Figure 2. Time-Resolved Decoding of Brain Responses during Dual Tasking.
(A) Experimental design: subjects had to discriminate a sound and a target letter embedded in a series of distractors. Three regions of interest from the primary visual, auditory, and motor cortices are depicted below, together with their time courses (for the motor cortex, activation in the hemispheres ipsi- and contralateral to the response hand were subtracted). Dotted black lines represent the rapid serial visual presentations (RSVPs), the sound (T1), and the relevant letter (T2, at Lag 9) onsets. The blue and red dotted lines represent the mean response time for Task 1 and Task 2, respectively. Note that the time courses are time locked to the relevant events (from top to bottom: the sound onset, the RSVP onset, and the response to Task 1).
(B) Mean (±SEM) subjects’ response times (top) and accuracy (bottom) as a function of inter-target lag for Task 1 (blue) and Task 2 (red). Regarding Task 2 performance, only trials with accurate Task 1 responses are presented.
(C) Left: sequence of brain activations (0–900 ms) related to Task 1 after subtraction of the irrelevant sound condition as shown in the source space (presented in Z scores compared to baseline) and in the sensors space (magnetometers). Right: temporal generalization of Task 1-classifiers trained at five latencies (200–600 ms after T1 onset) in each Lag condition (darker color for shorter Lags). Unseen trials in Lag 1 are represented in black. In these panels, 0 ms represents T1 onset.
(D) Same as (C) but for Task 2 after subtraction of the Distractor letter condition. Time 0 represents T2 onset.
Measures of reaction times on dual-task runs revealed a typical refractory period (Figure 2B): RT2 increased from 737 ms at Lag 9 to 957 ms at Lag 1 (F(3,27) = 31.70, p < 0.001), while RT1 remained unaffected (621 ms and 622 ms for Lag 9 and Lag 1, respectively). Subjects’ response accuracy also revealed an Attentional Blink (Figure 2B). The mean proportion of unseen trials increased with decreasing Lag (Lag 9: 21.42%; Lag 1: 37.04%, F(3,27) = 15.82, p < 0.001) and was larger for slow than for fast RT1 (main effect of RT1 speed based on a median split: F(3,27) = 53.16, p < 0.001; Lag 3 RT1 speed interaction: F(3,27) = 3.18, p = 0.04). Those findings replicate previous studies showing that the time spent to process Task 1 influences both the attentional blink and the psychological refractory period, hence suggesting that these two phenomena are closely related (Jolicoeur, 1998, 1999a, 1999b). No such lag effects on T2 processing were observed in the control runs where the sound was irrelevant, indicating that the Task 1, rather than the sound itself, was responsible for the interference onto Task 2.
MEG recordings at Lag 9 revealed two distinct processing chains for the two tasks. Figure 2A presents the average source activity at specific time points as well as the time course of activity measured in three regions of interests located in the primary auditory cortex, the primary visual cortex, and the primary motor cortex (see Experimental Procedures). The auditory cortex was activated by the presentation of the sound ~100 ms after stimulus onset. The comparison Relevant versus Irrelevant sounds, aiming at isolating Task 1 processes, revealed activations mainly in the parietal cortex from 200 to 600 ms (Figure 2C). The visual task-elicited activity in the visual cortex cadenced by the presentation of the letters (Figure 2A). The comparison Target versus Distractor letters, aiming at isolating Task 2 processes, revealed activity in the ventral visual cortex, which later propagated to the posterior parietal and frontal cortices from ~250 to ~900 ms (Figure 2D). We then used multivariate pattern analyses to investigate how these activations were affected by dual-task interference.
Dual-Task Interference Differentially Affects Early and Late Brain Responses
To uncover the dynamics of Task 1 brain networks, we trained a series of MVPA classifiers to categorize trials as belonging either to the Lag 9 condition (where the T1 task was performed in isolation, long before T2 appeared) or to the Irrelevant sound condition (where the T1 task was not performed; see Experimental Procedures). Similarly, Task 2 classifiers were trained to discriminate trials as belonging either to the Lag 9 condition (where the T2 task was performed long after T1) or to the Distractor letter condition (where the T2 task was not performed). Training two sets of classifiers, one for each task, allowed us to track the brain responses underlying Task 1 and Task 2 independently of each other. We trained at Lag 9 in order to ensure that classifiers were trained in a condition where Task 1 and Task 2 were performed in near isolation, without causing dual-task interference. We then tested for generalization to the shorter lags in which dual-task interference occurred. Since the only difference between the Lag 9 condition and the other lags is the temporal delay between the two target stimuli, this procedure minimizes the differences between the training and testing sets.
In order to sample the sensory, central, and response stages for each task, we selected classifiers trained at five latencies (t = 200, 300, 400, 500, and 600 ms). Each classifier trained at time t was then tested on its ability to categorize the data from other time points t’. The prediction performance decreased as the difference between the training time and the testing time (t-t’) increased (e.g., Figures 2C and 2D). The width of the generalization time window reflects the periods during which the differential brain activity is approximately stable. Each classifier is specific to a certain pattern of brain activity and the prediction performance over time reflects the time course of this pattern. This time course can be characterized by measuring the peak decoding amplitude, peak latency, onset, and offset in order to examine the impact of experimental manipulations on these variables.
In order to unravel the effect of dual-task interference on these brain processes, classifiers were trained at Lag 9 and then applied to Lags 1–4 as well as to trials in which T2 was undetected (hereafter called “unseen T2”). Task 1 processing was mildly affected by dual-task interference, as the time course of generalization performance did not vary with lag (Figure 2C). We only found that the time course of the classifier trained at 600 ms had a slightly shorter offset when the tasks overlapped, but this effect was not significant (X2(3) = 5.9, PFDR = 0.20). By contrast, Task 2 processing was heavily impacted by the inter-target lag and that this effect varied according to the processing stage (Figure 2D). The time courses of the classifiers trained at 200 and 300 ms were not altered by the inter-target lag. At 400 ms, the peak of the prediction performance decreased in amplitude (X2(3) = 18.36, PFDR < 0.001) and its latency was delayed when the inter-target lag decreased (X2(3) = 12, PFDR = 0.03). The onset and offset were also delayed (X2(3) = 13.85, PFDR = 0.02 and X2(3) = 24.09, PFDR < 0.01, respectively). Similar effects were observed for classifiers trained at 500 ms (peak latency, X2(3) = 17.48, PFDR < 0.01; onset, X2(3) = 15.12, PFDR = 0.01; offset, X2(3) = 10.2, PFDR = 0.06, amplitude, X2(3) = 24.12, PFDR < 0.001) and 600 ms (peak latency, X2(3) = 15.72, PFDR < 0.01; onset, X2(3) = 23.4, PFDR = 0.001; offset, X2(3) = 16.58, PFDR = 0.01, amplitude, X2(3) = 16.44, PFDR < 0.01).
These results show that, at short inter-target lag, late Task 2-related processes were delayed during dual-task interference, while early processes were left unaffected. Examining Task 1 processing at the same stage did not reveal any evidence of prolonged processes. This finding goes against the resourcesharing model, which predicts that at some stage both tasks should be prolonged because of shared limited resources. Contrarily, these results suggest that resources were serially allocated, first to Task 1, then to Task 2.
The above analyses are limited to a set of classifiers that were defined a priori. Our next analysis considers the entire sets of unfolding activations. When applied iteratively to every time sample, the decoding analysis results in a matrix of temporal generalization (King and Dehaene, 2014). This approach is not restrained to a priori defined spatio-temporal regions of interest and provides a synthetic view of the dynamic of each processing stage.
Dual-Task Interference Shortens Task 1 Processes
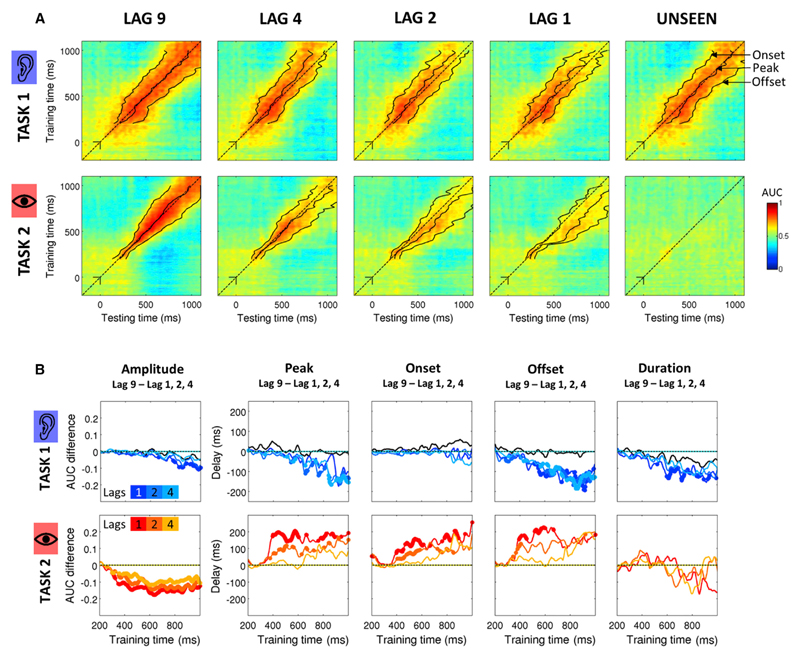
Figure 3 shows that Task 1 decoding performance sharply increased ~100 ms after stimulus onset (AUC close to 0.8) and remained strong until the end of the epoch. The diagonal-shaped decoding performance in Lag 9 shows that each classifier generalized over a period of time of ~200 ms, suggesting that task processing consisted in a cascade of partially overlapping processes. A first striking aspect of Figure 3A is that the temporal generalization of Task 1 classifiers was altered at short lags. The time courses of those classifiers exhibited shorter offsets (and therefore shorter durations) in Lags 1, 2, and 4 compared to Lag 9 (Figures 3A and 3B). At Lag 1, the offset was shortened by 36 ms for a classifier at 516 ms and by 176 ms for a classifier at 736 ms (as compared to Lag 9 offsets). A significant effect of inter-target lag was observed on the offsets of classifiers later than 288 ms (all PFDR < 0.05). By contrast, the onsets of these classifiers were left completely unaffected. This suggests that, although the total processing time of Task 1 was not affected by dual-task interference, the durations of the successive brain responses were shortened. Our interpretation is that once a brain area (or a set of areas) transmits information to the next one in the chain of processes, it is not abruptly shut down but instead remains partially active, with a temporally decaying profile, for a certain period of time. Our data indicate that this late activation period is shortened by the presence of Task 2. These results are in contradiction with the resourcesharing model, which predicted that those stages would be lengthened.
Figure 3. Temporal Generalization of Classifiers Reveals How Dual-Task Interference Impacts Task 1 and Task 2 Chains of Processes.
(A) Temporal generalization matrices for Task 1 (top rows) and 2 (bottom rows) for each Lag condition and for unseen trials. In each panel, a classifier was trained at each time sample (vertical axis: training time) and tested on all other time samples (horizontal axis: testing time). The dotted line corresponds to the diagonal of the temporal generalization matrix, i.e., a classifier trained and tested on the same time sample. For each classifier, we measured the onset, the peak, the offset, the duration, and the amplitude of the classification time course. Solid lines here represent the median peak latency, onset, and offset of each classifier.
(B) Colored lines indicate the median difference between Lag 9 and the other lags (dark, medium, and light colors for Lag 1, 2, and 4, respectively). Taking the peak latency as an example, a value of 0 on the y axis for a given condition means that the peak of the prediction performance had the same timing as in the Lag 9 condition. Negative and positive values indicate that the peak was shifted to earlier and later latency, respectively. Significant differences (signed-rank across subjects, FDR corrected) between the Lag 9 condition and the other condition of interest are depicted with a thick line. For display purposes, data points were smoothed using a moving average with a window of five samples.
The processing of Task 1 on unseen T2 trials provides further evidence. The comparison of Task 1 processes on Lag 9 and on Lag 1 unseen T2 trials revealed differences neither in the peak amplitude (all PFDR > 0.48), nor in the latency (all PFDR > 0.19), onsets (all PFDR > 0.4), and offsets (all PFDR > 0.7). Thus, while Task 1 processes were shortened on seen T2 trials, they unfolded normally on unseen T2 trials, as if T2 had not been presented (Figure 3A). Resource sharing implies that missing T2 should leave all resources available to T1 and therefore speed up its processing. Instead, the present results suggest that when T2 is unseen, processing of Task 1 can proceed normally without being shortened (see Supplemental Information for a detailed description of unseen T2 trials). Interestingly, these findings also present a challenge for the bottleneck model, since they show that Task 1 processing is not immune to dual-task interference.
An alternative interpretation of Task 1 shortening could however be a different type of causal relation between the two successive tasks: trials in which Task 1 duration is longer are more likely to lead to an unseen T2 (Jolicoeur, 1998; Marti et al., 2012; Sergent et al., 2005). In such a case, analyzing only the “seen” trials would lead to an apparent shortening of T1 processing—an effect that would become increasingly larger at shorter lags. While such an effect may contribute to our findings, further analyses suggest that it cannot fully account for the results. First, RT1 in seen T2 trials was similar in all lag conditions (p > 0.25). Second, although weaker, the shortening of T1-offset continued to be observed at Lag 1 relative to Lag 9 when we analyzed all trials, without sorting them into T2-seen and T2-unseen categories (Figure S1).
Another alternative interpretation would be that the shortening of T1 decoding does not reflect changes in the dynamics of Task 1-related brain responses but instead reflects a change in task-irrelevant background processes. Since the prediction performance produced by a classifier depends on the signal-to-noise ratio, any change in this prediction could reflect either changes in the amplitude of the brain response or changes in the noise. However, a classifier is highly selective of a certain pattern of brain activity. In fact, any change in the signal measured on MEG sensors that are orthogonal to the classifier’s hyperplane would by definition not affect prediction performance. Furthermore, it is unclear how irrelevant background activity could induce a dynamical set of topographies highly similar to the one evoked by task-relevant brain processes and affect the evoked decoding performance (see Supplemental Information for a detailed discussion).
Taken together, these results suggest that the shortening of Task 1-related decoding time courses truly reflects a termination of its corresponding processes.
Dual-Task Interference Impairs and Delays Task 2 Processing
We next examined how Task 2 unfolded during dual-task interference. Between ~200 and ~350 ms after T2 presentation, Task 2 could be successfully decoded. However, the temporal generalization of each classifier remained weak, indicating that during this period, target T2 passed through a series of short-lived brain responses (Figure 3A). After ~350 ms, the decoding performance of Task 2 classifiers was observed over longer time periods. The inter-target lag impacted only on the offset of classifiers trained from 344 ms onward (all PFDR < 0.05, Figure 3B). For instance, the prediction performance of the classifier trained at 392 ms was prolonged by 166 ms in Lag 1 as compared to Lag 9. The onsets and peak latencies were also affected by dual-task interference from 396 and 400 ms onward, respectively (all PFDR < 0.05). The direct comparison of Lag 1 and Lag 9 conditions revealed that the peak performance of a classifier observed at 400 ms in the Lag 9 condition was delayed by 214 ms in the Lag 1 condition, while its onset was delayed only by 76 ms. The duration of this deflection, i.e., the difference between the onset and the offset, similarly increased by 80 ms, although this effect did not reach significance. The delays observed on the onsets progressively increased for later classifiers (Figure 3B) and became comparable to the ones observed on peak latency for classifiers >500 ms. For instance, a classifier trained at 536 ms revealed a time course with similar delays on its onset and peak latency (152 ms and 148 ms, respectively). Furthermore, the delay and prolongation decreased as the inter-target lag increased. For instance, a classifier trained at 536 ms saw its peak being delayed by 97 ms in the Lag 2 condition as compared to the Lag 9 condition and by only 2 ms in the Lag 4 condition. Finally, correlating the single-trial time courses of each classifier with subjects’ reaction time revealed that peak latencies, onsets, and offsets of late classifiers (>500 ms) were positively correlated with RT2 at both Lag 9 and Lag 1. Interestingly, the prediction performances of the same classifiers were also positively correlated with RT1 but specifically at Lag 1 and not at Lag 9 (Figure S2).
Taken together, these findings indicate that between ~350 ms and ~450 ms, Task 2 brain responses were not only delayed but also prolonged in time. Beyond ~500 ms, however, brain responses were mainly delayed. In fact, this delay could be observed at the single-trial level and was directly related to a delay in subjects’ motor response, suggesting serial processing.
Only Task 2 Is Impaired during Dual-Task Interference
According to the resource-sharing model, the allocation of limited resources should not only prolong the execution of both tasks, but it should also decrease the amplitude of their brain activations. As the amplitude of neural responses directly affects signal-to-noise ratio, this predicts that decoding performance should decrease for both tasks. However, Task 1 decoding performance was similar at all Lag conditions (all PFDR > 0.25 between 200 and 600 ms, overall AUC > 0.7, Figure 3B). We only observed decreased performance for very late classifiers (>664 ms, i.e., after the motor response to T1) at Lag 1 (all PFDR < 0.05). By contrast, Task 2 decoding performance strongly decreased in all short-lag conditions compared to the Lag 9 condition. A significant drop in decoding performance was observed for classifiers later than 348 ms (all PFDR < 0.05) and was particularly pronounced at the shortest lag (Figure 3B). Together, the preservation of Task 1 decoding performance and the impairment of Task 2 decoding performance suggest that cognitive resources were not shared between tasks but were serially allocated, first to Task 1 and subsequently to Task 2.
An alternative interpretation would be that the decreased Task 2 decoding performance is unrelated to the amplitude of the brain response. Classifiers trained in a condition where the tasks were performed in isolation might not perform as well in a condition where multiple patterns of brain activity overlap. However, two topographies can overlap in time without any impact on the decoding performance of their corresponding classifiers if they are generated from independent sources (Figures S4A and S4B). We tested the selectivity of the classifiers used in the present study and found that Task 1 classifiers were not able to decode Task 2-related information and vice versa (Figures S4C and S4D). This suggests that the two sets of classifiers were orthogonal to each other and that the decrease in Task 2 decoding performance was genuinely related to a decrease in the amplitude of Task 2-related brain responses.
Taken together, the effects of dual-task interference on Task 1 and Task 2 processing depict a complex cognitive architecture in which the execution of a task consists of a sequence of processes partially overlapping in time. The design of the present experiment does not allow for a complete separation of each processing stage. However, the results revealed that these processes have different dynamics. Figure 4 allows a direct comparison of Task 1 and Task 2 processing dynamics and provides an overview of dual-task interference: processes are first organized in parallel and become serial only at a late stage (>500 ms). However, those late Task 1 and Task 2 processes were not merely performed one after the other but also repelled each other, a property that was not predicted by existing models of dual tasking.
Figure 4. Direct Comparison of Task 1 and Task 2 Processing Dynamics during Dual-Task Interference.
(A–D) Task collision in Lag 9 to 1. In each panel, the surface is delimited by the measured onset and offset of the prediction performance of each classifier (blue: Task 1, red: Task 2). Colored dots indicate significant differences between the Lag 9 condition (peak latency, onset, and offset) and the condition of interest (signed rank tests, FDR corrected). T1 is presented at time 0 and the corresponding diagonal is represented by a dashed line. Small black segments on this diagonal indicate T1 onset on x and y axes. Task 2 is represented similarly except that T2 onset varies in each panel. On the right of each panel are represented the time courses of classifiers (blue, Task 1; red, Task 2) trained at 300, 400, and 500 ms. The thick lines represent an AUC significantly different from chance level (FDR corrected). The gray dotted lines indicate the training time of each classifier.
Discussion
The present study aimed at understanding the brain mechanisms deployed to handle multiple tasks that overlap in time. Specifically, we tested the respective predictions of the two dominant models accounting for dual-task interference: serial bottleneck versus resource sharing. The results revealed that task processing is best understood as a chain of distinct processors. The chains of processes for Task 1 and 2 operated in parallel for several hundreds of milliseconds. Following this period, Task 1 processes were shortened while Task 2 processes were either hindered and prolonged or fully delayed. This suggests a “collision” between chains of processes: Task 1 and Task 2 late processes repelled each other. Those results strongly argue against the resource-sharing model but also show that the serial bottleneck model is incomplete. Consequently, we propose an alternative model of dual-task interference incorporating parallel and serial processing, and in which Task 1 and Task 2 processes actually compete for attentional resources and access to consciousness.
The Profiles of Task 1 and Task 2 Brain Responses Disconfirm the Resource-Sharing Hypothesis
Our findings revealed that Task 2 processes located in the ventral visual stream and in the posterior parietal cortex operated in parallel to Task 1 up to ~350 ms after stimulus onset. Between ~350 and ~450 ms, activations in the parietal cortex increased and extended to the temporo-parietal area. Decoding analyses revealed that these brain responses were observed in parallel to Task 1 but were prolonged in time while their amplitude decreased. This might correspond to a period in which limited resources are shared between tasks. However, Task 1 brain responses had shorter durations in Lags 1–4 compared to Lag 9 and this effect vanished when T2 was not consciously perceived. This finding contradicts the predictions of the resource-sharing model. Even if the totality of resources was successively allocated to each task, therefore emulating a serial bottleneck (Tombu and Jolicoeur, 2003), the model would not explain the fact that Task 1 processes were selectively shortened by the presence of Task 2. Therefore, these results suggest a competition between Task 1 and 2 rather than a sharing of limited resources.
Dual-Task Interference Cannot Be Fully Explained by a Serial Bottleneck
These results also challenge the classical serial bottleneck hypothesis, which typically proposes that Task 1 monopolizes attentional resources and therefore should not be affected by Task 2. The present results show instead that Task 1 is not immune to dual-task interference and that Task 2 can actually infringe on Task 1 processing.
Although these results are not compatible with the typical view of a bottleneck, we found that Task 2 processes beyond ~450 ms exhibited a clear serial profile: Task 1 and Task 2 brain activations were observed one after the other and barely overlapped. This is consistent with previous studies that showed that the lack of resources during Task 2 processing postponed late brain activity (i.e., the P3 component of the ERPs) (Dell’acqua et al., 2005; Sergent et al., 2005; Vogel et al., 1998). However, these studies were limited to the specific ERP components that they focused on, based on a priori knowledge of their latency and topography. The complete decomposition of tasks processing provided here reveals that Task 1 processes were shortened, while Task 2 processes were first diffused and then delayed (Vul et al., 2008). This suggests that the late processes of Task 1 and Task 2 repelled each other during dual-task interference. Therefore, the typical view of the serial bottleneck may have to be rethought in order to explain our findings.
Reconsidering the Brain’s Limitations to Multitasking
Our approach goes beyond the typical three-stage division of sensory, central, and motor processing stages. Instead, the results revealed a series of distinct processes that could operate in parallel to another task, rather than a single sensory stage. Furthermore, contrary to the classic depiction of a single central stage that would operate serially, we found evidence of multiple central processes that each exhibited a serial mode of functioning. Consequently, we propose a new theoretical framework that incorporates both parallel and serial processes and explains the present findings. We suggest that during the interference period, Task 2 is not passively waiting for the completion of Task 1. Instead, it competes for cognitive resources—much like two images compete for visibility during binocular rivalry. Specifically, when two incoming targets compete for top-down attentional signals from the posterior parietal cortex and the temporo-parietal area, inhibitory interactions may shorten Task 1-related processes on the one hand, and weaken and hinder the attentional engagement on Task 2 on the other hand (Dux and Marois, 2009; Nieuwenstein et al., 2005). The task that receives the strongest attentional enhancement triggers activation in parietal and frontal areas, allowing subjects to maintain and access the stimulus consciously.
This model fits well with the global neuronal workspace theory of consciousness (Dehaene et al., 1998; Sergent and Dehaene, 2004), which associates conscious perception to the synchronized activation of a large fronto-parietal network that broadcasts information in the cortex. Within this framework, our results suggest that although Task 2 competes with Task 1, it is inhibited during Task 1 processing, and the related sensory information is temporarily stored in a decaying sensory buffer (Marti et al., 2012; Sergent et al., 2005; Zylberberg et al., 2010). The attentional engagement on Task 2 is weakened and its conscious representation is delayed. Whether Task 2 will be consciously perceived or not depends on a balance between the duration of Task 1 processing and the degradation of Task 2 information in the buffer (Marti et al., 2012). If Task 2-related sensory activity is strong enough and Task 1 execution fast enough, then Task 2 can be accessed consciously although with a delay (Marti et al., 2010). Otherwise, this stimulus remains unperceived (attentional blink).
In conclusion, the decomposition of brain processes described in the present study revealed a surprisingly subtle functional architecture at play during multitasking. The architecture, simultaneously involving parallel and serial chains of processes, is a step toward a better comprehension of how the brain deploys attention over a continuous flow of sensory information and how this impacts the conscious representation of a stimulus.
Experimental Procedures
Subjects
The MEG recordings of ten participants previously analyzed in Marti et al. (2012) were included in the present analyses. The study was approved by the “Comité de Protection des Personnes” and all participants gave informed and written consents before testing and received a compensation of 120 € for their participation.
Experimental Protocol
Subjects performed a dual-task experiment composed of an auditory discrimination task (Task 1) and a visual discrimination task (Task 2) (Figure 2A). Subjects first had to discriminate a sound with a high (1,100 Hz) or a low (1,000 Hz) pitch presented for 84 ms. The second Task was to identify a black letter (Y or Z, 0.64°) embedded in a visual stream of 12 random black letters (duration: 34 ms separated by blank interval of 66 ms) presented on a white background (“Rapid Visual Stream Presentation” [RSVP]). The sound was presented together with the third item of the stream and separated from the target letter by 1, 2, 4, or 9 letters (“Lags 1, 2, 4, and 9,” respectively). In addition, a condition in which T2 was replaced by a “distractor letter” was also included. In a separate block, participants performed a control condition in which they performed the visual task but were instructed to ignore the sound (“Irrelevant sound” condition). Subjects were instructed to respond as fast as possible first to the sound, then to the letter. Subjects were also informed that sometimes the target letter would be absent, in which case they should not give any response. Trials in which T2 was presented but the participant failed to detect it were classified as “unseen.”
Trials started with the word “GO” (500 ms), followed by a fixation cross (1,000 ms). The rapid visual stream then started. Following the RSVP, a blank screen was presented for 3,000 ms before the beginning of the next trial. The experiment consisted of two training blocks (20 trials each) followed by five experimental blocks. In four blocks (100 trials each), subjects performed both Task 1 and 2, resulting in 80 trials by inter-target Lag condition, and in one block (50 trials) subjects performed only the visual task (i.e., irrelevant sound condition). The order of the blocks was counterbalanced between subjects. Subjects’ responses to Tasks 1 and 2, provided with their left and right middle and index fingers were counterbalanced across subjects (6/10 using left hand to respond to sounds).
MEG Recordings and Preprocessing
Subjects’ brain activity was recorded with a 306-channel whole-head magneto-encephalography system (Elekta Neuromag, 102 magnetometers and 102 pairs of orthogonal planar gradiometers) while performing a dual-task protocol. Head position was measured before each block with an isotrack polhemus system to compensate for head movements between blocks. Electro-oculogram and electro-cardiogram were continuously recorded during the experiment for offline rejection of eye movements and cardiac artifacts. Sampling rate was set to 1,000 Hz with an analog band-pass filter from 0.1 to 330 Hz. MaxFilter Software (Elekta Neuromag) was used to compensate for head movements, to interpolate bad channels, and to perform a signal space separation (Taulu et al., 2004) so as to minimize the magnetic interference external to the MEG helmet. The Fieldtrip package (Oostenveld et al., 2011) (http://fieldtrip.fcdonders.nl/) was used with MATLAB 7.11 for epoching, trial rejection, and baseline correction. Independent component analyses were applied separately to each type of sensor. To identify the components related to the cardiac artifact and to the eye movements, we computed correlations between each component and the ECG and between each component and the EOG and visually inspected their topography. Once identified, these components were subtracted out from the raw data. Signals were low-pass filtered below 30 Hz and down-sampled to 250 Hz.
Source Localizations
For each subject, an anatomical MRI (3T Siemens MRI scanner with a resolution of 1 × 1 × 1.1 mm) was acquired after the MEG acquisition. Subjects’ head was digitized and tracked within the MEG helmet in order to co-register MEG signals with subjects’ anatomy. Gray and white matters were then segmented with BrainVISA/Anatomist software tools (Geffroy et al., 2011) (http://brainvisa.info). Subjects’ head and cortical surfaces were reconstructed with the Brainstorm software (Tadel et al., 2011) (http://neuroimage.usc.edu/brainstorm/). Models of the cortex and the head were used to estimate the current-source density distribution over the cortical surface. The forward modeling was computed using overlapping spheres analytical model. Weighted minimum norm estimate (wMNE) was used for inverse modeling (depth-weighting factor: 0.5; dipole orientation constrained to be normal to the cortex).
In order to perform group analyses, we projected individual source estimate data on the standard MNI anatomical template. The contrasts between the conditions of interest were then computed. MEG signals are presented in Z scores relative to baseline and spatially smoothed over five neighboring vertices. Regions of interest (see Figure 2A) were visually defined a priori in the left and right primary auditory cortex (144 vertices), the primary visual cortex (276 vertices), and the primary motor cortex (208 vertices) with Brainstorm.
Multivariate Pattern Analyses
Time-Resolved MVPA
When comparing two experimental conditions, the difference in brain activations results in a series of specific topographical patterns at the sensor level. When applying MVPA to MEG or EEG data, it is possible to train a classifier at each time sample within each subject to isolate the topographical patterns that best differentiate the two conditions. In the present study, MVPA were applied using Scikit-Learn (Pedregosa et al., 2011). A 5-fold stratified cross-validation procedure was used for within-subjects analyses. For a given time sample, the MEG data were randomly split into 5 folds of trials and normalized (Z score of each channel-time feature within the cross-validation). The same proportion of each class was kept within each fold (stratification). A linear support vector machine (SVM [Chang and Lin, 2001]) was trained with a penalty parameter C fixed to 1 on 4 folds and tested on the left out trials in order to find the hyperplane (in this case a topography) that best separated the two classes without overfitting. A weighting procedure was applied in order to equalize the contribution of each class to the definition of the hyperplane. This procedure was iteratively applied for each time sample of each fold.
Generalization across Time
Classifiers trained at each time sample were also tested on their ability to discriminate conditions at all other time samples. The complete “temporal generalization” (King and Dehaene, 2014; King et al., 2014) results in a matrix of training time × testing time. The diagonal of this matrix corresponds to classifiers trained and tested on the same time sample. Training one classifier at time t and generalizing it time t’ was performed within the cross-validation so that t and t’ data came from independent sets of trials. An exemplary code for this temporal generalization pipeline can be found at http://martinos.org/mne/stable/auto_examples/decoding/plot_decoding_time_generalization.html.
Generalization across Conditions
In order to track Task 1-related and Task 2-related brain responses independently of each other, a series of MVPA classifiers were trained to categorize trials belonging either to the Lag 9 condition (where Task 1 was performed in near isolation) or to the Irrelevant sound condition (where Task 1 was not performed). Following the same logic, another series of classifiers were trained to discriminate trials belonging either to the Lag 9 condition (where Task 2 was performed in near isolation) or to the Distractor letter condition (where Task 2 was not performed). To evaluate how these brain responses were affected by the inter-target lag, we then applied the same classifiers to Lags 1–4 trials as well as to unseen T2 trials.
Statistical Analyses
For each test trial, classifiers generated a probabilistic output (Platt, 1999) to provide a continuous estimate comparable across subjects. Non-parametric effect sizes are reported with an area-under-the-curve (AUC) computed from the receiver operative curves (ROC), and representing predictions of true positives (e.g., a trial was correctly predicted to belong to Lag 9 condition) and predictions of false positives (e.g., a trial was incorrectly predicted to belong to Lag 9 condition). An AUC of 0.5 corresponds to chance level as it means that true positive and false positive are equiprobable. Conversely an AUC of 1 means a perfect prediction of a given class. AUC below 0.5 can occasionally be observed when classifiers are generalized across time or condition. This means that the probability of false positives is higher than the probability of true positives. In the context of M/EEG recordings, this can be explained by a reversal of the polarity of a given topographical pattern between the training time and the testing time (King et al., 2014).
Statistical analyses were performed across subjects, over a temporal window starting 200 ms before stimulus onset (either T1 or T2) and ending 1,100 ms after. We used signed rank tests with a threshold set at alpha = 0.05 to assess whether classifiers could predict the trials’ classes above the chance level (0.5). A correction for multiple comparisons was then applied with a false discovery rate (FDR).
Peak Measurement
For each subject, we measured the amplitude, the peak latency, the onset, and the offset of each classification time course. Data were first low-pass filtered at 10 Hz and the analyses were restrained to a 200–1,000 ms time window in which decoding performance was high in all experimental conditions. To measure the amplitude and the latency of the peak, we considered all time points for which the decoding performance exceeded the 95th percentile of the distribution. The median of these time points was considered as the peak latency and the median AUC as the peak amplitude. Although these estimators are not unbiased, the method allowed us to avoid numerical instabilities. The onset was defined by stepping backward from the peak and identifying the time point at which the AUC exceeded a threshold percentage of the peak. The choice of the threshold being arbitrary, we tried several values: 10%, 30%, and 50% of the difference between the mean AUC during the baseline period (from −200 ms to stimulus onset) and the peak amplitude. As the results were similar across values, we then kept the threshold to 50%. Similarly, the offset of the prediction performance was defined as the first time sample following the peak whose AUC was inferior to the threshold. In sum, this analysis resulted in four values (peak latency, onset, offset, and amplitude) for each training time that could be compared between conditions.
Statistical Analyses
The effect of the inter-target lag on these variables was evaluated at each time sample (across subjects) with Friedman tests. A correction for multiple comparisons (FDR) was then applied over time. We also directly compared peak measurements obtained from each short lag condition (1, 2, and 4) to the Lag 9 condition (see Figure 3B) with signed rank tests with FDR correction applied over time.
Supplemental Information
Supplemental Information includes four figures and can be found with this article online at http://dx.doi.org/10.1016/j.neuron.2015.10.040.
Highlights.
The brain activity was recorded while subjects performed a dual task
Multivariate pattern analyses were applied to decompose the chains brain processes
Chains of brain processes were initially parallel and then mutually exclusive
A new theoretical framework for multitasking is proposed
Acknowledgments
This research was supported by the Commissariat à l’Energie Atomique et aux Energies Alternatives (CEA), the Institut National de la Santé et de la Recherche Médicale (INSERM), the Human Frontier Science Program, a post-doctoral study grant from the Fyssen Foundation to S.M., and a senior grant of the European Research Council – the NeuroConsc program – to S.D. The Neurospin MEG facility was sponsored by grants from INSERM, CEA, Fondation pour la Recherche Médicale (FRM), the Bettencourt-Schueller Foundation, and the Région Ile-de-France. We are grateful to our reviewers for their useful comments and suggestions, to Darinka Trübutschek, Aaron Schurger, and Matthew Nelson for constructive discussions, and to UNIACT team for the recruitment and preparation of subjects.
Footnotes
Author Contributions
Conceived and designed the experiment: S.M., S.D. Performed the experiment: S.M. Analyzed the data: S.M. Contributed analysis tools: S.M., J.R.K. Contributed to the writing of the manuscript: S.M., J.R.K., S.D.
References
- Chang C, Lin C. LIBSVM: a library for support vector machines. Computer. 2001;2:1–27. [Google Scholar]
- Dehaene S, Kerszberg M, Changeux JP. A neuronal model of a global workspace in effortful cognitive tasks. Proc Natl Acad Sci USA. 1998;95:14529–14534. doi: 10.1073/pnas.95.24.14529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dell’acqua R, Jolicoeur P, Vespignani F, Toffanin P. Central processing overlap modulates P3 latency. Exp Brain Res. 2005;165:54–68. doi: 10.1007/s00221-005-2281-2. [DOI] [PubMed] [Google Scholar]
- Dux PE, Marois R. The attentional blink: a review of data and theory. Atten Percept Psychophys. 2009;71:1683–1700. doi: 10.3758/APP.71.8.1683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geffroy D, Rivière D, Denghien N, Souedet S, Laguitton S, Cointepas Y. BrainVISA: a complete software platform for neuroimaging. Python in Neuroscience Workshop (Paris) 2011 http://pythonneuro.sciencesconf.org/833/document. [Google Scholar]
- Jolicoeur P. Modulation of the attentional blink by on-line response selection: evidence from speeded and unspeeded task1 decisions. Mem Cognit. 1998;26:1014–1032. doi: 10.3758/bf03201180. [DOI] [PubMed] [Google Scholar]
- Jolicoeur P. Dual-task interference and visual encoding. J Exp Psychol. 1999a;25:596–616. [Google Scholar]
- Jolicoeur P. Restricted attentional capacity between sensory modalities. Psychon Bull Rev. 1999b;6:87–92. doi: 10.3758/bf03210813. [DOI] [PubMed] [Google Scholar]
- Kahneman D. Attention and Effort (Prentice-Hall) 1973 [Google Scholar]
- King JR, Dehaene S. Characterizing the dynamics of mental representations: the temporal generalization method. Trends Cogn Sci. 2014;18:203–210. doi: 10.1016/j.tics.2014.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King JR, Gramfort A, Schurger A, Naccache L, Dehaene S. Two distinct dynamic modes subtend the detection of unexpected sounds. PLoS ONE. 2014;9:e85791. doi: 10.1371/journal.pone.0085791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marti S, Sackur J, Sigman M, Dehaene S. Mapping introspection’s blind spot: reconstruction of dual-task phenomenology using quantified introspection. Cognition. 2010;115:303–313. doi: 10.1016/j.cognition.2010.01.003. [DOI] [PubMed] [Google Scholar]
- Marti S, Sigman M, Dehaene S. A shared cortical bottleneck underlying Attentional Blink and Psychological Refractory Period. Neuroimage. 2012;59:2883–2898. doi: 10.1016/j.neuroimage.2011.09.063. [DOI] [PubMed] [Google Scholar]
- Nieuwenstein MR, Chun MM, van der Lubbe RH, Hooge IT. Delayed attentional engagement in the attentional blink. J Exp Psychol Hum Percept Perform. 2005;31:1463–1475. doi: 10.1037/0096-1523.31.6.1463. [DOI] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, Schoffelen JM. FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci. 2011;2011:156869. doi: 10.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pashler H. Dual-task interference in simple tasks: data and theory. Psychol Bull. 1994;116:220–244. doi: 10.1037/0033-2909.116.2.220. [DOI] [PubMed] [Google Scholar]
- Pedregosa F, Weiss R, Brucher M. Scikit-learn: Machine Learning in Python. J Mach Learn Res. 2011;12:2825–2830. [Google Scholar]
- Platt JC. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. In: Smola AJ, Bartlett P, Schölkopf B, Schuurmans D, editors. Advances in Large Margin Classifiers. MIT Press; 1999. pp. 61–74. [Google Scholar]
- Raymond JE, Shapiro KL, Arnell KM. Temporary suppression of visual processing in an RSVP task: an attentional blink? J Exp Psychol Hum Percept Perform. 1992;18:849–860. doi: 10.1037//0096-1523.18.3.849. [DOI] [PubMed] [Google Scholar]
- Sergent C, Dehaene S. Neural processes underlying conscious perception: experimental findings and a global neuronal workspace framework. J Physiol Paris. 2004;98:374–384. doi: 10.1016/j.jphysparis.2005.09.006. [DOI] [PubMed] [Google Scholar]
- Sergent C, Baillet S, Dehaene S. Timing of the brain events underlying access to consciousness during the attentional blink. Nat Neurosci. 2005;8:1391–1400. doi: 10.1038/nn1549. [DOI] [PubMed] [Google Scholar]
- Sigman M, Dehaene S. Parsing a cognitive task: a characterization of the mind’s bottleneck. PLoS Biol. 2005;3:e37. doi: 10.1371/journal.pbio.0030037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tadel F, Baillet S, Mosher JC, Pantazis D, Leahy RM. Brainstorm: a user-friendly application for MEG/EEG analysis. Comput Intell Neurosci. 2011;2011:879716. doi: 10.1155/2011/879716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taulu S, Kajola M, Simola J. Suppression of interference and artifacts by the Signal Space Separation Method. Brain Topogr. 2004;16:269–275. doi: 10.1023/b:brat.0000032864.93890.f9. [DOI] [PubMed] [Google Scholar]
- Tombu M, Jolicoeur P. A central capacity sharing model of dualtask performance. J Exp Psychol Hum Percept Perform. 2003;29:3–18. doi: 10.1037//0096-1523.29.1.3. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Luck SJ, Shapiro KL. Electrophysiological evidence for a postperceptual locus of suppression during the attentional blink. J Exp Psychol Hum Percept Perform. 1998;24:1656–1674. doi: 10.1037//0096-1523.24.6.1656. [DOI] [PubMed] [Google Scholar]
- Vul E, Nieuwenstein M, Kanwisher N. Temporal selection is suppressed, delayed, and diffused during the attentional blink. Psychol Sci. 2008;19:55–61. doi: 10.1111/j.1467-9280.2008.02046.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zylberberg A, Fernández Slezak D, Roelfsema PR, Dehaene S, Sigman M. The brain’s router: a cortical network model of serial processing in the primate brain. PLoS Comput Biol. 2010;6:e1000765. doi: 10.1371/journal.pcbi.1000765. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.