Using Derivative Estimates to Describe Intraindividual Variability at Multiple Time Scales

Abstract

The study of intraindividual variability is central to the study of individuals in psychology. Previous research has related the variance observed in repeated measurements (time series) of individuals to traitlike measures that are logically related. Intraindividual measures, such as intraindividual standard deviation or the coefficient of variation, are likely to be incomplete representations of intraindividual variability. This article shows that the study of intraindividual variability can be made more productive by examining variability of interest at specific time scales, rather than considering the variability of entire time series. Furthermore, examination of variance in observed scores may not be sufficient, because these neglect the time scale dependent relationships between observations. The current article outlines a method of using estimated derivatives to examine intraindividual variability through estimates of the variance and other distributional properties at multiple time scales. In doing so, this article encourages more nuanced discussion about intraindividual variability and highlights that variability and variance are not equivalent. An example with simulated data and an example relating variability in daily measures of negative affect to neuroticism are provided.

As psychological methods have evolved, a movement has been made “to conceptualize key behavioral and behavioral change matters in more dynamical, change-oriented terms rather than the static, equilibrium-oriented terms that have tended to dominate our history” (Nesselroade, 2004, p. 45); this shift has brought with it a focus on intraindividual variability. Individual data are the combination of many different sources of variability (Nesselroade, 1991; Nesselroade & Boker, 1994). Constructs may fluctuate within days, within weeks (e.g., weekend effect), within months (e.g., hormonal effects), within years (e.g., seasonal effects), and within a lifetime. On each time scale, variables may differentially affect constructs such as mood; consider, for example, the effect of work demands on a within-day scale, global stress on a weekly scale, socioeconomic status on a monthly scale, resilience resources on an annual scale, and personality over the course of a lifetime. Some commonly used methods for modeling intraindividual change may not be ideal for modeling intraindividual variability, for example, growth curve modeling (McArdle & Epstein, 1987; Meredith & Tisak, 1990) and hierarchical linear modeling (Bryk & Raudenbush, 1987; Lairde & Ware, 1982; Pinheiro & Bates, 2000), because these fit a trend to the data and thus may average over intraindividual variability or partition this variability into the error terms of the models.

One common way that intraindividual variability has been examined is by calculating the intraindividual standard deviation or coefficient of variation (standard deviation divided by the mean) of a time series (e.g., Christensen et al., 2005; Cranson et al., 1991; Eid & Diener, 1999; Eizenman, Nessleroade, Featherman, & Rowe, 1997; Finkel & McGue, 2007; MacDonald, Hultsch, & Dixon, 2003; Mullins, Bellgrove, Gill, & Robertson, 2005). Although such studies provide initial insights into intraindividual variability, particularly as the standard deviation of a time series would seem intuitively to describe intraindividual variability, this approach is incomplete. These approaches have two limitations: (a) the standard deviation neglects the ordering of the observations, and (b) the sampling rate and time over which measurements are collected are frequently not considered, which may result in differing conclusions among researchers.

Consideration of Observation Ordering

When a standard deviation is calculated from a time series, the ordering of the information is not taken into account. To see why the ordering of observations is important, consider the following thought experiment. A researcher is interested in assessing whether three individuals differ in their variability on a construct. Three time series, such as those in Figure 1, are collected, and the standard deviation of each time series is calculated for each. These time series seem to correspond to individuals who differ in their variability; for example, Individual C might be considered more variable than Individual A. The researcher, however, will be disappointed to find that the standard deviations of each of these time series are exactly equal, as the time series consist of the same observations rearranged in different orders.

Figure 1.

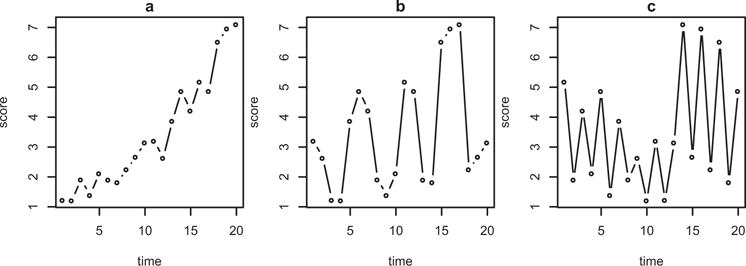
Three figures with different characteristics based on different arrangements of 20 observations. The variance of each of the three time series is exactly the same (s² = 3.64). If one calculates difference scores for each time series (x_t − x_{t − 1}), which are related to estimates of the first derivative, the variances of the differences scores differ dramatically ( $s_a^2=0.41$, $s_b^2=4.53$, $s_c^2=10.55$).

Although this likely would not occur in practice, the example highlights that standard deviation may not differentiate among individuals who appear to differ in variability. The information that the standard deviation neglects is the rate at which individuals are changing, information that cannot be captured unless one considers the ordering of the observations. Most descriptions of highly variable individuals involve not just a wide range of scores, but also high scores and low scores following each other in quick succession. That is, it is desirable to also consider the change in scores with respect to a change in time.

The change in one variable with respect to another is called a derivative. On a psychological measure, the first derivative can be used to express how quickly the scores are changing with respect to time, that is, the speed or velocity at which scores are changing. The second derivative can be used to express how quickly the first derivative is changing with respect to time, that is, whether the change in scores is accelerating or decelerating. With the first and second derivatives, the differences among individuals in Figure 1 would become apparent, because these measures take into account both the observed values and the ordering of the observations.

Consideration of Time Scale

Unfortunately, even the variance of intraindividual derivatives provides an incomplete understanding of variability. Some constructs may differentially affect other constructs depending on the time over which a time series is collected; for example, the relationship between mood variability and other constructs may differ when examined at daily versus monthly time scales. If this is the case, it is insufficient to theorize that a construct such as friend support is related to a decrease in intraindividual affect variability. Instead, the relationship between social support and affect variability may be limited to a weekly or monthly scale—social support could be less effective at mitigating hour-to-hour affect variability within the course of the work day. Consideration of the time scale over which relationships are examined could explicate differing relationships between constructs.

Time scale dependent relationships can be described by estimating derivatives, using differing numbers of observations. Consider a linear trend around which there is a short-term oscillation. By using a small number of observations to calculate derivative estimates, the short-term variability due to the oscillation can be described. This approach, however, neglects the long-term trend. Conversely, using many observations to calculate derivative estimates captures the long-term change but obscures the short-term oscillation. Calculation of derivative estimates at different time scales allows relationships that occur at differing time scales to emerge. This trade-off between being able to resolve finer detail and smoothing to enhance global features is well known in the time series literature; the principle is used in low and high pass filtering to focus on features that occur over a particular length of time (Gasquet & Witomski, 1999; Kwok & Jones, 2000; Rothwell, Chen, & Nyquist, 1998).

Multiple Time Scale Derivative Estimation

By examining the derivative estimates of a time series in addition to the observed scores, and by examining multiple time scales rather than a single time scale, researchers are able to understand intraindividual variability in significantly more detail. To accomplish this goal, it is necessary to first identify a method that can be used to estimate derivatives, using differing numbers of observations. Although several options exist (e.g., see Boker, Neale, & Rausch, 2004; Boker & Nesselroade, 2002; Ramsay & Silverman, 2005), this article uses a technique called generalized local linear approximation (GLLA; Boker, Deboeck, Edler, & Keel, in press; Savitzky & Golay, 1964). Although selection of this method is tangential to the primary objective of this article, the rationale for using GLLA includes the following: (a) it has the ability to use any number of observations to estimate a derivative (e.g., 3, 4, 5, 6, …), thereby automatically smoothing over different time scales; (b) it tends to produce a narrower sampling distribution than its predecessor (local linear approximation; Boker & Nesselroade, 2002), (c) it produces observed rather than latent estimates (e.g., Boker et al., 2004), and (d) it can be adapted to accommodate nonequally spaced observations (although we assume equally spaced observations in this article). Depending on the analytic needs imposed by one’s data, alternative choices for derivative estimation may be warranted.

The calculation of derivative estimates with GLLA, can be expressed as

$$\mathbf{Y}=\mathbf{X}\mathbf{L}{({\mathbf{L}}^{\prime }\mathbf{L})}^{-1}.$$ (1)

Matrix X is a reorganization of an individual’s observed time series and is called an embedded matrix. Matrix L is used to produce the weights that calculate the desired derivative estimates. The resulting matrix Y contains estimates of both the observed scores and derivatives of a time series.

The embedded matrix X is constructed with replicates of an individual time series that are offset from each other in time. Creation of X requires a time series X = {x₁, x₂, …, x_T} and the number of observations to be used for each derivative estimation (number of embedding dimensions).¹ If we were interested in using four observed values to estimate each derivative, X would consist of rows of four adjacent observations, with no pair of rows containing the same set of observations. For a time series with N observations, a matrix of embedding dimension four would have the form

$${\mathbf{X}}^{(4)}=\left(\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ x_2& x_3& x_4& x_5\\ ⋮& ⋮& ⋮& \\ x_{(N-3)}& x_{(N-2)}& x_{(N-1)}& x_N\end{array}\right).$$ (2)

For example, consider a time series X = {49, 50, 51, 52, 53, 54, 55, 56}, which consists of eight observations (N = 8). The embedded matrix X⁽⁴⁾, with four embeddings, would look like

$${\mathbf{X}}^{(4)}=\left(\begin{array}{cccc}49& 50& 51& 52\\ 50& 51& 52& 53\\ 51& 52& 53& 54\\ 52& 53& 54& 55\\ 53& 54& 55& 56\end{array}\right).$$ (3)

The number of embedded dimensions determines the number of observations used to calculate each derivative estimate. For additional examples related to the use of embedded matrices in psychology, see Boker et al. (2004) and Boker and Laurenceau (2006).

The L matrix produces weights that express the relationship between X and Y. Each column requires three pieces of information: (a) a vector ν consisting of values from 1 to the number of embeddings (columns in X⁽⁴⁾), (b) the time between successive observations in the time series Δ_t, and (c) the order α of the derivative estimate of interest (observed score order = 0, first derivative estimate order = 1, second derivative estimate order = 2, etc.). The values of each column can then be calculated using

$$L_{\mathit{\text{order}}}=\frac{{[{\mathrm{\Delta }}_t(\nu -\overline{\nu })]}^{\alpha }}{\alpha !},$$ (4)

where $\overline{\nu }$ is the mean of ν, and ! is standard notation for a factorial. If one wanted to calculate estimates up to the second derivative, one would use Equation 4 to calculate three column vectors (0th, 1st, and 2nd order) and to bind these vectors together to form L. For example, if one were to calculate up to the second order, using four embeddings (ν = {1, 2, 3, 4}) and Δ_t = 1,

$$\mathbf{L}=\left(\begin{array}{ccc}1& -1.5& 1.125\\ 1& -0.5& 0.125\\ 1& 0.5& 0.125\\ 1& 1.5& 1.125\end{array}\right).$$ (5)

It should be noted that the number of embeddings must be at least one greater than the maximum derivative order examined; this is related to the fact that calculating a linear or quadratic trend requires a minimum of two and three observations, respectively (Singer & Willett, 2003, p. 217). In addition, even if one is interested only in a higher order derivative, columns for all lower order derivatives must be included in L.

Using Equation 1 and the X and L that have been generated, one can calculate

$$\mathbf{Y}=\mathbf{X}\mathbf{L}{({\mathbf{L}}^{\prime }\mathbf{L})}^{-1}=\left(\begin{array}{ccc}50.5& 1.0& 0\\ 51.5& 1.0& 0\\ 52.5& 1.0& 0\\ 53.5& 1.0& 0\\ 54.5& 1.0& 0\end{array}\right).$$ (6)

The first, second, and third columns correspond, respectively, to estimates of the observed scores and the first and second derivative for each row of X. The estimates of observed scores are equal to the average for the observations in each row of X. The first derivative estimates, which are all equal to 1.0, indicate that for all rows, the scores are changing one unit with each one unit increase in time; this is equivalent to the slope within each row. The second derivative estimates are all equal to zero, indicating that within each row, the rate at which scores are changing is neither accelerating or decelerating.

Using GLLA Derivative Estimates

When using GLLA to calculate estimates of observed scores and derivatives at multiple time scales, subsequent analysis steps could proceed much as in previous studies and depending on the questions of the researcher. The primary change that occurs is a need for more specific hypotheses regarding intraindividual variability. A hypothesis would need to include the order of the derivative estimates, the distributional property that would be examined, and the time scale over which relationships are expected. One might hypothesize, for example, that more neurotic individuals tend to show higher variance in the first derivative estimates of negative affect over time scales of several days. Such a study would regress estimates of neuroticism against estimates of first derivative variance at a range of daily to weekly time scales.

The selection of the order of derivative estimates to examine depends on the statement one hopes to make about intraindividual variability. (For now, we focus on examining the variance of a distribution and ignore the specific time scale at which relationships may be observed.) A researcher who believes that a trait may relate to individuals using a wider or narrower range of scores on a scale would be able to examine such a relationship by using the variance of the observed scores. A researcher who believes a trait may relate to some individuals not changing much between two occasions and other individuals having rapid increases and/or decreases in score would be able to examine such a relationship by using first derivative estimates: The first derivative expresses the rate of change, or velocity, of scores; therefore, low variance would correspond to a small range of velocities, whereas high variance would correspond to a large range of velocities. A researcher who believes a trait may be related to whether individuals show quick increases in scores followed by quick decreases (or vice versa) would be able to examine such a relationship by using the second derivative estimates. The second derivative, or acceleration, is highest when scores either rapidly increase and then decrease or vice versa. Individuals with high variance in second derivative estimates would show a wide range of accelerations, whereas individuals with low variance would show more consistent acceleration.

Variability and Variance

It is also important to distinguish between variability and variance. Variance is one distributional property that could be used to describe intraindividual variability, but other distributional properties, such as skewness and kurtosis, may also be informative. When applied to observed scores, differences in skewness and kurtosis take on the expected interpretations; however, these alternative distributional properties offer unique substantive interpretations when applied to derivative estimates rather than the observed scores. Consider a time series with little overall trend. When the distribution of first derivative estimates is positively skewed, this would suggest an individual who exhibits only a few large positive slopes and but many smaller negative slopes. This person would appear to quickly become very distressed and would require much more time to slowly reduce his or her distress. When the distribution of first derivative estimates is negatively skewed, this would suggest an individual who exhibits many smaller positive slopes and only a few large negative slopes. This person would appear to require a lot of time to build up distress but would then be able to quickly alleviate distress by blowing off steam. It would be interesting to see if a trait could be used to predict individuals who display first derivative estimates with more positive or negative skew.

The kurtosis of the first derivative estimates also offers an intriguing avenue for characterizing intraindividual variability. Consider an individual with a leptokurtic distribution, which would correspond to many more small changes over time (peaked) and a few extra very large changes over time (additional observations in tails). An individual with a platykurtic distribution would display fewer very large changes over time and fewer small changes over time, primarily showing moderate changes most of the time. This first person, then, would appear not to change their distress level very much from day to day (fairly consistent amount of distress), although occasionally large positive and negative changes occur (e.g., days punctuated with good/bad luck). The second person, however, does not have the extreme changes and also has many fewer days with small changes in distress. Rather, this second person’s distress level changes by a more moderate amount almost every single day (e.g., most days a new drama arises).

In practice, we cannot assume that distributional properties, such as the mean of the first derivative, are, on average, equal to zero for all individuals. Consequently, when interpreting the results from a particular distributional property, the lower distributional properties must be kept in mind. For example, imagine that one finds that a trait is related to variance of the first derivative estimates. Individuals may still have differing means for the first derivative estimates; that is, some individuals may have an upward trend, and others may have a downward trend. The relationship between the trait and variance conveys only information regarding the variance around each individual’s central tendency. Similarly, if a significant relationship were shown between a trait and skewness, this would not rule out the potential that within individuals high and low on the trait, there could be a variety of distributions with differing means and variances. Consideration of this point is further discussed in the applied example.

Relationship to Time Series Methods

Using GLLA to estimate derivatives can be broadly categorized into the class of linear filters that are common in much of the time series analysis and signal-processing literatures (Gasquet & Witomski, 1999; Gottman, 1981). In signal processing, linear filters are often used to eliminate frequencies or components that may be undesirable, such as those associated with noise. For example, the time scale over which derivatives are estimated serves a function similar to that of low and high pass filters. Unlike typical linear filters, however, we are not utilizing the filters merely to remove a component, such as noise, from the data. GLLA derivative estimates focus on a specific time scale depending on the embedding dimension and time lag selected. By focusing in this way, we purposefully attempt to extract a derivative estimate at a particular time scale.

When estimating the 0th order derivatives, that is, the observed scores, the estimates produced by GLLA are similar to those of moving average algorithms. It is the use of filters corresponding to higher order derivatives that should be of particular interest in psychology. Rather than decomposing a signal into components, such as sine waves, a derivative filter literally provides information about how people are changing at a particular time scale. This substantive interpretation, which seems to map well onto how people discuss individual changes over time, motivates the selection of this particular filter.

Proposed Application

The combination of derivative estimates selected and distributional properties examined should directly relate to a researcher’s conceptualization of variability. This poses the question for theory: What does high intraindividual variability mean? Although answers are seemingly intuitive, consider the following example. You are told that someone you know is a driver with high intraindividual variability. One way a driver could show large variability is by having large variations in the distance from home that person drives on any given occasion (high variance in observed scores). The driver also could display a great deal of variance in his or her speed by using the entire range on the speedometer (high variance in the first derivative). That person also could have large variance in speed changes by slamming on the brakes or flooring the gas pedal (high variance in the second derivative). Because of the variety of possible interpretations, there is a need to be more specific when conceptualizing intraindividual variability.

We utilize GLLA as one of several possible methods to produce derivative estimates with a range of time scales. The analysis of the distributional properties of derivatives across multiple time scales will be referred to as derivative variability analysis (DVA). In the following sections, we pose questions such as the following: At what time scales (daily? weekly?) are individuals who are higher/lower on some trait more variable in their time series scores and derivative estimates? The first application consists of a simulation study, in which two types of time series are created. To each of these time series are added random events, the amplitudes of which are related to a traitlike variable. Analysis of these data demonstrate the ability of derivative-based analyses at multiple time scales to detect this relationship and the time scale at which it occurs. In the second application, we apply the method described to examine the relationships between intraindividual variability in negative affect and the trait of neuroticism.

Application 1: Simulation Study

We first consider an example with simulated data. Unlike typical simulations, we do not seek to define the parameter space over which a statistic is applicable. Rather, we create two different types of trajectories composed of many different, overlapping sources of variability, which are used to generate individual time series. Within the variability and measurement error of each time series is a component of the intraindividual variability that relates to a trait variable. With these examples, we explore whether DVA can be used to detect the portion of the intraindividual variability related to the trait variable, even though it is highly obscured.

For this simulation, time series are created with known characteristics. The variance of the observed scores of the time series and the variance of estimated derivatives are examined in relation to an exogenous predictor. The simulation demonstrates that some relationships may not be apparent in observed score variance but can be observed when using the variance of derivative estimates. The simulation also demonstrates that relationships occurring at specific time scales can be highlighted with DVA.

Methods

Simulated Data

Two very different types of time series were examined; the parameters selected for these time series are arbitrary, but this does not alter the substance of these examples. The first type of time series consisted of the linear combination of four sources of variability, which can be imagined to correspond to a construct that consists of an overall trend, with an approximately monthly oscillation that occasionally changes phase, combined with a few random life events that perturb the system for about a week, plus measurement error.

The oscillating trend was selected such that it would correspond to a cycle longer than 1 month, assuming that the space between observations is equal to 1 day. The oscillating trend was defined with 5 × sin(ω × time + δ), in which ω ~ N(0.15, 0.02); the 95% confidence interval for ω corresponds to cycles of 33.2 to 56.7 days. The parameter δ equaled 0 at t = 1 and had a 5% chance at each subsequent point in time of randomly resetting to a value drawn from a uniform distribution bounded by 0 and 2π; the reset chance of 5% was selected to represent a moderate probability of a serious disruption occurring on any particular day. The second source of variability, a linear trend, had a slope randomly drawn from a normal distribution with mean of 0 and standard deviation of 0.13. The mean of 0 was selected to allow for both positive and negative slopes. The standard deviation was selected such that the contributions of both the oscillating trend and linear trend were similar in amplitude for many time series; the oscillation has an amplitude from −5 to 5, whereas time series at one standard deviation from the mean on slope is expected to change 13 points over the 100 observations observed. The third source of variability consisted of randomly placed events that perturbed the system for about 7 days; this particular length was selected with the intention of representing a moderately disruptive event in one’s life. We used approximately one half of an oscillation to create this perturbation, defined by the equation sin(0.53 × t_w), where t_w = {0, 1, …, 6}, and 0.53 corresponds to the approximate ω value required for one half of a cycle of the desired length. The events were multiplied by a random uniform distribution consisting of the values −1 and 1, to allow for both positive and negative perturbations. Finally, independent, normally distributed errors were added to each time series with a mean of 0 and a standard deviation of 12.4, corresponding to a signal-to-noise ratio of approximately 5 to 1; these values were selected to represent a scale with reasonable reliability. Figures 2a and 2b depict two examples of these simulated data.

Figure 2.

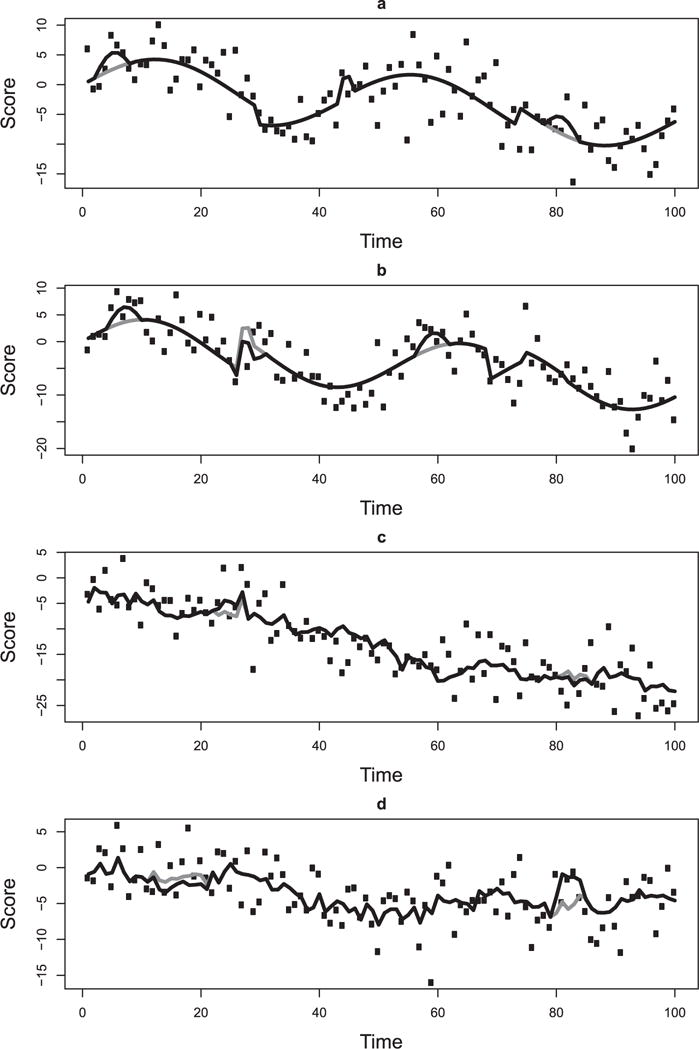
Examples of the data generated for the simulation study in Application 1. The points, which include the true signal plus error, are the data that would be analyzed. The black line represents the true scores. The gray parts of the line represent the original trajectory, before the random events were added to the trajectories. Examples of times series generated by overlapping sources of variability are shown in a and b, whereas c and d correspond to time series generated with an autoregressive process.

The second type of time series consisted of a linear combination of three sources of variability, which can be imagined to correspond to a construct where today’s value is highly related to yesterday’s value and somewhat related to the value of the day before, a few random life events that perturb the system for about a week, plus measurement error. The first source was a second-order autoregressive process, that is, x_t = a₁x_t−1 + a₂x_t−2 + γ_i. The random variable γ_i, often called the innovation, was drawn from a normal distribution with a mean of 0 and a variance of 1. The autoregressive parameters a₁ and a₂ were set to 0.7 and 0.31, respectively; in selecting these parameters, the considerations were that a₁ should be relatively large, such that adjacent observations are moderately to highly correlated, and that a₁ + a₂ > 1, so that the process would not be stationary. The second and third sources of variability, randomly placed events and independent normally distributed errors, were specified exactly as they were in the overlapping variability time series described earlier. Figures 2c and 2d depict two examples of these simulated data.

For both types of times series, each individual time series was paired with a value y_i drawn from a normal distribution (μ = 3, σ = 1). Two conditions were considered for each type of time series. In one condition, the amplitude of the randomly placed events for a particular time series was multiplied by the value y_i. In the other condition, the amplitude of the randomly placed events for a particular time series was multiplied by a value randomly drawn from the same distribution as y_i. In the first condition, the time series should display a small amount of additional intraindividual variability related to the trait variable y. In the second condition, no such relationships should occur. Moreover, because we know that the events are about seven observations in length, this is the time scale at which observation of relationships between the time series x variability and the trait score y are expected.

To be able to examine the expected results in the long run, a sufficiently large number of time series and single trait score sets must be analyzed. We examined 50,000 sets, with the assumption that this was sufficiently large, for each of the four conditions: overlapping variability related to trait, overlapping variability unrelated to trait, autoregressive related to trait, and autoregressive unrelated to trait. Time series were each 100 observations long. We analyzed each of the four groups as a single sample, using the procedure described in the next section. Although it would be unusual to acquire such a large sample, the analysis results should reflect the central tendency of expected results if this simulation were replicated with many smaller samples.

Analysis

The following outlines the broad conceptual steps that are taken in applying DVA to the simulated data and later to the set of applied data. Readers interested in applying DVA are referred to Appendixes A and B, which include R syntax and a detailed description of how to apply the syntax (R, 2008). This analysis focuses on applying the ideas from the introductory section, that is, applying DVA in the context of correlating properties of time series with a specific trait; DVA could be adapted to consider other derivatives, distributional properties, time scales, and even the relationships between two time series.

Step 1

Researchers should begin by selecting the conditions to be studied, including (a) the embedding dimension or dimensions, (b) the order of the derivatives, and (c) the distributional property or properties. First, when selecting embedding dimensions, researchers should consider several factors. On the low end, an embedding dimension of 3 is required for estimation of derivatives up to the second derivative. The highest recommendable embedding dimension depends on the length of the time series and the amount of missing data. Note that when using GLLA, an embedding dimension of 10 requires 10 consecutive observations to estimate a single derivative; several estimates are required to produce an estimate of a distribution. Consequently, even small amounts of missing data can rapidly reduce the number of estimates that can be generated from the data. It is important to consider the number of estimates that are produced by GLLA for each individual for a particular embedding and the number of individuals for whom enough estimates can be produced such that a distributional property can be examined.

Second, researchers should decide on the order of the derivatives to be examined; as described in the introductory section, the selection of the derivative order should be related to a researcher’s conceptualization of intraindividual variability—whether conceptualized as variability in observed scores, the rate at which scores change, or the rate at which scores accelerate and decelerate. Third, the distributional property to be examined must be selected. As discussed in the introductory section, the choice of distributional properties should also relate to a researcher’s conceptualization of intraindividudal variability, whether just variance or also including features such as skewness and/or kurtosis. For the simulated data example, the variance of the observed scores and first derivative estimates are examined. The embedding dimensions were selected both to encompass the length of the random events related to the trait of interest and to mimic the analysis of the applied data example; embedding dimensions from 3 to 30 are examined.

Step 2

The next step is to calculate a distributional property for an order of derivative at a particular embedding for each individual time series. Because each combination of distributional property, derivative order, and embedding dimension must be considered as an individual set of conditions, let us consider a specific example in which the variance of the first derivative estimates is being calculated for a specific embedding dimension. For example, let us assume that we are calculating values associated with an embedding dimension of 10. For each individual time series, one creates an embedded matrix X_i. GLLA, as described in the introductory section, is then used to produce the matrix of derivative estimates, Y_i. From Y_i the column corresponding to the first derivative estimates is selected. The variance can then be calculated from these estimates. The process of embedding matrices and calculating a distributional property is performed for each individual time series. The result is one estimate per individual, where the estimate equals a distributional property of interest, for a particular derivative order, at a particular embedding.

Step 3

The previous step produces a vector of estimates N individuals in length, which can then be correlated with a vector of trait scores for the corresponding individuals. For the specific example in Step 2, the resulting correlation addresses whether a trait is related to the variance of first derivative estimates at a time scale equivalent to the time spanned by 10 observations (i.e., an embedding dimension of 10). Correlations have been selected in the current article because of their interpretability; however, other applications of these methods may warrant the calculation of other statistics (e.g., slope estimates); regardless of the statistic selected in this step, the other steps for analysis remain unchanged.

Step 4

The standard errors produced when calculating a correlation may not be accurate when using DVA, because the assumptions may be violated. Consequently, hypothesis tests and confidence intervals produced by statistical programs should be ignored when using DVA. Rather, the bootstrap should be used to calculate confidence intervals that do not require distributional assumptions, that is, nonparametric confidence intervals. (Efron & Tibshirani, 1994). To bootstrap the data, pairs of variability and trait estimates are randomly drawn from the original data, with replacement, to form a bootstrap sample. The correlation is then calculated on this sample, and the process is repeated a large number of times, such that a distribution of correlations is formed.² In the example provided, the percentile confidence intervals are reported; for a 95% confidence interval, this method requires one only to sort the results from the boot-strap samples and select the upper and lower values for the middle 95% of the distribution.³

DVA will typically involve a large number of statistical tests, because correlations are calculated for each embedding dimension multiplied by the number of orders of derivatives and the number of distributional properties considered. Therefore, applications of this method should adopt stricter criteria than the typical 95% confidence interval to limit the frequency of Type I errors; not doing so could produce a large number of Type I errors and consequently mislead researchers. Until further research is done, we encourage the use of the conservative Bonferroni correction (α = .05/comparisons) to maintain the Type I error rate at .05 within each family of comparisons (Maxwell & Delaney, 2000). We have selected a family of comparisons to consist of all of the comparisons within a particular derivative order and distributional property, that is, all the tests conducted across the range of embedding dimensions. With the range of embedding dimensions selected for the simulation, 3 to 30, there are 28 tests conducted for each combination of distribution property and derivative order. Our corrected α level would then be equal to .00179 (.05/28), and we would form a 99.82% confidence interval for each embedding. Consequently, the probability of making a Type I error for the 28 comparisons is still equal to or less than .05. As with all statistical tests, researchers are encouraged to judiciously select a priori the tests to be performed; such a choice determines the extent to which results can be considered confirmatory, rather than exploratory.

Step 5

In Steps 2 through 4, focus was placed on calculating the correlation and confidence intervals for one specific combination of distributional property, derivative order, and embedding dimension. Step 5 is to repeat the process for each combination of conditions that were selected in Step 1.

In summary, the steps involve the following: (a) select distributional properties (variance, skewness, kurtosis), derivatives (observed score, first derivative, second derivative), and time scales (embedding dimensions) for analysis; (b) for a specific derivative and time scale, calculate a distributional property for each individual; (c) calculate the correlation or statistic of interest between a trait and the estimates from Step 2; (d) use a nonparametric procedure and a multiple-testing procedure to get accurate confidence intervals; and (e) repeat for all combinations of distributional properties, derivative orders, and time scales selected in Step 1.

Results

Figure 3 shows the DVA results for both types of time series. Although a typical application of DVA would include confidence intervals, they are not shown in the figure because the lines are expected to reflect the results in the population due to the simulation design.⁴ The upper and lower pairs of graphs correspond to the conditions in which the trait y are, respectively, unrelated and related to the amplitude of the random events added to each system. If we had regressed the trait against estimates of the standard deviation of time series, the results would be most similar to the results for the observed scores (solid line) at the lowest embedding dimension. That is, commonly used analyses would be the equivalent of only one point on one of the lines that we have shown, ignoring a substantial amount of potentially interesting information.

Figure 3.

Correlation for a given embedding dimension between trait scores and variance of the observed scores (line), first derivative estimates (filled circles), and second derivative estimates (open diamonds). The upper two panels correspond to the condition in which the trait and random events are unrelated. In the lower two figures, the trait and amplitude of the random events are related.

Using DVA, no relationships were expected when the trait and the event amplitude were unrelated, as observed in the upper pair of graphs. Relationships were expected when the trait and the event amplitude were related, as observed in the lower pair of graphs. When the trait is regressed on the observed score variance, these relationships are not apparent because of the many other sources of variability in each time series. The variances of the first and second derivative estimates reflect that there is a short-term relationship between the trait and the intraindividual variability; this result was present in each of the two types of time series that were simulated, suggesting that the result is not unique to a type of time series. In creating the time series, the random events were created to be 5 to 7 days in length. This feature of the data seems to correspond well with the peak of the relationship observed in the first derivative estimates. The peak of the relationship with second derivative variance is less well defined than that with first derivative variance; this is likely to be related to the variance of the sampling distribution of the second derivative estimates as well as the shape of the random events added to each system.

Conclusions

Although simulated data were used, this application highlighted several aspects of DVA. First, it demonstrated the examination of the relationship between a trait and a particular distributional property (variance) of different derivatives (0th to 2nd order) over multiple time scales (3 to 30 embeddings). Second, the results highlight the possibility that differing relationships can be observed depending on the derivative order and time scales examined. Third, examination of the standard deviation or coefficient of variation of the observed scores would yield results similar to the lowest embedding for the observed score variance; those result suggests that no relationships exist between the trait and time series.

Specification of the time scale, derivatives, and distributional properties impacts the conclusions one can draw about relationships with other constructs when examining intraindividual variability. It is tenable that relationships in applied research may occur at specific time scales. For example, if one considered the relationships between intraindividual variability on stress and the personality trait of dispositional resilience (Maddi & Kobasa, 1984), the application of DVA might suggest whether lability in stress is related to dispositional resilience, and whether these effects are universal or whether they occur at some specific time scale (e.g., daily, weekly, or monthly). It might be that the ability to shift efficiently between mood states in the shortterm is adaptive but that maintaining this lability over time may cease to be helpful and may even be related to poor psychological functioning when considered over a longer time span.

It should be noted that even events of a specific length in time will alter the estimation of derivatives at both longer and shorter time scales; consequently, adjacent embedding dimensions tend to produce similar correlation estimates. This blending of time scales is important to keep in mind when considering results, because the time scale of a relationship may actually be narrower than portrayed with DVA based on GLLA. Future research may better illuminate the conditions under which differing derivative estimation techniques may be used for more precise estimation of the time scale of a relationship.

Application 2: Applied Data Example

This applied example, exploring the relationship between neuroticism and negative affect, demonstrates the information that can be garnered with DVA. Given that neuroticism is defined either as an inherent propensity to experience negative affectivity or as a greater tendency for emotional lability (Costa & McCrae, 1980), the example examines the relationships between a trait measure of neuroticism and daily intraindividual variability in negative affect. Research has resulted in considerable debate surrounding these variables; some authors have proposed that there is conceptual and measurement overlap in neuroticism and negative affect (Ormel, Rosmalen, & Farmer, 2004) or negative affectivity (Fujita, 1991; Watson & Clark, 1984), suggesting redundancy in the constructs. That is, neuroticism is highly correlated with an individual’s typical level of distress. Others have considered predictive relationships among the constructs, implying that the constructs are related but are not the same (Bolger & Zuckerman, 1995; Mrocek & Almeida, 2004). In other words, neuroticism may make people more vulnerable to the negative consequences of stress, an indirect rather than a direct, effect (Suls & Martin, 2005). Using DVA, we can ultimately disentangle the extent to which neuroticism relates to level of distress (negative affect) or to volatility (change in negative affect) and whether the relationship between these constructs changes over a variety of time frames.

Methods

Participants

Participants were a subsample from the Notre Dame Longitudinal Study of Aging (see Wallace, Bergeman, & Maxwell, 2002, for details). Following the initial questionnaires assessing various aspects of the aging process, participants were invited to participate in a 56-day daily diary study. Of the 86 people invited, 66 (77%) participated in the daily data collection. The individuals who provided daily data were, on average, 3 years younger than those who declined to participate (t = 2.17, p < .05), but there were no significant differences by gender, race, marital status, or living situation (e.g., alone or with others). The participants who participated in the daily data collection were predominantly older (M_age = 79 years, SD = 6.21 years), female (75%), living either alone (54%) or with a spouse (45%), educated (98% through high school, 61% some post-high school), and White (90%; 5% African American, 5% Hispanic).

Measures

Daily negative affect was measured with the Positive and Negative Affect Schedule (Watson, Clark, & Tellegan, 1988). Participants were asked to select from a 5-point scale for each of the 20 affect items, examples of which include “irritable,” “distressed,” “attentive,” and “inspired.” Internal consistency reliability assessed on Day 1 was high (Cronbach’s α = .85). The sum of the 10 negative items on any given day was used as an index of negative affect, with higher scores indicating more negative affect. Daily data were collected over 56 days, with 1-, 2-, and 3-week packets counterbalanced within and between subjects.

Neuroticism was assessed with a subscale of the Revised NEO Personality Inventory (Costa & McCrae, 1991). The 12 items were scored such that higher scores indicated higher levels of neuroticism. Internal consistency reliability was high (Cronbach’s α = .88).

Analysis

In these analyses, the distributional properties variance, skewness, and kurtosis were examined with both observed score and the first derivative estimates. Estimates were examined from an embedding dimension of 3 days (the shortest value possible with GLLA if allowing for estimates up to the second derivative) to an embedding dimension of 30 days (approximately the longest value that seemed advisable given the length of the data and the presence of missing observations). As with the simulation, for each individual time series an estimate was made for each combination of distributional property (3 levels), derivative order (2 levels), and embedding dimension (28 levels; i.e., the number of embedding dimensions from 3 to 30). Each combination of estimates (e.g., skewness of the first derivative at an embedding dimension of 12) was then correlated with the neuroticism measure. Because of potential violations of assumptions, standard errors produced for the correlation estimates may be inaccurate. Therefore, we used bootstrapping to generate confidence intervals for each correlation. We required a minimum of 5 observed scores or derivative estimates to estimate a distributional property for an individual; this is very close to the minimum number of observations required to estimate kurtosis and may lead to poor estimates of distributional properties. A low minimum was used to include as much of the sample as possible, even at higher embedding dimensions, at the cost of larger standard errors around distributional estimates.

Because of the large number of relationships being examined (3 × 2 × 28 = 168 tests), there was a very high probability of making a Type I error. Each combination of distributional property and derivative order was therefore treated as a family of analyses (3 × 2 = 6 families). Within each family, each of the 28 comparisons was made with a 99.82% confidence interval. This confidence interval corresponds to the Bonferroni corrected alpha to maintain a familywise Type I error rate of .05 for 28 independent tests (Maxwell & Delaney, 2000), which is overly conservative in this case because tests within family are correlated. By using the 99.82% confidence interval in this example, the sum of all of our tests should be equivalent to conducting only 6 statistical tests with an alpha much less than .05. Percentile confidence intervals were generated with 100,000 pairwise bootstrap samples of the data within each combination of distributional property, derivative order, and embedding dimension (see footnote 2).

Results

Figure 4 plots the results for each combination of conditions, with the six graphs each corresponding to a combination of derivative order and distributional property. The confidence intervals suggest only a few occasions when the correlations between negative affect distributional properties and neuroticism significantly differ from zero; these are in the skewness of the first derivative estimates at an embedding dimension of 25, the kurtosis of the observed scores at an embedding dimension of 10, and the kurtosis of the first derivative estimates at embedding dimensions of 7, 9, 10, and 12. In interpreting the results, two cautions are recommended. The first is for the results consisting of a singular significant observation (skewness first derivative estimates of 25, and kurtosis observed score estimates of 10). It is odd that the adjacent values are not also significant, and so these results may be due to some chance fluctuation; that being said, these may be areas that could be more likely to produce significant results in future research. The second caution is that null results should be interpreted with caution, because these results have a high probability of being Type II errors given the Type I error corrections.

Figure 4.

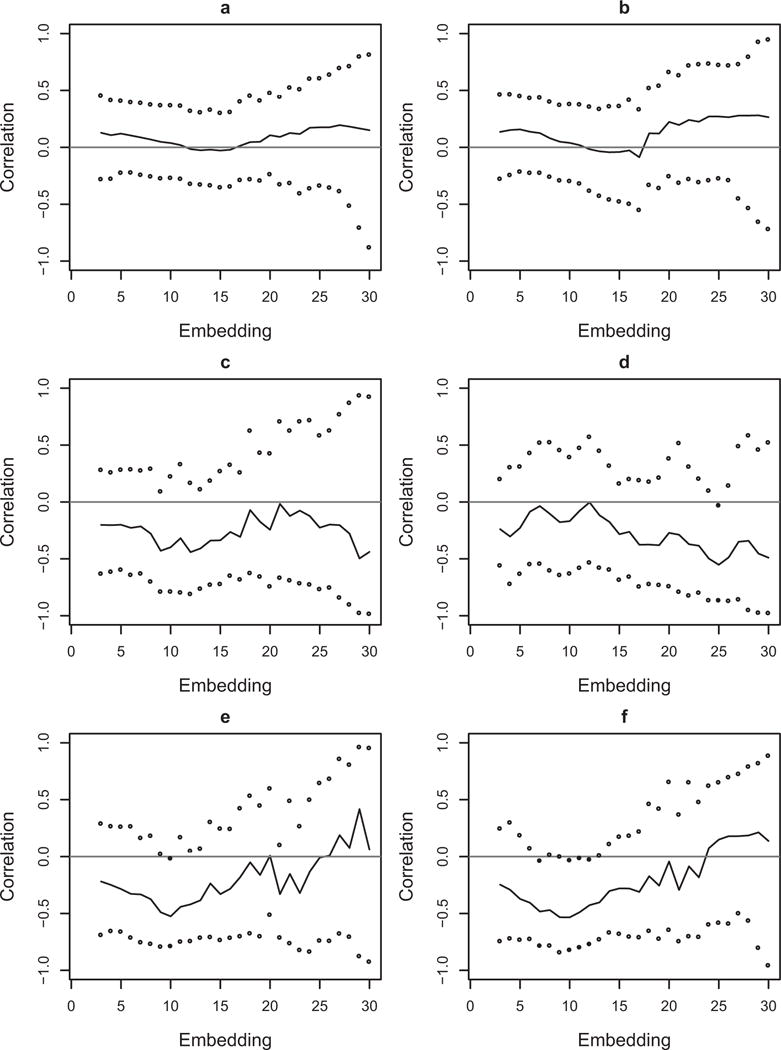
These figures represent the correlations (solid line) and 99.82% confidence intervals (circles) for observed scores (panels on the left) and first derivative estimates (scores on the right). The three rows correspond to the distributional properties variance, skewness, and kurtosis, respectively. Filled circles represent confidence intervals that do not contain zero. A horizontal line is provided at a correlation of zero for visual reference.

The kurtosis of the first derivative estimates suggest a relationship not apparent in the other distributional properties or in the observed scores. These results suggest a negative correlation between the estimated kurtosis of first derivative estimates of negative affect and neuroticism. Of the 7 embeddings that are near the zero correlation line (embeddings 7 to 13), four of the confidence intervals do not contain zero. Given the correction used on the confidence intervals, the probability of a Type I error rate has been controlled to be much less than .05 for the entire set of 28 tests; the probability of four significant results by chance is extremely small. These results suggest that at a weekly time scale, as neuroticism increases, the first derivative estimates tend to become more platykutic, whereas as neuroticism decreases, the first derivative estimates tend to be more leptokurtic. More neurotic individuals typically have distributions that include more moderate rates of change over most weeks, compared to less neurotic individuals, who experience smaller amounts of change on a weekly basis with the occasional more extreme change. Individuals with high or low neuroticism may still differ greatly in their means, variances, and skewness.

Conclusions

The results provide some interesting information regarding the conceptualization of neuroticism. On the basis of the definition of neuroticism, it was expected that the variance of the observed score or first derivative estimates would be correlated with neuroticism, particularly at shorter time scales. Because the results do not suggest such a relationship, it is unclear whether there is no such relationship, or whether this is a Type II error. Of interest, a result was observed at short time scales in the kurtosis of the first derivative estimates, which is concurrent with the definition of neuroticism. The results suggest that less neurotic individuals, relative to their mean rate of change, tend to have more weeks with small change and the occasional larger change. More neurotic individuals, however, are more likely to have moderate amounts of change each week (most weeks a new drama arises), relative to their mean rate of change.

It should be cautioned that individuals both high and low in neuroticism may have differences in their means, variances, and skewness. Therefore, in interpreting the data, it is possible that one neurotic individual may have scores with a positive trend, and another may have scores with a negative trend; the kurtosis results cannot inform us of this but can inform us that around each individual’s central tendency (whether positive or negative), the rates of change tend to be distributed around that trend in a more heavy-shouldered distribution compared to that of a less neurotic individual.

For contrast, one may consider regressing neuroticism against the standard deviation of each individual time series, as has been done in previous studies of intraindividual variability. With the results presented, one does not need to conduct this analysis, because the results should be very similar to those for the variance of the observed scores at the lowest embedding dimension—that is, the first point on Figure 4a. Although one would have additional power if conducting only a single statistical test, from the other figures it is clear that there is significantly more information that can be garnered from a time series. Given the cost and time associated with the collection of psychological data, it is important to learn as much as possible from these time series.

There are several limitations to the present work, several of which must be considered in all statistical applications but which are explicitly stated here because of the method’s novelty. First, one must be cautious about the interpretation of the correlations without regard to the confidence intervals because this may lead to misinterpretation or overinterpretation of results. As distributional properties, such as variance, are often skewed, spurious results can occur because of factors such as bivariate outliers; therefore, the calculation and interpretation of bootstrapped confidence intervals are important to deal with potential issues with distributional properties. Second, the results are subject to standard correlation assumptions, namely, that the errors in measurement of the two constructs are uncorrelated and that the constructs have a linear relationship. Third, for proper interpretation of results, it is critical that one considers the Type I error rate, power due to sample size, and the number of statistical tests performed. We have presented and suggested a conservative approach that is unlikely to yield Type I errors but could result in many Type II errors. Fourth, the current sample had 66 people measured on 56 days. This study is likely to have low power. Power for such studies could be increased by carefully selecting which statistical tests are conducted, such that less correction is required to avoid Type I errors, collecting multivariate indicators, and increasing either sample size or time series length.

The results presented here are unique from other applications where the standard deviation or the coefficient of variation of an entire time series is used to represent intraindividual variability. The information related to time scale of relationships will be helpful in designing future studies, because valuable research resources can be saved by sampling at rates corresponding to the relationships of interest. Through the richness of interpretation by examining multiple distributional properties, combined with derivatives, theory can move away from discussing individuals as more variable and discussing specifically how they are more variable (i.e., over which time scale? in their scores or derivatives? in their variance, skewness, or kurtosis?).

General Discussion

As research progresses toward a better understanding of the interface between method and theory, the understanding of intraindividual variability has moved toward a dynamic conceptualization of change (Nesselroade, 2006). Although fields such as developmental psychology have often described long-term trends in adaptation to life’s demands, increasingly the challenge is to understand intraindividual variability around those trends. Because, presumably, those long-term trends result from constituent experiences (e.g., momentary, daily, weekly, etc.), a natural scientific progression might be to unite findings across levels of analysis, investigating how daily life experience corresponds to the well-documented macroscopic trends observed with traditional developmental methods.

Examination of the distributions of derivative estimates provides a methodology that will begin to untangle the complexity of intraindividual variability. DVA highlights the importance of specifically considering the time scales at which relationships occur. Through the examination of derivative estimates, DVA detects relationships that might otherwise be obscured by other sources of variability. Furthermore, through the examination of distributional properties in addition to variance, nuanced understanding can be gained about differences in how different individuals change over time.

The applications of DVA and the theoretical insights that may result are much broader than the trait-state variability relationships presented. DVA could illuminate relationships between daily process and life span changes. This could be accomplished by melding the concepts presented in this article with the life span modeling ability of techniques such as hierarchical linear modeling. One could then address questions regarding how the regulation of daily fluctuations is related to long-term outcomes. DVA would also allow for the consideration of coupled time series more broadly than is currently available with other methods, including larger numbers of simultaneously coupled variables or consideration of constructs that may differentially affect each other at different time scales. The conceptual underpinnings of DVA can also be expanded in the future to accommodate unequally spaced data, because derivative estimation does not require equidistant observations.

DVA also has the potential for far-reaching consequences in informing theory. These include probing the relationships between traits and states or between short and longer term intraindividual variability, informing the conceptualization of constructs, and refining investigation of process-oriented models of change. The application of DVA concepts is primarily constrained only by the type and way in which data are collected, including the sampling rate and the length of time series collected.

Weekly measures, for example, allow for estimation of the second derivative with only 3 or more weeks; consequently, weekly measures allow for statements at only approximately monthly scales or longer, depending on how long data are collected. Because these limitations are inherent to study design, rather than to the concepts presented, the flexible nature of DVA is likely to encourage more creative sampling of constructs that change.

The information DVA provides may also be valuable in understanding how to pick a model to describe intraindividual variability. In many areas of psychology, researchers begin to understand the relationships between variables through the examination of correlations. Differing distributional properties over time may motivate the selection of one model over another; the time scale over which relationships with exogenous variable occur may also inform how exogenous variables should be included in a model. As an increasing diversity of methodologies for modeling intraindividual variability become available, the translation of DVA results into models should become increasingly apparent.

As psychologists move toward more dynamic understandings of change over time, additional methodological advances will be required to untangle the many sources of variability that contribute to observed time series. Methods flexible enough to allow for the examination of relationships at multiple time scales and methods able to identify and partial out variability of interest will become increasingly important as researchers try to disentangle antecedents, correlates, and sequelae of—as well as relationships between—long-term trends and short-term variability. DVA provides a tool for the understanding of intraindividual variability that parallels the first step taken in most psychological research: gaining nuanced understanding of the correlations between constructs. By providing a tool to further understand intraindividual variability, DVA will help inform both the collection of data (i.e., ideal sampling rates for particular relationships) and the modeling of data. Novel methods, such as those presented here, will allow psychological research to consider the causes, effects, and interrelation of the waves, tides, and currents of the seemingly chaotic sea of intraindividual variability.

Appendix A

Application of R Syntax

The following presents syntax that allows one to examine whether a particular trait is related to a specific distributional property of a time series, for a particular order of derivative, over a selected number of embeddings. The code presented is for the statistical program R (2008), which is available for free through the Internet and can be used on a wide variety of computer platforms.

The lines marked with the symbol # consist of comments regarding the function or implementation of this code. It is presumed that data have been scanned into R as two variables: (a) Data.Trait consisting of a vector with length N and (b) Data.TimeSeries an N × T matrix containing the time series for each individual. The variables N and T correspond to the total number of individuals and the total number of observations in each time series, respectively. The functions in Appendix B need to be copied and pasted into an active R Console prior to application of the code presented in this appendix.

The code is presented in five steps, corresponding to the five steps described in the Analysis section of Application 1. After the time series and trait data have been loaded into R, the first step for derivative variability analysis requires one to select (a) the embeddings (the time scale over which derivatives will be estimated) and (b) the order of the derivatives to be examined (observed scores, first derivatives, or second derivatives) and the distributional properties to be examined (variance, skewness, kurtosis). For now, assume that a single embedding dimension, a single derivative order, and a single distributional property have been selected for analysis.

The second step involves estimating the derivatives for each individual’s time series, using a particular embedding dimension, and then calculating the distributional property of interest from the estimates. This step can be accomplished by submitting to R temp <– CalculateProperty(Data.TimeSeries,Embedding, DerivativeOrder,Property)with the values selected in Step 1 substituted for the values between the parentheses. That is, Data.TimeSeries should be the matrix containing time series data, Embedding should be replaced with a value for an embedding dimension, DerivativeOrder should be replaced with “Observed Scores”, “ First Derivative”, or “Second Derivative”, and Property should be replaced with “ Variance”, “ Skewness”, or “ Kurtosis”. For example, one might use temp <– CalculateProperty(Data.TimeSeries,5, “Observed Scores”, “Skewness”)to calculate the observed score skewness at an embedding dimension of 5. The sample syntax, as written, saves the estimates to a variable call temp. Additional details about the function CalculateProperty are included in Appendix B, following the comment characters.

The third step involves calculating the correlation between the distributional property estimates generated in Step 2 and a trait of interest. In the fourth step, a bootstrapped confidence interval is produced for the estimate. Both steps are accomplished by submitting to R,  result <– TestRelationship(temp,Data.Trait,alpha,Bootsamples)where temp are the estimates from the previous step, and Data.Trait is the vector with the trait estimates for each individual (This does assume that the scores for a particular individual are saved in the same location for each vector; for example, that temp[6] and Data.Trait[6] correspond to the data for the same individual. This will be the case if the row number for an individual in the Data.TimeSeries matrix correspond to the vector position of an individual in Data. Trait.) The third value, alpha, corresponds to the Type I error rate desired for the confidence intervals. If one were selecting a single test, one could type .05 in place of alpha. If multiple tests are being conducted, to control the Type I error rate, alpha should be divided by the number of tests within a family or experiment (see Maxwell & Delaney, 2000, for a discussion of familywise and experimentwise control of Type I errors). In the applied example provided, Type I error rates were controlled within each family of comparisons involving 28 different embedding dimensions, so alpha was set equal to . 05/2 8. The selection of the number of times to resample the data while bootstrapping ( Bootsamples) depends on the value selected for alpha. See footnote 2 regarding the number of bootstrap samples. One might submit to R  result <– TestRelationship(temp,Data.Trait,.05/28,100000)with . 05/28 filled in for alpha and 100,000 filled in for the number of Bootsamples. The saved variable result contains the information about the correlation between the trait and the distributional property for the derivative estimates at a particular embedding. The correlation can be accessed by typing result$Correlation, and the confidence interval can be accessed by typing result$ConfidenceInterval.

This process produces only a single correlation and confidence interval. As in the applied example, one may wish to examine a range of conditions, for example, a range of embedding dimensions. So, corresponding to Step 5, the code presented can be easily extended to such situations. For example, if one wished to examine the variance of the first derivative over a range on embedding dimensions from 3 to 15, one might use the following syntax:

MinEmbedding <– 3
MaxEmbedding <– 15
results <– matrix(NA,MaxEmbedding,3)
for(value in MinEmbedding:MaxEmbedding) {
 temp <– CalculateProperty(Data.TimeSeries,value,
  “Observed Scores”, “Skewness”)
 temp2 <– TestRelationship(temp,Data.Trait,.05/28,100000)
 results[value,] <– c(temp2$Correlation,temp2$ConfidenceInterval)
 }

This would produce a matrix results where the row number corresponds to the embedding dimension and the columns correspond to the correlation (Column 1) and confidence interval (Columns 2 and 3).

Appendix B

R Syntax

 #Load library containing required functions. Prior to making
  #this call, be
 #sure that the e1071 package has been installed from the
  #CRAN libraries.
 #See “Package Installer” in R menus.
  library(e1071)
#Function to Embed Data
 Embed <– function(x,Dimen) {
  out <– matrix(NA,(length(x) — Dimen+1), Dimen)
  for(i in 1:Dimen) {out[,i] <– x[i:(length(x) — Dimen+i)]}
  return(t(out))
  }
#Function to Calculate properties of distribution of
 #derivative estimates
 CalculateProperty <– function(TimeSeries,Embedding,
   DerivativeOrder,Property)
  {
  N <– dim(TimeSeries) [1]
  estimates <– rep(NA,N)
  #Create L matrix to calculate derivative estimates
  L1 <– rep(1,Embedding)
  L2 <– c(1:Embedding)—mean(c(1:Embedding))
  L3 <– (L2^2)/2
  L <– cbind(L1,L2,L3)
  W <– L%*%solve(t(L)%*%L)
  #Set “DerivativeOrder” equal to a value
  if(DerivativeOrder = = “Observed Scores”) whichDerivative <– 1
  if(DerivativeOrder==“First Derivative”) whichDerivative <– 2
  if(DerivativeOrder==“Second Derivative”) whichDerivative <– 3
  #Apply following to each individual time series
  for(i in 1:N) {
   #Embed time series
   EMat <– Embed(TimeSeries[i,], Embedding)
   #Estimate deriatives and select derivative order of interest
   DerivativeEstimates <– (t(W)%*%EMat) [whichDerivative,]
   #If there are very few derivative estimates, don't create
    #estimate
   if(sum(!is.na(DerivativeEstimates)) <10) next
   #Calculate the requested distributional property for the
    #time series
   if(Property = = “Variance”) estimates[i]
    <– var(DerivativeEstimates,na.rm=TRUE)
   if(Property==“Skewness”) estimates[i]
    <– skewness(DerivativeEstimates,na.rm=TRUE)
   if(Property==“Kurtosis”) estimates[i]
    <– kurtosis(DerivativeEstimates,na.rm=TRUE)
   }
  #Return distribution estimates for all individuals
  return(estimates)
  }
#Function to calculate the correlation between a trait and the
  #distributional
#property of a selected derivative at a selected embedding dimension
 TestRelationship <– function(Estimates,Trait,alpha,Bootsamples) {
  #If there are very few pairs, don't create estimate
  percentdata <– sum((!is.na(Trait))*(!is.na(Estimates)))/
   length(Estimates)
  if(percentdata<0.5) {
   cat(“ERROR: You have more missing pairs of data than
    observed pairs.”)
   return(list(Correlation=NA,ConfidenceInterval = c(NA,NA)))
   }
  OriginalResult <– cor(Trait,Estimates,use=“complete.obs”)
  ResampledResults <– rep(NA,Bootsamples)
  Start <– Sys.time()
  #Boots trap Results
  for(i in 1:Bootsamples) {
   #Select from pairs of Trait & Estimate scores with replacement
   select <– floor(runif(length(Trait),1, (length(Trait)+1)))
   #Calculate and save correlation on boostrap sample
   ResampledResults[i] <– cor(Trait[select],Estimates[select],
    use=“complete.obs”)
   #If it has been a while, give an estimate as to how long
    #this is going to take.
   #This “if” statement can be deleted without altering performance.
   if((i%%50000) = = 0){
    time <– as.numeric(difftime(Sys.time(),Start,units=“mins”))
    time <– round(time/i*(Bootsamples–i),2)
    cat(“Approximate time to complete bootstrap: “,time,” minutes\n”)
    }
   }
 #Cal culate percentile confidence intervals
 CI <– sort(ResampledResults) [c(floor(alpha/2*Bootsamples),
   ceiling((1 – (alpha/2)) *Bootsamples))]
 #Return estimate or correlation in original data, and
   #confidence interval
 return(list(Correlation=OriginalResult,ConfidenceInterval=CI))
 }