Liter-scale production of uniform gas bubbles via parallelization of flow-focusing generators

Abstract

Microscale gas bubbles have demonstrated enormous utility as versatile templates for the synthesis of functional materials in medicine, ultra-lightweight materials and acoustic metamaterials. In many of these applications, high uniformity of the size of the gas bubbles is critical to achieve the desired properties and functionality. While microfluidics have been used with success to create gas bubbles that have a uniformity not achievable using conventional methods, the inherently low volumetric flow rate of microfluidics has limited its use in most applications. Parallelization of liquid droplet generators, in which many droplet generators are incorporated onto a single chip, has shown great promise for the large scale production of monodisperse liquid emulsion droplets. However, the scale-up of monodisperse gas bubbles using such an approach has remained a challenge because of possible coupling between parallel bubbles generators and feedback effects from the downstream channels. In this report, we systematically investigate the effect of factors such as viscosity of the continuous phase, Capillary number, and gas pressure as well as the channel uniformity on the size distribution of gas bubbles in a parallelized microfluidic device. We show that, by optimizing the flow conditions, a device with 400 parallel flow focusing generators on a footprint of 5 × 5 cm² can be used to generate gas bubbles with a coefficient of variation of less than 5% at a production rate of approximately 1 L/hr. Our results suggest that the optimization of flow conditions using a device with a small number (e.g., 8) of parallel FFGs can facilitate large-scale bubble production.

Graphical abstract

A parallelized microfluidic device is used to generate highly monodisperse gas bubbles at a production rate of ~ 1 L/hr.

Introduction

Gas bubbles represent a versatile template to fabricate materials with unique functionality and properties for a wide range of applications including medicine, ultra-lightweight materials, tissue engineering, and acoustic metamaterials.^1–7 The size as well as the size distribution of the gas bubbles are the key features that define the properties and functionality of these bubble-derived materials. In many instances, high uniformity in the size of gas bubbles is highly desirable or critical for specific applications. For example, the size uniformity of gas bubbles is essential in preparing acoustic metamaterials that can precisely manipulate the transport of sound waves. Additionally, producing highly size-uniform gas bubbles results in a more sharply defined resonance frequency in ultrasound imaging and therapy, significantly enhancing their utility.⁸ Conventional methods of gas bubble production in industry include mechanical agitation, sonication, and membrane extrusion. The sonication method can generate microbubbles in the size range of 1 to 50 µm diameter with a wide size distribution (> 30% CV) and production rates of ~5 L/hour.^{2, 9–11} Microfluidics has enabled the synthesis of highly monodisperse gas bubbles with precise control over their size, enabling the fabrication of novel engineered materials.^12–16 Despite the remarkable size uniformity afforded by microfluidics, these successes have been limited to laboratory-scale demonstrations, due to the limited throughput of gas bubble production using microfluidics (typically less than 1 mL/hr).¹⁷ Translation of these proof-of-concept microfluidic devices to large-scale production of highly uniform gas bubbles can allow these engineered materials to be manufactured commercially.

Recent efforts to increase the throughput of microfluidic generation of materials have focused on the large-scale production of highly uniform liquid emulsion droplets by parallel integration of T-junction or flow-focusing generators (FFGs) in a single microfluidic device.^18–25 To integrate a large number of parallelized droplet generators and to have each of them produce identical droplets, architectures have been developed that use a three-dimensional network of microchannels to uniformly distribute fluids to each droplet generator from a single set of injection ports. In particular, the ladder geometry, which takes advantage of distribution channels with large cross-sections and low hydrodynamic resistances, has enabled the parallelization of a large number of droplet generators in compact devices. By carefully designing the distribution network and tuning the channel resistances, it has been shown that up to 1,000 droplet generators can be integrated into a single microfluidic chip that has the production rate of several liters of liquid droplets per hour.²⁶

Despite these advances in the large-scale production of liquid droplets, the scale-up of microfluidic bubble production has not been as successful (e.g., 2 ml/hour production volume and 5.7 % CV using 8 FFGs²⁷). Previous studies have shown that the generation of uniform gas bubbles via parallelization is more challenging and difficult than that of uniform liquid droplets because of strong coupling between adjacent generators possibly due to high compressibility of the gas phase.²⁸ Although efforts have been made to design parallelized channels, these efforts have been limited to microfluidic devices with a relatively small number of generators (i.e., less than 16) and have not shown a similar level of success in throughput or size homogeneity as has been achieved for large-scale liquid drop production, largely due to the lack of detailed understanding on the critical factors that affect the size uniformity of gas bubbles and how those factors can be optimized.^{27, 29–31}

In this report, we identify key factors that control the size uniformity of gas bubbles generated in parallelized microfluidic droplet generators and investigate their effect on the bubble size distribution. In particular, we find that it is critical to consider both the variables that impact the flow resistance and also the uniformity of channel dimensions to narrow the bubble size distribution. By optimizing these factors, highly monodisperse bubbles (coefficient of variation (CV) < 5%, which is the criteria we use to represent extremely high size uniformity) are generated in a single device with 400 parallel FFGs at a production rate as high as 1 L/hr, ~1000 times higher than conventional microfluidic devices. We believe that the understanding derived from the investigation of uniform bubble formation can provide important guidelines in the scale-up production of emulsions and gas bubbles and ultimately aid in the translation of microfluidic generated gas bubbles to the commercial scale.

Experimental Methods

Fabrication of microfluidic device

As described in our previous report,²⁶ we have developed a robust fabrication method for a three-dimensional monolithic elastomer device (3D MED) by eliminating the need for aligning and bonding multiple pieces of elastomer layers. A 3D MED with a three dimensional structure is fabricated by double-sided imprinting using a hard silicon master and a soft PDMS master. A fabrication of 3D MED by double-sided imprinting using hard and soft masters is described in our previous report.²⁶ Briefly, we prepare the multi-height hard master by photo-lithography using negative tone photoresist SU-8 3000. For the first layer with the FFGs, we follow the standard protocol provided by the supplier (MicroChem Corporation). After UV exposure using the first photomask, a SU-8 layer of 600 µm thickness is spin-coated atop the first SU-8 layer, which is post baked at 95 °C for 14 hours. The second photomask that consists of through-holes and collection channels is aligned to the first layer using a mask aligner (ABM3000HR) and UV exposure (3,000 mJ/cm²) is performed. The multi-height SU-8 patterns are formed by removing the unexposed region of the photoresist in SU-8 developer. For the PDMS soft master, SU-8 of 1,250 µm thickness is formed on a silicon wafer (post baking at 95 °C for 20 hours) and UV (4,500 mJ/cm²) exposed through the photomask and developed to obtain the desired features. The PDMS soft master is obtained by replicating the single-layer SU-8 patterns. To characterize the dimensions of channel width of FFGs, we take optical images using an upright microscope (Carl Zeiss Axio Plan II) with a digital camera (AmScope MU1003-CK 10 MP) and then determine the channel widths and heights by using line profiling with ImageJ software and profilometry, respectively (Fig. S2B). In Supplementary Information, we describe examples of common fabrication errors that can lead to variations in channel dimensions.

Gas bubble generation using 3D MED

To test parallel bubble generation using an 8-FFG 3D MED (3D MED with 8 parallel FFGs), we use nitrogen gas and poly(vinylalcohol) (PVA, 87–90% hydrolyzed, average molecular weight: 13,000 – 23,000 g/mol, Sigma-Aldrich) solution as summarized in Table S1. PVA solution is injected into the 3D MED by using a syringe pump and then nitrogen gas is introduced into the device and controlled using a pressure regulator. For water-in-oil (W/O) liquid emulsion generation, we use de-ionized (D.I.) water as the dispersed phase and hexadecane solution with 2 wt% Span 80 as the continuous phase. To mass produce gas bubbles using a 400 FFG 3D MED, we use pressure driven flow by applying pressure to solution-filled stainless steel pressure vessels (One gallon, Alloy Products Corp.). To generate gas-in-water (G/W) bubbles, a 3D MED is filled with a continuous phase (2 wt% PVA in D.I. water) until trapped bubbles are completely removed. Subsequently, nitrogen gas is introduced to form G/W bubbles. The flow rates of the two-phases are controlled using pressure regulators. The diameter of bubbles in the microfluidic channel (D_p) is measured using optical microscopy (Nikon Diaphot 300 Inverted Microscope) and analyzed using ImageJ. The radius of spherical bubbles (r_s) is inferred by determining the volume of pancake-shaped bubbles (V_p) in the rectangular channel. We use the following equation,³²

$$V_{\mathrm{p}}=\frac{\pi h^3}{6}+\frac{\pi h}{4}(D_{\mathrm{p}}-h)(\frac{\pi h}{2}+D_{\mathrm{p}}-h)=\frac{4}{3}\pi r_{\mathrm{s}}^3$$ (1)

where h denotes the height of the channel. We take into account the height of each channel to estimate the diameter of spherical bubbles and the coefficient of variation (CV) in size. At least 300 bubbles are analyzed to determine the average bubble size.

Results and Discussion

In this study, we incorporate FFG droplet makers in our 3D MED using the ladder geometry, an architecture that has previously led to the large-scale production of highly uniform liquid droplets. In the ladder geometry individual droplet generators are connected to a set of liquid distribution channels in series. It has been shown that uniform distribution of liquids over N_f flow focusing generators (FFGs) connected to a single set of distribution channels can be achieved by adjusting the ratio of flow resistance in the distribution channel between FFGs (R_d) and that of each FFG (R_f) following,^{18, 33}

$$2N_{\mathrm{f}}(R_{\mathrm{d}}/R_{\mathrm{f}})<0.01.$$ (2)

The resistance of a rectangular channel can be calculated using

$$R=12\mu l/{\mathit{\text{wh}}}^3$$ (3)

where µ is the dynamic viscosity of the fluid and l, w, and h are the length, width, and height of the channel, respectively.

Although Eq 2 has provided an effective design rule for preparing parallelized microfluidic channels for the generation of uniform liquid droplets, its effectiveness in providing designs for a large-scale production of monodisperse gas bubbles has not been rigorously tested. We compare the generation of liquid droplets and gas bubbles using a device with 8-parallel FFGs that meet the conditions described in Eq 2 (Fig. 1). The dimensions of the channels are shown in Fig. 1A and B. Deionized water and hexadecane containing 2 wt% Span80 are used as the dispersed and continuous phases for water-in-oil emulsion production, respectively.

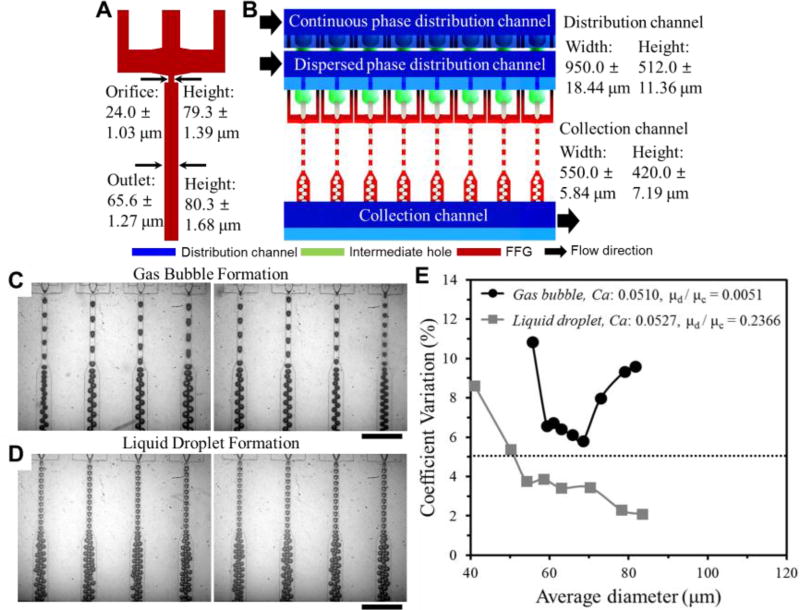
Fig. 1.

Schematic diagram for the ladder geometry design of 3D MED. (A) Geometry of FFG and dimension variation in 8 orifice and outlet channels. (B) 8 parallel bubble generation to investigate factors affecting size distribution. Optical micrographs of formation of gas bubbles (C) and liquid emulsion (D) in 8 parallel FFGs. Scale bars are 500 µm. See Electronic Supplementary Information for the movies. (E) Comparison of CV for gas bubble and liquid emulsion generation in 8 parallel FFGs.

Monodisperse liquid emulsions with a wide range of diameters are readily generated (Fig. 1C), whereas gas bubbles produced (nitrogen gas as disperse phase and 5 wt% PVA as continuous phase) are highly polydisperse (i.e., CV > 5 %; see Fig. 1D). While each FFG generates uniform gas bubbles, there is a significant discrepancy in the size of bubbles from different FFGs. Regardless of the average size of droplets or gas bubbles, gas bubbles produced from the 8-FFG 3D MED is always more polydisperse than liquid droplets (Fig. 1E). The difficulty associated with generating gas bubbles using parallelized devices has been reported previously, where it was shown that coupling among 4-parallel FFGs in gas bubble generation is more severe than that in liquid droplet generation; however, the source of polydispersity in large-scale bubble generation and efforts to minimize such size non-uniformity were not discussed in detail.²⁸

To understand the effect of various operating parameters on the size uniformity of gas bubbles in parallelized devices, we experimentally investigate the effect of Capillary number (Ca), continuous phase viscosity (µ_c) and gas pressure (P_gas) on the uniformity of bubble generation frequency (f_generation) and diameter (D_bubble) (Fig. 2B) while adjusting the conditions such that Eq 2 is always satisfied. In this experiment, we observe that the CVs for f_generation and D_bubble show broad minima when P_gas is between 0.0124 and 0.0179 mPa, and in this pressure range, D_bubble shows relatively weak dependence on P_gas (Fig. 2A inset). At P_gas below 0.0124 mPa, there are significant variations in D_bubble and f_generation from one FFG to another, although each FFG generates highly uniform bubbles (< 3% CV). Large variations in f_generation and D_bubble among different FFGs suggest that flow rates of dispersed and continuous phases are not uniform across different FFGs even though Eq 2 is satisfied under non-optimal P_gas.³⁴ However, within an optimal range of P_gas, the flow rate heterogeneity is reduced to produce monodisperse bubbles (< 5% CV).

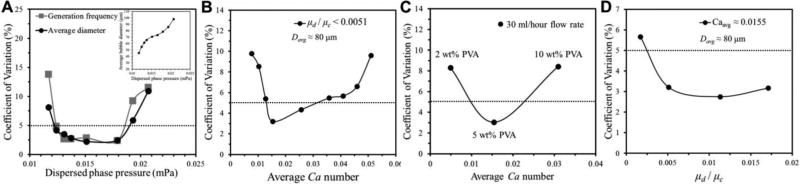
Fig. 2.

Testing the effect of operating conditions on the size uniformity of gas bubbles produced in the 8-FFG 3D MED. (A) Effect of gas pressure on the CV of bubble diameter and generation frequency under a constant water phase flow rate of 50 ml/hr flow. The inset plot shows average bubble size versus gas pressure. (B and C) Effect of Capillary number (Ca) and (D) continuous phase viscosity on the size uniformity of gas bubbles. In (B), Ca is varied by changing the flow velocity and keeping the solution viscosity constant, whereas in (c), Ca is varied by changing the solution viscosity under the same flow rate. To maintain Ca constant in (D) for varying viscosity ratio, the flow rate of the continuous phase is adjusted. The dotted line in each graph represents a CV of 5%, which we use as the criteria for high uniformity. The surface tension of PVA solution under varying concentration is shown in Table S1 (Suppelemental Information).

Next, we investigate the effect of Capillary number and continuous phase viscosity on the uniformity of f_generation and D_bubble in the 8-FFG 3D MED. The Capillary number (Ca = µ_cU/σ where µ_c and U are the viscosity and mean velocity of the continuous phase, respectively, and σ is the interfacial tension between the dispersed and continuous phases) represents the relative ratio of surface tension force to drag force during bubble break-up and has shown to be a critical factor in controlling the break-up mechanism.³¹ We change Ca by changing the flow rate of the continuous phase while keeping viscosity constant (5 wt% PVA). We find that monodisperse bubbles (< 5% CV) are generated in a specific range of Ca (0.0127 < Ca < 0.0358) (Fig. 2B). We also find that the CV of bubble size shows a minimum around Ca ~ 0.015 even if Ca is varied by changing the viscosity of the solution while keeping the flow velocity constant (Fig. 2C). In addition to Ca, we also find that there is an optimal range of µ_c that leads to the formation of monodisperse bubbles at a constant Ca (Fig. 2D). The µ_d is the viscosity of nitrogen (0.018 mPa·s) and the µ_c is controlled by changing the concentration of PVA (1.59 – 10.4 mPa·s) as shown in Table S1. Uniform bubbles are generated when µ_d/µ_c is greater than 0.0017. We also confirm that the wettability of PDMS does not depend significantly on the PVA concentration in the range of 2 to 10 wt%; thus, it is unlikely that the wetting property of PDMS is affecting the uniformity of gas bubbles (Fig. S1). Our result indicates that decreasing the viscosity of the continuous phase is desirable; that is, the amount of surfactants/stabilizers used for gas bubble stabilization should be kept to a minimum level because excess surfactants could lead to increased polydispersity of the bubbles by increasing µ_c.

From these results, it is clear that there is a very stringent set of conditions that must be met, in addition to Eq 2, to produce monodisperse gas bubbles using a parallelized-FFG device. Although we do not fully understand the exact mechanisms by which each of these factors affects the bubble size uniformity, we believe that the resistance of the FFG (R_f) likely depends very sensitively on these parameters (bubble size, capillary number, and viscosity ratio) because there is a two phase flow involving bubble suspensions in the FFGs and the dispersed phase is compressible (unlike liquid emulsions).^35–37 Thus, fluctuations in the size of orifices and channels of FFGs that result from the fabrication of highly parallelized large-scale devices can lead to significant variations in the R_f, possibly causing different bubble break-up dynamics in different FFGs, leading to the formation of polydisperse gas bubbles.

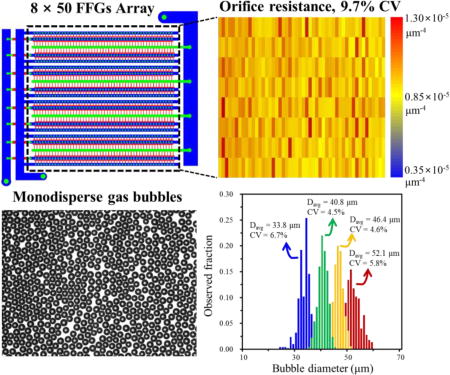
To test large-scale production of uniform gas bubbles using the solution parameters (Ca and µ_c) found using the 8-FFG 3D MED, we design a 400-FFG 3D MED with a ladder geometry (Fig. 3A), in which each row of distribution channels is connected to 50-FFGs and 8 distribution channels are connected to a single set of supply channels. Instead of the design rule provided in Eq 1, we use 2N_f(R_d/R_f) < 0.10 × 10⁻³ to enhance the bubble size uniformity. The resistance ratio of the supply channel to distribution channel is adjusted by using 2N_d(R_s/R_row) = 0.35 × 10⁻³, where N_d is the number of distribution channel and R_row (~ R_d/N_f) and R_s are channel resistance for distribution channel connected to N_f-FFGs and supply channel. The dimensions of the channels in this 400-FFG 3D MED are provided in Table S2 in the Supplementary Information. Using this 400-FFG 3D MED, we test the mass production of gas bubbles at Ca = 0.02 and u_d/u_c = 0.0113 (Fig. 3B) which are conditions that generated highly monodisperse bubbles in the 8-FFG 3D MED.

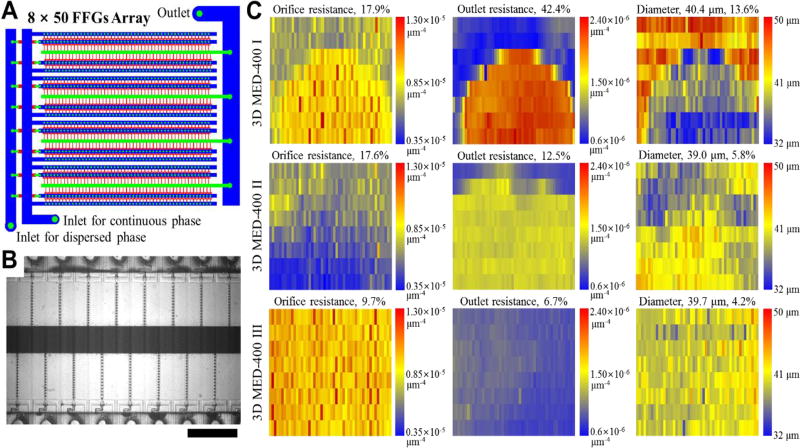
Fig. 3.

Large-scale integration of 400 FFGs for mass production of gas bubbles and the effect of channel dimension variations on the uniformity of gas bubbles. (A) The ladder-form 3D MED design contains 8 rows by 50 columns of FFGs. (B) Gas bubbles are produced by using the optimal flow conditions as determined using the 8-FFG 3D MED (See Supporting Information for movie). Scale bar indicates 1 mm. (C) Heat maps showing the channel resistance variations. Each rectangle in the heat maps represents a FFG. The first and second columns show the flow resistances of the orifice and outlet channels, respectively, and the third column shows the size of bubbles generated from 400 FFGs in 3D MED-400 I, II and III.

One of the key factors that we found affects the size uniformity of gas bubbles produced from a microfluidic device with parallelized FFGs is the uniformity of the FFG channel dimensions, which affects R_f in Eq 2. We test the importance of FFG channel dimension uniformity using two devices that have noticeable variations in the height (3D MED 400-I; 16.6% CV in the height of channels, see Supplementary Information) and in the width of FFG orifices and outlet channels (3D MED 400-II; 6.8% CV in the width of channels; see Supplementary Information). We find that such errors in the fabrication of masters for 3D MED can result in significant non-uniformity in channel dimensions (Fig. S2). The non-uniformity in the height of the FFGs likely originates from the non-uniformity in the thickness of the photoresist. The thickness of the spin-coated photoresist, for example, tends to be thicker around the edges.³⁸ Thus, to avoid such an issue, we recommend that the center region of the spin-coated photoresist or a spray coater is used to prepare a photoresist layer. Non-uniform channel widths, we believe, result from non-uniform and/or over-UV exposure.

Based on Eq 3, we calculate and plot the resistance of orifice and outlet channels of FFGs in each device as shown in Fig. 3. When gas bubbles are produced by tuning the applied pressure for the gas phase on the two device with higher fabrication error, more polydisperse gas bubbles (CV > 5%) are produced as expected. In the device with large height variations (3D MED 400-I, Fig. 3C), gas bubbles are produced with D_avg = 40.4 µm and CV = 13.6% under the optimized processing conditions (i.e., Ca, µ_c and P_gas). Changing the conditions outside these optimized ranges from the 8-FFG device leads to the production of even more polydisperse gas bubbles. With the second device (3D MED 400-II, Fig. 3C), the uniformity of the gas bubbles (D_avg = 39.0 µm and CV = 5.8%) produced is significantly enhanced compared to the first one, likely because the channel resistance dispersion of the second device is significantly smaller than that of the first one. While the size uniformity of gas bubbles from 400-FFG 3D MED scales with the overall uniformity of channel resistance, dependence of bubble size on the orifice/outlet resistance at the individual FFG-level is weak; that is, FFGs with high orifice/outlet resistance do not necessarily generate small gas bubbles (Table S3 in Supplementary Information).

In addition to variations in the dimensions of FFG orifice and outlet channels, we find that variations in the distribution channel dimensions can also significantly affect the size uniformity of gas bubbles (Fig. S3). Non-uniform pressure applied during double-sided imprinting can result in undesirable deformation of distribution channels (Fig. S3A), which can adversely affect the size uniformity of gas bubbles even if the FFGs have very uniform channel dimensions (Fig. S3B). Thus, it is critical that both the FFGs and the distribution channels are prepared with high uniformity (< 5% CV). To quantitatively determine the tolerance for channel dimension variability, a detailed study on the effect of channel dimension variations on the bubble size distribution is warranted.

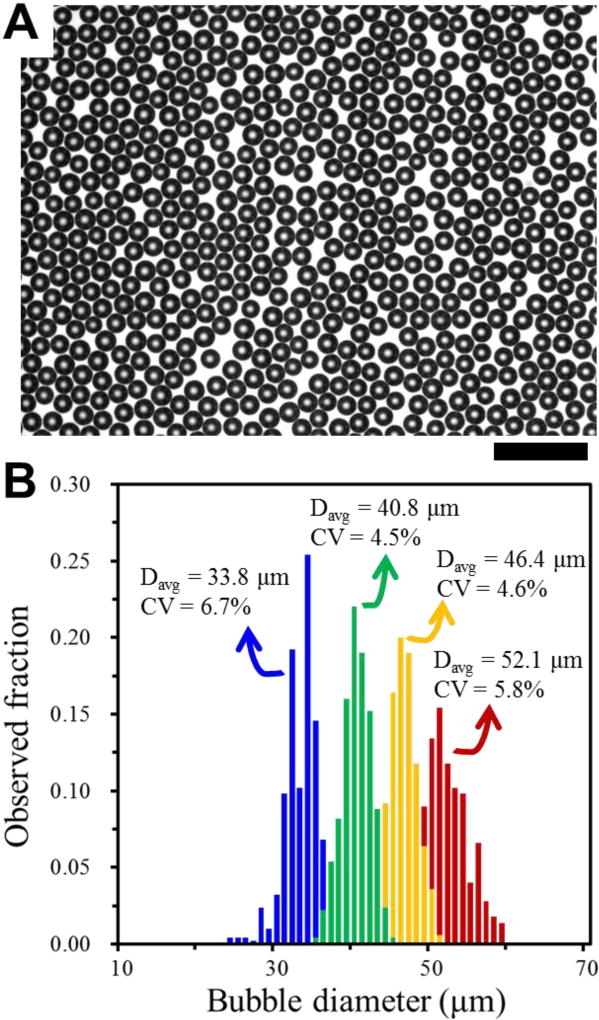
With a 400 FFG-parallel device that has uniform microchannels and distribution channels (3D MED 400-III), highly uniform bubbles are produced. Although the coefficient of variation of the FFG orifice (9.7% CV) and outlet resistances (6.7% CV) are above 5%, as long as the CVs of channel height and width are kept below 3% and the device is operated using the optimized Ca and µ_c from the 8-FFG device, highly uniform gas bubbles can be prepared. By controlling the gas pressure from 0.138 mPa to 0.179 mPa, the droplet diameter D_bubble can be controlled between 33.8 and 52.1 µm (Fig. 4), and highly monodisperse gas bubbles (< 5% CV) in the range of 40.8 and 46.2 µm can be generated at a production rate as high as 1 L/hour. Consistent with the trend seen in Figure 2A, there is a range of pressure (0.15 – 0.17 mPa) that minimizes the size heterogeneity. These results clearly show that it is critical to fabricate 3D MED devices with uniform channel dimensions and, subsequently, to use optimal operating conditions to produce highly uniform gas bubbles.

Fig. 4.

(A) Optical microscopy image of gas bubbles produced using 3D MED-400 III. Scale bar indicates 200 µm. (B) Size distribution of gas bubbles generated in the optimal range of gas pressure. Blue, green, yellow and green histograms represent the size distributions of gas bubbles generated with gas pressures of 0.138, 0.151, 0.165, 0.179 mPa, respectively.

We believe our approach of finding the optimized Ca and µ_c using an 8-FFG 3D MED offers an important strategy for successful and efficient scale-up of microfluidic bubble/droplet generations. Rather than using a device with hundreds or thousands of parallel FFGs, it is easier and more economical (e.g., less reagents is used) to use a device with a relative small number (e.g., 8 FFGs) of parallel FFGs to find the optimized Ca and µ_c, which subsequently can be used to operate parallelized devices with extremely large number of FFGs. The 8-FFG parallel device, can function as a pilot scale testing platform for identifying the optimized flow conditions (Ca and µ_c), which subsequently can be used in a device with a large number of FFGs to identify the optimized pressure range for large-scale monodisperse production.

Conclusions

In summary, we present mass production of highly uniform gas bubbles using a parallelized microfluidic device. We systematically studied the effect of gas pressure, Capillary number, and continuous phase viscosity on the gas bubble size uniformity, and have identified guidelines for choosing flow parameters to improve droplet size uniformity. We also have demonstrated the importance of uniformity in microchannel geometry in obtaining highly monodisperse gas bubbles from parallelized devices. Our results suggest that the dominant cause of droplet heterogeneity in parallelized devices is fabrication error and that the optimal parameters to minimize droplet heterogeneity are those that minimize the droplet diameter sensitivity to the fabrication error. We find that using a 8-FFG 3D MED provides an efficient method to identify optimized Ca and µ_c for the production of highly monodisperse gas bubbles in a 400-FFG 3D MED. Production of highly monodisperse gas bubbles using parallelized microfluidic devices will enable the fabrication of advanced materials such as acoustic metamaterials using bubbles as the basic building blocks. Moreover, highly uniform gas bubbles can potentially enhance the efficacy of ultrasound-based theranostic approaches since the interaction of microbubbles with ultrasound depends critically on the bubble size.