Abstract.
Optical coherence tomography (OCT) yields microscopic volumetric images representing tissue structures based on the contrast provided by elastic light scattering. Multipatient studies using OCT for detection of tissue abnormalities can lead to large datasets making quantitative and unbiased assessment of classification algorithms performance difficult without the availability of automated analytical schemes. We present a mathematical descriptor reducing the dimensionality of a classifier’s input data, while preserving essential volumetric features from reconstructed three-dimensional optical volumes. This descriptor is used as the input of classification algorithms allowing a detailed exploration of the features space leading to optimal and reliable classification models based on support vector machine techniques. Using imaging dataset of paraffin-embedded tissue samples from 38 ovarian cancer patients, we report accuracies for cancer detection for binary classification between healthy fallopian tube and ovarian samples containing cancer cells. Furthermore, multiples classes of statistical models are presented demonstrating accuracy for the detection of high-grade serous, endometroid, and clear cells cancers. The classification approach reduces the computational complexity and needed resources to achieve highly accurate classification, making it possible to contemplate other applications, including intraoperative surgical guidance, as well as other depth sectioning techniques for fresh tissue imaging.
Keywords: pattern recognition, image analysis, optical coherence tomography, classification, ovarian cancer
1. Introduction
Optical coherence tomography (OCT) allows for fast visualization of microscopic tissue structures based on elastic near-infrared light scattering up to to 3 mm in depth depending on the level of tissue absorbance. OCT is a laser-based interferometric technique that relies on morphologic contrast to create volumetric images, typically in cross-sectional view. Since the first publication of this technique applied to biological samples,1 constant improvements have been made to adapt the technology for clinical use.2 The development of clinical-grade OCT systems has been made possible by the availability of faster scanning laser sources and spectrometers, lasers with broader linewidths, as well as rugged imaging probes and fast scanning mechanisms.3 Extreme acquisition speeds have been reached, allowing optical data for entire volumes to be acquired in only a fraction of a second.4–6 OCT is now routinely used in cardiac surgeries,7–9 in dermatology,10 in ophthalmology,11 and to probe the gastrointestinal tract,6,12 to name a few examples.
“Qualitative” analysis of OCT images based on visual inspection can yield valuable information with several studies demonstrating its potential for diagnostics and screening.13,14 However, a limitation of qualitative analysis is that clinicians need to be trained to read complex optical images that can impede widespread adoption by the medical community. On the other end, automated tissue/pathology classification schemes relying on “quantitative” analysis could provide medical practitioners with standardized unbiased insight on the pathologies and lead to clinical translation in the context of, e.g., applications for intraoperative surgical guidance and as a complement to conventional histopathology analysis techniques.6,15
The contrast in OCT images comes from the intrinsic optical properties of biological specimens. Light backscattered by the tissue creates an intensity map modulated by the scattering and absorption properties at various depths. Quantitative metrics derived from OCT data (e.g., texture analysis, tissue segmentation, or spatial frequency analysis) can be used as surrogates of these optical properties. These mathematical features can be used in the scope of automated learning algorithms to, e.g., distinguish different tissue types, or detect the presence of differentiated cellular processes or morphological alterations associated with the genesis of cancer. This can be achieved by using large imaging datasets, including subsets of images belonging to each of the classes of interest, in order to produce a classifier, which is a multiparametric statistical model using a number of features associated with the images to classify into two or more classes.16–19 A classifier can receive vector inputs, such as in linear discriminant analysis (LDA), support vector machine (SVM), random forest (RF), boosted trees (BT), or directly take images or three-dimensional (3-D) volumes of data as input, such as in neural networks (NN) and convolutional neural networks (CNN).20 Based on classification results obtained from any of those techniques, one can extract the receiver operator characteristics (ROC) curve allowing the diagnostic potential of the technique to be evaluated. Important methodological aspects must be taken into account to train a reliable classifier that can be used for tissue characterisation in “real” situations, such as on-board instruments used by medical practitioners. Initially, a representative training dataset needs to be formed that captures the full heterogeneity present in each of the classes, ensuring intra- and interpatient variability is taken into consideration. For example, binary classification between benign/normal samples and tissue containing cancer cells in oncology would need to include: (1) benign/normal samples representing tissue subtypes within an organ (e.g., white matter and gray matter in brain), potential interpatient variations, and time-dependant variations that can affect the molecular composition of the tissue (e.g., menstrual cycle), (2) samples associated with the different types of pathology (e.g., cell type, nature of extracellular matrix) targeted for detection as well as samples associated with different disease stages and grades. Another consideration is the construction of an independent test dataset that should be constructed in such a way to capture a realistic degree of variance within each class in addition to be totally independent of the training dataset. Testing strategies implemented in “leave-one-patient-out” instead of “leave-one-sample-out” scheme should be preferred, ensuring that the classifier is not trained with a priori patient information.
Some classifiers were trained for OCT image classification with most studies considering two-class problems, including for glaucoma versus healthy eyes where statistical models were constructed using RF.21,22 A glaucoma study also demonstrated binary class statistical modeling as well as a comparison of five different classifiers.23 This study presents an accuracy of 96.6% using cross-validation for glaucoma detection. An atlas of the eye map was computed from OCT volumes to produce a “standardized map” for glaucomatous and healthy eyes, the deviation from that map for a given OCT is then classified using LDA and achieved over 90% in accuracy, sensitivity, and specificity.24 For macular degeneration, CNN has been used to distinguish between images of macular degeneration and healthy eye structures with a dataset built from eye images from 1606 patients.25 An attempt was also made with features extracted from OCT volumes instead of images, where they also discuss multiple classifier implementations and optimizations.26 For skin conditions, intensity-based features were fed to an NN classifier27 with accuracies of 80% or combined to polarization-sensitive features28 with an accuracy of 95.4%.
Clinical applications can necessitate classification into multiple classes, and some groups investigated classification in three or four distinct categories with OCT images. For eye lesions, high-classification performances (above 90% with seven classifiers) were obtained.29 Noteworthy, the dataset (over 3000 OCT images) was built using multiple images taken from the same 45 patients. To circumvent the limitations of many studies using a limited amount of clinical data to train the classifiers, a demonstration was made involving a pretrained CNN (on standardized dataset) fine-tuned to OCT images to yield accuracies of more than 86% for all three categories.30 A five-category classification using relevance vector machine attenuation and textures derived from OCT images of atrial tissue revealed an average accuracy of 80%.31 A new perspective was introduced by Gossage et al.,32 in which they calculated Brodatz textures to retrieve speckle information based on structure-poor OCT images. They succeeded in multiclass classification problems on various tissues, such as skin, testicular fat, and normal lungs with accuracies of 37.6%, 94.8%, and 65.3%, respectively. Finally, some groups classified multimodal acquisitions, such as OCT, Fourier transform infrared spectroscopy (FTIR) and various histology staining slides for oral lesions (four classes) with an average of 82.6% using SVM.33
Here, we present a multilayer descriptor allowing features extracted from OCT volumes to be represented as two-dimensional (2-D) images and used for ovarian tissue classification. We compared the classification performances of this descriptor with intensity features extracted from conventional grayscale images. We also compared shape color, texture, and wavelet decomposition against Haralick’s textural features. The imaging dataset consists of OCT images of ovarian cancer samples and healthy fallopian tubes from 38 patients. For each test configuration, we present the sensitivity, specificity, and accuracy, as well as the area under the ROC curve as a measure of the technique’s diagnostic value.
2. Methodology
2.1. Patients and Optical Coherence Tomography Dataset
Samples consisted of formalin-fixed paraffin-embedded (FFPE) ovarian and fallopian tube samples harvested from 38 women who underwent hysterectomy with bilateral oophorectomy at the Centre Hospitalier de l’Université de Montréal (CHUM) (Table 1). Samples were selected from the tissue bank protocol #BD04.002, approved by the research ethics board of the CHUM. All patients provided informed consent. Each tissue fragment measured between 1 and 25 mm with up to 3 mm in depth. A subset of the paraffin-embedded tissue samples dataset reported previously in Ref. 34 was selected from the three most common ovarian tumor types: high-grade serous tumors (HGS: 12 blocks), endometrioid tumors (En: 7 blocks), and clear cell tumors (CC: 7 blocks). Samples from healthy fallopian tubes were selected as well (12 blocks). Every block came from a different patient but could contain more than one sample associated with the given tissue type (either HGS, En, CC or healthy) from that patient. For example, a block in the healthy category could contain up to five healthy tissue fragments taken from the same patient. For each paraffin block, a slice was cut for hematoxylin and eosin (H&E) staining and histopathology leading to determination of tissue type and cancer cells identification if relevant. Each block was then installed on the bench top of an OCT system and imaged to extract tissue features within an area of with optical sampling depth of 5 mm. Depending on the specimen size, 3 to 5 scans were required to cover the entire sample surface. All scans were taken ensuring there was a spatial overlap between the images to be stitched together leading to full-size reconstructed images with structural features of interest. For each reconstructed OCT image, spatially registered regions of interests (ROIs) were defined on the corresponding H&E images. The volumetric regions ( or ) associated with each tissue fragments were all independent in the sense they were harvested from nonoverlapping regions in order to be representative of the pathology and inner-patient variability.
Table 1.
Numbers of patients and OCT regions for each class constituting the dataset. One FFPE block per patient was obtained and from each block between 3 and 6 independent and nonoverlapping 3-D ROIs were extracted from the OCT volumes to match the tissue types (HGS, En, CC, or healthy) identified by histopathology.
| # patients | # OCT regions | |
|---|---|---|
| Healthy | 12 | 95 |
| HGS | 12 | 90 |
| En | 7 | 51 |
| CC | 7 | 52 |
| Total | 38 | 288 |
The OCT system (OCS1310, Thorlabs, Newton, New Jersey) consists of a wavelength-swept Microelectromechanical System Vertical-Cavity Surface-Emitting infrared Laser (MEMS VCSEL; Thorlabs, Newton, New Jersey) centered at 1300 nm coupled with an interferometer and a data acquisition module (; ATS9350, Alazar Technologies, Canada). The swept-source has an average output power of 29 mW with an A-line scan rate of 100 kHz. The scan lens is a LSM03 objective (Thorlabs, Newton, New Jersey), with an effective focal length of 36 mm. The imaging head of the bench-top configuration yields a lateral resolution of and a depth resolution of in air. Data acquisition of a volume covers () in the -, -, and -directions, respectively.
Instead of using the commercial software supplied with the imaging system, custom software (MATLAB®, release 2016b, The MathWorks, Inc.) was used to export the raw data files containing the electrical signals from the detector (interferograms). Reconstructed OCT volumes require normalization with respect to the maximum intensity within the 3-D image to ensure the resulting gray levels for data acquired at different times can be compared and that the quantitative information associated with relative intensity differences can be used reliably as a basis for tissue classification. A Fourier transform was applied to the frequency-domain data leading—for each position on the surface—to a depth-resolved intensity profile (A-line intensity). The logarithm of each pixel was then computed leading to a 3-D image composed of intensity values labeled , where the integer indices and represent and lateral positions, respectively, and the index represents en-face planes, along the depth axis. Every volume was cropped along the depth axis (along an A-line) to ensure that the first intensity value corresponds to the surface of the tissue. Statistical metrics associated with global average, , standard deviation, , and maximum intensity values are then extracted from all normalized OCT volumes. The global statistics were then used to normalize the intensity associated with each pixel ensuring a volume representation consistent with a standard gray-level file format, namely, an eight-bit (256 values) range representation per pixel
| (1) |
A normalization was applied by dividing by three times the standard deviation [ in Eq. (1)] to maximize the representation between and 1 with the aim of mapping to finite pixel intensities. The denominator was chosen to limit the loss of information. By using three standard deviations, most of the intensities were included in the normalization interval to avoid excessive clipping of the out-of-range values during the conversion and since the number of discrete values that a pixel can take is limited, the values must be well spaced in the interval (i.e., dividing by a factor greater than 3 standard deviations would cause notable loss of sensibility during the conversion). The normalized values were then converted in pixel value using a linear transformation. The unique offset was chosen for all volumes to avoid saturation, including the outliers. This technique preserved the relative histogram of gray values from one volume to another but underrepresents darker gray levels. In this specific case, those tones were populated by paraffin, which did not represent the signal of interest and was removed thereafter. Finally, tissue segmentation was performed leading to the creation of a binary mask using the dilation, erosion, and thresholding operand to isolate paraffin areas within each image.35 Additional details concerning the segmentation process are further detailed in Appendix A.1. This step is important to ensure image classification is not affected by non-tissue-specific artifacts introduced by paraffin filling crypts and voids within the specimens.
2.2. Features and Descriptors
After dataset formatting and normalization, descriptors were extracted for tissue classification. Here, a multilayer descriptor was used to capture volumetric information more effectively when compared to simpler single B-scan image analysis techniques typically used in OCT classification. Classifiers must be robust enough to exhibit translation and rotation invariance, as small changes to the image position should not result in misclassification. An approach to increase a classifier’s robustness is to extract a descriptor based on second-order metrics, such as a subset of Haralick’s features36 or the image descriptors based on color, texture, shape, and wavelets (CTSW).37 Implementation of these two techniques is presented in the following section and further detailed in Appendices A.2 and A.3.
2.2.1. Overview of the preclassification steps
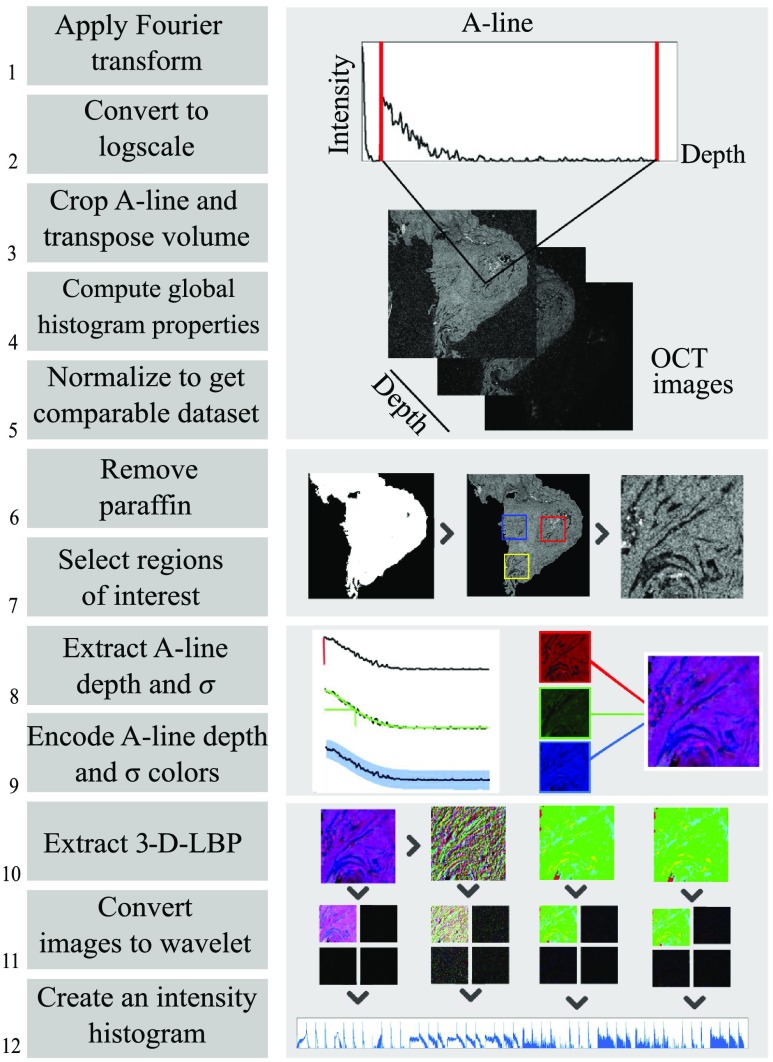
The preclassification process on OCT data implied a standardized exportation of data followed by a segmentation of the tissue before reducing volumes and extracting features. Figure 1 summarizes the dataflow for the multilayer descriptor from OCT volume acquisition to a classifiable vector. Steps 1 to 5 are required to format each en-face image of the acquired image stack and are described at the end of Sec. 2.1. The segmentation consisted of steps 6 and 7, where the paraffin was removed and ROIs were selected based on the corresponding H&E histological information. ROIs were selected to be containing only one tissue type. In the case of the multilayer descriptor analysis, steps 8 and 9 lead to the creation of a multichannel image, effectively reducing the dimensionality of the input data. A more detailed view of the process is given in Sec. 2.2.2 and finally, steps 10 to 12 illustrate the feature extraction process with the image descriptors based on CTSW technique, explained hereafter in Sec. 2.2.4, with the creation of a formatted input vector ready to enter the classification process. For Haralick’s features the dataflow follows Fig. 1 steps 1 to 7 followed by a conventional Haralick’s features calculation and vector concatenation (not shown, detailed in Sec. 2.2.3).
Fig. 1.
Preclassification steps with CTSW: (1 to 5) Reclassification steps to obtain en-face gray-level image stack (6 and 7) tissue segmentation (8 and 9) creation of three-channel images to represent OCT volume, and (10 to 12) CTSW descriptor extraction. 3D-LBP, three- dimensional local binary patterns.
2.2.2. Multilayer descriptor
Three-channel images are common in the image classification literature in the form of conventional color spaces, such as RGB or hue, saturation, and luminosity. The multilayer descriptor implemented here used the same structure, but each of the three channels was used to store an image feature derived from volumetric information rather than a color or a luminosity value.
The first channel was chosen to be the gray level of the first en-face OCT image yielding a backscattering map of the sample with morphological information relating to tissue architecture. For the remaining two channels, 2-D maps are computed based on simple mathematical operations applied to each A-line yielding images directly related with the heterogeneous nature of the tissue in terms of elastic scattering and absorption contrast. Specifically, the following two metrics were computed: (1) the depth associated with the half intensity (DHI) decrease of each A-line from which a 2-D image was created and (2) a 2-D map showing the standard deviation () for each A-line. The DHI information is directly related to the mean light attenuation within the tissue. Following accepted models for light attenuation in biological specimens,38,39 taking the depth at half intensity or the direct attenuation coefficient yields similar information. The intensity as a function of depth for any given OCT A-line flows an exponential decay, linearized by taking the logarithm. The remaining components of the light model are proportional to the product of the depth and attenuation coefficient . Taking one or the other results in the same information, represented as direct quantity or the inverse. To better model the variations of the slope along a typical A-line, a fit with a seventh-order polynomial was used, with the criterion of minimal least-square error. This order has been chosen to help fitting the trend variations in ovarian tissue while being low enough to allow smoothing. For fallopian tubes and ovaries, multiple layers and structures can arise within a sample, which can make labor intensive the linear fits generally used for attenuation quantification. The map of standard deviations gives a quantitative measure of tissue heterogeneity along the depth direction. Based on these three images (intensity of first OCT slice, DHI and ), a composite three-channel image was saved.
2.2.3. Haralick’ features
Haralick’s features were used for two main reasons: first, input data are naturally expressed as texture on which the Haralick’s analysis can be applied and, second, those descriptors are commonly used for image classification, and image classification performance can be compared with the proposed multilayer descriptor. For image analysis, the most common first-order (mean intensity and standard deviation) and second-order (energy, correlation, and contrast) metrics were selected. The gray-level cooccurrence matrices (GLCMs) were computed for 4 different orientations and 10 different distances (see Appendix A.2 for details). The second-order metrics were calculated for each of the 40 GLCMs. All second-order metrics were then concatenated with the first-order metrics to generate a vector of 122 elements per surface pixel of each B-scan (40 GLCMs × 3 second-order + 2 first-order elements) resulting in 366 elements (122 elements per layer × 3 channels) for the full multilayer descriptor.
2.2.4. Image descriptors based on color, texture, shape, and wavelets
Another feature extraction and analysis approach was used based on the combination of CTSW.37 For these analyses, the image descriptor was implemented directly on the multilayer data since it was designed for texture analysis in multichannel images. The first step was the calculation of local binary patterns (LBP)40,41 both intra- and interchannel throughout the descriptor. Then wavelet decomposition (Haar transform) was calculated to discriminate spatial frequency content in both axis of the image. A histogram was computed for each wavelet, and histograms are concatenated to build a classifiable vector. Further details relating to this algorithm are presented in the Appendix. This procedure is applied twice: once on the normalized volume and then on the depth filtered normalized volume using a moving average on five frames. This process considered information from the speckle and the from high spatial frequency structures within the tissue. The resulting classifiable vectors were then concatenated to create the final vector called H-descriptor.
2.3. Classification
2.3.1. Preclassification
Classification was performed on the vectors created from the calculated features for each image for Haralick’s method. In the following sections, Haralick 2-D will refer to classification using Haralick’s features calculated on intensity-based B-scan (gray level) images and Haralick 3-D will refer to classification using Haralick’s features calculated on the multilayer descriptor. A principal component analysis (PCA) was performed on the H-descriptor and the Haralick’s vectors prior to classification. The number of principal components was set, ensuring that the variance is almost 100% using a cumulative explained variance of (99.99%).
2.3.2. Implementation and cross validation of the classifiers
Following feature extraction over the entire dataset, the partition presented in Table 2 was created in preparation for the design of three distinct types of classifiers: (1) healthy versus HGS, (2) healthy versus cancer, and (3) a four-class classifier to attempt distinguishing between the four tissue types present in this study.
Table 2.
Data subsets used to build each classifier.
| Classes | ||||
|---|---|---|---|---|
| Healthy |
HGS |
En |
CC |
|
| 95 ROIs, 12 patients | 90 ROIs, 12 patients | 51 ROIs, 7 patients | 52 ROIs, 7 patients | |
| Case healthy versus HGS | I | II | — | — |
| Healthy versus cancer | I | II | ||
| Four classes | I | II | III | IV |
Performances were evaluated using a leave-one-patient-out cross-validation approach to cover the clinical variability and maintain the patient entities, to avoid any instances of bias created by tissue features from same patient. Because different machine learning approaches can perform differently, e.g., for different types of data and relative quantity of noise, several classification approaches (BT, SVM, NN, and LDA) were used and compared. Based on performance results, binary classification was based on an SVM technique while for four-category classification LDA was used.
2.3.3. Comparison criteria
The performance of the classification techniques (classifiers with different descriptors and classes) was evaluated by computing the confusion matrices, allowing for a precise assessment of misclassifications. This representation quantifies the region that has been well-classified and misclassified for each class. Each row of the confusion matrices indicates the correct diagnosis given by the pathology report and the column represented the classes that are predicted. The matrices are calculated for the three cases to evaluate the robustness with various levels of complexity.
Optimal accuracy, specificity, and sensibility were then computed. Those values summarize the main performance described in the confusion matrices. The accuracy indicates the ratio of region that was correctly classified. The specificity and sensibility are defined for binary systems. The specificity is defined as the probability of giving a negative result while the condition is negative while the sensitivity corresponds to the probability of giving a positive result for a case that is positive. ROC curves and the area under the curves (AUC) was also computed to evaluate the relation between the sensibility and specificity. The ROC curve represents the possible specificity–sensibility achievable with a trained classifier.
3. Results
3.1. Computation of Image Features
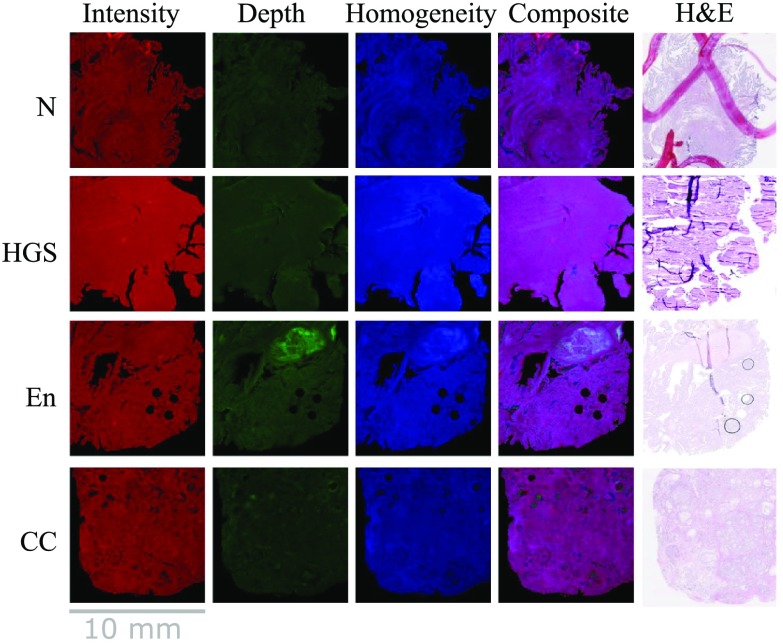
The multilayer descriptor was computed for each OCT volume in the dataset. Figure 2 shows one example per tissue class where the first image is the “intensity” image, taken in en-face configuration and formatted in red, the second image is the DHI map formatted in green, and the third image is the standard deviation image color coded in blue. The fourth column in the figure shows the resulting RGB composite image and the fifth column presents the H&E image corresponding to the tissue slice associated with the intensity image.
Fig. 2.
Creation of the composite images with sample of each layer and each class.
Haralick’s features for the gray-level images and for the multilayer descriptor were then computed. In the case of the multilayer descriptor, features from each channel were computed in parallel, and then the vectors were concatenated to produce the final vector. Figure 3 presents the extracted features for each class in the multilayer case. The vertical axis presents the values for each calculated feature in the same order for each image. The values are given by the amplitude of each feature. The samples are lined up along the horizontal axis for each class, so that any visible trend would be visible at a glance.
Fig. 3.
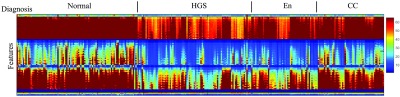
Haralick’s features of the dataset for the multilayer descriptor. The vertical axis presents the features (366 minus the all zero features for display) in each layer (intensity, DHI, and ), with the quantitative value associated with the scale bar. The horizontal axis contains every sample classified grouped by tissue class.
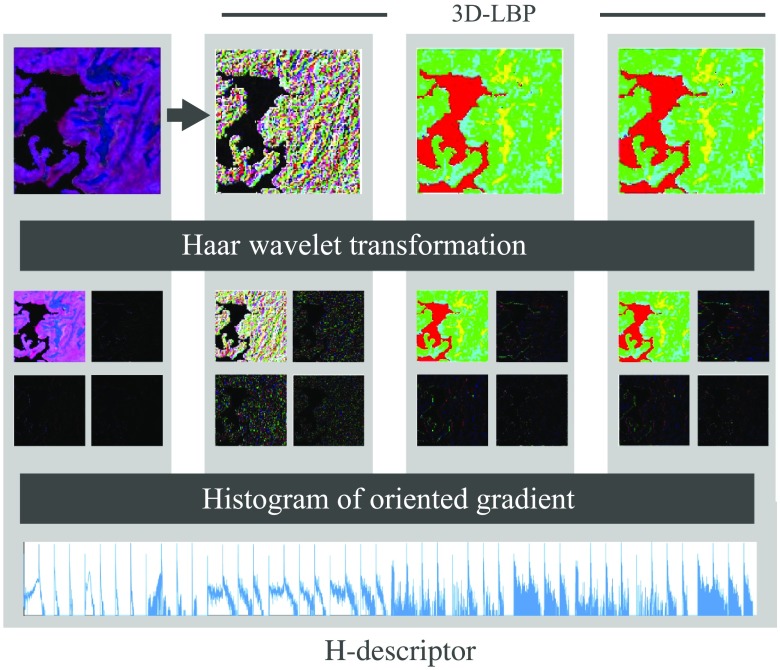
Figure 4 shows an example of wavelet decomposition and H-descriptor for a sample in the healthy category. The figure presents the intermediate computational steps to obtain the features based on the CTSW algorithm applied to the three-layer descriptor. The first row illustrates the 3D-LBP computation. The second row shows the wavelet decomposition using the Haar filter calculated for each layer. The third row shows a histogram of oriented gradients, in which, for every layer, a histogram was generated and concatenated to produce the H-descriptor for PCA preclassification.
Fig. 4.
Haralick’s features for multilayer images and CTSW algorithm. The multilayer descriptor serves as the principal image input to the algorithm. LBP are then extracted in the three orientations to generate the images in , , and planes. The Haar wavelet transform is then applied to the four images. Histograms are then generated and concatenated to build the output vector named H-descriptor.
3.2. Two-Class Problems
The multilayer descriptor was first tested against standard features from gray-level images. The basic test is a two-class problem. We addressed the case where the two classes are easily distinguishable at glance with a dataset built from the healthy and HGS specimens (first row in Table 2). The case where the two classes are heterogeneous and subtler to differentiate was addressed with a dataset built from the healthy against all the cancer specimens (second row in Table 2).
3.2.1. Healthy versus high-grade serous specimens
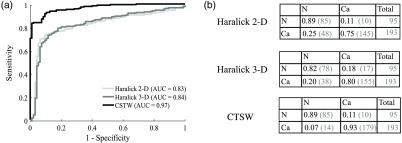
Figure 5 shows the classification performances using SVM. A single intensity image was used for Haralick 2-D, but the multilayer descriptor was used for Haralick 3-D and the CTSW features. The ROC curves are presented for each feature extraction technique, as well as the area under the ROC [Fig. 5(a)]. The associated confusion matrices are presented in Fig. 5(b), where the elements on the diagonal represent the proportion of samples correctly classified. The off-diagonal elements are the proportion of samples that were assigned to the wrong class. Each line in the confusion matrices represents the correct diagnosis [healthy (H) or HGS)] and the columns represent the calculated class (output from the classifier, either healthy or HGS). For example, the element (1, 1) of the confusion matrix quantifies the proportion of healthy samples that were correctly classified in the healthy category, whereas the element (2, 1) represents the proportion of HGS samples that were erroneously classified as healthy.
Fig. 5.
Classification performances for healthy versus HGS specimens: (a) ROC curve for each method with the corresponding AUC and (b) confusion matrices showing the fraction of samples being correctly classified on the diagonal and the number of misclassified samples in the off-diagonal elements. The number in parenthesis is the actual number of specimens with the column labeled “total” presenting the total number of samples in each class.
From the ROC curves in Fig. 5(a), the specificity, sensitivity, and accuracy of each classifier were calculated and are presented in Table 3. Those values were selected using the highest accuracy score along the available sets defined by the ROC. This set of specificity and sensitivity values can be interpreted as the combination along the ROC with the minimal distance to the perfect classification score (upper left corner).
Table 3.
Healthy versus HGS classification performances in terms of sensitivity, specificity, accuracy, and area under ROC curve for the three classifiers.
| Sensitivity (%) | Specificity (%) | Accuracy (%) | Area under ROC | |
|---|---|---|---|---|
| Haralick 2-D | 93.7 | 93.5 | 93.5 | 0.93 |
| Haralick 3-D | 83.3 | 94.7 | 89.2 | 0.91 |
| CTSW | 91.1 | 93.0 | 93.0 | 0.98 |
3.2.2. Healthy versus cancer specimens
Figure 6 shows the classification performances of the three classifiers built from the healthy and cancer specimens divided into two classes. The ROC as well as area under ROC is plotted for the three classifiers [Fig. 6(a)]. The confusion matrices for the three classifiers are detailed in Fig. 6(b). The first line and first column present the healthy class and the second line and column present the cancer class (Ca). The diagonal represents the proportion of samples associated in the correct class, whereas the off-diagonal terms represent the proportion of samples associated to the wrong class by the classifier.
Fig. 6.
Classification performances for healthy versus cancer specimens. (a) Shows the ROC curves for each method with the corresponding area under the ROC. (b) Details the associated confusion matrices for each method with the normalized success score (number of samples in parenthesis). The column total gives the total number of samples in each class.
From the ROC in Fig. 6(a), the sensitivity, specificity, and accuracy can be obtained for each classifier. The values of specificity and sensitivity were determined based on the highest accuracy score. Quantitative assessment of sensitivity, specificity and accuracy for each classifier are presented in Table 4.
Table 4.
Healthy versus cancer classification performances in terms of sensitivity, specificity, accuracy, and area under ROC for the three classifiers built.
| Sensitivity (%) | Specificity (%) | Accuracy (%) | Area under ROC | |
|---|---|---|---|---|
| Haralick 2-D | 83.9 | 81.1 | 79.9 | 0.83 |
| Haralick 3-D | 80.3 | 82.1 | 80.9 | 0.84 |
| CTSW | 92.8 | 89.5 | 91.7 | 0.97 |
3.3. Four-Class Problem
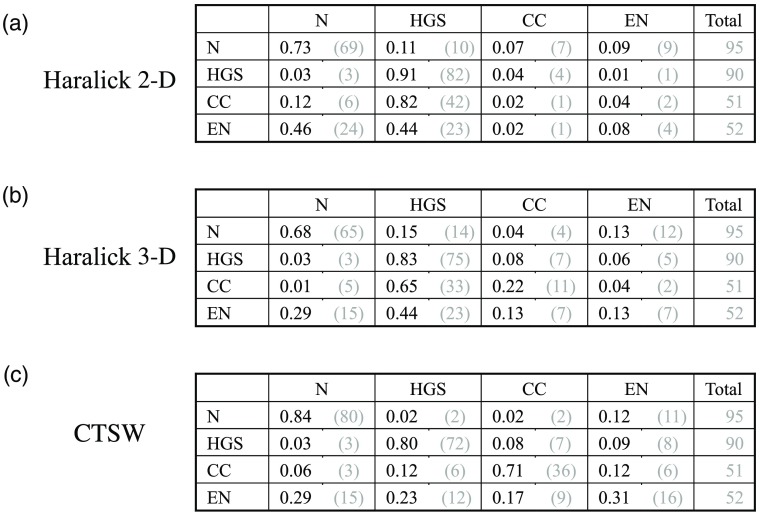
To further demonstrate the capabilities of the multilayer descriptor and the pertinence of volumetric OCT, we built classifiers to address four classes at the same time. The four categories of specimens were placed in the four classes: healthy specimens, HGS, En, and CC tumors. We trained three classifiers on a similar basis than the precedent section. Figure 7 shows the confusion matrices for the four-class problems for the three classifiers. The matrices are structured the same way as in Figs. 5(b) and 6(b), with four classes instead of two.
Fig. 7.
Classification performances for four classes: (a) to (c) present in order the confusion matrices for Haralick’s features on B-scan images (2-D), then based on the multilayer descriptor (3-D), and finally the CTSW algorithm performed on the multilayer descriptor.
Table 5 presents the accuracies for each class and for the three classifiers. Accuracy is calculated as the number of samples correctly classified in a certain category over the total number of samples of that category. For example, using the CTSW method, 80 healthy specimens were correctly assigned the category healthy and 15 were assigned other categories (2 in HGS, 2 in CC, and 11 in En) over the 95 healthy specimens, which yields an accuracy of 84%. The global accuracy for the Haralick’s features on intensity images was 54%, but including the multilayer descriptor increased this value to 55%. Using the CTSW algorithm in conjunction with the multilayer descriptor gave 71% global accuracy.
Table 5.
Four-class classification performances in terms of accuracy for the three classifiers and each class. The global accuracy is also given for the whole classifier.
| Normal (%) | HGS (%) | En (%) | CC (%) | Global (%) | |
|---|---|---|---|---|---|
| Haralick 2-D | 73 | 91 | 2 | 8 | 54 |
| Haralick 3-D | 68 | 83 | 22 | 13 | 55 |
| CTSW | 84 | 80 | 71 | 31 | 71 |
4. Discussion
A multilayer descriptor to represent volumetric OCT image information into a standard 2-D image was presented and implemented. This allows for additional insight into contextual data compared to traditional in-depth OCT images. This multilayer descriptor was then tested with two different algorithms to investigate the classification performances. It was also compared with a conventional gray-level feature extraction approach as a benchmark. Features from Haralick’s statistical and intensity-based features, as well as the color shape texture and wavelet decomposition technique were used to train classifiers using SVM. These classifiers were then validated and in a leave-one-patient-out scheme. To the best of our knowledge, the only other study addressing classification of ovarian tissue using OCT-based technique was published recently.42 We compare well with the results of the two well-defined classes study taken from 14 ovarian FFPE samples using full-field OCT (FF-OCT) to acquire en-face images. Applied on a test set of 20 images differentiating malignant tissue from normal, the FF-OCT study presents a sensitivity of 91.6% and specificity of 87.7%. We also compare well with other studies using two classes in other organs, such as the eyes23,24,26 or skin.27,28 As mentioned previously, results over 90% were presented in literature for glaucoma detection while skin classification was over 80%.
In comparison, ovarian classification may present a difference in complexity for the recognition, but the format used and the information retrieved from the volumes/samples allow ability to obtain similar result for binary issue. In the other hand, the multiclass results present a gain compare to the results of the three-class study base on speckle information for different kind of tissue32 (of 37.6%, 94.8%, and 65.3%,). Expecting the difference among the clinical cases, a possible explanation for the increase can be associated with the addition of structural and depth information present in the descriptors used. The multiclass problem for oral lesion offers a better result (average of accuracy per classes of 82.6%) for a four-class problem.32 But this gap can be explained by many factors. Predominantly, the solicitation of many modalities in the study of oral lesion can highlight different contrasts, which are not necessarily present in OCT and which may help the classification. In this optics, it may be interesting in further studies to combine the present descriptor for OCT with other modalities for ovarian classification. Moreover, the multiclass problem results compare well with other studies, even though they were performed on eyes32 and atrial tissue.31 Globally, the results seem to enhance that the format of information present additional useful to classify OCT for ovarian tissues recognition that represent low contrast.
A subset of OCT volumes from an existing ovarian cancer dataset was used. For the first test, the classifier’s capability to differentiate between the healthy and HGS classes, which are easily distinguishable by visual inspection of the OCT volumes, was assessed. The multilayer descriptor offered similar classification performances when used with the Haralick’s feature extraction, compared with the conventional Haralick’s texture performed on the intensity-only images. An AUC of 0.91 (83%, 95%, and 89% sensitivity, specificity, and accuracy, respectively) was achieved compared to 0.94 (94%, 94%, and 94% sensitivity, specificity, and accuracy, respectively). This is probably due to the addition of nonexplanatory information regarding textures, when using a small number of principal components for the classification (23 principal components for the 2-D version and 47 for the multilayer descriptor). The most pertinent features for classification and distinction between classes are not necessarily those expressing the highest explained variance in terms of principal components. In this context, the high number of features introduced by the multilayer descriptor is not appropriately reduced by an unsupervised analysis, such as PCA. Using the CTSW technique, the multilayer descriptor gave a higher AUC of 0.98 (91%, 93%, and 93% sensitivity, specificity, and accuracy, respectively).
The second test was designed to solve a more complex problem, namely, that associated with the classification between healthy and cancer specimens, which cannot be easily distinguished by simple visual inspection of the OCT volumes. In this case, the multilayer descriptor offered better performances when compared to analysis of more conventional texture metrics computed based on 2-D intensity images alone. The CTSW implementation with the descriptor yielded the best performances, 0.97 (93%, 89%, and 92% sensitivity, specificity, and accuracy, respectively). The conventional Haralick’s approach was less robust than in the case of two well-defined classes and achieved 0.83 AUC (84%, 81%, and 80% sensitivity, specificity, and accuracy, respectively) for the 2-D intensity images, comparable to an AUC of 0.84 with the multilayer descriptor (80%, 82%, and 81% sensitivity, specificity, and accuracy, respectively).
The third test pushed the limits of the multilayer descriptor with a four-class problem, using the healthy specimens in the first class and the three cancer types, each in a different class. The conventional Haralick’s technique on 2-D intensity images yielded 55% accuracy, which should be compared with the value of 25% corresponding to a random classification results. The Haralick’s features with the multilayer descriptor yielded an accuracy of 55%, comparable to the 2-D features. Finally, the CTSW algorithm used in conjunction with the multilayer descriptor gave an accuracy of 71%. The multilayer descriptor is well-suited for complex problems and yields significant improvement in classification performances, even in the unsupervised case. This can be explained by the fact that this descriptor leverages from 3-D spatial information as well as statistical information to better highlight more subtle differences between similar specimens of different classes. This descriptor must be fully exploited using an analysis that can discern the most relevant features.
In the context of ovarian cancer tissue identification, the use of OCT can provide pertinent insight on many levels, such as during the pathological examination of the specimens (for diagnostics), as well as during the surgical procedures (for surgical resection guidance). In both cases, there is a variety of specimens to analyze, with a large area in terms of histological resolution and field of view. Fallopian tubes, and more specifically ovaries, show a wide range of architectural variations due to hormonal levels, over the course of a lifetime and more rapidly over the course of the menstrual cycle. The reality of the clinical practice unfortunately must consider those variabilities. We tried to replicate this complexity in our dataset. In addition, most of ovarian cancers (over 70%) are HGS, and those lesions are now known to originate from the fallopian tubes. Those HGS lesions then migrate to the ovaries and the rest of the peritoneal and abdominal cavity as metastases. As the lesions and tumors migrate beyond the ovaries, cancer usually progresses at a fast rate and reaches stages III and IV, with the chances of survival of 10% to 20%. To this day, unfortunately, no efficient screening technique or tool exists to detect ovarian cancer in early stages. To circumvent this limitation, as well as to increase the lifetime of high-risk patients (those with family history of ovarian cancer of with hereditary conditions, such as BRCA I and/or BRCA II mutations), medical guidelines encourage prophylactic surgeries, an invasive procedure to remove the fallopian tubes and ovaries. This measure aims at limiting the spread of the disease but often results in unnecessary surgeries (or surgeries that could have been delayed). Once the organs have been removed, they should undergo thorough pathological examination to identify suspicious lesions in fallopian tubes and ovaries. OCT can be a promising imaging modality to perform a high-resolution assessment of the tissue without having to fix, slice, or cut the specimens. Even with OCT, the size of the organs yields a great amount of data, which could benefit from automated classification, using classifiers such as the ones built in this paper. Classification results can then be used by pathologist to help them register and localize suspicious lesions in the specimens that could be further analyzed with histology.
The classifiers can be both useful for surgical field inspection and pathological examination. In both cases, the emphasis should be placed on examination of the fimbriated end of the fallopian tube, which is easily accessible for OCT measurements both in the surgical field and during pathological evaluation. Healthy fallopian tubes must be clearly discerned from HGS lesions and tumors. Moreover, the ovary must be looked upon closely to see if there are any suspicious structures, such as glandular growth (closely related to endometrial cancer), solid carcinoma architecture (closely related to HGS cancer), or tubule-cystic architecture (present in cases of CC cancers). For pathological evaluation, a small probe that could be inserted within the tube could be used to acquire OCT images for the classifier. Small OCT probes have been developed specifically tailored to fallopian tube analysis.34,43 For ovaries analysis, as well as the exterior of the fimbriated end of the tubes, a wide-field scanning head, similar to the one used in this study, may be more appropriate. In the surgical workflow, a handheld probe may be more appropriate, but for a screening tool, a flexible mm-sized probe should be envisioned. Nevertheless, with similar imaging resolutions, the classifiers should be able to distinguish between cancer and healthy tissue in any probe configuration, given it got appropriate training and validation prior to imaging.
The dataflow can be divided into two steps: the formatting steps and the description extraction/classification. The first part was the more time-consuming. For one complete formatting and conversion from volume in 2-D images on a , the processing time on a I7 4820k 3.76 GHz with 32-Gb RAM took 65 s. One of the most time-consuming part was associated with the polynomial fitting of every A-line and the multiple hard drive writings and readings. With the commercial system used, OCT data were first written in a binary format that required conversion to a normalized image format. The raw data were read from the disk and normalized, and then the depth information was computed and saved in an RGB image format prior to the extraction of the classifiable vectors. However, this process can be accelerated by computing all the metrics during the acquisition process and then saving directly in the appropriate format limiting the I/O flow. This would require rewriting the commercial software platform for OCT acquisition, which was not the scope of this paper. On the other hand, the second part was quick for the features calculations: 0.12 s for CTSW and 0.26 s for Haralick’s textures per ROI. The classification part was negligible compared to the metric extraction (fraction of a second).
A definitive study to build a classifier would require a large clinical dataset of OCT images. In this study, we used paraffin-embedded specimens from a biobank. This biobank contains more samples from surgeries that were acquired over the years and fixed in paraffin. We could leverage from this biobank and others across Canada or in another country to minimize the bias from sample from a single institution and/or the acquisition through the same OCT system. An appropriate size of cohort for this study should range around 80 to 100 patients per class, to capture the inherent heterogeneity of ovaries during the menstrual cycle, and various time point during the life, and all these with or without hormonal therapy or contraceptive methods. We estimate that a minimum of three patients per subcategory would be a good start. The number of classes could be extended to also cover the low-grade serous and the mucinous tumors, which are also common. Some benign conditions could also be integrated, such as polycystic ovary syndrome and ovarian cysts. Hence, the minimal size of the cohort should be of 800 patients. If deep learning strategies are used to build and train a classifier, the number of patients should go higher and range in the 8000 to 10,000. The classifiers built here are meant to be a proof of principle to demonstrate the feasibility of accurate OCT classification performed on clinical data presenting low amount of structures. It is also intended to consider the clinical reality of pathology, in which samples may be viewed from any direction, not necessarily with the same markers from patient to patient. Next step on improving the complexity of classification technique would require a large database of OCT clinical images and volumes, not readily available. Once such database is available, CNN or other deep learning algorithms could be optimized to classify ovarian cancer OCT images.
The limitations of this study are the small number of patients, due to the limited availability of OCT images from clinical patients. As more OCT images of gynecologic specimens become available, the dataset can be expanded. Also, all the samples were taken from the same medical center, with the same OCT imaging system. It could be interesting to quantify the impact of different OCT system manufacturers on image acquisition and classification, as well as the variability of OCT scans from other medical or academic centers.
5. Conclusion
We demonstrated a multilayer descriptor encoding 3-D spatial information into common 2-D three-channel images (e.g., RGB format) to allow more efficient tissue classification. The descriptor was successfully implemented with two different feature extraction techniques and led to an AUC of 0.98 (91%, 93%, and 93% sensitivity, specificity, and accuracy, respectively) when classifying OCT volumes of paraffin-embedded ovarian cancer specimens and healthy fallopian tubes from 24 patients. Moreover, the descriptor showed significant classification performance improvements for multiclass approach and yielded an accuracy of 71%. The dataset used for this classifier was a collection of specimens from 38 patients, containing healthy fallopian tubes, HGS tumors, En tumors, and CC tumors. Of note, this kind of descriptor allows for more efficient handling of 3-D spatial information easily accessible through OCT systems.
Acknowledgments
The authors would like to thank Liliane Meunier and Christine Caron for assistance with tumor specimens and histology. We are grateful to Fouzi Benboujja and Michael Jermyn for fruitful discussions. Tumor banking was supported by the Banque de tissus et données of the Réseau de recherche sur le cancer of the Fond de recherche du Québec–Santé (FRQS), associated with the Canadian Tumor Repository Network. K.R., D.T., and A-M.M-M. are researchers of the Centre de recherche du Centre hospitalier de l’Université de Montréal (CRCHUM), which receives support from the FRQS. C.S.-P. is a scholar from Groupe de Recherche en Sciences et Technologies Biomédicales (GRSTB), financed by the FRQS. W.-J.M. and E.D.M are scholars of the Natural Sciences and Engineering Research Council of Canada (NSERC). N.G. and C.B. received support from NSERC. F.L. and D.T. received support from Movember Discovery Grants 2015 to 2017, Prostate Cancer Canada and Program interne de projets pilotes du continuum de recherche 2015-2017 from CRCHUM. D.T. receives salary support from the FRQS (Clinical Research Scholar, Junior 1) and Prostate Cancer Canada (Movember Rising Star Award).
Biography
Biographies for the authors are not available.
Appendix.
A.1. Tissue Segmentation
The tissue segmentation was computed in 2-D on the first en-face image of the stack, and the same mask was subsequently applied on the next layers. The first segmentation step consists of an erosion on the first image with a disk of 10-pixel radius. A large radius had been taken to reduce the effect of the speckle. Thereafter, a morphological reconstruction (imreconstruct, MATLAB®)44 was applied between the eroded image and the original image. This operation was followed by an image dilatation with the same disk’s size as for erosion. A final morphological reconstruction was applied between the inverse of the dilated image and the inverse on the image prior to dilatation. Since the operand was applied on the inverse images, a last inversion was necessary before, finally, creating a binary mask using a threshold define by the Otsu’s method (graythresh, MATLAB®).45
A.2. Haralick’s Features
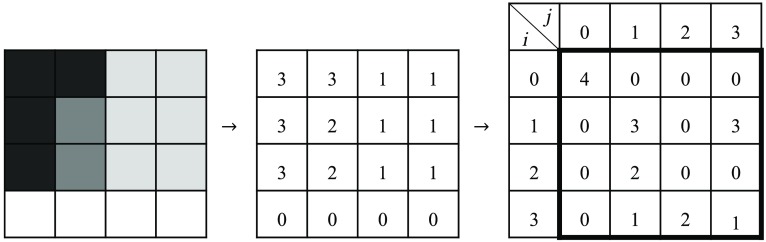
Haralick’s features were computed by using the normalized GLCM associated with a gray-level image and a vector.36 The GLCM represents how often a pixel shares a common brightness with the pixels that are separated from it by a fixed distance.
Figure 8 shows an example of the GLCM calculation. An intensity image is converted to a map of brightness ranges (example with 4 ranges from 0 to 3). To compute the GLCM, an offset vector (magnitude and direction) must be chosen. The previous example compares a reference pixel with its next horizontal neighbor on the right. Hence, the offset has distance of one and an orientation of 0 deg. The GLCM quantifies the number of couples sharing a ’th and ’th values. The ’th range is associated with reference pixel while the ’th represents the range of the neighbor pixel. For the GLCM calculation, 100 brightness ranges were used, and a collection of offsets was calculated for 0 deg, 90 deg, 180 deg, and 270 deg and 10 different distances (1, 3, 6, 10, 15, 20, 25, 50, 75, and 100 pixels). Longer vectors were included to evaluate slow variations and smaller ones for local information associated with shaper spatial variations and speckle. For each offset, a new GLCM was calculated.
Fig. 8.
Example of gray-level co-occurrence matrix () calculation.
Haralick’s features are well-known descriptors of intensity characteristics in images.36 They combine 14 features calculated on GLCM and they format image content in a classifiable vector. Three of the most common features were selected: correlation, contrast, and energy (derived from the angular second moment). The correlation [Eq. (2)] can be interpreted as the repetition in the image while the contrast [Eq. (3)] evaluates the variation in intensity
| (2) |
| (3) |
where is the normalized gray tone entry for the index and position for gray level and , , , and are the average value and the standard deviation defined as
| (4) |
| (5) |
| (6) |
| (7) |
Energy [Eq. (8)] quantifies the similitude between a pixel and its neighborhood. A high-energy score would translate as a more uniform image
| (8) |
Haralick’s features are used as a benchmark on an OCT image and are also computed for each channel of the multilayer descriptor.
A.3. Image Descriptor Based on Color, Texture, Shape, and Wavelets Features
The first calculation step of this descriptor consists of a local binary patterns descriptor in three-dimension (3D-LBP).37 The descriptor generates a sequence of eight bits for each dimension where both the position and the value of those bits encode spatial information. The position is associated to the spatial distribution of the neighbors. The value of each bit describes whether its given neighbor has or not a higher intensity then the given pixel. The local binary descriptor is defined for each pixel by comparing a pixel value with the one of its 8 nearest neighbors
| (9) |
where is a , channel position, is the Heaviside step function, is the function that return a gray level at a given position, and corresponds to the position of the neighbor associated with index . The LBP [Eq. (9)] associates the bit index of each pixel to one of the neighborhood localization, as shown in Fig. 9. One individual bit value is set to one if the corresponding neighbor is greater or equal to the center value and zero otherwise. Each pixel of the image is processed this way to generate the LBP descriptor.
Fig. 9.
Example of LBP calculation. An image of is composed of gray levels. The center pixel is selected for this calculation example. Every surrounding pixel’s intensity is then compared to the reference pixel to generate a binary map. The binary map is then organized into a sequence of eight bits generated from the values of the binary map read clockwise from the top left corner. This sequence of bit is then written as the value of the reference pixel in the 3D-LBP descriptor.
To transform this descriptor in a multichannel descriptor, Banerji et al.37 adapted the neighborhood function to return different index for three orthogonal planes, the first one to get the eight neighbors intrachannel and the second are the two interchannel planes. In this study, we defined the first neighborhood orientation to give a texture information for an en-face view of the multilayer descriptor (three maps are generated: one for each layer: the en-face image, the DHI, and the homogeneity layer) while the two other orientations present the relation among the three interchannel values. Since the multilayer accounts for volumetric data, classification performance may benefit from interchannel information.
For a three-channel image, the intermediate result consisted of three new images of three channels each. The colored image and the 3D-LBP descriptor were then decomposed with Haar wavelet transform. Each image was converted in an intensity histogram, and the resulting histograms were concatenated to create the H-descriptor. Finally, a PCA was performed on H-descriptor prior to classification.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Huang D., et al. , “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Drexler W., Fujimoto J. G., Optical Coherence Tomography—Technology and Applications, 2nd ed., Springer International Publishing, Berlin: (2015). 10.1007/978-3-319-06419-2 [DOI] [Google Scholar]
- 3.Drexler W., et al. , “Optical coherence tomography today: speed, contrast, and multimodality,” J. Biomed. Opt. 19(7), 071412 (2014). 10.1117/1.JBO.19.7.071412 [DOI] [PubMed] [Google Scholar]
- 4.Wang T., et al. , “Heartbeat OCT: in vivo intravascular megahertz-optical coherence tomography,” Biomed. Opt. Express 6(12), 5021–5032 (2015). 10.1364/BOE.6.005021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.De Boer J., Leitgeb R., Wojtkowski M., “Twenty-five years of optical coherence tomography: the paradigm shift in sensitivity and speed provided by Fourier domain OCT,” Biomed. Opt. Express 8(7), 3248–3280 (2017). 10.1364/BOE.8.003248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gora M. J., et al. , “Endoscopic optical coherence tomography: technologies and clinical applications,” Biomed. Opt. Express 8(5), 2405–2444 (2017). 10.1364/BOE.8.002405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tearney G. J., et al. , “Consensus standards for acquisition, measurement, and reporting of intravascular optical coherence tomography studies: a report from the International Working Group for Intravascular Optical Coherence Tomography Standardization and Validation,” J. Am. Coll. Cardiol. 59(12), 1058–1072 (2012). 10.1016/j.jacc.2011.09.079 [DOI] [PubMed] [Google Scholar]
- 8.Ughi G. J., et al. , “Clinical characterization of coronary atherosclerosis with dual-modality OCT and near-infrared autofluorescence imaging,” JACC Cardiovasc. Imaging 9, 1304–1314 (2016). 10.1016/j.jcmg.2015.11.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bouma B., et al. , “Intravascular optical coherence tomography,” Biomed. Opt. Express 8(5), 2660–2686 (2017). 10.1364/BOE.8.002660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Olsen J., Themstrup L., Jemec G. B. E., “Optical coherence tomography in dermatology,” G. Ital. Dermatol. Venereol. 150(5), 603–615 (2015). [PubMed] [Google Scholar]
- 11.Dong Z., Wollstein G., Schuman J. S., “Clinical utility of optical coherence tomography in glaucoma,” Invest. Ophthalmol. Visual Sci. 57(9), OCT556 (2016). 10.1167/iovs.16-19933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ughi G. J., et al. , “Automated segmentation and characterization of esophageal wall in vivo by tethered capsule optical coherence tomography endomicroscopy,” Biomed. Opt. Express 7(2), 409–419 (2016). 10.1364/BOE.7.000409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang E. W., et al. , “Low coherence interferometry approach for aiding fine needle aspiration biopsies,” J. Biomed. Opt. 19(11), 116005 (2014). 10.1117/1.JBO.19.11.116005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Scolaro L., et al. , “Molecular imaging needles: dual-modality optical coherence tomography and fluorescence imaging of labeled antibodies deep in tissue,” Biomed. Opt. Express 6(5), 1767–1781 (2015). 10.1364/BOE.6.001767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McLaughlin R. A., Sampson D. D., “Clinical applications of fiber-optic probes in optical coherence tomography,” Opt. Fiber Technol. 16(6), 467–475 (2010). 10.1016/j.yofte.2010.09.013 [DOI] [Google Scholar]
- 16.Fuchs T. J., Buhmann J. M., “Computational pathology: challenges and promises for tissue analysis,” Comput. Med. Imaging Graphics 35(7–8), 515–530 (2011). 10.1016/j.compmedimag.2011.02.006 [DOI] [PubMed] [Google Scholar]
- 17.Wang H., et al. , “Mitosis detection in breast cancer pathology images by combining handcrafted and convolutional neural network features,” J. Med. Imaging 1(3), 034003 (2014). 10.1117/1.JMI.1.3.034003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Napolitano G., et al. , “Machine learning classification of surgical pathology reports and chunk recognition for information extraction noise reduction,” Artif. Intell. Med. 70, 77–83 (2016). 10.1016/j.artmed.2016.06.001 [DOI] [PubMed] [Google Scholar]
- 19.Corredor G., et al. , “Training a cell-level classifier for detecting basal-cell carcinoma by combining human visual attention maps with low-level handcrafted features,” J. Med. Imaging 4(2), 021105 (2017). 10.1117/1.JMI.4.2.021105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Witten I. H., Frank E., “Part II. More advanced machine learning schemes,” in Data Mining, Witten I. H., et al., Eds., 4th ed., pp. 205–208, Morgan Kaufmann, San Francisco, California: (2017). [Google Scholar]
- 21.Asaoka R., et al. , “Validating the usefulness of the ‘random forests’ classifier to diagnose early glaucoma with optical coherence tomography,” Am. J. Ophthalmol. 174, 95–103 (2017). 10.1016/j.ajo.2016.11.001 [DOI] [PubMed] [Google Scholar]
- 22.Yoshida T., et al. , “Discriminating between glaucoma and normal eyes using optical coherence tomography and the ‘random forests’ classifier,” PLoS One 9(8), e106117 (2014). 10.1371/journal.pone.0106117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Burgansky-Eliash Z., et al. , “Optical coherence tomography machine learning classifiers for glaucoma detection: a preliminary study,” Invest. Ophthalmol. Visual Sci. 46(11), 4147–4152 (2005). 10.1167/iovs.05-0366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee S., et al. , “Atlas-based shape analysis and classification of retinal optical coherence tomography images using the functional shape (fshape) framework,” Med. Image Anal. 35, 570–581 (2017). 10.1016/j.media.2016.08.012 [DOI] [PubMed] [Google Scholar]
- 25.Lee C. S., Baughman D. M., Lee A. Y., “Deep learning is effective for classifying normal versus age-related macular degeneration optical coherence tomography images,” Ophthalmol. Retina 1, 322–327 (2016). 10.1016/j.oret.2016.12.009 [DOI] [Google Scholar]
- 26.Albarrak A., Coenen F., Zheng Y., “Volumetric image classification using homogeneous decomposition and dictionary learning: a study using retinal optical coherence tomography for detecting age-related macular degeneration,” Comput. Med. Imaging Graphics 55, 113–123 (2017). 10.1016/j.compmedimag.2016.07.007 [DOI] [PubMed] [Google Scholar]
- 27.Jørgensen T. M., et al. , “Machine-learning classification of non-melanoma skin cancers from image features obtained by optical coherence tomography,” Skin Res. Technol. 14(3), 364–369 (2008). 10.1111/srt.2008.14.issue-3 [DOI] [PubMed] [Google Scholar]
- 28.Marvdashti T., et al. , “Classification of basal cell carcinoma in human skin using machine learning and quantitative features captured by polarization sensitive optical coherence tomography,” Biomed. Opt. Express 7(9), 3721–3735 (2016). 10.1364/BOE.7.003721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang Y., et al. , “Machine learning based detection of age-related macular degeneration (AMD) and diabetic macular edema (DME) from optical coherence tomography (OCT) images,” Biomed. Opt. Express 7(12), 4928–4940 (2016). 10.1364/BOE.7.004928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Karri S. P. K., Chakraborty D., Chatterjee J., “Transfer learning based classification of optical coherence tomography images with diabetic macular edema and dry age-related macular degeneration,” Biomed. Opt. Express 8(2), 579–592 (2017). 10.1364/BOE.8.000579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gan Y., et al. , “Automated classification of optical coherence tomography images of human atrial tissue,” J. Biomed. Opt. 21(10), 101407 (2016). 10.1117/1.JBO.21.10.101407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gossage K. W., et al. , “Texture analysis of optical coherence tomography images: feasibility for tissue classification,” J. Biomed. Opt. 8(3), 570–575 (2003). 10.1117/1.1577575 [DOI] [PubMed] [Google Scholar]
- 33.Banerjee S., et al. , “Global spectral and local molecular connects for optical coherence tomography features to classify oral lesions towards unravelling quantitative imaging biomarkers,” RSC Adv. 6(9), 7511–7520 (2016). 10.1039/C5RA24117K [DOI] [Google Scholar]
- 34.Madore W.-J., et al. , “Morphologic 3D scanning of fallopian tube to assist ovarian cancer diagnosis,” Proc. SPIE 9689, 96894D (2017). 10.1117/12.2211204 [DOI] [PubMed] [Google Scholar]
- 35.Soille P., Morphological Image Analysis: Principles and Applications, Springer-Verlag, New York: (2003). [Google Scholar]
- 36.Haralick R. M., Shanmugam K., Dinstein I., “Textural features for image classification,” IEEE Trans. Syst. Man Cybern. SMC-3(6), 610–621 (1973). 10.1109/TSMC.1973.4309314 [DOI] [Google Scholar]
- 37.Banerji S., Sinha A., Liu C., “New image descriptors based on color, texture, shape, and wavelets for object and scene image classification,” Neurocomputing 117, 173–185 (2013). 10.1016/j.neucom.2013.02.014 [DOI] [Google Scholar]
- 38.Shalev R., et al. , “Processing to determine optical parameters of atherosclerotic disease from phantom and clinical intravascular optical coherence tomography three-dimensional pullbacks,” J. Med. Imaging 3(2), 024501 (2016). 10.1117/1.JMI.3.2.024501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Van Soest G., et al. , “Atherosclerotic tissue characterization in vivo by optical coherence tomography attenuation imaging,” J. Biomed. Opt. 15(1), 011105 (2010). 10.1117/1.3280271 [DOI] [PubMed] [Google Scholar]
- 40.Ojala T., Pietikainen M., Harwood D., “A comparative study of texture measures with classification based on feature distributions,” Pattern Recognit. 29(1), 51–59 (1996). 10.1016/0031-3203(95)00067-4 [DOI] [Google Scholar]
- 41.Harwood D., et al. , “Texture classification by center-symmetric auto-correlation, using Kullback discrimination of distributions,” Pattern Recognit. Lett. 16(1), 1–10 (1995). 10.1016/0167-8655(94)00061-7 [DOI] [Google Scholar]
- 42.Nandy S., Sanders M., Zhu Q., “Classification and analysis of human ovarian tissue using full field optical coherence tomography,” Biomed. Opt. Express 7(12), 5182–5187 (2016). 10.1364/BOE.7.005182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Keenan M., et al. , “Design and characterization of a combined OCT and wide field imaging falloposcope for ovarian cancer detection,” Biomed. Opt. Express 8(1), 124–136 (2017). 10.1364/BOE.8.000124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.“imreconstruct,” in Mathworks Documentation, The MathWorks Inc., Natick, Massachusetts: (2017). [Google Scholar]
- 45.“graythresh,” in Mathworks Documentation, The MathWorks Inc., Natick, Massachusetts: (2017). [Google Scholar]