Abstract
To adapt to the environment and survive, most animals can control their behaviors by making decisions. The process of decision-making and responding according to cues in the environment is stable, sustainable, and learnable. Understanding how behaviors are regulated by neural circuits and the encoding and decoding mechanisms from stimuli to responses are important goals in neuroscience. From results observed in Drosophila experiments, the underlying decision-making process is discussed, and a neural circuit that implements a two-choice decision-making model is proposed to explain and reproduce the observations. Compared with previous two-choice decision making models, our model uses synaptic plasticity to explain changes in decision output given the same environment. Moreover, biological meanings of parameters of our decision-making model are discussed. In this paper, we explain at the micro-level (i.e., neurons and synapses) how observable decision-making behavior at the macro-level is acquired and achieved.
Keywords: Decision-making behavior, Drift diffusion model, Spiking neural circuit, Synaptic plasticity, Learning mechanism
Introduction and motivation
Animal decision-making in behavior
Most animals can accurately control their behaviors to pursue benefits or avoid harm. For example, many insects have the ability to navigate by sunlight, accurately maintaining a fixed angle between flight and lighting direction. This behavior is highly stable and sustainable and must be regulated by an internal control system. This system, making decisions based on sensory input to carry out correct movements, is similar to a feedback control system in automatic control theory. Such decision-making behavior is more complex than a reflex and is usually achieved by the nervous system.
Choice behavior of Drosophila facing visual cues has been studied previously (Tang and Guo 2001; Zhang et al. 2007). In one experiment, flies were fixed in the center of a flight simulator and were only able to rotate in place. Two different color cues in the environment, green and blue, were presented to flies, and blue cues were associated with heat punishment. In the training session, flies were punished whenever the blue cue entered the frontal 90° sector of their visual field. The time that the flies spent in different flight directions was recorded. Flies showed no color preference before the training session but exhibited a preference for the green cues, which were not associated with heat punishment, after the training session. This result shows that flies can adjust flight behavior depending on visual input stimuli, suggesting that they can make decisions based on perceived color cues rather than random reflexes. We can make a reasonable assumption that a neural circuit for decision-making underlies this behavior and determines the direction of rotation (clockwise or counterclockwise) based on perceived color cues. The significant change in color preference before and after training suggests that a new decision-making neural circuit was formed. This behavioral experiment raises several questions. First, what is the decision-making process behind this behavior? Second, in the case of Drosophila, what kind of neural circuit in the central complex likely implements this decision-making process? Third, this neural circuit changed during the training session, so how was it corrected? Given these questions, this paper attempts to explain the structure of the decision-making neural circuit and its learning process in Drosophila behavioral experiments, using existing computational models of biological neurons and synaptic plasticity.
Related works in neural circuit modeling
Previous related studies on construction of neural circuits can be divided into four categories. First, there are artificial neural network models in engineering that focus on functionality and are not consistent with anatomical and electrophysiological evidence of biological nervous systems. These do not reflect the actual workings of the nervous system. Second, recurrent network models (Wang 2002) explain the process of decision-making. However, changes in decision-making or the learning process, which are exemplified by the Drosophila experiment described above, were not considered in these models. Third, some large-scale neural simulations (Ananthanarayanan and Modha 2007; Izhikevich and Edelman 2008; Markram 2006; Waldrop 2012) “seek ‘computer simulations that are very closely linked to the detailed anatomical and physiological structure’ of the brain, in hopes of ‘generating unanticipated functional insights based on emergent properties of neuronal structure’” (Carandini 2012). These simulations currently do not demonstrate connections between working mechanisms of neural circuits and specific observable behaviors (Eliasmith et al. 2012). Finally, some neural circuits (Bohte et al. 2002; Eliasmith et al. 2012; Foderaro et al. 2010; Natschläger and Ruf 1998; Zhang et al. 2013) were built using biological neuron models to solve application problems. However, ideas that are not biologically plausible were introduced from artificial neural networks, and external learning signals as indicators of errors were artificially imposed on the learning mechanisms and not integrated into circuits.
In the remainder of this paper, the decision-making process behind Drosophila behavior is discussed first. Then, the learnable neural circuit implementing the suggested decision-making process, which was comprised of different types of biological neurons, is presented. Three experiments are presented. In the first experiment, changes in the decision-making process resulting from punishment signals were investigated while considering biophysical characteristics of neurons. In the second experiment, simple circuits from the first experiment were integrated into a larger circuit to simulate Drosophila behavior. In the third experiment, neural mechanism underlying the behavior of Drosophila facing conflicting visual cues was investigated.
Decision-making model
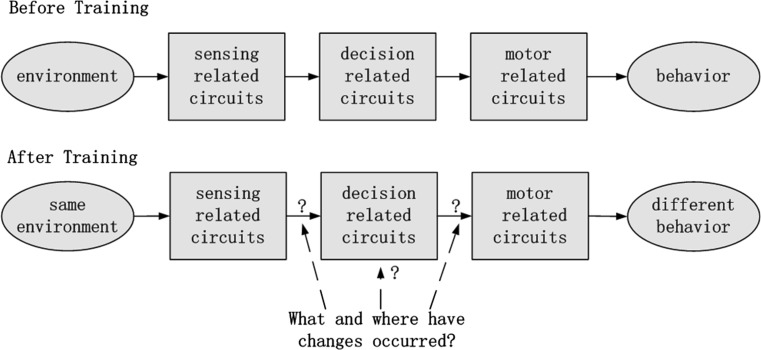
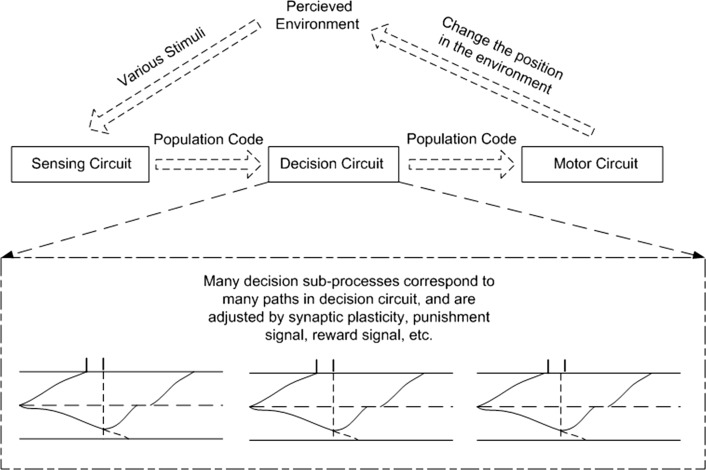
In the Drosophila experiment described above, the color stimuli in environment were fixed, but the behavior of flies before and after training changed, which suggests that, after training, some elements in circuits from sensing to decision to motor have changed, as illustrated in Fig. 1. We suggest that these changes result in reversal of output and occur in decision circuits.
Fig. 1.
Illustration of changes in decision-making process
To model complex continuous behavior of Drosophila, the decision-making process was decomposed into multiple simple discrete two-choice decision-making processes, as shown in Fig. 2. Attention mechanism was considered in the decision-making process. At each time step, the fly was given a probability to notice a single nearby color cue. Then, a decision (turn left or turn right) had to be made, and the fly shifted to a new state by executing the decision. The unbiased behavior of flies before training can be explained by attraction to both color cues. In addition, the biased behavior after training can be explained by attraction to a single color and repulsion from the other. Then, the change of behavior can be thought as a result of flipping the output of multiple two-choice decision-making processes.
Fig. 2.
Decomposition of decision making process
Drift diffusion model
A well-known model in two-choice decision-making is the drift diffusion model (Ratcliff 1978). We follow the order in Bogacz et al. (2006) to briefly introduce the drift diffusion model and its variants, and then we introduce our decision-making model as well as the relationships between these models. The equation of the drift diffusion model has been published previously and is shown in Eq. 1 (Bogacz et al. 2006), where A is the drift rate, c is a constant, and represents the noise term. Figure 3 illustrates the decision process of this model. This model assumes that evidence is accumulated for a single choice with a noise; when the evidence reaches one decision threshold, then a decision is made. The drift diffusion model is simple and can explain many characteristics of real data from response behavior experiments such as the trade-off between response time and response accuracy (Ratcliff and Rouder 1998). However, the biological meaning of parameters (drift rate A, starting point, decision bounds) in the drift diffusion model is difficult to define. Furthermore, the change of decision-making in a two-choice decision process was not investigated in these models. Thus, it cannot explain the change of behavior in the above Drosophila experiment.
| 1 |
Fig. 3.
Illustration of the diffusion model
The Ornstein–Uhlenbeck model (Busemeyer and Townsend 1993) added a third term (i.e., ) that is proportional to current accumulated evidence x as shown in Eq. 2 Bogacz et al. (2006). In this model, the change of evidence also depends on current accumulated evidence.
| 2 |
In the race model (Vickers 1970), separate evidence accumulators are used for two choices instead of a single accumulator in the drift diffusion model as shown in Eq. 3 (Bogacz et al. 2006). In the mutual inhibition model (Usher and McClelland 2001), mutual inhibition terms (i.e., and ) between the two separate accumulators were added as shown in Eq. 4 (Bogacz et al. 2006).
| 3 |
| 4 |
In the pooled inhibition model (also known as recurrent network model; Wang 2002), mutual inhibition was implemented by an additional inhibitory neuron pool (i.e., ). Moreover, this model was based on simulating pools of biological spiking neurons. This model made progress in the connection between the phenomenon decision-making model and the biophysical neural circuit model. The equation of this model can be simplified as shown in Eq. 5 (Bogacz et al. 2006). However, as in the other decision-making models, the pooled inhibition model only investigated the process of decision-making when the decision was solid. The change or flipping of decision output in a two-choice decision-making process when input stimulus remained constant was not investigated. This model still cannot explain the change of behavior in the above Drosophila experiment.
| 5 |
Decision-making model in this paper
The decision-making model in this paper is based on simulations of biological spiking neurons and is similar to the pooled inhibition model. In addition, the change or flipping of decision output in a two-choice decision-making process when input stimulus remains constant was investigated while considering synaptic plasticity. Before introducing the decision-making model, the model of the spiking neuron used in this paper is introduced.
Neuron model
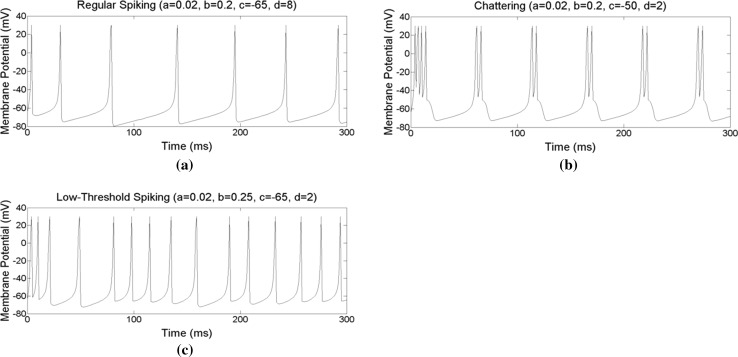
The spiking neuron model proposed by Izhikevich (2003) is used in this paper, as shown in Eqs. (6, 7, 8). Izhikevich’s neuron model is widely used in many studies (Qu et al. 2014; Samura et al. 2015; Li et al. 2016; Zhao et al. 2016. Three spiking patterns were used: regular spiking (RS), chattering (CH), and low-threshold spiking (LTS), as shown in Fig. 4. The RS and CH patterns are exhibited in excitatory neurons, and the LTS pattern is exhibited in inhibitory neurons. When presented with a prolonged stimulus, RS type neurons “fire a few spikes with short interspike period and then the period increases” (Izhikevich 2003). They were used as input neurons in this study, receiving stimuli and converting stimuli into spike trains. Neurons with a CH pattern “fire stereotypical bursts of closely spaced spikes” (Izhikevich 2003). They were used as control and output neurons because a burst of spikes can provide more stimuli in a short time period. As a result, the inhibitory neurons connected to these CH type neurons react quickly. The LTS type neuron was similar to the RS type and was used as interneurons (i.e., inhibitory neurons).
| 6 |
| 7 |
| 8 |
Fig. 4.
Three types of spiking patterns, a regular spiking, b chattering, c low-threshold spiking
Neural diffusion model
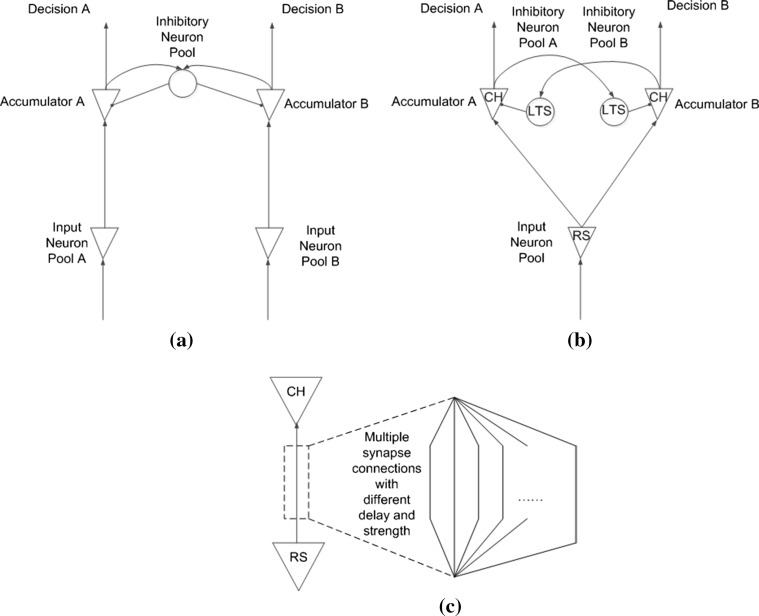
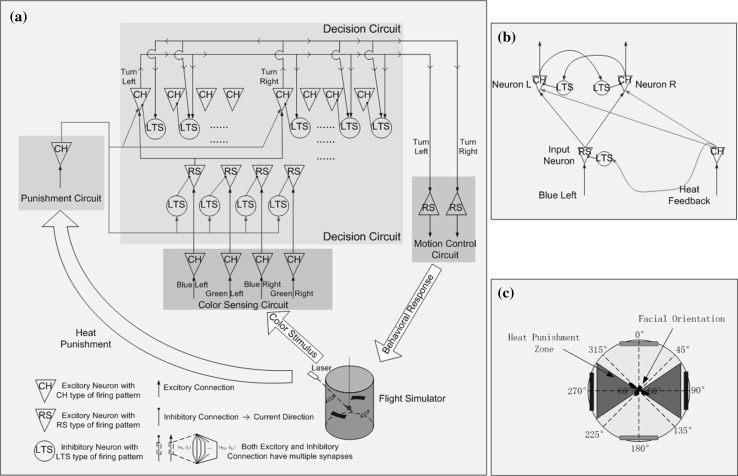
The architecture of the decision-making model in this paper is shown in Fig. 5b. As in the pooled inhibition model (Fig. 5a), input neuron pool is used to convert external stimuli to spiking trains, and two excitatory neuron pools as two separate evidence accumulators receive stimuli from the input neuron pool and race to fire. Inhibitory neuron pools are connected to excitatory neuron pools to generate competition between these two evidence accumulators. However, there are two major differences between our model and the pooled inhibition model. First, the two excitatory neuron pools share one input neuron pool in our model. In the pooled inhibition model, the two excitatory neuron pools use two separate input neuron pools and the result of competition between the two evidence accumulators depends on, to some degree, the relative strength of stimuli of these two separate input neuron pools. In addition, flipping the result of competition depends on flipping the relative strength of input stimuli. In other words, the decision flipping phenomenon was not explained by the pooled inhibition model itself but by flipping the input to the pooled inhibition model. However, in our model, the two evidence accumulators share the same stimulus source, and the result of competition between accumulators depends on differences in synaptic connections from input neuron pool to different excitatory neuron pools. As shown in Fig. 5c, there are multiple connections with different delays and strengths from input neuron pool to excitatory neuron pools. In addition, flipping or changing the result of competition occurs because changes in synaptic connections controlled by synaptic plasticity. Second, in our model, two separate inhibitory neuron pools facilitate competition between separate accumulators and help distinguish responsibility during punishment. The role and effect of these two separate inhibitory neuron pools, synaptic plasticity, and punishment signal are discussed in detail in the experiment section.
Fig. 5.
a Simplified architecture of the pooled inhibition model, b architecture of the decision making model, c synapse connections between a pair of neurons in the model
The equations for our model are presented in Eqs. (9–20). The relationship between our model and previous decision-making models can be easily observed from these equations. Our equations are based on Izhikevich’s equations for modeling membrane potential of biological neurons. The process of accumulating membrane potential to fire naturally corresponds to the process of accumulating evidence in the drift diffusion model. Moreover, the parameters in the previous models can be explained in terms of biological meaning. The starting point in the drift diffusion model corresponds to the parameters c in the Izhikevich model, which “describe the after-spike reset value of membrane potential v caused by the fast high-threshold conductances” (Izhikevich 2003). The decision threshold can be explained by peak membrane potential, and noise can be explained using local field potentials. The drift rate corresponds to the strength of input stimuli and synaptic connections. The term added in the Ornstein–Uhlenbeck model, which is proportional to current accumulated evidence, is contained in Izhikevich’s original equations as shown in Eq. (9), which “was obtained by fitting the spiking initiation dynamics to a cortical neuron” (Izhikevich 2003). The negative term u, which is also related to the potential v, “represents a membrane recovery variable which accounts for the activation of ionic currents and inactivation of ionic currents” (Izhikevich 2003). The parameters a, b, d also have an effect on accumulating evidence (or potential), but in a more complex way. The different spiking patterns shown in Fig. 4 are controlled by these three parameters. The parameters a, b, c separately describe “the time scale of the recovery variable u”, “the sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential v”, and the “after-spike reset of the recovery variable u caused by slow high-threshold and conductances” (Izhikevich 2003). The separate evidence accumulators in the race model and mutual inhibition term in the mutual inhibition model are explained by the separate excitatory and inhibitory neuron pools. In addition, the change of the decision-making process given the same input stimuli, which is the focus of this paper, is explained by synaptic plasticity. Figure 6 illustrates the decision-making process of our model in a similar way as the drift diffusion model.
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
Fig. 6.
Illustration of the decision making model in this paper
Synaptic plasticity
In our model, synaptic plasticity was considered to explain changing or flipping of decision output given the same input cues, as observed in the Drosophila experiment (Tang and Guo 2001; Zhang et al. 2007). Synaptic plasticity is an important foundation of learning and memory. The intensity and timing of stimuli encoded by synaptic connections can also affect transmission of information in a circuit. In keeping with previous studies (Bohte et al. 2002; Natschläger and Ruf 1998), multiple synaptic connections with different time delays and connection strengths were used between a pair of neurons, as shown in Fig. 5c. Stimuli received by neuron j from all presynaptic neurons i at time t are shown in Eqs. (22, 22), in which and are strength and delay of the kth synapse from neuron i to j, respectively, is the last firing time of neuron i. is a mathematical model for the response of the synapse to a pre-synaptic spike. The parameter t in is the time lasted from the received spike. is the time constant, and is set to 5.0 in our simulations.
| 21 |
| 22 |
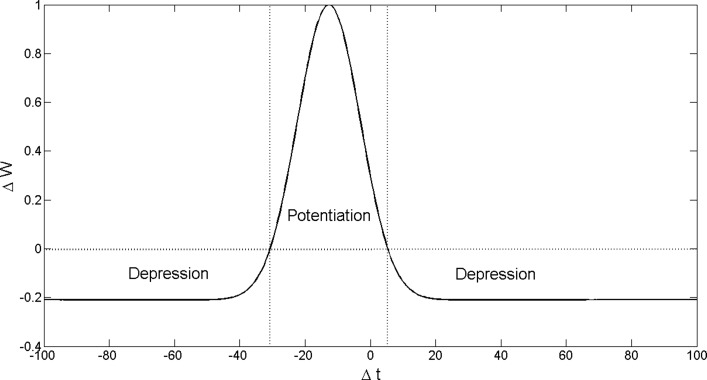
Adjusting the strength of synaptic connections in this study was based on spike timing-dependent plasticity (STDP) (Bell et al. 1997; Bi and Poo 1998; Gerstner et al. 1996; Markram et al. 1997), which adjusts connection strengths according to the relative timing of spikes of presynaptic and postsynaptic neurons. We used an alternative curve (Bohte et al. 2002; Natschläger and Ruf 1998), as shown in Eq. 23 ( in this paper) and Fig. 7, rather than the traditional STDP curve (Bi and Poo 1998). If the postsynaptic neuron fires a few milliseconds after the presynaptic neuron, the connection between the neurons is strengthened, whereas firing too early or late weakens the connection (Nishiyama et al. 2000; Wittenberg and Wang 2006).
| 23 |
Fig. 7.
The STDP curve used in this paper, describing how the strength of a synaptic connection is influenced by the firing time difference , where is the firing time of the presynaptic neuron at the synapse, is the firing time of the postsynaptic neuron
Experiments and results
Three experiments were conducted. In the first experiment, we investigated flipping the decision output of our decision-making model given the same input stimuli with the help of punishment feedback and synaptic plasticity. In the second experiment, we explored how the basic model reproduces complex behavior observed in the Drosophila experiment (Tang and Guo 2001; Zhang et al. 2007). In the third experiment, the neural mechanism underlying behavior of Drosophila facing conflicting visual cues was investigated. Note that because we did not intend to do data fitting in experiments, the noise term in our model was ignored, and each neuron pool contained only one neuron to make the dynamic process clearer. Data fitting and analysis of this model will be studied in the near future. In this study, the focus was on investigating the flipping of decisions and reproducing behavior in the Drosophila experiment.
Experiment 1: flipping the decision
Architecture of the circuit and its learning process
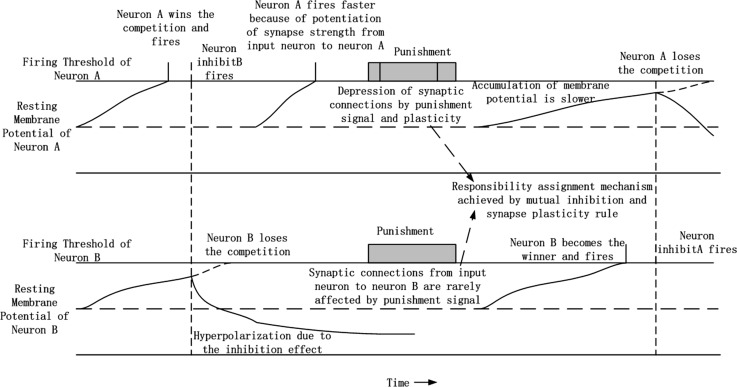
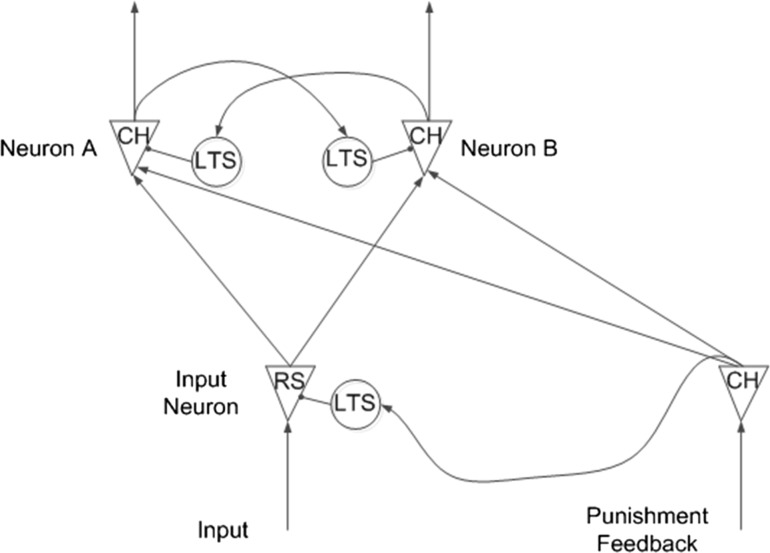
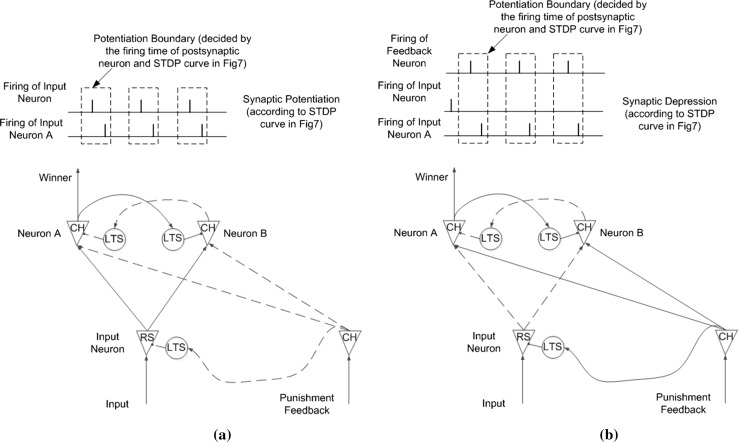
The architecture of the circuit used to investigate flipping the decision output is shown in Fig. 8, which is basically the same as Fig. 5b but with an additional punishment feedback component. A single input neuron converts constant current stimuli to spike trains. Spike trains from the input neuron are sent to two separate output neurons via multiple synaptic connections with different strengths and delays. In our experiment, there were 100 synaptic connections from each input neuron to each output neuron, with delays ranging from 1 to 100 ms and random strength. The two output neurons received stimuli from an input neuron and accumulated their membrane potentials at different rates due to differences in synaptic connections from the input neuron. The two output neurons inhibited each other via two separate inhibitory neurons. The final decision was made according to which output neuron won the firing competition. Synaptic connections from each input neuron to each output neuron were modified according to the STDP rule. Because of property of the STDP rule and the fact that firing of each output neuron was caused by stimuli from an input neuron, the average strength of synaptic connections between the winner output neurons and input neuron were potentiated, as shown in Fig. 9a. The potentiation of synaptic connections facilitates subsequent depolarization of the winner output neuron, and makes the same decision easier the next time. There is an additional punishment feedback neuron that helps achieve flipping the decision output. The punishment feedback neuron sends excitatory stimuli to both output neurons and inhibitory stimuli to the input neuron via an inhibitory neuron. The inhibitory effects between the two output neurons were set to be strong and persistent enough so that excitatory stimuli from the punishment feedback neuron would not change the winner output neuron. The inhibitory effect from the punishment feedback neuron on the input neuron was strong enough to stop firing of the input neuron. Then, the tight time correlation of firing between input neuron and winner output neuron, which is responsible to this punishment, is disrupted, and depression of synaptic connections occurs under the STDP rule as shown in Fig. 9b. After several rounds of punishment, the decision output flips. The new decision is then consolidated until the next association with punishment.
Fig. 8.
Architecture of the circuit used to simulate the process of flipping decision output
Fig. 9.
Learning mechanism of the decision making model. a Potentiation of the decision. b Depression of the decision with the help of punishment feedback
Simulation result
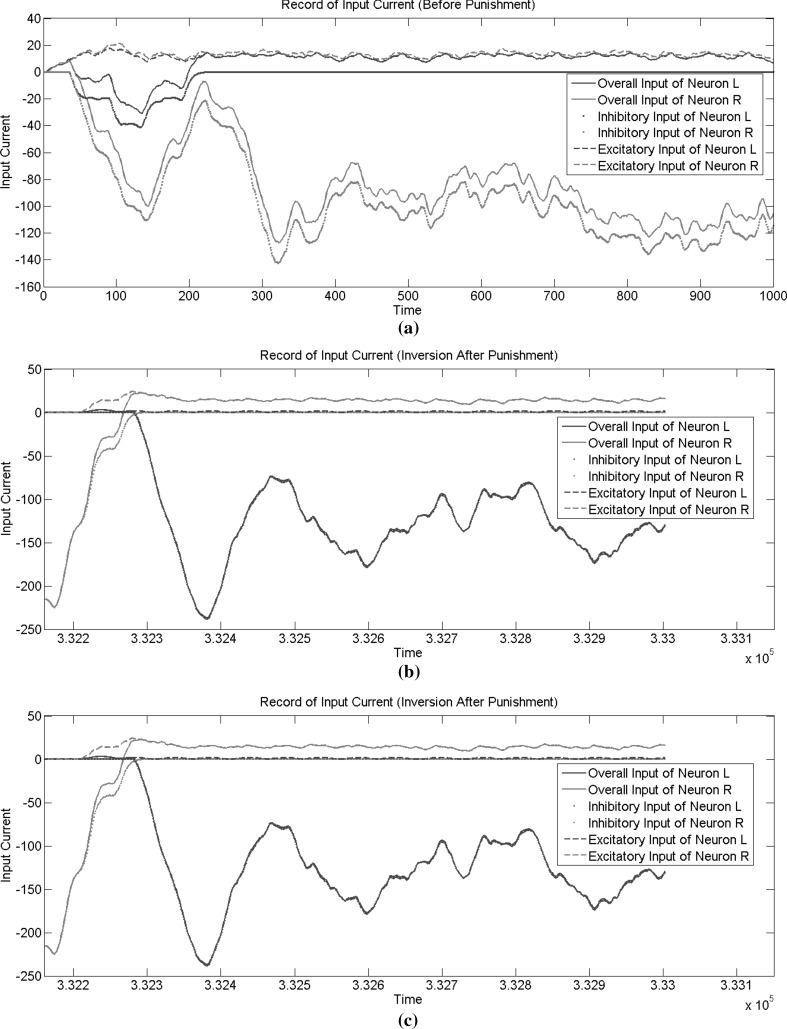
Synaptic plasticity changes the stimulus accumulation rate of the two output neurons, which corresponds to drift rate in the drift diffusion model. The input stimuli from the input neuron to the two output neurons were recorded, as shown in Fig. 10. We can see from Fig. 10a that neuron A won the competition and the competition for firing was very intense in the initial phase. That is because the strength of synaptic connections from the input neuron to each output neuron was randomly initialized, and the difference was small. The outcome of this competition was mostly determined by the difference in inhibitory effect, which can be considered a bias in decision-making. From Fig. 10a, we can see that the inhibitory effect of neuron A on neuron B was stronger in this simulation. Figure 10b shows the input stimuli of two output neurons after the first punishment stage. We can see that the previous winner neuron A became the loser of the competition. The excitatory input from the input neuron to neuron A was much smaller than that to neuron B, mainly because of depression of synaptic connections during the punishment stage. Then, after a second punishment phase, the winner neuron changed again, as shown in Fig. 10c. The strengths of synaptic connections from the input neuron to each output neuron in different stages of simulation are shown in Fig.11, which explains the changes in excitatory inputs shown in Fig. 10.
Fig. 10.
Record of the input current in different stage of simulation. a Before the first punishment. b After the first punishment stage. c After the second punishment stage
Fig. 11.
Strength of synaptic connections between input neuron and a neuron A, b neuron B at different stages. 100 synaptic connections with different time delay (1–100 ms) were set between each output neuron and input neuron. The size of the time delay is represented on the x-axis and the strength of the connection in that time delay is represented on the y-axis. Connection strength was randomly set at the start. Noticed that a little amount of connection recovery was set to ensure that input neuron and output neurons were always connected
Experiment 2: integration of multiple simple circuits
In this experiment, we investigated how our basic model could be used to build a larger circuit and reproduce behavior observed in the Drosophila experiment (Tang and Guo 2001; Zhang et al. 2007). The simulated environment is shown in Fig. 12c. There were two types of color cue in the environment: green and blue bars. The fly was assumed to be fixed in the center of the environment and could only rotate. The red sectors shown in Fig. 12c are heat punishment zones. In training sessions, the fly received punishment feedback whenever it rotated into the heat punishment zone, and feedback persisted until the fly left the punishment zone.
Fig. 12.
a Architecture of the neural circuit in this study. Some neurons and connections are omitted for clarity. b A basic decision unit in the circuit. c Diagram of simulated environment
Architecture of the circuit and its learning process
The architecture of the decision circuit used in this simulation was constructed from four parallel two-choice decision-making models and is shown in Fig. 12. Different input neurons in the decision circuit were stimulated according to the color and relative position of the perceived cue, then entered one of the four decision-making processes, and a decision about turning left or right was made. Four situations were considered: blue cue on the left (BL), green cue on the left (GL), blue cue on the right (BR), and green cue on the right (GR). According to the current orientation of the fly, each situation was given a probability to occur. For example, when the orientation of the fly was in the range of 22.5°–67.5° (see Fig. 12c), there was a 0.5 probability that the fly would perceive the green cue on the left and a 0.5 probability that it would perceive the blue cue on the right. After a decision was made, the simulated fly turned left or right by a constant degree and made a new decision based on the new perceived cue. The process of this simulation is illustrated in Fig. 13. The learning mechanism in this simulation was based on the STDP rule and punishment feedback as described in experiment 1.
Fig. 13.
Decision making and learning from the interaction with the environment
Simulation result
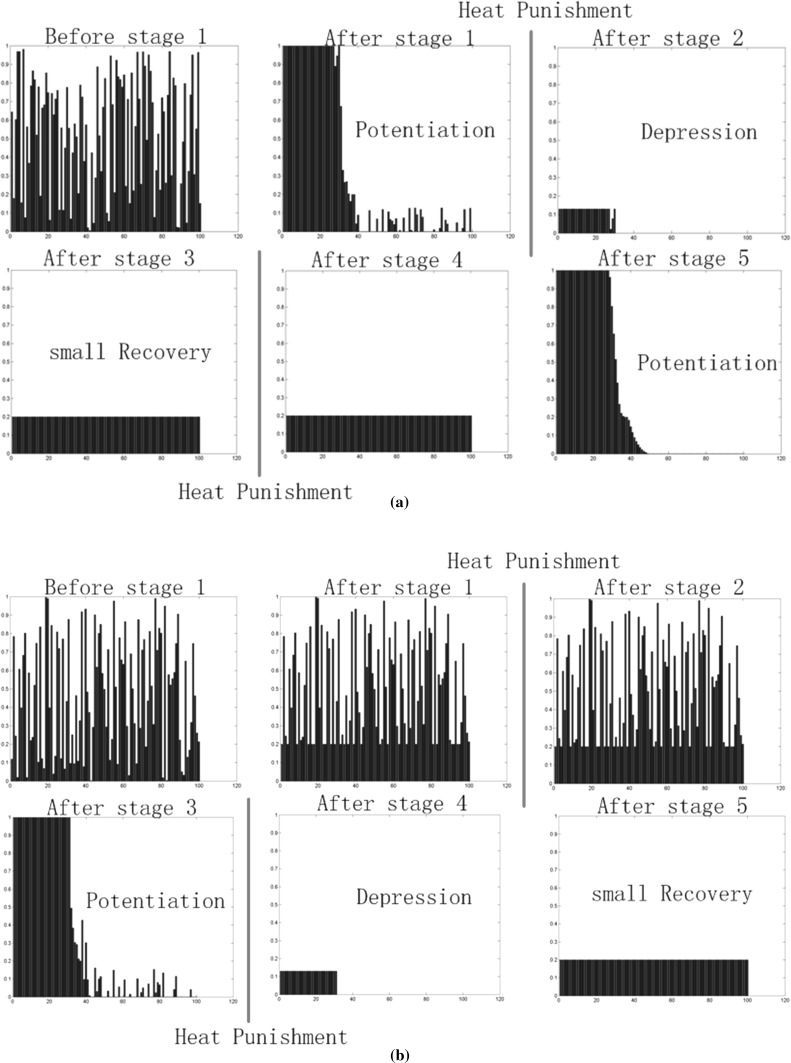
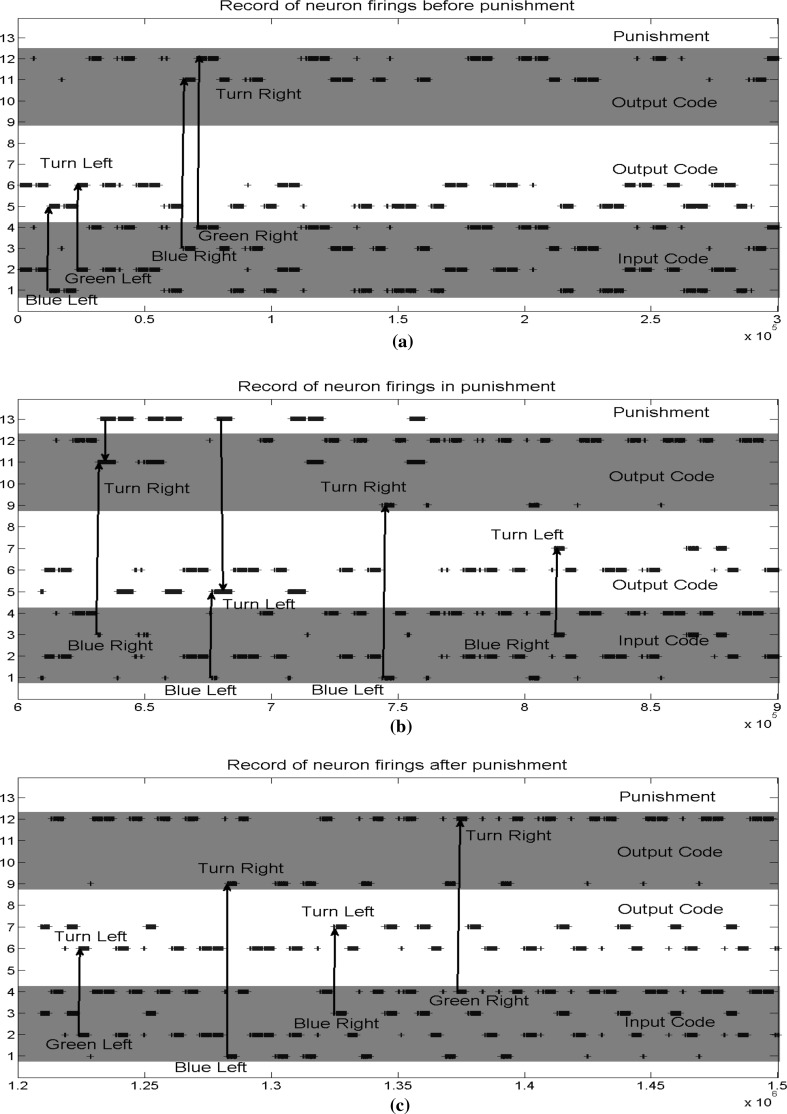
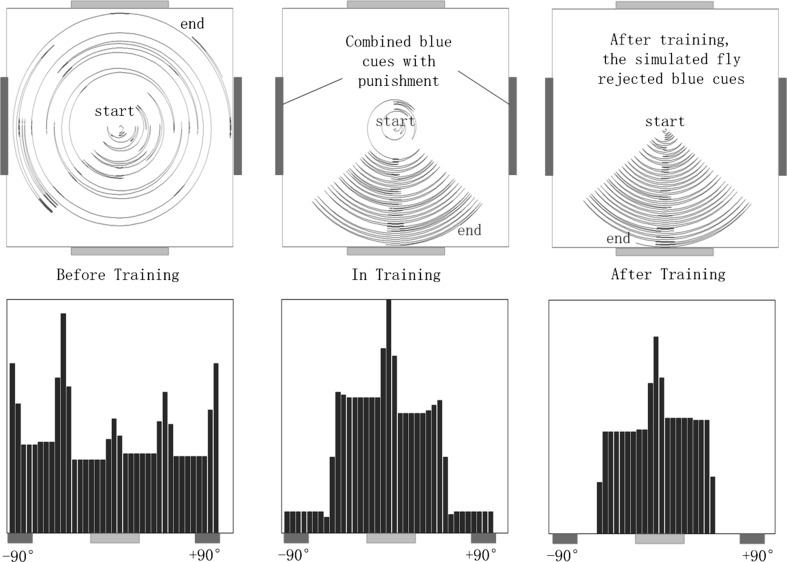
According to the results observed in Tang and Guo (2001) and Zhang et al. (2007), the fly should have shown no color preference before training. After training during which heat punishment was associated with a single color cue, preference for cues without heat punishment were expected in our simulation. Firing of neurons at different stages are shown in Fig. 14. Initial connections in the decision-making circuit were set so that the simulated fly tended to be attracted to every cue currently perceived. As shown in Fig. 14a, when the simulated fly perceived a blue cue on the left, it decided to turn left, and if the simulated fly perceived a blue cue on the right, it turned right. Similar results were obtained for the green cue. The resulting flight trajectories and histograms of time spent at each orientation are shown in Fig. 15. During the punishment training session, we combined heat punishment with a blue cue. As indicated in Fig. 14b, when the simulated fly perceived a blue cue on the right and turned right, it entered the punishment zone. Then, heat punishment was given, and the punishment feedback neuron took control of firing for that output neuron, which caused depression of synaptic connections as explained in experiment 1. Next, the simulated fly left the punishment zone and perceived a blue cue on the left. It turned left and received punishment again. After several rounds of punishment, the simulated fly learned to reject blue cues, as shown in Fig. 14b, c. Although reactions of the simulated fly to green cues were not changed, the repulsion to blue cues produced the observed relative preference for green cues, as shown in Fig. 15.
Fig. 14.
Record of the firings in different stage of simulation. Neuron 1−4 are input neurons, corresponding to blue cue on the left, green cue on the left, blue cue on the right, and green cue on the right separately. Neuron 5−8 are output neurons for decision of turning left. Neuron 9−12 are output neurons for decision of turning right. Neuron 13 is punishment feedback neuron. a Before training. b During training with punishment. c After training. (Color figure online)
Fig. 15.
Flight trajectories and histograms of the time spent in different directions, the distance between the simulated fly and the center of the environment is set proportional to time
Experiment 3: choice behavior of Drosophila facing conflicting cues
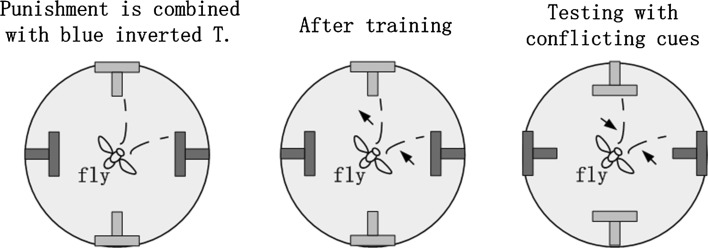
In the above two experiments, decision-making behaviors based on one kind of cues (i.e., color cues) were investigated. However, in the experiments in Tang and Guo (2001), shape cues were also set in addition to color cues, to investigate the decision-making behavior of Drosophila facing conflicting cues. The experiments in Tang and Guo (2001) is illustrated in Fig. 16, green upright T and blue inverted T cues are firstly placed in the environment, and train the flies to avoid blue inverted T cues, then recombine the color and shape of cues (i.e., using green inverted T and blue upright T) and record the preference of flies to these new cues. The Preference Index (PI) defined as Eq. 24 was used to evaluate the behavior of Drosophila, is the recorded time of flies facing blue upright T, is the recorded time of flies facing green inverted T. The large positive PI indicates strong preference to shape of cues, and the large negative PI indicates strong preference to color of cues. Tang and Guo (2001), the influence of color intensity of cues on PI was investigated. In the wild flies, PI changed with color intensity in a sigmoid curve manner. In the mushroom body damaged flies, PI changed with color intensity in a linear curve manner. Tang and Guo (2001) and Zhang et al. (2007) suggested that Drosophila has two types of cue selection ability, i.e., linear type and sigmoid type, and the type of choice ability of a fly is closely related to mushroom body.
| 24 |
Fig. 16.
Illustration of the color-shape choice experiment. (Color figure online)
The linear or nonlinear cue selection ability of Drosophila was not considered in the computing model in our first two experiments. Then can our decision-making model produce simulation results consistent with the real experiment observations? In this experiment, we combined the color-shape selection process with our decision-making circuit to investigate the influence of linearity and nonlinearity of color-shape selection ability on the behavior of the same decision-making circuit.
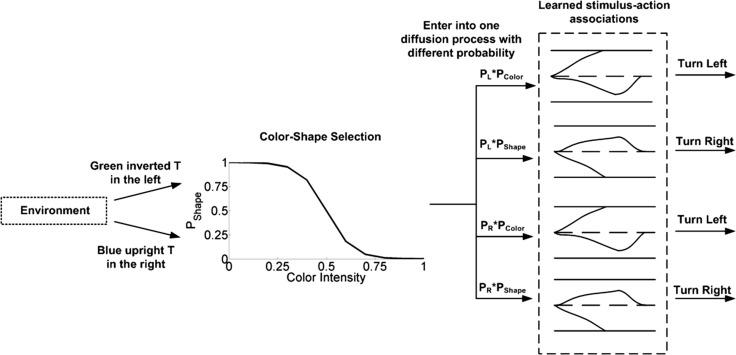
In this experiment, we added four basic decision-making units to the circuit used in experiment 2, the learning process was the same as in the experiment 2. Eight basic decision-making processes were considered, i.e., blue cue in the left, green cue in the left, upright T in the left, inverted T in the left, blue cue in the right, green cue in the right, upright T in the right, inverted T in the right. As in experiment 2, the simulated fly entered into one of the eight basic decision-making units according to the cues in the environment. Then it turned left or right a constant degree according to the output of the basic decision-making unit, and entered into the next decision-making process. In this experiment, the probability of the simulated fly entering a certain decision-making unit was determined by both the fly’s facial orientation and color intensity of cues. and separately represent the probability of the simulated fly choosing the left or right cues, and separately represent the probability of choosing color or shape cues. and were constant in this experiment (both were set as 0.5), and the values of and were determined by the color intensity and color-shape selection ability (either linear or sigmoid selection ability). Figure 17 illustrates the decision-making process where color-shape cue selection process is considered. The simulated fly perceived different cues from the environment, and entered into a certain decision-making unit with a probability determined by color-shape selection ability and current color intensity, then the decision-making unit triggered an action according to the learned stimulus-action association.
Fig. 17.
Illustration of the decision-making process with color-shape cue selection considered
Simulation result
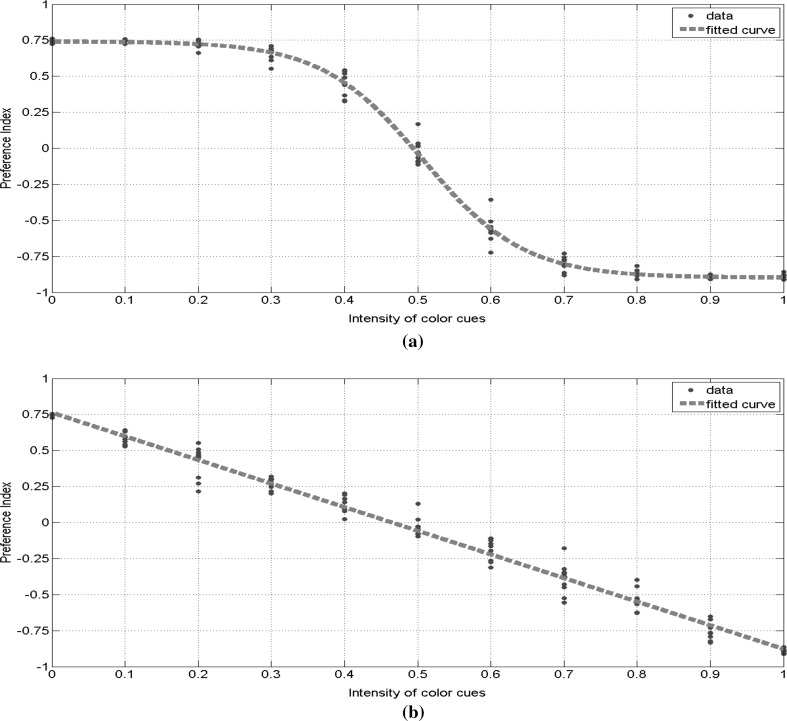
In this simulation, we considered two types of cue selection mechanism, corresponding to the two types of visual cue selection ability observed in Tang and Guo (2001) and Zhang et al. (2007), i.e., the sigmoid cue selection ability observed in wild flies and linear cue selection ability observed in mushroom body damaged flies. By changing the color intensity of cues, simulations were repeated under different levels of conflict between color and shape cues. The fitted PI curves on data produced by simulations are shown in Fig. 18. The nonlinear cue selection model produced nonlinear PI curve, and the linear cue selection model produced linear PI curve. The same decision-making circuit was used in all simulations, which means that the stimulus-action association was not changed. However, the change of cue selection ability caused two different behaviors. This result is consistent with the observation in Tang and Guo (2001) and Zhang et al. (2007). The consistence between our simulation results and real experiment observations indicates that the structure of our neural computing circuit has the potential to explain the micro-mechanism of decision-making process, it gives a possible implementation mechanism of how the cue selection ability affects behavior. With stimulus-action association unchanged, mushroom body may affect the behavior of Drosophila by regulating the cue selection ability.
Fig. 18.
a Boltzmann fit (with ) of preference indexes produced by simulations using sigmoid-shaped color-shape selection curve. b Linear fit (with ) of preference indexes produced by simulations using linear-shaped color-shape selection curve. (Color figure online)
The following question is that, how the cue selection function can be achieved by a neural circuit composed of spiking neurons? Model in Wang (2002) was originally designed as a decision-making model, but it also gives the feasibility of neural circuit implementation of the nonlinear cue selection function. The neural circuit model in Wang (2002) receives two independent input signals (for example, signal and ). A winner signal is determined between and with a probability related to their signal strength. And with the increasing of signal strength of , the probability of being the winner increases in a nonlinear manner. Although Wang’s model (2002) can be used to produce a nonlinear cue selection curve, the function and design of mushroom body was not investigated. We still need to explore more realistic neural circuit modeling to study how mushroom body affects the cue selection ability.
Conclusion
In this paper, we discussed the decision-making process underlying the observed behavior in the Drosophila experiment (Tang and Guo 2001; Zhang et al. 2007). We proposed that the change in behavior after punishment training given the same environmental stimuli could be explained by flipping multiple two-choice decision outputs. In addition, we proposed a neural circuit-based decision-making model, which is similar to previously described two-choice decision-making models such as the drift diffusion model (Ratcliff 1978) and the pooled inhibition model (2002). Our decision-making model utilizes the process of accumulating membrane potential to fire. The most significant difference between our model and previous models is that flipping the decision output given the same input stimuli was investigated. Moreover, the biological meaning of parameters in our decision-making models is discussed. In our experiments, we demonstrated how our basic decision-making model works, and we constructed a more complex circuit from the basic model in order to reproduce behaviors observed in Drosophila experiments (Tang and Guo 2001; Zhang et al. 2007). We focused on extracting questions from observed results, building a decision-making model to explain the results, and reproducing the results using the decision-making model. Future work will entail fitting our model to experimental data as in Wang (2002). This study furthers our understanding of how animal behaviors are regulated by neural circuits as well as the underlying encoding and decoding mechanisms from stimulus to response.
Acknowledgements
This work was supported by NSFC project (Project No.61375122), and in part by Shanghai Science and Technology Development Funds (Grant Nos. 13dz2260200, 135115 04300). We thank LetPub (www.letpub.com) and Accdon for their linguistic assistance during the preparation of this manuscript. The authors declare that there is no conflict of interest regarding the publication of this paper.
Contributor Information
Hui Wei, Email: weihui@fudan.edu.cn.
Yijie Bu, Email: yjbu15@fudan.edu.cn.
Dawei Dai, Email: dwdai14@fudan.edu.cn.
References
- Ananthanarayanan R, Modha DS (2007) Anatomy of a cortical simulator. In: Proceedings of the 2007 ACM/IEEE conference on supercomputing. ACM, p 3
- Bell CC, Han VZ, Sugawara Y, Grant K. Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature. 1997;387(6630):278–281. doi: 10.1038/387278a0. [DOI] [PubMed] [Google Scholar]
- Bi G-Q, Poo M-M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18(24):10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev. 2006;113(4):700. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Bohte SM, Poutré HL, Kok JN. Unsupervised clustering with spiking neurons by sparse temporal coding and multilayer RBF networks. IEEE Trans Neural Netw. 2002;13(2):426–435. doi: 10.1109/72.991428. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev. 1993;100(3):432. doi: 10.1037/0033-295X.100.3.432. [DOI] [PubMed] [Google Scholar]
- Carandini M. From circuits to behavior: a bridge too far? Nat Neurosci. 2012;15(4):507–509. doi: 10.1038/nn.3043. [DOI] [PubMed] [Google Scholar]
- Eliasmith C, Stewart TC, Choo X, Bekolay T, DeWolf T, Tang Y, Rasmussen D. A large-scale model of the functioning brain. Science. 2012;338(6111):1202–1205. doi: 10.1126/science.1225266. [DOI] [PubMed] [Google Scholar]
- Foderaro G, Henriquez C, Ferrari S (2010) Indirect training of a spiking neural network for flight control via spike-timing-dependent synaptic plasticity. In: 49th IEEE conference on decision and control (CDC). IEEE, pp 911–917
- Gerstner W, Kempter R, van Hemmen JL. A neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383:76–78. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proc Nat Acad Sci. 2008;105(9):3593–3598. doi: 10.1073/pnas.0712231105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM, et al. Simple model of spiking neurons. IEEE Trans Neural Netw. 2003;14(6):1569–1572. doi: 10.1109/TNN.2003.820440. [DOI] [PubMed] [Google Scholar]
- Li X, Chen Q, Xue F. Bursting dynamics remarkably improve the performance of neural networks on liquid computing. Cognit Neurodyn. 2016;10(5):415–421. doi: 10.1007/s11571-016-9387-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H. The blue brain project. Nat Rev Neurosci. 2006;7(2):153–160. doi: 10.1038/nrn1848. [DOI] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997;275(5297):213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- Natschläger T, Ruf B. Spatial and temporal pattern analysis via spiking neurons. Netw Comput Neural Syst. 1998;9(3):319–332. doi: 10.1088/0954-898X_9_3_003. [DOI] [PubMed] [Google Scholar]
- Nishiyama M, Hong K, Mikoshiba K, Poo M-M, Kato K. Calcium stores regulate the polarity and input specificity of synaptic modification. Nature. 2000;408(6812):584–588. doi: 10.1038/35046067. [DOI] [PubMed] [Google Scholar]
- Qu J, Wang R, Yan C, Du Y. Oscillations and synchrony in a cortical neural network. Cognit Neurodyn. 2014;8(2):157–166. doi: 10.1007/s11571-013-9268-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychol Rev. 1978;85(2):59. doi: 10.1037/0033-295X.85.2.59. [DOI] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol Sci. 1998;9(5):347–356. doi: 10.1111/1467-9280.00067. [DOI] [Google Scholar]
- Samura T, Ikegaya Y, Sato YD. A neural network model of reliably optimized spike transmission. Cognit Neurodyn. 2015;9(3):265–277. doi: 10.1007/s11571-015-9329-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang S, Guo A. Choice behavior of drosophila facing contradictory visual cues. Science. 2001;294(5546):1543–1547. doi: 10.1126/science.1058237. [DOI] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev. 2001;108(3):550. doi: 10.1037/0033-295X.108.3.550. [DOI] [PubMed] [Google Scholar]
- Vickers D. Evidence for an accumulator model of psychophysical discrimination. Ergonomics. 1970;13(1):37–58. doi: 10.1080/00140137008931117. [DOI] [PubMed] [Google Scholar]
- Waldrop MM. Computer modelling: brain in a box. Nature. 2012;482(7386):456–458. doi: 10.1038/482456a. [DOI] [PubMed] [Google Scholar]
- Wang X-J. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36(5):955–968. doi: 10.1016/S0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
- Wittenberg GM, Wang SS-H. Malleability of spike-timing-dependent plasticity at the CA3-CA1 synapse. J Neurosci. 2006;26(24):6610–6617. doi: 10.1523/JNEUROSCI.5388-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Guo JZ, Peng Y, Xi W, Guo A. Dopamine-mushroom body circuit regulates saliency-based decision-making in drosophila. Science. 2007;316(5833):1901–1904. doi: 10.1126/science.1137357. [DOI] [PubMed] [Google Scholar]
- Zhang X, Xu Z, Henriquez C, Ferrari S (2013) Spike-based indirect training of a spiking neural network-controlled virtual insect. In: IEEE 52nd annual conference on decision and control (CDC). IEEE, pp 6798–6805
- Zhao J, Deng B, Qin Y, Men C, Wang J, Wei X, Sun J. Weak electric fields detectability in a noisy neural network. Cognit Neurodyn. 2016;11:81–90. doi: 10.1007/s11571-016-9409-x. [DOI] [PMC free article] [PubMed] [Google Scholar]