Abstract
New memory formation depends on both the hippocampus and modulatory effects of acetylcholine. The mechanism by which acetylcholine levels in the hippocampus enable new encoding remains poorly understood. Here, we tested the hypothesis that cholinergic modulation supports memory formation by leading to structured spike timing in the hippocampus. Specifically, we tested if phase precession in dorsal CA1 was reduced under the influence of a systemic cholinergic antagonist. Unit and field potential were recorded from the dorsal CA1 of rats as they completed laps on a circular track for food rewards before and during the influence of the systemically administered acetylcholine muscarinic receptor antagonist scopolamine. We found that scopolamine significantly reduced phase precession of spiking relative to the field theta, and that this was due to a decrease in the frequency of the spiking rhythmicity. We also found that the correlation between position and theta phase was significantly reduced. This effect was not due to changes in spatial tuning as tuning remained stable for those cells analyzed. Similarly, it was not due to changes in lap‐to‐lap reliability of spiking onset or offset relative to either position or phase as the reliability did not decrease following scopolamine administration. These findings support the hypothesis that memory impairments that follow muscarinic blockade are the result of degraded spike timing in the hippocampus.
Keywords: acetylcholine, navigation, theta, memory, place cells, phase precession, spike timing, rhythmicity, Alzheimer's disease, aging
1. INTRODUCTION
New memory formation depends on both the hippocampus (Scoville & & Milner, 1957; Squire, 1992) and modulatory effects of acetylcholine (Ghoneim & Mewaldt, 1975; Hasselmo, 2006; Newman, Gupta, Climer, Monaghan, and Hasselmo, 2012). The mechanism by which acetylcholine levels in the hippocampus enable new encoding remains poorly understood. Here, we tested the hypothesis that cholinergic modulation supports memory formation by leading to structured spike timing in the hippocampus. Specifically, we test the necessity of muscarinic modulation for the generation of phase precession in hippocampal area CA1.
Temporal patterning of neural spiking is believed to be a key mechanism of neural coding (Bialek, Rieke, de Ruyter van Steveninck, & Warland, 1991; Maurer, Cowen, Burke, Barnes, & McNaughton, 2006a). In CA1, temporal patterning of neural spiking can be observed as phase precession, wherein neural spiking occurs at progressively earlier phases of the local field theta rhythm. When an animal is navigating through the firing field of a hippocampal place cell, such phase precession leads to a correlation between the position of an animal and the phase at which a cell fires on linear tracks (O'Keefe & Recce, 1993; Skaggs, McNaughton, Wilson, and Barnes, 1996; Maurer, Cowen, Burke, Barnes, and McNaughton, 2006b) and in open fields (Burgess, Recce, & O'keefe, 1994; Skaggs et al., 1996; Huxter, Senior, Allen, & Csicsvari, 2008; Jeewajee et al., 2014). The net result, when examined across many CA1 neurons, is a compressed sequence of place cell activity plays out over the theta cycle such that place cells representing the current position of the animal fire at early phases and that cells with fields further in front of the animal fire at later phases (Burgess et al., 1994; Skaggs et al., 1996; Dragoi & Buzsáki, 2006; Gupta, van der Meer, Touretzky, and Redish, 2012). Due to this compression, phase precession is believed to drive the formation of functional neural ensembles and stabilize spatial coding in the hippocampus (Mehta, Lee, & Wilson, 2002). Supporting this, manipulations that lead to degraded spike time precession also lead to impaired memory performance (Robbe et al., 2006; Robbe & Buzsáki, 2009).
An important determinant in the generation of temporal coding in CA1 neurons is the integrity of entorhinal input to the hippocampus (Schlesiger et al., 2015; Fernández‐Ruiz et al., 2017). Phase precession is generated by a shift in the predominant source of excitatory drive as an animal crosses a firing field to CA3 input from entorhinal input (Fernández‐Ruiz et al., 2017). This might correspond to shifts between prospective and retrospective firing of neurons in medial entorhinal cortex (de Almeida, Idiart, Villavicencio, & Lisman, 2012). Correspondingly, lesions of the medial entorhinal cortex lead to a loss of phase precession in CA1 (de Almeida et al., 2012; Schlesiger et al., 2015).
Because systemic administration of the muscarinic acetylcholine receptor antagonist scopolamine interferes with hippocampal–entorhinal interactions (Douchamps, Jeewajee, Blundell, Burgess, & Lever, 2013; Newman, Gillet, Climer, & Hasselmo, 2013; Newman, Climer, & Hasselmo, 2014), we hypothesized that the same manipulation may also impair phase precession in the hippocampus. Douchamps et al. (2013) found that scopolamine shifts the mean phase preference of CA1 neurons away from the phase of maximal entorhinal drive. We found that scopolamine also reduced the spatial coding of entorhinal grid cells (Newman, et al., 2014), an effect that would disrupt the patterned input to the hippocampus from the entorhinal cortex. We also found that scopolamine both delayed and muted the strength of the theta–gamma coupling selectively for high gamma rhythms (Newman et al., 2013), suggesting an impairment in the functional coupling between entorhinal cortex and the hippocampus (Colgin et al., 2009).
Given the importance of entorhinal input for the generation of temporal coding and the prior evidence that scopolamine impairs hippocampal–entorhinal interactions, we predicted that scopolamine would additionally impair temporal coding by hippocampal CA1 neurons. To test this, we had rats run laps on a circular track for food rewards before and after either a systemic scopolamine or saline injection. We recorded the activity of place cells in the dorsal portion of area CA1 and compared the temporal and spatial firing properties before and after scopolamine administration. The data show that, despite minimal disruption to spatial tuning, temporal coding in the forms of phase precession and phase coding of space were significantly reduced by the muscarinic antagonist. The observed reduction in temporal coding, when considered in the context of STDP, suggests that existing neural representations will be degraded during epochs of reduced cholinergic tone. An implication of this is that individuals with reduced cholinergic tone, such as elderly people or Alzheimer's patients, will not only suffer from a lack of new encoding, but also suffer from an active degeneration of existing neural representations.
2. METHODS
All animal procedures and surgery were conducted in strict accordance with National Institutes of Health and Boston University Animal Care and Use Committee guidelines.
2.1. Subjects
Recordings were made in 10 male Long‐Evans rats. All animals weighed 350–400 g at the time of surgery, were individually housed, were maintained at 90% of their free‐feeding weight following their full recovery after surgery, and were maintained on a 12:12 hr light‐dark cycle. All procedures were conducted during the light cycle.
2.2. Behavioral protocol
The rats completed laps on a circle track for a sweet cereal or chocolate drink reward in 20‐min‐long testing trials. The animals were only rewarded for laps completed in one direction (e.g., clockwise) selected to be consistent with early natural biases exhibited by the animal to run in that direction (Figure 1a). The rewards were delivered in a fixed position by an experimenter standing arm's length from the track. The track was centered in a well‐lit area surrounded by black curtains. Inside the curtained area, there were multiple landmarks (e.g., holding pedestal, experimenter) visible from the track. The track itself was a raised 8‐cm‐wide track with a diameter of 112 cm and 5‐cm‐tall walls on both the inside and outside edges. As shown in Figure 1b, testing sessions consisted of three 20 min trials: (1) a preinjection baseline trial; (2) an injection trial run 15 min post injection; and (3) a recovery trial 3–6 hr after the injection.
Figure 1.
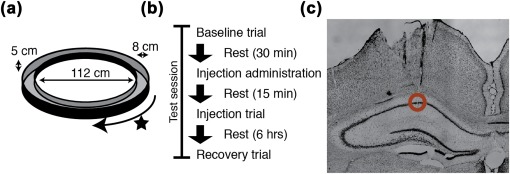
Schematic of experimental design. (a) Rats completed laps on a circular track for food reward. (b) Each test session consisted of a baseline trial run prior to the injection. The animals were left to rest on a pedestal for 15 min following the injection. Then an injection trial was run. Recovery trials were run 3–6 hr after the injection. (c) Independently moveable tetrodes were positioned in dorsal CA1. [Color figure can be viewed at wileyonlinelibrary.com]
2.3. Cholinergic manipulation
Cholinergic modulation was blocked through the use of scopolamine hydrobromide. The scopolamine, diluted in sterile saline to 0.5 mg/mL, was systemically administered via intraperitoneal (I.P.) injection at a dose of 0.5 mg/kg. To control for the effects of the injection procedure, the primary control condition consisted of a volume matched I.P. injection of sterile saline. Injections were administered within 5 min after the completion of the preinjection baseline trial and 15 min before the injection trial. Testing order between the scopolamine and saline conditions was counterbalanced across animals and testing sessions to match for overall experience with the testing process.
2.4. Electrophysiological recordings
Recordings were performed from the dorsal CA1 of the hippocampus with arrays of multiple independently movable tetrodes. The tetrodes were constructed out of four 12.7‐μm‐diameter nichrome wires (Sandvik, Bethel, CT USA) twisted together that were gold plated to bring the impedance at 1 kHz down to ∼250 kΩ in undiluted gold plating solution (Neuralynx, Bozeman, MT USA) or to ∼150 kΩ in the same solution diluted 90% with a solution of 1 mg/mL polyethelene glycol in distilled water. Tetrodes were loaded into a multiscrew hyperdrive giving an average of 300 μm intertetrode spacing. For implantation of electrodes, rats were anesthetized with isoflurane and a ketamine/xylazine mixture, the skull surface was exposed, and 5 to 9 anchor screws and one ground screw (located over the central cerebellum) were affixed to the skull. The tetrode bundle of the hyperdrive was centered over dorsal CA1, at 2.5 mm lateral and 3.5 mm posterior to bregma (Figure 1c). The screws and the drive were attached to the skull with dental acrylic. Tetrodes were lowered 1.3–1.75 mm into the brain at the time of surgery. The rats recovered for 7 days before behavioral testing and recording began. Tetrodes were stepped down to hippocampal area CA1 over the next 2–3 weeks. This was done by advancing each tetrode until clear sharpwave‐ripple complexes could be seen, and then each were slowly advanced until high‐amplitude low‐firing‐rate (0.1–5 Hz average) unit activity was observed.
Data collection was performed with the Axona Ltd. (Hertz, U.K) DacqUSB system. Signals recorded from the tetrodes were filtered and amplified to record local field potentials (bandpass 1–250 Hz; amplified ∼1,000–2,500×) and unit activity (bandpass 0.6–6.7 KHz; amplified ∼6,000–10,000×). Potential spike waveforms were identified by a rising slope that crossed a 65–100 μV threshold and stored to disk along with a 32‐bit time stamp. Cluster cutting was performed offline using the KlustaKwik spike sorting package (Rossant et al., 2016) and then Tint cluster cutting software (Axona Ltd., Hertz, U.K) or KlustaViewa (part of the Klustas toolkit) (Hazan, Zugaro, & Buzsáki, 2006; Rossant et al., 2016) were used to finalize the clusters. Recordings of the local field potential were referenced directly to the ground screw without a reversal of polarity (i.e., recorded: signal–ground). Head tracking was performed by the Axona Ltd. DacqUSB system by tracking the position of a large and small LED on the recording headstage attached for each session to track the position and head direction of the animal at a rate of 50 Hz.
2.5. Analyses
2.5.1. Data inclusion criteria
Valid sessions included a preinjection baseline trial, a timely postinjection trial (15 min postinjection), and a recovery trial within 24 hr of the injection. Those sessions for which the animal performed the task in all three trials (i.e., completed at least 5 complete laps on circle track) were included for analysis. Analyses were performed on well‐isolated units (minimum isolation distance of 10; (Schmitzer‐Torbert, Jackson, Henze, Harris, & Redish, 2005)) with an average firing rate of 0.1–5 Hz over a trial in hippocampal area CA1. Individual analyses imposed further cell inclusion criteria as indicated in the methods for each. Analyses were restricted to epochs of data where the animal was completing laps. That is, epochs during which the rat remained within 5.75 cm of the feeder or ventured to and from the feeder without completing laps were discarded.
2.5.2. Speed profile matching
The metrics of interest here are influenced by animal running speed (e.g., spike‐time rhythmicity and field potential theta frequency). To control for the influence of running speed on the results, the distribution of running speeds was matched between the baseline and injection trials for all analyses. This was particularly important in this context because scopolamine has been shown to slow running speed (Newman et al., 2013). To account for drug induced shifts to the running speed of the animal, all analyses were performed on subsampled data for which the running speed profile was matched between preinjection and postinjection trials. In all cases, the running speed was estimated by a Kalman velocity filter of the head tracking data. To match running speed profiles, the mean running speed was computed for each nonoverlapping 2.5 s epoch of the trial. A histogram of running speeds was then computed over the range of 0–150 cm/s in 5 cm/s bins for both trials. To match histograms, 2.5 s epochs from the corresponding bin were cut from the trial with the greater number of epochs as needed until the same number of epochs existed for each running speed bin in the two trial types.
The above subsampling matches speed profiles between baseline and injection trials but does not match speeds between conditions. To control for between‐condition differences in average speed, we performed a secondary speed matching control analysis to test if speed matching conditions altered the observed effects. To perform this matching, for each animal we aligned individual testing sessions from the saline condition with testing sessions from the scopolamine condition and subsampled the speed profiles to match the injection trials and then the baseline trials accordingly.
2.5.3. Spiking rhythmicity
The depth and frequency of spiking rhythmicity for individual cells were estimated as described elsewhere (Royer, Sirota, Patel, & Buzsáki, 2010). Briefly, the autocorrelogram was computed (max lag 700 ms, bin size 10 ms) for each cell and then fit with the following equation:
In this equation, t is the time variable from the autocorrelogram. The terms a, b, ω, t 1, and t 2 were parameters to be fit. The ω parameter set the frequency of the fit and a and b parameters determined the magnitude of the rhythmic modulation. The ratio of these terms (a/b) was used as the “theta index.” Analyses of these terms were only performed for cells for which the MATLAB function fit.m converged on a fit within 1000 iterations. Cells that failed to converge were assumed to have no significant theta rhythmicity.
2.5.4. Field potential analysis
The instantaneous phase of theta, used in analyses of theta phase locking or phase coding of space, was computed as the angle of the Hilbert transform at each time point of the bandpass filtered raw LFP. The filter was a third‐order Butterworth filter with cutoffs of 6 and 10 Hz and was convolved both forward and backward over the signal to avoid systematic phase shifts (using MATLAB function filtfilt.m). The frequency of the field theta rhythm was estimated as the center of mass of the distribution of instantaneous frequency estimates over the included epochs of the trial where instantaneous frequency was estimated as the inverse phase change over time. A second variation of the phase coding of space analysis used the Belluscio, Mizuseki, Schmidt, Kempter, and Buzsáki, (2012) method of theta phase estimation as indicated in the results section. Briefly, this method identifies the peaks and troughs of each theta cycle using 1–80 Hz broadband LFP and estimates theta phase as the linear interpolation between these extrema as pi‐to‐0 for the rising phases and 0‐to‐pi as the falling phases. To test for changes in the shape of the theta waveform, we used the asymmetry index described by Belluscio et al., (2012). Briefly, for each theta wave the trough and peak was identified on broadband signal (1–80Hz) and the ratio of the duration of the rising phase to the duration of the falling phase was computed. The log10 transform of this ratio was then taken as an index of the asymmetry of the theta wave. We then computed the mean asymmetry index over theta cycles within the speed‐matched epochs as the index for each trial.
2.5.5. Rate map generation
Linearized firing rate maps were created for each cell. This was accomplished by linearizing the position of the animal on the circle track as the angle of the animal relative to the center of the track. The position was then discretized into 3‐cm‐wide bins and the average firing rate was computed in each bin as the number of spikes observed divided by the occupancy time of that bin. This rate map was then smoothed with a Gaussian kernel (sigma = 1 bin). Because epochs in which the rat was within 5.75 cm of the feeder were discarded, this portion of the track was not included in the rate map. This process was performed separately for clockwise and counterclockwise movement to account for directional specificity of individual place fields (McNaughton, Barnes, & O'keefe, 1983).
2.5.6. Analysis of spatial tuning
The basic quality of spatial tuning was assessed using both spatial coherence (Kubie, Muller, & Bostock, 1990) and an information theoretic approach (Skaggs, McNaughton, Gothard, & Markus, 1993). The information theoretic analysis computed the amount of spatial information carried in the spiking of each cell. That is, for each cell, spatial information describes how much (in units of bits per second) the uncertainty about the position of the animal can be decreased based on the current firing rate of that cell. This describes how different the distribution of firing rates over space is from a uniform distribution. Spatial coherence analysis is complementary to spatial information—it evaluates how smoothly the rate map varies and serves here to indicate if the spatial tuning became noisier (even if not more uniform). Spatial coherence was quantified by taking the correlation between the rate map and a version of the rate map in which the firing rate at each pixel was replaced with the mean of the adjacent 2 pixels (the first adjacent pixel in both directions not including itself). Importantly, this was done on a nonsmoothed version of the rate map. Spatial information and spatial coherence were computed separately for rate maps from clockwise and counterclockwise running epochs. To compute a single value for each cell, the two values were linearly summed proportional to the percentage of time spent running in each respective direction.
Firing fields (place fields) were extracted when possible from the directional rate maps that yielded a spatial information score ≥0.5 bits/s. To do this, the smoothed rate map was examined for blocks of 3 or more adjacent bins with a mean firing rate of at least 10% of the maximum firing rate observed in the rate map. These firing fields were kept if they contained at least 50 spikes.
2.5.7. Phase precession and phase coding of space
To test for evidence of phase precession, the frequency of the field potential theta was compared to (subtracted from) the frequency of the spiking theta rhythmicity. We refer to this difference as the relative frequency gap. Positive values (i.e., higher frequency theta rhythmic spiking) were taken as evidence of phase precession. The term phase precession is also frequently used in the context of spatial coding to indicate that the phase at which a spike occurs shifts to progressively earlier phases as an animal moves through a field. However, because phase precession can be observed without any need for reference to space (i.e., as advancement of phase of first spike over successive cycles field potential rhythm), we refer to phase precession in the context of space as phase coding of space. The strength of phase coding of space was computed as the linear–circular correlation of between the (linear) position of the animal within a firing field and the (circular) phase of theta when each spike occurred. To facilitate aggregation of data across cells and fields, the positions within the field were standardized to the range of 0–1, reflecting the relative position between the start of the field (at 0) and the end of the field (at 1). Both the resulting rho value (as computed by the MATLAB function circ_corrcl.m of the Circular Statistics Toolbox; (Berens, 2009)) and the slope of the fit (Kempter, Leibold, Buzsáki, Diba, & Schmidt, 2012) were considered in quantifying the effects of the muscarinic antagonist on phase coding of space. In cases where an individual cell had multiple place fields (regardless of direction of movement), the correlation was computed over all spikes at a single time rather than being computed separately for each field.
2.5.8. Single‐pass analyses
To determine if the effects observed in the trial‐level analyses were the result of aggregating over many single passes through firing fields, we also examined the data at the level of single passes. Single passes were identified as complete passes through identified firing fields, including exiting the field prior to reentry. Only passes with more than one spike were processed. Three basic analyses were performed on the single‐pass data. The first assessed the variability across single passes of the position of the first (and last) spike of the pass. For this, the position of the first (or last) spike was recorded for each pass and the variance of this position was computed over all passes. The second was a similar analysis to quantify the variance in the theta phase at which the first (and last) spike of the pass occurred. We then computed the variance in the phase of firing over passes. Because theta phase is a circular metric, we used the circular variance script (circ_var.m) from the Circular Statistics Toolbox for MATLAB (Berens, 2009). In the third analysis, we computed the linear–circular correlation between spike position and phase as described above for each pass. In this case, we aggregated the rho values over passes by taking the mean over all passes within a trial for a given cell.
2.6. Statistics
Nonparametric statistics were used throughout the manuscript due to the lack of normality of the measures examined as revealed by a Kolmogorov–Smirnov goodness of fit test comparing the empirical data distribution to a normal distribution. In the case of nonpaired tests, rank‐sum tests were performed. In the case of paired tests, Wilcoxon signed‐rank tests were performed. To indicate which was used in each instance, the Z statistics are indicated as either Zr.s. for rank sum or Zs.r. for sign rank, respectively. Consistent with the use of nonparametric statistics, medians are reported as the key summary statistics. Chi‐square tests were used in instances where we sought to test if the change in percentage of neurons with a particular label could be considered significant. Because the number of available samples varies widely throughout the analyses, the number of observations used in each test is indicated explicitly. The threshold for significance was set with α = 0.05.
Data panels in figures show all data points for each condition. A horizontal line indicates the median of the sample and the associated 95% bootstrap confidence interval of the median is shown as a vertical error bar. The 95% bootstrap confidence intervals were computed using 10,000 iterations.
3. RESULTS
We sought to test if muscarinic receptor blockade reduces the quality of temporal coding in hippocampal neurons. To answer this question, we collected extracellular electrophysiological recordings of neuronal activity and field potential from dorsal CA1 in rats as they completed laps on a circle track for food rewards before and after systemically administering scopolamine. We then compared the temporal firing properties of those neurons before and during the influence of scopolamine. To summarize the results presented below, we found that spiking phase precession relative to field theta was significantly reduced, largely due to a slower rhythmic spiking frequency. While spatial tuning remained intact, phase coding of space was significantly reduced. These results are summarized in Figure 2.
Figure 2.
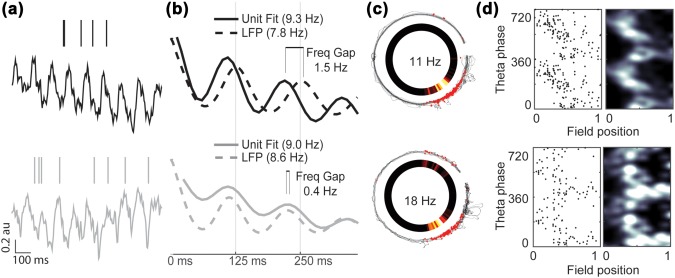
Phase precession in hippocampal place cells is reduced following systemic muscarinic receptor blockade despite preserved spatial tuning. (a) Representative spike raster and field theta from the preinjection baseline (top) and scopolamine injection (bottom) trials, showing perturbed precession during the injection trial. (b) Unit and field theta rhythmicity (solid and dashed lines, respectively) before and after scopolamine administration (top and bottom, respectively). The unit rhythmicity is reflected by the best fit line to the spike‐time autocorrelogram (see methods). (c) Spatial tuning is preserved. The animal trajectory is shown as a black trace with red dots indicating the position of the animal at each spike. The gap in the trajectory is the result of peri‐reward site epochs having been removed from all analyses. The firing rate of the neuron at each point of the track is shown in the inset pixelated ring. (d) Raw spike raster (left) and heat‐map (right) indicate that the linear–circular correlation between position within the field and theta phase was reduced. [Color figure can be viewed at wileyonlinelibrary.com]
As observed previously (Newman et al., 2014, 2013), rats ran slower on average under the influence of scopolamine (slowing from a median of 38cm/s to 26 cm/s; P < 0.001, Zs.r. =3.67, n = 12 sessions). Because the metrics of central interest to this study are known to co‐vary with running speed, we explicitly controlled for the running speed of the animals between conditions. That is, the pre‐scopolamine and scopolamine trials were subsampled to match the distribution of running speeds prior to all subsequent analyses. Neural firing rate changes are also of potentially of concern in this regard. However, we did not find a scopolamine related change in firing rate (0.48 vs 0.48 Hz, P = 0.41, Z s.r. = 0.83, n = 486 for all epochs; 0.54 vs 0.59 Hz, P = 0.97, Zs.r. = 0.04, n = 486 for speed‐matched epochs), thus, no subsampling was done with regard to firing rate.
3.1. Muscarinic blockade reduces phase precession
Our first analyses addressed whether muscarinic blockade reduced phase precession. To avoid unnecessary complication in the analysis, for example, by potential changes in spatial coding, we first examined phase precession as the relative difference between the frequency of theta‐rhythmicity observed in individual cell spike time autocorrelograms and field potential theta (Figure 3a & 3b). Prior to scopolamine administration, the median relative frequency gap was 0.54 Hz (spiking rhythmicity was 0.54 Hz faster than the field theta frequency) across the 389 significantly rhythmic well‐isolated cells aligned between the pre‐scopolamine and scopolamine trials. Following scopolamine administration, the median relative frequency gap decreased significantly to 0.33 Hz (P < 1 × 10−9, Z s.r. = 6.18, n = 389; Figure 3a). This observed reduction in the relative frequency gap suggests that, under the influence of scopolamine, fewer cells precessed relative to the field theta rhythm. We tested this explicitly by asking how many cells had a positive relative frequency gap. Prior to scopolamine, 86% of cells (334 of 389) had a positive relative frequency gap (i.e., phase precessed on average). Following scopolamine, the number of positive relative frequency gaps decreased to 73% of cells (283 of 389). A Chi squared test demonstrated this reduction in the ratio of cells with positive relative frequency gaps was significant (P < 1 × 10−5, χ2 = 20, df = 1; data not shown).
Figure 3.
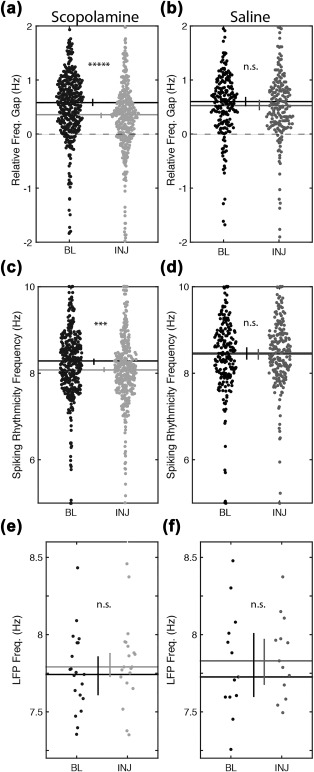
Phase precession, measured as the relative frequency gap between unit rhythmicity and field theta, was significantly reduced following muscarinic receptor blockade due to a shift in the frequency of unit rhythmicity, not field potential. (a) The relative frequency gap (unit freq. minus field theta freq.) during scopolamine injection trials is reduced relative to the preinjection baseline trials. (b) The relative frequency gap is unchanged during saline injection trials. (c,d) The frequency of rhythmic firing of units is reduced during scopolamine (c), but not saline (d), injection trials relative to the preinjection baseline trials. (e,f) Frequency of the field potential theta rhythm was not changed in either condition. Abbreviations: BL = preinjection baseline trial; INJ = injection trial; Freq = frequency. Horizontal lines indicate the medians. Error bars indicate bootstrap 95% confidence intervals. Significant indicators: *****P < 1 × 10−9; ***P < 1 × 10−5; n.s. = P > 0.05
Next, to better understand the origin of the change in the relative frequency gap, we sought to identify if either the field theta frequency or the spiking rhythmicity frequency were particularly affected. A post‐hoc analysis of field theta frequency revealed a nonsignificant increase from a median frequency of 7.74–7.79 Hz (P = 0.26, Z s.r. = 1.12, n = 21; Figure 3e). The analysis of spiking rhythmicity, however, revealed a significant decrease from 8.12 Hz to 7.99 Hz following scopolamine administration (p < 1 × 10−5, Z s.r. = 4.65, n = 389; Figure 3c). These results indicate that the reduced frequency gap was due largely to the shift in the frequency of spiking rhythmicity rather than an effect on field theta frequency.
A control condition was included to test that these observed effects were specific to the scopolamine manipulation and not, for example, the stress of the drug injection or the specific timing of the postinjection test relative to the preinjection baseline trial. In this control, a volume matched injection of sterile saline was administered instead of scopolamine and all other testing procedures were matched. In this control, we observed no change in the relative frequency gap (0.51 Hz vs 0.52 Hz, P = 0.79, Z s.r. = 0.27, n = 201; Figure 3b). Similarly, no changes were observed in either the field theta frequency (7.73 Hz vs 7.79 Hz, P = 0.75, Z s.r. = 0.31, n = 13; Figure 3f) or in the spiking rhythmicity frequency (8.42 Hz vs 8.41 Hz, P = 0.73, Z s.r. = 0.34, n = 201; Figure 3d). Although testing order was counterbalanced between scopolamine and saline conditions to match experience with the circle track between‐conditions, we performed a post‐hoc analysis to test if inadvertent differences in experience could account for between condition differences. We did not, however, find a significant difference between scopolamine and saline conditions in the amount of experience animals had with the circle track prior to testing (15.7 trials vs 13.6 trials, P = 0.63, Z r.s. = 0.48, df = 22). Given the lack of decreased phase precession in the saline condition, we conclude that the reduced relative frequency gap observed following scopolamine administration was not due to the injection or timing of the injection trial thereby supporting the conclusion that scopolamine triggered the reduction specifically.
A relevant concern when analyzing the frequency of field theta or spiking rhythmicity is that reduced rhythmicity could render the frequency estimates unreliable. In the case of field theta, a post‐hoc test of field theta amplitude revealed no significant change (0.15 vs 0.14 a.u., P = 0.20, Z s.r. = 1.27, n = 21; Figure 4a), as was observed in the saline condition (0.16 vs 0.15 a.u., P = 0.55, Z s.r. =0.59, n = 13; Figure 4b), suggesting that there should be no change in our ability to estimate the field theta frequency. In the case of estimating the frequency of the spike time autocorrelogram rhythmicity, the analysis utilized a curve‐fitting method that indicated when insufficient rhythmicity prevented a reliable estimate of the frequency. The above analyses were explicitly restricted to those cells with significant fits for both pre‐scopolamine and scopolamine trials.
Figure 4.
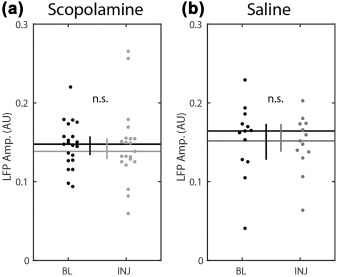
Local field theta amplitude was not significantly changed in either condition. Horizontal lines indicate the medians. Vertical bars indicate the 95% confidence intervals. Abbreviations: BL = preinjection baseline trial; INJ = injection trial; Freq = frequency; n.s. = P > 0.05. Error bars indicate bootstrap 95% confidence intervals
As a secondary control analysis designed to test whether the above mentioned results could be attributable to differences in running speed profiles between conditions (the prior speed matching procedure matched the distribution between trials), we further downsampled our sessions and data to match running speeds across conditions. When we did this, we found the same qualitative pattern of results. That is, the relative frequency gap decreased significantly after scopolamine (0.75 vs 0.40 Hz, P < 1 × 10−4, Z s.r. = 4.14, n = 59 cells) but not saline (0.68 vs 0.58 Hz, P = 0.53, Z s.r. = 0.63, n = 93), which was a significant difference between conditions (−0.39 vs −0.06 Hz, P < 0.001, Z r.s. = 3.49, df = 150). As observed in the full dataset, the frequency of rhythmic firing was significantly reduced following scopolamine (8.33 vs 8.14 Hz, P < 0.02, Z s.r. = 2.54, n = 59) but not saline (8.43 vs 8.38 Hz, P = 0.47, Z s.r. = 0.72, n = 93), which also was a significant difference between conditions (−0.18 vs 0.05 Hz, P < 0.02, Z r.s. = 2.45, df = 150). In this subsampling, theta frequency was marginally significantly increased following scopolamine (7.51 vs 7.64 Hz, P = 0.0499, Z s.r. = 1.96, n = 8), was not significantly changed in the saline condition (7.49 vs 7.57 Hz, P = 0.24, Z s.r. = 1.18, n = 8), and was not significantly different between conditions (0.15 vs 0.11 Hz, P = 0.77, Z s.r. = 0.29, df = 14). Given these results, we conclude that mean differences in speed between conditions cannot account for the observed effects of scopolamine on phase precession.
In our final analysis of spiking rhythmicity, we asked if the quality of the rhythmicity was significantly impacted by the muscarinic blockade. This analysis demonstrated that the strength of spiking rhythmicity was decreased significantly between baseline and scopolamine trials (0.88 vs 0.65, P < 1 × 10−9, Z s.r. = 6.34, n = 389; Figure 5b). This finding builds on the observed reduction in the frequency of spiking rhythmicity to indicate that hippocampal cells fired at both a slower frequency and with less regularity. No significant change in rhythmicity was observed in the saline condition (0.98 vs 0.81, P = 0.11, Z s.r. = 1.61, n = 201; Figure 5d).
Figure 5.
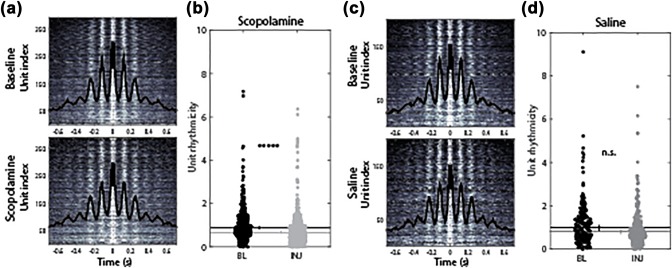
Rhythmicity is modestly, though significantly, reduced following muscarinic blockade. (a) Spike time autocorrelation over all cells during baseline (top) and scopolamine (bottom) trials shown as grayscale heat map. Black line indicates the average over all cells. (b) The strength of unit rhythmicity, as quantified by the fit to the theta amplitude parameter (Royer et al., 2010), was significantly reduced. (c,d) As in a and b, but for the saline condition, showing no significant change to the strength of unit rhythmicity. Abbreviations: BL = baseline; INJ = injection. Error bars indicate bootstrap 95% confidence intervals. Significant indicators: *****P < 1 × 10−9, n.s. = P > 0.05 [Color figure can be viewed at wileyonlinelibrary.com]
3.2. Muscarinic blockade reduces phase coding of space
Phase precession in place cells causes the position of an animal within a firing field to be correlated with the phase of theta at which a cell fires. Given the observed reduction in pure phase precession, our next question was whether muscarinic blockade also reduced phase coding of space. Here, we quantified this by performing a linear–circular correlation between the position in a field and the theta phase at each spike (Kempter et al., 2012). This analysis was performed on cells that had identifiable place fields both before and after scopolamine administration. Across these 154 cells, we found a modest but highly significant decrease in the median linear–circular correlation rho statistic (0.46 vs 0.41, P < 1 × 10−5, Z s.r. = 4.78, n = 154; Figure 6a). We further asked if the number of cells exhibiting a significant correlation between position and theta phase decreased following scopolamine administration. With this analysis we found a significant reduction in the percentage of cells with a significant correlation between position and spiking phase in the scopolamine condition (92% vs 83%, P < 0.02, χ2 = 5.88, df = 1; data not shown). In the saline injection condition, we did not find significant effects for either the linear–circular correlation rho value (0.38 vs 0.38, P = 0.93, Z s.r. = 0.09, n = 95; Figure 6b) or the percentage of significant correlations (82% vs 81%, P = 0.85, χ2 = 0.04, df = 1; data not shown). Comparing the change to the linear–circular correlation between the scopolamine and saline conditions showed that the scopolamine condition was significantly more negative than that observed in the saline condition (−0.06 vs 0.01, P = 0.001, Z r.s. = 3.27, df = 247; Figure 6c). These data show that scopolamine reduced the correlation between position and the theta phase of each spike, indicating reduced phase coding of space following muscarinic blockade.
Figure 6.
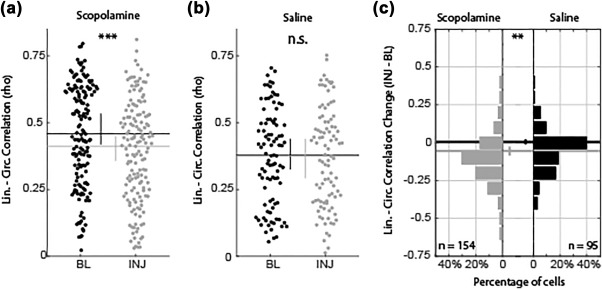
Phase coding of space was decreased following scopolamine administration. The linear–circular correlation between position in field and theta phase at which a spike occurs decreases following scopolamine administration (a) but not saline (b). The correlation decrease shown in (a) was carried by most cells showing modest, but significantly reliable, decrease between baseline and injection trials (c, left). Changes observed in the saline condition (c, right) were not reliably different from zero. Abbreviations: BL = baseline; INJ = injection; lin. = linear; circ. = circular. Error bars indicate bootstrap 95% confidence intervals. Significant indicators: ***P < 1 × 10−5; **P < 0.01; n.s. = P > 0.05
The above analysis, testing the effect of scopolamine on the phase coding of space is complicated by the fact that a reduction in the quality of spatial coding is sufficient to cause an apparent reduction to the linear–circular correlation rho value. To evaluate if such an effect could account for the observed effects on phase coding of space described above, we performed post‐hoc tests to assess the influence of scopolamine on the spatial coding of those cells included in the above analysis. We did not, however, find a significant decrease in the spatial information (si) carried by the neuronal firing (1.84 vs 1.66 bits, P = 0.16, Z s.r. = 1.40, n = 154; Figure 7a). Rather, we found a modest increase in spatial coherence (sc) of the firing rate maps (0.59 vs 0.63, P < 0.04, Z s.r. = 2.06, n = 154; Figure 7d). No significant changes to either metric were observed in the saline condition (si: 1.43 vs 1.49 bits, P = 0.08, Z s.r. = 1.75, n = 95; sc: 0.57 vs 0.57, P = 0.20, Z s.r. = 1.27, n = 95). The fact that the cells included in the analysis of phase coding of space did not have a significant loss of spatial tuning suggests that the reduced phase coding of space was unlikely to be driven simply by changes in spatial coding. While previous reports indicate we should have seen a modest decrease in tuning (Brazhnik, Muller, & Fox, 2003; 2004), it is worth emphasizing that the above analysis was restricted to those cells that had preserved place fields. Expanding the analysis to all cells revealed a significant decrease in both spatial information (si: 1.61 vs 1.82, P < 0.01, Z s.r. = 2.69, n = 474; Figure 7c) and spatial coherence (sc: 0.48 vs 0.42, P < 0.001, Z s.r. = 3.35, n = 474; Figure 7g) following scopolamine but not saline (si: 1.65 vs 1.56, P = 0.97, Z s.r. = 0.03, n = 238; sc: 0.54 vs 0.51, P = 0.44, Z s.r. = 0.77, n = 238; Figure 7d,h), consistent with previous observations (Brazhnik et al., 2004, 2003).
Figure 7.
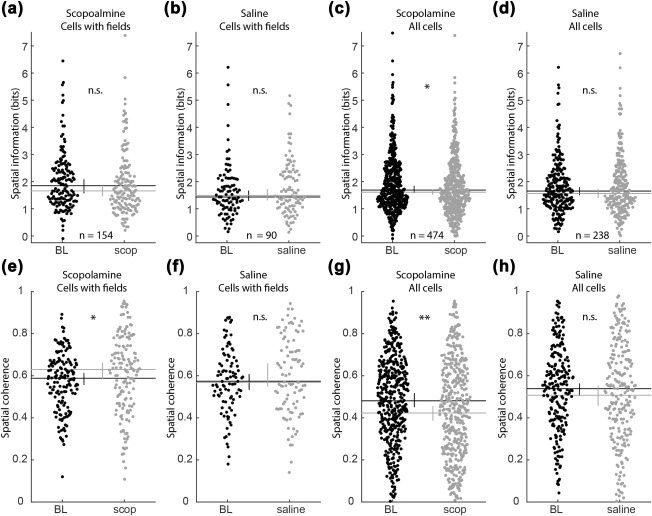
Changes in spatial tuning were not observed during changes in linear–circular correlations. (a–d) Spatial information of the rate maps did not change in among those cells with significant firing fields (i.e., those included in the analysis of phase coding of space in Figure 6) in either the scopolamine (a) or saline (b) conditions. When all cells were analyzed, spatial information was significantly reduced following scopolamine (c) but not saline (d). (e,f) Spatial coherence of the rate map increased modestly among cells that preserved their firing fields following scopolamine (e) but not saline (d). When all cells were analyzed, spatial coherence was significantly reduced following scopolamine (g) but not saline (h). Abbreviations: BL = baseline; INJ = injection; lin. = linear, circ. = circular. Error bars indicate bootstrap 95% confidence intervals. Significant indicators: **P < 0.001; *P < 0.05; n.s. = P > 0.05
Another potential concern in analyses of position–phase correlations is that a change in the shape of the theta wave could alter the underlying distribution of theta phases (e.g., if the rising phase became compressed). To test for this, we analyzed the shape of the theta wave for possible shifts by examining the theta asymmetry index (Belluscio et al, 2012). This analysis, however, revealed no significant difference between baseline and scopolamine injection trials (−0.07 vs −0.10, P = 0.19, Z s.r. = 1.31, n = 15; data not shown) like the lack of difference observed in the saline condition (−0.14 vs −0.14, P = 0.31, Z s.r. = 1.01, n = 9; data not shown). The lack of a significant change in the asymmetry index suggests that the shape of the theta waveform did not change substantially and, thus, was unlikely to substantial impact on our results. Nonetheless, we replicated the analysis of position–phase correlation using a variant wherein the Hilbert transform‐based method of phase estimation (used above) was replaced with the Belluscio et al., (2012) method of estimating phase by linearly interpolating between peaks and troughs of the theta wave. This variant would negate any changes in the duration of the rising or falling phases. The results, however, revealed the same basic pattern as described above—the position–phase correlation was significantly reduced during the scopolamine injection trial relative to the respective baseline trial among cells that maintained fields between trials (rho value of 0.42 vs 0.34, P < 1 × 10−5, Z s.r. = 4.58, n = 154; data not shown), whereas no change was observed following saline administration (0.34 vs 0.32, P = 0.55, Z s.r. = 0.60, n = 95; data not shown).
3.3. Phase coding reduced in single passes through field
To better understand the observed reduction in phase coding of space observed at the whole‐trial level, we turned to analyses of individual passes through the firing field. There are three accounts of how phase coding of space at the trial‐level could be reduced, each with distinct predictions for what happened within and between single passes of the firing field (Figure 8). The first is that the phase of theta at which a cell began and stopped firing became more variable. Consequently, even if the relationship between position and phase remained strong at the single‐pass level, it would appear weaker when compared over the whole trial; this is illustrated in Figure 8b(i). Similarly, a second account is that the position at which a cell began and stopped firing between passes through the field became more variable. Again, even if position and phase remained strongly related within passes, the relationship between position and phase may be weak when compared over the whole trial; this is illustrated in Figure 8b(ii). Neither the first nor the second accounts necessitate any change in the quality of phase coding from preinjection trials. A third account, however, is that phase coding itself was reduced, and thus, even at the level of single passes through the field, there should be a reduced correlation between position and phase; this is illustrated in Figure 8b(iii). To test these accounts, we analyzed the variability in phase and position of both the first and last spikes across passes, and the correlation of position and phase at the level of single passes.
Figure 8.
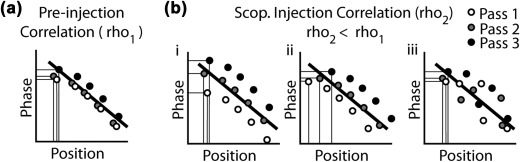
Three models of how phase coding of space at the trial‐level could be reduced are dissociable by the effects observed at the single‐pass level. (a) The standard negative relationship between position and phase that form the basis of phase coding of space. The trial‐level correlation aggregates over spikes that occur over distinct single‐passes, the spikes from each pass are depicted in different colors. The phase and position of the first spike are marked to illustrate the baseline level of variance. (b) The reduced correlation value observed in the scopolamine injection trial could be due to three different effects of scopolamine. The first (i) is an increase in the variance of the phase of spiking. The second (ii) is an increase in the variance of the position of spiking. The third (iii) is a reduction in the relationship between position and phase at the single‐pass level
Our analyses show that neither phase nor position of spiking became more variable over single passes and, thus, cannot account for the trial‐level decrease in phase coding of space. As shown in Table 1, in no case did we see a scopolamine related increase in variance in either the position or phase at which the first spike on each pass was observed. The same is true for the last spike on each pass. The only significant effect that we observed was a scopolamine‐related decrease in variability with respect to the position of the first spike (top row, Table 1). However, this cannot account for the decrease in trial‐level phase coding of space observed in the scopolamine condition. Reduced position variability over single passes would be expected to have the opposite effect; that is, it would facilitate finding an increased trial‐level linear–circular correlation rather than the observed decreased. No significant changes were observed in the saline condition.
Table 1.
Increased variability in the position or theta phase of spiking cannot account for the reduced trial‐level phase coding of space
| Condition | Spike | BL | INJ | Z s.r. | P | ||
|---|---|---|---|---|---|---|---|
| Variance in | Position | Scopolamine | First in pass | 0.031 | 0.019 | 2.77 | <0.01 |
| Last in pass | 0.029 | 0.027 | 0.19 | n.s. | |||
| Saline | First in pass | 0.027 | 0.026 | 0.01 | n.s. | ||
| Last in pass | 0.025 | 0.025 | 0.84 | n.s. | |||
| Theta phase | Scopolamine | First in pass | 0.38 | 0.35 | 1.49 | n.s. | |
| Last in pass | 0.53 | 0.50 | 0.77 | n.s. | |||
| Saline | First in pass | 0.40 | 0.36 | 1.59 | n.s. | ||
| Last in pass | 0.56 | 0.55 | 1.23 | n.s. |
Neither the position nor theta phase of spiking became more variable between single‐passes through firing fields. The only significant change was a reduction in the variability of the position at which the first spike occurred over passes in the scopolamine condition.
Examining the correlation between position and theta phase across single passes confirmed that this relationship was reduced even at the level of individual passes through the field (Figure 9). The linear–circular correlation between position and phase was significantly decreased following scopolamine (0.69 vs 0.63, P < 10 e−5, Z s.r. = 4.55, n = 147; Figure 9a) but not following saline (0.71 vs 0.70, P = 0.50, Z = 0.67, n = 114; Figure 9b). The decreased correlation coefficient observed at the level single passes, together with the lack of significant increases in variability in the position or phase of spiking, confirmed that the effect observed at the trial‐level reflects degradation in the phase coding of space by muscarinic blockade.
Figure 9.
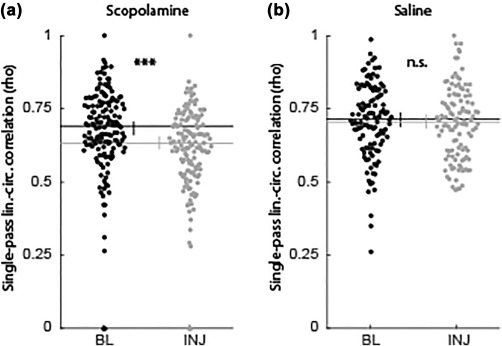
Reduced phase coding of space was observable at the single‐pass level. The linear–circular correlation between position and theta phase of spiking was significantly decreased at the level of individual passes through firing fields in the scopolamine condition (a) but not the saline condition (b). Abbreviations: BL = baseline; INJ = injection; lin. = linear; circ. = circular. Error bars indicate bootstrap 95% confidence intervals. Significant indicators: ***P < 1 × 10−5; n.s. = P > 0.05
4. DISCUSSION
We sought to test the necessity of cholinergic modulation for the generation of precise spike timing in the hippocampus of freely moving rats. We found that systemic blockade of muscarinic receptors significantly reduced phase precession of hippocampal spiking relative to the phase of local field theta. The quality of phase coding of space was also reduced, as observed through a reduction in the correlation between the position and phase of spiking. These effects were not due to a reduction in spatial coding of hippocampal place cells or due to increased variability in the position or phase of spiking over passes through the firing field. These findings demonstrate that muscarinic receptor signaling is necessary for the fine patterning of spike timing in the hippocampus.
4.1. Implications of reduced spiking timing
The decrease in fine patterning of spike timing observed here may help to explain the amnestic properties of muscarinic antagonists. Small changes in latency between the firing of a presynaptic and postsynaptic cell could make the difference between the induction of long‐term potentiation (LTP) or long‐term depression (LTD) (Bi & Poo, 1998). Thus, unless the fluctuations in timing were coherent across CA3 and CA1, the decreased phase coding that occured following scopolamine administration likely led to the degradation of the synaptic patterning between these areas. Such loss of patterning would thereby prevent the formation of novel memories while under the influence of scopolamine.
A more deleterious implication of disrupted spiking timing in the context of STDP is that ensembles which become activated while under the influence of the muscarinic antagonist could be expected to become degraded, causing forgetting of the associated content. Again, this is because the noisy spike timing would cause inappropriate synaptic updating, weakening synapses that should be strengthened and vice versa. Effectively, this would amount to injecting noise into the synaptic pattern that otherwise supports the activation of the appropriate CA1 neurons. If true, this would have serious implications in the case of conditions such as normal aging or Alzheimer's Disease that are associated with dramatically reduced cholinergic tone (Contestabile, 2011; Craig, Hong, & McDonald, 2011). It would predict that when such individuals access memories, they will cause abnormally large amounts of decay to the underlying neural representations.
4.2. Putative mechanism underlying reduced spike timing
The reduction in spike timing that was observed here may be the result of several possible mechanisms. Owing to the systemic administration of the muscarinic antagonist used here, it is not yet possible to know which mechanisms are to blame. There exist plausible mechanisms within the hippocampus, between the hippocampus and the entorhinal cortex, and due to changes in cortical processing.
Within the hippocampus, cholinergic modulation has a variety of influences that are relevant for the generation of precise spike timing and phase coding of space. For example, acetylcholine acts to inhibit presynaptic terminals from the Schaffer collaterals (Hasselmo & Schnell, 1994), putatively blocking the retrieval of previously formed associations in the context of new learning. In the current experiment, the blockade of muscarinic receptors would have reduced the magnitude of presynaptic inhibition and, thus, allowed for the activation of retrieved associations at inappropriate points within a firing field. Another potentially relevant mechanism of the observed effects within the hippocampus is the deactivation of OLM cells, which are made more excitable by acetylcholine (Leão et al., 2012). These cells serve to selectively gate the relative strength of input from area CA3 and entorhinal cortex to CA1 neurons and are likely a key contributor to the generation of phase precession as animals navigate through place fields (Fernández‐Ruiz et al., 2017). Reduced muscarinic activation could be expected to cause reduced firing rates among these cells, leading to increased processing of entorhinal inputs at inappropriate portions of a place field.
Changes to the entorhinal input to the hippocampus are another plausible mechanism for the observed reduction in temporal coding. Lesions of the medial entorhinal cortex lead to a loss of phase precession in CA1 (Schlesiger et al., 2015). Scopolamine administration likely reduces the strength of functional connectivity between the entorhinal cortex and hippocampus (Newman et al., 2013). Thus, the reduction of phase precession observed here may indicate that scopolamine serves to act effectively as a functional lesion of the entorhinal input to hippocampus. Notably, despite our previous finding that the same scopolamine manipulation degrades spatial tuning in entorhinal grid cells (Newman et al., 2014), we did not find significant reduction in the quality of spatial coding in the present study. However, this aligns with findings reported by Schlesiger et al. (2015) indicating that CA1 neurons continued to have spatial tuning following surgical lesions to the entorhinal cortex.
Finally, it is possible that the effects observed here are driven by changes in cortical processing at large. Acetylcholine plays an important role in a variety of cortical processing systems (Hasselmo, 2006; Hasselmo & Giocomo, 2006; Newman et al., 2012), including working memory (e.g., Croxson, Kyriazis, & Baxter, 2011) and attentional processing (Sarter, Hasselmo, Bruno, & Givens, 2005). Muscarinic blockade leads to impairments in each of these functions (e.g., Herrero et al., 2008; Bang & Brown, 2009). If the rats in the current study had generally impaired cognitive function, it is possible that the observed reduction in temporal coding was due to inconsistent strategy usage by the animals (e.g., Jackson & Redish, 2007).
It is worth noting that, while we subsampled the data to match the running speed between trials, it is likely that the slowed running speeds observed following scopolamine administration had physiological effects that subsampling did not address. For example, the relatively fast running speed during non‐scopolamine trials may have increased brain temperature, resulting in shifts in theta (Wells et al., 2013) with consequences for phase precession dynamics. Future work will test if and how such effects may be relevant to the effects described here.
4.3. Summary
The findings described here demonstrate that the spike timing of principal hippocampal CA1 neurons are significantly reduced following systemic blockade of muscarinic acetylcholine receptors. These results suggest the possibility that the loss of spike timing may be the mechanism by which muscarinic antagonists act to induce amnesia. We also suggest that, beyond preventing the formation of new memories, this loss of timing could lead to the active decay of existing representations. This work carries implication for understanding the cognitive deficits that accompany the degradation of the cholinergic system in aging and diseases such as Alzheimer's disease.
ACKNOWLEDGMENTS
The authors have no conflicts of interest to declare. They would like to thank the valuable contributions of all members of the Hasselmo Lab for their discussions and support in conducting this research. In particular, the CMBHOME toolbox first developed by Andrew Bogaard was central to making these analyses possible. We also appreciate the hard work and support provided by the BU animal care facilities in taking care of our test subjects for this work.
Newman EL, Venditto SJC, Climer JR, Petter EA, Gillet SN, Levy S. Precise spike timing dynamics of hippocampal place cell activity sensitive to cholinergic disruption. Hippocampus. 2017;27:1069–1082. https://doi.org/10.1002/hipo.22753
Funding information NIH, Grant/Award Numbers: F32MH090671, R01MH60013, and R01MH61492; Office of naval research MURI; Grant/Award Number: N00014‐10‐1‐0936
REFERENCES
- Bang, S. J. , & Brown, T. H. (2009). Muscarinic receptors in perirhinal cortex control trace conditioning. Journal of Neuroscience, 29, 4346–4350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belluscio, M. A. , Mizuseki, K. , Schmidt, R. , Kempter, R. , & Buzsáki, G. (2012). Cross‐frequency phase‐phase coupling between θ and γ oscillations in the hippocampus. Journal of Neuroscience, 32, 423–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens, P. (2009). CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software. [Google Scholar]
- Bi, G. Q. , & Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. Journal of Neuroscience, 18, 10464–10472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bialek, W. , Rieke, F. , de Ruyter van Steveninck, R. R. , & Warland, D. (1991). Reading a neural code. Science, 252, 1854–1857. [DOI] [PubMed] [Google Scholar]
- Brazhnik, E. , Borgnis, R. , Muller, R. U. , & Fox, S. E. (2004). The effects on place cells of local scopolamine dialysis are mimicked by a mixture of two specific muscarinic antagonists. Journal of Neuroscience, 24, 9313–9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brazhnik, E. S. , Muller, R. U. , & Fox, S. E. (2003). Muscarinic blockade slows and degrades the location‐specific firing of hippocampal pyramidal cells. Journal of Neuroscience, 23, 611–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess, N. , Recce, M. , & O'keefe, J. (1994). A model of hippocampal function. Neural Networks, 7, 1065–1081. [Google Scholar]
- Colgin, L. L. , Denninger, T. , Fyhn, M. , Hafting, T. , Bonnevie, T. , Jensen, O. , … Moser, E. I. (2009). Frequency of gamma oscillations routes flow of information in the hippocampus. Nature, 462, 353–357. [DOI] [PubMed] [Google Scholar]
- Contestabile, A. (2011). The history of the cholinergic hypothesis. Brain Research Reviews, 221, 334–340. [DOI] [PubMed] [Google Scholar]
- Craig, L. A. , Hong, N. S. , & McDonald, R. J. (2011). Revisiting the cholinergic hypothesis in the development of Alzheimer's disease. Neuroscience & Biobehavioral Reviews, 35, 1397–1409. [DOI] [PubMed] [Google Scholar]
- Croxson, P. L. , Kyriazis, D. A. , & Baxter, M. G. (2011). Cholinergic modulation of a specific memory function of prefrontal cortex. Nature Neuroscience, 14, 1510–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Almeida, L. , Idiart, M. , Villavicencio, A. , & Lisman, J. (2012). Alternating predictive and short‐term memory modes of entorhinal grid cells. Hippocampus, 22, 1647–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douchamps, V. , Jeewajee, A. , Blundell, P. , Burgess, N. , & Lever, C. (2013). Evidence for encoding versus retrieval scheduling in the hippocampus by theta phase and acetylcholine. Journal of Neuroscience, 33, 8689–8704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi, G. , & Buzsáki, G. (2006). Temporal encoding of place sequences by hippocampal cell assemblies. Neuron, 50, 145–157. [DOI] [PubMed] [Google Scholar]
- Fernández‐Ruiz, A. , Oliva, A. , Nagy, G. A. , Maurer, A. P. , Berényi, A. , & Buzsáki, G. (2017). Entorhinal‐CA3 dual‐input control of spike timing in the hippocampus by theta‐gamma coupling. Neuron, 93, 1213–1226.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghoneim, M. M. , & Mewaldt, S. P. (1975). Effects of diazepam and scopolamine on storage, retrieval and organizational processes in memory. Psychopharmacology, 44, 257–262. [DOI] [PubMed] [Google Scholar]
- Gupta, A. S. , van der Meer, M. A. A. , Touretzky, D. S. , & Redish, A. D. (2012). Segmentation of spatial experience by hippocampal theta sequences. Nature Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo, M. E. , & Giocomo, L. M. (2006). Cholinergic modulation of cortical function. Journal of Molecular Neuroscience, 30, 133–135. [DOI] [PubMed] [Google Scholar]
- Hasselmo, M. E. , & Schnell, E. (1994). Laminar selectivity of the cholinergic suppression of synaptic transmission in rat hippocampal region CA1: Computational modeling and brain slice physiology. Journal of Neuroscience, 14, 3898–3914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo, M. E. (2006). The role of acetylcholine in learning and memory. Current Opinions in Neurobiology, 16, 710–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazan, L. , Zugaro, M. , & Buzsáki, G. (2006). Klusters, NeuroScope, NDManager: A free software suite for neurophysiological data processing and visualization. Journal of Neuroscience Methods, 155, 207–216. [DOI] [PubMed] [Google Scholar]
- Herrero, J. L. , Roberts, M. J. , Delicato, L. S. , Gieselmann, M. A. , Dayan, P. , & Thiele, A. (2008). Acetylcholine contributes through muscarinic receptors to attentional modulation in V1. Nature, 454, 1110–1114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxter, J. R. , Senior, T. J. , Allen, K. , & Csicsvari, J. (2008). Theta phase‐specific codes for two‐dimensional position, trajectory and heading in the hippocampus. Nature Neuroscience, 11, 587–594. [DOI] [PubMed] [Google Scholar]
- Jackson, J. , & Redish, A. D. (2007). Network dynamics of hippocampal cell‐assemblies resemble multiple spatial maps within single tasks. Hippocampus, 17, 1209–1229. [DOI] [PubMed] [Google Scholar]
- Jeewajee, A. , Barry, C. , Douchamps, V. , Manson, D. , Lever, C. , & Burgess, N. (2014). Theta phase precession of grid and place cell firing in open environments. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 369, 20120532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kempter, R. , Leibold, C. , Buzsáki, G. , Diba, K. , & Schmidt, R. (2012). Quantifying circular‐linear associations: Hippocampal phase precession. Journal of Neuroscience Methods, 207, 113–124. [DOI] [PubMed] [Google Scholar]
- Kubie, J. L. , Muller, R. U. , & Bostock, E. (1990). Spatial firing properties of hippocampal theta cells. Journal of Neuroscience, 10, 1110–1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leão, R. N. , Mikulovic, S. , Leão, K. E. , Munguba, H. , Gezelius, H. , Enjin, A. , … Kullander, K. (2012). OLM interneurons differentially modulate CA3 and entorhinal inputs to hippocampal CA1 neurons. Nature Neuroscience, 15, 1524–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer, A. P. , Cowen, S. L. , Burke, S. N. , Barnes, C. A. , & McNaughton, B. L. (2006a). Organization of hippocampal cell assemblies based on theta phase precession. Hippocampus, 16, 785–794. [DOI] [PubMed] [Google Scholar]
- Maurer, A. P. , Cowen, S. L. , Burke, S. N. , Barnes, C. A. , & McNaughton, B. L. (2006b). Phase precession in hippocampal interneurons showing strong functional coupling to individual pyramidal cells. Journal of Neuroscience, 26, 13485–13492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNaughton, B. L. , Barnes, C. A. , & O'keefe, J. (1983). The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely‐moving rats. Experimental Brain Research, 52, 41–49. [DOI] [PubMed] [Google Scholar]
- Mehta, M. R. , Lee, A. K. , & Wilson, M. A. (2002). Role of experience and oscillations in transforming a rate code into a temporal code. Nature, 417, 741–746. [DOI] [PubMed] [Google Scholar]
- Newman, E. L. , Climer, J. R. , & Hasselmo, M. E. (2014). Grid cell spatial tuning reduced following systemic muscarinic receptor blockade. Hippocampus, 24, 643–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman, E. L. , Gillet, S. N. , Climer, J. R. , & Hasselmo, M. E. (2013). Cholinergic blockade reduces theta‐gamma phase amplitude coupling and speed modulation of theta frequency consistent with behavioral effects on encoding. Journal of Neuroscience, 33, 19635–19646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman, E. L. , Gupta, K. , Climer, J. R. , Monaghan, C. K. , & Hasselmo, M. E. (2012). Cholinergic modulation of cognitive processing: Insights drawn from computational models. Frontiers in Behavioral Neuroscience, 6, 24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Keefe, J. , & Recce, M. L. (1993). Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus, 3, 317–330. [DOI] [PubMed] [Google Scholar]
- Robbe, D. , & Buzsáki, G. (2009). Alteration of theta timescale dynamics of hippocampal place cells by a cannabinoid is associated with memory impairment. Journal of Neuroscience, 29, 12597–12605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbe, D. , Montgomery, S. M. , Thome, A. , Rueda‐Orozco, P. E. , McNaughton, B. L. , & Buzsáki, G. (2006). Cannabinoids reveal importance of spike timing coordination in hippocampal function. Nature Neuroscience, 9, 1526–1533. [DOI] [PubMed] [Google Scholar]
- Rossant, C. , Kadir, S. N. , Goodman, D. F. M. , Schulman, J. , Hunter, M. L. D. , Saleem, A. B. , … Harris, K. D. (2016). Spike sorting for large, dense electrode arrays. Nature Neuroscience, 19, 634–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Royer, S. , Sirota, A. , Patel, J. , & Buzsáki, G. (2010). Distinct representations and theta dynamics in dorsal and ventral hippocampus. Journal of Neuroscience, 30, 1777–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarter, M. , Hasselmo, M. E. , Bruno, J. P. , & Givens, B. (2005). Unraveling the attentional functions of cortical cholinergic inputs: Interactions between signal‐driven and cognitive modulation of signal detection. Brain Research Reviews, 48, 98–111. [DOI] [PubMed] [Google Scholar]
- Schlesiger, M. I. , Cannova, C. C. , Boublil, B. L. , Hales, J. B. , Mankin, E. A. , Brandon, M. P. , … Leutgeb, S. (2015). The medial entorhinal cortex is necessary for temporal organization of hippocampal neuronal activity. Nature Neuroscience, 18, 1123–1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitzer‐Torbert, N. , Jackson, J. , Henze, D. , Harris, K. , & Redish, A. D. (2005). Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience, 131, 1–11. [DOI] [PubMed] [Google Scholar]
- Scoville, S. A. , & Milner, B. (1957). Loss of recent memory after bilateral hippocampal lesions. Journal of Neurology, Neurosurgery, and Psychiatry, 20, 11–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skaggs, W. E. , McNaughton, B. L. , Gothard, K. M. , & Markus, E. J. (1993). An information‐theoretic approach to deciphering the hippocampal code. Neural Information Processing Systems, 1030–1037. [Google Scholar]
- Skaggs, W. E. , McNaughton, B. L. , Wilson, M. A. , & Barnes, C. A. (1996). Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus [Internet], 6, 149–172. Available from: http://onlinelibrary.wiley.com/doi/10.1002/(SICI)1098–1063(1996)6:2%3C149::AID‐HIPO6%3E3.0.CO;2‐K/abstract [DOI] [PubMed] [Google Scholar]
- Squire, L. R. (1992). Memory and the hippocampus: A synthesis from findings with rats, monkeys, and humans. Psychological Review, 99, 195–231. [DOI] [PubMed] [Google Scholar]
- Wells, C. E. , Amos, D. P. , Jeewajee, A. , Douchamps, V. , Rodgers, J. , O'keefe, J. , … Lever, C. (2013). Novelty and anxiolytic drugs dissociate two components of hippocampal theta in behaving rats. Journal of Neuroscience, 33, 8650–8667. [DOI] [PMC free article] [PubMed] [Google Scholar]


