Tundra water budget and implications of precipitation underestimation

Abstract

Difficulties in obtaining accurate precipitation measurements have limited meaningful hydrologic assessment for over a century due to performance challenges of conventional snowfall and rainfall gauges in windy environments. Here, we compare snowfall observations and bias adjusted snowfall to end‐of‐winter snow accumulation measurements on the ground for 16 years (1999–2014) and assess the implication of precipitation underestimation on the water balance for a low‐gradient tundra wetland near Utqiagvik (formerly Barrow), Alaska (2007–2009). In agreement with other studies, and not accounting for sublimation, conventional snowfall gauges captured 23–56% of end‐of‐winter snow accumulation. Once snowfall and rainfall are bias adjusted, long‐term annual precipitation estimates more than double (from 123 to 274 mm), highlighting the risk of studies using conventional or unadjusted precipitation that dramatically under‐represent water balance components. Applying conventional precipitation information to the water balance analysis produced consistent storage deficits (79 to 152 mm) that were all larger than the largest actual deficit (75 mm), which was observed in the unusually low rainfall summer of 2007. Year‐to‐year variability in adjusted rainfall (±33 mm) was larger than evapotranspiration (±13 mm). Measured interannual variability in partitioning of snow into runoff (29% in 2008 to 68% in 2009) in years with similar end‐of‐winter snow accumulation (180 and 164 mm, respectively) highlights the importance of the previous summer's rainfall (25 and 60 mm, respectively) on spring runoff production. Incorrect representation of precipitation can therefore have major implications for Arctic water budget descriptions that in turn can alter estimates of carbon and energy fluxes.

Key Points

• Water storage deficits are consistently overestimated when precipitation is not adjusted for underestimation

• End‐of‐snowmelt through July rainfall is a more effective measure of drought conditions than total warm season rainfall

• Precipitation bias lead to underestimated snowmelt runoff, due to overestimated antecedent water storage deficits and underestimated snowfall

1. Introduction

Arctic wetlands cover large areas of Alaska, Canada and Russia and their hydrology plays a major role in local to global energy, nutrient and global carbon exchange [Gorham, 1991; Gutowski et al., 2007]. The changing Arctic climate includes increased air temperatures [Kaufman et al., 2009] and precipitation caused by enhanced atmospheric poleward moisture transport [Zhang et al., 2013] and locally sourced precipitation from the increasingly ice‐free Arctic Ocean [Bintanja and Selten, 2014; Liu et al., 2012]. The urgency of parameterizing models with accurate water balance components to improve projections of the future state of the Arctic is well recognized [Lique et al., 2016]. Such an effort must be initialized with the fundamental derivation of realistic precipitation estimates.

Precipitation is a critical input variable for any water balance assessment but is challenging to measure accurately. Biases are primarily underestimates, which are attributed to a range of factors such as catch efficiency of gage type attributed to wind, water left on the walls of the gage (wetting loss), evaporation, shift from manual to automated recording techniques and treatment of trace precipitation events [Goodison et al., 1989; Groisman and Legates, 1994]. In the Arctic, errors are primarily attributed to wind, followed by wetting and trace losses [Mekis, 2005; Yang et al., 1998] due to high winds, long winters and the relatively low precipitation rates. Trace precipitation, which is the amount below a measurable limit, can account for nearly 80% of the total number of winter precipitation days [Benson, 1982].

Underestimation of measured snowfall and rainfall have been recognized for more than a century [Alter, 1937; Nipher, 1878; Warnick, 1953] with some studies estimating up to 50% error [Goodison et al., 1998; Groisman and Legates, 1994; Mekis and Vincent, 2011; Sevruk, 1982]. Specifically in arctic Alaska and Canada, some studies have reported weather station biases of up to 300–400% of end‐of‐winter snow accumulation [Black, 1954; Woo et al., 1983]. Adjustments to conventional measurements can provide reliable (or at least less biased) estimates [Adam and Lettenmaier, 2003; Dingman et al., 1980; Groisman and Legates, 1994; Mekis and Vincent, 2011; Yang et al., 2005], but uncertainty may still prevail [Vihma et al., 2016]. Snow (when effectively represented) is typically the major Arctic precipitation input [Kane and Yang, 2004; Woo, 1986] and require larger adjustments than rain [Benning and Yang, 2005; Mekis and Vincent, 2011]. Unadjusted snowfall may, therefore, have profound implications for climatological and hydrological model applications, including those informed by reanalysis products, which also rely on observations. There is a need for both improved quantification by and awareness within the research community about how precipitation biased descriptions could propagate through our understanding of biogeophysical systems.

Few efforts have focused on quantifying the impact of precipitation underestimation on water balance [Louie et al., 2002; Tian et al., 2007; Wang et al., 2015; Ye et al., 2012] and especially in the Arctic region where, in general, hydro‐climatological measurements are sparse due to logistical constraints [Bring et al., 2016]. Rarely are all individual water balance components measured simultaneously and/or there is a high degree of measurement or estimation uncertainty [Dingman et al., 1980]. Hydrological observations, both within and outside the Arctic region, are typically limited to basic meteorology (snowfall, rainfall and air temperature) and runoff [Kane and Yang, 2004], while the evapotranspiration and storage terms are often estimated and not directly measured [Shutov et al., 2006]. Inaccurate snowfall observations have been associated with large water budget imbalances (∼48% of unadjusted annual precipitation) in high latitude Canadian basins [Wang et al., 2015], while simulations forced with bias adjusted precipitation increase streamflow by 5 to 25% for most major rivers in northern latitudes [Tian et al., 2007]. However, ineffective representation of precipitation is a challenge not only affecting the hydrological sciences, but also disciplines that depend on water fluxes and storage estimates.

Arctic wetland hydrology plays a major role in the global climate systems, where the storage and flow of water controls the fate of extensive permafrost carbon stocks. The overestimated soil water storage deficit can result in a suppression of modeled evapotranspiration rates (due to water‐limitation) and therefore impact surface energy exchange in coupled atmospheric and hydrologic models. Further, an underestimation of snow depth can cause physical‐based models to produce colder winter soils than observations may otherwise suggest [Stieglitz et al., 2003]. The dry moisture status of near‐surface soils causes a cooling effect on deeper soils in summer and a warming effect in winter due to the insulating properties of organic soils [O'Donnell et al., 2009]. Carbon, water and energy simulations often rely on atmospheric reanalysis products that are informed by (underestimated) snowfall and rainfall observations [Dee et al., 2011]. Considering the combined impacts of (i) the direct and indirect role of soil moisture in controlling the form and magnitude of land‐atmosphere carbon fluxes [Gorham, 1991; Zona et al., 2016], (ii) the vast amounts of carbon stored in Arctic soils [Hugelius et al., 2014; Zimov et al., 2006], and (iii) the observed and projected trends of atmospheric warming in the Arctic [Chapman and Walsh, 1993; Holland and Bitz, 2003; Pithan and Mauritsen, 2014], it is of paramount importance that the scientific community continue to assess the prevalence of precipitation bias, make the necessary adjustments, and interpret findings appropriately thereafter.

Our objectives are to a) assess the 2006–2009 water budget of a low‐gradient tundra wetland near Utqiagvik (formerly Barrow) on the Arctic Coastal Plain in Northern Alaska; b) quantify the impact of unadjusted snowfall and rainfall measurements on the water budget; and c) assess how seasonal variability in rainfall controls water storage and, in particular, summer lows in water tables. The analyses are derived from existing methods for precipitation bias adjustment and field measurements that include end‐of‐winter snow depth and density, ablation, snowfall, rainfall, water table levels, runoff and evapotranspiration.

2. Site Description

The study area is referred to as the Biocomplexity watershed (0.3 km², 71.281 N, −156.596 W, elevation 4.5 m), which is located a few kilometers from the Beaufort and Chukchi Seas on the Barrow Environmental Observatory near Utqiagvik on the Arctic Coastal Plain, Northern Alaska (Figure 1) [Goswami et al., 2011; Zona et al., 2009]. Mean annual air temperature at Utqiagvik Airport is −12°C (1977–2009) with a June through August average air temperature of 3.3°C [Liljedahl et al., 2011]. Annual adjusted precipitation has been estimated to be 170 mm (1941–1970) [Dingman et al., 1980] and 173 mm (1977–2009) [Liljedahl et al., 2011].

Figure 1.

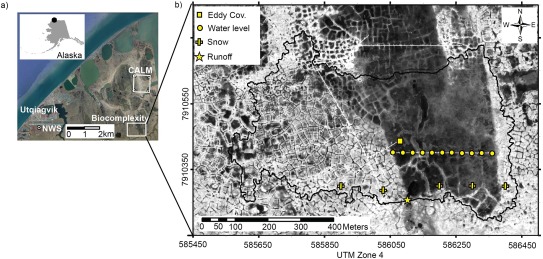
Locations of the long‐term meteorological data from the National Weather Service station at Utgiagvik Airport (NWS), the end‐of‐winter snow survey location (1999–2014) for (a) the Circumpolar Active Layer Monitoring Grid (CALM), and (b) the Biocomplexity watershed (0.3 km²) near Utgiagvik (formerly Barrow), Northern Alaska. Within the watershed are the west‐east transect of water table observations (Water level), 2008 and 2009 snow ablation monitoring sites (Snow), and runoff monitoring point (Runoff), eddy covariance tower and soil moisture measurements (Eddy Cov.). The dominating patterned ground features are low‐centered polygons, both without (mainly in the drained thaw lake basin) and with troughs, while high‐centered polygons are found in the upland area of the southcentral and easternmost portions. In general, the darker the shade the more surface moisture in the QuickBird panchromatic satellite image from 1 to 2 August 2002 [Manley et al., 2006]. The larger image of Utgiagvik area is from GoogleEarth.

About half of the watershed includes a vegetated drained thaw lake basin (DTLB) that drained no more than 300 years ago [Hinkel et al., 2003] and is now a poorly drained wet tundra meadow with Typic Aquiturbels soils underlain by ∼600 m thick permafrost [Brown and Johnson, 1965]. DTLB's [Mackay, 1963] occupy approximately 26% of the Arctic Coastal Plain [Hinkel et al., 2005] and 50% of the Utqiagvik Peninsula north of 71° latitude [Hinkel et al., 2003]. As typical in low‐gradient Arctic watersheds, low‐centered polygons are found within the DTLB, which is surrounded by upland tundra of older high‐ and low‐centered polygons. Landscape‐wide ice‐wedge degradation occurred sometime between 1948 and 2007, while only localized lateral expansion of some individual trough‐ponds have been observed since 2007 [Liljedahl et al., 2016]. The active layer depth at a nearby DTLB at Utqiagvik varied from 19 to 62 cm (mean 36 cm) in 1995–2009 and the average depth within the studied DTLB was 30 cm (2006), 26 cm (2007 and 2008), and 27 cm (2009) [Shiklomanov et al., 2011].

Arctic wetland vegetation is strongly correlated with subtle microtopographical landscape features [Billings and Peterson, 1980]. In Utqiagvik, wet tundra meadow communities predominate in the basin and upland tundra troughs, while mesic moss carpets, graminoids, and lichen cover the well‐drained domes of high‐centered polygons and elevated rims of low‐centered polygons [Tieszen, 1978]. Nonvascular vegetation represents a large portion of plant biomass and cover [Webber, 1978] and most of the live above‐ground biomass in the vegetated drained lake bed [Zona et al., 2010]. In a nearby DTLB, moss may reach depths of 20 cm at wet sites, but the bulk of their living biomass is usually within ∼1 cm of the soil surface [Engstrom et al., 2005; McEwing et al., 2015]. Vascular plant species composition is dominated by the graminoids Carex aquatilis (maximum LAI of 0.43), Eriophorum spp. (LAI ∼ 0.13) and Dupontia fisheri (LAI ∼ 0.02) [Zona et al., 2011]. Vegetation senescence in the region typically begins in mid to late August and extends to late September when snow typically begins to accumulate [Myers and Pitelka, 1979].

3. Methods

3.1. Meteorology

The 2006–2009 water balance analyses utilized meteorological measurements of wind speed, air temperature and relative humidity obtained from an eddy covariance tower [Zona et al., 2009], which is located inside the watershed. Footprint analyses show the tower sensors primarily representing the ground surface <70 m away [Zona et al., 2012]. Incoming solar radiation (direct and diffuse) was retrieved from the Atmospheric Radiation Measurement program located about 5 km north. Long‐term conventional daily precipitation (rainfall and snowfall, 1949–2014), air temperature and wind speed were retrieved from the National Climatic Data Center web archive for the Utqiagvik Wiley Post‐Will Rogers Airport station (STN 700260, WBAN 27502), which is located approximately 7 km from the studied watershed. We used three distinct methods in describing precipitation: End‐of‐winter snow depth measurements on the ground (Measured_CALM), unadjusted observed rainfall and snowfall (Measured_NWS) and adjusted observed rainfall and snowfall (Adjusted Measured_NWS).

The Measured_CALM precipitation was obtained from the annual average of the 121 end‐of‐winter snow depth measurements (1999–2014) across the 1 km² Circumpolar Active Layer Monitoring (CALM) study area (www.gwu.edu/~calm), which is located about 2 km north of the studied watershed (Figure 1). CALM snow water equivalent (SWE) values were estimated from the pre‐melt snow density measurements in 2008 and 2009 (average 0.32 g cm⁻³). The five snow density sites (Figure 1) were located to represent the two main features of the 0.3 km² watershed, which include upland tundra (high‐centered polygons, two sites) and the vegetated drained lake basin (low‐centered polygons, three sites). In addition to the pre‐melt snow density measurements, daily snow water equivalents were also calculated from five snow density measurements (Adirondack tube) and 50 snow depth measurements at each of the five sites following the method outlined by Rovansek et al. [1993]. Tundra snow accumulation near Utqiagvik is affected by wind, topography and vegetation [Dingman et al., 1980]. At the two study sites, snow is primarily caught in low lying areas between ice‐wedge polygons (i.e., in troughs) although the landscape‐scale average SWE is similar between ice‐wedge polygon types (high and low‐centered) [Liljedahl et al., 2016] and vegetated drained thaw lake margins (supporting information Figure S1). Net lateral snow transfer across the CALM grid boundary was assumed negligible.

The National Weather Service (NWS) station has experienced changes in its location and instruments throughout the years, with documentation limited to the following: The weather station was moved progressively to the southeast (<145 m in total) and further inland in 1955 and to the airport in 1966 (current location), but has always been located at 7 to 9 m.a.s.l. Wind instruments have remained at about 10 m above ground level (9.3 to 11.7 m). The rotating cups (Belfort MODEL 2000) were replaced with sonic sensors (Vaisala model 425) in June 2011. One wind screen has been in use since at least 1982 [e.g., Yang et al., 1998] and two screens (1.2 and 2.4 m diameter) since the installation of the new precipitation gauge. Snowfall and rainfall, here referred to as Measured_NWS, was measured with 8‐inch diameter heated tipping bucket (NWS 8 in/20.32 cm Standard Gauge) until 25 September 2003. The top of the gauge from the ground changed in 1966 (from 0.9 m to 1.8 m height). Weighing style gauge/load cell technology replaced the tipping bucket in 2003 (6.3 in/16 cm OTT Pluvio All‐Weather Precipitation Accumulation Gauge, AWPAG) with a sensor accuracy of at least 0.25 mm for individual precipitation events (supporting information Figure S2). Electronic weighing gauges, including the OTT Pluvio AWPAG, have shown reduced precipitation bias compared to heated tipping buckets [Rasmussen et al., 2012; Sevruk and Chvíla, 2005]. Field comparisons of heated tipping buckets and electronic weighing systems for snowfall have measured 24% less precipitation for tipping gauges primarily due to evaporative losses related to gauge heating [Savina et al., 2012]. The Double Fence Intercomparison Reference (DFIR) precipitation gauge has shown to catch 1.7 times more precipitation than the AWPAG with a Tretyakov wind shield inside a 2.4 m diameter Alter shield [Dover, 2008].

The third representation of precipitation (Adjusted Measured_NWS) was snowfall and rainfall adjusted for up to three main types of systematic errors, which include wind undercatch, trace events and also wetting loss (1949–2014). No evaporative losses were accounted for at the two gauges. We used bias adjustment methods that Yang et al. [1998] developed for NWS 8 in/20.32 cm Standard Gauge. The wind adjustment equation was applied to both types of gauges as we were unable to find wind adjustments specifically developed for the OTT AWPAG. Adjustment for wetting loss, which is attributed to wetting of the inner walls of the gauge orifice and container, included adding 0.03 and 0.15 mm to each measured daily rainfall and snowfall, respectively. The lowest amount of recorded daily precipitation was 3 mm throughout the time series, despite the differing precipitation gauges. Days with a trace precipitation event, i.e., precipitation observed below 3 mm, is defined by the notation “T” with a measurement of zero in the precipitation data. A conservative amount of 0.1 mm was given to all daily trace observations 1949–2014 following the method by Yang et al. [1998]. The change in gauge height and its effect on wind speed at the orifice was accounted for and the maximum wind speed at the gauge was set to 6.5 m s⁻¹. No daily average wind speed was recorded prior 1984. Calculation of adjusted precipitation 1949–1983 was informed by the 1984–2014 wind speed average at 10 m height (5.7 m s⁻¹).

A scaling factor (CALM factor) was derived by dividing the Measured_CALM by the Measured_NWS snowfall (1999–2014). Measured_CALM data were compared to conventional snowfall observations (i.e., to total snowfall up to the date of CALM measurements) and informed water balance analyses for 2006–2009. Gap‐filling of snowfall from the date of the CALM measurement through the snowmelt was made with Adjusted Measured_NWS rainfall and for snowfall, the CALM factor applied to Measured_NWS.

3.2. Runoff

Runoff was measured with a hand‐held velocity meter (Flo‐Mate^TM Model 2000, Marsh‐McBirney) in the morning (low‐flow) and evening (high‐flow) throughout the spring snowmelt runoff period. In the low‐rainfall summer of 2007, stream water level readings were obtained via daily site visits until flow ceased in late June and revisited through mid‐August after rainfall events. In 2008, stream water levels were recorded with hourly time lapse photos directed toward a metric staff gage and manually processed. In 2009, stream water levels were recorded hourly using a non‐vented pressure transducer (Onset U20–001‐04). Regular site visits (∼weekly) throughout the summer ensured that the pressure transducer was continuously immersed in the water column as the water level and frost table receded. The recorded data were processed with the software (HOBOware‐Pro, Onset Computer Corporation) to account for the effect of atmospheric pressure and water temperature. Snowmelt is known to be the main, and often only, runoff event in low‐gradient Arctic wetlands that lack any major snow drifts [Brown et al., 1968; Kane et al., 2008] and was here measured with the same method between the 3 years. Stage‐discharge relationships for streamflow predictions are unreliable during snowmelt due to the constantly changing channel morphology as snow and ice melts, therefore the daily measurements of low‐ (morning) and high‐flow (evening). Observations of summer stream water levels supported runoff estimates once the snowmelt‐derived flow ceased. The different methods in stream water level measurement techniques between years should have a negligible effect on our water balance assessments because a) daily low and high water levels were captured during the snowmelt and b) others have also found a minimal rainfall‐runoff response after the snow melt period at a similarly sized low‐gradient tundra watershed at Utqiagvik [e.g., Brown et al., 1968].

3.3. Evapotranspiration

The discontinuous time series of measured evapotranspiration from the eddy tower [Liljedahl et al., 2011] was gap‐filled using a hydrological model calibrated and validated for the watershed (for details on the method, see Liljedahl et al. [2016]). The model represents evapotranspiration via the Penman‐Monteith approach and separately accounts for soil (moss) evaporation, which was limited to the uppermost 10 cm of the soil column. The model validation of evapotranspiration rates includes three statistical methods; the relative index of agreement (I_a) [Willmott and Wicks, 1980], the root mean square of the error (RMSE) [Willmott, 1982] and the mean bias error (MBE).

3.4. Storage

The water table measurements were recorded relative to local ground surface within the vegetated drained thaw lake basin. In 2006, manual measurements were made at one location next to the flux tower. Water tables in 2007–2009 represented an average of 11 sites situated along an east‐west transect where measurements were marked with a 2.5 cm PVC tube. An artificially induced snowdrift (caused by an elevated boardwalk) developed each winter along the transect, which prevented measurement of water levels until about one week after peak runoff in 2007–2009.

Volumetric soil moisture was measured in the DTLB and in proximity of the eddy covariance towers using Time Domain Reflectometry (CS616 Campbell Scientific, Logan) moisture probes. The measurements were processed and presented as unfrozen soil moisture content in the units of percent saturation [Hinzman et al., 1991]. Here, the spring peak in soil moisture was assumed to represent saturated conditions (100%, all micro and macro pore spaces filled with liquid water). In winter, the organic soil was assumed to have 6% saturation.

3.5. Water Budget

Simultaneous measurements of all water balance components (precipitation, runoff, water level, soil moisture and evapotranspiration) were made during a 3 year period (2007–2009), while all but runoff were measured in 2006. The storage component of the annual water balance assessment was evaluated as

$$\Delta S_{Annual}=P\left(snow\right)+P\left(rain\right)-Q-ET$$ (1)

where ΔS is the storage change (mm), P precipitation as snow and rain (mm), respectively, Q measured runoff (mm) and ET evapotranspiration (mm). Change in storage was also calculated daily for the 2007–2009 period from the onset of snowmelt through start of winter (5 consecutive days below 0°C) for each respective year of the study as

$$\Delta S_{Daily}=M\left(snowmelt\right)+ P\left(rain\right)-Q-ET$$ (2)

where M represents the daily release of water via snowmelt (mm) as estimated via the degree‐day method calibrated to measured ablation [Liljedahl, 2011]. The effect of precipitation bias on the water budget was quantified by equation (2). In the unadjusted precipitation scenario, M and P_rain were based upon Measured_NWS precipitation, e.g., conventional snowfall and rainfall measurements. In the adjusted precipitation scenario, snow available for melt was initialized by Measured_CALM and Adjusted Measured_NWS represented rainfall (P_rain). Any snowfall after the onset of snowmelt was represented by Measured_NWS (unadjusted scenario) multiplied by the CALM factor (adjusted scenario) and added to the total snow available for M(snowmelt). The onset of snowmelt was defined as the onset of the ablation period where reductions in SWE occurred in consecutive days. Degree‐day factors, runoff and evapotranspiration remained as measured in the precipitation scenarios. The effect of the precipitation scenarios on storage anomaly was not carried over from 1 year to the next, since measured runoff and evapotranspiration were used. Accordingly, beyond the impact on the precipitation itself, the precipitation underestimation analysis was evaluated through the resulting differences in storage (ΔS_Daily) for each year without subsequent impacts on runoff and evapotranspiration.

4. Results

4.1. Meteorology

Large differences were shown between the methods used for estimating total winter precipitation (Figure 2 and supporting information Table S1). End‐of‐winter snow accumulation (Measured_CALM) was nearly four times larger (on average 3.7 with a range from 2.8 to 4.3) than what was recorded by the heated tipping gauge (Measured_NWS) in 1999–2003. During 2004–2014, the new weighing style gauge, which included an additional wind shield, reduced the bias, but the CALM snow survey still presented 2.5 times (1.8 to 3.9) more snow than what was recorded by the gauge. Winter precipitation estimates improved but remained underestimated following wind, wetting and trace adjustments and the bias was further reduced with the new sensor installation (Adjusted Measured_NWS was 62 mm (1999–2003) and 95 mm (2004–2014), which was 55 and 74%, respectively, of Measured_CALM). If left unadjusted, the long‐term average (1949–2014) total winter precipitation was 55 mm, while applying the CALM snow factors (3.7 for 1949–2003 and 2.5 for 2004–2014), results in 190 mm (Table 1). Long‐term average rainfall increased 24% from 67 (Measured_NWS) to 83 mm (Adjusted Measured_NWS). Application of adjustments to rainfall and the CALM adjustment factors to Measured_NWS snowfall produced an adjusted long‐term (1949–2014) annual precipitation estimate that is more than two times larger (274 mm) than what was originally observed (123 mm for Measured_NWS). Accounting for precipitation bias also increases the long‐term average contribution of snow to annual precipitation from 45% (Measured_NWS) to 69% (based on Adjusted Measured_NWS rainfall and the CALM factors applied to Measured_NWS snowfall).

Figure 2.

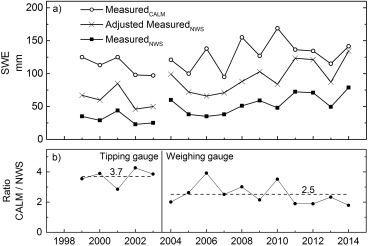
(a) Total winter precipitation estimated via three different methods and(b) the CALM factor (average 3.7 and 2.5, respectively), which is the Measured_CALM divided by the Measured_NWS value. The precipitation gauge was changed from a tipping to a weighing bucket in September 2003 that also included the installation of an additional wind screen.

Table 1.

Meteorology and Water Balance Components^a

	2006	2007	2008	2009	2006–2009	1949–2014
Meteorology (°C)
MAAT	−10.9	−9.7	−9.9	−10.1	−10.2	−11.9
SWI	11.8	18.9	11.5	15.3	14.4	10.3
Water balance (mm)
Ablation_END	11 Jun.	9 Jun.	14 Jun.	10 Jun.	11 Jun.
Summer_END	29 Sep.	1 Oct.	27 Sep.	22 Sep.	28 Sep.
PAnnual	221 (104)	142 (65)	240 (113)	268 (166)	218 ± 54	274 (123)
PWinter	150 (41)	118 (46)	180 (66)	164 (77)	153 ± 26	190 (55)
PSummer	71 (63)	25 (19)	60 (48)	104 (89)	65 ± 33	83 (67)
Runoff		52	53	112	72 ± 34	‐
ET b	141	165	139	161	152 ± 13	‐
ΔS	‐	−75 (−152)	48 (−79)	−5 (−107)	−38 ± 57	‐
Runoff/PWinter	‐	0.44	0.29	0.68	0.47 ± 0.20	‐

^aLong‐term (1949–2014) mean annual air temperatures (MAAT) represent the hydrologic year (1 September to 31 August). Summer and winter long‐term air temperature and precipitation represent months with mean monthly air temperatures above and below 0°C, respectively. Long‐term annual precipitation is the sum of summer and winter precipitation. Summer Warmth Index (SWI) is the sum mean monthly air temperature of all months >0°C. Long‐term precipitation is Measured_NWS winter precipitation multiplied by the 3.7 (1949–2003) and 2.5 (2004–2014) CALM factor plus Adjusted Measured_NWS summer precipitation. Water balance analyses in 2006–2009 represent onset of snowmelt through start of winter (5 consecutive days below 0°C), where winter precipitation includes end‐of‐winter snow accumulation measurements (Measured_CALM) plus any additional Measured_NWS snowfall through the onset of melt multiplied by the CALM factor and daily Adjusted Measured_NWS rainfall. Values in parentheses represents estimates based upon Measured_NWS precipitation, i.e., unadjusted precipitation.

^bFrom end‐of‐snowmelt.

Mean annual air temperatures (−10.2°C) and the Summer Warmth Index (14.4°C), which is the sum of all mean monthly air temperatures above 0°, were above the long‐term average (−11.9 and 10.3°C, respectively, 1949–2014) during the intensive study period (2006–2009). Summers of 2007 and 2009 were exceptionally warm and ranked among the top ten warmest summers recorded for Utqiagvik. These two summers had contrasting extremes in adjusted rainfall. Summer 2007 had the second lowest adjusted summer precipitation on record with about one third (25 mm) of the long‐term average (average 83 mm with a range from 12 to 115 mm, 1949–2014). Summer 2009 had 104 mm of adjusted rain (Figure 3a) or 127% of the adjusted long‐term average. Winter 2006–2007 (118 mm) and 2007–2008 (180 mm) had lower and average precipitation, respectively, compared to the long‐term adjusted value (190 mm).

Figure 3.

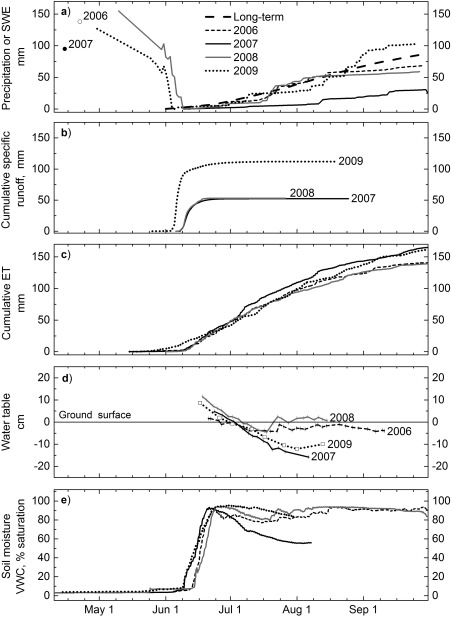
Measured water balance components 2006–2009. The individual components include water equivalent stored in the snow pack and cumulative (a) adjusted rainfall, (b) runoff, (c) modeled evapotranspiration, (d) vegetated drained thaw lake basin water levels and (e) near surface soil moisture at 10 cm depth. End‐of‐winter SWE and daily ablation were measured in 2008 and 2009, while only end‐of‐winter SWE was measured in 2006 and 2007. The runoff in 2007 and 2008 was nearly identical and therefore overlapping. Long‐term rainfall represents the adjusted 1947–2014 average.

4.2. Runoff

Runoff was primarily associated with the snowmelt in June (Figure 3d). High runoff lasted for about 3 days in early June when the DTLB temporarily became a shallow lake with up to ∼20 cm inundation surrounding the day of peak runoff (9 June in 2007 and 2008 and 5 June in 2009). During 2007–2009, total runoff averaged 72 mm and ranged from 52 (2008) to 112 mm (2009) (Table 1). No significant summer runoff was measured in this period. Only a trickle was observed at the outlet during a relatively large rain event (6.7 mm) in late August 2009 but it was too low to be measured effectively. Between 22% (2008) and 42% (2009) of the annual precipitation was partitioned into runoff. The partitioning of SWE into runoff showed larger interannual variability (29 to 68%) with an overall mean of 47% (Table 1). Winter 2007–2008, which followed the unusually low rainfall of summer 2007, had the highest winter precipitation (180 mm), but spring 2008 did not produce the largest runoff (only 53 mm). Instead, the greatest runoff was measured in 2009 (112 mm), which also followed a near‐average snow year (164 mm).

4.3. Evapotranspiration

Simulated and measured evapotranspiration (ET) show an overall good agreement (I_a 0.84–0.92, supporting information Table S2). Midday ET rates were slightly overestimated, which results in a total seasonal Mean Bias Error of up to 6 mm. Total summer ET averaged 152 mm (2006–2009) with the higher rates documented during the warmer 2007 (165 mm) and 2009 (161 mm) summers (Table 1 and Figure 3e). Evapotranspiration was the largest water loss component, while year‐to‐year variability in ET (±13 mm) was lower than that for adjusted summer (±33 mm), winter (±26 mm) and annual precipitation (±54 mm) during 2006–2009.

4.4. Storage

Each snow‐free season began with a flooding of the DTLB that was then followed by a steady draw‐down of the water table through mid‐July (Figures 3b and 3c). The early‐season inundation period typically lasted three weeks or more (based on 2008 and 2009 peak runoff and water table measurements). DTLB water tables remained close to the ground surface throughout summers with near‐normal June and July precipitation (2006 and 2008), temporarily receding to about 5 cm below the ground surface around mid‐July before approaching the ground surface with late summer and fall rainfall. The timing of water table recession below the ground surface was similar in all summers (last week of June‐first week of July), but the timing of minimum water table differed depending on the occurrence of late summer rain events. In years with typical early and mid‐summer (by 1 August) rainfalls, minimum water tables were observed in mid‐ to late July (−4.2 cm 2006, −4.5 cm 2008). In years with below‐average early and mid‐summer rainfall, the water table continued to lower into August (−16 cm 2007, −12 cm 2009). Soil pits dug in the DTLB in mid‐September 2007 confirmed unsaturated soils throughout the depth of the active layer. In 2009 water tables had begun to recover by mid‐August (−10 cm) due to extensive late summer rainfall that exceeded the long‐term average. Total summer water balance (P_Summer ‐ ET) was consistently negative in all 4 years (from −57 to −140 mm, Table 1). The overall change in storage for a respective water year ranged from −75 (2007) to 48 mm (2008) (Table 1). Two of the 3 study years showed a net loss in storage (2007 and 2009).

The melting of the snowpack (CALM measurements) in spring produced a rapid increase in surface and soil water storage (Figure 4). Measured spring runoff and high early through mid‐summer (June and July) ET rates then gradually reduced surface and soil water storage. We can see that a large amount of snowmelt‐derived input was retained as storage in summer 2008, which followed the unusually low rainfall summer of 2007, instead of being partitioned into runoff. Scenarios that utilize unadjusted snowfall and rainfall, while retaining the measured runoff and evapotranspiration, show suppressed peaks of storage recharge in early season that are less than half of the actual recharge. With rates of runoff and evapotranspiration remaining unchanged, the storage quickly become negative near the runoff peak during all years. The deficits further increased as the season progressed with total seasonal storage change (as informed by unadjusted precipitation) consistently exceeding deficits from the driest adjusted precipitation summer (i.e., 2007). Storage change derived from unadjusted conventional snowfall and rainfall observations ranged from −79 (2008) to −152 mm (2007), but this excludes the effect of underestimated storage state carrying over from 1 year to the next.

Figure 4.

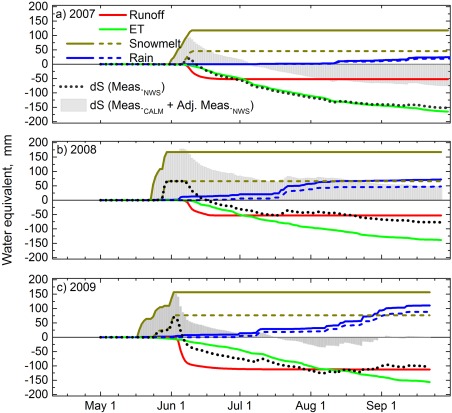
(a–c) Daily water balance of 2007–2009 using unadjusted or adjusted precipitation with storage estimated as the residual. The individual components include cumulative rain, snowmelt (Melt), runoff, evapotranspiration (ET) and storage change (dS). Shown are both adjusted (solid lines informed by CALM snow measurements and Adjusted Measured_NWS rainfall) and unadjusted precipitation (dashes representing Measured_NWS rainfall and snowmelt). Daily storage estimates are based upon adjusted (gray columns) or unadjusted precipitation (black dots). Snowmelt completion date, evapotranspiration and runoff are shown as measured in the field.

5. Discussion

We showed that actual end‐of‐winter snow accumulation on the ground over a 16 year period in a coastal Arctic Alaska is on average more than twice as large than what is recorded by conventional snowfall gauges. Total snowfall observations from individual winters represented down to 23% (2002) of SWE measured on the landscape. A shift in precipitation gauge type from a heated tipping bucket with one wind screen to a weighing style gauge and two wind screens in 2003 (OTT AWPAG) reduced the average snowfall bias from 370% to 250% (Figure 2). The magnitude in snowfall underestimation is in agreement with reports by others that also studied Arctic tundra end‐of‐winter snow accumulation on the ground [Benson, 1982; Black, 1954; Woo et al., 1983]. Testing of the OTT AWPAG by others presented a bias of 170% when compared to the internationally recognized reference gauge configuration Double Fence Intercomparison Reference, DFIR [Dover, 2008]. Accordingly, the DFIR is likely to also underestimate tundra snowfall. After including adjustments (Adjusted Measured_NWS rainfall and the CALM factor applied to Measured_NWS snowfall), the estimated long‐term annual precipitation more than doubled (from 123 to 274 mm). The share of snow on the annual precipitation increased from slightly less than half in unadjusted estimates to representing the majority of the final estimate of annual precipitation (from 45 to 69%), which is comparable to results (63%) presented by Dingman et al. [1980].

The underestimation of precipitation has major impacts on water balance analyses. Not accounting for snowfall and rainfall bias results in consistent loss of storage in each hydrologic year and with an amount that exceeds the true storage loss of the unusually low rainfall summer in 2007. The scenarios presents a conservative description of the effect of underestimated precipitation on soil and surface water status, because the storage change from each precipitation‐underestimate scenario was not carried over to the next water year. For example, unadjusted 2007 precipitation resulted in an estimated storage deficit of 152 mm. Unadjusted snowfall for the following winter (2007–2008) was 66 mm, which would support a soil and surface water recharge in spring 2008 of less than half of the 152 mm 2007 storage deficit. The consequence of no precipitation adjustment would include limited, if any, runoff and inundation during the 2008 snowmelt. Accordingly, analyses based on measured ET, runoff and conventional snowfall and rainfall observations that lack precipitation adjustments results in overestimated soil dryness, and therefore underestimation of both inundation period length and soil and surface water storage prior to freeze‐up. Further, these precipitation induced errors in storage estimates can propagate to impact estimates of other water balance components.

Underestimated soil and surface water storage can affect the following year's partitioning of snowmelt into runoff. Here we used our field measurements to show that the largest total winter precipitation (180 mm in 2008) does not produce the highest runoff. A doubling in runoff (112 mm in 2009 compared to 53 mm in 2008, which followed the dry summer of 2007) was observed in a year with typical snowfall (164 mm in 2009). Only 29% of winter precipitation was partitioned into runoff in 2008 compared to 68% in 2009. In 2008, the majority of snowmelt (up to 71%) recharged the large soil water storage deficit that was produced by the unusually dry soils and low rainfall summer of 2007. Our measurements support previous findings that show the importance of pre‐existing soil and surface water storage conditions in partitioning snow into runoff and soil and surface water recharge [Bowling et al., 2003; Kane et al., 2012]. Accordingly, overestimating soil dryness by relying on conventionally measured rainfall and snowfall can have dramatic impacts on runoff estimates if snowmelt water is allowed to recharge the overestimated soil and surface water deficits.

Our measurements suggest that the variations in pre‐existing conditions (i.e., soil and surface water storage prior snowmelt) are primarily a function of year‐to‐year differences in rainfall rather than evapotranspiration. The interannual variability in rainfall (±33 mm) was more than twice as large as that recorded for total evapotranspiration (±13 mm). Several non‐linear processes have been shown to moderate evapotranspiration from this wet landscape such as a limited ability of mosses to transfer moisture during large atmospheric demand (vapor pressure deficits >0.3 kPa) and an increased partitioning of available energy into ground heat flux [Liljedahl et al., 2011]; thus constraining interannual variability in evapotranspiration. Our results confirm findings from other low‐gradient arctic watersheds studies that show evapotranspiration and not runoff as the major pathway of water loss and evapotranspiration exceeding total summer rainfall [Boike et al., 2008; Kane et al., 1990, 2012; Mendez et al., 1998]. Although the impact of precipitation adjustment is not as large for rainfall (+23%) as for snowfall (+148%) during 2007–2009, the underestimated rainfall nevertheless adds to the overestimated soil water deficit by 5–15 mm.

Seasonal minimum water table depth occurred around mid‐July for summers that had close to average totals and temporal distributions of rainfall such as 2006 and 2008. The partial recovery of late season water table, due to late summer precipitation rates exceeding evapotranspiration rates, has previously been inferred via water balance analyses of low‐gradient Arctic wetlands [Kane et al., 2012]. However, we show that a summer with below‐average total rainfall may not necessarily experience a lower minimum water table or drier near‐surface soils than a summer with average or above‐average total rainfall due to the temporal distribution of the rainfall. For example, total rainfall in 2009 was nearly 125% of the long‐term average. Still, the water table minimum in late July 2009 was more similar to that measured for the unusually low rainfall of 2007 (30% of long‐term average rainfall) than the more typical total rainfall recorded in 2006 and 2008. Near‐surface soils were drier in June through July 2009 than in 2006 and 2008. Unlike 2006 and 2008 when a majority of the rainfall occurred in the early and mid‐season (June through July), the cumulative rainfall was below‐average through July in 2009. Furthermore, the near‐surface soils thawed (i.e., snowmelt ended) about a week earlier in 2007 and 2009 compared to 2006 and 2008. It can be misleading, therefore, to solely analyze statistics of total summer rainfall in assessing seasonal soil water conditions. Evapotranspiration can reach 4.7 mm d⁻¹ near solstice [Liljedahl et al., 2011], which receives the seasonal high in solar radiation. A combination of (below‐average) June through July rainfall, especially in combination with (early) timing of snowmelt, is a more effective metric than total seasonal rainfall in describing soil water variability during the growing period. Unlike in late summer, below‐average early summer rainfall cannot counter the evapotranspiration rates, which are higher in early summer compared to late summer.

Ineffective representation of precipitation can have a cascading effect on water balance studies, irrespective of whether the focus of a particular study is local or regional, and for both simple and complex models. Underestimated precipitation, which is more dramatic in snowfall, produces erroneous surface and soil water storage estimates in summer and prior to soil‐freezing, which in turn affects the partitioning of snowmelt water into runoff and soil water recharge the following spring. Accordingly, the effect of underestimated precipitation on runoff is exacerbated as both the snowmelt amount is underestimated and the storage deficit from the previous summer overestimated. Process‐based models are now commonly used for refining our understanding of permafrost hydrology and the role of hydrology on the larger Arctic system [Lique et al., 2016]. Not adjusting for precipitation undercatch can restrict the value in applying complex models to address our water‐related scientific questions about the Arctic landscape.

The World Meteorological Organization (WMO) has acknowledged the issue of precipitation underestimation by coordinating an evaluation of gauges during the last decade. For example, the current project WMO‐SPICE (Solid Precipitation Intercomparison Experiment) is an international assessment of the ability and reliability of automatic sensors, which are increasingly replacing manual methods, to accurately measure solid precipitation [Sevruk et al., 2009; WMO/CIMO, 2015]. The WMO‐SPICE effort has resulted in numerous recent publications that evaluate different approaches in measuring snowfall [Colli et al., 2015; Wolff et al., 2015; Yang and Simonenko, 2014].

Our findings emphasizes the benefits of maintaining simple end‐of‐winter landscape‐scale snow depth surveys that are co‐located with snowfall gauges to provide a “true” measure of total solid precipitation where sublimation losses are already accounted for. The end‐of‐winter snow depth surveys can in turn be used to evaluate a) automated snowfall measurement methods, b) effectiveness of daily snowfall bias adjustments methods, and c) a bulk snowfall correction factor for a particular landscape and, therefore, strengthen our overall understanding and representation of the Arctic system. For example, a simple but yet significant improvement for long‐term analyzes in landscapes like the Arctic Coastal Plain is to multiply the conventionally observed snowfall by 3.7 for a tipping gauge with one 1.2 m diameter wind screen and by 2.5 if the snowfall is recorded with a weighing gauge and two wind screens (1.2 and 2.4 m).

6. Conclusions

We conclude that ignoring precipitation underestimation, snow in particular, in water balance analyses that are derived from field measurements of runoff and evapotranspiration produces consistent and overestimated water deficits. In Arctic Alaska, conventional precipitation produced negative storage changes (−152 to −79 mm), which also exceeded the largest actual deficit (actual change in storage ranged from −75 to +48 mm). Thus, not accounting for precipitation bias in hydrological studies of Arctic tundra landscapes can not only dramatically underestimate the precipitation itself by only representing a fourth of the actual value, but also cause a chain reaction of underestimation that ripples through the other water balance components (soil and surface water storage, evapotranspiration, and runoff). In particular, our experiments and field observations highlight the risk of dramatically underestimating simulated snowmelt‐derived runoff by a) underestimating total winter precipitation and b) overestimating end‐of summer storage deficits, which results in an artificially large partitioning of snowmelt into soil and surface water storage recharge. Clearly, storage is a key component of the water balance of permafrost laden watersheds, even with a shallow (<40 cm) active layer. Further, our field measurements, albeit limited to four seasons, reveal that total summer rainfall (June–August) is an ineffective measure for evaluating minimum summer water levels when precipitation is effectively described. Instead, end‐of snowmelt through July total rainfall is a more effective drought index due to the consistent seasonality and amount of evapotranspiration, which rates peak near the solstice. We show that, although improved, snowfall remains underestimated (55 to 74% of measured value) after applying established bias adjustment protocols. Simple landscape‐scale end‐of‐winter snow surveys can help alleviate a significant problem in high latitude hydrological sciences and ultimately, refine local and global efforts that depend on effective descriptions of fluxes and stores of water in the Arctic.

Supporting information

Supporting Information S1

Liljedahl, A. K. , Hinzman L. D., Kane D. L., Oechel W. C., Tweedie C. E., and Zona D. (2017), Tundra water budget and implications of precipitation underestimation, Water Resour. Res., 53, 6472–6486, doi:10.1002/2016WR020001.