Exact and Approximate Statistical Inference for Nonlinear Regression and the Estimating Equation Approach

Abstract

The exact density distribution of the nonlinear least squares estimator in the one-parameter regression model is derived in closed form and expressed through the cumulative distribution function of the standard normal variable. Several proposals to generalize this result are discussed. The exact density is extended to the estimating equation (EE) approach and the nonlinear regression with an arbitrary number of linear parameters and one intrinsically nonlinear parameter. For a very special nonlinear regression model, the derived density coincides with the distribution of the ratio of two normally distributed random variables previously obtained by Fieller (1932), unlike other approximations previously suggested by other authors. Approximations to the density of the EE estimators are discussed in the multivariate case. Numerical complications associated with the nonlinear least squares are illustrated, such as nonexistence and/or multiple solutions, as major factors contributing to poor density approximation. The nonlinear Markov-Gauss theorem is formulated based on the near exact EE density approximation.

1. Introduction

According to the JSTOR database, the search for “nonlinear regression” returns 47,988 published items (on December 6, 2016) with the first article published by G.U. Yule in 1909. Since then, nonlinear regression has been studied along four lines of research: (1) Development of nonlinear least squares optimization algorithms. It is worthwhile to mention that the algorithm developed by Levenberg (1944) & Marquardt (1963) till now is the dominant method for sum of squares minimization and is widely used in modern numerical packages. (2) Developing curvature measures as a characterization of the model nonlinearity, starting from the pioneering 1961 paper by Beale and then continued by Bates & Watts (1980). (3) Connection of the curvature measures to criteria for existence and uniqueness of the nonlinear least squares estimate studied in the work by Demidenko (1989, 2000, 2006). (4) Derivation of the density of the nonlinear least squares estimator in small samples, mostly developed in the mid-eighties. The present paper continues the quest for the exact probability density distribution of the NLS estimate as continuation of the work by Pazman (1984), Hougaard (1985) and Skovgaard (1985). Needless to say how important the exact distribution of any estimator might be: it can be used as the benchmark for other approximations, to construct accurate confidence intervals and to test hypotheses with the exact type I error.

Studying statistical properties of nonlinear models in small samples is the most formidable problem of statistics. Although several general techniques are available, such as the saddlepoint and Edgeworth approximations (Goutis & Casella, 1999; Barndorf-Nielsen & Cox, 1979) they are still approximations in scope. To illustrate, consider the popular Lugannani & Rice (1980) and Fraser et al. (1999) saddle point approximation of order O(n^−3/2) for the cumulative distribution function (cdf) of the standardized maximum likelihood estimator with the sample size n used in the recent survey paper by Brazzale & Davison (2008)

$$F_n(b)\simeq \mathrm{\Phi }(b)+\varphi (b)\left(\frac{1}{b}-\frac{1}{q_n(b)}\right),$$

where Φ and ϕ are the cdf and density of the standard normal distribution, and q_n is a positive function of the Fisher information (we do not present the exact formula for brevity). However the cdf F_n(b) is not an increasing function of b which means that the density may become negative. In fact, many density approximations of the NLS estimator suggested by the previous authors may become negative as we learn from the next section. To the contrary, our exact density is always positive although derived under somewhat stringent conditions.

The study of the small-sample properties of nonlinear estimation tangles with numerical issues as nonexistence of the least squares solution and the presence of multiple solutions. Understandably, the previous authors who studied the distribution approximation for finite n even do not mention the possibility of the estimate nonexistence or multiplicity because their occurrence vanishes with n → ∞.

Several authors recognized the possibility of existence multiple local minima of the sum of squares in nonlinear regression and more generally multiple solutions of the estimating equation (M-estimator) leading to the concept of the intensity as a substitute of the density function (Skovgaard, 1990). This approach has been further developed in the following up work by Jensen & Wood (1998) and Almudevar et al. (2000). In contrast to that line of research, we aim at derivation of the explicit expression of the density distribution with applications to confidence interval and hypothesis testing in mind. Our method of derivation is different from those used by other authors: we use the fact that the estimating equation is linear in observations and derive the density by integrating out the multivariate density upon transformation.

For many years, it was believed that the distribution of the nonlinear least squares estimator, even if its unique, cannot be derived in closed form for a general model. We have derived this distribution and shown that it matches the distribution of a special case derived by Fieller (1932) more than 80 years ago. First, the exact distribution is derived for a nonlinear regression model with one parameter and then extended to models with an arbitrary number of linear parameters and a coefficient (partial linear least squares). Second, the exact density is generalized to the estimating equation approach with fixed sample size.

In short, unlike extensive research on the approximation of the distribution from the asymptotic point of view we derived the distribution directly for fixed n. We outline how this derivation can be extended to incorporate the possibilities of nonexistence of the NLS estimate and multiple solutions of the normal equation.

The Gauss-Markov theorem is the landmark result of statistical science (Casella & Berger, 1990; Schervish, 1995). The classic optimal estimation results with fixed n, such as uniformly minimum variance unbiased estimation, hold for the narrow exponential family of distributions (Bickel & Doksum, 2007) and therefore cannot be applied to nonlinear regression. Novel, non-quadratic loss function approaches are needed to expand the optimality theory to more complicated nonexponential distribution statistical models, such as nonlinear regression. As an example, we illustrate the application of the density of the M-estimator by showing that the nonlinear least squares is optimal in the local sense.

The organization of the paper is as follows. The exact density distribution and its comparison with density approximations in the univariate case are presented in Section 2. In that section, we generalize the density to weighted nonlinear least squares and apply the result to a nonlinear regression with a linear part. In Section 3, we generalize our derivation to the estimating equation approach and apply the exact density to a regression with unknown coefficient. Numerical complications arising in nonlinear optimization or the solution of the normal equation and its effect on the density are discussed in Section 4. Section 5 contains results for the multivariate density approximation for nonlinear regression and the estimating equation approach. The formulation of the nonlinear Gauss-Markov theorem and the local optimality of the nonlinear least squares is found in Section 6. In the final section, we outline open problems for exact statistical inference in nonlinear statistical problems with small sample.

2. One intrinsically nonlinear parameter

In this section, we consider nonlinear regression with one intrinsically nonlinear parameter. First, we derive the exact density for the Nonlinear Least Squares (NLS) estimator. Second, we compare the exact density with the near exact density developed previously. Third, we generalize our derivation to the weighted NLS with a known weight matrix. Fourth, we apply the weighted NLS to a regression with one intrinsically nonlinear parameter and an arbitrary number of linear parameters.

With only one nonlinear parameter, β, the nonlinear regression is written as

$$y_i=f_i(\beta )+{\epsilon }_i,i=1,2,\dots ,n,$$ (1)

where y_i is the ith observation of the dependent variable, f_i(β) is the nonlinear regression function, and {ε_i} are iid normally distributed errors with zero mean and variance σ². In many applications, the original regression function is written in the form f(β; x_i), where x_i is the explanatory (covariate) variable; we prefer the notation, f_i(β) = f(β; x_i), simply for brevity. Regarding regression functions {f_i(β)}, we assume them to have continuous derivatives up to the second order on a fixed interval, β ∈ (a, b); typically a = −∞ and b = +∞ (we refer to a and b as to the lower and upper domain parameters). Also, to comply with identifiability condition, we assume that two different parameter values cannot produce the same function values. That is, f_i(b₁) = f_i(b₂) for at least one i implies b₁ = b₂.

The NLS estimate, $\widehat{\beta }={\widehat{\beta }}_{\mathit{\text{NLS}}}$, minimizes the sum of squared residuals,

$${\displaystyle \sum _{i=1}^n{(y_i-f_i(b))}^2.}$$ (2)

One more comment regarding the notation: While $\widehat{\beta }$ denotes the estimator, b denotes a value it takes (it will also act as a dummy argument of functions). The NLS estimate can be found from the solution of the normal equation,

$${\displaystyle \sum _{i=1}^n(y_i-f_i(b))f_i(b)}=0,$$ (3)

where the dot over the function means the derivative, df_i/dβ = f_i, because symbol ′ is reserved for vector/matrix transposition. If the normal equation has a unique solution then the solution is the NLS estimate, otherwise, it may yield spurious solutions. Throughout the paper, we use the vector/matrix notation, y = (y₁, …, y_n)′ and f(β) = (f₁(β), …, f_n(β))′, so that $d\mathbf{f}/d\beta =\dot{\mathbf{f}}$, $d^2\mathbf{f}/d{\beta }^2=\ddot{\mathbf{f}}$. In this notation, the normal equation takes the form

$${(\mathbf{y}-\mathbf{f}(b))}^{\prime }\dot{\mathbf{f}}(b)=0.$$ (4)

The normal equation may have no solution. To avoid this complication, we may restrict our attention to regression with infinite tails: ||f(b)|| → ∞ when |b| → ∞. As was shown by Demidenko (2000), this assumption guarantees that equation (4) has at least one solution for each y.

Before formulating the main result, we introduce relevant quantities and functions:

$$\begin{array}{ll}A=A(b)=\Vert \dot{\mathbf{f}}(b){\Vert }^2,& B=B(b;\beta )={\ddot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta )),\\ C=C(b)={\dot{\mathbf{f}}}^{\prime }(b)\ddot{\mathbf{f}}(b),& D=D(b;\beta )={\dot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta )),\\ E=E(b)=\Vert \ddot{\mathbf{f}}(b){\Vert }^2,& Q=Q(b;\beta ,{\sigma }^2)=\frac{A^2+AB-CD}{\sqrt{{\sigma }^{2}A(AE-C^2)}}.\end{array}$$

As is seen from the following theorem, the exact density distribution of the NLS estimator is expressed through the standard normal cumulative distribution function (cdf), Φ and its density ϕ.

Theorem 1

Let the solution of the normal equation, the NLS estimate, uniquely exist for each y. Let ε_i be iid $\mathcal{N}(0,{\sigma }^2)$ and ${\dot{f}}_i\left(b\right)\ne 0$ for at least one i. Then the exact density of the NLS estimator is given by

$$p_{EX}(b;\beta ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\Vert \dot{\mathbf{f}}(b)\Vert exp\left[-\frac{1}{2{\sigma }^2}\frac{{\left({\dot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta ))\right)}^2}{\Vert \dot{\mathbf{f}}(b){\Vert }^2}\right]\times a_{EX}(b;\beta ,\sigma )$$ (5)

with the adjustment coefficient

$$a_{EX}(b;\beta ,\sigma )=\left(1+\frac{AB-CD}{A^2}\right)(2\mathrm{\Phi }(Q)-1)+\frac{2\sigma }{A}\sqrt{\frac{AE-C^2}{A}}\varphi (Q).$$ (6)

The proof is found in the Appendix and proceeds as follows. First, without loss of generality, we can assume that ${\dot{f}}_1\left(b\right)\ne 0$. Expressing the first observation (i = 1) through b and the other n − 1 observations, a well-known theorem for the density upon nonlinear transformation is applied. Second, we derive the mean absolute value of a linear function of a normally distributed vector in closed form. Third, we express the function value and its derivatives for i = 1 through the full component vectors.

We make a few remarks regarding the exact density, p_EX. First, we note that AE−C² ≥ 0 due to the Cauchy inequality, so the square root function appearing in the adjustment coefficient is well defined. Second, the adjustment coefficient, a_EX(b; β, σ) ≥ 0, so that the density cannot be negative. To prove that we rewrite the first term in (6) as

$$\frac{\sqrt{{\sigma }^{2}A(AE-C^2)}}{A^2}x(2\mathrm{\Phi }(x)-1),$$ (7)

where $x=(A^2+AB-CD)/\sqrt{{\sigma }^{2}A(AE-C^2)}.$ Since x(2Φ (x) − 1) ≥ 0 for all x, we have a_EX(b; β, σ) ≥ 0.

2.1. Comparison with the near exact density and other approximations

Early authors, including Pazman (1984), Hougaard (1985), and Skovgaard (1985), developed the so-called Near Exact (NE) density of the NLS estimator. This density coincides with (5) but has a different (simplified) adjustment coefficient,

$$a_{NE}(b;\beta )=1+\frac{AB-CD}{A^2}.$$ (8)

A nice feature of the NE density is that the cdf of the NLS estimator can be expressed through the standard normal cdf as

$$F_{NE}(b;\beta ,{\sigma }^2)=\mathrm{\Phi }\left(\frac{{\dot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta ))}{\sigma \Vert \dot{\mathbf{f}}(b)\Vert }\right),$$ (9)

which follows from straightforward differentiation. Equivalently, one can write, ${\dot{\mathbf{f}}}^{\prime }(\widehat{\beta })(\mathbf{f}(\widehat{\beta })-\mathbf{f}(\beta ))\Vert \dot{\mathbf{f}}(\widehat{\beta }){\Vert }^{-1}~\mathcal{N}(0,{\sigma }^2)$, where $\widehat{\beta }$ is the NLS estimate. However, in order for (9) to be a real b cdf, three conditions must be met: (1) the argument of Φ must be an increasing function of b for each β, (2) the argument must approach −∞ when b approaches its lower parameter domain and (2) the argument must approach +∞ when b approaches its upper parameter domain.

There are two important distinctions between the EX and NE densities: (1) There is a presence of Φ in the former density, (2) the exact adjustment coefficient contains σ but the NE does not. When σ → 0, the argument of Φ in (6) approaches +∞, implying that Φ → 1. The second adjustment coefficient vanishes when σ → 0, so that

$$\underset{{\sigma }^2\to 0}{\text{lim}}\frac{p_{EX}(b;\beta ,{\sigma }^2)}{p_{NE}(b;\beta )}=1.$$

In another extreme situation, when σ → ∞, we have Φ → 1/2, so that

$$\underset{{\sigma }^2\to \infty }{\text{lim}}\frac{p_{EX}(b;\beta ,{\sigma }^2)}{p_{NE}(b;\beta )}=0.$$

This observation suggests that the NE density approximation can be called “a small-variance approximation” because it coincides with the exact one when σ² approaches zero.

Skovgaard (1985, formula (3.6)) suggested another expression for the density of the NLS estimator. As in the case of previous authors, the formula differs by the adjustment coefficients. More specifically, it has the same argument Q at functions Φ and ϕ, but different coefficients on these functions:

$$a_{SK}(b;\beta ,\sigma )=\left(1+\frac{AB-CD}{A^2}\right)\mathrm{\Phi }(Q)+\frac{\sigma }{A}\sqrt{\frac{AE-C^2}{A}\varphi (Q).}$$ (10)

The difference between this and our a_EX (6) is in the coefficient at the first term. Clearly, the two expressions will be close when Q is large. It is possible to prove that the Skovgaard density is always positive because a_SK > 0.

A nonlinear model that can be reduced to a linear model has the form f(β) = g(β)x, where g is a strictly monotonic function. In the terminology of Pazman (1993), this model is an Intrinsically Linear (IL) model. For an IL model, AB − CD = 0 and AE − C² = 0, so we can approximate the density with a₁ = 1 and a₂ = 0, which leads to the IL approximation of $\widehat{\beta }$,

$$p_{IL}(b;\beta ,{\sigma }^2)=\frac{\Vert \dot{\mathbf{f}}(b)\Vert }{\sqrt{2\pi {\sigma }^2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\frac{{\left({\dot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta ))\right)}^2}{\Vert \dot{\mathbf{f}}(b){\Vert }^2}\right].$$ (11)

All three densities, (5), (8), and (11), are the same for an intrinsically linear nonlinear regression.

A further way to simplify the approximation of the density is to replace the derivative, $\dot{\mathbf{f}}\left(b\right)$, with the derivative evaluated at the true parameter value β:

$$p_{\mathit{\text{ILL}}}\left(b;\beta ,{\sigma }^2\right)=\frac{\left|{\dot{\mathbf{f}}}^{\prime }\left(\beta \right)\dot{\mathbf{f}}\left(b\right)\right|}{\sqrt{2\pi {\sigma }^2}\Vert \dot{\mathbf{f}}\left(\beta \right)\Vert }\text{exp}\left[-\frac{1}{2{\sigma }^2}\frac{{\left({\dot{\mathbf{f}}}^{\prime }\left(\beta \right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)\right)}^2}{{\Vert \dot{\mathbf{f}}\left(\beta \right)\Vert }^2}\right].$$ (12)

This approximation will be called the Intrinsically Linear-Linear (ILL) approximation. This approximation is satisfactory in close proximity to the true value and reduces to the standard normal density upon transformation $z={\dot{\mathbf{f}}}^{\prime }\left(\beta \right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)/\left(\sigma \Vert \dot{\mathbf{f}}\left(\beta \right)\Vert \right)$ under the assumption that ${\dot{\mathbf{f}}}^{\prime }\left(\beta \right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)$ is a monotonic function of b for each β. However, the area under the curve (12) is less than 1 if the range of z does not cover the entire line.

Finally, as follows from the standard asymptotic results (e.g. Gallant 1987), when n → ∞ the distribution of $\widehat{\beta }-\beta$ approaches the normal distribution with zero mean and varianc ${\sigma }^2/{\displaystyle {\sum }_{i=1}^n{\dot{f}}_i^2\left(\beta \right)}$, which implies the normal approximation,

$$p_N\left(b;\beta ,{\sigma }^2\right)=\frac{\Vert \dot{\mathbf{f}}\left(\beta \right)\Vert }{\sqrt{2\pi {\sigma }^2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}{\left(b-\beta \right)}^2{\Vert \dot{\mathbf{f}}\left(\beta \right)\Vert }^2\right]$$ (13)

routinely used in nonlinear regression analysis.

The problem with approximations (8), (11) and (12) is that the area under the “density” is not 1. The fact that the area under the curve specified by the near exact density is not 1 has been mentioned by other authors, including Hougaard (1988), but perhaps the most discouraging feature of the NE density approximation is that it may become negative. For example, for an exponential regression f(β) = e^βx, where x =(x₁, x₂, …, x_n)′, the adjustment coefficient evaluated at b = 0 is proportional to

$${\displaystyle \sum x_i^2+}{\displaystyle \sum x_i^2\left(1-e^{{\beta }_{x_i}}\right)e^{{\beta }_{x_i}}-\frac{{\displaystyle \sum x_i\left(1-e^{{\beta }_{x_i}}\right)}{\displaystyle \sum x_i^3}}{{\displaystyle \sum x_i^2}}}.$$

Assuming that max x > 0, some algebra shows that this quantity becomes negative when β → ∞. Although negative values of the density usually appear at the tails, it may lead to infinite confidence intervals with large σ; the same problem may arise when the area under the density is greater than one.

Example

Five density approximations, (8), (10), (11), (12) and (13), are compared with the exact density (5) for exponential regression, $f_i\left(\beta \right)=e^{\beta x_i}$, where x_i = i with i = 1, …, n = 6 and the true value, β = 0 and σ = 2.5. The results are depicted in Figure 1. The area under the four curves is evaluated numerically by integration over the interval (−4, 0.5) using function integrate in R with 10⁷ subdivisions (R Core Team, 2014). As seen from this figure, the problem with the NE density approximation starts when the NLS estimate takes values below −0.5, resulting in a considerable deviation of the area under the “density” from 1. The negative density is due to the negative values of the adjustment coefficient which falls below zero starting from b = −0.5. The IL and ILL approximations are close to each other and to the EX/NE densities. From a statistical prospective, the NLS estimator has a long left tail which is less visible in the NE approximation. The NE density deviates from the true one because the curvature of the exponential model is unbounded (Pazman, 1984).

Figure 1.

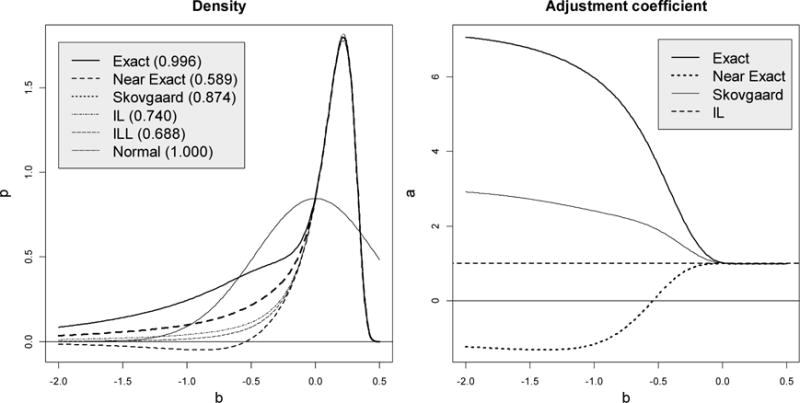
Exact and four density approximations for the exponential regression f_i(β) = e^iβ with i = 1, 2, …, 6, σ = 2.5 and the true β = 0. The figure in the parentheses shows the area under the curve (must be 1).

An obvious remedy for possible negative values of the adjustment coefficient (and the density) in the NE approximation is to take the absolute value, |a_NE(b; β)| or set it zero. This suggestion can be justified by the fact that function x (2Φ (x) − 1) in (7) can be well approximated by |x|. After ignoring the second adjustment coefficient in a_EX, we arrive at |a_NE(b; β)|.

2.2. Nonlinear regression with linear parameters

A nonlinear regression with m additive linear parameters takes the form

$$\mathbf{y}=\mathbf{X}\text{γ+}\mathbf{h}\left(\beta \right)+\epsilon ,$$ (14)

where it is assumed that the n × (m + 1) matrix, [X,h(b)], has full rank for all b. We can reduce this regression to a univariate linear regression by fixing β and applying least squares for γ, yielding $\stackrel{\sim }{\mathbf{y}}=\mathbf{W}\mathbf{y}$ and f(b) = Wh(b), where W = I − P and P = X(X′X)⁻¹X′ is the projection matrix, so that W^1/2 = W. Sometimes, this procedure is called the partially linear least squares, or the Golub-Pereyra algorithm by the name of the original authors, Golub & Pereyra (2003). The reduced sum of squares can be rewritten as

$$\left(\mathbf{y}-\mathbf{X}\mathrm{\gamma }-\mathbf{h}\left(b\right)\right)\prime \mathbf{W}\left(\mathbf{y}-\mathbf{X}\mathrm{\gamma }-\mathbf{h}\left(b\right)\right),$$

where γ may be taken as the true parameter because WX = 0. Formally, the nonlinear regression is f(b) = Xγ − h(b), but since $\dot{\mathbf{f}}\left(b\right)=\dot{\mathbf{h}}\left(b\right)$ and WX = 0, it is sufficient to use f(b) = h(b) with matrix W = I − X(X′X)⁻¹X′. Consequently, the distribution of $\widehat{\beta }$ does not depend on linear parameters γ. To obtain the joint density, (a) write the density of $\widehat{\mathbf{\gamma }}={\left(\mathbf{X}\prime \mathbf{X}\right)}^{-1}\mathbf{X}\prime \left(\mathbf{y}-\mathbf{h}\left(b\right)\right)$ conditional on $\widehat{\beta }=b$,

$$\widehat{\mathrm{\gamma }}|b~\mathcal{N}\left({\left(\mathbf{X}\prime \mathbf{X}\right)}^{-1}\mathbf{X}\prime \left(\mathbf{h}\left(\beta \right)-\mathbf{h}\left(b\right)\right),{\sigma }^2{\left(\mathbf{X}\prime \mathbf{X}\right)}^{-1}\right),$$ (15)

then (b) the joint density for $\widehat{\mathbf{\gamma }}$ and $\widehat{\beta }$ is the product of p_EX and this normal conditional density.

2.3. Possible improvements of Theorem 1

The exact density of the NLS estimator is derived under a stringent assumption on the uniqueness of the solution of the normal equation. If this assumption does not hold the area under p_EX may be different from 1, below is a motivating example.

Example (provided by a referee)

Define the circle nonlinear regression as f(β) = (cos β, sin β) on β ∈ (−π, π], n = 2. The normal equation has two solutions, ${\widehat{\beta }}_1=a\text{tan}\left(y_2/y_1\right)$ and ${\widehat{\beta }}_2={\widehat{\beta }}_1-\pi \times s\text{ign}\left({\widehat{\beta }}_1\right)$. One solution is the NLS estimate as the minimizer of the residual sum of squares (2) and another is the maximizer, the spurious solution. The conditions of Theorem 1 are violated and it is not difficult to find that the area under p_EX density is 2. This example, gives rise to the following improvement of Theorem 1.

Find the density of the NLS estimator under condition that the second derivative of the residual sum of squares is positive: this condition eliminates the spurious solution of the estimating equation corresponding to the maximum of the criterion function.

An advantage of the proof of Theorem 1 is that we can easily incorporate the condition on the positiveness of the second derivatives because it is expressed as a linear function of observations. Indeed, in the notation of the proof from the Appendix, let in addition to the normal equation $\left(z-g\left(b\right)\right)\prime \dot{\mathbf{f}}\left(b\right)=0$we define the condition of the positiveness of the second derivative as

$$\left(\mathbf{z}-\mathbf{g}\left(b\right)\right)\prime \ddot{\mathbf{f}}\left(b\right)=u+{\sigma }^{-1}{\Vert \dot{\mathbf{f}}\left(b\right)\Vert }^2,$$

where z = σ⁻¹(y − f(β)) are normalized observations and g(b) = σ⁻¹(f(b) − f(β)), and u < 0. The joint density of (b, u) can be derived by integrating out y₂, …, y_n following the line of the proof. Finally, to obtain the marginal distribution of b we condition on u > 0 by integration the bivariate density over (−∞, 0). For example, for the circle regression the density of the NLS (with the spurious solution eliminated) is proportional to

$$\begin{array}{l}-{\displaystyle {\int }_{-\infty }^0{(2\pi {\sigma }^2)}^{-1}}u{e}^{-\frac{1}{2}{\left\{{\sigma }^{-1}(\text{cos}b-\text{cos}\beta )-(u+{\sigma }^{-1})\text{cos}b\right\}}^2}{ }^{-\frac{1}{2}{\left\{{\sigma }^{-1}(\text{sin}b-\text{sin}\beta )-(u+{\sigma }^{-1})\text{sin}b\right\}}^2}du\\ ={(2\pi {\sigma }^2)}^{-1}{e}^{-\frac{1}{2{\sigma }^2}}\left(1+{\sigma }^{-1}\text{cos}(b-\beta )\frac{\mathrm{\Phi }({\sigma }^{-1}\text{cos}(b-\beta ))}{\varphi ({\sigma }^{-1}\text{cos}(b-\beta ))}\right).\end{array}$$

This integral has been evaluated in closed form using a technique presented in the proof based on the formula ${\displaystyle {\int }_a^{b}u\varphi \left(u\right)du=\varphi \left(a\right)-\varphi \left(b\right)}$. Remarkably, the circle regression gives rise to a new family of distributions on the circle (Mardia & Jupp, 2000). In Figure 2 we depict the empirical (using 100,000 simulations) and theoretical densities of the NLS estimator in the circle regression, wrapped around the unit circle, under two scenarios of true parameters: the densities match perfectly. The density has a peak, the distance from the unit circle, at the true β, and the density with σ = 2 is more “uniform.”

Figure 2.

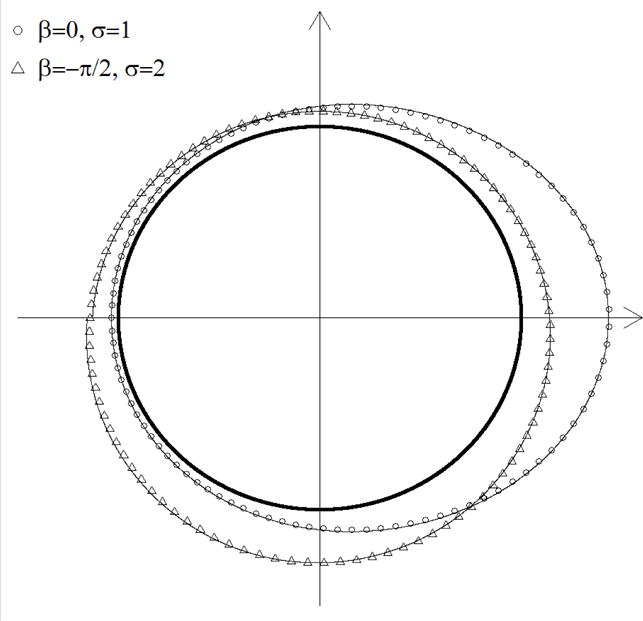
The theoretical and empirical densities of the NLS estimate in circle regression wrapped around the unit circle under two scenarious (symbols represent simulations and curves represent the analytic density).

Another possible improvement of Theorem 1 is to incorporate the criterion on the global minimum into the derivation of the density. Indeed, the global criterion is usually formulated as follows: if b is a local minimizer such that ║y − f(b)║² < ║y − f(b₀)║², where b₀ is known, then b is the global minimizer of the sum of squared residuals (Demidenko, 2006, 2008). Express the above inequality as ║y − f(b₀)║² −║y − f(b)║² = 2u where u > 0, or equivalently as y′(f(b)−f(b₀)) = u−(║f(b) ║²−║f(b₀)║²)/2. Since this equation is linear in y we can derive the joint density of b and u and then find the marginal density of b by integrating out u. The same method can be utilized to incorporate an existence criterion into density derivation which is also expressed as the difference of the sums of squared residuals (Demidenko, 1989, 2000).

3. Extension to the estimating equation approach

Theorem 1 can also be generalized to the case when any function, say r, is used instead of ḟ in the normal equation (4). This leads to the estimating equation (EE) approach:

$$\left(\mathbf{y}-\mathbf{f}\left(b\right)\right)\prime \mathbf{r}\left(b\right)=0,$$ (16)

where r(b) is a nonnull vector function such that r′(b)ḟ(b) ≠ 0 for all b and, as before, {y_i − f_i(β)} are iid $\mathcal{N}\left(0,{\sigma }^2\right)$. The solution of this equation is usually referred to as the M-estimator, or the EE estimator. Here we assume that the solution of (16) exists and is unique for each y (the discussion on the alternative intensity function is deferred to Section 5.2). Without loss of generality, one can assume r′(b)ḟ(b) > 0. It is well known that the EE approach yields a consistent M-estimator of β under mild conditions (Huber, 1981; Schervish, 1995). In particular, the estimating equation approach appears in the framework of the quasi (pseudo) -likelihood and the generalized estimating equation approach (Godambe, 1960; Gong & Samaniego, 1981; Zeger et al., 1988, Pawitan, 2001), robust statistics, and the instrumental variable approach in connection with the measurement error problem (Fuller, 1987).

Theorem 2

The exact density of the M-estimator, ${\widehat{\beta }}_{EE}$, defined by estimating equation (16), is given by

$$p_{EE}\left(b;\beta ,{\sigma }^2\right)=\frac{\Vert \mathbf{r}\left(b\right)\Vert }{\sqrt{2\pi {\sigma }^2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\frac{{\left(\mathbf{r}\prime \left(b\right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)\right)}^2}{{\Vert \mathbf{r}\left(b\right)\Vert }^2}\right]\times a_{EX}\left(b;\beta ,\sigma \right)$$ (17)

with adjustment coefficients computed by the same formulas as in Theorem 1, but

$$\begin{array}{l}A={\Vert \mathbf{r}(b)\Vert }^2,D=\mathbf{r}\prime (b)(\mathbf{f}(b)-\mathbf{f}(\beta )),B=\dot{\mathbf{r}}\prime (b)(\mathbf{f}(b)-\mathbf{f}(\beta )),\\ C=\mathbf{r}\prime (b)\dot{\mathbf{r}}(b),E={\Vert \dot{\mathbf{r}}(b)\Vert }^2,G=\left|\mathbf{r}\prime (b)\dot{\mathbf{f}}(b)\right|.\end{array}$$

The Near Exact and IL approximations have adjustment coefficients

$$a_{NE}\left(b;\beta \right)=\frac{G}{A}+\frac{AB-CD}{A^2},a_{IL}\left(b\right)=\frac{G}{A}.$$

The proof is a slight modification of that for Theorem 1 and is found in the Appendix. Basically, we replace $\dot{\mathbf{f}}$ with r and $\ddot{\mathbf{f}}$ with $\dot{\mathbf{r}}$ and repeat the three steps of the proof outlined in the preceding section. Note that we use the absolute value in G, so $\mathbf{r}\prime \left(b\right)\dot{\mathbf{f}}\left(b\right)$ may be negative.

As in the case of the NE distribution for the NLS estimator, it is straightforward to check that the EE estimator has the cdf given by

$$F_{EE}\left(b;\beta ,{\sigma }^2\right)=\mathrm{\Phi }\left(\frac{\mathbf{r}\prime \left(b\right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)}{\sigma \Vert \mathbf{r}\left(b\right)\Vert }\right).$$ (18)

Similar to our previous comment, in order for this function to be a cdf, F_EE as a function of b must satisfy three conditions.

Linear instrumental variable check: Let f(β) = βx and r(β) = (r₁, r₂, …, r_n)′ be a fixed vector such that r′x > 0, so that the estimating equation takes the form (y−βx)′r = 0. This estimator emerges as the instrumental variable approach (Fuller, 1987). As follows from linear theory, ${\widehat{\beta }}_{EE}=\left(\mathbf{y}\prime \mathbf{r}\right)/\left(\mathbf{r}\prime \mathbf{x}\right)~\mathcal{N}\left(\beta ,{\sigma }^2\Vert \mathbf{r}\Vert /{\left(\mathbf{r}\prime \mathbf{x}\right)}^2\right)$. But from Theorem 2, B = C = E = 0 and a₁ = G/A = (r′x) ║r║², a₂ = 0, which yields

$$\begin{array}{c}{p}_{EE}\left(b;\beta ,{\sigma }^2\right)=\frac{\Vert \mathbf{r}\Vert }{\sqrt{2\pi {\sigma }^2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\frac{{\left(b-\beta \right)}^2}{{\Vert \mathbf{r}\Vert }^2/{\left(\mathbf{r}\prime \mathbf{x}\right)}^2}\right]\times \frac{\left(\mathbf{r}\prime \mathbf{x}\right)}{{\Vert \mathbf{r}\Vert }^2}\\ =\frac{1}{\sqrt{2\pi {\sigma }^2{\Vert \mathbf{r}\Vert }^2/{\left(\mathbf{r}\prime \mathbf{x}\right)}^2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\frac{{\left(b-\beta \right)}^2}{{\Vert \mathbf{r}\Vert }^2/{\left(\mathbf{r}\prime \mathbf{x}\right)}^2}\right],\end{array}$$

the same density as follows from the linear theory. All three densities, NE, IL and ILL, coincide for linear regression.

3.1. Nonlinear regression with an unknown coefficient

In this section, we apply the theory of the estimating equation to regression with one intrinsically nonlinear parameter and an unknown coefficient at the nonlinear function,

$$\mathbf{y}=\nu \mathbf{h}\left(\beta \right)+\epsilon ,$$ (19)

assuming that the n × 2 matrix [h(b), h(b)] has a full rank for all b, and ν ≠ 0. After eliminating ν through linear least squares, we arrive at the estimating equation for β,

$$\mathbf{y}\prime \left(\mathbf{I}-\frac{\mathbf{h}\left(b\right)\mathbf{h}\prime \left(b\right)}{{\Vert \mathbf{h}\left(b\right)\Vert }^2}\right)\dot{\mathbf{h}}\left(b\right)=0,$$

which is equivalent to

$$\left(\mathbf{y}-\nu \mathbf{h}\left(b\right)\right)\prime \left(\mathbf{I}-\frac{\mathbf{h}\left(b\right)\mathbf{h}\prime \left(b\right)}{{\Vert \mathbf{h}\left(b\right)\Vert }^2}\right)\dot{\mathbf{h}}\left(b\right)=0,$$

where ν is the true value. Thus, letting

$$\mathbf{f}=\nu \mathbf{h},\mathbf{r}=\dot{\mathbf{h}}-\frac{\mathbf{h}\prime \dot{\mathbf{h}}}{{\Vert \mathbf{h}\Vert }^2}\mathbf{h},$$

Theorem 2 applies (the argument, b, is omitted for brevity). The required condition, $G=\mathbf{r}\prime \left(b\right)\dot{\mathbf{f}}\left(b\right)>0$ follows from the Cauchy inequality,

$$G=\nu \left({\Vert \dot{\mathbf{h}}\Vert }^2-\frac{{\left(\mathbf{h}\prime \dot{\mathbf{h}}\right)}^2}{\Vert \mathbf{h}\Vert }\right)>0$$

since matrix $\left[\mathbf{h},\dot{\mathbf{h}}\right]$ has full rank. The exact and near exact densities require the derivative vector, $\dot{\mathbf{r}}$, which is straightforward to obtain in terms of derivatives of h,

$$\dot{\mathbf{r}}=\ddot{\mathbf{h}}-\frac{\mathbf{h}\prime \dot{\mathbf{h}}}{{\Vert \mathbf{h}\Vert }^2}\dot{\mathbf{h}}-\frac{1}{{\Vert \mathbf{h}\Vert }^4}\left[\left({\Vert \dot{\mathbf{h}}\Vert }^2+\mathbf{h}\prime \ddot{\mathbf{h}}\right){\Vert \mathbf{h}\Vert }^2-2{\left(\mathbf{h}\prime \dot{\mathbf{h}}\right)}^2\right]\mathbf{h}.$$

Fieller (1932) example. In this example, we test (17) through a distribution derived almost one hundred years in a very special case. Namely, we apply the estimating equation theory to the nonlinear regression

$$\mathbf{y}=\nu \left(1+\beta \mathbf{x}\right)+\epsilon .$$ (20)

In previous notation we have h(b) = 1+bx, r(b) = x − (1+bx)′x(1+bx) ║1+bx║⁻². For this model the exact distribution of the NLS estimator of β reduces to the distribution of the ratio of two normally distributed random variables. Indeed, the NLS estimator of β is

$$\widehat{\beta }=\frac{\widehat{\nu \beta }}{\widehat{\nu }},$$ (21)

where $\widehat{\nu \beta }$ and $\widehat{\nu }$ are the least squares slope and intercept, respectively. They have a bivariate normal distribution with marginal distributions $\widehat{\nu \beta }~\mathcal{N}\left(\nu \beta ,{\sigma }^2/{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}\right)$ and $\widehat{\nu }~\mathcal{N}\left(\nu ,{\sigma }^2/{\displaystyle \sum x_i^2/\left(n{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}\right)}\right)$, respectively, and correlation coefficient $-{\displaystyle \sum x_i/\sqrt{n{\displaystyle \sum x_i^2}}}$. Fieller (1932) initially derived and Hinkley (1969) extended the distribution of the ratio of two normally distributed random variables, Z = X₁/X₂ with means μ_i, variances ${\sigma }_i^2\left(i=1,2\right)$, and correlation coefficient ρ. Thus the Fieller result applies with μ₁ = νβ, ${\sigma }_1^2={\sigma }^2/{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}$ and μ₂ = ν, ${\sigma }_2^2={\displaystyle \sum x_i^2}/(n{\displaystyle \sum {\left(x_i-\overline{x}\right)}^2}$ and $\rho =-{\displaystyle \sum x_i}/\sqrt{n{\displaystyle \sum x_i^2}}$ as the benchmark testing of our EE distribution specified in Theorem 2. After some algebra, one can show that our density p_EX and the density of the ratio are identical while other known density approximations, such as NE or Skovgaard do not coincide with the density of the ratio.

3.1.1. Example: Michaelis-Menten model

The Michaelis-Menten model is a popular model in many application fields, especially in chemistry (Seber & Wild, 1989; Hadeler et al. 2007). It has a hyperbolic shape and describes the data with the right asymptote,

$$y_i=\frac{\nu x_i}{\beta +x_i}+{\epsilon }_i.$$ (22)

We use Puromycin data on the velocity of a chemical reaction from the example provided in Bates & Watts (1988, p. 269), n = 12 with the true parameter values β = 0.064 and ν = 212.7 estimated from the data, where x is the substrate concentration and y is the velocity of the enzymatic reaction. The estimated residual standard error was σ = 10.9; we use σ = 40 here to amplify the difference between the densities. Four densities of the NLS estimator $\widehat{\beta }$ with the associated 75% density limits are depicted in Figure 3 (we use the 75% confidence level, not 95%, for the illustrative purpose).

Figure 3.

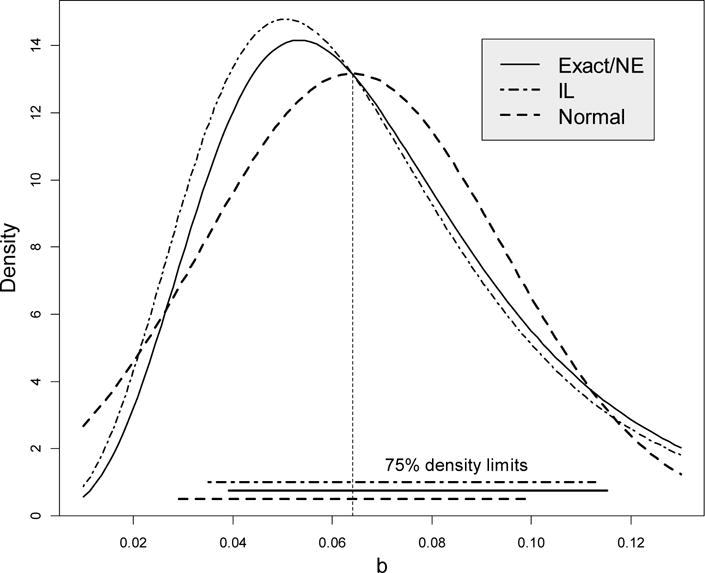
Four densities of the NLS estimator of β = 0.064 in the Puromycin example (σ = 40) with the 75% density limits. The exact and near exact densities practically coincide.

The exact and near exact densities practically coincide; that is why only three curves are seen. The IL density deviates only slightly from the exact/NE densities. The normal approximation is adequate only in a close proximity to the true value, but deviates from the exact density elsewhere due to the implied symmetry. Consequently, the normal density limits are narrow and symmetric around β. The Exact/NR and IL limits are wider and shifted to the right due to skewness of the estimates. The same conclusions, on average, can be drawn regarding confidence intervals for β.

In Figure 4, the exact expected value of $\widehat{\beta }$ and its MSE are computed using the function integrate in R based on the exact density as a function of the standard error of residuals. For σ larger than 40, the negative bias becomes considerable (left plot). For σ > 30 the normal approximation variance, routinely used in existing statistical packages, considerably exceeds the exact value and inflates the p-value as follows from the right plot.

Figure 4.

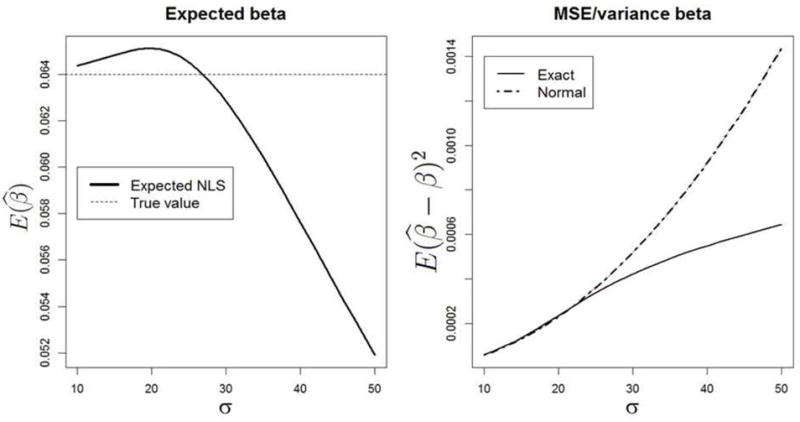
Computation of the expected value and the MSE of the NLS estimator using the numerical integration of the exact density.

The NLS estimate in the Michaelis-Menten model may not exist especially for large σ; complications associated with nonexistence are discussed below in Section 4. Criteria for the NLS existence for this model are developed in Hadeler et al. (2007). A simple criterion based on the concept of the existence level (Demidenko, 2000, 2004), is as follows. Denote $S_1={\displaystyle {\sum }_{i=2}^n{y}_i^2}$ and $S_2={{\displaystyle {\sum }_{i=1}^n\left(y_i-\overline{y}\right)}}^2$; if there is a starting value for ν and β with the sum of squares less than min(S₁, S ₂), the NLS estimate exists.

Now we derive the joint distribution of the estimator for two parameters, the linear coefficient, $\widehat{\nu }=\mathbf{y}\prime \widehat{\mathbf{h}}/\widehat{\mathbf{h}}\prime \widehat{\mathbf{h}}$ and $\widehat{\beta }$, where $\widehat{\mathbf{h}}=\mathbf{h}(\widehat{\beta })=\mathbf{x}/(\widehat{\beta }+\mathbf{x})$. As in (15), we note that the distribution of $\widehat{\nu }$ conditional on $\widehat{\beta }=b$ is normal with mean νh′(β)h(b)/h′(b)h(b) and variance σ²/h′(b)h(b). Therefore, the joint distribution is the product of this conditional normal distribution and the marginal density, p_EX(b; β, σ²).

3.2. Nonlinear regression with an unknown coefficient and linear parameters

The regression with one intrinsically nonlinear parameter, a linear part and an unknown coefficient takes the form

$$\mathbf{y}=\mathbf{X}\text{γ+}\nu \mathbf{h}\left(\beta \right)+\epsilon ,$$ (23)

where γ is an m-dimensional parameter vector and ν and β are scalars. It is assumed that the n × (m + 2) matrix, [X, h(β), h(β)], has full rank for all β. This regression is an obvious combination of (14) and (19) with applications arising from two-compartment modeling as the solution to ordinary differential equations. For example, Gallant (1987) uses model (23) with h(β) = e^βz.

After elimination of the linear parameters, γ, we come to a one-parameter nonlinear least squares problem with coefficient ν treated as in the above section. Thus, the same formula for the density of $\widehat{\beta }$ applies with f = νh and h replaced with f = νWh and Wh, as in Section 2.2.

4. Numerical complications

The goal of this section is to examine how numerical complications arising when minimizing the sum of squares or solving the normal equation affect the density of the NLS estimator distribution. Apparently, two kinds of complications are possible: the solution does not exist and there are multiple solutions.

4.1. What happens when the NLS estimator does not exist

In the traditional asymptotic approach, nonexistence of the NLS estimate is not an issue because according to the classical maximum likelihood theory this probability vanishes when n → ∞. However, in practice the probability that the NLS estimate does not exist cannot be ignored, see an example below. Only a handful of papers discuss the nonexistence of the NLS estimate either in terms of sufficient criteria Demidenko (1989, 2000, 2008) or necessary and sufficient conditions for specific nonlinear regression models Hadeler et al. (2007), Jukíc & Markovic (2010), and Jukíc (2014), to name a few. The purpose of this section is to illustrate how the probability of nonexistence affects the density distribution using simplistic examples of nonlinear regression where this probability is tractable.

The NLS estimate does not exist for some observations y₁, …, y_n when σ² is large and the regression curve has finite tails, namely, when ║f(b)║ does not go to infinity when |b| → ∞. To illustrate, let us consider an exponential regression $f_i\left(\beta \right)=e^{{\beta }_{x_i}}$ with two observations (n = 2). For simplicity, we assume that x₁ = 1 and x₂ = 2, implying that the regression curve is a half parabola in the observation space R². The normal equation turns into a cubic polynomial 2θ³ + (1 − 2y₂)θ − y₁ = 0 where θ = e^b. Although the cubic equation has at least one real root, there may be no positive roots which means that the NLS estimate does not exist.

Using some algebra on the cubic equation similar to Demidenko (2000), one can show that there are no positive roots for θ if y₁ ≤ 0 and y₂ < 1.2 |y₁|^2/3 + 0.5. These explicit conditions allow computation of the probability that the NLS estimate does not exist for given β and σ expressed as an integral,

$$\text{Pr}\left(\widehat{\beta }\text{does not exist}\right)={\sigma }^{-1}{\displaystyle {\int }_{-\infty }^0\varphi \left(\frac{y_1-e^{\beta }}{\sigma }\right)}\mathrm{\Phi }\left(\frac{1.2{\left(-y_1\right)}^{2/3}+0.5-e^{2\beta }}{\sigma }\right)d{y}_1.$$ (24)

These probabilities as functions of σ are depicted in Figure 5 for β = ln 0.5 and β = 0. The closer the true point is on the regression curve to zero or the larger σ, the greater the probability. For example, in regression with the true value β = ln 0.5 = −0.7 and the standard deviation, σ = 1, a quarter of all iterations would diverge to −∞ if standard nonlinear regression software such as nls in R were used.

Figure 5.

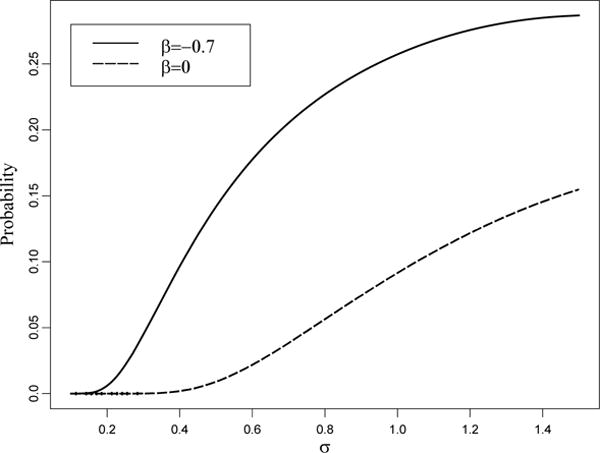
Probabilities that the NLS estimate does not exist in the exponential regression with two observations (n = 2) computed as the integral (24). The smaller the value of β the greater the probability.

Now we investigate the effect of nonexistence on the density of the NLS estimator. Two exact densities with the true value β = 0 and σ = 0.5, σ = 1 computed by formula (5) are depicted in Figure 6. Both densities have a long left tail, especially for σ = 1. The areas under the densities evaluated by numerical integration are shown in the upper-left corner. While for σ = 0.5 this area is 1, as it supposed to be, the area under the density for σ = 1 is less than 1 which reflects the fact that in approximately 20% of cases the NLS estimate does not exist. In general, numerical evaluation of the area under the density is a good test that points out to a nonignorable nonexistence of the NLS estimate.

Figure 6.

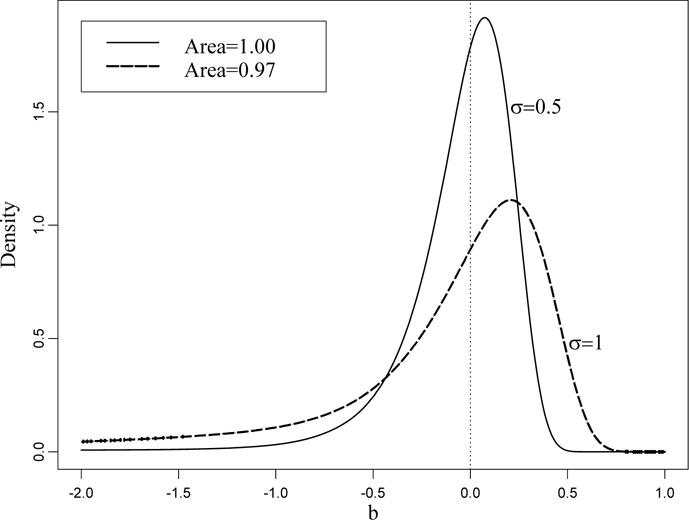
Two densities for an exponential regression with β = 0 and different σ. For σ = 0.5, there is a tiny probability that the NLS estimate does not exist. For σ = 1 this probability is about 0.1, as follows from the previous figure.

4.2. What happens when the normal equation has multiple roots

In this section, we analyze the effect of violation of another assumption under which the exact and near exact densities were derived, namely, when the normal equation has multiple roots. Lehmann & Casella (1998, p. 451) and Skovgaard (1990) presented the analysis of multiple solutions in general terms by showing that the maximum likelihood estimator lacks consistency. Here, we illustrate the consequences with an example similar to that from the previous section, the parabolic regression, f₁(b) = b and f₂(b) = b², −∞ < b < ∞ (n = 2), see Figure 7. Then the normal equation reduces to a cubic equation which admits a closed-form solution. As was shown in Demidenko (2000), the sum of squares (y₁ −b)² + (y₂−b²) has two local minima if y₂ > 3/4^1/3 |y₁|^2/3 +1/2. In the figure, the data point y leads to two local minima as the distance to the parabolic curve; the positive value is the true NLS estimate and the negative value is the false NLS estimate. For given β and σ, one can compute the probability of two local minima as the integral

$$\text{Pr}\left(\text{multiple roots}\right)={\sigma }^{-1}{\displaystyle {\int }_{-\infty }^{\infty }\varphi \left(\frac{y_1-\beta }{\sigma }\right)\mathrm{\Phi }\left(\frac{{\beta }^2-\frac{3}{4^{1/3}}{\left|y_1\right|}^{2/3}-0.5}{\sigma }\right)}d{y}_1.$$ (25)

For example, for β = 0.5 and σ = 0.5 the probability that the sum of squares has two local minima is 0.026. In Figure 7, the circle around (0.5, 0.5²) shows the 95% confidence region of (y₁, y₂). Probability (25) equals the density-weighted area of the intersection of this circle with the shaded area.

Figure 7.

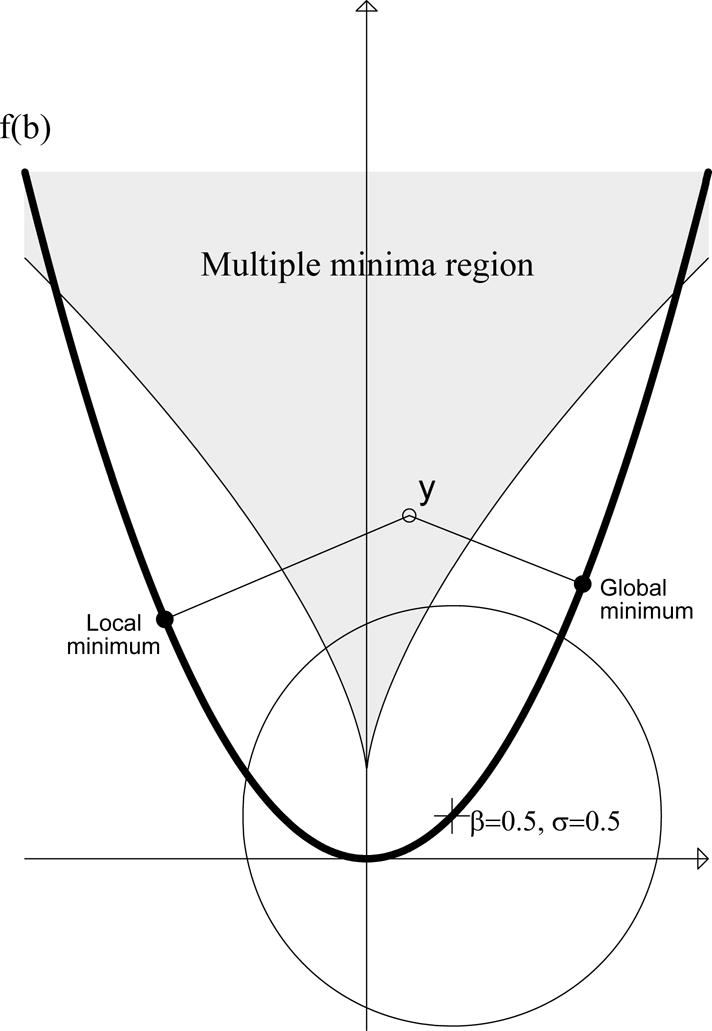
Parabolic regression on the plane (n = 2). If y = (y₁, y₂) is from the shaded region the sum of squares, (y₁ − b)² + (y₂ − b²)², has two local minima.

Now we turn our attention to how multiple roots (local minima) affect the densities. Although the NLS estimate should yield the absolute minimum of the sum of squares it may not hold in practice where a possibility of local minimum is a reality. In Figure 8, five densities are shown for β = 0.5 and σ = 0.5. The first two densities are theoretical and the last three densities are empirical, estimated with the Gaussian kernel based on 100,000 simulations. Three strategies for handling multiple roots are studied through simulations: The “Global minimum” strategy is when the global minimum is taken, which leads to the true NLS estimate. The “False minimum” is when the wrong local minimizer is taken as the false NLS estimate. The “50/50” strategy is when the true or the false estimate is randomly chosen with equal probability. We notice that the NE density has a prominent dip and differs from the EX density in the interval (−0.5, 0.25). The probability of the false NLS estimate computed by formula (25) is 0.026. The left bump around −0.5 in the densities reflects the possibility of the false estimate. In fact, when y is close to the center of the multiple minima region (b = 0), the roots of the normal equation have the same magnitude but different signs. The existence of multiple roots makes the area under the EX density larger than 1; for this example, it is 1.10. As in the case of the NLS nonexistence, the deviation of the area under the density from 1 is indicative of the nonuniqueness of the NLS estimate.

Figure 8.

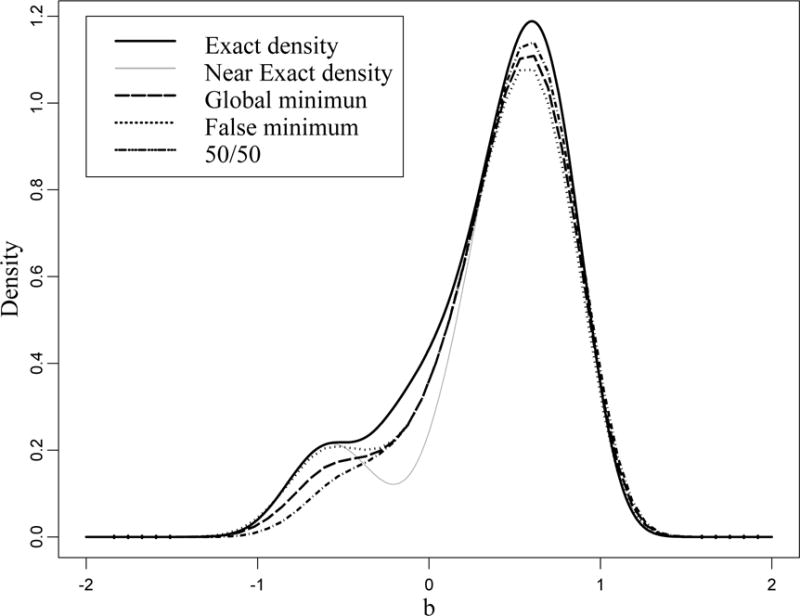
Two theoretical and three empirical densities from simulations (N = 100,000) estimated with the Gaussian kernel for parabolic regression, β = 0.5, σ = 0.5. The left bump reflects the existence of the false NLS estimate. The probability that the sum of squares has two local minima, computed by formula (25), is 0.026.

5. Multivariate case

In multivariate nonlinear regression, parameter β is an m-dimensional vector, so we use boldface now,

$$y_i=f_i\left(\mathit{\beta }\right)+{\epsilon }_i.$$

The NLS estimator, $\widehat{\mathit{\beta }}$, is the solution to the vector normal equation

$$\mathbf{F}\prime \left(\mathbf{b}\right)\left(\mathbf{y}-\mathbf{f}\left(\mathbf{b}\right)\right)=\mathbf{0},$$ (26)

where F(b) =∂f/∂b is the n × m derivative (Jacobian) matrix assuming det(F′(b)F(b)) ≠0 for all b and that f(b₁) = f(b₂) implies b₁ = b₂ to ensure the identifiability. As in the univariate case, we assume that the solution of (26) uniquely exists for each y ∈Rⁿ. The exact density for a multivariate nonlinear regression model cannot be derived in closed form, so we deal with approximations.

5.1. Density approximations for the NLS estimator

The NE density for the multivariate case was derived by Pazman (1984, 1993) using a geometric approach,

$$\begin{array}{c}{p}_{NE}\left(\mathbf{b};\mathit{\beta },{\sigma }^2\right)=\frac{\text{det}\left[\mathbf{F}\prime \left(\mathbf{b}\right)\mathbf{F}\left(\mathbf{b}\right)+\left({\mathbf{I}}_m\otimes {\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)}^{\perp }\right)\mathbf{H}\left(\mathbf{b}\right)\right]}{{\left(2\pi {\sigma }^2\right)}^{m/2}\sqrt{\text{det}\left(\mathbf{F}\prime \left(\mathbf{b}\right)\mathbf{F}\left(\mathbf{b}\right)\right)}}\\ \times \text{exp}\left[-\frac{1}{2{\sigma }^2}\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\prime \mathbf{P}\left(\mathbf{b}\right)\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\right],\end{array}$$ (27)

where H(b) is a (nm) × m stack matrix with the ith m × m block as the Hessian matrix of f_i, namely, H_i = ∂²f_i/∂b², and P(b) = F(b)(F′(b)F(b))⁻¹F′(b) is the n × n projection matrix. Notation ^⊥ is used to indicate the row distance vector to the plane spanned by vector columns of matrix F(b), namely, (f(b) − f(β))^⊥ = (f(b) − f(β))′(I_n − P(b)). Skovgaard (1985), Hougaard (1985) and Pazman (1999) derived expression (27) using the saddlepoint approximation.

We make several comments on density (27). First, the Kronecker product in (27) can be expressed explicitly as

$$({\mathbf{I}}_m\otimes {(\mathbf{f}(\mathbf{b})-\mathbf{f}(\mathit{\beta }))}^{\perp })\mathbf{H}(\mathbf{b})={\displaystyle \sum _{i=1}^n{(f(\mathbf{b})-f(\mathit{\beta }))}_i^{\perp }{\mathbf{H}}_i(\mathbf{b})}.$$ (28)

Second, for m = 1, after some algebra, we arrive at the previous expression (5) with adjustment coefficient (8). Third, density (27) is equivalent to saying that

$${(\mathbf{F}\prime (\widehat{\mathit{\beta }})\mathbf{F}(\widehat{\mathit{\beta }}))}^{-1/2}\mathbf{F}\prime (\widehat{\mathit{\beta }})(\mathbf{f}(\widehat{\mathit{\beta }})-\mathbf{f}(\mathit{\beta }))~\mathcal{N}(0,{\sigma }^2\mathbf{I}).$$ (29)

The IL approximation can be used as a simplification of p_NE by omitting term (28),

$$p_{IL}\left(\mathbf{b};\mathit{\beta },{\sigma }^2\right)=\frac{\sqrt{\text{det}\left(\mathbf{F}\prime \left(\mathbf{b}\right)\mathbf{F}\left(\mathbf{b}\right)\right)}}{{\left(2\pi {\sigma }^2\right)}^{m/2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\prime \mathbf{P}\left(\mathbf{b}\right)\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\right].$$

Again, one can prove that this density is exact for the intrinsically linear regression model, the nonlinear model that can be reduced to linear after reparametrization. The ILL approximation is a further simplification when matrices are evaluated at the true value:

$$p_{\mathit{\text{ILL}}}\left(\mathbf{b};\mathit{\beta },{\sigma }^2\right)=\frac{\sqrt{\text{det}\left(\mathbf{F}\prime \left(\mathit{\beta }\right)\mathbf{F}\left(\mathit{\beta }\right)\right)}}{{\left(2\pi {\sigma }^2\right)}^{m/2}}\text{exp}\left[-\frac{1}{2{\sigma }^2}(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right))\prime \mathbf{P}\left(\mathit{\beta }\right)\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\right].$$

The complications outlined in Section 4 apply to these densities as well. Namely, (27) can be negative and the volume under the densities may be not 1. Pazman (1984) expressed the deviation of (27) from the true density in terms of the minimum radius of intrinsic curvature as a part of the nonoverlapping assumption. The problem is that, in most nonlinear regression models, this minimum reaches zero if parameter space is not restricted, so that the nonoverlapping assumption does not hold. For example, the radius of intrinsic curvature approaches zero when β → −∞ in the exponential model $f_i\left(b\right)=e^{-b{x}_i}$ with 0 < x₁ < … < x_n. Of course, one can restrict the parameter space, say, β > 0, but that restriction would become questionable.

5.2. Density approximations for the estimating equation approach

In the multivariate EE approach, the M-estimator is found from the vector equation

$$\mathbf{R}\prime \left(\mathbf{b}\right)\left(\mathbf{y}-\mathbf{f}\left(\mathbf{b}\right)\right)=\mathbf{0},$$ (30)

where R(b) is a n × m matrix such that matrix R′(b)F(b) is positive definite. In a special case when R = F, the estimating equation approach reduces to NLS. Following the line of the proof in the univariate case, we obtain the NE approximation of the density of the M-estimator,

$$\begin{array}{c}{p}_{NE}\left(\mathbf{b};\mathit{\beta },{\sigma }^2\right)=\frac{\text{det}\left[\mathbf{F}\prime \left(\mathbf{b}\right)\mathbf{R}\left(\mathbf{b}\right)+\left({\mathbf{I}}_m\otimes {\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)}^{\perp }\right)\mathbf{E}\left(\mathbf{b}\right)\right]}{{\left(2\pi {\sigma }^2\right)}^{m/2}\sqrt{\text{det}\left(\mathbf{R}\prime \left(\mathbf{b}\right)\mathbf{R}\left(\mathbf{b}\right)\right)}}\\ \times \text{exp}\left[-\frac{1}{2{\sigma }^2}\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\prime \mathbf{P}\left(\mathbf{b}\right)\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\right],\end{array}$$ (31)

where E(b) is a (nm) × m stack matrix, with the ith m × m block, E_i = ∂r_i/∂b and r_i = r_i(b), being the ith row vector of matrix R(b), and the projection matrix is given by

$$\mathbf{P}\left(\mathbf{b}\right)=\mathbf{R}\left(\mathbf{b}\right){\left(\mathbf{R}\prime \left(\mathbf{b}\right)\mathbf{R}\left(\mathbf{b}\right)\right)}^{-1}\mathbf{R}\prime \left(\mathbf{b}\right).$$

Simple algebra shows that (31) reduces to (17) when m = 1. The IL approximation is an obvious simplification,

$$p_{IL}\left(\mathbf{b};\mathit{\beta },{\sigma }^2\right)=\frac{\text{det}\left(\mathbf{F}\prime \left(\mathbf{b}\right)\mathbf{R}\left(\mathbf{b}\right)\right)}{{\left(2\pi {\sigma }^2\right)}^{m/2}\sqrt{\text{det}\left(\mathbf{R}\prime \left(\mathbf{b}\right)\mathbf{R}\left(\mathbf{b}\right)\right)}}\text{exp}\left[-\frac{1}{2{\sigma }^2}\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\prime \mathbf{P}\left(\mathbf{b}\right)\left(\mathbf{f}\left(\mathbf{b}\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)\right].$$

The saddlepoint approximation to the density in more general settings expressed in terms of the cumulant generating function were developed by Field (1982) and Strawderman et al. (1996), among others (see a nicely written paper by Goutis & Casella (1999) as a general introduction to the saddlepoint approximation). One can show that the saddlepoint approximation yields p_IL. There is a bulk of work on the distribution of the M-estimator in a less idealistic situation when there are several solutions of the EE with the density counterpart termed the intensity function derived in a general form. For example, Almudevar et al. (2000) provide an explicit solution for the density only for a linear Huber’s robust regression.

The multivariate version of the EE densities can be applied to nonlinear regressions with linear part and unknown coefficients, such as Xγ+ν₁f₁(β₁) + ν₂f(β₂), similar to regression with one intrinsically nonlinear parameter.

5.3. Possible improvements of multivariate density derivation

We have indicated that our derivation of the univariate density may be improved by brushing off spurious solutions or by accounting for nonexistence of the estimate. Many previous derivations of the multivariate density relied on the saddle point approximation. We provide an outline of an alternative derivation of the density as a generalization of the univariate case in the Appendix. As before, we assert that this derivation is flexible enough to incorporate conditions on positive definiteness of the Hessian, or at least positiveness of the diagonal elements, and existence criteria once they are expressed as linear functions of observations.

6. Gauss-Markov theorem for nonlinear regression

The aim of this section is to show how the density results can be used to study methods of optimal parameter estimation. Classic quadratic loss function criteria for optimality do not work in this setting because (a) the moments may not exist, such as in Fieller problem, and therefore the concept of unbiasedeness is invalid, and (b) the distribution is highly asymmetric.

Gauss-Markov theorem is the landmark result of linear regression with normally distributed variables: if y = Xβ + ε, where components of error vector ε are iid normally distributed with zero mean and matrix X has full rank, then the maximum likelihood (least squares) estimators of the beta-coefficients are unbiased and have minimum variance for any finite n. This result holds for the NLS estimator in nonlinear regression in large sample (n → ∞). The paramount question: does it hold for finite n? One can guess that this question was on the mind of statisticians since the Gauss-Markov theorem was proved for linear regression. Two challenging questions should be answered before even formulating the problem:

1. What family of competitive estimators should be considered?

2. How to define the most precise estimator with a known cdf which may have infinite mean or variance like in the Fieller test example when the traditional mean square error loss function does not work?

To answer the first question we suggest to consider the EE approach with the family of estimators defined by equation (30). To motivate our choice we refer to linear regression restricting to linear estimators that reduces to equation R′(y − Xβ) = 0, where matrix R has full rank and matrix R′X is nonsingular (‘linear’ means that matrix R does not depend on β). The EE estimator ${\widehat{\mathit{\beta }}}_{\mathbf{R}}={\left({\mathbf{R}}^{\prime }\mathbf{X}\right)}^{-1}{\mathbf{R}}^{\prime }\mathbf{y}$ is unbiased with the covariance matrix $\mathit{\text{cov}}({\widehat{\mathit{\beta }}}_{\mathbf{R}})={\sigma }^2{({\mathbf{R}}^{\prime }\mathbf{X})}^{-1}({\mathbf{R}}^{\prime }\mathbf{R}){({\mathbf{X}}^{\prime }\mathbf{R})}^{-1}\ge {\sigma }^2{({\mathbf{X}}^{\prime }\mathbf{X})}^{-1}=\mathit{\text{cov}}({\widehat{\mathit{\beta }}}_{LS})$, as the Gauss-Markov theorem says (the last inequality follows from the fact that matrix I − X(X′X)⁻¹X′ is nonnegative definite). Restriction on unbiased estimators is crucial—the EE approach defined by (30) can be viewed as the unbiasedeness counterpart.

To answer the second question, we invoke the concept of the confidence interval (CI) termed here as inverse cdf (see Casella & Berger, 1990, pp. 417–418). Hereafter in this section we consider the one-parameter statistical estimation problem. Let the cdf of an estimator be defined as F(b; β) such that F(b; β) is a strictly decreasing function of β for every fixed b and lim_β→−∞ F(b; β) = 1, lim_β→∞ F(b; β) = 0. If α is the significance level, say, α = 0.05 and $\widehat{\beta }$ is the EE estimator, the lower and the upper limits of the CI for β are the solutions to the equations F( $\widehat{\beta }$; β) = 1 − α/2 and F( $\widehat{\beta }$_; β) = α, respectively. The solutions exist and unique as follows from the assumptions on cdf F, although the existence of the limiting values for F are not crucial— if the the solution does not exist the CI limit is set to ∞.

Definition 3

Let the cdfs of two estimators of the true β be F₁(b; β) and F₂(b; β). We say that the first estimator is more precise if its inverse cdf CI is a subinterval of the second for every α > 0.

It is easy to see that the two estimators are unbiased and normally distributed with cdfs Φ((b − β)/σ₁) and Φ((b − β)/σ₂) the first estimator is more precise if and only if σ₁ ≤ σ₂.

Now we turn our attention to formulation of the extended Gauss-Markov theorem; as mentioned before one intrinsically nonlinear parameter nonlinear regression with known σ is discussed here. Also we restrict ourselves with near exact approximation of the density distribution since the cdfs for the NLS and EE estimators admit a closed-form expression via Φ defined by (9) and (18). The family of nonlinear regressions has to be constrained as well to comply with the uniqueness of the cdf solutions in inverse cdf CI. We adopt the following definition of the unidirected regression (Demidenko, 2006):

Definition 4

A nonlinear regression is called unidirected if the vector derivatives constitute a sharp angle for any pair of parameter values, i.e. ḟ′(β₁)ḟ(β₂) > 0 for every β₁ and β₂.

It is easy to see that for a unidirected regression the inverse cdf CI based on the cdf (9) is unique for any α. Indeed, if $\widehat{\beta }$ is the NLS estimator the lower and upper limits of the CI are the solutions to the equation H.(β; $\widehat{\beta }$) = σΦ⁻¹(1 − α/2), where

$$H.\left(\beta ;b\right)=\frac{\left|{\dot{\mathbf{f}}}^{\prime }\left(b\right)\left({\dot{\mathbf{f}}}^{\prime }\left(b\right)-\mathbf{f}\left(\beta \right)\right)\right|}{\Vert \dot{\mathbf{f}}\left(b\right)\Vert }$$

But for the unidirected function H is a strictly increasing function of β for any fixed b, including b = $\widehat{\beta }$ so that the solutions are unique.

Now we turn our attention to the EE estimator as the solution to (16) defined by function r. In general terms, the Gauss-Markov theorem for nonlinear regression proves that r(b) = ḟ(b) yields a more precise EE estimator than any other choice of function r(b). The expression for cdf (18) is crucial here.

Theorem 5. Local near-exact Gauss-Markov theorem for nonlinear regression

Let (1) be a unidirected nonlinear regression and r(b) be such that r′(b)ḟ(β) > 0 for every b and β. Denote

$$H_{\mathbf{r}}\left(\beta ;b\right)=\frac{\left|{\mathbf{r}}^{\prime }\left(b\right)\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\beta \right)\right)\right|}{\Vert \mathbf{r}\left(b\right)\Vert }$$

Then (a) the EE estimator with r = r_∗ is the most precise if H_r(β; b) ≤ H_r∗(β; b) for all β and b. (b) The NLS/ML estimator is locally precise meaning that

$$\underset{|b-\beta |\to 0}{\text{lim}}\frac{H_{\mathbf{r}}(\beta ;b)}{H.(\beta ;b)}\le 1$$

for any function r = r(b).

Proof

1. As follows from (18) the inverse cdf (1−α)100% CI can defined as the interval I_r = {β: H_r(β; b) ≤ σΦ⁻¹(1−α/2)}. If r_∗ is such that $H_{\mathbf{r}}(\beta ;b)\le H_{{\mathbf{r}}_{\ast }}(\beta ;b)$ then the interval $\left\{\beta :H_{{\mathbf{r}}_{\ast }}(\beta ;b)\le \sigma {\mathrm{\Phi }}^{-1}(1-\alpha /2)\right\}$ is a subinterval of I_r.

2. For the NLS/MLE estimator we have

   $$\underset{|b-\beta |\to 0}{\text{lim}}\frac{H.(\beta ;b)}{|b-\beta |}=\underset{|b-\beta |\to 0}{\text{lim}}\frac{|{\dot{\mathbf{f}}}^{\prime }(b)(\mathbf{f}(b)-\mathbf{f}(\beta ))|}{\Vert \dot{\mathbf{f}}(b)\Vert |b-\beta |}=\frac{|{\dot{\mathbf{f}}}^{\prime }(\beta )\dot{\mathbf{f}}(\beta )|}{\Vert \dot{\mathbf{f}}(\beta )\Vert }=\Vert \dot{\mathbf{f}}(\beta )\Vert .$$

   For the EE estimator with any r = r(b) we have

   $$\underset{|b-\beta |\to 0}{\text{lim}}\frac{H_{\mathbf{r}}(\beta ;b)}{|b-\beta |}=\frac{\left|{\mathbf{r}}^{\prime }(\beta )\dot{\mathbf{f}}(\beta )\right|}{\Vert \mathbf{r}(\beta )\Vert }\le \Vert \dot{\mathbf{f}}(\beta )\Vert$$

   due to Cauchy-Schwarz inequality, end of proof.

We make a few comments regarding this theorem: (a) function H provides a criterion for search of the most precise EE estimator through the vector function r(b). (b) the Gauss-Markov theorem holds in the local sense, for tight CI.

7. Future work

The present work on the density distribution for the estimating equation approach can be extended in several theoretical research directions. First, the density distribution of the variance estimate, ${\widehat{\sigma }}^2={\displaystyle {\sum }_{i=1}^n{(y_i-f_i(\widehat{\beta }))}^2/(n-m)}$ should be derived and the confidence intervals for the parameters should be corrected based on this density. We believe that this knowledge may show the way to find a better estimator of σ².

Second, the extension to the estimating equation approach developed in this paper opens the possibility of studying the small-sample properties of the weighted nonlinear regression (Carroll & Ruppert, 1988), and the quasi/pseudo-likelihood approach (Gong & Samaniego, 1981; Zeger et al. 1988) with a normally distributed response variable. In the former approach, which is sometimes called generalized nonlinear least squares, the weight matrix is a function of the regression parameters and the estimating equation takes the form

$${\mathbf{F}}^{\prime }(\mathbf{b})\mathbf{W}(\mathbf{b})(\mathbf{y}-\mathbf{f}(\mathbf{b}))=\mathbf{0},$$

where W(b) is the weight matrix, which turns into estimating equation (30) by letting R(b) = W(b)F(b).

Third, following the line of our density derivation, one may study the small-sample properties of the Generalized Estimating Equation (GEE) approach, often applied to the analysis of longitudinal and cluster data (Fitzmaurice & Molenberghs, 2009), with estimating equation ${\displaystyle {\sum }_{k=1}^K{\mathbf{X}}_k^{\prime }{\mathbf{W}}_k(\mathbf{b})({\mathbf{y}}_k-{\mathbf{X}}_k\mathbf{b})=\mathbf{0}}$ and the weight matrix ${\mathbf{W}}_k(\mathbf{b})={\left({\mathbf{D}}_k(\mathbf{b}){\mathbf{R}}_k{\mathbf{D}}_k(\mathbf{b})\right)}^{-1}$, where R_k is the correlation matrix and D_k(b) is the diagonal matrix of standard deviations.

Fourth, the exact (or improved) statistical inference can be extended to statistical models when variance-covariance matrices are subject to estimation using the estimating equation approach (Paige & Trindade, 2009).

Fifth, the normal approximation density can be improved for multivariate nonlinear regression (Vonesh et al., 2001) and, more generally, nonlinear mixed models (Demidenko, 2013).

Sixth, the near exact density approximation of estimating equation approach allows formulation of the nonlinear Gauss-Markov theorem. We have derived a local version of the theorem; more work has to be done in this direction, intriguing from the theoretical and important from practical perspective. In particular, the question whether NLS/ML estimator remains precise in the global sense is open and awaiting the solution. It is possible that for a concrete regression function one may find a better estimator.

Seventh, the idea finding the exact distribution conditional on the difference of residual sum of squares in Section 2.3 may be applied to adjust for nonexistence of the NLS, frequently forgotten in the literature of higher order asymptotics, because the criteria of existence usually have the form ${\Vert \mathbf{y}-\mathbf{f}(\beta )\Vert }^2-{\Vert \mathbf{y}-\mathbf{f}({\beta }_0)\Vert }^2<0$ where β₀ is a fixed parameter value (Demidenko 1989, 2008).

On the practical side, as was mentioned above, the existing commercial statistical packages, such as SAS and STATA, or freely available R rely on the normal approximation which yields symmetric Wald confidence intervals. Arguments against computationally intensive confidence intervals in nonlinear models were adequate several decades ago, but not today. In addition to Wald confidence intervals and p-values, software offering nonlinear regression should be augmented with more precise numerical and statistical features, such as testing whether the found minimum of the sum of squares is global and improved asymmetric profile-confidence intervals and associated p-values such as implemented in the recent R package nlreg (Brazzale et al., 2007, Brazzale & Davison, 2008).

Appendix

A. Proof of Theorem 1

The following lemma is an obvious reformulation of a textbook result on the density of the multivariate distribution under a nonlinear transformation.

Lemma 6

Let random vector y = (y₁, y₂, …, y_n) have density p_y(y₁, y₂, …, y_n) and random variable b be a unique solution to a nonlinear equation,

$$g(b,y_1,y_2,\dots ,y_n)=0,$$ (32)

where g is a nonlinear function such that $\frac{\partial }{\partial y_1}g(b,y_1,y_2,\dots ,y_n)\ne 0$. Moreover, let y₁ be expressed from (32) via inverse function, y₁ = h(b, y₂, …, y_n). Then the density of b is given by

$$p(b)={\displaystyle {\int }_{-\infty }^{\infty }\cdots {\displaystyle {\int }_{-\infty }^{\infty }\left|\frac{\partial h}{\partial b}\right|p_{\mathbf{y}}(h(b,y_2,\dots ,y_n),y_2,\dots y_m)d{y}_2\cdots d{y}_m}}.$$

Since the normal equation does not depend on σ, we can assume that σ is fixed and known. Moreover, we can normalize the normal equation by replacing the observations and the regression function with y_i/σ and f_i(β)/σ, respectively, so that observations will have unit variance. Also, without loss of generality, we can assume that ${\dot{f}}_1(b)\ne 0$ for all b. The proof has three steps.

#1. Express y₁ through the NLS estimator b and y₂, …., y_n. as

$$y_1=h\left(b,y_2,\dots ,y_n\right)=f_1\left(b\right)-\frac{{\displaystyle {\sum }_{i=2}^n\left(y_i-f_i\left(b\right)\right){\dot{f}}_i\left(b\right)}}{{\dot{f}}_1\left(b\right)}$$

and apply Lemma 3 to obtain the density of the NLS estimator as an integral:

$$p_{\mathit{\text{NLS}}}\left(b;\beta \right)={\left(2\pi \right)}^{-n/2}{\displaystyle {\int }_{R^{n-1}}\left|\frac{\partial h}{\partial b}\right|e^{-\frac{1}{2}{h}^2-\frac{1}{2}{\displaystyle {\sum }_{i=2}^n{\left(y_i-f_i\left(b\right)\right)}^2}}d{y}_2\cdots d{y}_n}.$$ (33)

The needed derivative is obtained using elementary calculus, $dh/db=R+{\displaystyle {\sum }_{i=2}^n{z}_i{q}_i}$, where $z_i=y_i-f_i\left(\beta \right)~\mathcal{N}\left(0,1\right)$ and

$$\begin{array}{l}R=\frac{1}{{\dot{f}}_1\left(b\right)}{\displaystyle \sum _{i=1}^n{\dot{f}}_i^2\left(b\right)+{\displaystyle \sum _{i=2}^n\left(f_i\left(\beta \right)-f_i\left(b\right)\right)q_i\left(b\right)}}\\ q_i=\frac{{\ddot{f}}_1\left(b\right){\dot{f}}_i\left(b\right)}{{\dot{f}}_1^2\left(b\right)}-\frac{{\ddot{f}}_i\left(b\right)}{{\dot{f}}_1\left(b\right)},i=2,3,\dots ,n.\end{array}$$

Introducing the (n − 1) × 1 vectors z, q and g with the ith components z_i, q_i and $g_i={\dot{f}}_i\left(b\right)/{\dot{f}}_1\left(b\right)$, respectively, rewrite integral (33) in a compact form as

$$p_{\mathit{\text{NLS}}}\left(b;\beta \right)={\left(2\pi \right)}^{-n/2}{\displaystyle {\int }_{\mathbf{z}\in R^{n-1}}\left|R+{\mathbf{q}}^{\prime }\mathbf{z}\right|e^{-\frac{1}{2}{\left({\mathbf{z}}^{\prime }\mathbf{g}-p\right)}^2-\frac{1}{2}{\Vert \mathbf{z}\Vert }^2}d\mathbf{z}},$$ (34)

where $p=\left[{\left(\mathbf{f}\left(b\right)-\mathbf{f}\left(\mathit{\beta }\right)\right)}^{\prime }\dot{\mathbf{f}}\left(b\right)\right]/{\dot{f}}_1\left(b\right)$.

#2. Express integral (34) as an expectation of |R + q′z| over a normally distributed vector using cdf Φ. Using an elementary fact (a > 0),

$${\displaystyle {\int }_{-\infty }^{\infty }|u|e^{-a{u}^2+cu}du=\frac{1}{a}+\frac{c\sqrt{a\pi }}{2a^2}{e}^{\frac{1}{4a}{c}^2}\left(2\mathrm{\Phi }\left(\frac{c}{\sqrt{2a}}\right)-1\right)},$$

which follows from equality ${\displaystyle {\int }_a^{b}u\varphi \left(u\right)du=\varphi \left(a\right)-\varphi \left(b\right)}$ where ϕ = Φ′. After some algebra, we obtain

$$E_{X~\mathcal{N}(\kappa ,{\tau }^2)}\left(\left|X\right|\right)=\frac{e^{-\frac{1}{2{\tau }^2}{\kappa }^2}}{\tau \sqrt{2\pi }}\left[2{\tau }^2+\kappa \tau \sqrt{2\pi }{e}^{\frac{1}{2{\tau }^2}{\kappa }^2}\left(2\mathrm{\Phi }\left(\frac{\kappa }{\tau }\right)-1\right)\right].$$ (35)

We apply this formula to (34) letting X = R + q′z and expressing the integrand through a density of a (n − 1) dimensional normal variable. Using the formula

$${(\mathbf{I}+\mathbf{g}{\mathbf{g}}^{\prime })}^{-1}=\mathbf{I}-\frac{\mathbf{g}{\mathbf{g}}^{\prime }}{1+{\Vert \mathbf{g}\Vert }^2},$$

we represent

$${\Vert \mathbf{z}\Vert }^2+{\left({\mathbf{z}}^{\prime }\mathbf{g}-p\right)}^2={\left(\mathbf{z}+\mathit{\mu }\right)}^{\prime }\left(\mathbf{I}+\mathbf{g}{\mathbf{g}}^{\prime }\right)\left(\mathbf{z}+\mathit{\mu }\right)+\frac{p^2}{1+{\Vert \mathbf{g}\Vert }^2},$$

where μ=−p(I + gg′)⁻¹ g = −p(1 + ||g||²)⁻¹ g. Using this result, we can rewrite the exponential part as

$$\begin{array}{l}{\left(2\pi \right)}^{-\left(n-1\right)/2}{e}^{-\frac{1}{2}{\left({\mathbf{z}}^{\prime }\mathbf{g}-p\right)}^2-\frac{1}{2}{\Vert \mathbf{z}\Vert }^2}\\ ={\left(2\pi \right)}^{-\left(n-1\right)/2}{e}^{-.5c}{e}^{-\frac{1}{2}{\left(\mathbf{z}+\mathit{\mu }\right)}^{\prime }{\left(\mathbf{I}-\frac{\mathbf{g}{\mathbf{g}}^{\prime }}{1+{\Vert \mathbf{g}\Vert }^2}\right)}^{-1}\left(\mathbf{z}+\mathit{\mu }\right)}\\ =\frac{e^{-\frac{p^2}{2(1+{\Vert \mathbf{g}\Vert }^2)}}}{\sqrt{\text{det}\left(\mathbf{I}+\mathbf{g}{\mathbf{g}}^{\prime }\right)}}\left[{\left(2\pi \right)}^{-(n-1)/2}\sqrt{\text{det}\left(\mathbf{I}+\mathbf{g}{\mathbf{g}}^{\prime }\right)}{e}^{-\frac{1}{2}{(\mathbf{z}+\mathit{\mu })}^{\prime }{\left(\mathbf{I}-\frac{\mathbf{g}{\mathbf{g}}^{\prime }}{1+{\Vert \mathbf{g}\Vert }^2}\right)}^{-1}(\mathbf{z}+\mathit{\mu })}\right].\end{array}$$

But det (I + gg′) = 1 + ||g||², so finally the distribution of R + q′z is a constant times the normal distribution, or symbolically,

$$X=R+{\mathbf{q}}^{\prime }\mathbf{z}~\mathcal{N}\left(R+\frac{p}{1+{\Vert \mathbf{g}\Vert }^2}{\mathbf{g}}^{\prime }\mathbf{q},{\Vert \mathbf{q}\Vert }^2-\frac{{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}^2}{1+{\Vert \mathbf{g}\Vert }^2}\right).$$

Combining this result with formula (35) and letting X = R + q′z with

$$\kappa =R+\frac{p}{1+{\Vert \mathbf{g}\Vert }^2}{\mathbf{g}}^{\prime }\mathbf{q},{\tau }^2={\Vert \mathbf{q}\Vert }^2-\frac{{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}^2}{1+{\Vert \mathbf{g}\Vert }^2},$$

we obtain the following result. Let $\mathbf{z}~\mathcal{N}\left(0,\mathbf{I}\right)$, p and R be scalar and g and q be vectors. Then

$${\left(2\pi \right)}^{-n/2}{\displaystyle {\int }_{\mathbf{z}\in R^{n-1}}\left|R+{\mathbf{q}}^{\prime }\mathbf{z}\right|e^{-\frac{1}{2}{\left({\mathbf{z}}^{\prime }\mathbf{g}-p\right)}^2-\frac{1}{2}{\Vert \mathbf{z}\Vert }^2}d\mathbf{z}=\frac{\sqrt{1+{\Vert \mathbf{g}\Vert }^2}}{\sqrt{2\pi }}{e}^{-\frac{p^2}{2+(1+{\Vert \mathbf{g}\Vert }^2)}}\times \left(a_1+a_2\right)},$$ (36)

where

$$a_1=\frac{R+\frac{p}{1+{\Vert \mathbf{g}\Vert }^2}{\mathbf{g}}^{\prime }\mathbf{q}}{1+{\Vert \mathbf{g}\Vert }^2}\left(2\mathrm{\Phi }\left(\frac{R+\frac{p}{1+{\Vert \mathbf{g}\Vert }^2}{\mathbf{g}}^{\prime }\mathbf{q}}{\sqrt{{\Vert \mathbf{q}\Vert }^2-\frac{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}{1+{\Vert \mathbf{g}\Vert }^2}}}\right)-1\right),$$ (37)

$$a_2=\frac{1}{1+{\Vert \mathbf{g}\Vert }^2}\sqrt{\frac{2}{\pi }}{e}^{-\frac{{\left(R+\frac{p}{1+{\Vert \mathbf{g}\Vert }^2}{\mathbf{g}}^{\prime }\mathbf{q}\right)}^2}{2\left({\Vert \mathbf{q}\Vert }^2-\frac{{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}^2}{1+{\Vert \mathbf{g}\Vert }^2}\right)}}\sqrt{{\Vert \mathbf{q}\Vert }^2-\frac{{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}^2}{1+{\Vert \mathbf{g}\Vert }^2}}.$$ (38)

Note that without the absolute value, we obtain an easier expression,

$${\left(2\pi \right)}^{-n/2}{\displaystyle {\int }_{\mathbf{z}\in R^{n-1}}\left(R+{\mathbf{q}}^{\prime }\mathbf{z}\right)e^{-\frac{1}{2}{\left({\mathbf{z}}^{\prime }\mathbf{g}-p\right)}^2-\frac{1}{2}{\Vert \mathbf{z}\Vert }^2}d\mathbf{z}=\frac{\sqrt{1+{\Vert \mathbf{g}\Vert }^2}}{\sqrt{2\pi }}{e}^{-\frac{p^2}{2(1+{\Vert \mathbf{g}\Vert }^2)}}a},$$ (39)

where

$$a=\frac{R+\frac{p{\mathbf{g}}^{\prime }\mathbf{q}}{1+{\Vert \mathbf{g}\Vert }^2}}{1+{\Vert \mathbf{g}\Vert }^2}.$$ (40)

#3. Express the density through the n-dimensional vector f and its derivatives and simplify. Letting

$$\begin{array}{l}{a}_i={\dot{f}}_i\left(b\right),b_i={\ddot{f}}_i\left(b\right),{\mathrm{\Delta }}_i=f_i\left(\beta \right)-f_i\left(b\right),\\ A={\displaystyle \sum _{i=1}^n{a}_i^2,D={\displaystyle \sum _{i=1}^n{a}_i{\mathrm{\Delta }}_i},B={\displaystyle \sum _{i=1}^n{b}_i{\mathrm{\Delta }}_i,C={\displaystyle \sum _{i=1}^n{b}_i{a}_i},E={\displaystyle \sum _{i=1}^n{b}_i^2}}}\end{array}$$

for brevity, some tedious algebra yields

$$\begin{array}{l}\frac{1}{1+{\Vert \mathbf{g}\Vert }^2}\left(R+\frac{p{\mathbf{g}}^{\prime }\mathbf{q}}{1+{\Vert \mathbf{g}\Vert }^2}\right)\\ =\frac{1}{A}{a}_1^2\left[\frac{A}{a_1}+{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)-\frac{a_1^2}{A}\frac{1}{a_1^2}D{\displaystyle \sum _{i=2}^n{a}_i\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)}}\right]\\ =\frac{a_1}{A}\left[A+\frac{b_1}{a_1}{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i{a}_i-{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i{b}_i-\frac{D}{A{a}_1}\left(b_1{\displaystyle \sum _{i=2}^n{a}_1^2-a_1{\displaystyle \sum _{i=2}^n{a}_i{b}_i}}\right)}}\right]\\ =\frac{a_1}{A}\left[A+\frac{b_1}{a_1}\left(D-{\mathrm{\Delta }}_1{a}_1\right)-B+b_1{\mathrm{\Delta }}_1-\frac{D}{A{a}_1}\left(b_1\left(A-a_1^2\right)-a_1\left(C-a_1{b}_1\right)\right)\right]\\ =\frac{a_1}{A}\left[A+\frac{b_1}{a_1}D-b_1{\mathrm{\Delta }}_1-B+b_1{\mathrm{\Delta }}_1-\frac{D}{A{a}_1}\left(b_{1}A-a_{1}C\right)\right]\\ =\frac{a_1}{A}\left[A+\frac{b_1}{a_1}D-B-D\frac{b_1}{a_1}+\frac{DC}{A}\right]=\frac{a_1}{A}\left[A-B+\frac{DC}{A}\right]\end{array}$$

and

$$\begin{array}{l}{\Vert \mathbf{q}\Vert }^2+{\Vert \mathbf{q}\Vert }^2{\Vert \mathbf{g}\Vert }^2-{\left({\mathbf{g}}^{\prime }\mathbf{q}\right)}^2\\ ={\displaystyle \sum _{i=2}^n{\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)}^2}+\left[{\displaystyle \sum _{i=2}^n{\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)}^2}\right]{\displaystyle \sum _{i=2}^n\frac{a_i^2}{a_1^2}-{\left({\displaystyle \sum _{i=2}^n\frac{a_i}{a_1}\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)}\right)}^2}\\ =\frac{1}{a_1^4}{\displaystyle \sum _{i=2}^n{\left(a_i{b}_1-a_1{b}_i\right)}^2+\frac{1}{a_1^6}{\displaystyle \sum _{i=2}^n{\left(a_i{b}_1-a_1{b}_i\right)}^2{\displaystyle \sum _{i=2}^n{a}_1^2-\frac{1}{a_1^6}{\left({\displaystyle \sum _{i=2}^n{a}_i\left(a_i{b}_1-b_i{a}_1\right)}\right)}^2}}}\\ =\frac{b_1^2}{a_1^4}{\displaystyle \sum _{i=2}^n{a}_i^2+\frac{1}{a_1^2}}{\displaystyle \sum _{i=2}^n{b}_i^2-\frac{2b_1}{a_1^3}{\displaystyle \sum _{i=2}^n{a}_i{b}_i+\frac{1}{a_1^6}\left(b_1^2{\displaystyle \sum _{i=2}^n{a}_i^2-2a_1{b}_1}{\displaystyle \sum _{i=2}^n{a}_i{b}_i+a_1^2{\displaystyle \sum _{i=2}^n{b}_i^2}}\right)\left(A-a_1^2\right)}}\\ -\frac{1}{a_1^6}{\left(b_1{\displaystyle \sum _{i=2}^n{a}_i^2-a_1{\displaystyle \sum _{i=2}^n{a}_i{b}_i}}\right)}^2=\frac{b_1^2}{a_1^4}\left(A-a_1^2\right)\frac{1}{a_1^2}\left(E-b_1^2\right)-\frac{2b_1}{a_1^3}\left(C-a_1{b}_1\right)\\ +\frac{1}{a_1^6}\left[(b_1^2\left(A-a_1^2\right)-2a_1{b}_1\left(C-a_1{b}_1\right)+a_1^2\left(E-b_1^2\right)\right]\left(A-a_1^2\right)-\frac{1}{a_1^6}{\left(b_1\left(A-a_1^2\right)-a_1\left(C-a_1{b}_1\right)\right)}^2\\ =\frac{1}{a_1^4}\left(C^2-AE\right).\end{array}$$

Plugging these expressions back into (36), we obtain the exact density of the NLS estimator (5) with the adjustment coefficients, which follow from (37) and (38). Note that the NE density approximation with adjustment coefficient (8) follows from (39). Thus, this approximation is obtained from density (33) by ignoring the absolute value of the derivative/Jacobian.

B. Proof of Theorem 2

This proof follows the proof of Theorem 1 closely. Express y₁ through the NLS estimator b and y₂, …., y_n. as

$$y_1=h\left(b,y_2,\dots ,y_n\right)=f_1\left(b\right)-\frac{{\displaystyle {\sum }_{i=2}^n\left(y_i-f_i\left(b\right)\right)r_i\left(b\right)}}{r_1\left(b\right)}$$

and find the derivative $dh/db=R+{\displaystyle {\sum }_{i=2}^n{z}_i{q}_i}$, where

$$\begin{array}{l}R=\frac{1}{r_1\left(b\right)}{\displaystyle \sum _{i=1}^n\dot{f}\left(b\right)r_i\left(b\right)+{\displaystyle \sum _{i=2}^n\left(f_i\left(\beta \right)-f_i\left(b\right)\right)q_i\left(b\right)}}\\ q_i=\frac{{\dot{r}}_1\left(b\right)r_i\left(b\right)}{r_1^2\left(b\right)}-\frac{{\dot{r}}_i\left(b\right)}{{\dot{r}}_1\left(b\right)},i=2,3,\dots ,n.\end{array}$$

Introducing the (n − 1) × 1 vectors z, q and g with the ith components z_i, q_i and g_i = r_i(b)/r₁(b), respectively, and p = [(f(b) − f(β))′r(b)]/r₁(b). We notice that the derivative ${\dot{f}}_i$ appears only in the expression of R; in the rest of the expressions, r_i acts as ${\dot{f}}_i$ and subsequently ${\dot{r}}_i$ acts as ${\ddot{f}}_i$. Thus, we need to work on the terms containing R,

$$\begin{array}{l}\frac{1}{1+{\Vert \mathbf{g}\Vert }^2}\left(R+\frac{p{\mathbf{g}}^{\prime }\mathbf{q}}{1+{\Vert \mathbf{g}\Vert }^2}\right)\\ =\frac{1}{A}{a}_1^2\left[\frac{G}{a_{1}A}+{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i}\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)-\frac{a_1^2}{A}\frac{1}{a_1^2}D{\displaystyle \sum _{i=2}^n{a}_i}\left(a_i\frac{b_1}{a_1^2}-b_i\frac{1}{a_1}\right)\right]\\ =\frac{a_1}{A}\left[\frac{G}{A}+\frac{b_1}{a_1}{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i{a}_i-{\displaystyle \sum _{i=2}^n{\mathrm{\Delta }}_i{b}_i-\frac{D}{A{a}_1}\left(b_1{\displaystyle \sum _{i=2}^n{a}_i^2-a_1{\displaystyle \sum _{i=2}^n{a}_i{b}_i}}\right)}}\right]\\ =\frac{a_1}{A}\left[\frac{G}{A}+\frac{b_1}{a_1}(D-{\mathrm{\Delta }}_1{a}_1)-B+b_1{\mathrm{\Delta }}_1-\frac{D}{A{a}_1}\left(b_1\left(A-a_1^2\right)-a_1\left(C-a_1{b}_1\right)\right)\right]\\ =\frac{a_1}{A}\left[\frac{G}{A}+\frac{b_1}{a_1}D-b_1{\mathrm{\Delta }}_1-B+b_1{\mathrm{\Delta }}_1-\frac{D}{A{a}_1}\left(b_{1}A-a_{1}C\right)\right]\\ =\frac{a_1}{A}\left[\frac{G}{A}+\frac{b_1}{a_1}D-B-D\frac{b_1}{a_1}+\frac{DC}{A}\right]=\frac{a_1}{A}\left[\frac{G}{A}-B+\frac{DC}{A}\right].\end{array}$$

Thus, we come to the formula for density in Theorem 2 by replacing $\dot{\mathbf{f}}(b)$ with r(b) and $\ddot{\mathbf{f}}(b)$ with $\dot{\mathbf{r}}(b)$.

C. Outline of the multivariate density derivation

Partition the Jacobian matrix F(b), the data vector y and the regression function f(b) as follows:

$$\mathbf{F}(\mathbf{b})=\left[\begin{array}{c}{\mathbf{F}}_1^{m\times m}(\mathbf{b})\\ {\mathbf{F}}_2^{(n-m)\times m}(\mathbf{b})\end{array}\right],\mathbf{y}=\left[\begin{array}{c}{\mathbf{y}}_1^{m\times 1}\\ {\mathbf{y}}_2^{(n-m)\times 1}\end{array}\right],\mathbf{f}(\mathbf{b})=\left[\begin{array}{c}{\mathbf{f}}_1^{m\times 1}(\mathbf{b})\\ {\mathbf{f}}_2^{(n-m)\times 1}(\mathbf{b})\end{array}\right],$$

assuming that the square matrix F₁(b) is nonsingular for every b. Using the normal equation express y₁ through the NLS estimator b and z₂ = y₂ − f₂(β),

$${\mathbf{y}}_1=\mathbf{h}(\mathbf{b},{\mathbf{z}}_2)\stackrel{\text{def}}{=}{\mathbf{f}}_1(\mathbf{b})-{\left({\mathbf{F}}_1^{\prime }\left(\mathbf{b}\right)\right)}^{-1}{\mathbf{F}}_2^{\prime }(\mathbf{b})({\mathbf{z}}_2+({\mathbf{f}}_2(\mathit{\beta })-{\mathbf{f}}_2(\mathbf{b})),$$

and apply the multivariate version of Lemma 6 to obtain the density of the NLS estimator as an integral over R^n−m,

$$p_{\mathit{\text{NLS}}}(\mathbf{b};\mathit{\beta })={\left(2\pi \right)}^{-n/2}{\displaystyle {\int }_{R^{n-m}}\left|\text{det}\left(\mathbf{R}+{\displaystyle \sum _{i=m+1}^n{z}_{2i}{\mathbf{Q}}_i}\right)\right|e^{-\frac{1}{2}{\Vert \mathbf{h}(\mathbf{b},{\mathbf{z}}_2)-{\mathbf{f}}_1(\beta )\Vert }^2-\frac{1}{2}{\Vert {\mathbf{z}}_2\Vert }^2}d{\mathbf{z}}_2},$$

where $\begin{array}{l}\mathbf{R}={\mathbf{F}}_1(\mathbf{b})+{\left({\mathbf{F}}_1^{\prime }\left(\mathbf{b}\right)\right)}^{-1}{\mathbf{F}}^{\prime }(\mathbf{b})\mathbf{F}(\mathbf{b})+{\displaystyle \sum _{i=2}^n(f_i(\beta )-f_i(b)){\mathbf{Q}}_i,}\\ {\mathbf{Q}}_i=-{\left({\mathbf{F}}_1^{\prime }\left(\mathbf{b}\right)\right)}^{-1}{\mathbf{H}}_{2i}\end{array}$ and H_2i = ∂²f_i2/∂²b. Approximate

$$\text{det}\left(\mathbf{R}+{\displaystyle \sum _{i=m+1}^n{z}_{2i}\mathbf{Q}}\right)\simeq |\mathbf{R}|{\displaystyle \sum _{i=m+1}^n\text{tr}({\mathbf{R}}^{-1}{\mathbf{Q}}_i)z_{2i}}.$$

using the Jacobi’s formula and proceed as in the univariate case since the right-hand side may be treated as a normally distributed random variable and as such exact density can be derived beyond this point. Note that if the absolute value of the determinant in p_NLS expression is approximated as det(R) we obtain the NE density.