Effects of Pedal Speed and Crank Length on Pedaling Mechanics during Submaximal Cycling

ABSTRACT

During submaximal cycling, the neuromuscular system has the freedom to select different intermuscular coordination strategies. From both a basic science and an applied perspective, it is important to understand how the central nervous system adjusts pedaling mechanics in response to changes in pedaling conditions.

Purpose

To determine the effect of changes in pedal speed (a marker of muscle shortening velocity) and crank length (a marker of muscle length) on pedaling mechanics during submaximal cycling.

Methods

Fifteen trained cyclists performed submaximal isokinetic cycling trials (90 rpm, 240 W) using pedal speeds of 1.41 to 1.61 m·s⁻¹ and crank lengths of 150 to 190 mm. Joint powers were calculated using inverse dynamics.

Results

Increases in pedal speed and crank length caused large increases knee and hip angular excursions and velocities (P < 0.05), whereas ankle angular kinematics stayed relatively constant (P > 0.05). Joint moments and joint powers were less affected by changes in the independent variables, but some interesting effects and trends were observed. Most noteworthy, knee extension moments and powers tended to decrease, whereas hip extension power tended to increase with an increase in crank length.

Conclusions

The distribution of joint moments and powers is largely maintained across a range of pedaling conditions. The crank length induced differences in knee extension moments, and powers may represent a trade-off between the central nervous system’s attempts to simultaneously minimize muscle metabolic and mechanical stresses. These results increase our understanding of the neural and mechanical mechanisms underlying multi-joint task performance, and they have practical relevance to coaches, athletes, and clinicians.

During cycling, power delivered to the pedals is produced by muscles that span the ankle, knee, and hip and by power produced in the upper body that is transferred across the hip joint (6,25). The investigation of the power contributions of the various muscle groups (i.e., joint action powers) to total mechanical power gives us invaluable insights into mechanical and physiological processes underlying exercise and cycling performance. For example, the analysis of joint action powers has increased our understanding of intermuscular coordination strategies as a function of cycling intensity (9,10), pedaling rates (9,30), or cycling duration (26).

During submaximal cycling, the neuromuscular system has the freedom to selectively use combinations of the various power producing joint actions to meet the task requirement. This selection may represent some optimization such as minimizing muscle activation (30), muscle stress (15), or overall metabolic cost (20). This notion is supported by analyses of preferred pedaling rates. Cyclists freely choose pedaling rates that are associated with minimized values for joint moments (13,16,22), muscle stress (15), negative muscle work (29), and muscle activation (30). Although metabolic cost is not minimized at the preferred pedaling rate (23), it is likely that the minimization of metabolic cost contributes to the intermuscular coordination strategy in terms of joint power distribution. In support of this notion, Korff et al. (20) demonstrated that metabolic cost is minimized when cyclists use their preferred pedaling technique. Thus, it is likely that the movement strategy adopted during submaximal cycling may represent an optimization based on some combination of metabolic and neural demand as well as muscular stress. However, their interaction within the context of intermuscular coordination has not been fully elucidated. In submaximal cycling, a thorough understanding of these factors is important from both a mechanistic and an applied perspective. Regarding the former, cycling is a repetitive movement with generally constrained joint and muscle kinematics, and so, it is an ideal task to gain mechanistic insights into the interacting roles of mechanical muscle actions and intermuscular coordination. Regarding the latter, knowledge of the mechanical muscle properties, which govern the movement strategy adopted during submaximal cycling, increases our understanding of endurance cycling performance (18,19) and could give insights into more effective training and intervention strategies for cyclists as well as intervention strategies for clinical applications.

From a theoretical point of view, three variables are of particular importance within this context: pedal speed, cycle frequency, and crank length. Pedal speed (the mathematical product of crank length and crank angular velocity) is indicative of muscle shortening velocities of monoarticular muscles (24,34). Cycle frequency is indicative of activation-deactivation dynamics (7,24). Crank length is indicative of muscle excursions of monoarticular muscles (14). Thus, each of these variables represents a different physiological phenomenon. Pedal speed is of particular importance because of the dependency of muscular force (2) and muscular efficiency (4) on muscle shortening velocity. The primary purpose of this study was therefore to investigate the effect of pedal speed on joint angular excursions, velocities, moments, and powers.

Pedal speed can be altered by varying pedaling rate at a constant crank length, varying crank length at a constant pedaling rate, or a combination of the two. However, it is challenging to isolate the effect of pedal speed using either of these experimental paradigms. When pedaling rate is altered with a constant crank length (e.g., 3,10), both pedal speed (muscle shortening velocities) and pedaling rate (activation deactivation dynamics) are altered concomitantly. Here, we chose to vary crank length and hold pedaling rate constant to ensure that any effects of pedal speed would not be confounded by concomitant changes in pedaling rate. In particular, we sought to isolate the effect of muscle shortening velocities on joint powers independent of activation-deactivation dynamics. However, changing crank length results in altered muscle excursions, which could lead to different joint moments because of the muscles working on different regions of their respective force–length relationships. If this was the case, joint powers could also be different across crank lengths. Previous research has shown that joint action powers are unaffected by changes in pedaling rate when crank length is held constant (3,10), meaning that in these studies, pedal speed and pedaling rate were changed concomitantly. Within the context of the primary purpose of this study, it was also important to ensure that crank length (i.e., muscle excursions)—independent of pedal speed—would not be a confounding factor. Thus, the second purpose was to investigate the effect of crank length (independent of pedal speed) on joint angular velocities, joint moments, and joint powers.

METHODS

Participants

Fifteen trained cyclists (12 men [76 ± 7 kg], 3 women [66 ± 7 kg]) age 19 to 44 yr, all regularly competing in regional cycling races, volunteered to take part in the study. Experimental procedures were approved by the institutional review board of the University of Utah and the Research Ethics Committee of Brunel University. Participants received a verbal and written explanation of all procedures and gave their written informed consent.

Procedure

Participants visited the laboratory on 4 separate occasions. During the first two visits, they practiced cycling with the nonstandard crank lengths (150 and 190 mm). Practice was not provided for the standard crank lengths (165, 170, and 175 mm), as participants regularly cycled on cranks within this range. On each familiarization day, participants performed two 10-min trials of submaximal cycling (one on the shortest crank [150 mm] and one on the longest crank [190 mm]). Each trial consisted of 8-min cycling at a self-selected power output (e.g., ~75–150 W), followed by 2-min cycling at a power output of 240 W. All practice sessions were performed on the same isokinetic cycling ergometer as used for the experimental data collection.

During the third and fourth visits, participants performed the experimental submaximal cycling protocol, with two or three crank lengths tested on each visit. The order of the crank lengths was randomized, as was the number of crank lengths tested on each experimental day (three crank lengths on the first day and two on the second or vice versa). Data collection took place on two separate days to minimize fatigue across the experimental trials. For each participant, data collection began at the same time on both experimental days. On the first day, body mass, thigh length (greater trochanter to lateral femoral condyle), leg length (lateral femoral condyle to lateral malleolus), foot length (heel to toe), and “kinematic foot length” (pedal spindle to lateral malleolus) were measured. All anthropometric measures were collected by the same investigator.

The experimental trials consisted of two 30-s trials of isokinetic cycling at each crank length (150, 165, 170, 175, and 190 mm). One trial was performed at a pedaling rate of 90 rpm, and the other trial was performed at a constant pedal speed of 1.60 m·s⁻¹ (equivalent to the middle condition of 170-mm crank length and 90 rpm). Table 1 details the crank lengths, pedaling rates, and pedal speeds used in both experimental conditions. The order of the two experimental trials was randomized, and a minimum of 3-min recovery was given between them. Participants were asked to maintain a target power output of 240 W against the isokinetic resistance (10); feedback regarding their instantaneous crank power was provided by means of a calibrated SRM power measurement system (Schoberer Rad Messtechnik, Jülich, Germany). To verify that the subjects cycled at the required power output, the average power that was delivered to the right pedal was obtained (see methodological details below). Assuming bilateral symmetry, this value should be approximately 120 W. Across all trials, subjects produced an average power output of 118.4 W (±6.8 W).

TABLE 1.

Crank lengths, pedaling rates, and pedal speeds used in both experimental conditions.

Cycle ergometer

All cycling trials were performed on an isokinetic ergometer, constructed from a Monark cycle ergometer frame and flywheel (Monark Exercise AB, Vansbro, Sweden). The ergometer flywheel was coupled to a 3.75-kW direct current motor (Baldor Electric Company model CDP3605, FortSmith, AR) and controlled by a speed controller equipped with regenerative braking (Minarik model RG5500U, Glendale, CA). Two reference measurements were recorded on each participant’s training bicycle and used to set the ergometer position; “seat height,” as defined by the distance between the top of the saddle and the pedal spindle when the crank was positioned to allow maximum displacement between these two points, and “handlebar drop,” as defined by the vertical drop from the top of the saddle and the top of the handlebars. When crank length was changed on the ergometer (SRM multilength crank; Schoberer Rad Messtechnik, Jülich, Germany), the height of the seat and the handlebars were both altered to maintain these two reference measurements (seat height, handlebar drop) across all crank lengths. “Handlebar reach,” as defined by the horizontal distance between the saddle and the handlebars, remained constant across all crank lengths. Participants wore cycling shoes with cleats that locked onto the pedal interface (Speedplay Inc., San Diego, CA).

Instrumentation

The instrumentation and procedures used to obtain cycling kinematic and kinetic data have been described in several previous studies from our laboratory (3,10,25). Normal and tangential pedal forces were recorded on the right pedal using two three-component piezoelectric force transducers (Kistler 9251; Kistler USA, Amherst, NY). The right pedal and crank were equipped with digital position encoders (S5S-1024-IB, US Digital, Vancouver, WA), and the pedal and crank angles were used to resolve the normal and tangential pedal forces into absolute vertical and horizontal components. The position of the right iliac crest was recorded with a two-segment instrumented spatial linkage (26). Pedal forces, pedal position, crank position, and instrumented spatial linkage position were all sampled at 240 Hz using Bioware software (Kistler USA) and filtered with a fourth-order zero-lag Butterworth low-pass filter at a cutoff frequency of 8 Hz.

The position of the hip joint was calculated from the position of the iliac crest, assuming a constant offset, measured in a static condition (31). The location of the ankle joint was determined using the angular positions of the crank and pedal and the distance from the pedal spindle to the lateral malleolus, assuming that the position of the lateral malleolus relative to the pedal surface was fixed throughout the pedal cycle (17). The position of the knee joint center was calculated by means of the law of cosines, using the locations of the hip and ankle joints as well as thigh and leg lengths. Joint angles were calculated from joint positions and segment lengths. Linear and angular velocities and accelerations of the limb segments were determined by finite differentiation of position data with respect to time.

Segmental masses, moments of inertia, and segmental center of mass locations were estimated using the regression equations reported by de Leva (21). Sagittal plane joint intersegmental forces and net muscle moments about the joint (joint moments) were derived at the ankle, knee, and hip using standard inverse dynamics techniques (9), as previously described (3). Joint powers were defined as the product of joint moments and joint angular velocities. Power delivered to the right pedal was defined as the product of the component of pedal force acting normal to the crank and the linear velocity of the pedal.

Derivation of dependent variables

All complete pedal cycles during the 30-s trial were analyzed. Joint angular velocities and joint powers were determined over extension and flexion phases and calculated as average values over these pedal cycles. Extension and flexion phases were defined based on the numerical sign of the corresponding joint angular velocity. In addition, we determined peak joint action powers during extension and flexion phases.

Statistical analysis

One-way analyses of variance (ANOVAs) with repeated measures were performed to determine the effects of pedal speed on all dependent variables. Here, pedal speed was the independent variable (see Table 1 for details). Similarly, to examine the effect of crank length (independent of pedal speed) on the dependent variables, 1-way ANOVAs with repeated measures were performed for each dependent variable. Here, crank length was the independent variable, and data at the five crank lengths were analyzed (Table 1).

If an ANOVA indicated a significant main effect, post hoc pairwise comparisons (Bonferroni) were performed to locate where those differences occurred. In addition, effect sizes to describe pairwise differences were calculated. Effect sizes were interpreted on the basis of Cohen (8) classification scheme: effect sizes less than 0.5 were considered to be small, effect sizes between 0.5 and 0.8 were considered to be moderate, and effect sizes greater than 0.8 were considered to be large. The alpha level was set at 0.05, and all statistical procedures were performed using SPSS 15.0 (SPSS Inc., Chicago, IL).

RESULTS

Effects of pedal speed

The main effect of pedal speed on knee and hip angular excursions was significant (P < 0.001). Post hoc t tests revealed that angular excursions increased with increasing pedal speed. All pairwise comparisons were significant (P < 0.05) for both joint angular excursions. The main effect of pedal speed on ankle angular excursion was nonsignificant. The main effects of pedal speed on extension and flexion velocities at the knee and hip were significant (P < 0.001) (see Table 2 for details of statistical tests). The main effects of pedal speed on ankle extension and flexion velocities were nonsignificant (P > 0.05). Post hoc pairwise comparisons revealed that extension and flexion velocities at the knee and hip increased with increases in pedal speed (Table 2). The analysis of effect sizes revealed that the largest effect sizes (ES > 0.8) were observed for the most extreme pedal speed comparisons (Fig. 1B). Figure 1 illustrates the changes in joint angular velocities across pedal speeds.

TABLE 2.

Details of the statistical analyses for the effects of pedal speed and crank length on the dependent variables.

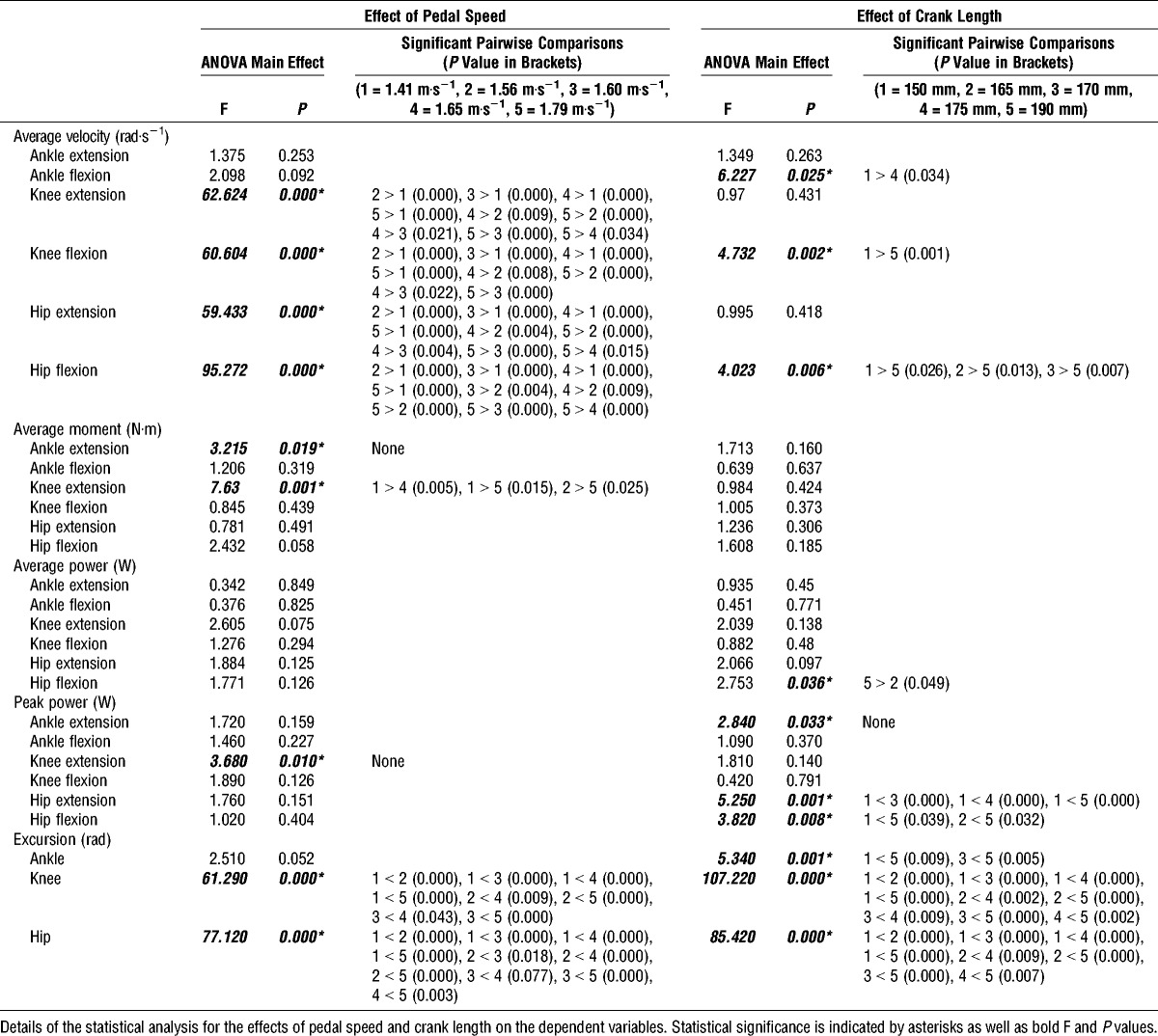
FIGURE 1.

Changes in joint kinetics and joint kinematics across pedal speeds. Joint profiles and associated descriptive statistical data tables and are presented for the ankle (1), knee (2), and hip (3) to show the effect of pedal speed on excursion (A), angular velocity (B), moment (C), and power (D). Statistical data tables display mean and standard deviations in bold, with effect sizes for the pairwise comparisons in the remaining cells. For clarity, joint profiles are only presented for the slowest (light gray), middle (gray), and fastest (black) pedal speeds.

Changes in pedal speed affected knee extension moment (P < 0.001). Post hoc pairwise comparisons revealed a greater knee extension moment at 1.41 m·s⁻¹ compared with 1.65 and 1.79 m·s⁻¹ and at 1.56 m·s⁻¹ compared with 1.79 m·s⁻¹ (Table 2). The magnitudes of the effects describing these pairwise comparisons were moderate (0.5 < ES < 0.8) and small (ES, < 0.5) (Fig. 1C). Although the ANOVA indicated a significant main effect for pedal speed on ankle extension moment (P = 0.019), post hoc pairwise comparisons did not reveal any significantly different pedal speed pairs (Table 2). Pedal speed did not affect flexion moment at the ankle, knee, or hip (P > 0.05). The effect of pedal speed on hip extension moment was also nonsignificant (P > 0.05). Pedal speed did not affect joint powers at the ankle knee or hip (P > 0.05) (Table 1). All effect sizes describing the difference between pairs of joint powers across pedal speeds were small (Fig. 1D). Figure 1 illustrates relationship between knee extension velocity, knee extensor moment, and knee extension power across pedal speeds. Pedal speed had a significant effect on peak knee extension power (P = 0.01). However, all follow-up pairwise comparisons were nonsignificant.

Effects of crank length

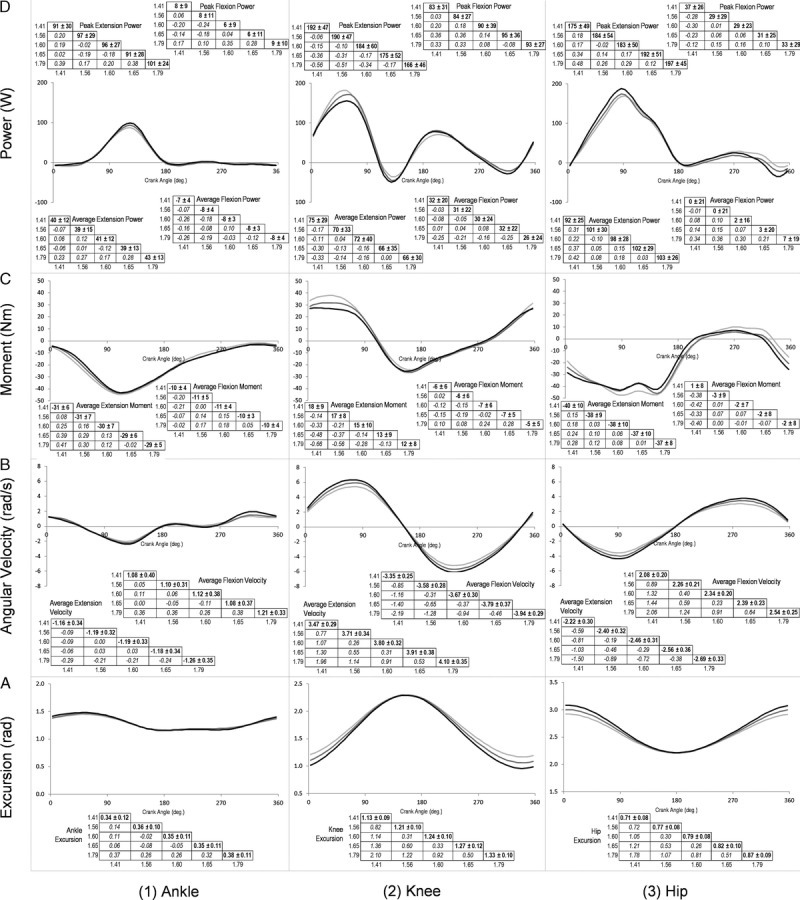
With pedal speed held constant, the main effect of crank length on ankle, knee, and hip angular excursions was significant (P < 0.001). Post hoc t tests revealed that at a crank length of 190 mm, ankle angular excursions were greater than that at 170 and 150 mm (P < 0.05). At the hip and knee joints, angular excursions increased with increasing crank length. All pairwise comparisons were significant (P < 0.05) for both joint angular excursions. The effect of crank length on extension velocities at the ankle, knee, and hip was nonsignificant (P > 0.05) (Table 2). Crank length significantly affected flexion velocities at the ankle, knee, and hip (P < 0.05) (Table 2). Post hoc pairwise comparisons between crank length pairs revealed that ankle flexion velocity was greater at a crank length of 175 mm compared with 150 mm. Furthermore, knee flexion velocity was greater at a crank length of 190 mm compared with 150 mm, and hip flexion velocity was greater at a crank length of 190 mm compared with 150, 165, and 170 mm (Fig. 2B). The magnitude of each of these effects was small (ES, <0.5) (Fig. 2B).

FIGURE 2.

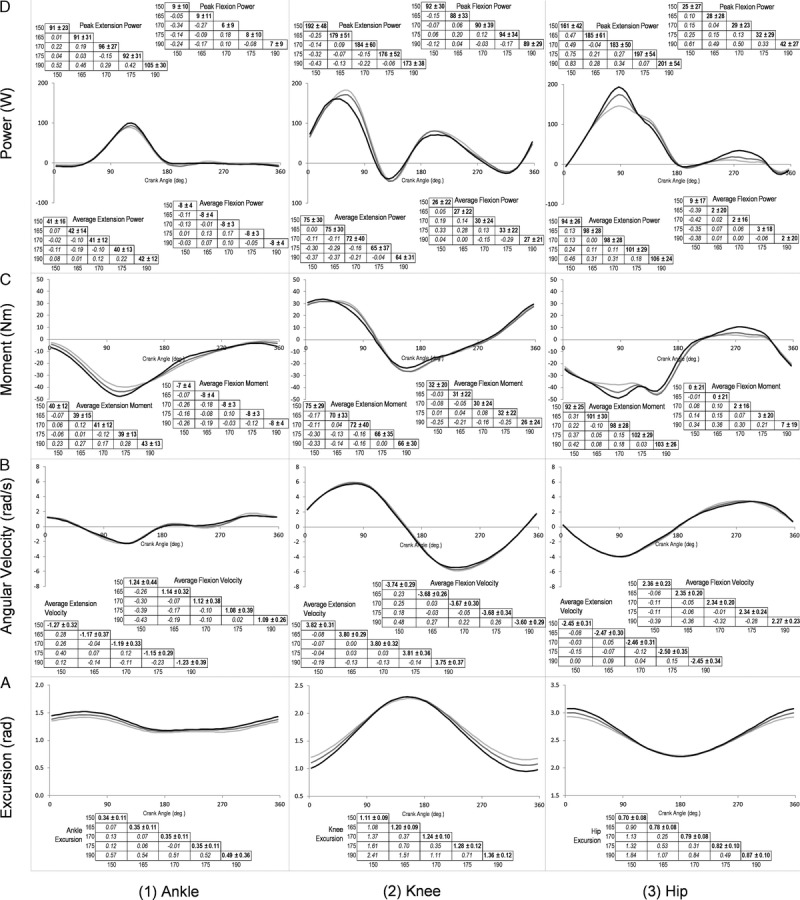
Changes in joint kinetics and joint kinematics across crank lengths. Joint profiles and associated descriptive statistical data tables and are presented for the ankle (1), knee (2), and hip (3) to show the effect of crank length on excursion (A), angular velocity (B), moment (C), and power (D). Statistical data tables display mean and standard deviations in bold, with effect sizes for the pairwise comparisons in the remaining cells. For clarity, joint profiles are only presented for the shortest (light gray), middle (gray), and longest (black) crank length.

At a constant pedal speed, the effect of crank length on flexion power at the ankle and knee joints were nonsignificant (P > 0.05). With pedal speed held constant, crank length did not affect extension or flexion moments at the ankle, knee, or hip (P > 0.05) (Table 2 and Fig. 2C). Changes in crank length did not affect extension power at the ankle, knee, and hip (P > 0.05). Crank length significantly affected hip flexion power (P < 0.05), with post hoc pairwise comparisons revealing that hip flexion power was greater at a crank length of 190 mm compared with 165 mm. However, the analysis of the effect sizes revealed that the magnitude of this effect was small (ES, 0.39) (Fig. 2D). Crank length significantly affected peak ankle extension power (P = 0.033), peak hip extension power (P = 0.001), and peak hip flexion power (P = 0.008). Post hoc t tests revealed that at a crank length of 150 mm, peak hip extension power was significantly smaller than at crank lengths of 170, 175, and 190 mm. Peak hip flexion power was greater at a crank length of 190 mm compared with 165 and 150 mm. For peak ankle extension power, none of the follow-up tests were significant.

DISCUSSION

The purpose of this study was to investigate the effect of pedal speed on joint angular excursions, velocities, moments, and powers in submaximal cycling. In this study, pedal speed was altered by changing crank length and keeping pedaling rate constant. To ensure that our results would not be confounded by changes in muscle excursions, we also determined the effect of crank length on these variables. Both manipulations had similar effects on joint excursions, which indicates that muscle length changes were similar for both manipulations. Interestingly, the greater leg excursion required to accommodate larger crank lengths was achieved by greater knee and hip joint excursions (signified by moderate and large effect sizes between conditions). Conversely, crank length–dependent changes in ankle joint excursions were smaller (Figs. 1A and 2A). Consistent with this finding, changes in ankle angular velocities across pedal speeds and crank lengths were negligible (signified by small effect sizes; Figs. 1B and 2B). It has previously been shown that the plantarflexors stiffen the ankle joint to allow for energy transfer from the proximal to distal segments (12). Our results suggest that this requirement to stiffen the ankle joint is accomplished by relatively constant ankle kinematics across crank lengths (Figs. 1A, B, 2A, and B). In addition, we found significant differences in extension and flexion velocities of both the knee and hip joints across pedal speeds, which is consistent with previous findings (23). Our results thereby confirm that pedal speed is related to the shortening velocities of the muscles spanning the knee and hip but not the ankle joint.

Our results also indicate significant effects of pedal speed on ankle and knee extension moments (Figs. 1C and 2C). Specifically, knee extension moment decreased with an increase in pedal speed. This effect was not observed when crank length was manipulated independent of pedal speed; it can therefore be attributed to changes in pedal speed per se. For all other actions, pedal speed or crank length did not affect the corresponding joint moments. The overall small pedal speed and crank length–dependent changes in joint moments suggest that during submaximal cycling, the CNS may attempt to minimize muscular mechanical stress across conditions. Support for this conjecture comes from (22,30,32) who found that joint moments and muscle forces are minimized at a cyclists preferred cadence. However, the significant effect of pedal speed on knee extension moment warrants further discussion.

One possible explanation for the pedal speed–dependent change of knee extension moment is the conjecture that the central nervous system would also seek to preserve joint powers across pedaling conditions. Bearing in mind that knee extension velocity increased with increasing pedal speed and that joint power is the mathematical product of joint moment and joint angular velocity, the opposing effects of pedal speed on knee extension moment and angular velocity could have canceled each other out to produce constant knee extensor power across pedal speeds. Indeed, neither pedal speed nor crank length significantly affected average joint powers. However, there was a tendency for knee extensor power to decrease in response to both pedal speed and crank length (ES, 0.33 and 0.37 for the most extreme comparisons). Conversely, there was a tendency for hip extensor power to increase in response to both increases in pedal speed and crank length. This was likely due to the large crank length–dependent increases in hip extension velocity, which were accompanied by small decreases in joint moments. The nonsignificant trends for changes in knee and hip extension power were similar across both manipulations. Thus, they can be attributed to crank length rather than pedal speed manipulations. It is therefore possible that the changes in operating muscle length across extremely different crank lengths may indeed require intermuscular coordination to be altered to achieve the goal of the task effectively. One could speculate that even more extreme changes in crank length or pedal speed would make this effect more apparent. Future research should explore this possibility explicitly.

In addition to the nonsignificant trends in average joint powers, we found significant effects of crank length on peak joint action powers. Specifically, increases in crank length resulted in increased peak hip extension and flexion powers. This effect was more pronounced when crank length (as opposed to pedal speed) was manipulated; it can therefore be attributed to changes in crank length. Although nonsignificant, peak knee extension power tended to decrease with increases in pedal speed and crank length. Thus, while the averaged joint action powers did not differ substantially, the way in which those actions were performed differed considerably. To further explore the meaningfulness of the relationship between crank length and joint powers, we performed additional regression analyses to determine the relationships between joint action powers and crank lengths. These analyses revealed that crank length was not significantly related to joint action powers. Specifically, the coefficients of determination were 1.7% (P = 0.83) for knee extension power and 2.1% (P = 0.34) for hip extension power. Thus, although the pairwise comparisons might seem noteworthy, these regression analyses failed to discover any influence of crank length on joint power production for these actions.

The present results in combination with previous findings suggest that within the limits tested in this investigation, the distribution of joint moments and joint action powers are somewhat robust neuromechanical properties, which may govern the CNS’s control strategies. The maintenance of joint powers might be due to localized muscle metabolism and metabolic stress or might reflect synergistic multi-joint extension and flexion actions. Muscle metabolic stress is related to muscle power (rate of energy release (33)). Increasing muscle power will likely increase rates of metabolic by-product production (5) that influences the central nervous system via afferent feedback (1). This feedback may, thereby, influence reliance on various muscles and joint actions during submaximal cycling. If localized metabolic stress is an important criterion in the selection of activation patterns, maintenance of relative muscle or joint action powers might be expected across a range of conditions just as we and others (6,10,11) have observed. Furthermore, the maintenance of joint moments may reflect the CNS’s strategy to keep muscular mechanical stress constant across conditions possibly to avoid fatigue (22,30,32). The somewhat conflicting requirements of maintaining metabolic and muscular stress may explain our observed effects of crank length on knee extension moment powers. One can speculate that the joint-specific differences in joint moments and powers are a result of the various constraints imposed on the system. In particular, they may represent a trade-off between minimizing muscular mechanical as well as metabolic stress while keeping the external power output constant. Further research is warranted to specifically test this hypothesis.

There are a number of limitations that need to be considered. When changing crank length, we elected to maintain the maximum leg extension as others have done (3,27,28). This maintained joint angles at the leg’s most extended position but altered joint angles throughout the rest of cycle where most power is produced. Also, we chose to maintain the anterior–posterior position of the saddle (except for small differences associated with sliding the seat post up and down at the angle imposed by the ergometer frame). Consequently, our peak values during extension occurred with the foot closer to the hip joint with shorter cranks and further away with longer cranks. The resulting differences in joint angles may have played a role in the leg extension action and may be partially responsible for the differences in peak joint power values. One alternative approach could have been to maintain the seat height relative to the crank axle. This would have helped to maintain joint angles during the middle portion of the leg extension phase. However, it would have resulted in 2-cm increases in leg extension with the 190-mm cranks, which we sought to avoid. Another approach would have been to move the saddle anteriorly when increasing crank length and posteriorly when decreasing crank length. This approach would also have helped to maintain joint angles during leg extension but would have increased differences during the flexion phase. These alterations of joint angles may have influenced joint power within each cycle. Nonetheless, the average joint powers for the four main power producing actions did not differ across the range of crank lengths evaluated.

Together, with previous studies of metabolic cost (28) and maximal power (3,24,27), our results have implications for athletes, clinicians, and researchers. The 27% range of crank lengths evaluated in this investigation is substantially larger than the 6% range (165–175 mm) typically available for adult bicycles, indicating that cyclists can change crank lengths without concern of changing their power production strategies. Furthermore, cyclists and triathletes wishing to adopt a more horizontal torso position to reduce aerodynamic drag could use shorter cranks to eliminate thigh to torso contact, which might compromise ventilation and/or power production. Cycling enthusiasts who have musculoskeletal impairments such as femoral-acetabular impingement or knee osteoarthritis might use shorter cranks to reduce maximum hip and knee flexion and thereby reduce the risk of symptomatic flare-ups triggered by larger joint angular excursions. Similarly, in rehabilitation settings, individuals recovering from injury or surgery might benefit from using a progression of shorter to longer cranks to gradually improve range of motion over time. Finally, our results suggest that biomechanical evaluation in laboratory settings may be performed on a single “lab standard” crank length. That is, biomechanical results obtained using one length (e.g., 170 mm) will provide results that are valid for cyclists who use other crank lengths on their own bicycles. From a basic sciences perspective, our data lay the groundwork for further research investigating the potentially conflicting requirements of minimizing metabolic and muscular stresses during submaximal cycling (35).