Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Oct 12.
Published in final edited form as: Appl Magn Reson. 2016 Apr 7;47(5):527–538. doi: 10.1007/s00723-016-0775-7

Eight-Channel Monopole Array Using ICE Decoupling for Human Head MR Imaging at 7 T

Xinqiang Yan 1,2,3,✉, Long Wei 2,3, Suoda Chu 1, Rong Xue 1,4, Xiaoliang Zhang 5,6,✉
PMCID: PMC5638452  NIHMSID: NIHMS910455  PMID: 29033501

Abstract

Due to the unique structure of radiative coil elements, traditional decoupling methods face technical challenges in reducing the electromagnetic coupling of the radiative arrays. In this study, we aim to investigate the possibility of using the recently introduced induced current elimination (ICE) decoupling technique for cylindrical shaped radiative coil array designs. To evaluate the method, an eight-channel transmit/receive monopole array with the ICE decoupling, suitable for human head imaging at 7 T, was built and comparatively investigated. In vivo human head images were acquired and geometry factor maps were measured and calculated to evaluate the performance of the ICE-decoupled monopole array. Compared with the monopole array without decoupling methods, the ICE-decoupled monopole array had a higher signal-to-noise ratio and demonstrated improved parallel imaging ability. The experimental results indicate that the ICE decoupling method is a promising solution to addressing the coupling issue of radiative array at ultrahigh fields.

1 Introduction

Ultrahigh field (7 T and beyond) magnetic resonance imaging (MRI) using radiofrequency (RF) coil arrays promises high signal–noise ratio (SNR), high spatial resolution and high contrast in MR imaging and spectroscopy [1–10]. However, attenuation of RF signals caused by the localized radio frequency magnetic field (B1) of typical coil arrays degrades the sensitivity in the deep area of the high dielectric, conductive biological samples, such as human body [11, 12]. To increase the MR SNR gain in the deep area of the human head or body, radiative coil arrays, such as dipole [13] and monopole [14] arrays have been proposed for ultrahigh field MRI applications, showing better SNR performance in the deep area [13, 14].

Minimizing the electromagnetic (EM) coupling among coil elements is critical to RF coil array designs, given that better decoupling could lead to higher SNR and better parallel imaging [15–20]. Due to the unique structure of radiative coil elements, EM coupling between elements in radiative coil arrays cannot be readily addressed by using traditional decoupling methods such as element overlapping [21] and L/C decoupling network [22–27]. Consequently, no decoupling treatments have been utilized to radiative array coils so far, which dramatically limits their imaging capability and performance. The induced current elimination (ICE) decoupling technique [28, 29] proposed recently has demonstrated its feasibility in designing microstrip transmission line (MTL) arrays [28, 30, 31] and traditional L/C loop arrays [32]. This decoupling method uses an independent decoupling element which forms a meta-material to eliminate the current induced by electromagnetic coupling. This method does not need physical connections between coil elements and decoupling elements, which is essential for dipole and monopole transceiver arrays.

In this study, we aim to investigate the feasibility and performance of the ICE decoupling method in cylindrical multichannel coil arrays for human head imaging at ultrahigh magnetic fields. To do this, an eight-channel transmit/receive (TX/RX) monopole array using this decoupling method was designed and fabricated for human head MR imaging at 7 T. A monopole array without decoupling treatments was also designed and fabricated for quantitative comparison.

Bench test results and in vivo human head MR images obtained from the eight-channel ICE-decoupled monopole array were presented. To further validate the ICE decoupling method in monopole arrays, Q values, scattering (S-) parameters, SNR and parallel imaging capability of the ICE-decoupled monopole array were evaluated and compared with the monopole elements without decoupling treatments.

2 Materials and Methods

2.1 Design and Construction of the ICE-Decoupled Monopole Array Coil

The monopole antenna is composed of a conductor which is perpendicular to the ground plane. The length of the conductor is quarter wavelength at the desired frequency.

The eight-channel ICE-decoupled monopole array coil was mounted on a cylindrical acrylic former with an outer diameter of 25 cm, as shown in Fig. 1a. For each monopole element, two capacitors Cs and Cp (Voltronics Corp., NJ, USA) were applied for matching and finely tuning [33–36]. Each decoupling element, which consists of a conductor and a capacitor in series (referred to as Cd), was placed between adjacent monopole elements, as shown in Fig. 1c. The length of the monopole elements and the decoupling elements were about 25 cm. All conductor strips were made of high quality copper tape (3 M, St, Paul, MN) with a width of 10 mm. The ground plate, which was perpendicular to the monopole elements and decoupling elements, had a dimension of 40 × 40 cm2. The upper corners of the ground were cut to fit in the MRI bore [14]. The ground plate was cut by a number of slots to reduce the eddy currents. Chip capacitors with a value of 1 nF were connected across the slots to ensure the RF connectivity.

Fig. 1.

Fig. 1

Open in a new tab

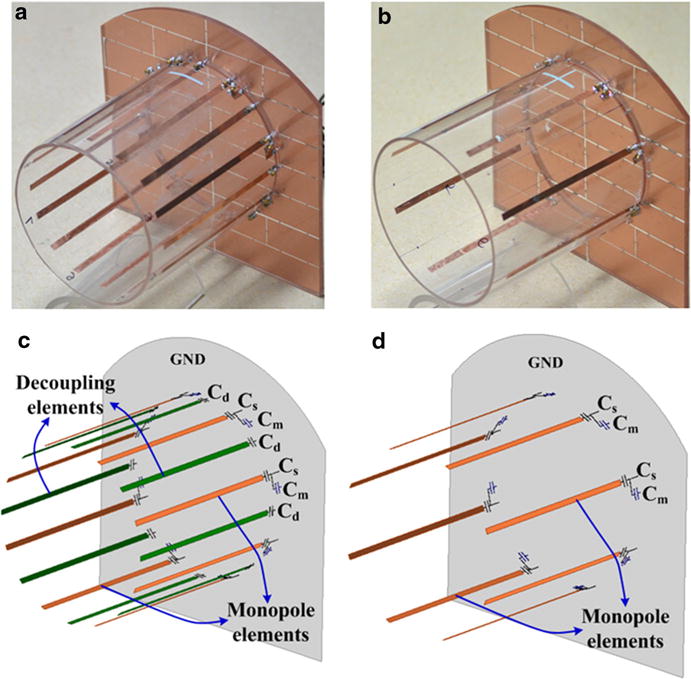
a Photograph of the 8-channel ICE-decoupled monopole transceiver coil array. b Photograph of the 8-channel monopole transceiver coil array without decoupling methods. c Schematic presenting of the monopole elements and decoupling elements of an 8-channel ICE-decoupled monopole array. c Schematic presenting of the monopole elements of an 8-channel monopole array without decoupling methods

Additionally, an 8-channel monopole array without decoupling methods was built for comparison, as shown in Fig. 1b. The dimensions of the monopole array without decoupling methods were exactly the same with the ICE-decoupled monopole array as described above. The matching circuits were also applied for this array to make a fair comparison, as shown in Fig. 1d.

The two monopole arrays described above were used for both transmission and reception, and were matched to 50 Ω and tuned to 297.2 MHz, which is the Larmor frequency of our 7 T MRI system. The RF signal from the power amplifier was equally split into eight transmit sources by an eight-way Wilkinson power splitter. The eight transmit sources drove the eight monopole elements with an increment of 45 degree between adjacent monopole elements. Eight Transmit/Receive switches and conventional 50-Ω preamplifiers were made to operate the array coils.

2.2 Bench Tests

The S-parameter matrices including reflection coefficients (S11) and transmission coefficients (S21) of the ICE-decoupled monopole array and monopole array without decoupling methods were measured using an Agilent E5071C network analyzer. The S-parameter matrices were recorded when the coils were loaded with human head. The S11 measurements were also used to calculate the unloaded Q value (QUL) and the Q value (QL) loaded with human head.

2.3 MRI Experiments

In vivo human head MR imaging experiments were performed on a whole-body MRI scanner (7 T MAGNETOM, Siemens Healthcare, Erlangen, Germany) in the same healthy volunteer. The human MRI experimental protocol was approved by the local Institutional Review Board (IRB) and the volunteer has signed an informed consent form.

We acquired the gradient recalled echo (GRE) images in the transverse and sagittal planes using the 8-channel ICE-decoupled monopole array and the monopole array without decoupling methods. The imaging acquisition parameters were as follows: flip angle (FA) = 25 degree, TR = 120 ms, TE = 6 ms, FOV = 250 × 250 mm2, matrix = 256 × 256, slice thickness = 5 mm, bandwidth = 260 Hz/pixel.

The transverse GRE images were also shown for signal-to-noise (SNR) comparison between the ICE-decoupled monopole array and the monopole array without decoupling methods. The SNR was determined by: SNR = SI/SD × 0.655, where SI is the signal intensity and SD is the standard deviation of the noise. The signals were measured from a square of 15 × 15 pixels in each of the five positions at the center and periphery of the images. The standard deviation was calculated from a 50 × 50 square in the image background. To demonstrate the parallel imaging performance of the two monopole arrays, accelerated GRE images and residual images with reduction factors of 2, 3 and 4 in the sagittal plane were shown. GRAPPA reconstructions were performed with in vivo data. Additionally, geometry (g-) factor (defined in [16]) maps and average g-factors were calculated using an RF coil array design and analysis software Musaik (Speag, Switzerland).

3 Results

3.1 Bench Tests

The S11 and S21 matrices of the eight-channel ICE-decoupled monopole array and monopole array without decoupling methods are shown in Fig. 2. The measured S11 of all coil elements in both arrays were better than −25 dB, indicating all coil elements are well matched to 50 Ω.

Fig. 2.

Fig. 2

Open in a new tab

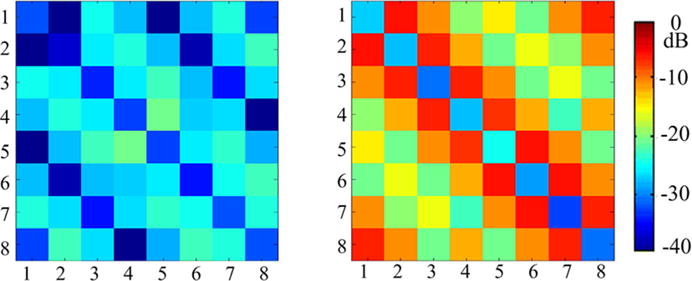
S11 and S21 measurements of the 8-channel monopole array with (left) and without (right) ICE decoupling method loaded with human head. Without decoupling treatments, mean S21 between adjacent, next adjacent and opposite elements of the monopole array was about −7.1, −11.5 and −15.6 dB, respectively, whereas the mean S21 between adjacent, next adjacent and opposite elements were reduced to −25.4, −25.1 and −40.3 dB, respectively, when the ICE decoupling method was employed. This indicates the coupling between any two monopole elements was reduced to a sufficient small value using the ICE decoupling method

For the monopole array without any decoupling treatment, the S21 between adjacent, next adjacent and opposite elements were about −7.1, −11.5 and −15.6 dB, respectively. This indicates that obvious coupling existed, which could decrease the sensitivity of the monopole elements and the capability of parallel imaging. When the ICE decoupling method was employed, the mean S21 between adjacent, next adjacent and opposite elements were about −25.4, −25.1 and −40.3 dB, respectively. This indicates that the coupling between any two monopole elements was reduced to a sufficient small value by using the ICE decoupling method. We could also find that the ICE method had excellent decoupling capability for both the non-adjacent and the adjacent elements, which is especially important for the volume array design.

Figure 3 shows the noise covariance matrices of the ICE-decoupled monopole array and the monopole array without decoupling treatments. The average noise covariance between adjacent, next adjacent and opposite elements were 13, 12 and 9 %, respectively; whereas the average noise covariance between adjacent, next adjacent and opposite elements of the monopole array without decoupling treatments were 61, 35 and 19 %, respectively. These results were consistent with the S-parameter results and also indicated the excellent decoupling capability of the ICE method for monopole array.

Fig. 3.

Fig. 3

Open in a new tab

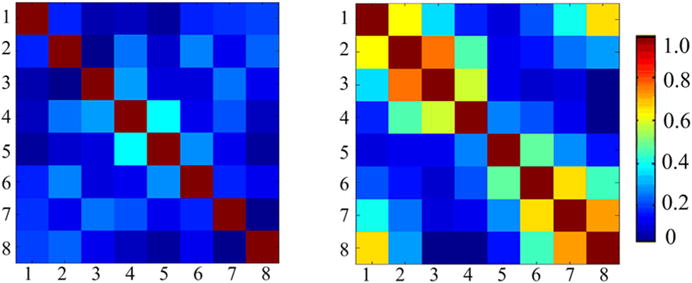
Noise covariance matrices of 8-channel monopole arrays with (left) and without ICE decoupling (right). The average noise correlations between adjacent, next adjacent and opposite elements were 13, 12 and 9 %, respectively; whereas the average noise correlations between adjacent, next adjacent and opposite elements of the monopole array without decoupling treatments were 61, 35 and 19 %, respectively

For the monopole array without decoupling methods, the average QUL and QL of a single monopole element were 9.1 and 3.0, respectively. For the ICE-decoupled monopole array, the average QUL and QL of a single monopole element were 110.2 and 33.2. The improvement of Q values was probably because of the better decoupling performance (Figs. 2, 3) and shielding effect of the decoupling elements [32].

3.2 Human Head Imaging, SNR and Parallel Imaging

Figure 4a and b show the individual GRE images acquired from each coil element and their combinations with the RSS (root-sum-of-squares) method in the transverse and sagittal planes. These human head images were acquired from a healthy volunteer using the ICE-decoupled monopole array. These images indicate that the ICE decoupling technique is feasible in designing transmit/receive monopole array for human head imaging at the ultrahigh field of 7 T. Due to the unique B1 distribution of the monopole element [14] and the shielding effect of the decoupling element [32, 33], the ICE-decoupled monopole array has sufficient SNR at both the peripheral area and the central area of the brain.

Fig. 4.

Fig. 4

Open in a new tab

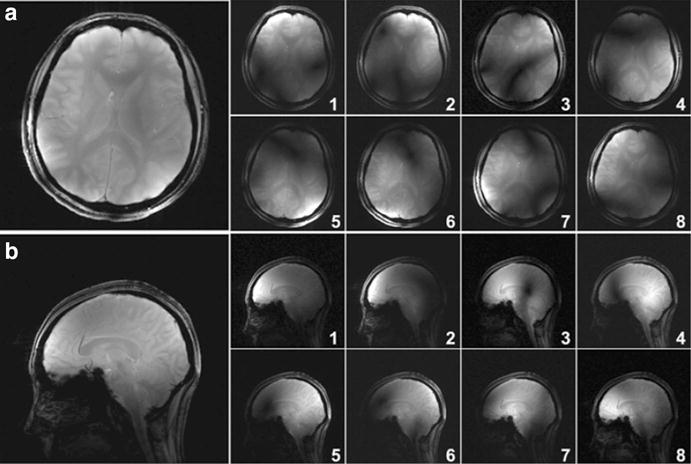
Human head GRE images acquired with a 7 T Siemens scanner using the ICE-decoupled monopole array. a Combined GRE image and individual sub-images from each coil element in the transverse plane with parameters: FA = 25 deg, TR = 120 ms, TE = 6 ms, FOV = 250 × 250 mm2, matrix = 256 × 256, slice thickness = 5 mm. b Combined GRE image and individual sub-images from each coil element in the sagittal plane using the same sequence. The ICE-decoupled monopole array has sufficient SNR at both the peripheral area and the central area of the brain. These images indicate that monopole arrays using the ICE decoupling technique are feasible for human head imaging at the ultrahigh field of 7 T

Figure 5 shows the SNR comparison of human head images for the ICE-decoupled monopole array and the monopole array without decoupling methods at 7 T. These images were reconstructed from raw data without using filters, and were shown in the same signal intensity scale. Images from individual channels were combined with RSS method. The noise areas used here were carefully chosen to avoid including artifacts. Local SNR at four peripheral areas and the central area of the brain were calculated and marked in the images. For the monopole array without decoupling methods, SNR at the central area was higher than that of the peripheral areas [14]. On the other hand, the ICE-decoupled monopole array displayed a different SNR pattern, with the SNR at the peripheral areas higher than that of the central area. This is probably because of the better decoupling performance (Figs. 2, 3) and shielding effect of the decoupling elements. Meanwhile, the ICE-decoupled monopole array kept similar SNR at the center of the brain, which is consistent with the previous work [33, 37]. An overall SNR gain of 13–80 % was achieved for the 8-channel monopole array when the ICE decoupling method was applied.

Fig. 5.

Fig. 5

Open in a new tab

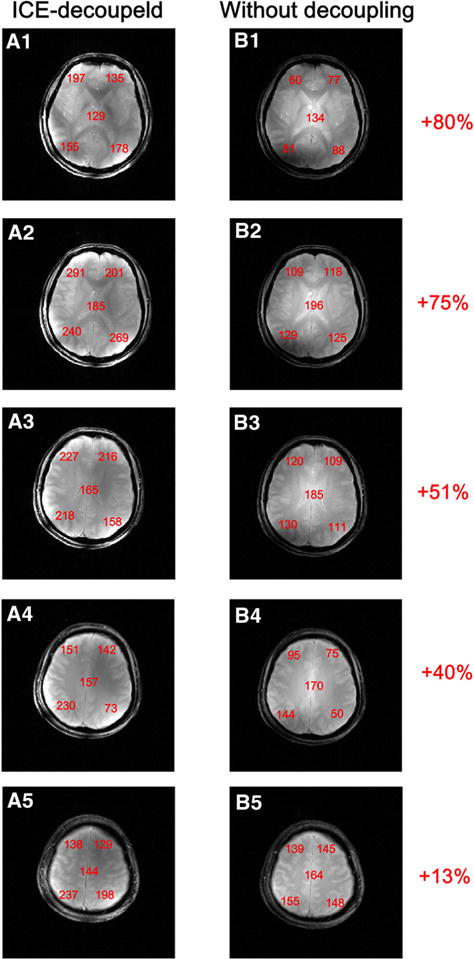
Human head GRE images acquired using the ICE-decoupled monopole array (A1–A5) and the monopole array without decoupling methods (B1–B5). The local SNR’s were measured and marked in boldface numbers. In the SNR measurements, the signals were measured from a square of 20 × 20 pixels in each of the five positions at the center and periphery of the images. An overall SNR gain of 13–80 % was achieved by using the ICE decoupling method for the 8-channel monopole array over the monopole array with no decoupling treatments

Figure 6a and d show the accelerated images of the human head with reduction factors (R) of 1 (no acceleration), 2, 3, and 4 in the sagittal plane using the ICE-decoupled monopole array and the monopole array without decoupling methods. Figure 6b and e show the residual images of the accelerated images and unaccelerated images. Residual images of the ICE-decoupled monopole array were relatively smaller than those of the monopole array without decoupling methods, indicating better parallel ability was obtained by using the ICE decoupling method. For the ICE-decoupled monopole array, the residual images were neglectable and no significant image reconstruction related noise amplifications were observed, even at a high acceleration factor of 4, as shown in Fig. 6a and b.

Fig. 6.

Fig. 6

Open in a new tab

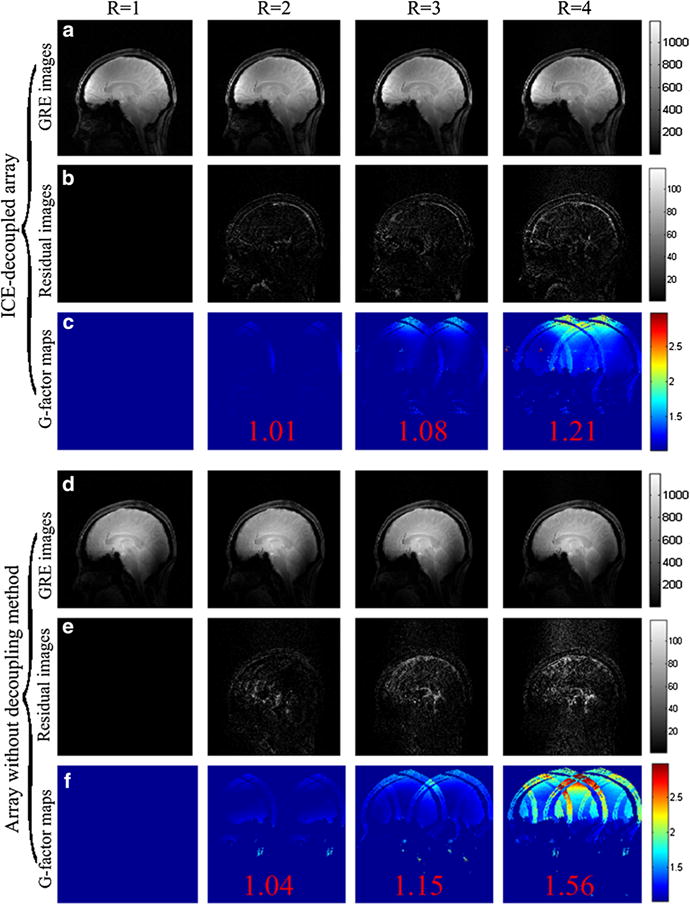
GRE images, residual images, and g-factors maps of the ICE-decoupled monopole array (a–c) and the monopole array without decoupling methods (e–f) with the acceleration factor R of 1 (no acceleration), 2, 3 and 4 in the sagittal plane. Average g-factors are marked in red color in the g-factor maps (Fig. 6c and f). The average g-factors of the ICE-decoupled monopole array with R of 2, 3 and 4 were 1.01, 1.08, and 1.21, respectively, whereas the average g-factors of the monopole array without decoupling methods with R of 2, 3 and 4 were 1.04, 1.15, 1.56, respectively. The maximum g-factors of the ICE-decoupled monopole array at R = 2, 3 and 4 were 1.35, 1.96, and 2.68, respectively, whereas the average g-factors of the monopole array without decoupling methods at R = 2, 3 and 4 were 1.43, 2.53, and 5.02, respectively. These results demonstrates that the parallel imaging capability of 8-channel monopole array was highly improved by using the ICE decoupling method

Figure 6c and f show the g-factor maps of the ICE-decoupled monopole array and the monopole array without decoupling methods with R of 2, 3, and 4. The average g-factors of the ICE-decoupled monopole array at R = 2, 3 and 4 were 1.01, 1.08, and 1.21, respectively, whereas the average g-factors of the monopole array without decoupling methods at R = 2, 3 and 4 were 1.04, 1.15, and 1.56, respectively. The maximum g-factors of the ICE-decoupled monopole array at R = 2, 3 and 4 were 1.35, 1.96, and 2.68, respectively, whereas the maximum g-factors of the monopole array without decoupling methods at R = 2, 3 and 4 were 1.43, 2.53, and 5.02, respectively. Both the average and maximum g-factors of the monopole array were highly improved using ICE decoupling method, which is consistent with the comparison of S-parameter matrices and residual images. Considering the SNR of accelerated images is inversely proportional to the g-factor [16], the g-factor results suggest that better quality-accelerated images of the monopole array can be achieved using the ICE decoupling method.

4 Discussions and Conclusion

For the eight-channel human head monopole array, the monopole elements were closely placed and the distance between the two adjacent elements is 9 cm, which is only approximately 1/10 of the wavelength at the frequency of 297.2 MHz. Without decoupling treatments, the isolation between adjacent and next adjacent elements were only −7.1 and −11.5 dB, respectively. Therefore, the electromagnetic coupling among the monopole elements was quite strong and could not be ignored.

In this study, the magnetic wall or induced current eliminated decoupling method was applied to reduce the coupling between adjacent and non-adjacent elements of the eight-channel monopole array. Eight-channel monopole array with this decoupling method was designed and constructed for human head imaging at 7 T. The feasibility of the 8-channel magnetic wall-decoupled monopole array has been validated through bench tests and in vivo MRI imaging experiments. For the ICE-decoupled monopole array, the isolation between any two monopole elements was better than −25 dB. This indicates that the ICE decoupling method could reduce the coupling between non-adjacent elements and adjacent elements to a sufficiently small value. An L-shaped capacitive network was applied and each monopole element was well matched to 50 Ω.

Compared with the monopole array without decoupling methods, the ICE-decoupled monopole array shows higher SNR at the peripheral areas and meanwhile keeps similar SNR at the central area of the brain. The overall SNR gain was in range of 13–80 % for different axial slices. This is probably due to its better decoupling performance and the shielding effect of the decoupling elements, which acts as a magnetic wall and increases the B1 field at the peripheral areas.

For the monopole array without decoupling methods, the average g-factor of human head in the sagittal plane was as high as 1.56 and obvious image reconstruction related noise amplifications were observed when the acceleration factor achieved 4. This is due to the obvious coupling among monopole elements as described above, whereas the ICE-decoupled array demonstrated excellent parallel imaging capability, with the average g-factor of only 1.21 when the acceleration factor achieves 4. The maximum g-factor was also reduced from 5.02 to 2.68 by using the ICE decoupling method. These results again indicate that high quality images could be obtained using the ICE-decoupled monopole array.

It has been demonstrated in our previous work that Q values could be improved by using ICE decoupling owing to the shielding effect of decoupling elements [32]. Unlike the MTL [28] and loop arrays [32], Q values of the 8-channel monopole array were highly improved with a factor of about 10. This can be understood that all decoupling elements contributed obvious shielding effect to each monopole element.

From the in vivo images and parallel imaging results, the ICE decoupling method has demonstrated its feasibility of designing volume-type transmit/receive monopole arrays for human head parallel imaging at ultrahigh fields. Although the ICE decoupling method is only validated for the monopole array in this work, this decoupling method would also be suitable for other kinds of radiative arrays, such as the dipole coil arrays.

Acknowledgments

This study was supported in part by the Chinese National Major Scientific Equipment R&D Project (Grant No. ZDYZ2010-2), the Ministry of Science and Technology of China Grant (2012CB825500, 2015CB351701), the National Natural Science Foundation of China Grant (51228702, 91132302), the Chinese Academy of Sciences Grants (XDB02010001, XDB02050001), and National Institutes of Health (NIH) R01EB008699 and R21EB020283.

References

  • 1.Yacoub E, Shmuel A, Pfeuffer J, Van de Moortele PF, Adriany G, Andersen P, Vaughan JT, Merkle H, Ugurbil K, Hu XP. Magn Reson Med. 2001;45:588–594. doi: 10.1002/mrm.1080. [DOI] [PubMed] [Google Scholar]
  • 2.Zhang X, Ugurbil K, Chen W. Magn Reson Med. 2001;46:443–450. doi: 10.1002/mrm.1212. [DOI] [PubMed] [Google Scholar]
  • 3.Lei H, Zhu X, Zhang X, Ugurbil K, Chen W. Magn Reson Med. 2003;49:199–205. doi: 10.1002/mrm.10379. [DOI] [PubMed] [Google Scholar]
  • 4.Zhu X, Zhang Y, Tian R, Lei H, Zhang N, Zhang X, Merkle H, Ugurbil K, Chen W. Proc Natl Acad Sci USA. 2003;100:4352. [Google Scholar]
  • 5.Ibrahim TS, Mitchell C, Schmalbrock P, Lee R, Chakeres DW. Magn Reson Med. 2005;54:683–690. doi: 10.1002/mrm.20596. [DOI] [PubMed] [Google Scholar]
  • 6.Wiggins GC, Potthast A, Triantafyllou C, Wiggins CJ, Wald LL. Magn Reson Med. 2005;54:235–240. doi: 10.1002/mrm.20547. [DOI] [PubMed] [Google Scholar]
  • 7.Zhang X, Ugurbil K, Sainati R, Chen W. IEEE Trans Biomed Eng. 2005;52:495–504. doi: 10.1109/TBME.2004.842968. [DOI] [PubMed] [Google Scholar]
  • 8.Zhang X, Zhu XH, Chen W. Magn Reson Med. 2005;53:1234–1239. doi: 10.1002/mrm.20462. [DOI] [PubMed] [Google Scholar]
  • 9.Thomas BP, Welch EB, Niederhauser BD, Whetsell WO, Jr, Anderson AW, Gore JC, Avison MJ, Creasy JL. J Magn Reson Imaging. 2008;28:1266–1272. doi: 10.1002/jmri.21576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Chang G, Deniz CM, Honig S, Egol K, Regatte RR, Zhu Y, Sodickson DK, Brown R. J Magn Reson Imaging. 2014;39:1384–1393. doi: 10.1002/jmri.24305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Hoult DI, Magn J. Reson Imaging. 2000;12:46–67. doi: 10.1002/1522-2586(200007)12:1<46::aid-jmri6>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
  • 12.Collins CM, Yang QX, Wang JH, Zhang X, Liu H, Michaeli S, Zhu XH, Adriany G, Vaughan JT, Anderson P, Merkle H, Ugurbil K, Smith MB, Chen W. Magn Reson Med. 2002;47:1026–1028. doi: 10.1002/mrm.10153. [DOI] [PubMed] [Google Scholar]
  • 13.Raaijmakers AJ, Ipek O, Klomp DW, Possanzini C, Harvey PR, Lagendijk JJ, van den Berg CA. Magn Reson Med. 2011;66:1488–1497. doi: 10.1002/mrm.22886. [DOI] [PubMed] [Google Scholar]
  • 14.Hong SM, Park JH, Woo MK, Kim YB, Cho ZH. Magn Reson Med. 2014;71:1944–1952. doi: 10.1002/mrm.24844. [DOI] [PubMed] [Google Scholar]
  • 15.Sodickson DK, Manning WJ. Magn Reson Med. 1997;38:591–603. doi: 10.1002/mrm.1910380414. [DOI] [PubMed] [Google Scholar]
  • 16.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
  • 17.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
  • 18.Lee RF, Giaquinto RO, Hardy CJ. Magn Reson Med. 2002;48:203–213. doi: 10.1002/mrm.10186. [DOI] [PubMed] [Google Scholar]
  • 19.Sodickson DK, McKenzie CA, Ohliger MA, Yeh EN, Price MD. Magma. 2002;13:158–163. doi: 10.1007/BF02678591. [DOI] [PubMed] [Google Scholar]
  • 20.Adriany G, Van de Moortele PF, Wiesinger F, Moeller S, Strupp JP, Andersen P, Snyder C, Zhang X, Chen W, Pruessmann KP, Boesiger P, Vaughan T, Ugurbil K. Magn Reson Med. 2005;53:434–445. doi: 10.1002/mrm.20321. [DOI] [PubMed] [Google Scholar]
  • 21.Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. Magn Reson Med. 1990;16:192–335. doi: 10.1002/mrm.1910160203. [DOI] [PubMed] [Google Scholar]
  • 22.Zhang X, Webb A. J Magn Reson. 2004;170:149–155. doi: 10.1016/j.jmr.2004.05.004. [DOI] [PubMed] [Google Scholar]
  • 23.Pinkerton RG, Barberi EA, Menon RS. Magn Reson Med. 2005;54:499–503. doi: 10.1002/mrm.20583. [DOI] [PubMed] [Google Scholar]
  • 24.Wu B, Zhang X, Qu P, Shen GX. J Magn Reson. 2006;182:126–132. doi: 10.1016/j.jmr.2006.04.013. [DOI] [PubMed] [Google Scholar]
  • 25.Wu B, Qu P, Wang C, Yuan J, Shen GX. Concepts in Magnetic Resonance Part B: Magnetic Resonance. Engineering. 2007;31B:116–126. [Google Scholar]
  • 26.Wu B, Wang C, Krug R, Kelley DA, Xu D, Pang Y, Banerjee S, Vigneron DB, Nelson SJ, Majumdar S, Zhang X. IEEE Trans Biomed Eng. 2010;57:397–403. doi: 10.1109/TBME.2009.2030170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Yan X, Ma C, Shi L, Zhuo Y, Zhou XJ, Wei L, Xue R. Appl Magn Reson. 2014;45:437–449. [Google Scholar]
  • 28.Li Y, Xie Z, Pang Y, Vigneron D, Zhang X. Med Phys. 2011;38:4086–4093. doi: 10.1118/1.3598112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Yan X, Xie Z, Pedersen JO, Zhang X. Concepts in Magnetic Resonance Part B: Magnetic Resonance. Engineering. 2015;45:183–190. [Google Scholar]
  • 30.Yan X, Pedersen JO, Wei L, Zhang X, Xue R. IEEE Trans Biomed Eng. 2015;62:1652–1659. doi: 10.1109/TBME.2015.2401976. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Yan X, Xue R, Zhang X. Appl Magn Reson. 2015;46:1239–1248. doi: 10.1007/s00723-015-0712-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Yan X, Zhang X, Feng B, Ma C, Wei L, Xue R. IEEE Trans Med Imaging. 2014;33:1781–1787. doi: 10.1109/TMI.2014.2313879. [DOI] [PubMed] [Google Scholar]
  • 33.Yan X, Zhang X, Wei L, Xue R. Quant Imaging Med Surg. 2014;4(2):79–86. doi: 10.3978/j.issn.2223-4292.2014.04.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Yan X, Xue R, Zhang X. Quant Imaging Med Surg. 2014;4:225–231. doi: 10.3978/j.issn.2223-4292.2014.08.03. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Yan X, Wei L, Xue R, Zhang X. Appl Magn Reson. 2015;46:541–550. doi: 10.1007/s00723-015-0656-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Yan X, Zhang X. Quant Imaging Med Surg. 2015;5:546–551. doi: 10.3978/j.issn.2223-4292.2015.07.06. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Yan X, Zhang X, Wei L, Xue R. Appl Magn Reson. 2015;46:59–66. doi: 10.1007/s00723-014-0612-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES