A continuum-mechanical skeletal muscle model including actin-titin interaction predicts stable contractions on the descending limb of the force-length relation

Abstract

Contractions on the descending limb of the total (active + passive) muscle force—length relationship (i. e. when muscle stiffness is negative) are expected to lead to vast half-sarcomere—length inhomogeneities. This is however not observed in experiments—vast half-sarcomere—length inhomogeneities can be absent in myofibrils contracting in this range, and initial inhomogeneities can even decrease. Here we show that the absence of half-sarcomere—length inhomogeneities can be predicted when considering interactions of the semi-active protein titin with the actin filaments. Including a model of actin—titin interactions within a multi-scale continuum-mechanical model, we demonstrate that stability, accurate forces and nearly homogeneous half-sarcomere lengths can be obtained on the descending limb of the static total force—length relation. This could be a key to durable functioning of the muscle because large local stretches, that might harm, for example, the transverse-tubule system, are avoided.

Author summary

Muscle force generation is a complex process depending on muscle length, activation, and other time-dependent properties. Contractions on the descending limb of the force—length relation (i. e. when the maximum isometric force decreases with increasing muscle length) are interesting, since this behaviour is expected to result in non-physiological length inhomogeneities of the muscle microstructure. Previously, different mechanisms have been suggested that could have a stabilising effect on the muscle microstructure. However, superposition of several phenomena makes it difficult to separate the influence of a single mechanism in an experimental setup. Within a model, individual phenomena can be knocked out to quantify the influence of a single process. Here we show, using a physiologically motivated model of the whole muscle, that variable mechanical properties of the large protein titin (controlled by calcium as a second messenger) can guarantee stability of the muscle microstructure during contractions on the descending limb of the force—length relation.

Introduction

The isometric active force—length relation of muscle fibres [1] and many muscles [2–4] is composed of strikingly linear segments. Based on this observation, the sarcomere microstructure, and the sliding filament theory [5, 6], a geometric model of the filament overlap has been established and validated [1], which shaped our understanding of muscle structure and functioning.

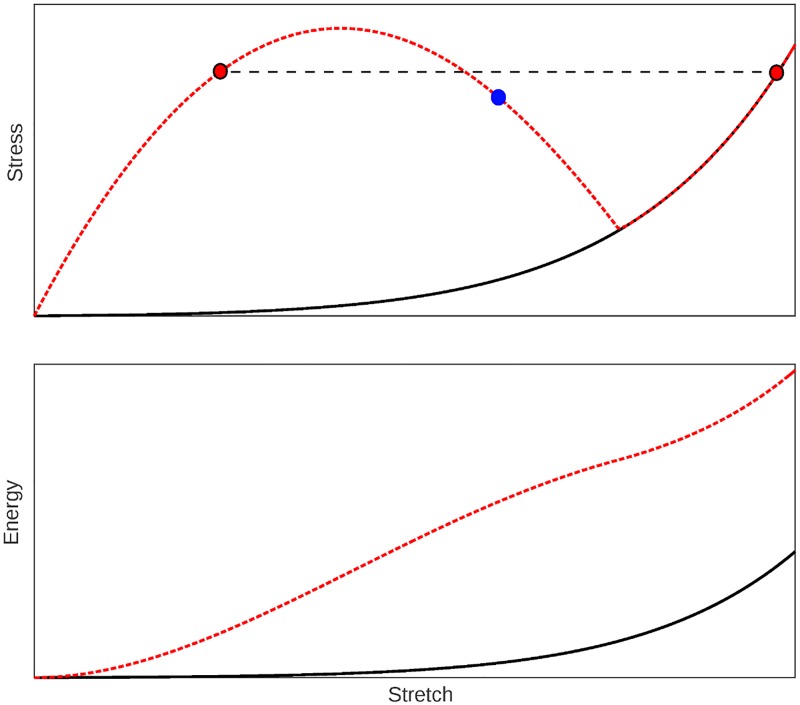
From a mechanical point of view, the negative slope of the force—length relationship at long muscle lengths (descending limb) was and is of special interest for muscle physiologists and modellers due to its inherent instability. It has been suggested early [7] that contractions on the descending limb of the force—length relation will result in unstable behaviour leading to the formation of short and long half-sarcomeres in series during fixed-length muscle contractions (cf. Fig 1 top).

Fig 1. Schematic of passive and fully activated stress–stretch relations and corresponding energy—stretch relations.

Top: Consider the case that muscle force is completely described by the passive stress (black solid curve) and total isometric stress (red dashed curve). Then, a fixed-length contraction of two in-series-arranged half-sarcomeres on the descending limb of the total stress—stretch relation (blue dot) is unstable. Small initial half-sarcomere length differences lead to a stronger, shorter half-sarcomere and a weaker, longer half-sarcomere. Hence, the short half-sarcomere will shorten further, stretching the longer half-sarcomere until static force equilibrium is established again on ascending albeit different limbs of the total stress—stretch relation (red dots). Such behaviour is not observed in experiments [8, 9]. Bottom: Passive, convex energy (black curve) and total, non-convex energy (red dashed curve).

A number of human and animal skeletal muscles work on the descending limb of the active force—length relation [10]. Moreover, passive forces in single muscle fibres [11–13] and some entire skeletal muscles, e. g. the rabbit extensor digitorum longus, extensor digitorum II, and soleus [3, 4] or the frog semitendinosus [14], appear only at lengths that correspond to the descending limb of the active force—length relation [13, 15] leading to a descending limb in the total force—length relation. Simulation of these muscles is particularly challenging using continuum-mechanical finite element models, which typically superimpose the passive stress tensor with an active stress that includes the active force—length relation [16, 17]. The descending limb of the resulting total stress—stretch relation (Fig 1 top) causes instability of these models, which explains why previous continuum-mechanical models focused on muscles with significant passive forces occurring at short muscle length, i. e., that have no descending limb in the total force—length relation [17–21].

With respect to the above described approach of superimposing passive and active stress contributions, two aspects require further consideration. First, the energy corresponding to a total stress—stretch relation with a descending limb is described by a non-convex function, cf. Fig 1 (bottom), whereas a unique solution requires convexity. Second, the force—length relation is a static muscle property and, in light of muscle contraction phenomena like force enhancement (muscle force is increased after stretch compared to the corresponding isometric muscle force at the same final length) [22–24], it should not be used as a dynamic one [25]. Thus, the force—length relation should not be interpreted as a hyperelastic stress—stretch relation.

Unstable half-sarcomere behaviour on the descending limb can be mitigated by the damping effect of the force—velocity relation [26] and might possibly even be prevented by the interaction of the semi-active protein titin with the actin myofilament [27–29]. By calcium-induced actin—titin binding within the isotropic band of the half-sarcomere, the molecular spring length of titin would dramatically reduce. This would lead to an increased passive force when the (weaker) half-sarcomere is lengthened, which may prevent the evolution of a heterogeneous half-sarcomere—length distribution and instability on the descending limb of the force—length relation.

Recently (see [30]), we included a biophysical model describing force enhancement based on actin—titin interaction [31] in a continuum-mechanical finite element model [19, 32]. The ‘sticky—spring’ model [31] assumes that, in the presence of calcium, titin’s PEVK (rich in proline (P), glutamic acid (E), valine (V), and lysine (K)) region can bind to actin. This leads to increased titin forces during and after active stretch. The resulting titin-induced half-sarcomere-based stresses have been homogenised and added to the continuum-mechanical stress tensor consisting of passive and active stress contributions. We used the proposed model to analyse muscle forces during and after active stretch starting on the plateau and the descending limb of the force—length relation by comparing the results obtained by the models with and without actin—titin interaction. In that contribution, we neglected the force—velocity relation.

In this study we demonstrate that actin—titin interactions [27–29] stabilise half—sarcomere lengths during fixed—length contractions and active stretches (neglecting inertia effects) on the descending limb of the force—length relation. Moreover, we demonstrate that the force—velocity relation does not stabilise half-sarcomeres in a similar way, as it has been discussed controversially in the past (cf. e. g. [33, 34]).

Material and methods

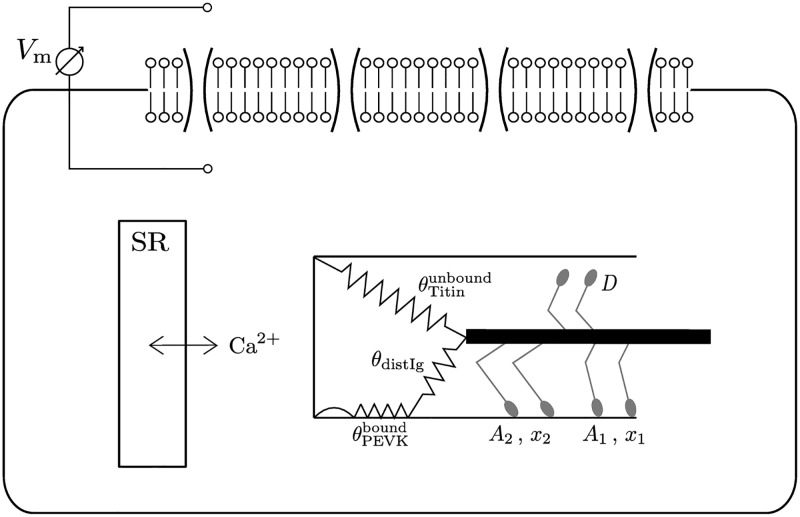
In previous work [30], we included the biophysical ‘sticky—spring’ force enhancement model [31] into our continuum-mechanical skeletal muscle modelling framework [19, 32, 35]. Since this model is also the basis of the present work, we briefly review it here. Fig 2 provides a schematic overview of the presented multi-scale skeletal muscle model.

Fig 2. Overview of the multi-scale skeletal muscle model.

Each box indicates a submodel. The coupling between the submodels is illustrated by the arrows in combination with the exchanged variables. (For further details see [19, 30, 32].)

The multi-scale muscle model

Muscles consist of muscle fibres arranged in parallel and these fibres are connected to each other laterally through the extracellular matrix, to which a significant portion of the fibre force can be transmitted [36, 37]. Thus, not only the arrangement of sarcomeres in series within a muscle fibre, but also their spatial arrangement within a muscle has to be considered to examine half-sarcomere—length inhomogeneities. Likewise, a large number of half-sarcomeres needs to be considered to obtain a statistically meaningful distribution. Consequently, a multi-scale continuum model is chosen in the present study.

The multi-scale skeletal muscle model [19, 32] embeds one-dimensional muscle fibre (finite element) meshes into the three-dimensional mesh of the muscle geometry. Note that the spatial locations of the computational half-sarcomeres, that make up the computational muscle fibres, is directly coupled to the actual (deformed) configuration of the three-dimensional continuum-mechanical model and hence enables force transmission along adjacent muscle fibres [37, 38]. The computational muscle fibres are used to compute the propagation of the action potential by solving the discrete monodomain equation [39]. The nonlinear reaction term of the monodomain equation is coupled to a model of the excitation—contraction coupling at the half-sarcomere level, describing the electro-physiology of the membrane, calcium release from the sarcoplasmic reticulum (SR), and cross-bridge cycling, cf. Fig 3. In previous works [19, 30, 32], we used a complex biophysical model [40] to simulate the excitation—contraction coupling on the cellular level. Since a detailed description of individual processes (e. g. the activity of single ion channels) is less important within the scope of this work, we replaced the biophysical model of the excitation—contraction coupling [40] with a phenomenological description of the membrane electro-physiology [41] coupled to a simplified Huxley-type model [42]. The coupling is realised by assuming that the slow variable of the phenomenological electro-physiological model [41] (a dimensionless representation of the conductance of a slow inward (repolarising) current [43]) behaves qualitatively similar to the calcium concentration in the myoplasm, which is required as input for the cross-bridge dynamics model [42]. Neglecting nearest-neighbour cooperative effects and distortion dependencies, the model predicts a linear force—velocity relation (see [42]). The linear approximation of the force—velocity relation is considered to be sufficient for the expected small range of contraction velocities due to the fact that only fixed-length contractions and quasi-static stretch experiments are considered in this work. The maximum shortening velocity of the muscle is assumed to be v_max = 15 L₀/s [3, 44], where L₀ denotes the fibre length of the resting muscle.

Fig 3. Schematic representation of the half-sarcomere model.

The half-sarcomere model consists of a phenomenological description of the membrane voltage and the intracellular calcium concentration [41], that is coupled to a simplified Huxley-type model [42] and the ‘sticky—spring’ titin model [31].

The resulting coupled model of the excitation—contraction coupling is solved at each discretisation point of the muscle fibre meshes [19]. The normalised half-sarcomere-based cross-bridge force, γ, and the binding probability of titin to bind to the actin filament, ζ, are computed from

$$\begin{array}{c}\hfill \gamma =\frac{A_1{x}_1+A_2{x}_2}{A_2^{\text{max}}{x}_0}\text{and}\zeta =\frac{A_2}{A_2^{\text{max}}}.\end{array}$$ (1)

Therein, A₁ and A₂ are the number of cross-bridges in the attached pre-power stroke and post-power stroke states, respectively, and x₁ and x₂ denote the corresponding average cross-bridge distortions. Further, $A_2^{\text{max}}$ is the number of cross-bridges in the attached post-power stroke state during an isometric tetanic contraction (stimulation frequency 100 Hz), and x₀ denotes the cross-bridge distortion induced by the power-stroke under isometric conditions [42]. While the binding probability of titin, ζ, is assumed to be independent of the contraction velocity, the cross-bridge force is a function of the half-sarcomere velocity, i. e., $\gamma =\gamma \left({\dot{l}}_{\text{hs}}\right)$. In detail, γ = 0 indicates passive behaviour, and γ = 1 corresponds to an isometric contraction at a stimulation frequency of 100 Hz. The cross-bridge force is first scaled using the relation between active force and sarcomere length (f_l) [1] and then homogenised ($T_{\mathrm{H}}:\gamma f_{\mathrm{l}}\to {\overline{\gamma f}}_{\mathrm{l}}$) to be incorporated into the continuum-mechanical stress tensor, which is evaluated at the macroscale using the discrete representation of the three-dimensional muscle geometry. The homogenisation is also performed for the binding probability of titin ($T_{\mathrm{H}}:\zeta \to \overline{\zeta }$).

Solving the balance of momentum at the macroscale, one obtains the contraction-induced deformation of the muscle geometry and the induced reaction forces. The local muscle deformation (represented by the fibre stretch, λ_f) is interpolated ($T_{\mathrm{I}}:{\lambda }_{\mathrm{f}}{l}_{\text{hs}}^{\text{ref}}\to l_{\text{hs}}$) using the shape functions of the three-dimensional finite elements to the discretisation points of the muscle fibre meshes, where they are used to evaluate the microscopic force—sarcomere length relation f_l = f_l(l_hs) [1]. In the following, we refer to these interpolated lengths as half-sarcomere lengths, l_hs. The resting half-sarcomere length in the undeformed, stress-free reference configuration (λ_f = 1) is assumed to be $l_{\text{hs}}^{\text{ref}}=1.0\mu \text{m}$ [11]. Further, the velocity is determined from the interpolated local muscle deformations, where an average over four time steps of the continuum-mechanical model (Δt_mech = 0.1 ms) is computed to increase the numerical stability.

As in our previous work [30], we additionally solve a half-sarcomere-based force enhancement model [31] (the ‘sticky—spring’ model) at the discretisation points of the muscle fibre meshes. The ‘sticky—spring’ model assumes that in the presence of calcium titin’s PEVK region can bind to the thin filament, which reduces titin’s free molecular spring length to its distal Ig (immunoglobulin) region. The model distinguishes between titin filaments that are bound to actin, and titin filaments that are not bound to actin. The stress—stretch relations of both unbound and bound titin filaments is directly obtained from fitting experimental data [45, 46]. In the model, the stress in unbound titin filaments ${\theta }_{\text{titin}}^{\text{unbound}}$ results directly from this relation, i. e. ${\theta }_{\text{titin}}^{\text{unbound}}={\theta }_{\text{titin}}^{\text{unbound}}\left(l_{\text{hs}}\right)$. The titin stresses induced by bound titin filaments is calculated by solving force equilibrium between titin’s distal Ig region and the actin—titin interconnection, i. e. θ_distIg(l_hs, l_hs[0]) = θ_PEVK(l_hs, l_hs[0]). (For further details, we refer to [31].) The ‘sticky—spring’ model assumes that the actin—titin interconnection behaves like a linear elastic spring, where the corresponding spring constant k_PEVK is a function of the half-sarcomere length at which titin was bound to actin l_hs[0]. The relation k_PEVK(l_hs[0]) was determined from numerical simulations [31]. Consequently, the stress induced by bound titin filaments depends on the actual half-sarcomere length l_hs and the half-sarcomere length at which the titin filament was bound to the thin filament l_hs[0], i. e. ${\theta }_{\text{titin}}^{\text{bound}}={\theta }_{\text{titin}}^{\text{bound}}\left(l_{\text{hs}},l_{\text{hs}}{}_{\left[0\right]}\right)$. Similar to the active stresses, the resulting titin stresses are homogenised ($T_{\mathrm{H}}:{\theta }_{\text{titin}}\to {\overline{\theta }}_{\text{titin}}$) and added to the continuum-mechanical stress tensor. The resulting macroscopic first Piola-Kirchhoff stress tensor reads

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathit{P}=& -p(det\mathit{F}){\mathit{F}}^{T-1}+{\mathit{P}}_{\text{passive}}(\mathit{F},\mathcal{M})+\hfill \\ & +{\mathit{P}}_{\text{active}}(\overline{\gamma },\mathit{F},\mathcal{M})+{\mathit{P}}_{\text{titin}}(\overline{\zeta },{\overline{\theta }}_{\text{titin}}\mathit{F},\mathcal{M}).\hfill \end{array}\end{array}$$ (2)

Therein, P_active and P_titin are the active and titin-induced stress contributions, where

$$\begin{array}{c}\hfill \begin{array}{cc}& {\mathit{P}}_{\text{active}}={\overline{\gamma f}}_{\mathrm{l}}{P}^{\text{max}}{I}_4^{-1/2}\mathit{F}\mathcal{M}\text{and}\hfill \\ & {\mathit{P}}_{\text{titin}}=[\overline{\zeta }{\overline{\theta }}_{\text{titin}}^{\text{bound}}+(1-\overline{\zeta }){\overline{\theta }}_{\text{titin}}^{\text{unbound}}]P^{\text{max}}{I}_4^{-1/2}\mathit{F}\mathcal{M},\hfill \end{array}\end{array}$$

(see [19, 30]). Further, P_passive denotes the three-dimensional, transversely isotropic, hyperelastic passive stress tensor. Note that P_passive is a smeared-out representation of the overall passive mechanical stiffness of the muscle including the extracellular connective tissue, passive contributions of the muscle fibres (e. g. cytoskeletal structures like nebulin or desmin) and matrix—fibre connectivity, but excludes the passive contribution of the titin filaments. This is realised by fitting the passive material parameters to experimental data from uniaxial compression tests, cf. [19]. Since within the scope of this publication we do not want to simulate a specific muscle we scaled the passive material properties (compared to [19, 32]) in order to obtain the property of a descending limb in the static total stress-stretch relation. Furthermore, (·)^T indicates a transposed tensor, F denotes the deformation gradient tensor, $\mathcal{M}={\mathit{a}}_0\otimes {\mathit{a}}_0$ is a structural tensor, where a₀ denotes a referential unit vector pointing in the muscle fibre direction, I₄ = a ⋅ a = Fa₀ ⋅ Fa₀ is the fourth (mixed) invariant of the right Cauchy-Green deformation tensor C = F^T F and P^max is the maximum isometric tension. Finally, p is the hydrostatic pressure that enters the equation as a Lagrange multiplier due to the incompressibility constraint [47]. Note that the active and titin-induced stresses only act along the muscle fibre direction, while rather small [30] cross-fibre contributions are not considered. For material parameters of the titin model and the continuum-mechanical model, we refer to our previous publications (for the ‘sticky—spring’ model see [31], for the continuum-mechanical model see [30]). The entire model is implemented within the open-source software library OpenCMISS [48].

Numerical simulations

To avoid influences of the geometry, a generic cubic muscle specimen with initial edge length L₀ = 1cm is considered, in which the muscle fibres are aligned with one of the edges of the cube.

For the simulations, the muscle specimen is first passively stretched to a certain length L. Then, all embedded muscle fibres are simultaneously activated (tetanic stimulation, frequency 100 Hz) in their middle, while keeping the total length of the muscle specimen fixed. Note that individual segments of the simulated muscle are not constrained and can shorten against each other. Active forces are computed by subtracting the passive forces from the total forces obtained at a certain muscle length.

For the analysis, four models are compared: (i) model ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ includes actin—titin interactions and the force—velocity relation, (ii) model M_ATI includes actin—titin interactions but omits the force—velocity relation, (iii) model M^Fv omits actin—titin interactions but includes the force—velocity relation, and (iv) model ${\text{M}}_{\text{x}}^{\text{x}}$ omits both actin—titin interactions and the force—velocity relation. In the models without actin—titin interaction, the titin-induced stresses do not vanish but describe the stresses induced by the titin filaments when they are not bound to actin, i. e., ${\mathit{P}}_{\text{titin}}={\overline{\theta }}_{\text{titin}}^{\text{unbound}}{P}^{\text{max}}{I}_4^{-1/2}\mathit{F}\mathcal{M}$.

Stability analysis

The following stability analysis considers the static equilibrium and thus neglects the force—velocity relation. In this case, γ and ζ coincide, i. e., ζ = γ, cf. Eq (1). Moreover, this analysis does not distinguish between macroscopic and microscopic quantities, i. e., $\overline{(·)}=(·)$ and $l_{\text{hs}}={\lambda }_{\mathrm{f}}=I_4^{1/2}$.

Within the theory of hyperelasticity, convexity guaranties the existence of a global minimiser and hence a unique solution. A sufficient condition for the existence of deformations minimizing a given hyperelastic potential W(F) = W(F, adj F, det F) is the polyconvexity condition:

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{{\partial }^{2}W}{\partial \mathit{F}\otimes \partial \mathit{F}}·(\mathit{H}\otimes \mathit{H})\ge 0,\hfill \\ & \frac{{\partial }^{2}W}{\partial adj\mathit{F}\otimes \partial adj\mathit{F}}·(\mathit{H}\otimes \mathit{H})\ge 0,\hfill \\ & \frac{{\partial }^{2}W}{\partial det{\mathit{F}}^2}\ge 0,\hfill \end{array}\end{array}$$ (3)

where H ≠ 0 denotes an arbitrary second-order tensor [49]. Regarding the stress tensor in Eq (2), the incompressible Mooney—Rivlin material and the anisotropic stress contribution making up for the first two terms on the right-hand side of Eq (2) are known to satisfy the polyconvexity condition (see Eq (3)) cf. [49, 50]. Further, due to the fact that the active and titin-induced stresses are not conservative, no strain energy can be defined for the last two terms on the right-hand side of Eq (2) [51, 52]. Rather than introducing pseudo-energies for these stress contributions, the definition of the first Piola—Kirchhoff stress tensor of the theory of hyperelasticity $\mathit{P}=\frac{\partial W}{\partial \mathit{F}}$ is used to eliminate the energy in Eq (3).

For the sake of readability, we introduce a short-hand notation for the active and titin-induced stress contributions:

$$\begin{array}{c}\hfill \widehat{\mathit{P}}=\widehat{S}(\gamma ,I_4)\mathit{F}\mathcal{M}={\mathit{P}}_{\text{active}}+{\mathit{P}}_{\text{titin}},\end{array}$$ (4)

where $\widehat{S}(\gamma ,I_4)$ denotes a scalar-valued function of the cross-bridge force γ and the fourth (mixed) invariant I₄. Then, the active and titin-induced stress tensors satisfy the condition of Legendre—Hadamard ellipticity if

$$\begin{array}{c}\hfill \frac{\partial \widehat{\mathit{P}}}{\partial \mathit{F}}·(\mathit{G}\otimes \mathit{G})\ge 0,\end{array}$$ (5)

where G ≠ 0 denotes an arbitrary second-order rank-one tensor, i. e., G = h ⊗ k ∀h, k.

For a given cross-bridge force $\stackrel{*}{\gamma }$ and deformation $\stackrel{*}{I_4}$ the ellipticity condition can be written as [52]

$$\begin{array}{c}\hfill 2\stackrel{*}{I_4}\frac{\mathrm{d}\widehat{S}(\stackrel{*}{\gamma },\stackrel{*}{I_4})}{\mathrm{d}{I}_4}+\widehat{S}(\stackrel{*}{\gamma },\stackrel{*}{I_4})\ge 0.\end{array}$$ (6)

To evaluate this condition, as a worst case scenario, we assume full activation ($\stackrel{*}{\gamma }=1$), such that

$$\begin{array}{c}\hfill \widehat{S}\left(I_4\right)=I_4^{-1/2}{P}^{\text{max}}[f_{\mathrm{l}}\left(I_4\right)+{\theta }_{\text{titin}}^{\text{bound}}\left(I_4\right)].\end{array}$$ (7)

Inserting Eq (7) into Eq (6), and using $I_4^{-1/2}>0,P^{\text{max}}>0$, the sum of the active and titin-induced stress tensors satisfies the rank-one ellipticity condition if

$$\begin{array}{c}\hfill \frac{\mathrm{d}{f}_{\mathrm{l}}\left(\stackrel{*}{I_4}\right)}{\mathrm{d}{I}_4}+\frac{\mathrm{d}{\theta }_{\text{titin}}^{\text{bound}}\left(\stackrel{*}{I_4}\right)}{\mathrm{d}{I}_4}\ge 0.\end{array}$$ (8)

Relation (8) states that the sum of the slopes of the active force—length relation and the titin-induced stress has to be positive for all muscle lengths. This condition is equivalent to the condition for a monotonically increasing scalar-valued function, due to the one-dimensional nature of the active and titin-induced stresses.

While the titin-induced stress ${\theta }_{\text{titin}}^{\text{bound}}$ is a monotonically increasing function [31], the active force—length relation [1] possesses a descending limb with negative stiffness. Keeping in mind that also the passive stress, which we omitted from this derivation, adds positive stiffness to the total behaviour, the result of the ellipticity condition can be interpreted as follows: the positive stiffness induced by the passive stresses and the titin-induced stresses have to compensate together for the negative stiffness on the descending limb of the force—length relation.

Results

The behaviour of the half-sarcomere model

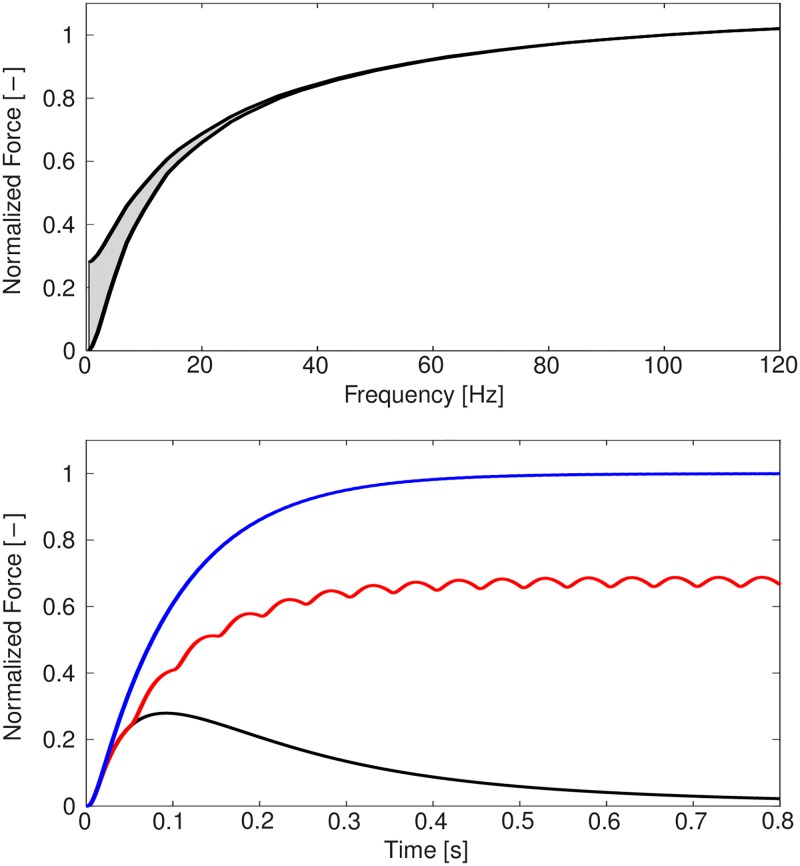
First, we demonstrate that the newly introduced phenomenological half—sarcomere model of the excitation—contraction coupling is able to reproduce the expected physiological behaviour in response to stimulation. Fig 4 shows modelled isometric force responses due to different stimulation frequencies (top) and the model’s force—frequency relation (bottom). It can be observed that the model predicts a physiological twitch shape, twitch summation, and twitch-tetanus ratio.

Fig 4.

Top: Isometric force responses of the microscopic half-sarcomere model due to different stimulations. Single—twitch (black), submaximal contraction at 20 Hz (red), and tetanic contraction at 100 Hz (blue). Bottom: Force—frequency relation of the half-sarcomere model. Under conditions of not completely fused twitches, the range between the minimum and maximum values of the active force is shown.

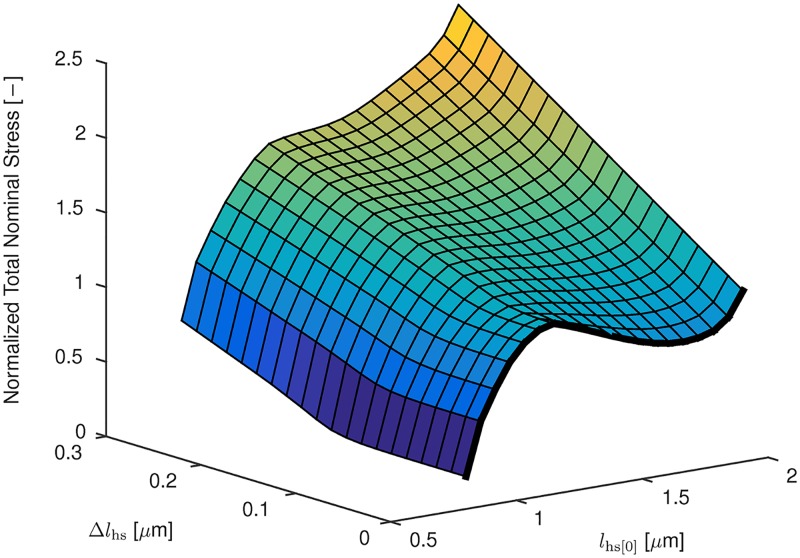
Next, the quasi-static behaviour of the microscopic half-sarcomere model with actin—titin interaction is considered in isolation. To this end, isometric contractions have been carried out at different half-sarcomere lengths, l_hs[0]. Moreover, for different initial half-sarcomere lengths, l_hs[0], i. e., the half-sarcomere lengths at which the activation started, quasi-static (i. e. the force—velocity relation was omitted) active stretch experiments have been performed for different active stretch increments, Δl_hs = l_hs − l_hs[0]. The results are summarised in a three-dimensional surface plot in Fig 5. While the relation between the total stress in a half-sarcomere and l_hs[0] (i. e., the total isometric force—length relation; thick black line in Fig 5) is not monotonically increasing, the total stress increases monotonically with the active stretch increment. In other words, the partial derivative of the total stress with respect to the active stretch increment is always positive, although the static total stress—stretch relation has a descending limb.

Fig 5. Total stress of the half-sarcomere model with actin—titin interaction versus the half-sarcomere length at which activation started, l_hs[0], and the active stretch increment, Δl_hs.

The thick black curve at the right edge of the surface corresponds to the static total stress—stretch relation shown in Fig 8 (top).

Fixed-length contractions

Having established the behaviour of the microscopic half-sarcomere model, macroscopic whole-muscle simulations are investigated in the following. Fixed-length contractions at different muscle lengths have been carried out using the previously described four models, namely the ${\text{M}}_{\text{ATI}}^{\text{Fv}}$, M_ATI, M^Fv, and ${\text{M}}_{\text{x}}^{\text{x}}$ models. Fig 6 compares the resulting active force—length relations. Models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI reproduce the force—sarcomere length relation as proposed in [1] at the macroscopic whole muscle level, while models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$ predict similar forces on the ascending limb and the plateau but deviating forces on the descending limb. In fact, there is a striking agreement between the stretch regions corresponding to the descending limb of the total stress—stretch relation and the occurrence of deviations from the expected linear force decrease in the models without actin—titin interaction (${\text{M}}_{\text{x}}^{\text{x}}$, M^Fv). This analysis compares results after 2.5 seconds simulation time. At this time, transient effects caused by the force—velocity relation have disappeared and models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$ predict similar results. At the very end of the descending limb of the total force—length relation and beyond (L/L₀ > 1.6), the forces induced by bound titin filaments had to be relaxed by up to 25% to obtain convergence of models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI. This can be explained by the large stiffness of the bound titin filaments at these lengths (cf. Fig. B1(A) of [31]) leading to numerical problems.

Fig 6. Isometric active force—length relations of the different models.

Models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI reproduce the force—length relation as proposed in [1] that is included at the half-sarcomere level of all models. Models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$ predict different forces on the descending limb. Under steady-state conditions (after 2.5 s) the results of models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$, as well as those of models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI, coincide.

To further investigate the origin of the different behaviours of the models, Fig 7 shows the distribution of half-sarcomere lengths within the muscle specimen in fixed-length contractions at different muscle lengths after 2.5 seconds. While almost homogeneous half-sarcomere—length distributions are predicted by models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI for all muscle lengths, the models without actin—titin interaction predict homogeneous half-sarcomere—lengths only on the plateau and for very long muscle lengths, and strongly heterogeneous distributions on the descending limb of the total force—length relation.

Fig 7. Distribution of half-sarcomere lengths, l_hs, in the cubic muscle specimen for different muscle lengths ranging from L/L₀ = 1.1 to 1.7 during fixed-length contractions of models ${\text{M}}_{\text{x}}^{\text{x}}$, M^Fv, M_ATI, and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$.

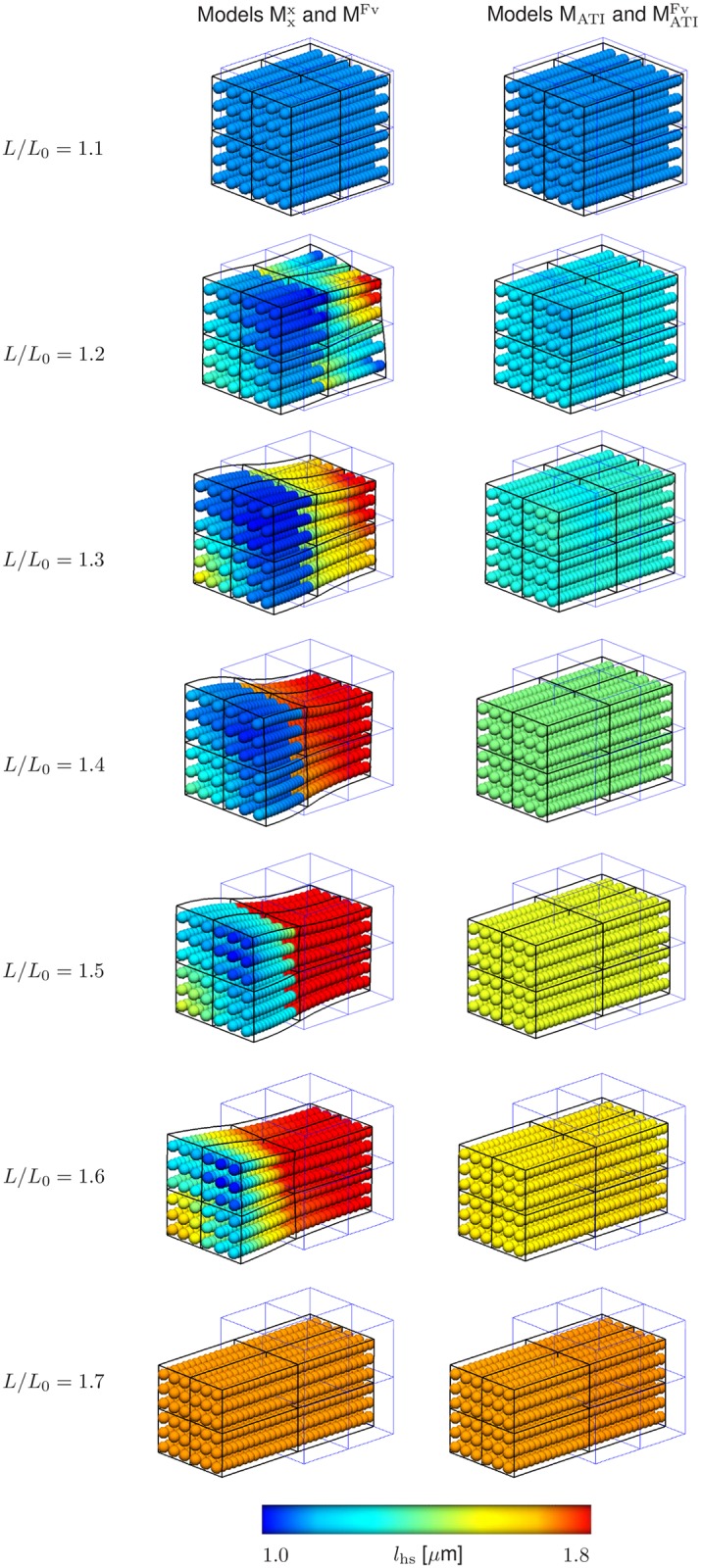
Results after 2.5 s are displayed (steady-state conditions), where the results of models ${\text{M}}_{\text{x}}^{\text{x}}$ and M^Fv (left), as well as those of M_ATI and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$(right) coincide.

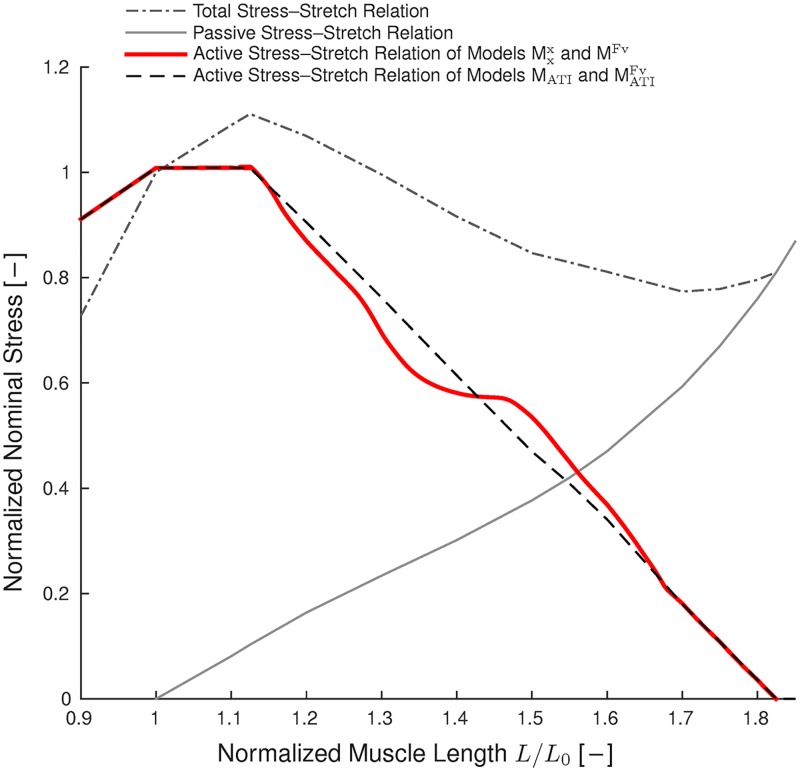
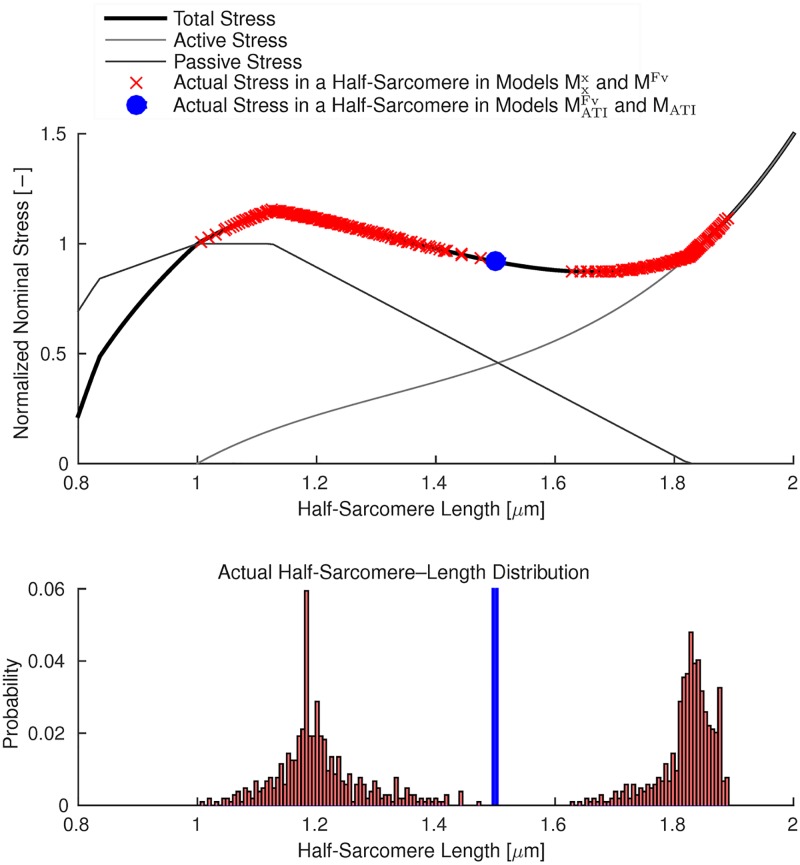
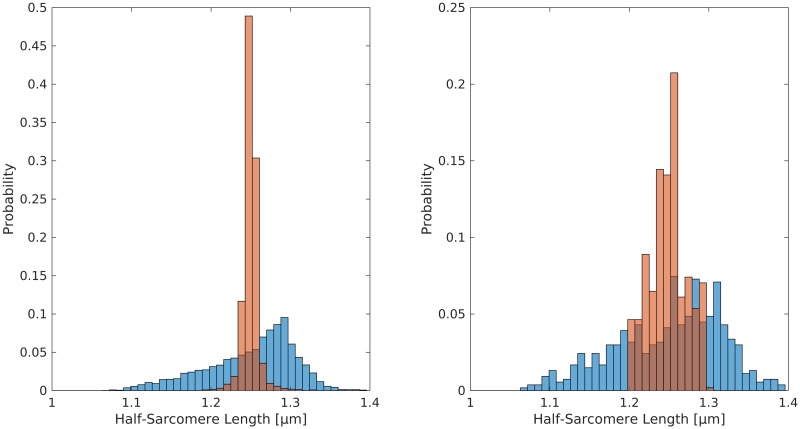
For the simulation with L/L₀ = 1.5, Fig 8 (top) shows the stresses obtained with models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI (blue dot) and the distributions of half-sarcomere lengths obtained with models ${\text{M}}_{\text{x}}^{\text{x}}$ and M^Fv (red crosses) superimposed on the total force—length relation. Under steady-state conditions (after 2.5 s), the models without actin—titin interactions (M^Fv, ${\text{M}}_{\text{x}}^{\text{x}}$) predict identical half-sarcomere length distributions that significantly deviate from the expected value of 1.5 μm. In detail, models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$ predict half-sarcomere lengths ranging from 1.0 μm to 1.9 μm, cf. Fig 8 (bottom).

Fig 8.

Top: Total, active, and passive force—length relations. Superimposed on the total stress curve are, for a muscle length of L/L₀ = 1.5, the half-sarcomere lengths predicted by models ${\text{M}}_{\text{x}}^{\text{x}}$ and M^Fv (red crosses), and models M_ATI and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ (blue dot). The value predicted by models M_ATI and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ coincides with the theoretically predicted stress—stretch value. Bottom: Histogram of half-sarcomere lengths in models ${\text{M}}_{\text{x}}^{\text{x}}$ and M^Fv (red), and models M_ATI and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$(blue, scaled for readability). Under conditions of steady state (after 2.5 s), the results of models ${\text{M}}_{\text{x}}^{\text{x}}$ and M^Fv, as well as those of models M_ATI and ${\text{M}}_{\text{ATI}}^{\text{Fv}}$, coincide.

Summarising the results shown in Figs 6, 7 and 8, a homogeneous half-sarcomere length distribution and active forces that are in accordance with the isometric force—length relation can only be obtained on the descending limb of the total force—length relation, when actin—titin interactions are included in the model. Further, it can be observed that the force—velocity relation cannot prevent the formation of half-sarcomere length inhomogeneities (models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI, and likewise models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$, predict similar results under steady-state conditions).

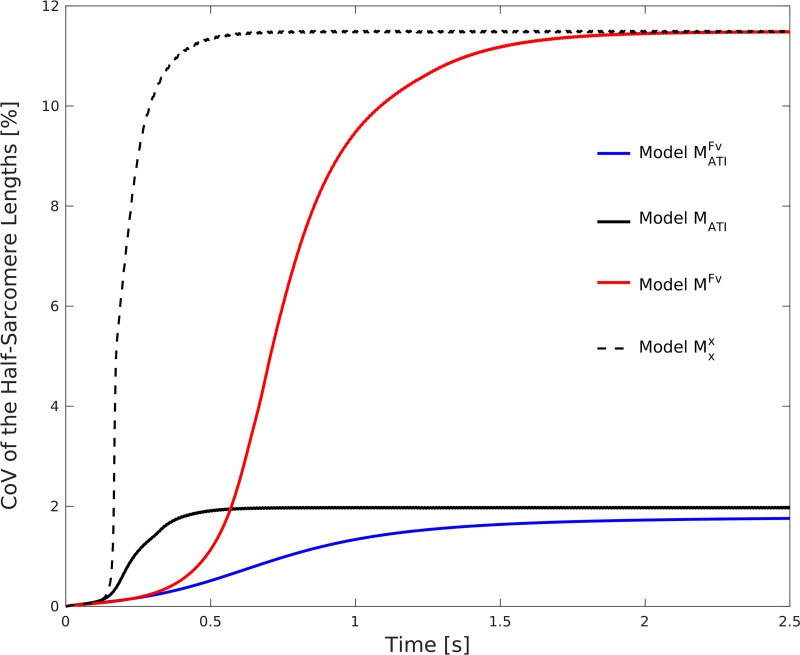
The previous results in this section considered steady-state results after 2.5 seconds, when transient effects caused by the force—velocity relation have disappeared. Fig 9 shows that the force—velocity relation delays the development of half-sarcomere—length heterogeneities. Note that the steepness of the force—length relation determines the rate of formation of half-sarcomere length heterogeneities, i. e. a steeper force—velocity relation decelerates the development of heterogeneities. For this analysis, the simulation with L/L₀ = 1.2 is considered, in which inhomogeneities develop more slowly then at longer muscle lengths. While model ${\text{M}}_{\text{x}}^{\text{x}}$ predicts a high coefficient of variation (CoV; standard deviation/mean*100%) of the half-sarcomere lengths for the entire simulation time, the heterogeneities in model M^Fv appear only gradually but eventually reach the same high level. In contrast, model M_ATI predicts a constantly low coefficient of variation of the half-sarcomere lengths.

Fig 9. Coefficient of variation (CoV; standard deviation/mean*100%) of the half-sarcomere lengths during an isometric contraction at muscle length L/L₀ = 1.2, for models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ (blue line), M^Fv (red line), M_ATI (black solid line) and ${\text{M}}_{\text{x}}^{\text{x}}$ (black dashed line).

While actin—titin interactions can damp the magnitude of half-sarcomere—length heterogeneities, the force-velocity relation damps the their temporal evolution.

Active stretch experiments

In order to test if the proposed model can predict the experimentally observed reduction in the half-sarcomere—length heterogeneity after active stretch [9], the previous model is slightly modified. To obtain an initially inhomogeneous distribution of the half-sarcomere lengths, we either introduced heterogeneous passive material properties or assumed that the maximum number of available cross-bridges per half-sarcomere shows random fluctuations. This was realised by scaling the corresponding material parameters (either the two isometric Mooney-Rivlin parameters and the two anisotropic parameters, or the maximum isometric force P_max, for further details see [30]) in each finite element with a random value from a normal distribution with mean one and a standard deviation of 0.025. For both model variants, the initial passive stretch and the subsequent fixed-length contraction (phases I and II, Fig 10) yielded heterogeneous half-sarcomere lengths. For the model variant with variable passive properties the mean ± standard deviation of the half-sarcomere length distribution were 1.05 ± 0.01 μm. For the model variant with variable active properties the mean ± standard deviation of the half-sarcomere length distribution were 1.05 ± 0.03 μm. To verify that the linear approximation of the force—velocity relation is justified, the maximum shortening and lengthening half-sarcomere velocities occurring in these simulations have been analysed. They are in the range of |v| < 0.25 v_max.

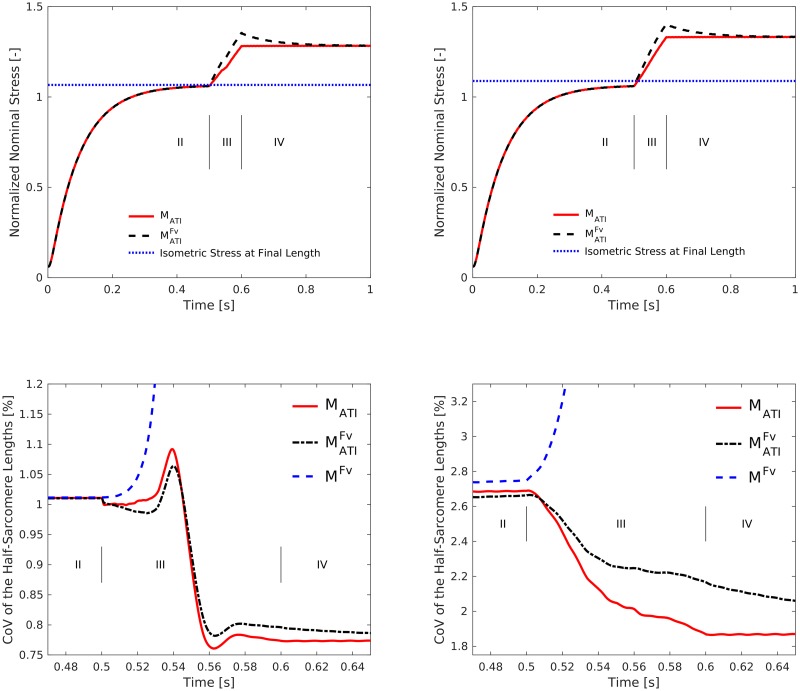
Fig 10. Active stretch experiments.

Initial half-sarcomere length inhomogeneity is introduced via variation of passive (left column) and active (right column) material properties (see text). Top: Total stress evolution in models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ (black dashed line) and M_ATI (red line) following a protocol of passive stretch from L/L₀ = 1.0 to 1.05 (phase I, i.e., computing the passive stretch as shown in Fig 6), full activation at fixed length (phase II), active stretch at a velocity of v/v_max = 13.3% from L/L₀ = 1.05 to 1.25 (phase III), and subsequent fixed-length contraction (phase IV). Additionally, the stress resulting from a fixed-length contraction (model ${\text{M}}_{\text{ATI}}^{\text{Fv}}$) at the same final length L/L₀ = 1.25 is shown (blue dotted line). The kink in the red line during the active stretch marks the transition from the plateau to the descending limb of the force—length relation. Note that we excluded stresses from models M^Fv and ${\text{M}}_{\text{x}}^{\text{x}}$ from these figures, since these models cannot reproduce the expected forces on the descending limb (previously shown, see e. g. Fig 6). Bottom: Coefficient of variation (CoV, standard deviation/mean*100%) of the half-sarcomere lengths corresponding to the above stretch experiments.

When modifying passive (Fig 10 left column) or active (Fig 10 right column) material properties, active stretch experiments show qualitatively similar results for total stresses (Fig 10 top row) and the evolution of the coefficient of variation (CoV) of the half-sarcomere lengths (Fig 10 bottom row) in models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$, M_ATI, and M^Fv. The transient differences between models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI during and after the active stretch (phases III and IV) are caused by velocity-dependent effects. The differences (force enhancement) between the stresses of models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI compared to the stress of of a fixed length reference contraction (blue dotted line) at the same final length after 1 s (Fig 10 top) are evoked by actin—titin interactions (phase IV). The simulations of the model variant with distributed active properties show a higher magnitude of (residual) force-enhancement. This can be explained by the higher half-sarcomere length heterogeneity for the simulations with this model variant (cf Fig 10 bottom) and the resulting higher titin forces. When including actin—titin interactions, i. e. for models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI, active stretch reduced significantly the CoV of the half-sarcomere lengths (cf. Fig 10 bottom). During phases III and IV, the CoV of the half-sarcomere lengths reduced by approximately 25% compared to its value before the active stretch. This behaviour deviates clearly from simulations with model M^Fv, where the CoV of the half-sarcomere lengths monotonously increases first moderately and then rapidly to more than 20.

For both model variants, i. e. with either heterogeneous active or heterogeneous passive material properties, the CoV of the half-sarcomere lengths for models ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ and M_ATI is not strictly decreasing and shows for all simulations parts with a positive time derivative (or at least equal zero). This behaviour is a consequence of the model assumption that the mechanical titin properties are more uniformly distributed than the passive and/or active material properties, i. e. in general the CoV of the half-sarcomere lengths decreases when the time derivative of the homogeneous distributed forces is greater than the time derivative of the heterogeneous distributed forces.

Moreover, Fig 11 compares the final distribution of the half-sarcomere lengths resulting from the active stretch simulation (L/L₀ = 1.05 to 1.25) of model ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ with variable passive material parameters (cf. Fig 11 left) and variable active material parameters (cf. Fig 11 right) to the distribution of half-sarcomere lengths of a fixed-length contraction at L/L₀ = 1.25 (blue). For both model variants the half-sarcomere lengths are less heterogeneously distributed after an active stretch than for a fixed length contraction at the same final length.

Fig 11. Histogram of half-sarcomere lengths in model ${\text{M}}_{\text{ATI}}^{\text{Fv}}$ with distributed material properties after an active stretch from L/L₀ = 1.05 to 1.25 (red) and after a fixed-length contraction at the same final length L/L₀ = 1.25 (blue).

This figure compares steady-state results, i. e. transient effects of the force-velocity relation have disappeared. Left: Variable passive properties, right: Variable active properties.

Thus, under the assumption that the material properties of titin are more homogeneously distributed than the passive and/or active material properties, the model can predict and explain, based on actin—titin interaction, the experimentally observed reduction in the half-sarcomere length heterogeneity after active stretch [9].

Discussion

We analysed the effect of actin—titin interactions and the force—velocity relation on half-sarcomere lengths and muscle force during fixed-length muscle contractions and active stretches. Static convexity analysis revealed that the total stress—stretch relation including passive, active, and force enhancement-related contributions has to be monotonically increasing to obtain stability, and this prediction was confirmed by the numerical experiments. Thus, actin—titin interactions can be sufficient to obtain stable half-sarcomere operation, i. e. a nearly homogeneous half-sarcomere—length distribution, on the entire descending limb of the active force—length relation, and lead to active isometric forces in accordance with the descending limb of the classic force—length relation (Fig 6). In contrast, if actin—titin interaction is not included in the model, homogeneous half-sarcomere—lengths and active isometric forces in accordance with the descending limb of the force—length relation are generally not obtained, and unstable behaviour is observed during fixed-length contractions at lengths corresponding to the descending limb of the total force—length relation. The force—velocity relation can delay but not prevent the development of heterogeneities in the half-sarcomere length, and steady-state results coincide with those of the models without the force—velocity relation. The latter finding holds for both, models that include and models that do not include actin—titin interactions.

In the present paper, a simple cubic muscle without pennation was considered to minimize the potential influence of the muscle geometry [16, 53] on sarcomere lengths of adjacent muscle fibres and thus on our results. Thus, more homogeneous sarcomere lengths in adjacent muscle fibres can be expected from our model simulations (see Fig 7). In real muscle, complex geometries, which include, for example, elastic aponeuroses functioning as attachment areas for muscle fibres, various pennation angles, and different muscle compartments [54–56], might lead to different lengths of adjacent muscle fibres. These length differences will be much more pronounced during active contractions coupled with three-dimensional muscle deformation, changes in pennation angle, as well as storage and release of elastic energy due to the deformation of an aponeurosis in longitudinal and transversal direction. Recently, heterogeneous length changes along the fascicles of human medial gastrocnemius were reported during submaximal plantar flexion [57]. Due to the extracellular matrix (ECM), which provides elastic linkages between adjacent muscle fibres [58], local differences in the length of these adjacent fibres might result in development and transmission of local forces along the muscle fibre direction. Local forces in fibre direction can affect sarcomere length changes in general and thus can elevate or limit half-sarcomere length inhomogeneities. For example, in our model, the passive elastic properties led to coupling of half-sarcomere lengths, which can be observed in Fig 7 (left), where regions of distinct, relatively homogeneous half-sarcomere lengths developed during contractions at intermediate lengths (1.2–1.6 μm). In summary, more complex muscle geometries might additionally influence sarcomere inhomogeneities on the descending limb of the force-length relation. To address this issue, implementation of more complex muscle architectures are required in future studies. However, modelling more complex geometries is straight forward within this finite element framework [35].

The distribution of half-sarcomeres during a fixed-length contraction at a length corresponding to the descending limb of the total force—length relation depends on the structure of the preparation and on the model. When considering a preparation consisting of only half-sarcomeres in series (e. g. a myofibril) and neglecting actin—titin interaction, half-sarcomeres would aggregate at two points on ascending albeit different limbs of the total force—length relation exhibiting the same total stress (Fig 1 top). The number of short and long half-sarcomeres would not be unique, and the distribution of the short and the long half-sarcomeres along the myofibril would be arbitrary. Since the continuum-mechanical model accounts additionally for transverse forces connecting the myofibrils and muscle fibres to each other in lateral directions, the half-sarcomere lengths obtained from simulations without actin—titin interaction are more diverse (Fig 7 left), and their frequency distribution shows two accumulation zones (Fig 8 bottom). Contrary to a myofibril, longer and shorter half-sarcomeres are grouped together in a muscle (Fig 7 left) due to forces of the passive matrix.

The calcium-induced binding of titin’s PEVK region to the actin filament reduces the molecular spring length of the titin filament, which significantly increases the passive stiffness of the half-sarcomere and yields a positive overall stiffness on its entire range of operation (including the entire descending limb of the active force—length relation, cf. Fig 5). The increased stability of the models including actin—titin interaction, which causes a homogeneous distribution of the half-sarcomere lengths in these models, can be attributed to the absence of a region with negative stiffness. Thus, the source of the theoretical instability, namely the imbalance between serially-arranged stronger (shorter) half-sarcomeres and weaker (longer) half-sarcomeres on the descending limb of the total force—length relation (cf. Fig 1), is absent in the models including actin—titin interactions (cf. Figs 6 and 7 right).

Further, actin—titin interaction leads to homogenisation of initially inhomogeneous half-sarcomere lengths during active stretch on the descending limb of the total force—length relationship in our models (Figs 10 and 11), an effect consistent with literature [9]. Assuming homogeneous titin properties across sarcomeres, bound titin is stiffer in initially longer half-sarcomeres [31]. (This result of the titin model is in accordance with recent muscle fibre experiments [59]). Hence, in subsequent stretches, titin forces increase disproportionately in half-sarcomeres, which are initially longer. This leads to disproportionate elongation of initially shorter half-sarcomeres and homogenisation of half-sarcomere lengths during active stretch compensating for initial inhomogeneities.

Within the scope of our study, the force—velocity relation delayed but did not prevent the development of half-sarcomere—length inhomogeneities on the descending limb of the total force—length relation (Fig 9). Thus, in general, the effect of actin—titin interaction on stability is different than that of the force—velocity relation. However, the force—velocity relation might stabilize the system for a short time (less than 0.5 s in our model, cf. Fig 9). The exact time, however, depends on the steepness of the force—velocity relation—steeper relations (lower values of v_max) damp the system more effectively. We used a linear force—velocity relation, which is a reasonable approximation within the scope of the considered fixed-length contractions and quasi-static stretches.

The sarcomere—length non-uniformity theory [60–63] proposes that series—arranged (half-)sarcomeres can develop non-uniform lengths in muscle contractions due to the unstable behaviour on the descending limb of the force—length relation. Applying stretches beyond the plateau region of the force—length relation to a model of such half-sarcomeres in series resulted in non-uniform half-sarcomere lengths, and the subsequent isometric forces deviated from the theoretical sarcomere force—length relation [64], cf. Figs 6 and 7 (left). With the assumption of variations in the properties of half-sarcomeres within a myofibril (for example, strong and weak half-sarcomeres), this theory can also predict non-uniform half-sarcomere lengths and deviating forces in the range of the plateau region of the force—length relation.

However, the existence of sarcomere—length inhomogeneities in real muscle and predictions based on the sarcomere—length non-uniformity theory are a matter of debate [60, 65, 66]. A series of studies reported sarcomere—length inhomogeneities in myofibrils and muscle fibres after stretch [67–70] or even during fixed-length tetanic contractions [61]. In contrast, it has been reported that sarcomeres produce no instabilities on the descending limb [71]. Furthermore, it has been observed that, following stretch, half-sarcomere lengths were perfectly stable and sarcomere—length inhomogeneities were even reduced [9]. While the former results are in accordance with our simulations neglecting actin—titin interactions, the latter results are in accordance with our simulation results when including actin—titin interactions. Hence, actin—titin interaction might be particularly important for stable operation of muscles working on the descending limb of the force—length relation. Moreover, history- and activation-dependent actin—titin interactions can explain the phenomenon of force enhancement more completely than the sarcomere—length inhomogeneity theory [31] (especially forces exceeding the maximum isometric force by large amounts, e. g. [59, 72]).

The presumption that instabilities might exist on the descending limb results from generalising the force—length relationship (which is a static muscle property determined by a set of isometric experiments at different muscle lengths) to dynamic contractions. Many theoretical considerations and recent studies, for example, using Hill-type or continuum-mechanical muscle modelling, are based on this presumption by default. In view of the cited contradictory results with respect to the occurrence of sarcomere—length inhomogeneities in muscle contractions, this seems illicit at least for a subset of muscles. In fact, many experiments on whole muscle preparations [22, 73], isolated muscle fibres [9, 74, 75], and even single sarcomeres [76] reveal that the steady-state force following active stretch (when transient, velocity-dependent forces have vanished) on the plateau and the descending limb of the force—length relationship is higher than the force resulting from an isometric contraction at the same final length. This history-dependent behaviour, called (residual) force enhancement [22–24, 75], might be attributed to activation-dependent behaviour of the titin filament [27–29, 31, 66].

Taking all the available experimental findings into account, we conclude that, although there might be a descending limb in the isometric total force—length relation of a half-sarcomere/muscle, a half-sarcomere of a muscle exhibiting history-dependent effects never experiences negative stiffness (cf. the forces resulting from an active stretch increment in Fig 5), and thus instabilities and half-sarcomere heterogeneities are neither expected nor observed in such muscles [71]. Thus, the validity of mathematical models using hyperelastic stress—stretch relations that are based on the isometric force—length relationship describing these muscles has to be questioned.

Conclusion

Our simulations show that actin—titin interactions can enable stable half-sarcomere operation on the descending limb of the active force—length relation during fixed-length muscle contractions and active stretches. Moreover, it has been demonstrated that the force—velocity relation can delay but not prevent the development of half-sarcomere length heterogeneities. Thus, actin—titin interactions and the force—velocity relation affect the stability of the system differently. It may be speculated that a key function of actin—titin interaction is to enable stable, predictable half-sarcomere operation avoiding large local stretches—that may for example damage the T-tubule system—for muscles working through the entire range of the force—length relation.

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

Support was provided by the European Research Council (ERC) under the European Union’s Seventh Framework Program (FP7/2007-2013) ERC grant agreement n° 306757, https://erc.europa.eu/. Moreover, the authors TH and OR would like to thank the German Research Foundation (DFG) for the financial support of the project within the Cluster of Excellence in Simulation Technology (EXC 310/1) at the University of Stuttgart, http://www.dfg.de/en/. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.