RIFS: a randomly restarted incremental feature selection algorithm

Abstract

The advent of big data era has imposed both running time and learning efficiency challenges for the machine learning researchers. Biomedical OMIC research is one of these big data areas and has changed the biomedical research drastically. But the high cost of data production and difficulty in participant recruitment introduce the paradigm of “large p small n” into the biomedical research. Feature selection is usually employed to reduce the high number of biomedical features, so that a stable data-independent classification or regression model may be achieved. This study randomly changes the first element of the widely-used incremental feature selection (IFS) strategy and selects the best feature subset that may be ranked low by the statistical association evaluation algorithms, e.g. t-test. The hypothesis is that two low-ranked features may be orchestrated to achieve a good classification performance. The proposed Randomly re-started Incremental Feature Selection (RIFS) algorithm demonstrates both higher classification accuracy and smaller feature number than the existing algorithms. RIFS also outperforms the existing methylomic diagnosis model for the prostate malignancy with a larger accuracy and a lower number of transcriptomic features.

Introduction

Modern biological technologies are rapidly revolutionized and improved in the recent years, and the biological OMIC data has been accumulated at an accelerated speed¹. Human complex disease like cancers and cardiovascular diseases are known to be associated with more than one genetic factor^2,3 and the classic single-factor correlation analysis tends to detect statistically significant factors⁴. So the existing complex disease diagnosis panels usually use the genetic information of multiple genes^5,6.

The development of a disease diagnosis panel relies on the efficiency of the feature selection technologies⁷. A biological OMIC technology generates thousands or even millions of data entries for a single sample, but a biomedical project seldom recruited more than 1,000 samples due to various limitations, e.g. cost and patient availability⁸. The biomarker screening procedure may generate the overfit models due to the paradigm of “large p, small n”, where p and n are the numbers of features and samples, respectively^9,10. Besides the aforementioned statistical reason, biomedical research results also show that not all the genes are biologically involved in a given disease onset and development processes¹¹.

It is a computationally infeasible task to find a global optimal feature subset within a reasonable period¹², and the existing feature selection algorithms may be roughly grouped as filter and wrapper approximate algorithms^13,14. A filter algorithm evaluates each feature’s association with the class label using a statistical significance measurement¹⁵. Many biomedical biomarker were screened by the filter algorithms due to their linear time requirement, and sometimes is the only choice for large datasets like SNP and methylation polymorphisms^16,17. But a filter algorithm only ranks the features by single-feature associations with the class labels, and the user is responsible for choosing the number of top-ranked features¹⁸. A wrapper algorithm evaluates each heuristically selected feature subset using a classification algorithm and tends to achieve better classification performance than the filters since a wrapper algorithm directly optimizes the target classification algorithm. A wrapper usually runs much slower than a filter algorithm, due to its consideration of inter-feature relationships¹⁹.

This study proposed a modified incremental feature selection strategy for the filter algorithms. An Incremental Feature Selection (IFS) algorithm evaluates the classification performance of the top-k-ranked features iteratively for k ∈ (1, 2, …, n), where n is the total number of features. IFS usually stops at the first observation of performance decrease^13,20. This study proposes an IFS strategy by selecting features incrementally from a randomly-chosen starting feature and output the best solution from multiple Randomly re-started IFS (RIFS) procedures. The comparison with the existing filters and wrappers demonstrates that RIFS outperforms them by both higher classification accuracies and smaller feature numbers.

Material and Methods

Binary classification problem

This study evaluates a feature subset using the binary classification performance. A binary classification problem has two groups of samples, i.e. the Positive (P) and Negative (N) samples^13,21. P and N are also used to denote the numbers of positive and negative samples. The binary classification problem is the simplest classification model, and usually a heuristic rule was employed to find the solution. And this is also the most widely adopted problem setting for biomedical researchers, e.g. disease versus control samples in the Genome-Wide Association Study (GWAS)²², and the samples of two phenotypes in the clinical survival analysis²³, etc.

Two groups of feature selection algorithms

This study compares the proposed algorithm with two major groups of feature selection algorithms, i.e. filters and wrappers^24–26. Three filters, i.e. T-test based ranking (Trank)²⁷, false positive classification rate (FPR)²⁸, and Wilcoxon-test based ranking (Wrank)²⁹, are evaluated when they select the same numbers of features as to the proposed algorithm in this study. Wrappers can directly recommend a list of features without the user-determined number of features³⁰. Three wrappers, i.e. Lasso, Random Forest (RF) and Ridge Regression (Ridge), were compared with RIFS in this study. So this study investigated both the classification performances and the numbers of features for these feature selection algorithms. Two of the algorithms, Trank and Wrank, are from the Python scipy package, and all the other algorithms are from the Python scikit-learn package. Wrapper algorithms may achieve differently using different parameters. We assume that the default parameters of a wrapper algorithm should work well in most cases. To carry out a fair comparison, the RIFS’s parameters were optimized over four datasets ALL1/ALL2/ALL3/ALL4, and this study conducted the comprehensive comparison between RIFS and the existing algorithms on all the 17 transcriptome datasets. The Lasso parameter Alpha was set to 0.1. All the other parameters of feature selection algorithms utilized the default values.

Performance measurements

A binary classification algorithm optimizes the parameters of a model and predicts that a new sample belongs to the positive (P) or negative (N) group. The sizes of the positive and negative groups are denoted as P and N, respectively. A positive sample is defined as a true positive or false negative one if it is predicted as positive or negative. And a negative sample is defined as a false positive or a true negative if its prediction is positive or negative. The numbers of true positives, false negatives, false positives and true negatives are denoted as TP, FN, FP and TN, respectively. The binary classification performance is evaluated by the following measurements, as similar in¹³. This study defines sensitivity (Sn) and specificity (Sp) as the percentages of correctly predicted positive and negative samples, i.e. Sn = TP/(TP + FN) and Sp = TN/(TN + FP). The overall accuracy is defined as Acc = (TP + TN)/(TP + FN + TN + FP). F-score is also known as F-measure or F ₁-score and has been widely used to evaluate the performance of a binary classification model³¹. F-score is defined as 2 × (Precision × Sn)/(Precision + Sn), and Precision = TP/(TP + FP).

Five representative classification algorithms were evaluated on the datasets, and the maximal accuracy achieved by these five algorithms on a given feature subset of a dataset was defined as the maximal accuracy mAcc. Support Vector Machine (SVM) is a popular binary classification algorithm. K Nearest Neighbors (KNN) algorithm is an intuitive distance-based classification algorithm. Decision Tree (DTree) will generate an easy-to-interpret classifier. And Naïve Bayesian classifier (NBayes) assumes that all the features are independent to each other. Logistic Regression (LR) trains a linear classification function, which may suggest the weights of the chosen features.

All the algorithms were tested under two major Python releases, i.e. 2.7.13 and 3.6.0.

Biomedical datasets

Data pre-processing is one of the most important steps for a data modeling problem. This study focused on the feature selection problem, and only checked the datasets for the issue of missing data. A feature was excluded from further analysis if it has missing data for some samples.

The proposed algorithm in this study was compared with the existing algorithms using 17 datasets, as similar in¹⁴. Each of the 17 datasets has two class labels, i.e. a binary classification problem. Six transcriptome datasets, i.e. DLBCL³², Pros³³, ALL³⁴, CNS³⁵, Lym³⁶ and Adeno³⁷, were publicly available at the Broad Institute Genome Data Analysis Center. The two datasets Colon ³⁸ and Leuk ³⁹ were provided in the R/Bioconductor packages colonCA and golubEsets, respectively. The dataset ALL modeled as four binary classification datasets, i.e. ALL1/ALL2/ALL3/ALL4, based on different phenotype annotations, as described in Table 1. Five more recent datasets, i.e. Mye (accession: GDS531)⁴⁰, Gas (accession: GSE37023)⁴¹, Gas1/Gas2 (accession: GSE29272)⁴², T1D (accession: GSE35725)⁴³ and Stroke (accession: GSE22255)⁴⁴, were publicly available at the NCBI Gene Expression Omnibus (GEO) database. The raw data from the NCBI GEO database was normalized into the gene expression matrix with the default parameters of the RMA algorithm⁴⁵, and all the other datasets were downloaded as the normalized data matrix.

Table 1.

Summary information of the 17 binary classification datasets.

ID	Dataset	Samples	Features	Summary
1	DLBCL	77	7,129	DLBCL (58) vs follicular lymphoma (19)
2	Pros	102	12,625	prostate cancer (52) vs control (50)
3	Colon	62	2,000	colon cancer (40) vs normal (22)
4	Leuk	72	7,129	ALL (47) vs AML (25)
5	Mye	173	12,625	presence (137) vs absence (36) of focallesions of bone
6	ALL1	128	12,625	B-cell (95) vs T-cell (33) ALL
7	ALL2	100	12,625	ALL with (65) vs without (35) relapse
8	ALL3	125	12,625	ALL with (24) vs without (101) multidrug resistance
9	ALL4	93	12,625	ALL with (26) and without (67) the t(9;22) chromosome translocation
10	CNS	60	7,129	medulloblastoma survivors (39) vs treatment failures (21)
11	Lym	45	4,026	germinalcentre (22) vs activated B-like DLBCL (23)
12	Adeno	36	7,457	colon adenocarcinoma (18) vs normal (18)
13	Gas	65	22,645	gastric cancer (29) vs non-malignants (36)
14	Gas1	144	22,283	non-cardia gastric cancer (72) vs normal (72)
15	Gas2	124	22,283	cardia gastric cancer (62) vs normal (62)
16	T1D	101	54,675	T1D (57) vs control (44)
17	Stroke	40	54,675	ischemic stroke (20) vs control (20)

Datasets 1–15 are the cancer transcriptomes, while the last two are transcriptome datasets of type I diabetes and stroke, respectively.

A recent study proposed that methylomes outperformed transcriptomic profiles in separating prostate cancers from the control samples⁴⁶. We demonstrated that a good choice of transcriptomic features might also achieve a similarly good classification model compared with methylomes. The dataset GSE55599 was downloaded from the Gene Expression Omnibus (GEO) database⁴⁷. The binary classification problem worked on the 32 prostate carcinoma samples and 10 benign prostatic hyperplasia samples. Each sample has 47,231 probesets, i.e. features.

RIFS, a randomly re-started incremental feature selection algorithm

The incremental feature selection algorithm was modified to have a start position k and the consecutive performance decreasing cutoff D, which was denoted as the algorithm sIFS(k, D). For a binary classification problem with n features and m samples, the features are ranked based on their association significance with the binary class labels. A feature’s association significance with the class label is calculated by the statistical significance P value of the t-test²⁷. Features are denoted as f _i, i ∈ {1, 2, …, n}, based on their ranks. The algorithm will consecutively add the next element to the feature subset until the binary classification accuracy decreases consecutively D times. The pseudo-code of the algorithm sIFS(k, D) is shown as follows.

The Randomly re-started Incremental Feature Selection (RIFS) algorithm is proposed based on the unit algorithm sIFS(k, D). Our hypothesis is that a summarization of multiple sIFS(k, D) algorithms may generate a feature subset with better classification accuracy than the classical algorithms sIFS(1, 1). The pseudo-code of RIFS was shown as follows.

Randomly seeded k-fold cross validation

A k-fold cross validation (KFCV) strategy is utilized to calculate the overall classification performance. The dataset was randomly split into k folds and used each fold to validate the model trained from the rest of k−1 folds. Given a binary classification dataset with positive and negative samples in the subsets P and N, respectively, KFCV randomly splits P and N into k equally-sized subsets, respectively. P = {P ₁, P ₂, …, P _k} and N = {N ₁, N ₂, …, N _k}. Iteratively, P _i ∪ N _i is selected as the testing dataset, and the other samples are used as the training data for a given classification algorithm. The classification performance measurements Sn, Sp and Acc are calculated based on this round of iteration.

RIFS selects features using the incremental rule from the given starting feature, and only the feature subset with the best classification performance will be kept for further analysis. Due to that different data splitting will generate different classification performances, multiple random seeds will be employed to produce KFCV calculations. The classification performance measurements are averaged over all the rounds of KFCV experiments. To eliminate the effects of over-fitting and random splitting, this study carried out 20 random runs of 10-fold cross-validation and chose the classification accuracy maximized over five classifiers, i.e. SVM, KNN, DTree, NBayes, and LR.

Experimental procedure

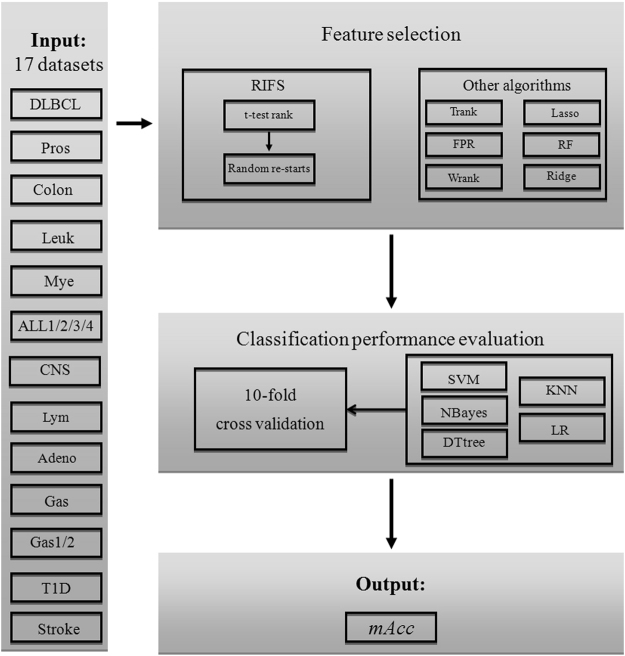
RIFS was compared with two major classes of feature selection algorithms, i.e. three filters and three wrappers. The performance measurement was calculated using 10-fold cross-validation, and the classification accuracy was the maximum value mAcc of the five classification algorithms, i.e. SVM, KNN, DTree, NBayes and LR. The detailed procedure was illustrated in Fig. 1.

Figure 1.

Experimental setting of this work. 17 datasets were chosen to compare RIFS with three filters and three wrappers, and the classification performances were calculated using 10-fold cross-validations.

All the experiments were carried out in an Inspur Gene Server G100, with 256GB memory, 28 Intel Xeon® CPU cores (2.4 GHz), and 30TB RISC1 disk space.

Results and Discussion

Two optimization rules for the IFS strategy

This study proposes two hypothetical modifications of the Incremental Feature Selection (IFS) strategy^13,20,48 based on the experiment data, as shown in Fig. 2. The optimization goal is to maximize the binary classification accuracy using the selected feature subset. The classification performance in this demonstration step was calculated by one round of 10-fold cross validation.

Figure 2.

Demonstrative examples of RIFS rules and evaluation of the best starting percentage. (a) Two features starting from the rank i = 31 for the dataset ALL2. 4 features starting from the rank i = 443 for the dataset ALL3. (b) Accuracy curve of IFS(757) for the dataset T1D. (c) Accuracy curve of IFS(37) for the dataset Colon. (d) The maximum accuracy is calculated for each of the four datasets, i.e. ALL1/ALL2/ALL3/ALL4, with different percentages of all the features as the starting points.

Randomly re-start the IFS strategy

We generalize the classical version of IFS as the IFS(i), which chooses a subset of consecutively ranked features starting from the rank i. Our hypothesis is that there may exist a feature subset IFS(i) with a classification accuracy better than IFS(0). This hypothesis is supported by the two examples in Fig. 2(a). The two features with the ranks 31 and 32 achieved 79.5% in the overall accuracy for the dataset ALL2, better than 77.0% in accuracy for the top two ranked features by IFS(0), as shown in Fig. 2. The four features with the ranks 443, 444, 445 and 446 outperformed the top four ranked features by 1.3% in accuracy for the dataset ALL3. Their statistical significances measured in P-values are 0.036990, 0.036994, 0.037100 and 0.037105 for these four low-ranked features, respectively. So the IFS strategy may be improved by the randomly re-starting rule.

Stop at one decrease does not work well

We also observe that a big increase in the classification performance may be achieved by adding two consecutively ranked features, even when there is a decrease by adding the first one. For example, the feature screening process IFS(37) got the first accuracy decrease (1.5%) for the dataset Colon when adding the four^th feature (ranked 40). But IFS(37) achieved an increase (1.4%) in accuracy even compared with the situation before adding the four^th feature, as shown in Fig. 2(b). Another case was the feature screening process IFS(757) for the dataset T1D, as in Fig. 2(c). The integration of the third feature decreased the accuracy by 1.3%, but the next feature (ranked 760) increased the accuracy by 5.4%, which was also higher than the two consecutively ranked features 757 and 758 by 4.1% in accuracy. So the stop strategy of IFS(i) needs to tolerate at least one accuracy decrease.

How many starting points are enough for most datasets?

We investigated the best number of starting points for RIFS using the four datasets, ALL1/ALL2/ALL3/ALL4, as shown in Fig. 2(d). RIFS was set to stop if three consecutive tries do not increase the classification performances. Five choices of the numbers of starting points were evaluated, i.e. pStartingPercentage = 15%, 25%, 35%, 45%, 55% of the total feature number, respectively. The classification performance in this parameter optimization step was calculated by one round of 10-fold cross validation. The classification algorithms achieved 100% in mAcc for all the six values of the parameter pStartingPercentage on the dataset ALL1. It seems that the dataset ALL1 is easy to separate, and some other algorithms also achieved 100% in mAcc, as demonstrated in¹⁴. The measurement mAcc for the dataset ALL2 was improved from 79.5–80.6% when the parameter pStartingPercentage increased from 15–55%, and the maximum value 80.6% was achieved after pStartingPercentage = 45%. The measurement mAcc remained 88.3% for all different values of pStartingPercentage for the dataset ALL3. And the best mAcc = 94.9% was achieved after pStartingPercentage = 45%. So the default value 45% was set for the parameter pStartingPercentage.

How much tolerance for consecutive performance decreases is enough?

A greedy feature selection algorithm tends to stop when the optimization goal decreases during the feature screening process, e.g. the classical IFS strategy. Our hypothesis is that after a minor decrease in the classification performance, adding the next feature may achieve a much better overall performance improvement.

We evaluated the RIFS stopping criteria pStoppingDepth = 1, 2, 3, 4 and 5, i.e. RIFS stops when pStoppingDepth consecutive performance decreases are detected. The four datasets ALL1/ALL2/ALL3/ALL4 were chosen for the evaluation. The parameter pStartingPercentage was set to 10%, 20%, 30%, 40% and 50%, and the performance measurement is mAcc by the 10-fold cross validation strategy. The classification performance in this parameter optimization step was calculated by one round of 10-fold cross validation. Figure 3 demonstrated that RIFS achieved the best mAcc when pStoppingDepth reached 4 for all the four datasets using the 5 values of pStartingPercentage. So the experimental data supported our hypothesis that it may not be the best choice to stop immediately after one performance decrease was detected. And the default value of pStoppingDepth was chosen as 4.

Figure 3.

How many steps are tolerated without performance improvements. The classification performance is measured in mAcc.

A comprehensive evaluation of RIFS with the default parameter values pStartingPercentage = 45% and pStoppingDepth = 4 was carried out for all the 17 transcriptome datasets, as shown in Fig. 4. The classification performance in the following comparative analysis steps was calculated by 20 random rounds of 10-fold cross validation. RIFS achieved at least 0.804 in mAcc for these datasets, and even achieved 1.000 in mAcc for 6 out of the 17 datasets. The following sections will compare RIFS with the existing feature selection algorithms by the performance measurement mAcc.

Figure 4.

The classification performances of RIFS on the 17 transcriptome datasets. The measurement mAcc is used as the vertical axis, and the horizontal axis lists the 17 datasets. The detailed mAcc values are also given on the top of each column.

Comparison with filters on the 17 transcriptomes

RIFS with the default parameter values pStartingPercentage = 45% and pStoppingDepth = 4 was compared with the filter algorithms. A filter algorithm assumes that features are independent to each other, and evaluates the association of a feature with the class label independently. So users need to determine how many features will be chosen, after all the features are evaluated and ranked by the filter algorithm. In order to conduct a fair comparison, if RIFS selects k features, this study selects the same number k of top-ranked features evaluated by a filter. 10-fold cross-validation strategy was employed to calculate the binary classification performances of RIFS and the three filter algorithms, i.e. Trank, FPR, and Wrank. RIFS improves the feature selection procedure based on a filter algorithm, so it is anticipatable that RIFS outperforms the filter algorithms.

RIFS performed the best compared with the three filter algorithms on all the 17 datasets, as shown in Fig. 5(a). The four datasets ALL1, Lym, Adeno and Stroke, seem to be easy to be separated, since three feature selection algorithms including RIFS achieved 100% in mAcc. RIFS outperformed the three filter algorithms on all the other 13 datasets. And CNS seems to be a difficult binary classification dataset. RIFS achieved 87.4% in mAcc, and improved the other filter algorithms by at least 11.6% in mAcc. RIFS usually selects no more than 10 features, and the maximal number of features selected by RIFS was 27 for the dataset Mye.

Figure 5.

Performance comparison of RIFS with 3 filters and 3 wrappers. The vertical axis is the performance measurement mAcc and F-score, and the horizontal axis gives the dataset names. Since all the filter algorithms select the same number of features as RIFS, only the numbers of features by RIFS are shown. The last table gives the numbers of features selected by the wrappers algorithms and RIFS. (a) Comparison with 3 filters. (b) Comparison with 3 wrappers.

The experimental data suggests that an orchestration of low-ranked features may achieve very good classification performances even for the difficult datasets like CNS and ALL2. No filter algorithms achieved mAcc better than 76.0%, and RIFS only achieved 80.4% and 87.4% in mAcc for the datasets ALL2 and CNS, respectively.. This provides an additional piece of evidence for the rule “Randomly re-start the IFS strategy” of RIFS.

RIFS achieved F-score >  = 0.900 on 13 out of the 17 transcriptome datasets, and the maximal F-scores on 12 datasets compared with the 3 filters, as shown in Fig. 5(a). The maximal F-score improvement 0.049 compared with RIFS’s F-score = 0.916 was achieved by Trank and FPR on the dataset Gas1. The next biggest F-score improvement 0.038 compared with RIFS was achieved by Trank on the dataset ALL3. The data suggested that ALL3 was a difficult dataset for the filter algorithms.

Comparison with wrappers on the 17 transcriptomes

RIFS with the default parameters pStartingPercentage = 45% and pStoppingDepth = 4 performed the best compared with the three wrapper algorithms, i.e. Lasso, RF and Ridge, on all the transcriptome datasets except for Myel, as also shown in Fig. 5(b). RIFS achieved 100% in mAcc for 6 out of the 17 datasets, and its average mAcc is 94.5%. The next best algorithm based on the average mAcc is Lasso. Lasso achieved the average mAcc 90.4% and mAcc = 100% for the three datasets Leuk, ALL1 and Lym. Lasso was also the only wrapper algorithm outperforming RIFS with 2.4% in mAcc on the dataset Mye. Except for this case, RIFS performed better than all the wrapper algorithms on all the datasets, and achieved an average improvement 3.5% in mAcc for the best of the three wrapper algorithms on the 17 transcriptomic datasets.

Another performance measurement for a feature selection algorithm is the number of features selected by the algorithm. Besides the excess consumption of computational power in training and predicting by a classification model with a large number of features, the overfitting problem is also inevitable to be fixed⁴⁹. Due to the high data production cost in the biomedical area, the number of samples is usually much smaller than that of features in a biomedical dataset⁵⁰. And the final clinical deployment of a classification model has a cost positively correlated with the number of features in the model. So a biomedical classification model with a higher accuracy and a smaller number of features is preferred in the clinical settings.

RIFS recommended a smaller list of features for training classification models with higher accuracy except for six cases, as shown in the table under the line plot in Fig. 5. Both RIFS and Lasso recommended 11 features for the dataset Colon, but RIFS outperformed Lasso with an improvement 3.3% in mAcc. Lasso selected the same number of features as RIFS for the dataset Lym, and both achieved 100% in mAcc. And Lasso outperformed RIFS with an improvement 2.4% in mAcc on the dataset Mye. For the three datasets ALL3, Gas1 and T1D, Lasso recommended fewer features than RIFS, but RIFS achieved improvements in mAcc 6.7%, 1.5% and 11.4%, respectively. Overall, RIFS suggested an average number of features 8.882, while the three wrapper algorithms chose 25.706, 54.706, and 8428.353 features, respectively.

RIFS achieved the maximal F-score on 13 out of the 17 transcriptome datasets compared with the 3 wrapper algorithms. Except for the dataset ALL3, RIFS achieved at least 0.800 in F-score on all the other 16 datasets. The maximal F-score improvement 0.076 compared with RIFS was achieved by the algorithm Lasso on the dataset Gas1. RIFS didn’t work well on the three gastric cancer datasets Gas/Gas1/Gas2 and the dataset Mye compared with the 3 wrappers. RIFS achieved the biggest F-score improvement 0.237 on the dataset ALL3 compared with the three wrappers.

Transcriptome performs similarly well with methylome

RIFS was employed to screen the transcriptomes of prostate samples and detected two features with 100% discrimination accuracy of prostate cancers. A recent study suggested that top-ranked methylome features outperformed the top-ranked transcriptome features by at least 5.7% in the measurement Area Under the ROC Curve (AUC)⁴⁶. A combination of three methylome features achieved 100% in both the overall accuracy and AUC, while three expression features only achieved 0.978 in AUC. RIFS detected two features ILMN_1708743 and ILMN_1727184 as the biomarkers to discriminate the samples of prostate carcinoma and benign prostatic hyperplasia, as illustrated in Fig. 6. We may see that these two biomarkers can easily separate the 32 prostate carcinoma and ten benign prostatic hyperplasia samples. There is only one sample which is very close to the prostate carcinoma samples in the two-dimensional plane. And a non-linear-kernel SVM can achieve 100% in mAcc for this binary classification problem.

Figure 6.

Dot plot of the two features detected by RIFS. There is only one benign prostatic hyperplasia sample which is very close to the prostate carcinoma ones.

How random seeds impact the feature subsets?

Different random seeds generate different series of random numbers, so we evaluated how random seeds affect the performance of RIFS. To conduct a fair comparison, RIFS was run with the default random seed 0 in the above experiments. This section executed RIFS on the dataset Mye using integers from 0 to 20 as the random seeds. Default values were chosen for the two RIFS parameters pStartingPercentage = 45% and pStoppingDepth = 4. Table 2 shows that the random seeds 1/4/10/11/14/15/19 generated the same feature subset as the random seed 0, and the 27 features achieved the best mAcc = 89.8%. And the random seeds 3/13/16/18 even found a feature subset of 13 features and achieved 89.0% in mAcc. So if a user may prefer a smaller feature subset, multiple tries of different random seeds are recommended.

Table 2.

Results of RIFS with different random seeds.

Random seeds	Rank	NumF	mAcc
1,2,4,10,11,14,15,19	379	27	89.8%
3,13,16,18	179	13	89.0%
5,6,9,12,20	66	17	89.2%
7	1	18	88.7%
8,17	63	21	89.1%

The first column gives the random seeds. Some random seeds generated the same feature subset, so they were summarized in the same row. The columns Rank, NumF and mAcc give the rank of the first feature, the feature number and the classification measurement mAcc of the best feature subset.

Conclusions

RIFS demonstrated a new perspective of feature selection that two individually low-ranked features might work together to make a highly accurate classification model. RIFS can detect features with accurate classification performances, by significantly expanding the searching space. RIFS also tries to avoid the local optimal solutions by tolerating more than one classification performance decreases. There is a balance between the running time and the classification performance, but the user has the flexibility of choosing better classification accuracy for a long running time or an acceptable accuracy within a short period.

Author Contributions

F.Z. conceived the project, designed the experiment and wrote the manuscript. Y.Y. coded the initial algorithm in R and completed the performance comparison with the existing algorithms. R.Z. re-implemented the R.I.F.S. algorithm with improved rules and conducted all the performance comparison procedures using Python. A demonstration of how RIFS performs on the methylation data was also carried out by R.Z. X.F., W.Z. and S.L. helped draft and proof-read the manuscript.

Competing Interests

The authors declare that they have no competing interests.