Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Sep 13;9(40):34618–34624. doi: 10.1021/acsami.7b06949

Metamaterial Combining Electric- and Magnetic-Dipole-Based Configurations for Unique Dual-Band Signal Enhancement in Ultrahigh-Field Magnetic Resonance Imaging

Rita Schmidt †,‡,*, Andrew Webb †
PMCID: PMC5639467  PMID: 28901137

Abstract

graphic file with name am-2017-06949d_0006.jpg

Magnetic resonance imaging and spectroscopy (MRI and MRS) are both widely used techniques in medical diagnostics and research. One of the major thrusts in recent years has been the introduction of ultrahigh-field magnets in order to boost the sensitivity. Several MRI studies have examined further potential improvements in sensitivity using metamaterials, focusing on single frequency applications. However, metamaterials have yet to reach a level that is practical for routine MRI use. In this work, we explore a new metamaterial implementation for MRI, a dual-nuclei resonant structure, which can be used for both proton and heteronuclear magnetic resonance. Our approach combines two configurations, one based on a set of electric dipoles for the low frequency band, and the second based on a set of magnetic dipoles for the high frequency band. We focus on the implementation of a dual-nuclei metamaterial for phosphorus and proton imaging and spectroscopy at an ultrahigh-field strength of 7 T. In vivo scans using this flexible and compact structure show that it locally enhances both the phosphorus and proton transmit and receive sensitivities.

Keywords: metamaterial, dual-band, magnetic resonance imaging, ultrahigh field, in vivo

Introduction

Magnetic resonance imaging (MRI) is one of the most important modalities for clinical disease diagnosis, and it plays a key role in fundamental preclinical research. Its major advantages include nonionizing radiation, lack of penetration effects, ability to acquire fully isotropic three-dimensional (3D) data, and ability to produce a variety of image contrasts between tissues using different data acquisition parameters. The major disadvantage of MRI arises from its low sensitivity, which is a result of the small energy difference between energy levels. Alternative noninductive detection methods have been explored at very low magnetic fields (≪1 T), including optical atomic magnetometers1 and superconducting quantum interference devices,2 but these are not suitable for the much higher field strengths (1.5–7 T) used in human imaging. Magnetic resonance force microscopy,3−5 which uses a nanoscale cantilever for mechanical detection of the MR signal, is a method that has extremely high sensitivity, with the ability to detect single electronic spins, but it is not applicable to human imaging because the sample must be placed in a vacuum at low temperatures.

An alternative method to increase the sensitivity is to incorporate novel materials into the setup: one such example is a metamaterial. Metamaterials and artificial materials represent a novel group of structures, creating new means to control wave propagation.6−9 Applications commenced with optical superlensing,6,10 continued with transformation optics11 and invisibility cloaking,12 and presently have incorporated a wide range of device miniaturization and efficiency enhancements.13−15 Several studies in MRI have investigated potential improvements using metamaterials in the detection sensitivity,16,17 RF transmit efficiency,18 and decoupling between the individual coils in a multicoil array.19,20 In this study, we explore a completely new metamaterial implementation for MRI, namely, a dual-nuclei resonant structure. We have designed a hybrid metamaterial, comprising a two-dimensional (2D) metamaterial surface and a high permittivity dielectric substrate, and explored the properties controlling the two resonant modes corresponding to the Larmor frequencies of the two different nuclei. Most of the nonproton nuclei that are of interest for in vivo acquisition21 have a Larmor frequency that is far away from that of protons, due to the very different gyromagnetic ratios. The two nuclei we chose to focus on in this study are phosphorus22−24 (with γ, the gyromagnetic ratio, of 17.4 MHz/T) and proton (γ of 42.58 MHz/T).

While initial publications on acquiring a 31P signal date back to 1974,25,26 phosphorus magnetic resonance spectroscopy (MRS) is not in wide clinical use due to its low signal-to-noise ratio (SNR). The low SNR arises from low concentration and a low gyromagnetic ratio compared to those of 1H, present in high concentration as water or lipid in tissue (SNR ∝ γ2B0c where B0 is the magnetic field strength and c is the concentration). In vivo 31P MRS acquisition is always performed in combination with 1H imaging, because the latter provides localization for the 31P volume-of-interest and complementary diagnostic information. This requirement is the motivation behind dual-nuclei excitation and acquisition. Therefore, we explored a new flexible and compact metamaterial that can be added as a pad to an existing RF coil setup and augment the SNR for both the 31P and 1H imaging using a single structure.

Several studies have demonstrated metamaterial designs for MRI, which have included swiss-rolls,18,27 split-rings,16,28 wires,17 and magnetoinductive waveguides.29 These structures shape the RF magnetic field, enabling local increases in the MRI transmit and receive efficiency. Two proposed metamaterials have recently garnered interest. One is based on a metamaterial with negative permeability,28 implemented using split-rings, and its feasibility has recently been demonstrated at 3 T using a thin (11 mm) metamaterial slab. The second proposal is based on a metamaterial with negative permittivity,17 using a metasurface based on a set of wires or conductive strips: this has been demonstrated at 1.517 and 7 T30 and showed a local enhancement in SNR. Both designs are based on a quasi-static approximation applicable for relatively low RF frequencies relevant for MRI (≲300 MHz). In this approximation, the magnetic and electric fields can be analyzed separately, and therefore, a system of either magnetic dipoles (split-rings28 or short wires that function equivalently to split-rings31−33) or electric dipoles (long wires17) can support resonant modes at the frequencies of interest. In our study, at 7 T, the quasi-static approximation is well-suited for 31P (121 MHz) but is marginal for 1H (298 MHz). Therefore, full electromagnetic (EM) simulations were used to determine the resonant modes. Our main aim in this study was to design a new type of metamaterial with the capability to enhance the signal for both nuclei (31P and 1H), using the same structure. This new feature arises from a combination of the above two types of metamaterials, creating a novel dual-nuclei metamaterial.

Design of the Dual-Nuclei MRI Metamaterial

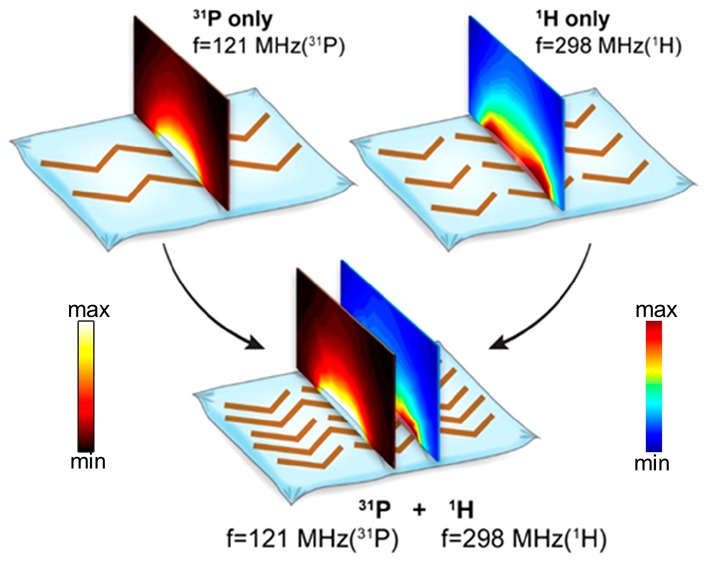
Several studies have examined metamaterials for dual-band settings in the IR and microwave ranges using negative refraction.34−36 Such structures rely on different characteristics depending on the RF frequency range, for example, using 3D structures (with perpendicular setups for dual bands)36 or a subunit that incorporates dual dimension settings.34 For the frequency range in the applications in optics and microwaves, the metamaterials were devised to generate negative refraction, requiring both negative permittivity and negative permeability. For the lower frequencies, which are of interest in our work, implementation based on previous works would result in large 3D structures that are not well-suited to the very restricted space in the MRI environment. In contrast to previous works, two frequency bands can be realized based on the same substrate at the frequencies relevant for MRI: one frequency band produced via coupling with a set of long strips and the other with a set of short strips. Such a metamaterial does not require the property of negative refraction. A set of long strips produces resonant modes for the low frequency band of interest, and a set of short strips produces resonant modes for the high frequency band of interest. In this study, the two structures are harnessed to generate a unique single metamaterial structure for dual-nuclei purposes (as shown in Figure 1). This allows us to generate frequency bands shifted from each other by a factor of two and more. Such frequency band shifts are required for MRI dual-nuclei implementations, due to the very different gyromagnetic ratios of the nuclei of interest compared to that of protons. The exception for this are 19F and 1H, which are very close to each other (γ of 19F is 0.94 vs 1H), and therefore can be implemented with very close resonant systems.37 In our current study, the gyromagnetic ratio of 31P is 40% of the gyromagnetic ratio of 1H. A new metamaterial structure and RF field distributions of the resonant modes, relevant for 31P and 1H, are shown in Figure 1.

Figure 1.

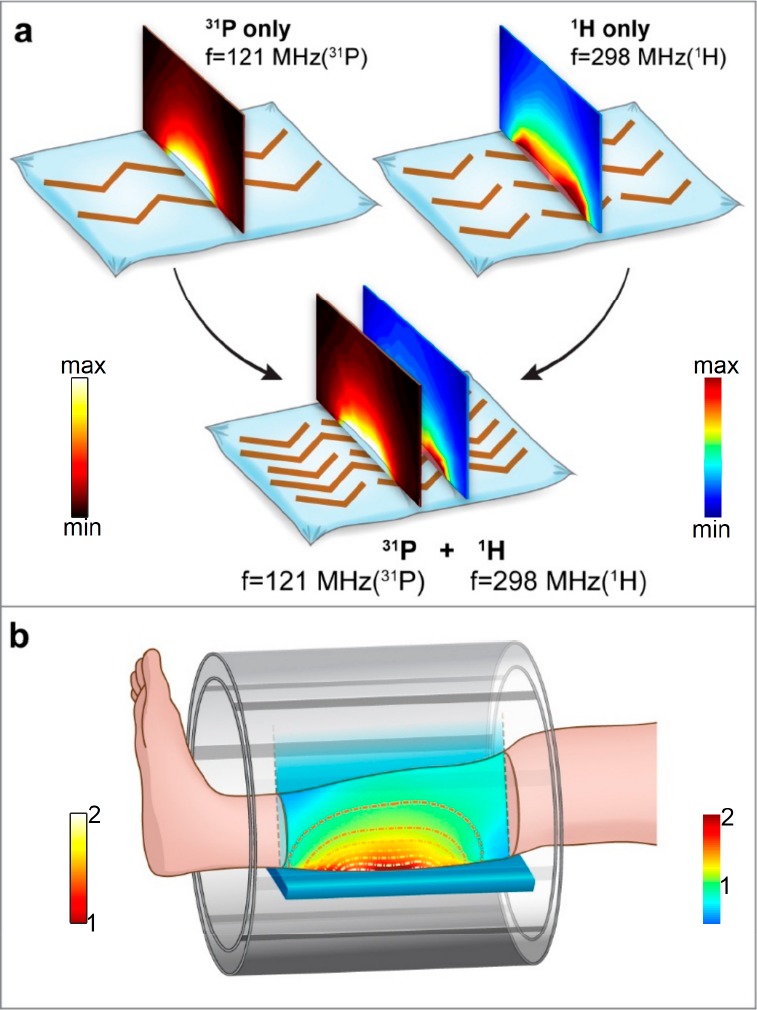
Figure 1

Open in a new tab

Schematic view of the hybrid metamaterial pad and its dual-nuclei behavior. (a) Schematic view of the metamaterial pad combined from subsetups: (top left) 31P nucleus band, tuned to 121 MHz; (top right) 1H nucleus band tuned for 298 MHz. On top of the structure, a central cross section of the magnetic field |H| is shown (for the combined structure two maps for two bands are shown). (b) Schematic view of the setup in MRI including the RF “birdcage” coil and a metamaterial placed behind the leg. A cross section through the leg shows the distribution in the central slice. A scaled color map shows the enhancement ratio distribution for the proton image, and a contour map on top shows an enhancement ratio for the phosphorus. In a and b, the 31P maps and the contours are displayed with a “hot” color map, and the 1H maps are displayed with a “jet” color map.

In a previous study, we reduced the dimensions of a hybrid metamaterial based on copper strips combined with a high dielectric substrate by using a CaTiO3 suspension.30 In the current work, we further reduced the metamaterial dimensions by utilizing zigzag-shaped copper strips instead of straight-line strips. The zigzag shape enables extension of the electric dipole to the length required by the desired frequency while maintaining the physical dimensions of the pad (see Figure S1 that compares a metamaterial based on a set of zigzag-shaped strips versus straight-line strips).

To generate the relevant set of modes, we used a set of long copper zigzag-shaped strips immersed in water acting as a dielectric substrate (εr = 80) as the structure for the 31P frequency (121.7 MHz) at 7 T to produce a compact setup (overall dimensions 14 × 23 × 1 cm3). The setup for the higher frequency band was designed using a matrix of short copper strips. The magnetic dipoles are generated in this setting by the short strips. It has been shown in several previous works31−33 that short wires are equivalent to split-rings. In our case, it is especially advantageous to use the short strips configuration, because we can integrate them with the long zigzag strips in a similar manner in one setup. Figures S2.1 and S2.2 summarize the distributions of the H- and E-fields in the main three planes for both frequencies.

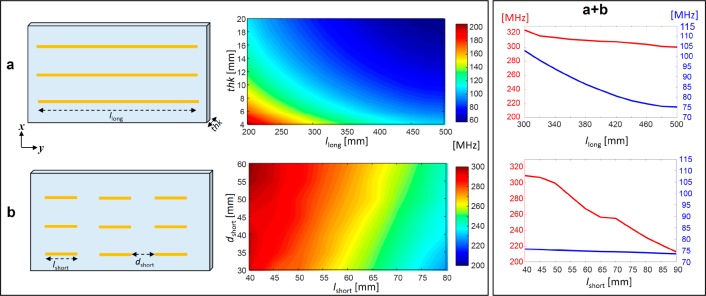
Our analysis shows that, although some parameters such as the dimensions and electric properties of the dielectric substrate substantially affect both frequencies, there are also properties that have a major effect on only one frequency band and a very minor effect on the other. This allows us to independently control the tuning of each frequency band. Long strip lengths (llong) mainly affect the low frequency band, with a minor effect on the high frequency. The effect on the high frequency is due to the effective impedance change of the overall system. Conversely, short strip lengths (lshort) and the spacing between them affect the high frequency band and have a minor effect on the low frequency. Figure 2 shows the effect of the parameters that allow separate mode tuning in the combined structure. Variation of llong in the range of 30–50 cm had a marked effect (∼35%) on the low frequency band, and a much smaller effect (∼6%) on the high frequency band. On the other hand, variation of lshort in the range 4–9 cm had only a very small effect (∼4%) on the low frequency band, while having a significant effect (∼38%) on the high frequency band. Another feature worth noting is the similar characteristics of these resonant modes to transverse electric (TE) mode behavior. This is especially relevant for MRI since the RF H-field must be perpendicular to the main static magnetic field (B0) in order to create the required phase coherence between the spins.

Figure 2.

Figure 2

Open in a new tab

Parametric dependence of the resonant mode for the low and high bands. (a) Schematic view of the structure including three long strips in a dielectric substrate and frequency dependence versus strips length (llong) and thickness of the dielectric (thk). (b) Schematic view of the structure including a matrix of 3 × 3 short strips in a dielectric substrate and the frequency dependence versus strips length (lshort) and spacing (dshort) between the strips. (a+b) Dependence of the dual-band frequencies in the combined structure as a function of llong and lshort: blue plot for the low frequency band, and red plot for the high frequency band. The parameters that were kept constant in all simulations were dielectric layer width and height (180 mm and 500 mm, respectively) and the distance between the strips of the same type (40 mm in the x axis). In b and a+b, the structure thickness was set to 1 cm. In the combined setup, for the plot showing the dependence of the long strips, lshort = 60 mm, and dshort = 20 mm, and for the plot for the short strips, the llong was set to 500 mm.

Results

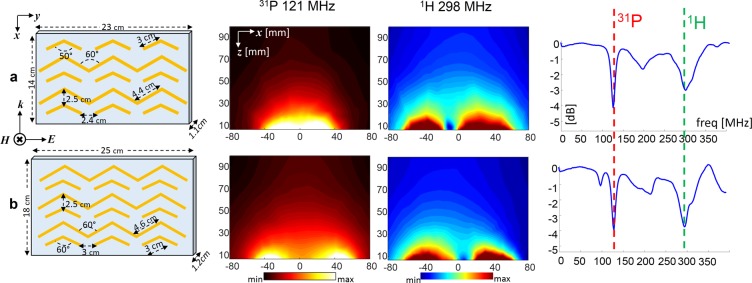
To optimize the required penetration depth and the overall distribution, the dual-nuclei configurations can include different numbers of short and long strips. Figure 3 demonstrates two dual-nuclei configurations with different penetrations of the 31P band into tissue. Figure 3 also shows the frequency response of the implemented setups, measured with a pick-up loop, demonstrating the dual-nuclei bands of interest as expected in simulations.

Figure 3.

Figure 3

Open in a new tab

Comparison of configurations. (a) Dual-nuclei with two long strips. (b) Dual-nuclei with three long strips. From left to right: (left) For each setup, the schematic structure and the dimensions are shown; (center) Central cross section in the xz plane are displayed for the 31P and 1H frequency bands; (right) plots of the frequency response (measured with a pick-up loop adjacent to the structure). The 31P maps are displayed with a “hot” color map, and the 1H maps are displayed with a “jet” color map. The border of the structure is at z = 5.5 mm.

Another optimization criterion is the electric field distribution. The power deposition in a sample or patient is most commonly quantified via the specific absorption rate (SAR), which is proportional to the sample conductivity and the square of the electric field. The maximum intensity of the electric field is reduced by replacing the straight-line strips by the zigzag-shaped strips (see Figure S1). This indicates that further optimization of the electric field distribution is possible, perhaps by using a snake-shaped dipole antenna as implemented for ultrahigh-field MRI.38

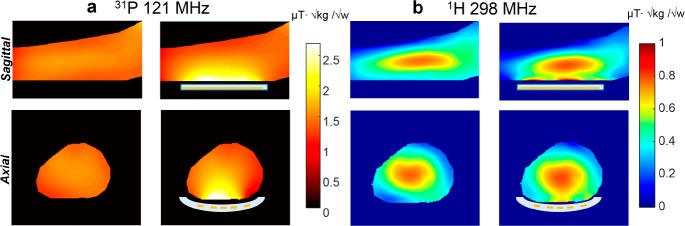
One of the major applications of 31P spectroscopy is the study of metabolism in muscle physiology of the lower extremities in diseases such as muscular dystrophy. Therefore, we examined the local enhancement that can be achieved for imaging the lower extremities. A full EM simulation is shown in Figure 4, demonstrating strong local enhancement at both frequencies. The simulation includes a “birdcage” transmit and receive RF coil for each of the frequencies, the metamaterial structure shown in Figure 3a, and a human model of the lower extremities. The maximum enhancement of the RF field, normalized to the square root of the maximum SAR (B1+ / √SAR), is a factor of 2 for 31P and 2.3 for 1H.

Figure 4.

Figure 4

Open in a new tab

EM simulations using a human body model of the lower extremities. (a) EM simulations at the 31P frequency with and without metamaterial, placed under the calf muscle. (b) EM simulations for 1H with and without metamaterial. Sagittal and axial cross sections through the calf are shown. The B1+ maps are normalized to the square root of the maximum local SAR averaged over 10 g. The 31P maps are displayed with a “hot” color map, and the 1H maps are displayed with a “jet” color map. A schematic cross-sectional overlay of the metamaterial (white) is shown in the images.

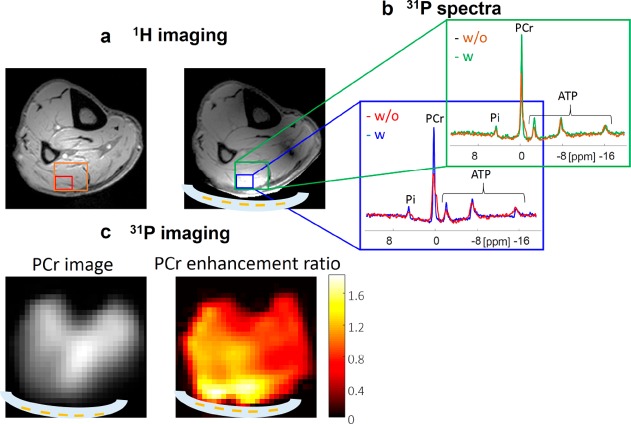
The metamaterial was experimentally realized by placing the copper strips on a very thin plastic substrate, which was placed in a water pad sealed in a flexible plastic container. The flexibility of this structure allows close contact with the calf. The experiment was performed using a transmit/receive double-tuned birdcage coil. 1H scanning comprised a gradient echo sequence with a low-tip angle excitation. This type of sequence produces images in which the SNR is proportional to the product of the RF transmit field (B1+) and the complex conjugate of the receive sensitivity (B1–*) (see the Experimental Section for more details). A chemical shift imaging (CSI) pure phase encoded method was used for the 31P spectroscopic imaging. Figure 5 shows experimental imaging and spectroscopy results from a human calf muscle, with measured local enhancement similar to the simulation results (see also Figure S3 for the corresponding phantom results). The maximum enhancement ratios of the SNR, for the same excitation tip angle, were calculated from the images as 1.8 for 31P and 2.1 for 1H (the noise was calculated as a standard deviation in a region placed outside the objects in the image). The measured signal enhancement was slightly lower than in the simulation (shown in Figure 4), which might be partially explained by a small local coupling between the coil and the metamaterial that was not included in the simulations.

Figure 5.

Figure 5

Open in a new tab

In vivo results. (a) 1H images with and without the metamaterial. (b) 31P spectra of two size voxels (single voxel with maximal enhancement and four-combined voxels) with and without the metamaterial. (c) Phosphocreatine (PCr) image with the metamaterial in place and a map of the enhancement ratio with the metamaterial compared to without the metamaterial. The maximum enhancements (for the same excitation tip angle) were 1.8 and 2.1 for 31P and 1H, respectively. A schematic cross-sectional overlay of the metamaterial (white) is shown in the images.

Discussion and Conclusion

In this study, we have demonstrated for the first time a metamaterial that can be used to enhance the sensitivity of two different nuclei in MRI scans. The prototype demonstrates a local enhancement by combining two substructures, one based on electric dipoles and the other on magnetic dipoles, and optimally arranging them for the two frequency bands. Specifically in the demonstrated 31P/1H example, we have shown an enhancement ratio of approximately a factor of two in the SNR for both nuclei. This enhancement can be converted into a higher imaging resolution or alternatively reduced scanning times: the latter consideration is especially important for 31P spectroscopic imaging that can typically take tens of minutes. Furthermore, although our focus here was a 31P/1H dual-nuclei metamaterial, this method can be extended to other important nuclei. Figure S4 shows a potential design for sodium and proton imaging, which have Larmor frequencies even further apart (the gyromagnetic ratio of sodium is 0.26 times that of the proton).

An additional aspect requiring analysis is the metamaterial’s finite structure implementation with a relatively low number of units. Considering the dielectric environment of the modes of interest in this study, the distances between the strips are in the range λ/6 to λ/8 (where λ is the effective wavelength). Thus, although the subunits are not orders of magnitude smaller than the wavelength, they are small enough in order to produce metamaterial properties. To examine the resonant mode with the low number of units as shown in Figure 3, we performed a series of simulations varying the number of strips. Figures S2.1–S2.3 show that the resonant mode field distributions for both frequency bands are maintained for the low number of units actually used compared to the higher number of units, with a slight shift of the modal frequency. Local peaks in the fields close to the metamaterial surface can be seen in Figure 3. These arise from two different sources, the relatively low number of subunits and local coupling between the long and short strips. This local inhomogeneity can be reduced by a higher density of the subunits (as shown in Figures S2.1–S2.3). However, it is important to note that, because the effect takes place near the structure and the relevant imaging area is 1–2 cm from the structure, the presence of these small peaks has negligible impact on the imaging performance in the region of interest.

In addition to conventional methods of improving the sensitivity of the RF coils, there is growing interest in exploring complementary methods that utilize the EM properties of materials for signal enhancement.39,40 For example, passive pads based on a suspension of Perovskite materials (CaTiO3 and BaTiO3) with relative permittivities (εr) of 100–300 have been shown to locally increase the SNR.41−43 The convenience of passive dielectric pads is that they are simply added to the existing RF coil setup. However, significant improvements for 31P MRS require very high relative permittivity values, in the range 500–1000 or very bulky pads,44−46 both of which make it difficult to integrate into a clinical setup. In this work, our goal was a new flexible and compact structure that can provide patient comfort and ease of use in a realistic environment; that is, it can be integrated into closely fitting receive arrays. The flexibility of the metamaterial also provides an additional advantage, which is the close contact to the region-of-interest, maximizing the available SNR. The approach introduced in this work is a further step toward new design principles of metamaterials for manipulating RF magnetic and electric fields. Such manipulation can be optimized for different goals in MRI, such as enhancing the local signal (as shown in this work), reducing SAR (due to a reduced electric field), or improving signal homogeneity, especially for ultrahigh-field MRI. In the current implementation, we used the metamaterial as a passive pad; however, it could also be implemented as an active resonator and serve as a building block in future RF coil design.

Experimental Section

Analysis and Simulations

3D EM simulations were performed using finite integration technique (FIT) software (CST Microwave Studio, Darmstadt, Germany). The first step used the eigenmode solver to analyze the spatial distribution and the resonant frequencies of the relevant mode. The EM mode used for MRI must have an H-field component perpendicular to the main static magnetic field and should propagate into the object being imaged. We choose here a “TE01-like” mode that satisfies the first criterion and is also the mode with the deepest penetration. Simulations included analysis of the frequency dependence of the modes as a function of the distance between the short and long strips and the thickness of the dielectric substrate. Water was chosen as the dielectric substrate. Figures S1 and S2 show full details of the mode characterization.

The RF transmit field is defined as a left circularly polarized field transverse to the main B0 magnetic field: the transmit field B1+ = (B1x + B1y) / 2 and the receive field B1– = (B1x – B1y) / 2. The magnitude of the RF transmit field defines the excitation tip angle θ applied to the spins in the excited volume, θ = γB1+τ where γ is the gyromagnetic ratio and τ is the pulse duration. The SNR of the image is proportional to sin(θ) • B1–* / √P, where P is the accepted power of the coil. All RF transmit (B1+) maps were normalized to an accepted power of 1 W. The simulations were performed separately for 31P and 1H with a setup that included 8-rung high-pass quadrature birdcage coils for 31P and 1H (i.d. = 19 cm and rung length = 14 cm for 31P; i.d. = 19.5 cm and rung length = 14 cm for 1H), corresponding to the transmit coil used for the experimental measurements.30 The coil was loaded with the human model data set “Gustav” provided by the CST software. The mesh resolution was 2.0 × 2.0 × 2.0 mm3. The simulations compared the RF field distribution with and without the metamaterial positioned below the calf region.

Characterization of Materials

The metamaterial prototype included two long strips of 26 cm in total length and a 3 × 3 matrix of short strips (6 cm length) (as shown in Figure 3a). The distance between the strips was 2.5 cm. The implemented structure was constructed from 25 μm thick copper strips, 5 mm wide each. The full structure size was 14 × 23 × 1.1 cm3 including a 1.1 cm thick water layer. The dielectric layer and the copper strips were sealed in a plastic container. The pad was placed under the calf muscle of the leg to assess the local enhancement of the prototype.

Phantom and in Vivo Experiments

Phantom and in vivo images of a volunteer were acquired on a Philips Achieva 7 T MRI system. The phantom setup consisted of a plastic cylinder containing polyvinylpyrrolidone (∼1.8 M) in water and salt added to achieve dielectric properties of εr = 48 and σ = 0.3 S/m (in order to mimic the electric properties of calf muscle), in which 500 mM phosphoric acid was dissolved.

All experimental protocols were approved by the Leiden University Medical Centre Medical Ethics Committee, and all methods were carried out in accordance with Leiden University Medical Centre guidelines and regulations. Phantom and in vivo scans were acquired using custom-built double-resonant birdcage coils reported in ref (30). The 1H images were produced by a low-tip-angle gradient-echo sequence with the following scan parameters: field-of-view (FOV) = 24 × 24 cm2, spatial resolution = 1.5 × 1.5 × 5.0 mm3, TR/TE = 10/3.4 ms, and flip angle = 5°. The 31P spectroscopic imaging consisted of a nonselective 2D CSI sequence. The CSI scan parameters for the phantom were as follows: FOV = 13 × 13 cm2, phase encoding matrix = 13 × 13, flip angle = 45°, echo time = 1.2 ms, repetition time = 2000 ms, and number of averages = 2. For the in vivo scans, the parameters were as follows: FOV = 20 × 20 cm2, phase encoding matrix = 10 × 10, flip angle = 45°, echo time = 1.3 ms, repetition time = 2000 ms, and number of averages = 12.

Acknowledgments

We are grateful to I. Ronen for help with the in vivo experiments. R. Schmidt thanks N. Sobel from the Weizmann Institute of Science for hosting her as a visiting scientist.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.7b06949.

  • Additional characterizations, simulations, and phantom verification experiments; and a potential design for a sodium and proton imaging setup (PDF)

This work was supported by an ERC advanced grant 670629 NOMA MRI and NWO Topsubside 20645 (A.G.W.).

The authors declare no competing financial interest.

Supplementary Material

am7b06949_si_001.pdf (594.3KB, pdf)

References

  1. Xu S.; Yashchuk V. V.; Donaldson M. H.; Rochester S. M.; Budker D.; Pines A. Magnetic Resonance Imaging with an Optical Atomic Magnetometer. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (34), 12668–12671. 10.1073/pnas.0605396103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. McDermott R.; Lee S.; Haken B. t.; Trabesinger A. H.; Pines A.; Clarke J. Microtesla MRI with a Superconducting Quantum Interference Device. Proc. Natl. Acad. Sci. U. S. A. 2004, 101 (21), 7857–7861. 10.1073/pnas.0402382101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Sidles J. A. Noninductive Detection of Single-Proton Magnetic Resonance. Appl. Phys. Lett. 1991, 58 (24), 2854–2856. 10.1063/1.104757. [DOI] [Google Scholar]
  4. Rugar D.; Yannoni C. S.; Sidles J. A. Mechanical Detection of Magnetic Resonance. Nature 1992, 360 (6404), 563–566. 10.1038/360563a0. [DOI] [Google Scholar]
  5. Rugar D.; Züger O.; Hoen S.; Yannoni C. S.; Vieth H. M.; Kendrick R. D. Force Detection of Nuclear Magnetic Resonance. Science 1994, 264 (5165), 1560–1563. 10.1126/science.264.5165.1560. [DOI] [PubMed] [Google Scholar]
  6. Smith D. R.; Pendry J. B.; Wiltshire M. C. K. Metamaterials and Negative Refractive Index. Science 2004, 305 (5685), 788–792. 10.1126/science.1096796. [DOI] [PubMed] [Google Scholar]
  7. Pendry J. B.; Schurig D.; Smith D. R. Controlling Electromagnetic Fields. Science 2006, 312 (5781), 1780–1782. 10.1126/science.1125907. [DOI] [PubMed] [Google Scholar]
  8. Engheta N.; Ziolkowski R.. Electromagnetic Metamaterials: Physics and Engineering Explorations; Wiley-IEEE Press: Hoboken, NJ, 2006. [Google Scholar]
  9. Cai W.; Shalaev V.. Optical Metamaterials: Fundamentals and Applications; Springer: New York, 2009. [Google Scholar]
  10. Fang N.; Lee H.; Sun C.; Zhang X. Sub–diffraction-limited Optical Imaging with a Silver Superlens. Science 2005, 308 (5721), 534–537. 10.1126/science.1108759. [DOI] [PubMed] [Google Scholar]
  11. Chen H.; Chan C. T.; Sheng P. Transformation Optics and Metamaterials. Nat. Mater. 2010, 9 (5), 387–396. 10.1038/nmat2743. [DOI] [PubMed] [Google Scholar]
  12. Schurig D.; Mock J. J.; Justice B. J.; Cummer S. A.; Pendry J. B.; Starr A. F.; Smith D. R. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 2006, 314 (5801), 977–980. 10.1126/science.1133628. [DOI] [PubMed] [Google Scholar]
  13. Dolling G.; Wegener M.; Soukoulis C. M.; Linden S. Negative-index Metamaterial at 780 nm Wavelength. Opt. Lett. 2007, 32 (1), 53–55. 10.1364/OL.32.000053. [DOI] [PubMed] [Google Scholar]
  14. Dolling G.; Enkrich C.; Wegener M.; Soukoulis C. M.; Linden S. Low-loss Negative-index Metamaterial at Telecommunication Wavelengths. Opt. Lett. 2006, 31 (12), 1800–1802. 10.1364/OL.31.001800. [DOI] [PubMed] [Google Scholar]
  15. Yu N.; Capasso F. Flat Optics with Designer Metasurfaces. Nat. Mater. 2014, 13, 139–150. 10.1038/nmat3839. [DOI] [PubMed] [Google Scholar]
  16. Freire M. J.; Jelinek L.; Marques R.; Lapine M. On the Applications of μ, r = – 1 Metamaterial Lenses for Magnetic Resonance Imaging. J. Magn. Reson. 2010, 203, 81–90. 10.1016/j.jmr.2009.12.005. [DOI] [PubMed] [Google Scholar]
  17. Slobozhanyuk A. P.; Poddubny A. N.; Raaijmakers A. J.; van den Berg C. A.; Kozachenko A. V.; Dubrovina I. A.; Melchakova I. V.; Kivshar Y. S.; Belov P. A. Enhancement of Magnetic Resonance Imaging with Metasurfaces. Adv. Mater. 2016, 28 (9), 1832–1838. 10.1002/adma.201504270. [DOI] [PubMed] [Google Scholar]
  18. Wiltshire M. C. K.; Pendry J. B.; Young I. R.; Larkman D. J.; Gilderdale D. J.; Hajnal J. V. Microstructured Magnetic Materials for RF Flux Guides in Magnetic Resonance Imaging. Science 2001, 291 (5505), 849–851. 10.1126/science.291.5505.849. [DOI] [PubMed] [Google Scholar]
  19. Hurshkainen A. A.; Derzhavskaya T. A.; Glybovski S. B.; Voogt I. J.; Melchakova I. V.; van den Berg C. A.; Raaijmakers A. J. Element Decoupling of 7T Dipole Body Arrays by EBG Metasurface Structures: Experimental Verification. J. Magn. Reson. 2016, 269, 87–96. 10.1016/j.jmr.2016.05.017. [DOI] [PubMed] [Google Scholar]
  20. Georget E.; Luong M.; Vignaud A.; Giacomini E.; Chazel E.; Ferrand G.; Amadon A.; Mauconduit F.; Enoch S.; Tayeb G.; et al. Stacked Magnetic Resonators for MRI RF Coils Decoupling. J. Magn. Reson. 2017, 275, 11–18. 10.1016/j.jmr.2016.11.012. [DOI] [PubMed] [Google Scholar]
  21. Bottomley P. A. Human In Vivo NMR Spectroscopy in Diagnostic Medicine: Clinical Tool or Research Probe?. Radiology 1989, 170 (1), 1–15. 10.1148/radiology.170.1.2642336. [DOI] [PubMed] [Google Scholar]
  22. Bottomley P. A. Noninvasive Study of High-energy Phosphate Metabolism in Human Heart by Depth-resolved Phosphorus-31 NMR Spectroscopy. Science 1985, 229, 769–773. 10.1126/science.4023711. [DOI] [PubMed] [Google Scholar]
  23. Arnold D. L.; Matthews P. M.; Radda G. K. Metabolic Recovery After Exercise and the Assessment of Mitochondrial Function In Vivo in Human Skeletal Muscle by Means of 31P NMR. Magn. Reson. Med. 1984, 1 (3), 307–315. 10.1002/mrm.1910010303. [DOI] [PubMed] [Google Scholar]
  24. Oberhaensli R.; Bore P.; Rampling R.; Hilton-Jones D.; Hands L.; Radda G. Biochemical Investigation of Human Tumours In Vivo with Phosphorus-31 Magnetic Resonance Spectroscopy. Lancet 1986, 328 (8497), 8–11. 10.1016/S0140-6736(86)92558-4. [DOI] [PubMed] [Google Scholar]
  25. Hoult D. I.; Busby S. J. W.; Gadian D. G.; Radda G. K.; Richards R. E.; Seeley P. J. Observation of Tissue Metabolites Using 31P Nuclear Magnetic Resonance. Nature 1974, 252, 285–287. 10.1038/252285a0. [DOI] [PubMed] [Google Scholar]
  26. Ackerman J. J.; Grove T. H.; Wong G. G.; Gadian D. G.; Radda G. K. Mapping of Metabolites in Whole Animals by 31P NMR Using Surface Coils. Nature 1980, 283 (5743), 167–170. 10.1038/283167a0. [DOI] [PubMed] [Google Scholar]
  27. Radu X.; Garray D.; Craeye C. Toward a Wire Medium Endoscope for MRI Imaging. Metamaterials 2009, 3 (2), 90–99. 10.1016/j.metmat.2009.07.005. [DOI] [Google Scholar]
  28. Algarin J. M.; Freire M. J.; Breuer F.; Behr V. C. Metamaterial Magnetoinductive Lens Performance as a Function of Field Strength. J. Magn. Reson. 2014, 247, 9–14. 10.1016/j.jmr.2014.08.006. [DOI] [PubMed] [Google Scholar]
  29. Syms R. R. A.; Young I. R.; Ahmad M. M.; Rea M. Magnetic Resonance Imaging Using Linear Magneto-inductive Waveguides. J. Appl. Phys. 2012, 112, 114911. 10.1063/1.4768281. [DOI] [Google Scholar]
  30. Schmidt R.; Slobozhanyuk A.; Belov P.; Webb A. Flexible and Compact Hybrid Metasurfaces for Enhanced Ultra High Field In Vivo Magnetic Resonance Imaging. Sci. Rep. 2017, 7, 1678. 10.1038/s41598-017-01932-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Dolling G.; Enkrich C.; Wegener M.; Zhou J. F.; Soukoulis C. M.; Linden S. Cut-wire Pairs and Plate Pairs as Magnetic Atoms for Optical Metamaterials. Opt. Lett. 2005, 30 (23), 3198–3200. 10.1364/OL.30.003198. [DOI] [PubMed] [Google Scholar]
  32. Zhou J.; Zhang L.; Tuttle G.; Koschny T.; Soukoulis C. M. Negative Index Materials Using Simple Short Wire Pairs. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 041101. 10.1103/PhysRevB.73.041101. [DOI] [Google Scholar]
  33. Shalaev V. M. Optical Negative-index Metamaterials. Nat. Photonics 2007, 1 (1), 41–48. 10.1038/nphoton.2006.49. [DOI] [Google Scholar]
  34. Yuan Y.; Bingham C.; Tyler T.; Palit S.; Hand T. H.; Padilla W. J.; Smith D. R.; Jokerst N. M.; Cummer S. A. Dual-band Planar Electric Metamaterial in the Terahertz Regime. Opt. Express 2008, 16 (13), 9746–9752. 10.1364/OE.16.009746. [DOI] [PubMed] [Google Scholar]
  35. Chen K.; Adato R.; Altug H. Dual-band Perfect Absorber for Multispectral Plasmon-enhanced Infrared Spectroscopy. ACS Nano 2012, 6 (9), 7998–8006. 10.1021/nn3026468. [DOI] [PubMed] [Google Scholar]
  36. Kwon D. H.; Werner D. H.; Kildishev A. V.; Shalaev V. M. Near-infrared Metamaterials with Dual-band Negative-index Characteristics. Opt. Express 2007, 15 (4), 1647–1652. 10.1364/OE.15.001647. [DOI] [PubMed] [Google Scholar]
  37. Nikulin A.; Glybovski S.; Melchakova I.; Belov P.; Enoch S.; Abdeddaim R.. A Dual-frequency MRI Coil for Small Animal Imaging at 7 T Based on Metamaterial-inspired Wire Structures. Int. Congr. Adv. Electromagn. Mater. Microwaves Opt., 10th; 2016; pp 241–243.
  38. Steensma B.; Andrade A. V. O.; Klomp D.; van den Berg N.; Luijten P.; Raaijmakers A.. Body Imaging at 7 T with Much Lower SAR Levels: an Introduction of the Snake Antenna Array. Proceedings of the International Society for Magnetic Resonance in Medicine, Singapore, May 7–13, 2016; International Society for Magnetic Resonance in Medicine: Concord, CA, 2016; Vol. 25, p 0395.
  39. O’Brien K. R.; Magill A. W.; Delacoste J.; Marques J. P.; Kober T.; Fautz H.-P.; Lazeyras F.; Krueger G. Dielectric Pads and Low-B1+ Adiabatic Pulses: Complementary Techniques to Optimize Structural T1w Whole-brain MP2RAGE Scans at 7 T. J. Magn. Reson. Imag. 2014, 40 (4), 804–812. 10.1002/jmri.24435. [DOI] [PubMed] [Google Scholar]
  40. Franklin K. M.; Dale B. M.; Merkle E. M. Improvement in B1-inhomogeneity Artifacts in the Abdomen at 3T MR Imaging Using a Radiofrequency Cushion. J. Magn. Reson. Imag. 2008, 27 (6), 1443–1447. 10.1002/jmri.21164. [DOI] [PubMed] [Google Scholar]
  41. Haines K.; Smith N. B.; Webb A.G. New High Dielectric Constant Materials for Tailoring the B1 Distribution at High Magnetic Fields. J. Magn. Reson. 2010, 203, 323–327. 10.1016/j.jmr.2010.01.003. [DOI] [PubMed] [Google Scholar]
  42. Webb A. G. Dielectric Materials in Magnetic Resonance. Concepts Magn. Reson., Part A 2011, 38A (4), 148–184. 10.1002/cmr.a.20219. [DOI] [Google Scholar]
  43. Yang Q. X.; Wang J.; Wang J.; Collins C. M.; Wang C.; Smith M. B. Reducing SAR and Enhancing Cerebral Signal-to-Noise Ratio with High Permittivity Padding at 3 T. Magn. Reson. Med. 2011, 65, 358–362. 10.1002/mrm.22695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Vaidya M. V.; Sodickson D. K.; Collins C. M.; Lattanzi R.. Extending the Sensitivity of a Transmit/Receive Radiofrequency Coil with Dielectric Materials at 7 T. Proceedings of the International Society for Magnetic Resonance in Medicine, Milan, Italy, May 10–16, 2014; International Society for Magnetic Resonance in Medicine: Concord, CA, 2014; Vol. 22, p 0406.
  45. Rupprecht S.; Lee B.-Y.; Zhu X.-H.; Chen W.; Yang Q. X.. Signal-to-Noise Ratio Improvement for MR Proton Spectroscopy at 3T Using a Ultra-high Dielectric Constant (uHDC) Material Sleeve. Proceedings of the International Society for Magnetic Resonance in Medicine, Milan, Italy, May 10–16, 2014; International Society for Magnetic Resonance in Medicine: Concord, CA, 2014; Vol. 22, p 0403.
  46. Koolstra K.; Börnert P.; Brink W. M.; Webb A. G. Improved Image Quality and Reduced Power Deposition in the Spine at 3T Using Extremely High Permittivity Materials. Magn. Reson. Med. 2017, 10.1002/mrm.26721. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am7b06949_si_001.pdf (594.3KB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES