How Water’s Properties Are Encoded in Its Molecular Structure and Energies

Abstract

How are water’s material properties encoded within the structure of the water molecule? This is pertinent to understanding Earth’s living systems, its materials, its geochemistry and geophysics, and a broad spectrum of its industrial chemistry. Water has distinctive liquid and solid properties: It is highly cohesive. It has volumetric anomalies—water’s solid (ice) floats on its liquid; pressure can melt the solid rather than freezing the liquid; heating can shrink the liquid. It has more solid phases than other materials. Its supercooled liquid has divergent thermodynamic response functions. Its glassy state is neither fragile nor strong. Its component ions—hydroxide and protons—diffuse much faster than other ions. Aqueous solvation of ions or oils entails large entropies and heat capacities. We review how these properties are encoded within water’s molecular structure and energies, as understood from theories, simulations, and experiments. Like simpler liquids, water molecules are nearly spherical and interact with each other through van der Waals forces. Unlike simpler liquids, water’s orientation-dependent hydrogen bonding leads to open tetrahedral cage-like structuring that contributes to its remarkable volumetric and thermal properties.

1. Introduction: Why Is Water So Important?

Among materials, water holds a special prominence. It is highly abundant on Earth (occupying 1.4 × 10⁹ km³²⁻⁴). It plays a central role in Earth’s geophysics and geochemistry, and in most of the world’s industries. It is critical for life. It occupies about half the volume inside biological cells, and it controls various important biological actions. It is a basic human need. Therefore, it is also a major source of human conflict and war. Quests for life in the universe are searches for planetary bodies that are capable of supporting liquid water. Water’s boiling and freezing points define the main temperature scales of Celsius and Fahrenheit. Some of our grandest global challenges—distributing clean water, producing cheap and clean energy, providing greater food security, green ways to produce modern chemicals, and curing diseases—depend on a better understanding of water at the molecular level. We expand on these points below.

1.1. Water Is Essential for Life

All forms of life depend on water.^5,6 Liquid water constitutes about half the volume of every living biological cell.⁷ Water can act as a solvent, reactant, product, catalyst, chaperone, messenger, and controller. Interactions with water are a major driving force for biomolecular structure and function in living systems. They are dominant forces in the folding of proteins and nucleic acids, the partitioning of solutes across membranes, and the binding of metabolites and drugs to biomolecules. Specific water molecules often play critical roles in biological mechanisms. To better understand healthy life, and control disease, we need faster and more accurate computational classical and quantum models of water.

Life depends on the solubilities of gases in water. Humanity depends on sea life for food, and they require conditions under which oxygen (O₂) has sufficient solubility in water. Marine plants require carbon dioxide (CO₂), which must be dissolved in water, in order for photosynthesis to produce carbohydrates, which releases oxygen. Gas solubilities in water depend on temperature, pressure, and salinity.

Also important for biology are water’s surface tension and capillary action. The heights and branching of trees depends on water’s capillary action. Due to an interplay of the forces of adhesion and surface tension, water exhibits capillary action whereby water rises into a narrow tube against the force of gravity. Water adheres to the inside wall of the tube and surface tension tends to straighten the surface causing a surface rise and more water is pulled up through cohesion. The process continues as the water flows up the tube until there is enough water such that gravity balances the adhesive force. For example, when water is carried through xylem up stems in plants, the strong intermolecular attractions (cohesion) hold the water column together and adhesive properties maintain the water attachment to the xylem and prevent tension rupture caused by transpiration pull.⁸

1.2. Water Is a Basic Human Need. It Is a Root of Human Conflicts

Despite water’s abundance, its distribution is increasingly problematic for the world’s growing populations; see Figure 1 and Appendix A.3.

Figure 1.

Water covers 71% of Earth’s surface. Most of it is salt water. Only 2.5% of it is fresh water. And, only 1.2% of that fresh water is in rivers and lakes. The rest of Earth’s fresh water is trapped as ice in polar caps and glaciers (68.8%) or underground (30.0%).

The availability of drinking water is limited, and it is shrinking worldwide. By the year 2030, the world’s 8.5 billion people⁹ will consume 6 trillion cubic meters (6000 km³) of water per year.¹⁰ While today 11% of the global population lives with poor access to clean drinking water,¹¹ it is estimated that in 2030 half the world’s population will be living under severe water stress.¹² It is increasingly challenging to get clean water to where it is needed. Early civilizations settled near rivers. But now, clean water is increasingly provided through water purification, desalination,^4,13,14 and transport. Therefore, clean water increasingly requires access to energy. Also, water distribution increasingly poses technical challenges, requiring advances in separating water from salts and oils at low energy costs, for example.

Water conflict is a term used to describe a clash between countries, states, or groups over access to water resources. While traditional wars have rarely been waged over water alone,¹⁵ water conflicts date back at least to 3000 B.C.¹⁶ The U.S. Dust Bowl drought of the 1930s, which covered nearly 80% of the United States at its peak, drove mass migration. More recent droughts occurred in the southwestern United States in the 1950s, and in California and the southern United States in just the past few years. Water has been regarded as a component of conflicts in the Middle East,¹⁷ in Rwanda, and in the Sudanese war in Darfur. Eleven percent of the world’s population, or 783 million people, are still without access to good sources of drinking water.¹¹ Increased water scarcity can compound food insecurity, and put pressure on human survival.

1.3. Water Plays a Major Role in Earth’s Geophysical and Geochemical Cycles

Water plays a role in climate and weather. It is the most abundant greenhouse gas in the atmosphere, accounting for 40–70% of Earth’s retention of heat. The planet’s geochemistry is linked to the cycling of water in seas, lakes, and rivers. For example, water is transported through a hydrological cycle of evaporation, condensation, precipitation, surface and channel runoff, and subsurface flow, driven by energy from the sun. The annual flux of water through the atmosphere is about 4.6 × 10⁵ km³/year¹⁸ and is coupled to water’s cycling in oceans and seas between the surface and bulk.

1.4. Water Is Crucial for Industrial Processes

Almost every manufactured product uses water in at least one part of its production process. Major consumers of water are industries that produce metal, wood, food, and paper, as well as industries based on chemicals, gasoline, and oils. Water is used for fabricating, processing, washing and cleaning, diluting, cooling, or transporting products. Worldwide, agriculture and power generation are the main consumers. Agriculture accounts for 70% of all water consumption, compared to 20% for industry and 10% for domestic use. Electrical power production uses more water than any other industrial process. For example, in 2005 the United States used around 0.76 trillion L of water/day to produce electricity (excluding hydroelectric power), most of which is surface water.¹⁹ It takes about 95 L of water to produce 1 kWh of electricity. In the food industry, about 1000 L of water is needed to produce $1’s worth of sugar.

Industrial processes are a major source of pollutants, accounting for nearly half of the water pollution in the United States.²⁰ Pollutants include asbestos, lead, mercury, nitrates, phosphates, sulfur, oil, and petrochemicals as well as pharmaceuticals, illicit drugs, and personal care products.²¹ The world’s move toward greener chemistry—the reduction of hazardous substances in producing chemicals and reducing pollution—requires new ways to replace organic solvents with water, to better understand water’s role in reaction mechanisms, and to better understand how solutes and toxins partition into the environment.²²⁻²⁵

Better ways are needed to separate water from other materials, such as organic solids, bacteria, and hydrocarbons.²⁶ Each year, 20 billion barrels of water are used in the United States to extract oil and gas. In Oklahoma, the wastewater that results from hydrocarbon extraction is so voluminous that it has been claimed to cause earthquakes.²⁷

2. In Some Ways, Water Is a Normal Material; In Other Ways, It Is Unusual

In certain ways, water is a fairly normal material. For example, at low temperatures, water is a solid (ice). Heating causes melting, a phase transition to the liquid state. Further heating causes boiling, a phase transition to the vapor state. Therefore, at this level, water’s pressure–temperature (pT) phase diagram—which expresses these general features—resembles the phase diagram of other materials. And, like other polar liquids in general, water readily dissolves salts and ions, but does not so readily dissolve nonpolar molecules, such as oils.

However, in other ways, water is complex and anomalous. Its quirkiness is reflected in various experimental observables, and requires understanding through different types of theory, simulations, and modeling. Water is more cohesive than materials made of molecules of equivalent size and shape. Water molecules associate with each other relatively tightly. Therefore, H₂O has relatively high values of surface tension, melting point, and boiling point. And, water has density anomalies that are manifested in various ways (see Figure 2). For example, ice floats on liquid water. In most other materials, the solid sinks in the liquid. Related to this, the slope of water’s pT equilibrium phase boundary between the solid and liquid is negative, whereas it is positive for other materials. Therefore, applying pressure melts water’s solid into a liquid, whereas applying pressure drives most liquids to freeze into a solid. And, while typical materials have only one or two solid phases, water has more than a dozen phases of its solid, ice (see also Figure 10). Water is a polar molecule, so its liquid can dissolve polar and ionic solutes. Its thermodynamic signatures for dissolving nonpolar molecules are different from those of most other solvents. To signify that difference, it has been given its own name: the hydrophobic effect.

Figure 2.

Water has volumetric anomalies. Shown here for liquid water are the temperature dependences of its heat capacity (C_P), molar volume (v), thermal expansion coefficient (α), and isothermal compressibility (κ_T) for water (black lines) and a Lennard-Jones simple fluid (σ = 2.9 Å, ϵ = 0.8 kcal mol^–1) (gray lines). Water’s heat capacity is relatively large, because water stores energy in both its van der Waals and hydrogen bonds. Water has a minimum volume (red circle), i.e., a temperature of maximum density, TMD, at 4 °C, whereas the volumes of simpler liquids increase monotonically. Cold water has a negative thermal expansion coefficient between 0 and 4 °C (red circle); heating shrinks it. Water has a negative derivative of compressibility at temperatures lower than 46 °C (red circle); heating makes it less compressible. (Data collected from from ref (28).)

Figure 10.

Water’s temperature–pressure phase diagram shows its many solid phases. There are 17 known crystalline forms of water. Not pictured in this diagram are proton-ordered variations (such as ice XI which is a proton-ordered form of ice I_h, where waters orient in a repeated manner rather than the more typical random fashion) and metastable forms (such as ice XVI, which is formed by solute evacuation from clathrate hydrates).

3. How Do We Know Water’s Structure–Property Relationships?

Much of what is known about water’s structure–property relationship comes from bulk measurements, such as the enthalpies, entropies, and heat capacities of pure water in its various phases; changes in those thermal quantities upon melting or boiling, or changes due to dissolving solutes; changes due to applied pressure; changes of electrical properties in applied electric fields; and measured surface tensions, for example. However, to learn how material properties are encoded within molecular structures requires more than just experiments. It also requires models, theories, and simulations. Without modeling, we cannot interpret observable properties in terms of water’s molecular structure, energetics, and population distributions. Making the structure–property connection requires knowing the driving forces. Because no single type of model currently gives a full picture, we look here through the lenses of different models and theories.

Water has been modeled variously: as a simple continuous medium for fast calculations of solvation or dielectric properties; or as simplified statistical mechanical sphere-like particles with hydrogen bonding arms; or by using fixed-charge or polarizable atomically detailed models in computer simulations; or at the (computationally expensive) quantum mechanical level for insights into the nature of electronic structure and the bonding of the atoms (see Figure 3). Each of these approaches has its own target problems and its own research communities.

Figure 3.

Different water models serve different purposes. (left) Coarse-grained and reduced-dimensionality models. These allow for the most extensive sampling of configurations, and are useful for modeling the statistical mechanics, partition functions, entropies, and heat capacities. (middle) Atomically detailed semiempirical models are used in molecular dynamics and Monte Carlo simulations of liquid and solid states. (middle left) Fixed-charge models. (middle right) Polarizable models. (right) Quantum mechanical (QM) models represent the atomic nuclei and electrons explicitly, for studying bonding. QM modeling is computationally expensive.

There are several classic reviews on the properties of water and water modeling.²⁹⁻³³ Guillot summarized computer simulations of semiempirical models.³⁴ Ben-Naim has reviewed different types of models of water and solvation, including its anomalous properties.^35,36 A website Water Structure and Science gives an extensive collection of physical, chemical, and biological properties of water, from experiments, simulations, and theory.³⁷ Recently, a thematic issue on Water—The Most Anomalous Liquid was published in Chemical Reviews (2016, 116 (13)) with in-depth reviews of various methodologies. And, Sun and Sun recently reviewed the role of hydrogen-bond cooperativity in water’s anomalous properties.³⁸ The present review goes beyond—but is is similar in spirit to—refs (39 and 40).

This review describes structure–function principles; here is a brief overview.^34,40

1. Water is tetrahedral. It forms hydrogen bonds. Water has strong orientational interactions in addition to van der Waals attractions and repulsions.

2. This leads to cage-like structuring, not only in the solid phases (ices) but also even in liquid water. In 1892, W. C. Röntgen (who was also the discoverer of X-rays) postulated that liquid water is a mixture of two fluids: a low-density one and a high-density one.^29,41 In 1933, Bernal and Fowler⁴² suggested that the tetrahedral geometry of water molecules might be responsible for water’s unusual properties.

3. Liquid water is a mixture of types of structure. Over the following two decades, more microscopic models emerged, of how water’s structure gives water’s macroscopic properties.^43,44 From these liquid water appears to be a mixture of types of structure. Among the first quantitative models was that of Pople in 1951,⁴⁵ which went beyond treating waters as being of just two types—crystal-like or not—and supposed that waters had distributions of hydrogen bonding.

3.1. Modeling Water’s Quantum Mechanics, Electrons, and Hydrogen Bonding

The most fundamental level of water modeling is quantum mechanical. At this level, a water molecule is understood by solving the Schrödinger equation for 10 electrons in the molecule, obtaining the covalent bonding of two hydrogen atoms and one oxygen atom. The hybridization of the molecular orbitals is sp³, which means that a water molecule has tetrahedral structure, even though the three atoms are coplanar. This tetrahedral structure is reflected in the network-like structures in condensed phases of water (resembling those of tetrahedral elements such as Si or Ge).

The molecular orbitals (MOs) of water are shown in Figure 4. The four orbitals to the left of the dashed line each contain two electrons. To the right of the dashed line is the first empty orbital (lowest unoccupied molecular orbital, or LUMO); this plays a role in water hydrogen bonding. The lone-pair orbitals of water are a linear combination of the 1b1 (highest occupied molecular orbital, or HOMO) and 3a1 MOs. The two lone pairs of water are perpendicular to the molecular plane. The two covalent bonding orbitals are directed along the OH bond directions and are a linear combination of the first two orbitals in Figure 4. These four orbitals have maximum electron densities along the tetrahedral directions (sp³ hybridization). A hydrogen bond (HB) forms between the positively charged hydrogen atom of the donor molecule and the lone pair electrons of the acceptor molecule.

Figure 4.

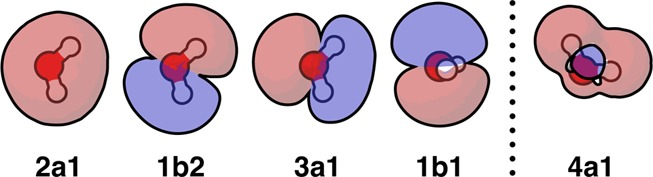
Molecular orbitals of water, labeled by their symmetries.

A hydrogen bond occurs when a hydrogen atom that is bound covalently to an electronegative atom (such as oxygen, nitrogen, or fluorine) shifts its charge distribution when another nearby electronegative atom attracts it. A hydrogen bond can be regarded as an electrostatic polarization, both intramolecular and intermolecular,⁴⁶ but also entails a quantum mechanical charge-transfer component. The power of ab initio quantum mechanical modeling is in its ability to reveal the nature of bonding within water molecules in small clusters. But quantum modeling at the highest theoretical level is computationally expensive, so only very small clusters can be studied this way.

Simulations of larger structures—of sizes up to several hundred water molecules, in liquid form and in ices⁴⁷—can be modeled by starting from an ab initio force field that gives a highly accurate quantum chemical representation of water and clusters, and then approximating the oxygen polarizability by fitting functions to gain computational speed.⁴⁸⁻⁵⁴ This level of modeling shows how the shifting of the distribution of water’s electrons is needed to account for hydrogen-bond cooperativity⁵⁵ effects (whereby hydrogen bonds become stronger in the presence of other hydrogen bonds).

The properties that are captured by modeling these systems are water’s diffusion properties, its polarizability and dielectric function,⁵⁶ optical spectroscopic properties,⁵⁷ the anomalous isotope effect in ice,⁵⁸ the density anomaly,⁵⁹ IR spectra,⁵⁷ structures of small water clusters,⁶⁰ and H-bond dynamics.⁶¹

Modeling such collections of water quantum mechanically requires simplifications and approximations. An important methodology is density functional theory (DFT) of electronic structure. Rather than to compute wave functions of all the many individual electrons and nuclei of multimolecule systems, DFT computes far fewer quantities, namely the overall spatial electron density. In the Born–Oppenheimer approximation (BO), the atomic nuclei are described by the laws of classical physics and the electronic wave functions are computed at each time step (or at each different nuclei position). In Car–Parrinello (CP) molecular dynamics,⁶² the motions of electrons and ions are treated together and the electronic wave functions are propagated as classical degrees of freedom.⁶³ An advantage of CP is its computational efficiency.

Quantum modeling—with its ability to account for the electrons and their distributions—is a powerful way to study the nature of the bonding among water molecules, in small clusters. However, for modeling water on the larger scale—such as in its bulk liquid state, or as it undergoes phase changes to solid or vapor states, or as a solvent for ions or nonpolar molecules, or at chemical or biological surfaces—the most popular current approaches are theories and simulations at a coarser-grained or more approximate level.

3.2. Water Is Often Modeled through Semiempirical Classical Simulations Using Atomistic Potentials

Beginning around 1970, a popular approach has been to model water using semiempirical classical (i.e., not quantum) intermolecular potentials, which are sampled according to the laws of statistical physics through the use of Monte Carlo (MC) or molecular dynamics (MD) in computer simulations. In 1969, MC simulations of pure water were performed by Barker and Watts.⁶⁴ They assumed an orientation-dependent water–water pair potential consisting of a central Lennard-Jones particle surrounded by four charges, two partially positive ones centered on hydrogen atom locations and two neutralizing negative charges placed at orthogonal p-orbital locations about the oxygen center.⁶⁵ In 1971, MD simulations were performed by Rahman and Stillinger based on a symmetrical tetrad arrangement of charges centered on the Lennard-Jones site.^66,67 The latter evolved into the popular ST2 model for liquid water.^68,69 ST2 gave some of the first detailed insights into the distributions of structures in liquid water. Prior to these works, there was no way to know more than just bulk averages of experimentally observable properties, and no way to see how water’s properties were encoded in water’s molecular structure and energetics. In 1983, Stillinger noted that, because of water’s tetrahedral capacity to form multiple hydrogen bonds, liquid water is a hydrogen-bonded network that, although transient and amorphous, nevertheless has much of the ice-like character of its solid. The special directionality of the hydrogen bonds is responsible for many of the anomalous water properties.⁷⁰ He also noted that the H-bonding network in the liquid resembled the known ice network structures and he showed how the optimal structure of the water dimer is the key to understanding the strengths and properties of the hydrogen bonding. Stillinger’s computer simulations related the radial distribution functions (RDFs) of liquid water to the average number of nearest neighbors, which is close to four, because of water’s tetrahedral character, rather than the larger number of nearest neighbors that results from simpler van der Waals liquids, which pack more like marbles in a jar. Experimental measurements showed that the average number of hydrogen bonds in liquid water is in fact around 3.5 (estimates of fewer neighbors have been shown to be incorrect⁷¹).

In the 1980s, simpler and computationally more efficient models emerged, such as Jorgensen’s transferable intermolecular potential (TIP) models^72,73 and Berendsen’s simple point charge (SPC) model.⁷⁴⁻⁷⁶ The TIP and SPC models are now major workhorses for simulating water. The TIP3P model has become widely used because it is able to capture water’s liquid properties with sufficient accuracy, with only three point sites (hence, the 3P designation) of interaction, so it is computationally efficient. Because the ST2 model has five sites of point interactions, it is more costly than TIP3P. TIP3P and related models are widely used in molecular mechanics packages such as CHARMM and AMBER, as they are considered the preferred water types in the default force fields for these packages.^77,78 Like TIP3P, Berendsen developed the three-point SPC model of water with the same benefits of efficiency and transferability. SPC is simple, having hydrogen bond lengths of 1 Å and a tetrahedral bond angle of 109.47°. Then, in order to better capture liquid-state properties in a three-point water model, SPC/E was developed to include the missing condensed-phase electronic polarization.⁷⁴ The resulting model better reproduces pure liquid water properties including the density, diffusion constant, and liquid structure. SPC is the default model for the GROMOS package and force field. Intermediate in cost-performance trade-off are the four-point models, such as TIP4P.⁷⁹⁻⁸² Some water model parameters are given in the Appendix in Table 5, and some properties are listed in Table 6.

Table 5. Parameters of Some Water Molecular Models^a.

model	type	σ [Å]	ε [kJ mol–1]	l1 [Å]	l2 [Å]	q1 [e0]	q2 [e0]	θ [deg]	ϕ [deg]
SPC	a	3.166	0.65	1	–	0.41	–0.82	109.47	–
SPC/E	a	3.166	0.65	1	–	0.4238	–0.8476	109.47	–
TIP3P	a	3.15061	0.6364	0.9572	–	0.417	–0.834	104.52	–
iAMOEBAb	a	3.6453	0.8235	0.9584	–	0.29701	–0.59402	106.48	–
TIP4P	b	3.15365	0.648	0.9572	0.15	0.52	–1.04	104.52	52.26
TIP4P-Ew	b	3.16435	0.680946	0.9572	0.125	0.52422	–1.04844	104.52	52.26
TIP4P/2005	b	3.1589	0.7749	0.9572	0.1546	0.5564	–1.1128	104.52	52.26
ST2	c	3.1	0.31694	1	0.8	0.24357	–0.24357	109.47	109.47
TIP5P	c	3.12	0.6694	0.9572	0.7	0.241	–0.241	104.52	109.47
TIP5P-Ew	c	3.097	0.7448	0.9572	0.7	0.241	–0.241	104.52	109.47

^aData collected from ref (37).

^biAMOEBA is a polarizable water model.

Table 6. Calculated Physical Properties of Some Water Models at 25 °C and 101.3 kPa^a.

model	dipole moment [D]	dielectric const	self-diffusion, 10–5 [cm2 s–1]	density max [°C]	expansion coeff, 10–4 [°C–1]
SPC	2.27	65	3.85	–45	7.3b
SPC/E	2.35	71	2.49	–38	5.14
TIP3P	2.35	82	5.19	–91	9.2
iAMOEBA	2.78	80.7	2.54	4	2.5
TIP4P	2.18	53	3.29	–25	4.4
TIP4P-Ew	2.32	62.9	2.4	1	3.1
TIP4P/2005	2.305	60	2.08	5	2.8
TIP5P	2.29	81.5	2.62	4	6.3
TIP5P-Ew	2.29	92	2.8	8	4.9
exptl	2.95	78.4	2.3	3.984	2.53

^aData collected from ref (37).

^bAt 27 °C.

Some recent models are more coarse-grained. An example is the monatomic water (mW) model of Molinero and Moore, which uses a parametrized Stillinger–Weber potential.⁸³ Water’s hydrogen bonding is mimicked through an angle-dependent three-body potential term encouraging tetrahedral configurations. The mW model is computationaly efficient and gives the energetics, structure, and density of liquid water, as well as water’s anomalies⁸⁴ and phase transitions with comparable accuracy as most atomistic water models. The mW model was, among others, applied to studies of ice nucleation,⁸⁵ confined water,⁸⁶ hydrophobicity,⁸⁷ and clathrate hydrates.⁸⁸ A slightly more complex class of single-point models called the soft sticky dipole (SSD) model is also popular for efficient simulation of water.⁸⁹ SSD is an extension of the hard sphere BBL model,⁹⁰ and it uses point multipoles for electrostatic interactions with surrounding molecules and a tetrahedral spherical harmonic potential for hydrogen bonding between neighboring water molecules. SSD and its extended variants have been used to study liquid water structure and dynamics,⁹¹⁻⁹⁵ ice nucleation,⁹⁶ and confined water,⁹⁷ and it shows promise for general aqueous solvation investigations.^98,99

Even more coarse-grained are those models in which water’s atoms are collectively represented by a single interaction site.^100−107 Or, multiple water molecules can even be represented by a single site.^108−111 Yet another approach is to approximate each water molecule as being spherically symmetrical, using so-called isotropic core-softened potentials.^112−115 Rather than to represent hydrogen bonding as tetrahedral and dependent on orientations, these spherically symmetric models treat water–water interactions by supposing that there is tight binding at close water–water distances and weaker binding at greater water–water separations. Such models show that some volumetric anomalies can be captured without explicitly accounting for orientation-dependent hydrogen bonding.

Other recent modeling has been toward more refinement or detail, for example by incorporating three-body or many-body terms, such as in the E3B and MB-pol models.^116−118 It has been argued that fixed-charged models are approaching their limits of optimizability through parameter variations.^82,119,120 Further improvements beyond fixed-charge models are being sought by including polarizabilities, whereby the charge distributions within the molecule can shift depending on the molecular conformation or environment. The development of analytical potentials representing the many-body effects were recently reviewed in ref (121). So far, however, polarizable models have not yet become mainstream, partly because they are computationally expensive.

3.3. The Mercedes-Benz Coarse-Grained Model That Captures Water’s Orientational–Translational Coupling

Some of water’s major features are a consequence of its cage-like structuring and the prominent entropies and heat capacities that arise from it. Fine-grained atomically detailed simulations can be too “in the weeds” to capture these properties. Alternatively, water can be modeled using statistical mechanical liquid theories, which are good at expressing distributions of populations because of the various ways that statistical mechanics can compute averages over large ensembles. But, liquid-state theories often require potentials that have special simplicity, such as spherical symmetry, so they miss key aspects of how water’s properties arise from its tetrahedral cage-like structures.

Thus, into this breach arose the Mercedes-Benz (MB) model and its variants. It gets its name from the fact that the two-dimensional (2D) version of the MB model looks like the Mercedes-Benz logo—a circle with three radial arms that represent hydrogen bonds (see Figure 3, left). The power of MB-type models is that they do capture the translational–orientational coupling that comes from water’s orientation-dependent hydrogen bonding, while at the same time they also allow for the statistical mechanical averaging that is needed to express structural distributions, entropies, heat capacities, and free energies of large systems.⁴⁰ The Mercedes-Benz (MB) model¹²² and its variants have been studied by Monte Carlo,^123−126 integral equations,^127,128 and mean-field analytics.^129−133 Throughout this review, we often present 2D images from this and other similar models (Rose water model¹³⁴) to convey structure–property relations in a simple way.

4. How Are Water’s Properties Encoded in Its Molecular Structure and Energetics?

Our starting point for understanding water’s unique properties is its tetrahedral hydrogen bonding organization (see Figure 5).^135−137 In classical terms, the collective interactions between water molecules can be represented by (i) a radial dispersion attraction with steric repulsion at short-range and (ii) electrostatic interactions between spatially localized groupings of charge. In this way, hydrogen bonding is a consequence of these localized electrostatic interactions leading to nearly tetrahedral arrangement of surrounding water molecules. Water is often compared to simpler liquids, which do not structure as strongly and can be more easily treated with uniform interactions. Below, we describe structure–property relationships of water, as seen from various theoretical and modeling studies.

Figure 5.

Water molecules form hydrogen bonds, giving tetrahedral structuring. The attractive interactions between water molecules can be represented with a uniform dispersion term and strong localized electrostatics, giving rise to the tetrahedral arrangement of hydrogen bonds about each water.

4.1. Water Is More Cohesive than Simpler Liquids, due to Its Hydrogen Bonding

Liquid water tends to be a more cohesive than other simple liquids, because water–water attractions arise from hydrogen bonding in addition to van der Waals interactions that are typical in simpler liquids. For example, a higher temperature is required to melt ice than to melt solids of simple liquids. And, a higher temperature is required to boil liquid water than to boil other simpler liquids. In addition, water has a relatively high surface tension, of 72.8 mN m^–1 at room temperature, due to its high cohesion, the highest of the common nonionic, nonmetallic liquids.

Table 1 compares the properties of water (H₂O) and hydrogen sulfide (H₂S), which have similar atomic structures. Both have sp³ hybridized orbitals, with bond angles (of HOH and HSH) being 104.45° and 92.1°, respectively. Oxygen and sulfur belong to the same group of the periodic table. But, because sulfur has twice as many electrons as oxygen, it is larger and less electronegative. Therefore, the O–H bond is much more polar than the S–H bond. Even though H₂S has almost twice the molar mass of H₂O, it is a gas at room temperature and pressure, while H₂O is a liquid, indicating greater cohesion in water. Because of its hydrogen bonding, water has a higher melting point, boiling point, and heat of vaporization, as well as a higher heat capacity (which reflects the higher capability for storing thermal energy through these additional types of bonds).

Table 1. H₂O Is More Cohesive than H₂S, Despite Their Similar Structures, Because Water Forms Hydrogen Bonds.

property	H2O	H2S
molar mass [g mol–1]	18.015	34.081
boiling pointa [K]	373.12	212.85
melting pointa [K]	273.15	187.45
enthalpy of vaporizationb [kJ mol–1]	40.657	18.622
entropy of vaporizationb [J mol–1 K–1]	108.95	87.9
critical temperature [K]	647.1	373.2
critical pressure [MPa]	22.06	8.94
critical molar volume [cm3 mol–1]	55.9	98.5
critical density [kg m–3]	322	347
critical compressibility	0.229	0.284
specific heat capacityc (CV) [J mol–1 K–1]	74.539	26
specific heat capacityc (Cp) [J mol–1 K–1]	75.3	34.6

^aAt 101.3 kPa.

^bAt boiling.

^cAt 25 °C and 101.3 kPa.

A useful way to compare the energetics of water and simpler materials is with an energy ladder; see Figure 6. States of lower energy are lower on the ladder. The laws of thermodynamics say that the densities of liquids and solids are determined, at any given temperature and pressure, by the molecular arrangement that has the lowest free energy. Figure 6, left, shows a simple material. The lowest-energy state of a simple material is the solid, typically held together by van der Waals forces. Introducing energy (say, by raising the temperature to the melting point) melts the solid, leading to fewer weaker, more disordered van der Waals interactions in the liquid state. Introducing even more energy breaks the remaining van der Waals contacts, boiling the liquid. Figure 6, right, illustrates how water is more cohesive than the simpler liquid. The melting temperature of water is higher than that for the liquid on the left in part because of the hydrogen bonding (which is tetrahedral in real water, shown as hexagonal here in a two-dimensional toy version of water). The boiling temperature of water is higher than that for the simpler material also because hydrogen bonding contributes cohesion to water. Figure 6 also shows the nature of the two states of liquid water: that cold water tends to retain a little more cage-like, ice-like structure and hot water tends to retain less of it.

Figure 6.

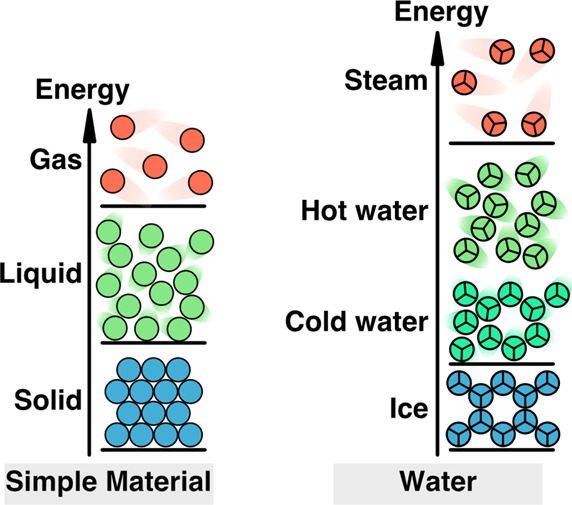
Energy–volume relationship of water, vs simpler materials. (left) Simple materials (cold) achieve low energies by tight-binding into solids, (warmer) achieve higher energies by forming looser liquid states, and (hot) achieve the highest energies when most bonds are broken in the gas phase. The black bars indicate transitions: heating melts the solid, then boils the liquid. (right) Water (very cold, ice) achieves its lowest energies through open low-density hydrogen bonded structures, (cold liquid water) achieves intermediate energies through some breakage of cages, leading to increased density, (hot liquid water) achieves higher energies by breakage of more bonds, leading to looser liquid, and (hot) achieves its highest energies, like simpler materials, by breaking most bonds, to reach the low-density gas phase.

4.2. Water’s Volumetric Anomalies Arise from a Competition between van der Waals Attractions and Hydrogen-Bond-Driven Expansion

Water has volumetric anomalies. For example, ice floats. The solids of most other materials are compact and more dense, leading them to sink to the bottom of their own liquid. For water, the solid is less dense than its liquid. This is because cold water is dominated by its hydrogen bonding, which is tetrahedral, leading to only four neighbors of any given water molecule. Cold water at low pressure tends to maximize its hydrogen bonding, which tends to cause its structure to be open and loose. Simpler materials, such as argon, pack more like hard spheres, having higher densities because each molecule has up to 12 nearest neighbors. Only under higher pressures will the open structure of ice collapse to form dense, interconnected lattices. Figure 7 shows how the tetrahedral nature of the strong hydrogen bonding tends to lead to open structures, competing with the weaker and omnidirectional van der Waals interactions that simply favor more neighbors and higher densities.

Figure 7.

Densities of some phases of water, illustrated in a 2D model. At high pressures, ices are dense, having some broken hydrogen bonds. At lower pressures (say, 1 bar), ices are less dense, having more optimal hydrogen bonding. Liquid water is more disordered, but still has much residual cage-like structuring.

Figure 8 interprets these ladders of molecular organization in terms of the different populations, energies, and molecular volumes of the states.^40,129,130 Thermodynamics says that the densities of liquids and solids are determined, for any given temperature and pressure, by the volumetric state that has the lowest free energy. This can be expressed approximately using the energy-ladder diagrams of Figure 8. On both diagrams, the bottom energy levels show the stable states of the cold material and the top energy levels show the stable states of the hot material. Figure 8, top, shows a normal simple material: At low temperature, the material populates its low energy levels, so the material is a high-density solid. At high temperature, the material populates its high energy levels, so it is a low-density gas. In between, the material is a liquid, having intermediate density. Figure 8, bottom, shows how water is different from this. We illustrate this using five energy levels. (level 1) At low temperature below freezing, water’s energies are dominated by hydrogen bonding, so water’s structure is ice, which is low density. (level 2) Slightly warmer, above freezing, in cold liquid water, some hydrogen bonds are broken and some van der Waals interactions are made, leading to slightly denser water. (level 3) Heating still further, to warm liquid water, breaks more hydrogen bonds and makes more van der Waals contacts, so water then becomes still denser. (level 4) Heating further, to hot liquid water, now leads to breaking both hydrogen bonds and van der Waals interactions, leading to reduced density, as would be observed in a normal simpler liquid. (level 5) Higher temperatures boil the liquid, turning it into a gas, which has much lower density.

Figure 8.

Water’s density (D) anomalies are correlated with shifts in Density of State (DoS) populations. (left) Same energy ladders as in Figure 6. (top right) Increasing temperature leads to shifting populations from ice-like on the left to vapor-like on the right. (bottom right) Heating a simple material drives it from solid (high density) to liquid (slightly lower density) to gas (very low density). Heating water drives it from ice (low density) to cold water (higher density) to hot water (lower density) to gas (very low density).

Some of water’s anomalies can be explained using Figure 8. First, ice floats on water because ice has lower density due to its open hydrogen-bonded tetrahedral structures. A second anomaly is that water has a temperature of maximum density (TMD, of approximately 4 °C) in its liquid range, whereas other materials are maximally dense in their solid states. Upon going from its melting point at 0 °C to its TMD at 4 °C, liquid water gets denser because heating melts some low-density, cage-structure waters into higher density van der Waals contact structures. This is also reflected in a third anomaly: just above 0 °C, water has a negative thermal expansion coefficient, indicating its increasing density with temperature. Then, heating beyond the TMD, liquid water expands like other materials do because heating loosens the intermolecular bonding.

There are practical consequences of water’s density anomalies. One is shown in Figure 9. Whereas simpler materials freeze from the bottom up, lakes filled with water freeze from the top down, since ice is less dense than liquid water.

Figure 9.

Lakes freeze from the top, not the bottom. Ice floats because it is less dense than the liquid. So, even in wintry frozen lakes, fish can live at the bottom, where water is liquid.

Another anomaly is water’s nuclear isotope effect. Typically, molecules having a heavier isotope form a higher-density material than molecules having the lighter isotope. Molecules with the heavier isotope form tighter intermolecular bonds. For example, at low temperatures, ²⁰Ne is denser than ¹⁸Ne. But for water, it is the opposite. That is, ice having the lighter hydrogen isotope (H₂O) is denser than ice having the heavier deuterium isotope (D₂O). The reason for this results from an anomaly due to a subtle quantum effect of the zero-point energies.^58,138 In the primary isotope effect, the covalent, intramolecular OH distance is observed to be longer than the OD distance. In the secondary isotope effect, the H-bond donor–acceptor (oxygen–oxygen) distance R changes upon isotopic substitution, being shorter for H than for D in ice. In general this occurs in materials with strong H-bonds, while in materials with weaker H-bonds the opposite effect occurs.^139−144 Surprisingly, the anomalous isotope effect reflected in the volume of water per molecule becomes greater at room temperature water—the volume per molecule of D₂O is slightly larger than H₂O, suggesting that H-bonds in H₂O water are stronger than in D₂O.

5. Water Has Many Solid Crystalline (Ice) Phases

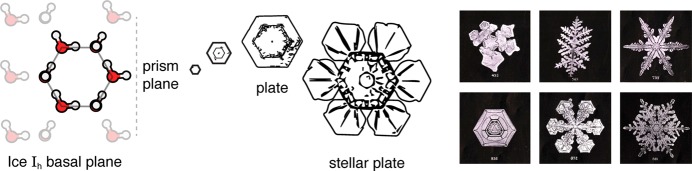
The phase diagram of solid water shows many crystalline phases (Figure 10). The molecular structures of some of them are shown in Figure 11. The most familiar form of ice is hexagonal, ice I_h. Hexagonal ice has a relatively open structure and a lower density than that of liquid water. The term hexagonal comes from its crystal structure, as shown in Figure 12, when looking at the basal plane of the crystal. This is the basal plane because the rotational symmetry in this plane gives rise to six prism planes. Water ordering and crystal growth have been shown to be enhanced on the prism planes relative to the basal planes.^145,146 The densities and crystal forms of various ices are given in Table 4.

Figure 11.

Different ice forms have different densities, driven by different temperatures and pressures. At the extremely high pressures on top (ice X), the red oxygen atoms and white hydrogen atoms are compressed so tightly that the hydrogen bond and covalent bond lengths in water are the same.

Figure 12.

Snowflakes have sixfold symmetries because of the elementary hexagonal structures formed by hydrogen bonding in ice I_h crystals. (right) Photos from Wilson Bentley taken in the winter of 1901–1902.¹⁴⁷

Table 4. Crystal Structure and Density of Various Ice Forms^a.

ice form	crystal structure	density [g cm–3]
Ih	hexagonal	0.92
Ic	cubic	0.93
II	rhombohedral	1.17
III	tetragonal	1.14
IV	rhombohedral	1.27
V	monoclinic	1.23
VI	tetragonal	1.31
VII	cubic	1.50
VIII	tetragonal	1.46
IX	tetragonal	1.16
X	cubic	2.51
XI	orthorhombic	0.92
XII	tetragonal	1.29
XIII	monoclinic	1.23
XIV	orthorhombic	1.29
XV	pseudoorthorhombic	1.30
XVI	cubic	0.81

^aData collected from ref (37).

Why do snowflakes have such beautiful symmetries? Snowflake structures are a result of water’s hexagonal symmetries, which are the basis for sixfold directional growth in this plane. Snowflakes start as small six-sided plate crystals or prisms. Depending on the temperature and humidity, they may continue to grow as plates or become needles, stellar plates, or dendrites, among others, as seen in Figure 12.^147−149 Defects in crystal growth lead to the immense variety of snowflake shapes, captured in the historic photographs from Wilson Bentley’s early studies.¹⁴⁷

Some ices are proton-disordered and some are proton-ordered. This terminology refers to whether a given ice structure is achievable by multiple degenerate microscopic water configurations, or just one. In its tetrahedral lattice about the oxygen atom centers, each water molecule has six possible orientations. There is a disorder (and a corresponding entropy of R ln (3/2)¹⁵⁰) that arises from these options that are available to the molecule. Ice I_h is proton-disordered because, at each lattice site, a water molecule can have different orientations. In proton-ordered ices, a water molecule can have only one configuration at each lattice site. You can experimentally craft proton-ordered forms of ice by promoting proton tunneling via the introduction of a defect (KOH can provide excess OH^– ions, for example) at very cold temperatures. Then, the protons will arrange until the water molecules all order perfectly in regular directions. The entropy for these ordered forms of ice is 0, satisfying the “perfectly crystalline solid” requirement of the third law of thermodynamics. A famous (but fictional) example of a proton-ordered ice is ice-nine, made popular in Kurt Vonnegut’s novel Cat’s Cradle.¹⁵¹ In that novel, it was imagined that this form of ice could nucleate whole bodies of water to freeze on contact, killing people instantly, leading to a global catastrophe. Fortunately, Vonnegut’s ice-nine is fictitious. In reality, ice IX is a proton-ordered form of ice III, and only exists at very low temperatures and high pressures, so it is not threatening to life on Earth.

6. Does Supercooled Water Have a Liquid–Liquid Critical Point?

Water can be supercooled. That is, water can be prevented from freezing—and remain a liquid—even below its normal freezing point, by careful experiments that avoid nucleation. In principle, water can be supercooled to about 150 K, which is the temperature at which devitrified (ultraviscous) water spontaneously freezes to cubic ice.^152−154 In practice, this point has yet to be reached because water undergoes homogeneous nucleation first. This is a kinetic point at which nucleation of the crystal happens spontaneously. The limit reached so far is about 227 K, by evaporative cooling experiments.¹⁵⁵ The region between the spontaneous crystallization temperature of devitrified water and the homogeneous nucleation temperature is called no-man’s land.

Two key properties of interest of supercooled water are the isothermal compressibility κ_T = (∂ ln ρ/∂ ln p)_p and the isobaric heat capacity C_p = T (∂S/∂T)_p, where p is the pressure, T is the temperature, ρ is water’s density, and S is the entropy (see Figure 13). In 1976 Angell and Speedy showed that, as they lowered the temperature of supercooled water, these two quantities appeared to grow large, and possibly diverge, when extrapolated to −45 °C.¹⁵⁶

Figure 13.

Supercooling water to low temperatures leads to a large divergent compressibility (top) and heat capacity (bottom). These quantities appear to diverge for temperatures approaching −45 °C. It is not clear whether this means water is approaching a typical spinodal point (i.e., the system must freeze to ice), or a point of phase transition between two liquid states. Data collected from refs (163) and (156).

What molecular structures of water can explain these apparent divergences of supercooled water? The large values of the heat capacity and compressibility indicate large variances in the energies and densities of the underlying molecular organization of water. One conjecture is that this divergence simply indicates a system reaching a spinodal point, beyond which there is no metastable liquid phase and beyond which the system must freeze. An alternative conjecture is that this divergence reflects a phase transition between two different metastable liquid phases.^157−159 To come to a deeper understanding, supercooled water has been studied by structural experiments. For example, X-ray structure factors have been used to determine radial distribution functions¹⁶⁰ and X-ray absorption and X-ray Raman scattering^161,162 have been used to determine first coordination shells in supercooled water.

The idea of a liquid–liquid coexistence is that there are two species of water, A and B, with temperature-dependent concentrations x_A(T) and x_B(T),¹⁶⁴ a high-density liquid (HDL) and a low-density liquid (LDL).¹⁶⁵ LDL could be thought of as more cage-like and HDL as less cage-like, for example. Urquidi et al. interpreted their experiments in terms of two types of dynamically interconverting microdomains having, on average, bonding characteristic of water in ice I_h and ice II.¹⁶⁶ These hypothetical liquids derive some experimental justification from known low-density and high-density amorphous ices (LDA and HDA, respectively).¹⁶⁷ LDA is formed by depositing water vapor on single-crystal metallic surfaces, and HDA is obtained applying pressure to ice I_h. The idea of a liquid–liquid critical point is partly motivated by the observation of a first-order phase transition between LDA and HDA.

The properties of supercooled water have been explored by computer simulations. Supercooled water likely has a critical point below the homogeneous nucleation temperature, so it cannot be probed directly by experiments, hence the need for computer simulations of liquid water in no-man’s land.^168−170 Definitive results have been difficult to obtain because (1) phase equilibria are slow processes that challenge computational resources and (2) any possible free energy barriers are small and subtle, requiring extensive computational sampling, and different models can give different results.^{162,171−177} At the center of this animated debate has been the ST2 water model.¹⁷⁸ Recent modeling, however, does appear to support the view that supercooled water undergoes a liquid–liquid phase transition.^179−181 Further support comes from a study in 2015 by Smallenburg and Sciortino, who proved that tetravalent model systems similar to water have two stable supercooled liquid phases.¹⁸²

7. How Is Water Structured around Solutes That Are Nonpolar?

Water is called the universal solvent because it dissolves a wide variety of substances. Water is polar, so it readily dissolves charged or polar solutes. Water also dissolves some molecules that have nonpolar character, such as aromatics and surfactants. However, water is not a good solvent for nonpolar molecules such as hydrocarbons (oils). This is the basis for the expression that “oil and water don’t mix”. This avoidance tendency of oils for water is the basis for many important processes, such as the following. Surfactants and soaps spontaneously form micelles in water; it is the basis for their cleaning actions. Lipids spontaneously form bilayers, forming the structures of cell membranes, which defines the “self” of the cell. Drugs and metabolites either partition into lipid bilayers or not, depending on their degree of nonpolarity, dictating whether or not they have biological or medicinal properties. Protein molecules, which tend to contain about equal numbers of polar and nonpolar amino acids, fold into compact structures—the nonpolar parts forming a core, minimizing their contact with water. These folded structures perform most of the chemical and mechanical properties of living cells. Many of the binding processes in biology—of proteins to other proteins or to DNA or to drugs and metabolites—are driven predominantly by the degree to which nonpolar molecules tend to avoid solvation in water. Many of the methods of separation or analysis of analytical chemistry, such as reversed-phase chromatography, are governed by the varying affinities of solutes for water. Toxins and pollutants partition into environments, including into otherwise clean water, depending on their degrees of nonpolarity.

You can study solutes dissolved in water using partitioning experiments. These experiments measure the solute concentration in water and the solute concentration in an oil or vapor phase that is in equilibrium with the water. Polar solutes tend to concentrate more in water, whereas nonpolar solutes tend to concentrate more in oil phases. The space of all possible solute molecules is huge. Therefore, the goal of determining solvation in water of a broad range of solutes has been made simpler using the companion ideas of model-compound partitioning and additivity relationships. The idea is that an arbitrary solute can be thought of as a collection of smaller component substituent moieties, such as individual methylene or carbonyl or alcohol groups. The free energy of partitioning of these components can be measured in a partitioning experiment. The free energies of solvation of all the moieties can be added together to compute the solvation free energy for the whole solute molecule. For example, by measuring the concentrations in water of a series of alcohols—methanol, ethanol, propanol, butanol, etc.—Tanford determined that the free energy of transferring each individual methylene group into water was 825 cal mol^–1.¹⁸³ That number has then been used to estimate the free energy of solvation of methylene groups in arbitrary solutes, as an additive term for each such group.¹⁸⁴

The promise of such model-compound studies has been twofold. First, it has offered the prospect that, by simple experiments on a small number of small molecules, many chemical processes could be predicted on a much larger set of molecules, including the folding of proteins, formation of lipid bilayers, binding of drugs to proteins, partitioning of toxins in the environment, and the transport of drugs through cell membranes, for example. Second, model compound experiments could give insights into how water is structured around solutes.

The idea of hydrophobicity scales arose in the 1970s from these model-compound-plus-additivity studies. Correspondingly, a compound was said to lie along a single axis—from polar to nonpolar. The notion was that a solute’s partitioning into one hydrocarbon would be the same as into any other hydrocarbon (alkanes, alkanols, or cyclohexane, or octanol, for example), irrespective of the chemical details of the particular hydrocarbon or solute. However, it is now clear that nonpolarity is not independent of chemical details, and that hydrophobicity scales differ from one another, so the notion of “hydrophobicity scale” is more qualitative than quantitative.¹⁸⁵

Similarly, model-compound studies have been found to be more correlational than quantitatively predictive, due to nonadditivities. Figure 14 shows an example of a nonadditivity in free energies of transfer of xylenol solutes into water. The methyl groups of 2,6-xylenol (Figure 14, right) sterically crowd a first-shell water molecule, leading to poorer solvation. In short, perturbing this single water molecule affects the whole solvation cage, causing a loss of 1.4 kcal mol^–1 of solvation free energy, out of a total solvation free energy of −6.3 kcal mol^–1 in the mostly unperturbed 3,5-xylenol (Figure 14, left).¹⁸⁶ Ordinarily, it would be expected that if one solvent molecule were perturbed, say, out of 20 solvent molecules in a first solvation shell, then a solvation free energy of −6.3 kcal mol^–1 would have been affected by only about 1/20 = 0.3 kcal mol^–1; see 2,4-xylenol (Figure 14, middle). But when the solvent is water, very small perturbations that lead to changes in even one hydrogen bond in one water molecule can have outsized energetic consequences.

Figure 14.

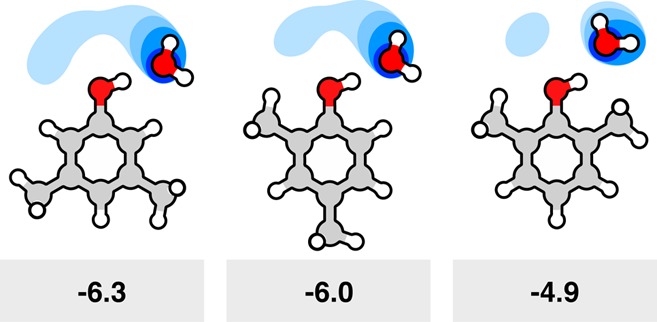
Solvation free energies can be nonadditive because the solute can perturb waters away from their cage-like favored structures. In a series of xylenol molecules, the different methyl group arrangements perturb the water solvation of the (red) hydroxyl group of each solute, particularly in the first solvation shell. The (blue) water occupancy from molecular simulations shows how displacing water from the ideally H-bonded structure leads to a decrease in the ΔG_solv (here in units of kcal mol^–1).

Insights about solvation structures can be obtained by decomposing solvation thermodynamics into its two components (Figure 15): (i) a nontransient cavity forms in the solvent and then (ii) the solute enters and interacts with the solvent cavity.^29,187−190 The first step describes the reversible work spent on the water–water interactions to open a cavity of appropriate size and shape (reorganization free energy). The second step expresses the free energy of the solute–water interactions (binding free energy). In general, the driving forces of the solvation process can be subtle and complex,^29,187−197 but we give a general overview below.

Figure 15.

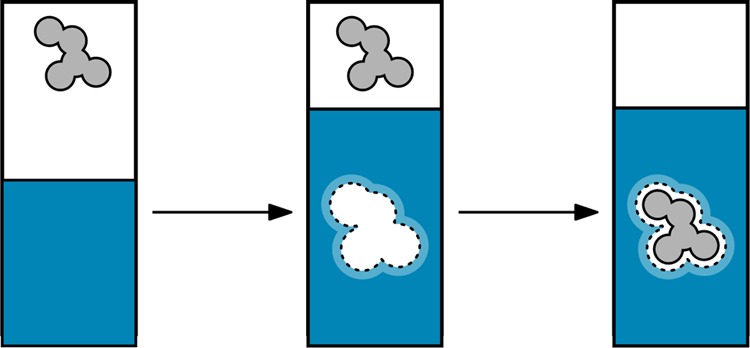
The solvation process can be decomposed into two steps. (left) Prior to solvation, the solute (gray) is in the vapor phase (white). (middle) A cavity opens in the water solvent (blue). (right) The solute inserts into the cavity.

7.1. Oil and Water Do Not Always Mix: The Hydrophobic Effect

A longstanding rule-of-thumb about mixtures is that “like dissolves like”. In general, when two species A and B are combined in a mixture, the AA and BB attractions tend to be stronger than the AB attractions. The fact that oil and water often do not mix is consistent with this rule. But, there is an important difference between water and simpler systems. In simpler systems, immiscibility is because of energies. For oil and water, the thermodynamic signature of the immiscibility (at room temperature) is entropic. This is manifested in the different temperature dependences of solvation; see Figure 16. This figure shows how the entropy, enthalpy, and free energy depend on temperature when dissolving toluene in water. Interestingly, even though the entropy and enthalpy of aqueous solvation of nonpolar solutes change substantially with temperature, the solvation free energy is relatively independent of temperature.

Figure 16.

Dissolving oil is entropically favorable in hot water, but entropically unfavorable in cold water. For toluene in water.¹⁹⁸ The solvation free energy depends little on temperature. The enthalpy and entropy depend more strongly on temperature, and they compensate. In cold water, the solute induces more ordering than in bulk waters, and the cages have good H-bond and solute interactions.¹⁹⁹ In hot water, insertion of oil breaks potential water–water hydrogen bonds, leading to both higher entropies and higher enthalpies.

The structural explanation of aqueous solvation dates back at least 70 years.^200,201 Liquid water can be viewed as an ensemble of cage-like structures, not a single ice-like structure.²⁰² Cold water has more population of open-cage states.²⁰³ Introducing a small hydrophobic particle shifts the equilibrium further toward these more open and ordered states,¹⁸⁷ and water has slower dynamics in the first few solvation shells.^204,205 Hotter water has less cage-like organization.^40,206−208 Introducing a solute into hot water acts more like traditional “like-dissolves-like” situations, where the solute insertion into water is unfavorable for energetic reasons.

The solubilities of nonpolar molecules depend on their sizes. Consider a series of nonpolar solutes in water, having increasing radii. They will induce first-shell water structuring that differs depending on the solute size; see Figure 17.

Figure 17.

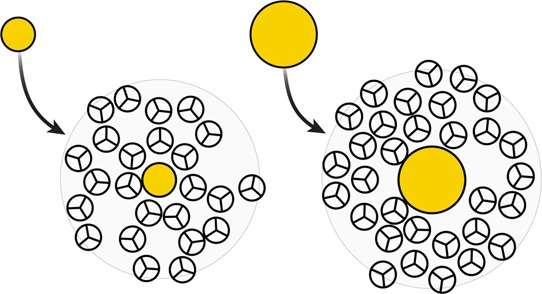
A small solute is compatible with water’s natural cages. A large solute does not fit in a cage. In cold water, small solutes can fit in the available cavities with minimal perturbation of the water structure. This process is favored by enthalpy and opposed by entropy. However, in cold water, big solutes do not fit in preexisting cavities. First-shell solvating water molecules around large nonpolar solutes are more disordered. Dissolving large solutes in cold water is opposed by enthalpy (breaks hydrogen bonds) and favored by entropy.

In short, a small nonpolar solute (say, the size of xenon) does not dissolve well in water at room temperature for entropy reasons. Small solutes can fit into natural hydrogen bonded water cages, but they distort those cages, which is entropically unfavorable.^{40,207,209,210} In contrast, a large nonpolar solute (say, a sphere bigger than 1 nm diameter) does not dissolve well in water at room temperature for enthalpy reasons. A large solute cannot fit within water’s common small hydrogen-bonding cages. A large solute must enter into a larger unstructured volume of water, where hydrogen bonding is largely already broken. The different physics of the transfer of a small big hydrophobic object in water is reflected also in the magnitude of the transfer solvation free energy per unit surface area. For small solutes this quantity is about 25 cal mol^–1 Å^–2. This reflects the cost of ordering water molecules around the solute. For big solutes the solvation free energy per unit area tends to the value of the water macroscopic surface tension, which is about 75 cal mol^–1 Å^–2. This reflects the cost of breaking the HB network around the solute.⁴⁰

The solvation free energy of a hydrophobe can also be understood in terms of the probability of finding a cavity in water of the appropriate size. Information theory links those two quantities.²¹¹ This way of considering hydrophobic solvation is of particular interest in biology in order to understand the wetting–dewetting of biological surfaces.²¹²

7.2. How Do Two Hydrophobes Interact in Water?

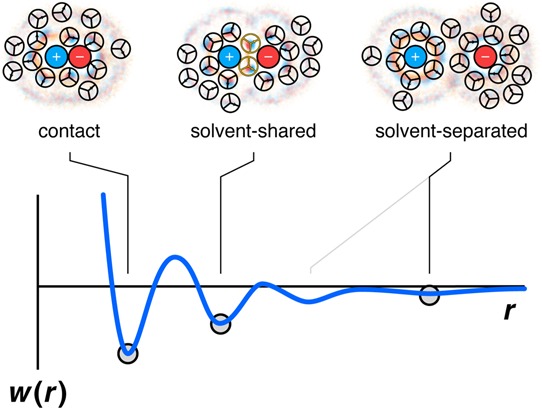
The potential of mean force (PMF) is the free energy of bringing two particles together in a solvent from a large original distance apart to a separation r from each other. Figure 18 shows the PMF of two hydrophobic spheres in water. The curve has some minima and maxima. The first minimum (contact minimum) represents the free energy of the two particles brought into direct contact. This configuration is favorable because the direct-contact state minimizes the total water-accessible surface of the two hydrophobes, relative to all other separations. The particles cannot approach closer than this due to steric repulsion. The second minimum (solvent-separated minimum) is favorable because then the spheres fit compatibly within water’s caging structure.^{211,213−220} The unique aspect of water here is its ability to form cage structures, causing the solvent-separated state to be relatively stable for some hydrophobes.

Figure 18.

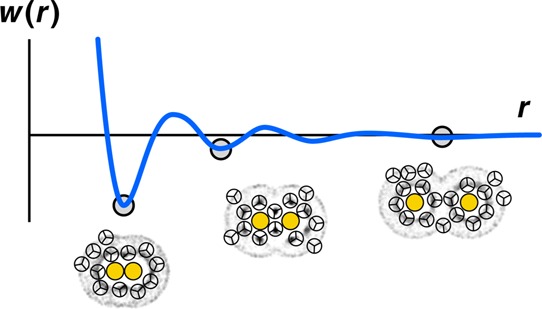
Water is structured differently around two hydrophobes at different separations. The PMF is the reversible work spent to bring two hydrophobic particles from infinite distance to the distance r. The leftmost minimum shows that two hydrophobes in contact are stable in water. The middle minimum (solvent-separated state) shows partial stability when two hydrophobes are both in water cages, separated by a layer of water. The maxima (unstable states) are hydrophobe separations that have unfavorable water configurations.

7.3. Water Pulls Away from Hydrophobic Surfaces

Water molecules tend to avoid hydrophobic surfaces. Waters do not form hydrogen bonds with such surfaces.^209,221 Even more unfavorable is when water becomes squeezed between two hydrophobic surfaces. Such confinements can be sufficiently unfavorable that water molecules between nonpolar planes will vaporize inside, and escape the confinement. This has been called a drying transition or dewetting. A more subtle consequence is that water at a hydrophobic surface will have larger density fluctuations than it will have in the bulk.^222−229 Lum, Chandler, and Weeks noted that this repulsion between a hydrophobic solute surface and surrounding waters depends on the size of the solute: bigger flatter surfaces tend to exclude water more strongly.²²¹ Therefore, large hydrophobic objects will tend to cluster together, to squeeze out the water molecules in between them.^{209,227,228,230−241} MD simulations show that (1) while dewetting does happen in the melittin tetramer protein,²²⁵ (2) it does not happen in the two-domain protein BphC,^223,224 and (3) the dewetting phenomenon can disappear in the presence of small additional interactions, and depends on force field parameters.²²⁶ While water may not fully deplete near hydrophobic surfaces, it may have larger fluctuations than it has in the bulk.

8. Water Forms Solvation Structures around Ions

8.1. Ions are Kosmotropes or Chaotropes, Depending on Whether They Order or Disorder Waters

Put an ion in water. In the ion’s first solvation shell, water molecules will adopt different types of structure depending on the size and charge of the ion.²⁴² Gurney defined some ions as being structure makers or kosmotropes, and other ions as being structure breakers or chaotropes.²⁴³ Water’s structure-making or structure-breaking tendencies are defined by experiments that show how each type of ion changes the viscosity of water, or its entropy of solvation in water, for example.^126,242 If a type of salt ion is added to water that has a negative Jones–Dole viscosity B coefficient or has a negative entropy of solvation, that type of ion is called a structure maker.²⁴⁴

In 1957, Samoilov²⁴⁵ also proposed water structuring around ions is reflected in a dynamical property, namely the activation energy required to strip a water molecule away from the first solvation shell of an ion. A first-shell water molecule around a kosmotropic ion is more tightly bound to the ion than that water is bound to another water. He referred to this as a positive activation energy. In contrast, a first-shell water molecule around a chaotropic ion is bound more weakly to the ion than that water is bound to another water. He called this a negative activation energy.²⁴⁵ The structures and dynamics of water in ion hydration shells have been studied extensively by diffraction and spectroscopic measurements, as well as by computer simulations (for reviews, see refs (242 and 246−248).).

Figure 19 shows that small ions cause electrostatic ordering of solvating waters, while large ions cause hydrophobic ordering (shown in the Mercedes-Benz-plus-dipole model^40,126). A small ion’s charge can come close to a water molecule, resulting in a strong electrostatic attraction for the water’s dipole. This is the nature of kosmotropic ordering of water around small ions such as Li⁺ and F^–. In contrast, the charge at the center of a large ion cannot come close to a water molecule, so the electrostatic interactions with water are weak. Around large ions, water molecules form hydrogen bonds with other water molecules, as they would do around nonpolar solutes. Chaotropic ordering of water around large ions such as Cs⁺ and I^– resembles hydrophobic water structuring.^40,126

Figure 19.

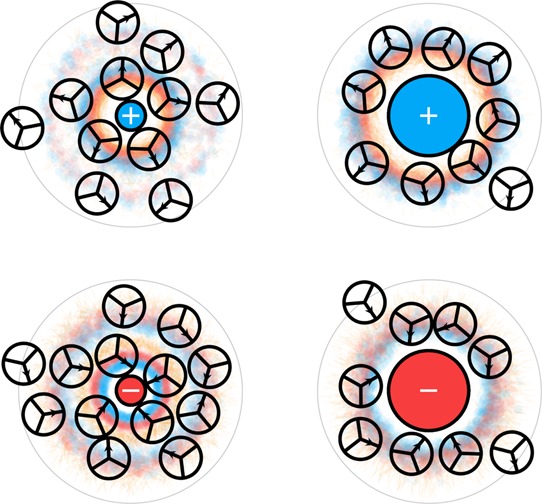
Around small ions, waters become electrostatically ordered. Around large ions, waters become hydrophobically ordered. The coloring shows the probability density of water dipole positive (blue) and negative (red) charges as well as water–water hydrogen bonding arms (orange). About small ions, water is highly electrostricted.

An anion does not have the same effects as a cation of the same size. The negative charge on water’s dipole is at the center of the water molecule. The positive charge on water’s dipole is near the outside of the water molecule. Therefore, an anion can come closer and interact more strongly with a water’s dipole than a cation can. This leads to a notable difference between anion and cation size required to achieve a given level of water ordering.^{126,249−251}

8.2. In the Hofmeister Effect, Salts Can Drive Nonpolar Molecules To Aggregate or Disaggregate in Water

At very low concentrations, nonpolar solutes will dissolve in water. Increasing its concentration causes a solute to reach its solubility limit, and to then aggregate. Now, to these hydrophobe–water solutions, add salt. Some types of salts will increase the solubilities of nonpolar solutes (called salting in), and other types of salts will decrease the solubilities (called salting out).^252−254 These effects of salts on hydrophobe solvation were first discovered by Hofmeister,^255,256 and are widely applied to dissolving or precipitating proteins, which are partly composed of hydrophobic amino acids. The Hofmeister effect is commonly modeled by the Setschenow equation:²⁵⁴ ln(c_i/c_i(0)) = −k_sc_s, where c_i and c_i(0) are the solubilities of the hydrophobe in a solution of salt and water, respectively, and c_s is the concentration of the salt. k_s is the salt’s Setschenow coefficient; it depends on the type of salt, as well as on the nature of the hydrophobic solute.^{254,257−260} At small salt concentrations, the cation and anion effects on the hydrophobe solubility are typically independent and additive.^261,262 The Hofmeister series is a list in which different types of ions are rank-ordered in terms of how strongly they modulate hydrophobicity.

Small ions tend to cause salting out: adding salt reduces hydrophobic solubilities in water. Large complex ions tend to cause salting in: adding salt increases nonpolar solubilities in water. Molecular dynamics simulations of Smith²⁶³ and Kalra et al.²⁶⁴ indicate that salting out is because the hydrophobe is excluded from the first hydration shell of the ion. Salting in is because the hydrophobe can occupy the ion’s solvation shell. And, like chaotrope/kosmotrope properties, Hofmeister effects tend to correlate with the charge densities on the ions.

Figure 20 illustrates the structural basis for Hofmeister effects.^40,126 Small ions exclude hydrophobes because small ions bind water molecules quite tightly. This exclusion increases the hydrophobe concentration in the remaining volume of the solution, driving the hydrophobes to aggregate with increasing ion concentration. Large ions do not exclude hydrophobes because large ions do not bind waters so tightly. Therefore, adding large ions to solution does not drive increased hydrophobe concentration in the remaining solution volume. The black bars in Figure 20 show the hydrophobe exclusion volume of different ions, as well as the well-known observation that the smaller ions tend to have the larger exclusion volumes.²⁶⁵

Figure 20.

Hydrophobes are excluded around small ions. Hydrophobic solutes (gold) insert more readily into the inner solvation shells of large ions than small ions. (orange) Hydrophobe density. (light gray lines) First and second solvation shells (black and gray bars underneath) show the effective size of the ion, from the perspective of external solutes.

8.3. When Two Ions Interact in Water, Both Solvation Shells Determine the Solution Properties

Figure 21 shows the PMF of two ions coming together in water. It shows how the solvation-shell waters are structured at different ion separations. When the ions are far apart, each ion’s solvation shell is structured as described above for the isolated ions. When the two ions are separated by about one layer of water, the bridging waters between them will be structured by multiple interactions. Each bridging water interacts with other bridging waters through hydrogen bonding, and each bridging water interacts with each ion through its water dipole. When the two mobile ions come into contact, the ion–ion electrostatics can also contribute substantially to the free energy. Extensive computer simulations using different water models show that the shape of the PMF depends on all these factors. The resulting free energy from the sum of the factors can be quite different for ions of different sizes and shapes.²⁶⁶

Figure 21.

The water structure around an ion pair depends on the cation–anion distance. At large separations, each ion has its own solvation shell. At intermediate separations, the ion pair is stabilized by bridging waters. Ion–ion contacts of opposite charge are stabilized by electrostatic attractions, in addition to the water forces. (blue) Positive charge density of the waters. (red) Negative charge density of the waters. (orange) Density of the water–water hydrogen bonding arms.

There is an interesting puzzle of ion pairing. Some salts are more soluble in water than others. When a salt is composed of a small anion and a small cation, say LiF, it is relatively insoluble in water. When a salt is composed of a big anion and big cation, say CsI, it is also relatively insoluble in water. But, when a salt is composed of a small ion and a large ion, say CsF, then it is relatively soluble. Collins explained this through his law of matching water affinities.²⁵¹

The structural basis for Collins’ law is shown in Figure 22. Two small ions stick together (their contact state is most stable) because their ion–ion charge attractions dominate the energetics. Two large ions stick together because they act like hydrophobes (since their charge interactions are weak, because the two ions cannot come sterically close together). But the middle diagram in Figure 22 shows that small–large ion pairs tend to be most stable in their solvent-separated states, hence these are the least “sticky” of the salt types. The reason this state is stable is because the small ion attracts a water cage around it for electrostatic reasons, and the large ion is compatible with a water cage for hydrophobic reasons.²⁶⁷ When ions are stable in water-separated states, they will also tend to dissolve well in water.

Figure 22.

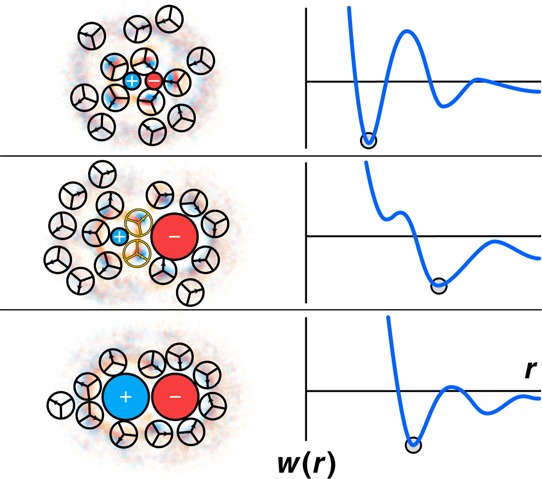
The water structure around an ion pair depends on the size of each ion. Water is more electrostricted around small ions.²⁶⁶ The ion–ion contact state is most stable for small +/small – , because of electrostatic attractions. The contact state is also most stable for large +/large – , because of hydrophobic-like water structuring. The most stable state for large-ion/small-ion pairs is solvent separated.

Therefore, the properties of aqueous solutions of even the simplest ions result from a subtle balance of geometry, hydrogen bonding, and charge interactions. When additional forces are also involved, such as when ions are near curved surfaces or protein binding sites, it can further tip that balance.²⁶⁸ On the other hand, aqueous solvation of solutes that are polar but not ionic can be simpler.^269,270 For example, around alcohols, water–water hydrogen bonds can be replaced by water–alcohol hydrogen bonds, but much of the rest of the water structuring is unaffected. In these cases, charge and geometry are less complicating factors.

9. Water in Confined Spaces and at Liquid–Vapor Interfaces

Water is commonly in contact with surfaces. Examples include water permeating through granular or porous or supramolecular structures or gels,²⁷¹ or inside crowded biological cells, or bound to proteins or DNA, or at interfaces with air or oils.²⁷² Surfaces can constrain or induce water structuring,²⁷³ by promoting or interfering with water–water hydrogen bonding. For example, since water cannot form hydrogen bonds to hydrophobic surfaces, water tends to move away from them toward locations most compatible with forming water–water hydrogen bonding instead.^272,274 An example of a hydrophobic surface is the air–water interface. At surfaces with air, water can lose hydrogen bonds simply because of the geometric constraint imposed by the surface;^272,275 see Figure 23. Some recent experiments suggest that the lost hydrogen bond is due to the OH group,^272,275 while others suggest that it is the lone pair on the oxygen pointing away from water’s surface.^276−278 Air–water interfaces are also slightly enriched in hydronium ions (H₃O⁺), but not hydroxide (OH^–).^272,274,279 Hydronium ions are only weak H-bond acceptors, so they cannot compete with water–water hydrogen bonds in the bulk liquid, and therefore hydronium ions tend instead to concentrate at surfaces.

Figure 23.

Water molecules orient at interfaces to favor hydrogen bonding. Air above liquid water acts like a hydrophobic surface. In order to minimize the loss of H-bonding interactions, interfacial water will tend to orient such that either a single proton or electron lone pair points toward the air.²⁷⁵

Hydrophobes in water tend to concentrate at air–water interfaces. This is because hydrophobes tend to localize wherever they are able to break the fewest water–water hydrogen bonds. Surfaces have a lower density of water–water hydrogen bonds than bulk water has.²⁷² Acids and bases can also differentially localize at surfaces, depending on the preferences of the protonated or deprotonated forms of a molecule. For example, consider acetic acid in a solution with water at a bulk pH equal to the pK_a (i.e., 4.8). In the bulk, there will be equal concentrations of the protonated and deprotonated forms. But at water’s surface, acetic acid is found predominantly in its protonated form.²⁷⁴ At pH ≪ pK_a, both the bulk and the surface of water are enriched in the protonated species. At pH ≫ pK_a the deprotonated species dominates the bulk, and the surface is depleted of both forms.²⁷² Other types of ions, too, are enriched or depleted at water surfaces depending on the preferential interactions of those ions with surface vs bulk waters.^{272,280−283}

9.1. Water Is Structured in Nanotubes Partly by Hydrogen Bonding

Water inside nanotubes can be sterically constrained;²⁷¹ see Figure 24. Water’s organization inside such confined spaces can depend on the size and shape of the cavity. In narrow hydrophobic pores (Figure 24, left), waters can form hydrogen bonded chains, where each water hydrogen bonds to one water neighbor in front and one behind. According to semiempirical simulations by Hummer et al., such water wires can explain how water is transported up to 3 orders of magnitude faster in nanotubes than in the bulk.^284,285 Water’s normal slow mobility in the bulk is because it moves by breaking and making hydrogen bonds to neighboring waters. Its high mobility in nanotubes is because water does not break or make hydrogen bonds to the nanotube walls as it flows. However, other studies show the opposite; namely that water flow is retarded in certain kind of nanotubes.^286,287

Figure 24.

Nanoconfined water is geometrically constrained (left) in a tube of diameter 8 Å and (right) in a tube of 11 Å. The hydrogen bonding between two waters or between water and the surface depends on the size and shape of the confinement.²⁷¹

Putting water into some physical confinement can shift water’s pT phase diagram. Different confining surfaces can either raise²⁸⁸ or lower water’s melting point.²⁸⁹ Smaller nanotubes tend to lead to higher boiling points and depressed freezing points of water.²⁷¹ Also different forms of ice may form within confined spaces. Depending on the diameter, as well as their interior surface characteristics, nanotubes may exhibit ion selectivity, similar to that of the ion channels, which is attributed mostly to the formation of ion hydration shells.^290,291

9.2. Icy Frontiers: Ice Changes under Confinement and in Clathrate Cages around Hydrocarbons

Several of water’s ices are observed under pressures that are greater than 100 atm and are applied omnidirectionally. What happens if water is squeezed in only a single direction, such as between two smooth plates? Such a situation has been studied for ice that contracts upon freezing in a bilayer form, sometimes called Nebraska ice because “Nebraska” is a Native American term meaning “flat water” and because the modeling was performed at the University of Nebraska.²⁹² Modeling has explored the stabilities of known ice polymorphs.^293,294 Computer simulations have predicted phases of ice not yet seen experimentally,^96,295 and have explored the structuring of ice that is confined within nanotubes,^296−299 ranging from linear chains, to helical H-bonded spirals, to stacked pentagonal rings, and more.²⁹⁷ These repeating patterns are similar to the optimal water cluster arrangements for small numbers of water molecules,³⁰⁰ apparently consistent with the principle that water adopts structures having maximal hydrogen bonding subject to the given geometric constraints.

Sometimes ice itself is the constraining vessel. Other molecules can be captured within ices, in the form of clathrate hydrates. Clathrate hydrates are ice cages that encapsulate small molecules, typically hydrocarbons. There are several regular clathrate structures, and Figure 25 shows the two most common forms. The shape and size of the caged solutes, as well as the pressure and temperature, will direct the type of clathrate structure adopted by the surrounding water.

Figure 25.

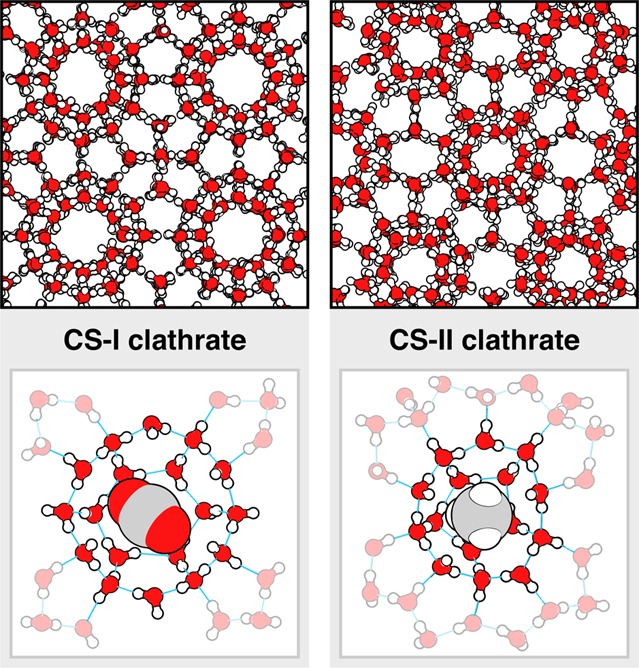
Clathrate ice structures can act as cages for gas molecules. Two of the most common clathrates are the cubic structure type I (CS-I or sI) and cubic structure type II (CS-II or sII). The imaged clathrates are oriented to highlight CS-I’s simple cubic and CS-II’s face-centered-cubic lattice structures, and respective cage cutaways with space-filling CO₂ and CH₄ guests are shown below.

Among the most notable clathrate hydrates is methane clathrate.³⁰¹ These are found naturally in large quantities on the cold ocean floor. Clathrate hydrates can be problematic commercially because they limit gas and oil extraction by clogging up the transport of hydrocarbons through pipelines. Despite this troublesome aspect, their large natural abundance and high methane density mean methane clathrates represent an enormous potential energy source.³⁰² However, extraction is problematic and is at present not economically competitive with standard drilling techniques.

Under the proper conditions, clathrate hydrates can be grown, often by doping ice using a hydrogen-bonding solute that can catalyze hydrate formation through the uptake of surrounding gas solutes.^303−306 They are promising for gas storage and transport, such as for sequestering CO₂. Growing such clathrate hydrates also provides an avenue for finding new structures of pure-water ices. Solutes can be extracted from clathrate hydrates by vacuum evacution to empty the ice cages, leading to new potential phases of pure ice.^307,308 Such a strategy was recently applied by Falenty, Hansen, and Kuhs to evacuate Ne gas from a Ne CS-II clathrate hydrate.³⁰⁹ The resulting ice XVI structure is the lowest-density ice polymorph that is observed experimentally. Not unexpectedly, it is more delicate than the unevacuated Ne clathrate, collapsing at temperatures above 145 K.

10. Molecular Structure Governs Water’s Dynamical Properties

10.1. Water Diffuses More Rapidly above Its Glass Transition Temperature Than below It

By studying water’s diffusion and viscosity properties, it is found that water is a complex glassy material. Cooling a liquid slowly causes it to freeze to a stable crystalline state. But cooling a liquid rapidly can lead to kinetically trapped states that are glassy, i.e., which do not have regular order and in which transport is sluggish.³¹⁰ Water undergoes such a glass transition to an amorphous solid. In water, the characteristic relaxation times become of the order of 100 s and the rate of change of the volume and entropy decreases abruptly (but continuously) to that of a crystalline solid.³¹¹ Glassy water dynamics can be explored using computer simulations of supercooled water. But, such simulations have been challenging because the time scales are very slow—15 orders of magnitude slower than in normal liquid water.³¹² Glassy water is studied either through the dynamics of the molecules and HB network directly^313−316 or by relating the dynamics to equilibrium properties.^312,317,318

But, even as glassy materials go, water is unusual. A key diagnostic is the rate of change of a material’s viscosity with temperature as the temperature approaches its glass transition point.^319−321 Plotting the logarithm of the viscosity of a liquid vs the inverse of the temperature of the liquid, Angell defines strong glass formers as those having straight lines on this Arrhenius-type figure. He defines fragile glass formers as having curved lines, where the viscosity is insensitive to temperature in the hot liquid and strongly dependent on temperature in the cold liquid. Strong glass formers are regarded as having memory of their molecular arrangements above their glass transition. Fragile liquids forget their glass structure much faster upon crossing the glass transition into the liquid phase. Water is more complicated than either of these behaviors, because of the complexity of structure in the supercooled liquid state. The high-density and low-density components of water each have different viscosity characteristics.

10.2. Cold and Supercooled Water Diffusion and Viscosity Depend on the Relative Population of High and Low Density Water

In simple liquids (and in hot water), increasing the pressure increases the viscosity and decreases the diffusivity because applying pressure leads to crowding of the molecules, making their motion more sluggish. However, cold water behaves differently. At temperatures below 306 K the viscosity of water decreases with increasing pressure.^322,323 Below 283 K the diffusivity of water molecules increases upon increasing the pressure of the system.³²⁴ Anomalous behavior is also observed in the sound velocity in cold water.³²⁵ What explains these results? According to Le Chatelier’s principle, applying pressure squeezes a system into a denser state. In the case of cold water, applying pressure shifts water structures, crunching cage-like waters into van der Waals clusters. This breakage of hydrogen bonding frees up waters to move faster.^{163,167,323,326−329}

10.3. Protons and Hydroxide Ions Diffuse Rapidly in Water

Small molecules and ions diffuse through liquids. Their diffusion rates typically depend on the radius of the diffusant and the viscosity of the solvent. However, when the liquid is water, there is a remarkable exception. Water’s own component breakdown products—its protons and hydroxide ions—diffuse much faster than other ions do in water. The mobility of H⁺ is 7 times the mobility of Na⁺, and the mobility of OH^– is 2.5 times the mobility of Cl^–; see Table 3. This implies that there is a distinctive transport mechanism for H⁺ and OH^– compared to other ions in water. Ionic diffusion in water plays crucial roles in processes in biology (e.g., proton transfer in enzymes and biological channels), in industry (e.g., transfer of ions through fuel cell membranes), and in environmental processes (e.g., ion transfer on ice surfaces facilitating atmospheric reactions). Water ionization is a key component of aqueous acid–base chemistry.

Table 3. Selected Physicochemical Properties of Liquid Water^a.

property	value
density	997.047013 kg m–3
molar volume	18.0685 cm3 mol−1
molar concentration	55.345 mol dm–3
molality	55.508472 mol kg–1
dielectric constant	78.375
magnetic susceptibility	–1.64 × 10–10 m3 mol–1
electric conductivity	0.05501 × 10–6 Ω–1 cm–1
limiting molar conductivity	H+: 349.19 cm2 Ω–1 mol–1
	OH–: 199.24 cm2 Ω–1 mol–1
ionic mobility	H+: 3.623 × 10–7 m2 V–1 s–1
	OH–: 2.064 × 10–7 m2 V–1 s–1
thermal conductivity	0.610 W m–1 K–1
speed of sound	1496.69922 m s–1
refractive index	1.33286 (λ = 589.26 nm)
pH	6.9976
pKw	13.995
surface tension	0.07198 N m–1
kinematic viscosity	0.8935 × 10–6 m2 s–1
dynamic viscosity	0.8909 mPa s
bulk viscosity	2.47 mPa s
diffusion coefficient	0.2299 Å2 ps–1
dipole moment	2.95 D (at 27 °C)
adiabatic compressibility	0.4477 GPa–1
isothermal compressibility	0.4599 GPa–1
expansion coefficient	0.000253 °C–1
adiabatic elasticity	2.44 GPa
Joule–Thomson coefficient	0.214 K MPa–1
vapor pressure	3.165 kPa
cryoscopic constant	1.8597 K kg mol–1
ebullioscopic constant	0.5129 K kg mol–1
polarizability	1.636 × 10–40 F m2

^aQuantities dependent on temperature and/or pressure are given at 25 °C and 101.325 kPa. See also Table 1. (Data collected from ref (37).)

Water’s autoionization, H₂O ⇌ H⁺ + OH^–, is a rare event. It occurs on the ∼10 h time scale.³³⁰ In aqueous solutions, the proton (H⁺) does not exist in unhydrated form. The proton in water forms a hydronium ion, H⁺(H₂O) or H₃O⁺, which is itself short-lived.³³¹ The hydronium ion can donate three hydrogen bonds. Hydronium makes strong hydrogen bonds,³³² which can influence more than 100 surrounding waters,³³³ and can form hydronium chains. Manfred Eigen suggested that the proton is localized on an individual water molecule, and that the H₃O⁺ gets further solvated by three water molecules, i.e. H₃O⁺(H₂O)₃ or H₉O₄⁺; this is called the Eigen cation;^334,335 see Figure 26. Alternatively, Georg Zundel suggested that H⁺ is shared equally between two water molecules, forming the (H₂O)H⁺(H₂O) or H₅O₂⁺ cation, called the Zundel cation;³³⁶ see Figure 26. Other types of structures for the hydrated proton have also been proposed,^337−339 as well as for the hydrated hydroxide ion (OH^–(H₂O)_n).^{274,340−345}

Figure 26.

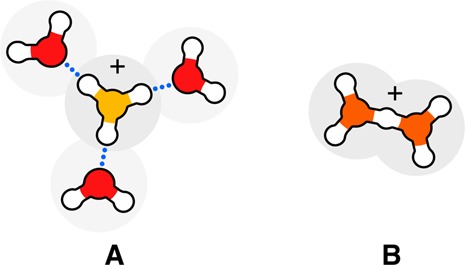
In liquid water, protons are hydrated. (A) On the Eigen cation, the proton H⁺ is localized on one water molecule. The resulting H₃O⁺ is hydrogen bonded to three surrounding water molecules. (B) On the Zundel cation, the H⁺ is shared between two water molecules.

Simple diffusion does not explain the anomalously high electric mobilities of H⁺ and OH^–. A mechanism was proposed in 1806 by Theodor von Grotthuss;^346,347 see Figure 27. Protons hop along a hydrogen bond network of neighboring water molecules, like a “bucket brigade” by cleaving and forming covalent bonds. Recent computer simulations give additional insights. First, it is found that the Eigen and Zundel cations are only limiting ideal structures, and that there are delocalized defects, giving a broader distribution of structures.^341,348,349 Second, the proton transfer in water is not exclusively by stepwise hopping, but includes broad pathways, time scale distributions, modes of transfer, and concerted motion of multiple atoms.³⁵⁰ This migration of charge involves bursts of activity along proton wires.^351−353 A proton can jump 4–8 Å across several water molecules on the subpicosecond time scale, followed by resting spells.³⁵² Third, it is found that the transition state in proton transfer is the formation of special water pairs having rare ultrashort hydrogen bonds, which can lead to a multiplicity of tortuous routes in three dimensions.³⁵⁴

Figure 27.

Fluctuations driving the autoionization of water involve the concerted motion of many atoms. A water wire links the H₃O⁺ and OH^– ions. The Grotthuss mechanism (A) of proton propagation involves three consecutive steps (1–3). In contrast, a cooperative motion of the water wire (B) that results in a concerted motion of three protons is shown.

Water molecules can diffuse rapidly through nanotubes. It has been suggested that an excess of proton charge defects near the entrance of dry hydrophobic carbon nanotube can aid the loading of water.³⁵⁵ Relying on charge defect delocalization and Grotthuss shuttling to help grow a chain of water molecules in the tube, this wetting process is specific to a hydrated excess proton alone. Other monatomic cations, such as K⁺, have the opposite effect: they block the wetting process and make the nanotube even more dry. A wetting mechanism of this type can be important in biological systems, for example in understanding the hydration of hydrophobic protein pores, where the charge defect is, for instance, created by peripheral amino acid residue deprotonation.

11. Challenges for Improving Water Models

To create new technologies for producing clean water, reclaiming polluted water, predicting climate and weather, inventing green chemistry, separating chemicals and biomolecules, and designing new drugs to cure diseases requires an ever deeper understanding of water structure–property relationships. It requires ever better models of various types and at different levels. Modeling is needed that can handle water that contains salts and oils and biomolecules, often in high concentrations, in the presence of complex and structured media and surfaces, and often under different conditions of temperature and pressure. Semiempirical models of water have generated insights and quantitative predictions over a broad spectrum of inquiries. But, there are opportunities for the future. More efficient computational models are needed to give better sampling of water’s distributions of configurations, including its cage-like states, to give more accurate entropies, heat capacities, and temperatures of transitions. We need improved water models for solvating ions of high charge density. We need continued work in polarizable models. We need to go beyond current fixed-charge models, if we are to study pH or acid–base behavior, because protons cannot dissociate in present models. We need more efficient quantum simulation models for acid–base chemistry, for bond-making and bond-breaking reactions, for water’s ices and solid states, and for understanding principles of bonding.

There is also great value in improved analytical and semianalytical and coarse-grained models. They can give insights into principles; they give ways to explore dependences on variables such as temperatures, pressures, and concentrations; and they should be able to give computationally efficient ways to address engineering questions in complex systems. Moreover, combining methods can also be valuable: quantum plus semiempirical modeling for bond-breaking reactions, or coarse-grained plus atomistic semiempirical models for noncovalent changes in large biomolecular complexes, for example.

12. Summary

We reviewed here how water’s properties are encoded in its molecular structure and energies, as interpreted through the lens of various models, theories, and computer simulations. Anomalous properties of water arise from the cage-like features of its molecular organization, arising from the tetrahedral hydrogen bonding among neighboring molecules. The challenge in modeling is due to the coupling between rotational and translational freedom of neighboring molecules. It is responsible for some volumetric anomalies, such as the lower density of ice than liquid water, the backward part of the liquid–solid pT phase diagram, and water’s aversion for nonpolar surfaces and solutes. Water’s behavior as a solvent for nonpolar and charged molecules can be explained through a combination of its caging structures and water’s electric dipole.

Glossary

Abbreviations

HB

hydrogen bond

LJ

Lennard-Jones

MO

molecular orbital

LUMO

lowest unoccupied molecular orbital

HOMO

highest occupied molecular orbital

DFT

density functional theory

HDL

high density liquid

LDL

low density liquid

MB

Mercedes-Benz

TIP

transferable intermolecular potential

SPC

simple point charge

MD

molecular dynamics

PMF

potential of mean force

RDF

radial distribution function

CIP

contact ion pair

SIP

solvent-shared ion pair

GB

generalized Born

PB

Poisson–Boltzmann

RISM

reference interaction site model

SEA

semi-explicit assembly

i-PMF

interpolation potential of mean force

SAMPL

Statistical Assessment of the Modeling of Proteins and Ligands

Biographies

Emiliano Brini received his M.Sc. degree in chemistry from the University of Bologna in 2008, and did a Ph.D. in chemistry with N. F. A. van der Vegt at Technische Universitaet Darmstadt. He is currently a postdoc with Ken A. Dill at the Laufer Center for Physical and Quantitative Biology at Stony Brook University. His research focuses on solvation and protein physics.

Christopher J. Fennell received his Ph.D. in chemistry from the University of Notre Dame, and after working as a postdoctoral researcher at the University of California, San Francisco, he became a Laufer Junior Fellow at the Laufer Center for Physical and Quantitative Biology at Stony Brook University. He is currently an assistant professor of chemistry at Oklahoma State University with a research focus in computational and theoretical chemistry.

Marivi Fernandez-Serra obtained her B.Sc. and M.Sc. in physics at Universidad Autonoma de Madrid, Spain, in 2001. She received her Ph.D. in physics in 2005, from the University of Cambridge. After this she worked as a postdoc at CECAM (Center for Atomic and Molecular Simulations) in Lyon, France. Currently she is an associate professor of physics and has been at Stony Brook University since 2008. Her research is in the field of computational condensed matter physics. She develops and applies methods to study the atomic and electronic dynamics of complex materials. One of her main research areas is the study of fundamental properties of liquid water using quantum mechanical simulations. In her group they apply their methods to study the interface between water and functional elements such as electrodes, photocatalytic semiconductors, and oxide materials.

Barbara Hribar-Lee studied chemistry at University of Ljubljana, Slovenia. She received her Ph.D. at the same university in 1998. In 2000–2001 she did her postdoctoral research with Ken A. Dill at the University of California, San Francisco. She is a professor of physical chemistry at the Faculty of Chemistry and Chemical Technology (FCCT), University of Ljubljana. Her research is in the fields of statistical mechanical theories of water and hydration, partly quenched systems, solutions of (poly)electrolytes, and intermolecular interactions and their role in the stability of protein solutions.

Miha Lukšič studied chemistry at the Faculty of Chemistry and Chemical Technology (FCCT), University of Ljubljana, Slovenia. In 2010 he obtained his Ph.D. in physical chemistry at the same university. He was a visiting researcher at the University of Regensburg (Germany), the National Autonomous University of Mexico (Mexico), and the University of California, San Francisco. In 2012–2014 he worked as a postdoctoral fellow at the Laufer Center for Physical and Quantitative Biology at Stony Brook University. He is currently an assistant professor of physical chemistry at the FCCT, University of Ljubljana. His research interests are in statistical mechanical theory of water and hydration, partly quenched systems, solutions of (poly)electrolytes, and lately in electrochromic cell devices.

Ken A. Dill received S.B. and S.M. degrees in mechanical engineering from the Massachusetts Institute of Technology, obtained a Ph.D. in biology with B. H. Zimm at the University of California, San Diego, and did postdoctoral research with P. J. Flory at Stanford University. He was on the faculty of the University of California, San Francisco, until 2010, and since then has been the Louis and Beatrice Laufer Professor of Physics and Chemistry at Stony Brook University and the Director of the Laufer Center for Physical and Quantitative Biology. His research has been on water statistical mechanics, the protein-folding problem, aspects of nonequilibrium statistical physics, and biophysical mechanisms and evolution of cells.

Appendix

A.1. Modeling Large Complex Solutes Requires Approximations and Efficient Computational Methods

For studying water that contacts large or complex surfaces, efficient computational methods are needed. Several fast approximate models, described below, have been useful.^356−365

A.1.1. Modeling Water as a Continuum: Surface Tension, Born and Poisson Models

For modeling how water molecules interact with solutes, a simple and computationally inexpensive strategy is to treat water as a miniature unstructured continuous medium. For example, you can approximate the free energy of dissolving nonpolar solutes in water as ΔG = γA, where A is the surface area of the solute and γ is the free energy per unit area of association of the solute with water (like a surface tension). In this approach, water’s role is modeled as a continuum represented by a single bulk-like quantity, γ in this case, rather than as individual molecules buffeted by thermal motions. Different values of γ are obtained for different types of chemical moieties by experiments on model compounds. For solutes having multiple chemical moieties, the total solvation free energy is assumed to be the sum of free energies of the component moieties.¹⁸⁵

A different continuum approximation is useful for treating the solvation of ions or polar molecules. For solutes that have electrostatic character, the relevant bulk-like property of water is its dielectric constant ε. When two charged objects interact with each other in a polarizable medium, such as liquid water, their interactions are weakened by the screening effect that results from the effect of the ions polarizing the medium. At room temperature, at charge–charge separations of greater than the Bjerrum length of water (roughly 7–8 Å), this screening is an effect of sheilding one charge from another. Implicit-solvent models treat water as a continuum, rather than as individual molecules. Implicit-solvent models treat water as having a dielectric constant, which reduces the ion–ion interaction energy.^356−363

For solute molecules that have both nonpolar and charged moieties, another type of additivity relationship is used. The free energy of solvation, ΔG_solv, is taken to be the sum of electrostatic (ΔG_el) and nonpolar (ΔG_nonpolar) components.^364,365

A.1.1.1. Poisson Implicit-Solvent Models of Water

One type of implicit-solvent model is the Poisson or Poisson–Boltzmann approach.^366−370 In this case, all charge–charge interactions are taken into account through Coulomb’s law, summed together by solving the Poisson equation of electrostatics for the given distribution of fixed full and partial charges. In the presence of mobile charges, such as dissolved salt ions—which are free to distribute around the fixed charges—the Poisson–Boltzmann equation is solved for the electrostatic potential due to both fixed and mobile charges.³⁶⁹ Poisson-type modeling requires choosing where to locate the dielectric boundaries, and what dielectric constants should be used to approximate the different regions. As implicit-solvent models go, solving the Poisson equation can be computationally expensive.^371,372

A.1.1.2. Born and Generalized Born Implicit-Solvent Models of Water

A less computationally expensive way to approximate the screening effect of water around charges is the generalized Born model.^{357,364,373,374} In the underlying Born model, the electrostatic potential around a simple ion with radius a and charge q is³⁶⁴

1

where ε_w is the dielectric constant of water. In the case where a solute molecule can be modeled as several charges embedded in spheres, and the separation between them is sufficiently large compared to the radii, the solvation free energy of a molecule can be given by a sum of individual Born terms, and pairwise Coulomb terms.³⁶⁴ In the generalized Born model the two terms are replaced by one, substituting the radius of the sphere and the distance between two charges by a single function, f_GB, that interpolates between the two:³⁶⁴

2

GB simulations tend to be faster than those of PB. To achieve similar accuracies, GB models are often parametrized on a corresponding PB model by choosing proper effective atomic radii.^375−378

The advantage of continuum models is their computational speed. Therefore, they are often applied in modeling large or complex solutes, such as biomolecules, or multicomponent systems, such as in chemical separations.^379−381 The continuum models sacrifice molecular detail or specific hydrogen bonding,^{356,364,374,382} and thus water–water, water–solute, and solute–solute correlations.³⁸³ For example, implicit models are often qualitatively incorrect in situations involving solvated charges near curved surfaces²⁶⁸ or where solute surfaces are complex or corrugated.³⁸⁴

A.1.2. Modeling Liquids Using the Reference Interaction Site Model (RISM)

A compromise between explicit-solvent and continuum models are the integral-equation theories of molecular liquids. They aim to combine a relatively detailed molecular description with relatively low computational cost. The fundamental relationship for the integral equation theories is the Ornstein–Zernike (OZ) integral equation which, for a m-component system, is³⁸³

3

where r is the interparticle separation distance. Here, c(r) is the direct correlation function. The total correlation function is given by h(r) = g(r) – 1. To solve the OZ equation, another relation is needed between the functions c(r) and h(r), called a closure relation. Different closures are used for different problems.³⁸³

One such approach to solvation in aqueous solutions is the reference interaction site model (RISM), proposed by Chandler and Andersen.³⁸⁵ It treats the solute and solvent molecules as sets of sites having spherical symmetry, where the interactions between pairs of sites are treated through their correlation functions. RISM has been applied to dipolar liquids by Hirata and Rossky³⁸⁶ (XRISM). The RISM theory has been used in combination with the hypernetted-chain (HNC) closure to study the solvation of monatomic solutes (alkali halides and argon-like particles) in aqueous solutions,^195,387 small peptides,³⁸⁸ and polar organic molecules.³⁸⁹ However, these early RISM models did not handle well large molecular solutes, which contain atoms that are buried inside away from solvent exposure,³⁹⁰ or the polarizabilites of polar liquids.

Further developments led to the 3D-RISM model, in which a set of three-dimensional (3D) integral equations (one equation for each solvent site) was derived by integrating over the orientational degrees of freedom.^390−392 3D-RISM has been applied to studying the ionic atmosphere of DNA,^393−395 receptor–ligand pairs docking and binding affinities,^396−398 self-assembly of rosette nanotubes,³⁹⁹ tubulin protofilaments,⁴⁰⁰ and amyloid fibrils.⁴⁰¹ However, 3D-RISM gives limited accuracy in density distributions,^402−404 or hydration free energies of organic solutes,⁴⁰⁵ or distribution coefficients for drug-like molecules between organic and aqueous phases.⁴⁰⁶ These limitations have motivated more recent advances.^{392,405,407−409} Misin et al.⁴⁰⁸ demonstrated a pressure-corrected 3D-RISM that gives accurate salting-out constants for a wide range of organic compounds in aqueous sodium chloride solutions. Improved methods to predict hydration free energies and entropies of small drug-like molecules are now also available.⁴⁰⁹ So far, the RISM approaches have been less widely used than implicit-solvent modeling because of the greater computational expense of RISM.

A.1.3. The SEA Water Model: Explicit-Model Physics at Implicit-Model Speeds

SEA (semi-explicit assembly) is a model that aims to compute solvation free energies using the physics of semiempirical models, such as TIP3P, but at much faster computational speeds.^{186,410−412} In order to calculate the solvation free energy of a solute in water SEA uses two steps: (1) First is a pre-runtime simulation of idealized spheres (having different radii, different charges, and different van der Waals interactions with water) in explicit water, representing all the possible component pieces a solute could have. (2) Then, at runtime, SEA assembles the appropriate ideal spheres and sums terms into a total free energy of solvation. SEA is as fast as implicit-solvent models, because of its free-energy additivities in the assembly step. SEA has been found to be as accurate as explicit-solvent models in blind tests, called SAMPL;^413−415 see secA.2. While SEA is only as accurate as its underlying explicit-solvent model, nevertheless its accuracy stems, in part, from its intrinsic capture of water–water multibody effects in the presimulations. With the development of the field version of the technique and its dynamic solvent accessible surface boundary (Figure 28), SEA can also be applied to solvents beyond pure water by simply updating the surface accessibility and solvation coefficient tables for solvated LJ particles in the new environments.^412,415,416

Figure 28.

The water-accessible surface depends on the charge on the solute (gray). (left) Water-accessible surface (green) around an uncharged solute. (right) When the solute is charged (blue), the water surface is electrostricted (red) around neighboring solute atoms.

A.1.4. The i-PMF Method for Computing Potentials of Mean Force

In the spirit of the SEA approach, i-PMF is a method for fast and accurate calculations of the potential of mean force (PMF) between pairs of charged or uncharged solutes in water.⁴¹⁷ The PMF is the reversible work averaged over all possible configurations of the solvent molecules required to bring two solute particles in the solution from infinite separation to a distance r. The i-PMF method is divided into presimulation and runtime steps. In the presimulation step, extensive MD simulations are performed with a classical force field to compute the PMFs of various pairs of solutes in the solvent. These computed PMFs are compiled into tables. Next, interpolations are performed to fill in additional solute radii and separations r. At runtime, a PMF can be computed rapidly for particles of arbitrary charges, interaction energies, and radii. Figure 29 shows an example of Na⁺ and Cl^– ions in SPC/E water at infinite dilution. Figure 29 also illustrates the nature and magnitude of the errors from the miniature-medium models, GB and PB, which do not account for the particulate nature of water, and from 3D-RISM, which treats waters in an explicit but simplified way.⁴¹⁸ Because i-PMF is an interpolator, its runtime speed is about 5 orders of magnitude faster than the underlying MD simulations that it interpolates.

Figure 29.

Different models give different predictions for the Na⁺–Cl^– PMF in water.^417,418

A.2. The SAMPL Competition for Modeling Solvation in Water

How can we evaluate and improve computational models of solvation? Different methods have different errors and different computational speeds. A community-wide mechanism has recently been developed for blind testing of solvation models. The event, called SAMPL (Statistical Assessment of the Modeling of Proteins and Ligands) is held every second year. In the SAMPL event, a set of small-molecule (often drug-like) structures is provided to the predictor community, who then uses their various methods to predict the solvation free energies. Experimental measurements are then performed subsequently, and the prior blind predictions of the different groups are then evaluated comparatively.^419−423

A.3. How Is Water Globally Distributed on Earth?

The total amount of water on Earth is around 1.39 × 10⁹ km³; see Table 2. Of this, only around 0.77% is fresh water. Water makes up about 71% of the Earth’s surface, but only about 0.05% of the Earth’s total mass. Rivers are the source of most of the fresh surface water people use; that is about 1/10000th of 1% of Earth’s total water. Of Earth’s total water, 97.5% of it is saline, 95.5% of which is in oceans. Only 2.5% of all water is fresh water, and most of that is trapped as glaciers and snow.

Table 2. Global Distribution of Water on Earth^a.

water source	water volume [km3]	fresh water [%]	total water [%]
oceans, seas, bays	1 338 000 000	–	96.54
ice caps, glaciers, permanent snow	24 064 000	68.7	1.74
groundwater	23 400 000	–	1.69
fresh	10 530 000	30.1	0.76
saline	12 870 000	–	0.93
soil moisture	16 500	0.05	0.001
ground ice, permafrost	300 000	0.86	0.022
lakes	176 400	–	0.013
fresh	91 000	0.26	0.007
saline	85 400	–	0.006
atmosphere	12 900	0.04	0.001
swamp water	11 470	0.03	0.0008
rivers	2 120	0.006	0.0002
biological water	1 120	0.003	0.0001

^aPercentages are rounded and do not add to exactly 100%. (Data collected from refs (2 and 3).)

A.4. Selected Physicochemical Properties of Liquid Water

Table 3 lists selected physicochemical properties of liquid water. The crystal structures and densities of various ice forms are listed in Table 4.

A.5. Parameters for Some Water Models

The parameters for some water molecular models are listed in Table 5. Different water models used in Table 5 are shown in Figure 30.

Figure 30.

Different water models used in Table 5.

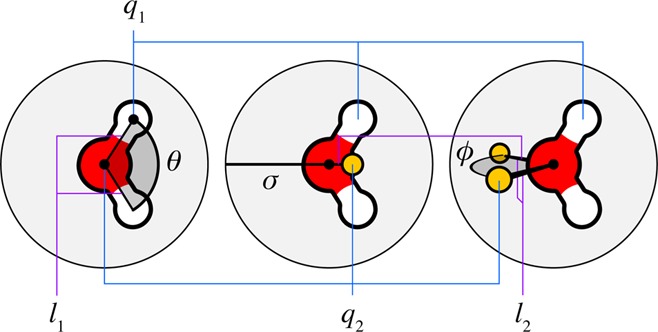
The water–water pair interaction potential (u_ww) for non-polarizable pointcharge water models is calculated using the parameters from Table 5 through eq 4:

4

where r_OO is the distance between two oxygens, and r_ij is a distance between charges q_i and q_j, located on different water molecules.

A.6. Calculated Physicochemical Properties of Some Water Models

The calculated physicochemical properties of some water models are listed in Table 6.

The authors declare no competing financial interest.

Author Status

^# C.J.F., M.F.-S., B.H.-L., and M.L.: Authors are listed in alphabetical order.