Design of Strain-Limiting Substrate Materials for Stretchable and Flexible Electronics

Abstract

Recently developed classes of electronics for biomedical applications exploit substrates that offer low elastic modulus and high stretchability, to allow intimate, mechanically biocompatible integration with soft biological tissues. A challenge is that such substrates do not generally offer protection of the electronics from high peak strains that can occur upon large-scale deformation, thereby creating a potential for device failure. The results presented here establish a simple route to compliant substrates with strain-limiting mechanics based on approaches that complement those of recently described alternatives. Here, a thin film or mesh of a high modulus material transferred onto a prestrained compliant substrate transforms into wrinkled geometry upon release of the prestrain. The structure formed by this process offers a low elastic modulus at small strain due to the small effective stiffness of the wrinkled film or mesh; it has a high tangent modulus (e.g., >1000 times the elastic modulus) at large strain, as the wrinkles disappear and the film/mesh returns to a flat geometry. This bilinear stress–strain behavior has an extremely sharp transition point, defined by the magnitude of the prestrain. A theoretical model yields analytical expressions for the elastic and tangent moduli and the transition strain of the bilinear stress–strain relation, with quantitative correspondence to finite element analysis and experiments.

1. Introduction

Significant progress in materials science, mechanical designs, and manufacturing approaches in stretchable and flexible electronics^[1–4] has led to a broad range of recent system-level device demonstrators,^[5–11] with emerging commercial examples in biomedical devices and wearable electronics.^[12–14] The soft mechanical behaviors of these systems represent key points of uniqueness relative to conventional technologies, where the requirements include: (i) low effective modulus and ability to accommodate large strain deformations with elastic response, to minimize mechanical constraints on biological tissues;^[15] and (ii) small strains in the active materials to eliminate the possibility of device failure.^[16–18] One solution to the latter challenge involves development of active materials that themselves have high fracture strains.^[19–24] Alternatives rely on mechanics design in the substrate and in geometrically shaped material structures to maintain compatibility with the highest performance electronic materials, such as inorganic semiconductors. Here, materials (e.g., network materials,^[25] network collagen fibrils,^[26] biological tissue^[27]) that have the “J-shaped” stress–strain behavior can be important. In some designs toward this goal,^[25] curved microstructures in network layouts yield mechanics that involves compliant (low elastic modulus) response at small strain due to bending and twisting deformations. An effective stiffening occurs at large strain (high tangent modulus) as the microstructures straightened and transition from a bending to a stretching dominated response. The resulting materials properties satisfy the requirements outlined in the previous paragraph, although the ratio of the high tangent modulus to low elastic modulus can reach values of only ≈10. In addition, the transition between these two regimes occurs over a wide range of strains, instead of a more desirable sharp, bilinear response.

This paper introduces a simple strategy that overcomes these limitations. We begin with a description of a basic embodiment, consisting of a thin film of a stiff material bonded to a prestrained, compliant substrate (Figure 1). Release of the prestrain leads to wrinkling of the thin film into sinusoidal form.^[28] At small strain, such a system has low elastic modulus, close to that of the compliant substrate, because the stiffness of the wrinkled film is negligible. Beyond an applied strain that stretches the wrinkled film into its original, flat geometry, the stiff film yields a high tangent modulus. The result is a bilinear stress–strain behavior with an extremely sharp transition point, and an exceptionally high ratio (e.g., >10³) of tangent to elastic moduli. Comprehensive theoretical, numerical, and experimental studies of this composite material, and of advanced embodiments, reveal key variables that govern the strain-limiting behavior, under both uni- and multidirectional strain.

Figure 1.

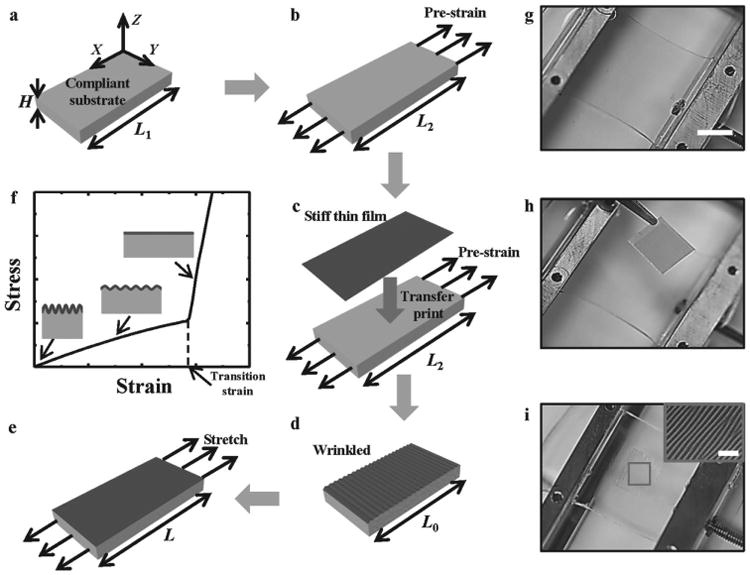
Schematic illustrations and optical images of the process for fabricating strain-limiting structures. a,b) Compliant substrate without and with the prestrain. c) Transfer printing a stiff thin film onto the prestrained substrate. d) Releasing the prestrain to form the wrinkled film. e) Stretching the strain-limiting structure. f) Bilinear stress–strain behavior of the strain-limiting structure. g–i) Optical images (scale bar, 1 cm; inset scale bar: 0.5 mm) of the process for applying prestrain to the substrate, transfer printing a stiff thin film on the prestrained substrate, and releasing the prestrain to form the wrinkled film.

2. Results and Discussions

The schematic diagrams in Figure 1a–e illustrate the fabrication process. A compliant, elastomeric substrate with an initial length L₁ and thickness H (Figure 1a) is stretched to length L₂ (Figure 1b), to induce a prestrain ε_pre = (L₂ – L₁)/L₁ in the substrate. A stiff thin film with thickness h is bonded onto the prestrained substrate (Figure 1c). Release of the prestrain in the substrate leads to wrinkling of the thin film (Figure 1d) to a length L₀. This system of materials is then stretched to length L (Figure 1e), which defines the applied strain ε = (L – L₀)/L₀. At small applied strain, the elastic modulus E of the system is the same as the elastic modulus E_S of the compliant substrate, i.e., E = E_s. This is because the membrane force in the wrinkled film remains constant during stretching such that the wrinkled film has a negligible stiffness and does not contribute to the tensile stiffness of the system. As the applied strain increases, the film begins to return to its flat state. At a strain comparable to the prestrain, the film becomes flat again and therefore contributes to the stiffness of system to yield the tangent modulus E_tangent = (E_fh + E_sH)/(h + H) by the rule of mixtures,^[29] where E_f is the elastic modulus of the film. As illustrated in Figure 1f, the behavior follows a bilinear stress–strain relation, with a transition strain ε_transition = (L₂ – L₀)/L₀ that separates the two linear regimes. For a thin film (e.g., h = ≈10⁻³H) much stiffer than the substrate (e.g., E_f = ≈10⁶E_s), the tangent modulus E_tangent is much larger than the elastic modulus E_s of the system, thereby providing a strain-limiting response. Figure 1g–i shows optical images for various stages in the fabrication, corresponding to Figure 1b–d, respectively, for the case of a polyimide (PI) thin film and a silicone (Silbione) substrate. PI has been widely used in stretchable electronics.^[30,31] Their elastic properties appear in Table 1, together with those of Cu (as the stiff thin film), and polydimethylsiloxane (PDMS, Sylgard 184, 10:1 ratio of prepolymer and curing agent) and Ecoflex for the compliant substrate.

Table 1.

Maximum prestrain and material properties of representative systems.

	PDMS [Es = 1 MPa, νs = 0.5]	Ecoflex [Es = 60 kPa, νs = 0.5]	Silbione [Es = 3 kPa, νs = 0.5]
Cu (Ef= 119 GPa, νf = 0.34, εY = 0.3%)	0.8%	6.0%	45%
PI (Ef= 2.5 GPa, νf= 0.34, εY = 2%)	2.6%	20%	150%

The total energy consists of the membrane energy and bending energy in the thin film, and the elastic strain energy in the compliant substrate. Minimization of the total energy gives the wrinkle wavelength and amplitude.^[28,32] For a semi-infinite substrate, its initial length L₁ is recovered upon release of the prestrain, i.e., L₀ = L₁ in Figure 1d, and the transition strain for the bilinear stress–strain relation is simply the prestrain, i.e., ε_transition = ε_pre. This relation ε_transition = ε_pre holds approximately for a very thick substrate when its bending stiffness overwhelms that of the film, i.e., Ē_fh³/(Ē_sH³) ≪ 0.01. The transition strain for a relatively thick substrate [Ē_fh³/(Ē_sh³) < ≈ 0.01] will be discussed in Equations (3) and (7). Here ${\overline{E}}_{\mathrm{s}}=E_{\mathrm{s}}/(1-{\nu }_{\mathrm{s}}^2)$ and ${\overline{E}}_{\mathrm{f}}=E_{\mathrm{f}}/(1-{\nu }_{\mathrm{f}}^2)$ are the plane-strain moduli of the substrate and film, respectively, and ν_s and ν_f are the corresponding Poisson's ratios. The critical strain for wrinkling is ε_c = (3Ē_s/Ē_f)^2/3/4, which is ≈0.3% or much less for the materials in Table 1. Once wrinkled, the compressive membrane strain in the film remains at −ε_c. The bending strain reaches a maximum upon complete release of the prestrain, and is given by $2\sqrt{{\varepsilon }_{\mathrm{c}}({\varepsilon }_{\text{pre}}-{\varepsilon }_{\mathrm{c}})}\approx 2\sqrt{{\varepsilon }_{\mathrm{c}}{\varepsilon }_{\text{pre}}}$ since the prestrain is usually much larger than ε_c. The maxi mum strain in the film, which is the same as the bending strain since the membrane strain is negligible, should be less than the yield strain ε_Y of the film in order to avoid plastic deformation, which gives a maximum prestrain of

$${\varepsilon }_{\text{pre}}<\frac{{\varepsilon }_{\mathrm{Y}}^2}{4{\varepsilon }_{\mathrm{c}}}={\varepsilon }_{\mathrm{Y}}^2{\left(\frac{{\overline{E}}_{\mathrm{f}}}{3{\overline{E}}_{\mathrm{s}}}\right)}^{2/3}$$ (1)

As shown in Table 1, the maximum prestrain for PI is much larger than that for Cu because PI has a relatively large yield strain ε_Y = 2%.^[25] The maximum prestrain for Silbione is much larger than those for Ecoflex and PDMS, which is consistent with Equation (1). This is because Silbione has very low elastic modulus and therefore imposes small stress on the film at the same prestrain.

Applications of strain-limiting materials may require relatively thin substrates.^[33] For substrates with bending stiffness two (or more) order(s) of magnitude or above that of the film, i.e., Ē_fh³/(Ē_sH³) <≈0.01, numerical results for the substrate with finite thickness^[34] suggest that the analysis described above is still valid. However, the substrate no longer recovers its initial length L₁ upon release of the prestrain, due to the film stiffness. The residual force Ē_fhε_c in the substrate resulting from the membrane strain −ε_c in the film, gives the new length L₀ of the substrate as (Figure 1d)

$$L_0=L_1+\frac{L_1}{4}{\left(\frac{9{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}$$ (2)

This value increases with the ratio of film-to-substrate bending stiffness, as shown in Figure S1 in the Supporting Information of the normalized length L₀/L₁ versus thickness ratio H/h for the PI film on several substrates. The transition strain for the bilinear stress–strain relation is

$${\varepsilon }_{\text{transition}}=\frac{{\varepsilon }_{\text{pre}}-\frac{1}{4}{\left(\frac{9{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}}{1+\frac{1}{4}{\left(\frac{9{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}}$$ (3)

It degenerates to ε_transition = ε_pre for a semi-infinite substrate (H → ∞). This expression suggests that the prestrain must exceed [9Ē_fh³/(Ē_sh³)]^1/34 for the system to exhibit a bilinear stress-strain relation. Besides the transition strain, the other critical property is the tangent modulus, and is obtained from the rule of mixtures^[29] as

$${\overline{E}}_{\text{tangent}}=\frac{{\overline{E}}_{\mathrm{f}}h+{\overline{E}}_{\mathrm{s}}H}{h+H}\approx {\overline{E}}_{\mathrm{s}}+\frac{h}{H}{\overline{E}}_{\mathrm{f}}$$ (4)

Figure 2a shows the bilinear stress–strain curves for a 1 μm-thick PI film on a 1 mm-thick Silbione substrate. The results from finite element analysis (FEA) and experiments agree well with the theory. The prestrain ε_pre is 15.1%, 25.6%, and 36.0% for the transition strain ε_transition to be 10%, 20%, and 30%, respectively. Here the prestrain must be larger than the transition due to the finite thickness of the substrate. Figure 2b shows the linear relation between ε_transition and ε_pre in Equation (3) for the PI film on several substrates given in Table 1 with the substrate-to-film thickness ratio H/h = 1000. The intercept of each curve with the horizontal axis denotes the minimal prestrain for wrinkling obtained from Equation (3), below which the film remains straight (but stretched) upon release of the prestrain. The right end of each curve denotes the maximum prestrain, determined from Equation (1) to avoid plastic yielding, but with ε_pre replaced by ε_transition to account for the finite thickness of the substrate (see Note 1 in Supporting Information for details). A more compliant substrate gives a larger range of prestrain that avoids plastic yielding, but also requires a larger prestrain to trigger wrinkling. The maximum prestrain can reach 150% for PI/Silbione. Figure 2c shows the linear relation between the tangent modulus Ē_tangent and film stiffness Ē_fh in Equation (4) for the PI film on several substrates with thickness ratios H/h = 1000, 3000, and 5000. A thinner substrate clearly gives a higher tangent modulus, reaching >1000 times of the elastic modulus as shown in Figure 2c.

Figure 2.

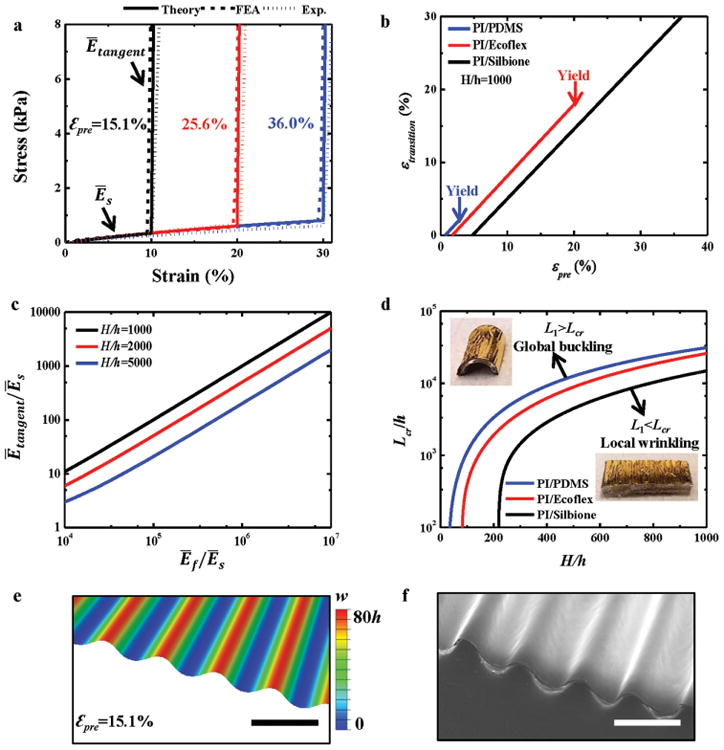
Theoretical, numerical, and experimental results from a unidirectional strain–limiting structure. a) Bilinear stress–strain curves of 1 μm-thick PI film on 1 mm-thick Silbione substrate subjected to various prestrains. b) The transition strain versus the prestrain for the PI film on several substrates with thickness ratio H/h = 1000. c) The tangent modulus normalized by the substrate modulus, Ē_tangent/Ē_s, versus the normalized film modulus Ē_f/Ē_s for several thickness ratios H/h. d) The critical film length that separates local wrinkling from global buckling. e,f) Numerical results and optical images (scale bar, 1 mm) of the morphology and out-of-plane displacement for a 1 μm-thick PI film on a 1 mm-thick Silbione substrate subjected to 15.1% prestrain.

There exists, however, a lower limit of the substrate thickness, below which global buckling occurs (top inset, Figure 2d), similar to Euler buckling of beams.^[35] This lower limit is given by Ē_fh³/(Ē_sH³) = 0.064 (see Note 2 in Supporting Information for details). For the substrate thickness above this lower limit, global buckling may still occur if the initial length L₁ is above a critical length L_cr^[35] (see Note 2 in Supporting Information for details)

$$L_{\text{cr}}=8.7\sqrt{\frac{EI}{{\overline{E}}_{\mathrm{s}}H}[\frac{1}{{\left(\frac{{\overline{E}}_{\mathrm{s}}}{{\overline{E}}_{\mathrm{f}}}\right)}^{2/3}+{\left(\frac{{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}}-\frac{1}{{0.064}^{1/3}}]}$$ (5)

where

$$EI=\frac{{({\overline{E}}_{\mathrm{s}}{H}^2+{\overline{E}}_{\mathrm{f}}{h}^2)}^2+4{\overline{E}}_{\mathrm{s}}{\overline{E}}_{\mathrm{f}}{H}^{3}h}{12({\overline{E}}_{\mathrm{s}}H+{\overline{E}}_{\mathrm{f}}h)}$$ (6)

is the effective bending rigidity. The normalized critical length L_cr/h, which separates local wrinkling from the undesirable global buckling modes, is shown versus the substrate-to-film thickness ratio H/h for PI film on several substrates. For PI/Silbione and H/h = 1000, the length of the stiff thin film (L₁) should be less than 15 000 times the thickness h. Figure 2e,f shows the morphology and out-of-plane displacement of 1 μm PI film on 1 mm Silbione, obtained by FEA and experiment, respectively, at 15.1% prestrain, which corresponds to 10% transition strain. The morphologies for 25.6% and 36.0% prestrain, corresponding to 20% and 30% transition strain, respectively, appear in Figure S2 in the Supporting Information.

Figure 3a shows a strain-limiting design for biaxial stretching. Here, the thin film in Figure 1c is replaced by a thin mesh (width W and spacing S, Figure 3a) on a biaxially pre-strained, compliant substrate. The thin mesh wrinkles in both x and y directions (Figure 3a) upon release of biaxial prestrains ${\varepsilon }_{\text{pre}}^x$ and ${\varepsilon }_{\text{pre}}^y$. Such a design can achieve anisotropic strain-limiting behavior by applying different prestrains in x and y directions. Figure 3b shows the stress–strain curves for x-, y-and 45°-stretching of a 1 μm-thick PI mesh (width W = 0.1 mm and spacing S = 0.4 mm) on a 1 mm-thick Silbione substrate subjected to the prestrains ${\varepsilon }_{\text{pre}}^x=30.8\%$ and ${\varepsilon }_{\text{pre}}^y=15.7\%$. For stretching along x or y directions, the stress–strain curves are clearly bilinear, and have the same elastic modulus Ē_s, same tangent modulus given by Ē_tangent ≈Ē_s+ [W/(W + S)]E_fh/H but different transition strains given by

Figure 3.

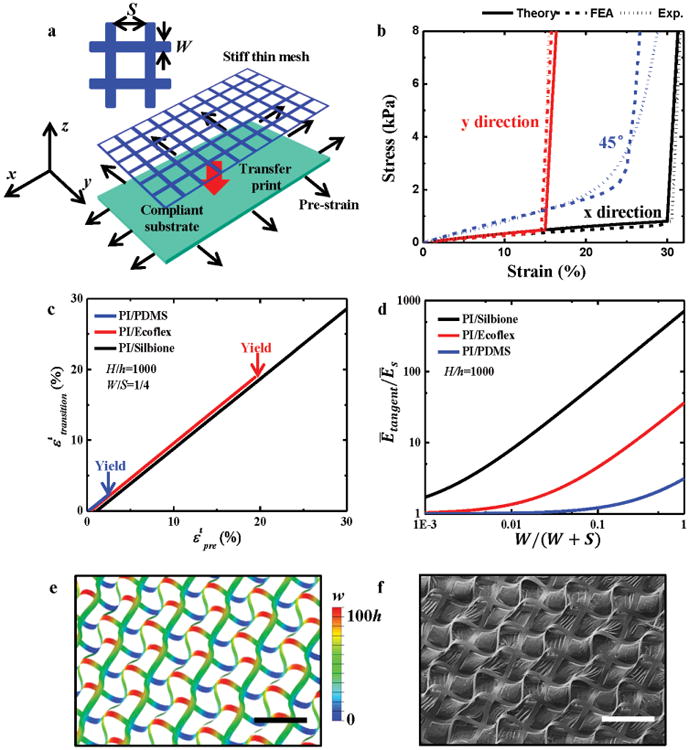
a) Schematic illustrations of the fabrication process that uses biaxial stretching. b) Stress-–strain curves for x-, y-, and 45°-stretching of 1 μm-thick PI mesh (width W = 0.1 mm and spacing S = 0.4 mm) on 1 mm-thick Silbione substrate subjected to prestrains of ${\varepsilon }_{\text{pre}}^x=30.8\%$ and ${\varepsilon }_{\text{pre}}^y=15.7\%$. c) The transition strain versus the prestrain for the PI mesh on several substrates with thickness ratio H/h = 1000 and W/S = 1/4. d) The tangent modulus normalized by the substrate modulus, Ē_tangent/Ē_s, versus (W/(W + S)) for PI mesh on several substrates with thickness ratio H/h = 1000. e,f) Numerical results and optical images (scale bar, 200 μm) of morphology and out-of-plane displacement for 1 μm-thick PI mesh (width W = 0.1 mm and spacing S = 0.4 mm) on 1 mm-thick Silbione substrate subjected to prestrains of ${\varepsilon }_{\text{pre}}^x=30.8\%$ and ${\varepsilon }_{\text{pre}}^y=15.7\%$.

$${\varepsilon }_{\text{transition}}^i=\frac{{\varepsilon }_{\text{pre}}^i-\frac{W}{6(W+\mathrm{s})}{\left(\frac{9{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}}{1+\frac{W}{6(W+\mathrm{s})}{\left(\frac{9{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}\right)}^{1/3}}$$ (7)

where the superscript i denotes either x or y. The transition strain in the x or y direction depends only on the prestrain in the same direction, and is 30% for ${\varepsilon }_{\text{pre}}^x=30.8\%$ and 15% for ${\varepsilon }_{\text{pre}}^y=15.7\%$, respectively in Figure 3b. The transition strain is comparable to the prestrain because the minimal prestrain [W/(W + S)][9E_fh³(Ē_sh³)]^1/3/6 to initiate wrinkling is much smaller than that for uniaxial stretching due to the factor W/(W + S). For x- or y- stretching, the theory agrees well with FEA and experiments (Figure 3b). For stretching along 45° (Figure 3b) and other directions (Figure S3, Supporting Information), FEA and experiments all show the strain-limiting behavior, though they do not display a sharp transition point. Figure 3c shows the linear relation between ${\varepsilon }_{\text{transition}}^i$ and ${\varepsilon }_{\text{pre}}^i$ in Equation (7) for the PI film on several substrates with the thickness ratio H/h = 1000 and width-to-spacing ratio W/S = 1/4. The minimal prestrain for wrinkling, corresponding to the intercept of each curve with the horizontal axis, is relatively small such that ${\varepsilon }_{\text{transition}}^i\approx {\varepsilon }_{\text{pre}}^i$. The right end of each curve denotes the maximum prestrain for plastic yielding, and it increases as the substrate modulus decreases. Figure 3 d shows the linear relation between the tangent modulus Ē_tangent and [W/(W + S)]Ē_fh/H for the PI film on several substrates with the thickness ratio H/h = 1000. The right limit W/(W + S) = 1 in Figure 3d (i.e., spacing S approaching 0) corresponds to Figure 2c for the thin film, while the limit W/(W + S) = 0 (i.e., no mesh) gives the substrate modulus. Figure 3e,f shows the morphology and out-of-plane displacement of a 1 μm PI mesh (width W = 0.1 mm, spacing S = 0.4 mm) on a 1 mm Silbione substrate, obtained by FEA and experiment, respectively, at the prestrains ${\varepsilon }_{\text{pre}}^x=30.8\%$ and ${\varepsilon }_{\text{pre}}^y=15.7\%$. The results agree reasonably well, even though the optical image in Figure 3f shows slight delamination between the stiff thin mesh and compliant substrate. FEA (Figure S4, Supporting Information) also confirms that the effect of delamination, if any, is small (see Note 3 in the Supporting Information for details).

3. Conclusions

A thin film or mesh of a stiff material bonded onto a prestrained, compliant substrate wrinkles upon release of the prestrain. The resulting system is naturally strain-limiting—it has low elastic modulus, comparable to that of the substrate, at small strain because the wrinkled film or mesh has negligible stiffness in this regime; it has high tangent modulus (e.g., >1000 times the elastic modulus) at large strain when the wrinkled stiff film or mesh becomes flat. The result is a bilinear stress–strain response with a very sharp transition point. A theoretical model provide analytical expressions for the elastic and tangent moduli and the transition strain of the bilinear stress–strain relation, all in agreement with FEA and experiments.

For biomedical device applications, the low elastic modulus response can match or reach values below those of targeted biological tissues, thereby avoiding any mechanical constraint on natural motions. The high tangent modulus, on the other hand, serves to shield the stretchable and flexible electronics from large deformations that might otherwise lead to fracture and device failure.

4. Experimental Section

Finite Element Analysis

ABAQUS commercial software^[36] was used to study the mechanics response of the strain-limiting structure. The compliant substrates (PDMS, Ecoflex and Silbione) were modeled by the hexahedron element (C3D8R), while the stiff thin films (Cu and PI) were modeled by the composite shell element (S4R).

Preparation of Strain-Limiting Structure

PMMA (100 nm) coated on a glass slide (70 × 50 × 1.0 mm³) served as a sacrificial layer to facilitate release. Spin casting on top of this substrate yielded a film of PI (1≈100 μm in thickness, HD Microsystems, USA). Photolithographic patterning of this PI followed by thermal curing (2 h at 250 °C in a vacuum oven) defined the desired planar or mesh structure. Undercut etching removed the PMMA layer to allow release for subsequent integration with a prestrained compliant and tacky elastomeric substrate (Silbione RT 4717 A/B, Bluestar silicones, France) mounted on a manual stretcher.

Measurements of Stress–Strain Responses

Mechanical properties of all samples were measured with a dynamic mechanical analyzer (TA instruments, Q800). Characterizing the applied force versus the displacement under uniaxial tensile loading at room temperature yielded data for determination of the mechanical modulus. Each of the reported results corresponds to an average of measurements on three samples.