Frequency-Selective Computed Tomography: Applications During Periodic Thoracic Motion

Abstract

We seek to use computed tomography (CT) to characterize regional lung parenchymal deformation during high-frequency and multi-frequency oscillatory ventilation. Periodic motion of thoracic structures results in artifacts of CT images obtained by standard reconstruction algorithms, especially for frequencies exceeding that of the X-ray source rotation. In this study, we propose an acquisition and reconstruction technique for high resolution imaging of the thorax during periodic motion. Our technique relies on phase-binning projections according to the frequency of subject motion relative to the scanner rotation, prior to volumetric reconstruction. The mathematical theory and limitations of the proposed technique are presented, and then validated in a simulated phantom as well as a living porcine subject during oscillatory ventilation. The four-dimensional image sequences obtained using this frequency-selective reconstruction technique yielded high spatio-temporal resolution of the thorax during periodic motion. We conclude that frequency-based selection of CT projections is ideal for characterizing dynamic deformations of thoracic structures that are ordinarily obscured by motion artifact using conventional reconstruction techniques.

I. INTRODUCTION

SEVERAL imaging modalities are available to provide four-dimensional descriptions of transient tissue deformations (i.e., three spatial dimensions, one temporal dimension) [1]. X-ray computed tomography (CT) is often used in this regard due to its excellent spatial resolution, despite the risks associated with the use of ionizing radiation [2]. However scanner rotation speed limits temporal resolution using standard image reconstruction algorithms [3]. This may limit the quality of images during dynamic subject motion, especially for deformations at high frequencies. As a result, temporally-resolved imaging during rapid, periodic motion, e.g., high-frequency and multi-frequency oscillatory ventilation [4],[5], is difficult to acquire. Especially with faster rotation times, larger axial coverage, and the ability to significantly reduce radiation exposure utilizing newly emerging CT technologies [6],[7], there is a renewed interest in assessing dynamic physiologic phenomena via CT.

With CT imaging, the X-ray source and detector array rotate about the subject, while X-rays are projected at varying angles. The resulting projections on the opposing detector array are characterized by linear attenuation coefficients, representing the tendency of various biological tissues to absorb or scatter X-rays [8]. The raw data acquired by the scanner comprises projections at multiple angles. A two-dimensional image of the spatially-distributed linear attenuation coefficients can then be obtained by reconstruction of the projection data.

Various reconstruction algorithms are available for clinical purposes, such as filtered back-projection or iterative reconstruction [9], with each achieving a particular balance between image quality and computational cost. Standard reconstruction algorithms assume that the subject is stationary during scanner rotation, such that each acquired projection captures the same spatial orientation through a different angle. However if the subject is moving during image acquisition, the projection data will contain multiple spatial orientations and projection angles [10]. In such situations, standard reconstruction algorithms will blur the resulting image due to motion artifact [11]. This becomes especially problematic during repetitive periodic motion of anatomic structures at rates equal to or faster than the scanner rotation frequency [4],[12]. Motion artifact mitigation and/or temporally resolved image reconstruction in three dimensions is possible using appropriate gating or triggering techniques [12]. However such techniques selectively target image acquisition at the same subject state repeatedly over the course of multiple motion cycles, rather than acquiring multiple transient states within one cycle.

Image acquisition during periodic subject motion has been well-described in the fields of cardiac and thoracic imaging, for which cardiogenic motion (in the frequency range of 1 to 2 Hz) and spontaneous breathing (0.1 to 0.7 Hz) present sources of motion artifact. Gating techniques for such applications may utilize external signals for either retrospective gating or prospective triggering of the image acquisition cycle. In thoracic CT, a variety of external signals including respiratory flow, pressure, or abdominal motion may be used to target image timing according to lung volume or respiratory phase (i.e., end-expiration and end-inspiration) [13]–[15]. In cardiac CT, an electrocardiogram (EKG) may be used to target image timing according to cardiac phase and heart rate, identifying a period for which the mediastinal contents remain relatively stationary (i.e., diastole) [12],[16]–[18]. However conditions involving highly-dynamic subject states, such as high-frequency oscillatory ventilation (HFOV), do not provide comparable motionless time windows. HFOV is an alternative form of mechanical ventilation that may be used during severe refractory hypoxemia in the Acute Respiratory Distress Syndrome (ARDS). In contrast to conventional forms of mechanical ventilation, HFOV delivers tidal volumes that may be smaller than anatomic dead space, at rates of 2 to 20 Hz [19]. Thus imaging during HFOV has been limited to planar views [20] or phase-averaged volumetric images [4],[21]–[23], resulting in poor spatio-temporal resolution.

To achieve high-resolution CT images during such highly dynamic states, an alternative approach must be implemented that does not rely on the reconstruction of sequentially acquired projections triggered by physiological events [24],[25]. In this study, we propose the use of frequency-selective 4D-CT (FSCT) for capturing periodic subject motion with both high spatial and temporal resolutions. Our approach relies on the continuous acquisition of many projections during multiple scanner rotations over a specified length of axial coverage, followed by a retrospective analysis of the resulting phase distribution of subject motion obtained from projection data.

II. METHODS

A. Theory

Consider an X-ray source rotating through a circular trajectory at frequency f_rot, with an opposing detector array acquiring projections at varying angles, during periodic subject motion at frequency f_sub. The phase of subject motion ϕ_sub can be expressed as a function of time:

$${\varphi }_{\text{sub}}\left(t\right)=\left(2\pi f_{\text{sub}}t\right)\text{mod}2\pi ,t\ge 0$$ (1)

where each distinct value of ϕ_sub between 0 and 2π corresponds to a particular spatial orientation, cyclically repeated during the periodic motion. Similarly, the phase of the scanner rotation is:

$${\varphi }_{\text{rot}}\left(t\right)=\left(2\pi f_{\text{rot}}t\right)\text{mod}2\pi ,t\ge 0$$ (2)

where ϕ_rot is equivalent to the projection angle relative to the initial projection angle at time t = 0. To reconstruct a “still” image of the subject at one particular phase ϕ_rec, projections must be acquired at times t_k such that ϕ_sub (t_k) = ϕ_rec:

$$tk=\frac{{\varphi }_{\text{rec}}+2\pi k}{2\pi f_{\text{sub}}},\text{where}k=0,1,2,\dots$$ (3)

The relative X-ray projection angle at each t_k is given by:

$${\varphi }_{\text{rot}}\left(t_k\right)=\left[\left(\frac{f_{\text{rot}}}{f_{\text{sub}}}\right)\left({\varphi }_{\text{rec}}+2\pi k\right)\right]\text{mod}2\pi ,\text{where}k=0,1,2,\dots$$ (4)

Multiple distinct “still” images of the subject throughout the periodic motion may be reconstructed by first partitioning subject phase into N_bin equally spaced bins on the interval 0 to 2π:

$$n_{\text{bin}}=\{\begin{array}{ll}0,& 2\pi \frac{0}{N_{\text{bin}}}\le {\varphi }_{\text{sub}}<2\pi \frac{1}{N_{\text{bin}}}\\ 1,& 2\pi \frac{1}{N_{\text{bin}}}\le {\varphi }_{\text{sub}}<2\pi \frac{2}{N_{\text{bin}}}\\ ⋮& ⋮⋮\\ N_{\text{bin}}-1,& 2\pi \frac{N_{\text{bin}}-1}{N_{\text{bin}}}\le {\varphi }_{\text{sub}}<2\pi \frac{N_{\text{bin}}}{N_{\text{bin}}}\end{array}$$ (5)

and then grouping the sequentially acquired projections according to the corresponding subject phase bin:

$$n_{\text{bin}}\left(t\right)=\lfloor \left(\frac{{\varphi }_{\text{sub}}\left(t\right)N_{\text{bin}}}{2\pi }\right)\text{mod}{N}_{\text{bin}}\rfloor ,t\ge 0$$ (6)

where ⌊⌋ denotes rounding the enclosed argument to the largest integer less than or equal to itself. Equation (6) can be rewritten as:

$$n_{\text{bin}}\left(t\right)=\lfloor \left(f_{\text{sub}}t{N}_{\text{bin}}\right)\text{mod}{N}_{\text{bin}}\rfloor ,t\ge 0$$ (7)

Binning the acquired projections according to subject phase yields N_bin sinograms, each containing a sufficient number of angles required for image reconstruction. The phase-binned sinograms may then be reconstructed independently to produce N_bin images in a sequence representing dynamic subject state during periodic motion. Each image represents subject state over a limited range of motion characterized by the size of each phase bin. Increasing N_bin reduces the size of each phase bin, thereby reducing motion artifact in the reconstructed images.

Fig. 1a shows an example of transient variations in subject motion phase during scanner rotation, according to (1) and (2). Standard CT reconstruction is performed on sequentially acquired projections, resulting in variable subject motion phase obtained during one scanner rotation, illustrated in Fig. 1b. FSCT reconstruction is instead performed on subsets of projection data binned according to subject motion phase. Fig. 1c illustrates more uniform subject motion phase obtained in each binned subset of projection data using the FSCT approach described in (5).

Fig. 1.

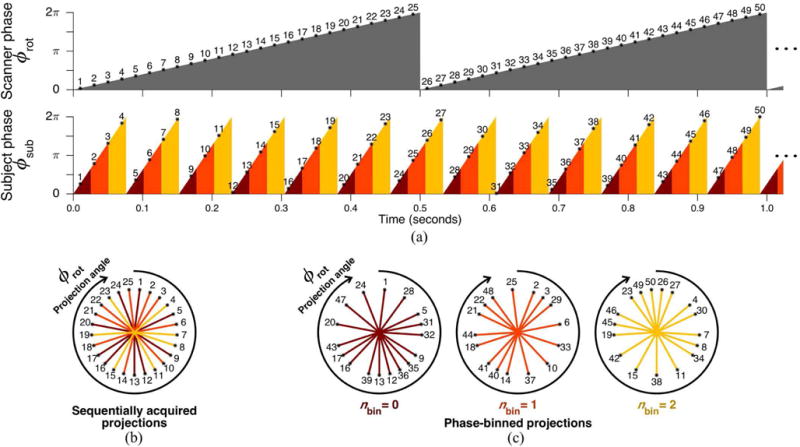
Illustration of FSCT concept for arbitrarily selected parameters. (a) Scanner phase ϕ_rot as a function of time for a 2.0 Hz rotation frequency, with 25 projections acquired per rotation as indicated by numbered asterisks. Projections are numbered according to chronological order of acquisition. Subject phase ϕ_sub as a function of time for a 13.13 Hz periodic motion cycle. Subject phase is labeled according to 3 equally sized bins, indicated by color (red, orange, yellow). (b) Standard CT reconstruction is performed on sequentially acquired projections, averaging together variable subject phase acquired throughout one scanner rotation. (c) FSCT reconstruction is performed on phase-binned subsets of projections, each containing a limited range of subject phase.

B. Feasible Sampling Criterion

In practical applications, the number of unique projection angles is given by the number of projections acquired per scanner rotation N_pro. Projections are acquired at a fixed rate and with equal angular spacing throughout each scanner rotation. Therefore projection angle ϕ_rot may be considered a discrete variable rather than a continuous function of time, such that ϕ for the p^th sequentially acquired projection is given by:

$${\varphi }_{\text{rot}}\left(p\right)=\frac{2\pi p}{N_{\text{pro}}}\text{mod}2\pi ,p=0,1,2,\dots$$ (8)

Each unique value of ϕ_rot (p) may be indexed by n_pro such that:

$$n_{\text{pro}}\left(p\right)=p\text{mod}{N}_{\text{pro}},p=0,1,2\dots$$ (9)

Acquisition of the p^th projection occurs at time point t_p:

$$t_p=\frac{p}{N_{\text{pro}}{f}_{\text{rot}}},p=0,1,2,\dots$$ (10)

with subject motion phase:

$${\varphi }_{\text{sub}}\left(p\right)=p\frac{2\pi f_{\text{sub}}}{N_{\text{pro}}{f}_{\text{rot}}}\text{mod}2\pi ,p=0,1,2,\dots$$ (11)

and subject phase bin index n_bin:

$$n_{\text{bin}}\left(p\right)=\lfloor p\frac{N_{\text{bin}}{f}_{\text{sub}}}{N_{\text{pro}}{f}_{\text{rot}}}\text{mod}{N}_{\text{bin}}\rfloor .$$ (12)

Each projection is therefore assigned a pair of indexes 〈n_pro, n_bin〉 characterizing the associated projection angle and subject motion phase bin. All unique combinations of n_pro and n_bin must be sampled to appropriately reconstruct the complete image sequence with minimal spatial aliasing, although it is possible to poorly select f_sub, f_rot, and N_bin such that the acquired projections repeat non-unique pairs 〈n_pro(p), n_bin(p)〉 before complete sampling. The relative periodicity between scanner rotation and subject motion is determined by the number of projection acquisitions which may occur before a repetition in the pair 〈ϕ_rot(p), ϕ_sub(p)〉, hereafter referred to as R_pro. Projection angle index n_pro is periodic in p with period N_pro, therefore R_pro must be an integer multiple of N_pro:

$$R_{\text{pro}}=R_{\text{rot}}{N}_{\text{pro}}$$ (13)

where R_rot is the smallest integer number of rotations which may complete before a repetition in 〈ϕ_rot(p), ϕ_sub(p)〉 occurs. Substituting this expression for R_pro for p in (11) yields:

$${\varphi }_{\text{sub}}\left(R_{\text{pro}}\right)=\frac{R_{\text{rot}}2\pi f_{\text{sub}}}{f_{\text{rot}}}\text{mod}2\pi$$ (14)

Thus the pair 〈ϕ_rot(p), ϕ_sub(p)〉 repeats non-unique combinations when an integer number of scanner rotations have completed such that:

$$R_{\text{sub}}=R_{\text{rot}}\frac{f_{\text{sub}}}{f_{\text{rot}}}$$ (15)

where R_sub is the smallest integer number of motion cycles that may complete before a repetition in 〈ϕ_rot(p), ϕ_sub(p)〉 occurs. If f_sub and f_rot are incommensurable, then no finite values of R_rot and R_sub exist. Instead, both R_rot and R_sub will be infinite, since an exact repetition in 〈ϕ_rot(p), ϕ_sub(p)〉 will never occur. However if f_sub and f_rot are commensurable, then R_rot may be found by continued fraction expansion [26].

Finally the number of unique pairs 〈ϕ_rot(p), ϕ_sub(p)〉 for a given f_rot and f_sub is limited by an upper bound, determined as the number of projections acquired per scanner rotation N_pro multiplied by the number of scanner rotations which may occur before repetition R_rot. To ensure that undersampling does not occur, the product N_pro · R_rot must be greater than the total number of samples to be acquired, which is given by the product N_pro · N_bin:

$$\frac{N_{\text{pro}}{R}_{\text{rot}}}{N_{\text{pro}}{N}_{\text{bin}}}=\frac{R_{\text{rot}}}{N_{\text{bin}}}\ge 1$$ (16)

Note that this feasible sampling criterion does not depend on N_pro, but rather only on N_bin, f_rot, and f_sub. Fig. 2 illustrates the space of feasible sampling, a selection of N_bin and frequency ratio (f_sub/f_rot) This fractal-like criterion is characterized by the Thomae function, a modified Dirichlet function that is non-zero only at rational values of its argument.

Fig. 2.

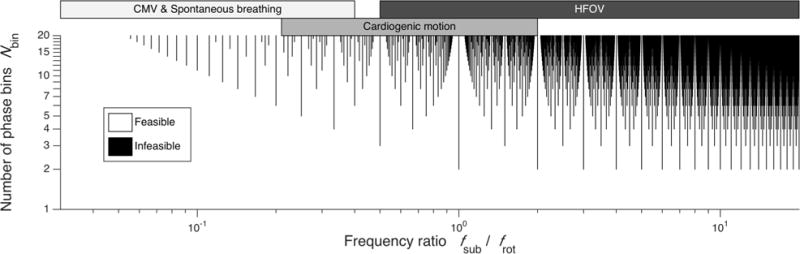
The space of feasible sampling, showing the combinations of N_bin and frequency ratio (f_sub/f_rot) for which the projection angles and subject phase bins are either completely (white) or incompletely (black) sampled before repetitious sampling. Parameter selection along the black lines may not provide sufficient sampling for image reconstruction. Typical ranges of f_sub and f_rot corresponding to conventional mechanical ventilation (CMV), spontaneous breathing, cardiogenic motion, and high-frequency oscillatory ventilation (HFOV) are shown.

C. Optimal Sampling Condition

The minimum scanning duration for a feasible selection of N_bin and frequency ratio (f_sub/f_rot) depends on the length of time required to completely sample all unique pairs of phase bin and projection angle. Under ideal circumstances, each newly acquired projection corresponds to a previously unsampled pair 〈n_pro(p), n_bin(p)〉, i.e., with minimal redundancy. In this case, the scanning duration measured in number of scanner rotations (N_rot) is lower-bounded by the number of motion phase bins:

$$\frac{N_{\text{rot}}}{N_{\text{bin}}}\ge 1$$ (17)

However (17) assumes that the acquired projections uniformly sample both subject phase bins and projection angle bins without redundancy. More generally, the degree of redundant sampling depends on the frequency ratio (f_sub/f_rot), as indicated by Fig. 2. Due to the discrete nature of phase-binning, redundant sampling of indices 〈n_pro(p), n_bin(p)〉 may occur before an exact repetition of phases 〈ϕ_rot(p), ϕ_sub(p)〉 is encountered. For any choice of N_bin, the ideal sampling condition given by (17) is ensured with equality when:

$$\frac{f_{\text{sub}}}{f_{\text{rot}}}=\frac{c}{N_{\text{bin}}}$$ (18)

where c is any positive integer such that c and N_bin are coprime. If (18) is satisfied, then N_bin scanner rotations may be used to reconstruct N_bin motion phase bins. Some examples of optimal frequency ratios for desired N_bin values are provided in Table I, according to (18). Deviating from the frequency ratios given by (18) may result in substantially increased scanning duration required to properly reconstruct the image sequence.

TABLE I.

Optimal Sampling Conditions to Minimize Scanning Duration

Nbin	Optimal fsub/frot ratio
1	Any
2	1/2,3/2,5/2,7/2,9/2, …
3	1/3,2/3,4/3,5/3,7/3, …
4	1/4,3/4,5/4,7/4,9/4, …
5	1/5,2/5,3/5,4/5,6/5, …
⋮	⋮
Nbin	c/Nbin, with c and Nbin coprime

Under such conditions, required scanning duration N_rot = N_bin.

D. Simulated Phantom

An oscillating imaging phantom was simulated using a Shepp-Logan design [27], with two ellipses modified by sinusoidal oscillations in size, intensity, and/or centroid position at a rate of 9.924 Hz, as shown in Fig. 3. Image size was 256 by 256 pixels. An X-ray CT scanner was simulated with 1000 detectors, 1600 projections per rotation, and 3.509 Hz rotation frequency (285 ms period). These frequencies were chosen to maximize the number of feasible choices for N_bin. Projection acquisition was performed using the Radon transform in MATLAB (The Mathworks Inc., Natick, MA), assuming parallel beam projection and a flat detector array. A total of 224,000 projections over 140 scanner rotations were acquired during continuous phantom oscillation.

Fig. 3.

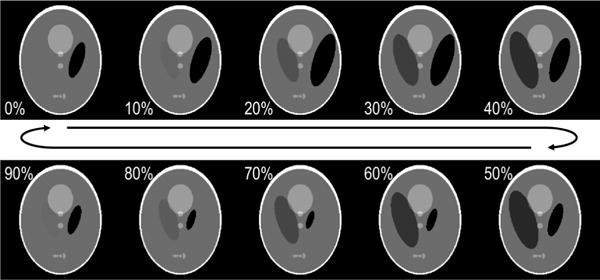
Simulated phantom shown at 10 discrete phases equally spaced throughout a continuous and periodic deformation cycle. Two ellipses of the standard Shepp-Logan phantom [27] were modified with sinusoidal oscillations in size, intensity, and/or centroid position. Image size was 256 × 256 pixels.

Image reconstruction was performed by filtered back-projection using the inverse Radon transform, with linear interpolation and Ram-Lak ramp filtering. Standard reconstruction was performed using either 1 complete rotation (1600 sequentially acquired projections), or 140 rotations (224,000 sequentially acquired projections). FSCT reconstruction was performed by phase-binning the projection data according to the 9.924 Hz phantom cycle, using a range of N_rot between 1 and 140 rotations, and a range of N_bin between 1 and 100 motion phase bins¹. FSCT reconstruction error was computed as the mean and standard deviation of voxel-wise absolute intensity difference between the reconstructed image and the phantom image across all reconstructed phase bins. The reference phantom image for each phase bin was selected at the motion phase corresponding to the midpoint of the phase bin.

E. Thoracic Imaging in vivo

One pig weighing 45 kg was scanned with approval from the University of Iowa Institutional Animal Care and Use Committee (Protocol number 5031314). The animal was sedated using an intravenous infusion of propofol at 9 mg kg⁻¹ hr⁻¹, and paralyzed with intermittent doses of rocuronium at 1 mg kg⁻¹. EKG waveforms were obtained using a Philips patient monitor equipped with the M3001A measurement module (Philips Healthcare, Andover, MA). The animal was ventilated by a FabianHFO ventilator/oscillator (Acutronic Medical Systems AG, Hirzel, Switzerland) using pressure-controlled ventilation at a rate of 24 min⁻¹ with 5 cmH₂O positive end-expiratory pressure, 20 cmH₂O peak inspiratory pressure, and I:E ratio 1:2. The animal was positioned in the gantry of a SOMATOM Force CT scanner (Siemens Healthineers, Forchheim, Germany) such that the axial field of view was centered approximately 3 cm caudal to the carina. Scanning was performed during 1) ventilation with pressure-controlled conventional mechanical ventilation (CMV); 2) high-frequency oscillatory ventilation (HFOV) set at 5 Hz; 3) HFOV set at 20 Hz; and 4) multi-frequency oscillatory ventilation (MFOV) using a broadband excitation waveform containing energy set at 5 Hz, 10 Hz, 15 Hz, and 20 Hz [5]. Each of the oscillatory waveforms was delivered at 10 cmH₂O mean airway pressure, 100 cmH₂O peak-to-peak pressure, and 10 L min⁻¹ bias flow. The animal was continuously scanned at 80 kVp tube voltage and 150 mA tube current for a total duration of approximately 30 seconds, at a 4.0 Hz scanner rotation frequency (250 ms period). The Force scanner acquired 1120 projections per rotation using 920 detectors per row and 96 detector rows. Transverse beam width was 0.48 mm at the isocenter, with 0.6 mm spacing between detector rows. As part of another study under this protocol, a total of 177 mL Isovue-370 contrast agent (Bracco Diagnostic Inc., Monroe Township, NJ) was given over approximately one hour. Scanning for this study was performed 20 minutes following the final 54 mL dose.

The ventilatory and cardiac frequencies were estimated from the ventilator settings and EKG heart rate monitor, however these estimates lacked sufficient precision for the FSCT reconstruction technique. Since the in vivo projection data contained substantial frequency content at both ventilatory and cardiac frequencies, temporal variations in each set of projection data were examined to determine frequency content prior to selection of FSCT reconstruction frequencies. The acquired projections were re-sampled at intervals of 2π radians in projection angle, producing subsets of the projection data containing transient variations in subject position sampled at the frequency of the scanner rotation (f_rot). In the two-dimensional discrete Fourier transform (2D-DFT) of this subset of projection data, the dimensions of the transformed projection data correspond to detector position and time. Integrating the magnitude of the 2D-DFT along the dimension corresponding to detector position produced a spectrum of oscillatory energy in the projection data as a function of temporal frequency, relative to scanner rotation frequency (i.e., frequencies greater than 0.5 f_rot will be aliased). Spectral peaks identified in the oscillatory energy spectrum correspond to either ventilatory or cardiogenic sources of motion. Thus ventilatory and cardiac frequencies were determined from the projection data, using a priori knowledge obtained from physiologic monitors (e.g., ventilator settings, EKG-derived heart rate) to determine de-aliased frequency content.

FSCT reconstruction was performed by first phase-binning the projection data according to either ventilatory or cardiac cycle as described in the Theory section, and subsequently reconstructing each phase-binned sinogram using a Feldkamp-type cone-beam reconstruction algorithm [28] (Michigan Image Reconstruction Toolbox, J. A. Fessler, University of Michigan, Ann Arbor, MI) and MATLAB (The Mathworks Inc., Natick, MA).

III. RESULTS

Fig. 4 shows the simulated phantom at time t = 0 seconds, alongside standard CT reconstructions and FSCT reconstruction of projection data acquired over 140 scanner rotations. The FSCT image is only shown at the first of 10 motion phase bins. A transient profile is shown through a single row from the phantom and FSCT images, resolving the periodic motion of the phantom over multiple 9.924 Hz oscillation cycles. A static profile through the same row is provided for the standard reconstructed images. The standard reconstructions are affected by motion artifacts that obscure finer details in lung structure, whereas the FSCT reconstruction yields crisp spatial boundaries within each bin and smooth transient motion between bins.

Fig. 4.

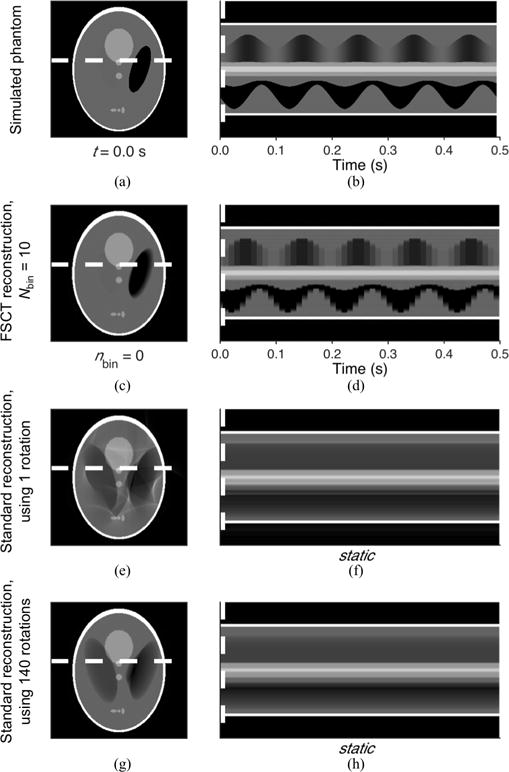
Comparison between standard CT reconstruction (e,g) and FSCT reconstruction (c) of the simulated phantom oscillating at 9.924 Hz (a). A transient profile shown through a single row (white dashed line) is provided for the simulated phantom (b) and FSCT reconstructed image (d), resolving periodic motion over multiple 9.924 Hz oscillation cycles. A static profile through the same row is provided for the standard reconstructed images (f,h).

Fig. 5 shows the error of FSCT reconstruction performed using varying subsets of the total acquired projection data and varying phase bin sizes. Error was assessed by the mean and standard deviation of voxel-wise intensity difference between each reconstructed image compared to the reference phantom images. The lower bound for adequate scanning duration given by (17) is indicated by the dashed line, delineating two domains with different behavior of the reconstruction error with respect to the amount of sampling and number of bins. The minimum sampling criterion is not satisfied at short scanning durations and large number of bins, thus aliasing and streak artifact caused by undersampling produce substantial reconstruction errors. The minimum sampling criterion is satisfied at long scanning durations and small number of bins, with mean voxel-wise intensity difference converging with increased sampling. However when N_bin becomes too small, the reconstruction error increases as a result of the increased bin size and motion artifact. For reference, the standard reconstruction using 1 rotation, shown in Fig. 4e, corresponds to the location N_bin = 1 and N_rot = 1 in the bottom-left corner of Figs. 5a and 5b. Likewise, the standard reconstruction using 140 rotations, shown in Fig. 4g, corresponds to the location N_bin = 1 and N_rot = 140 in the top-left corner of Figs. 5a and 5b.

Fig. 5.

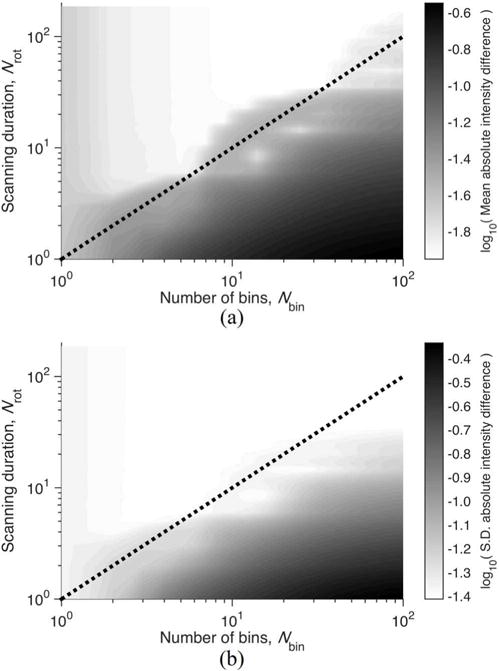
Contours of error in FSCT reconstructed image of simulated phantom for varying selection of scanning duration N_rot and number of bins N_bin. Error was assessed by (a) mean and (b) standard deviation of voxel-wise absolute intensity difference between the reconstructed image and the phantom image across all reconstructed phase bins. The lower bound for adequate sampling given by (17), is indicated by the dashed line, using N_det = 1000, N_pro = 1600, f_rot = 3.509 Hz, f_sub = 9.924 Hz.

A. Thoracic Imaging in vivo

Fig. 6 shows frequency content in the projection data acquired during in vivo mechanical ventilation. The spectral peaks correspond to either cardiogenic or ventilatory oscillations, potentially aliased relative to the scanner rotation frequency. FSCT reconstruction frequencies were chosen for each set of projection data based on the spectral peaks, using a priori knowledge to de-alias higher frequency content. Fig. 7 shows example images reconstructed at both cardiac and ventilatory frequencies using the FSCT approach. Transient profiles from each image are presented through a single slice from the transverse plane, resolving the motions of various intrathoracic organs and tissues across subject phase bins, equally spaced throughout the periodic motion cycle.² Motion artifact is present in each image wherever extraneous motion occurs at non-harmonic frequencies relative to the reconstruction frequency—for example, cardiogenic motion produces blurring in images reconstructed at the ventilatory frequency, and vice versa.

Fig. 6.

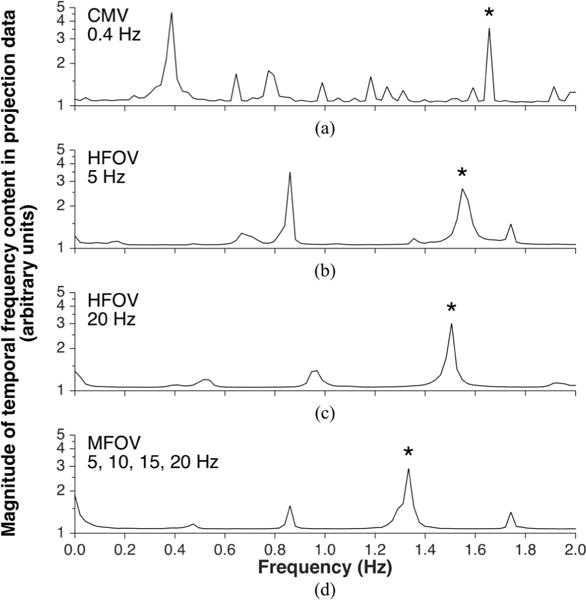
Frequency content in the projection data acquired during in vivo mechanical ventilation of a pig, using either conventional mechanical ventilation (a), high-frequency oscillatory ventilation (b,c), or multi-frequency oscillatory ventilation (d). Frequency on the horizontal axis obtained from discrete Fourier transform using the scanner rotation frequency f_rot = 4 Hz as the sampling frequency. Thus subject motion frequencies greater than 0.5 f_rot are aliased. Spectral peaks correspond to either ventilatory motion or cardiogenic motion. Spectral peaks corresponding to heart rate are indicated by asterisks.

Fig. 7.

Example images reconstructed from projection data acquired over 30 seconds of scanning during in vivo mechanical ventilation of a pig, using (a) conventional mechanical ventilation at 0.4 Hz (24 min⁻¹), (b) high-frequency oscillatory ventilation at 5 Hz (300 min⁻¹), (c) high-frequency oscillatory ventilation at 20 Hz (1200 min⁻¹), and (d) multi-frequency oscillatory ventilation using a broadband waveform containing energy at 5, 10, 15, and 20 Hz. Both ventilatory and cardiac frequencies were reconstructed from the same projection data. Transient profiles from each image are presented through a single slice from the transverse plane over 1 to 6 seconds, showing resolved motion across subject phase bins equally spaced throughout the periodic motion cycles.

It should be emphasized that each pair of ventilatory and cardiac reconstructions presented in Fig. 7 were obtained from the same projection data. Furthermore the transient profiles are shown through the same spatially-oriented slice. Therefore, any differences in image quality or structural clarity between these paired reconstructions are a direct consequence of modulating the reconstruction frequency and/or number of phase bins.

IV. DISCUSSION

In this study, we have presented an algorithm for reconstructing temporally-resolved CT images of periodic subject motion. This frequency-selective 4D-CT (FSCT) imaging technique involves continuously acquiring X-ray projections during multiple rotations of the source around the oscillating subject, then sorting the acquired projections into multiple subject phase bins, each yielding a complete sinogram for reconstruction of an image sequence.

Respiratory-gated and non-gated 4D-CT are suitable for use during irregular, spontaneous breathing with low subject motion frequency compared to scanner rotation frequency [10],[29]. FSCT extends 4D-CT imaging across a much wider range of application in terms of subject motion frequencies, yet imposes a restricting assumption of regular, periodic motion. Nevertheless, the limitations imposed by the feasible sampling criterion (16) do not restrict practical 4D-CT reconstruction at low frequencies such as spontaneous breathing. This is indicated in Fig. 2 by the available selection of N_bin up to 20 for low f_sub relative to f_rot. However at high frequencies of subject motion, the choice of N_bin may be infeasible depending on (16).

Traditional retrospective gating for cardiac CT can be performed by continuously acquiring both EKG and X-ray projections as the subject slowly translates through the scanner [30]. The projection data is then selectively filtered prior to reconstruction, retaining projections corresponding to the diastolic phase and discarding the rest. Despite the potential for high radiation exposure during the scan, a large portion of the projection data may actually not be used for the image reconstruction. Alternatively with prospective triggering, EKG detection of diastole initiates the scanner to emit and detect X-ray beams through a subset of projection angles, typically covering 180° plus half the angle of the detector array [31]. The subject is then translated to scan a different transverse plane upon the next diastolic triggering event. This type of acquisition is informally known as “step-and-shoot” in regard to the repeated process of “stepping” to the next transverse plane followed by “shooting” the X-ray beam for acquisition. Compared to retrospective gating, prospective triggering reduces the amount of ionizing radiation required for cardiac imaging. For either of these EKG-based methods, the temporal resolution of the image is determined by the duration of acquisition within each cardiac cycle [32]. In other words, temporal resolution depends on how much cardiac motion is averaged in the reconstruction: faster scanner rotation reduces the duration of acquisition within each cardiac cycle, and thus results in less motion artifact.

Multi-segment reconstruction is another effective strategy for improving the temporal resolution of a thoracic image. This approach involves reducing the duration of image acquisition each cardiac cycle by acquiring a subset of projection data (i.e., 180° plus half of the detector fan angle) over multiple cardiac cycles [33]. Multi-segment reconstruction results in a more consistent state of the mediastinum during each acquisition compared to standard EKG-triggering approaches. However the extended scanning protocol increases susceptibility to image corruption from other extraneous motions such as respiration [34]–[36]. Several other techniques have been developed for mitigating motion artifact and radiation exposure in cardiac imaging, such as compensation algorithms that modify the projection data to approximate a motionless image of the thorax based on estimated motion models [37]–[41].

Alternative strategies for volumetric imaging during dynamic motion using X-ray CT, such as quasi-static [42] or temporally-averaged [4],[43] approaches, tolerate some amount of either temporal or spatial blurring when using sequential projection acquisition. FSCT fully resolves the spatio-temporal dynamics of subject motion, yet only throughout the cycle of one specified reconstruction frequency. Thus, FSCT images represent a periodic, dynamic steady state of the subject. Imaging high-frequency motions (i.e., greater than the scanner rotation frequency) is an important potential application of the FSCT technique, opening a relatively unexplored area of research in CT imaging. Reconstruction algorithms incorporating direct sinogram alterations introduce some uncertainty in the resulting image due to the use of numerically estimated motion models used to approximated the actual subject motion [37]–[41]. Motion estimation approaches maintain reasonably low exposure to ionizing radiation. Our FSCT technique is intended to provide high-fidelity images of the subject during actual periodic motion, albeit at the expense of increased radiation exposure. Thus at present FSCT may be more suitable for research purposes, rather than clinical diagnostic use.

The selection requirements for FSCT imaging parameters were characterized for a given subject motion frequency f_sub and desired number of images N_bin, yielding a feasible sampling condition (16) as well as an optimal sampling condition (18). The use of a circular X-ray source trajectory allows improved temporal resolution compared to similar phase-correlated reconstruction of projections acquired during a spiral or helical trajectory [24],[25]. FSCT imaging is feasible for periodic subject motions at nearly any frequency an appropriate frequency ratio (f_sub/f_rot) is used to ensure full sampling without repetition (Fig. 2). Thus FSCT can be used to obtain temporally-resolved image sequences of both high- and low-frequency anatomic motion. Fig. 7 demonstrates several successful reconstructions using FSCT across a wide range of frequencies (0.4 Hz to 20 Hz) relative to the scanner rotation frequency (4 Hz). Ideally, scanner parameters such as f_rot could be tuned to minimize feasible scanning duration given a specific subject motion frequency f_sub. In practical applications, most commercially available CT scanners offer a small number of choices for f_rot and N_pro preset by the manufacturer. However unlike conventional CT imaging, the temporal resolution for FSCT is determined not only by the rotation speed of the scanner, but also by a combination of imaging and reconstruction parameters.

Other potential uses of FSCT span a variety of physiologic applications involving periodic motion, including analysis of airway, lung tissue, or blood vessel deformation, tumor localization and tracking, cardiac wall motion abnormalities, as well as joint motion. Future work may also involve four-dimensional image registration to quantify regional strains of thoracic structure during periodic motion [42],[44]. Four-dimensional registration approaches identify smooth transformations between volumetric images through a temporal dimension (or in this case specifically, subject motion phase) [45],[46]. A periodic constraint may be applied to FSCT-registration, ensuring continuity and smoothness of the computed transformation throughout the entire reconstructed sequence, including the wrap-around from the final image to the initial image.

A. Limitations

Some limitations of our technique should be noted. First, the extensive scanning duration required for FSCT reconstruction exposes the subject to prohibitive radiation dosage, i.e., up to two orders-of-magnitude greater than standard X-ray CT imaging. Accordingly, clinical implementation of FSCT imaging in patients may not be warranted without substantial reductions in radiation exposure. Exact control of scanner rotation frequency f_rot according to (18) may allow minimization of redundant projection acquisition and thus minimization of scanning duration. Iterative reconstruction of each phase-binned sinogram may allow dose reductions at the expense of increased computational cost [47]. It may be possible to reduce radiation dose further by minimizing the number of acquired projection angles per subject phase bin using half-scan approaches for cone-beam reconstruction [48],[49]. Reductions in scanning duration may be achievable using specialized dual-source CT scanners equipped with two independent X-ray sources and corresponding detector arrays positioned at different projection angles through the subject [50],[51]. Finally, prospective triggering approaches generally reduce radiation exposure compared to retrospective gating approaches [52],[53]. Prospective FSCT imaging may also be possible by synchronizing X-ray beam actuation to specified phases of a particular periodic subject motion cycle, with frequency known a priori. In this way, prospective triggering could reduce the total radiation dose by selectively avoiding radiation exposure during non-reconstructed phases.

Although the FSCT technique was evaluated quantitatively in computational simulations, evaluation of the experimentall obtained images presented in Fig. 7 was qualitative. Quantitative assessment of anatomic structures in FSCT images, such as segmented volumes of intrathoracic structures, may require “step-and-shoot” implementation.

Finally, the FSCT technique proposed herein uses only one value of f_sub per image sequence. It is possible to reconstruct multiple image sequences from the same raw projection data, simply by using a different value of f_sub for each sequence. Fig. 7 shows several cases in which two image sequences were reconstructed: one at the ventilatory frequency and another at the cardiac frequency. However the resulting images will contain resolved motion at only the one specific reconstruction frequency, as well as any harmonics or integer multiples of the reconstruction frequency. All other extraneous motion in the subject will cause motion artifact and blurring. For this reason, blurring around the heart is apparent in images reconstructed at the ventilatory frequency, whereas blurring in the lungs is apparent in images reconstructed at the cardiac frequency. It may be possible to combine information from both reconstructed images to reduce apparent motion artifact [54]. Additionally, FSCT may not be appropriate for temporally resolving physiologic processes that are either irregular, aperiodic, or otherwise occur on multiple time scales, such as diffusive equilibration during angiography or tracer gas washout.

V. CONCLUSION

Frequency-selective CT imaging produces a temporally-resolved volumetric image sequence of periodic subject motion at a specified reconstruction frequency. This novel technique enables imaging of both low- and high-frequency dynamic periodic motion at a specified frequency, with minimal extraneous motion artifact. The FSCT approach may offer improved imaging fidelity of dynamic subject motion compared to more conventional ‘quasi-static’ approaches. When combined with registration techniques [45], FSCT may provide detailed four-dimensional information of distributed tissue deformation previously inaccessible using standard reconstruction approaches.

GLOSSARY OF NOMENCLATURE

FSCT

Frequency-selective computed tomography

f_rot

Frequency of scanner rotation

f_sub

Frequency of subject motion

k

Index

n_bin

Index of subject phase bin

n_pro

Index of projection angle

N_bin

Number of subject phase bins

N_pro

Number of projections acquired per scanner rotation

N_rot scanner

Total scanning duration, measured in number of rotations

p

Index of sequentially acquired projections

R_pro

Number of projections acquired before repetitious sampling

R_rot

Number of scanner rotations completed before repetitious sampling

R_sub

Number of subject motion cycle completed before repetitious sampling

t

Time

t_k

Times corresponding to the same subject phase

t_p

Time of acquisition for p^th projection

π

Number of radians in a semi-circle

ϕ_rec

Reconstructed phase of subject motion

ϕ_rot

Phase of scanner rotation

ϕ_sub

Phase of subject motion