Parameterization of Noncovalent Interactions for Transition State Interrogation Applied to Asymmetric Catalysis

Abstract

The use of computed interaction energies and distances as parameters in multivariate correlations is introduced for postulating noncovalent interactions. This new class of descriptors affords multivariate correlations for two diverse catalytic systems with unique noncovalent interactions at the heart of each process. The presented methodology is validated by directly connecting the noncovalent interactions defined through empirical dataset analyses to the computationally derived transition states.

Graphical Abstract

Selectivity in chemical reactions and specifically in catalytic processes is commonly a complex function of various noncovalent interactions (NCIs) occurring prior to or at the transition state (TS). Although the determination and quantification of such interactions is highly desirable in order to predict, improve, and understand reaction performance, this is a difficult goal using purely empirical observations as NCIs are often low energy (0–2 kcal/mol) and dynamic.¹ In this vein, computational analysis of TSs can provide insight into significant influences in the selectivity-determining step(s).² However, as is always a consequence of TS interrogation, a detailed understanding of the roles of all reaction components is obligatory.

Considering this, we have reported a complimentary physical organic strategy, which uses multidimensional linear regression to compare specific structural descriptors to the observed output, for reactions with ambiguous mechanistic possibilities.³ This tactic has allowed us to evaluate a number of complex reactions, providing predictions for output improvement as well as mechanistic insight on the basis of the parameters required to develop a mathematical model.^3a,4 The parameters used include spectroscopic,⁵ geometric,⁶ atomic charge,⁷ and detailed size descriptors.⁸ However, a key limitation thus far has been the absence of suitable parameters to describe attractive NCIs.^2b,9 Indeed, only polarizability¹⁰ or quadrupole moments¹¹ are reported as descriptor surrogates for this purpose. Therefore, a more precise parameter set is required to define these essential underlying phenomena, which occur in a wide swath of processes. Herein we introduce computed π-stacking/CH-π interaction energies and distances as parameters in multivariate correlation analysis (Figure 1). As described below, this strategy can also link the statistical models to computationally-derived TS analysis to reveal the ensemble of NCIs responsible for effective catalysis.

Figure 1.

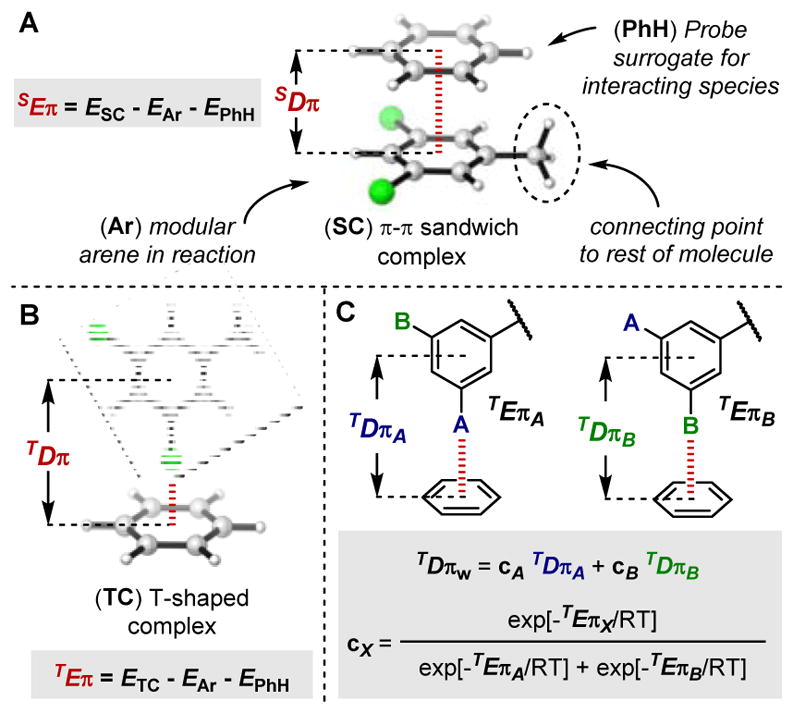
Computed energies Eπ and distances Dπ as parameters. (A) General idea and π-π sandwich complex. (B) T-shaped complex. (D) Determination of weighted parameters.

The interactions of π-systems, which is a core set of NCIs invoked in catalytic processes, have been subject to extensive experimental and computational studies.^2b,9,12 In particular, Houk and Wheeler’s teams have reported computed interaction energies of numerous sandwich and parallel-displaced arene dimers (Figure 1A), which linearly correlate with the Hammett σ_m parameter.¹³

These reports inspired us to compute representative interaction energies (E_π) to be used as descriptors for putative π-interactions. Indeed, for any reaction with substrates and/or catalysts containing an aryl moiety Ar (Figure 1A), one can hypothesize that stacked or T-shaped interactions transpire during the reaction sequence (Figure 1A–1B). In addition to the interaction energy Eπ, the corresponding distance Dπ can be measured, which is defined as the distance between the centers of the two interacting moieties (Figure 1A–1B). This parameter is dependent on both distinct geometric and electronic features, since it is influenced by the attractive energy as well as substituent size. Moreover, when a NCI can occur in greater than one conformer, the associated properties can be weighted according to their energies, as depicted in Figure 2D, represented as E/Dπ_w. For each of the case studies presented below, the relevant complexes were calculated at the B97-D/def2TZVP level of theory, since this functional paired with a triple-zeta basis set has been reported to be a practical, economical compromise to compute NCIs.¹⁴ As simple probes are used to compute the parameters, a library of descriptors can be acquired with minimal computational load.

Figure 2.

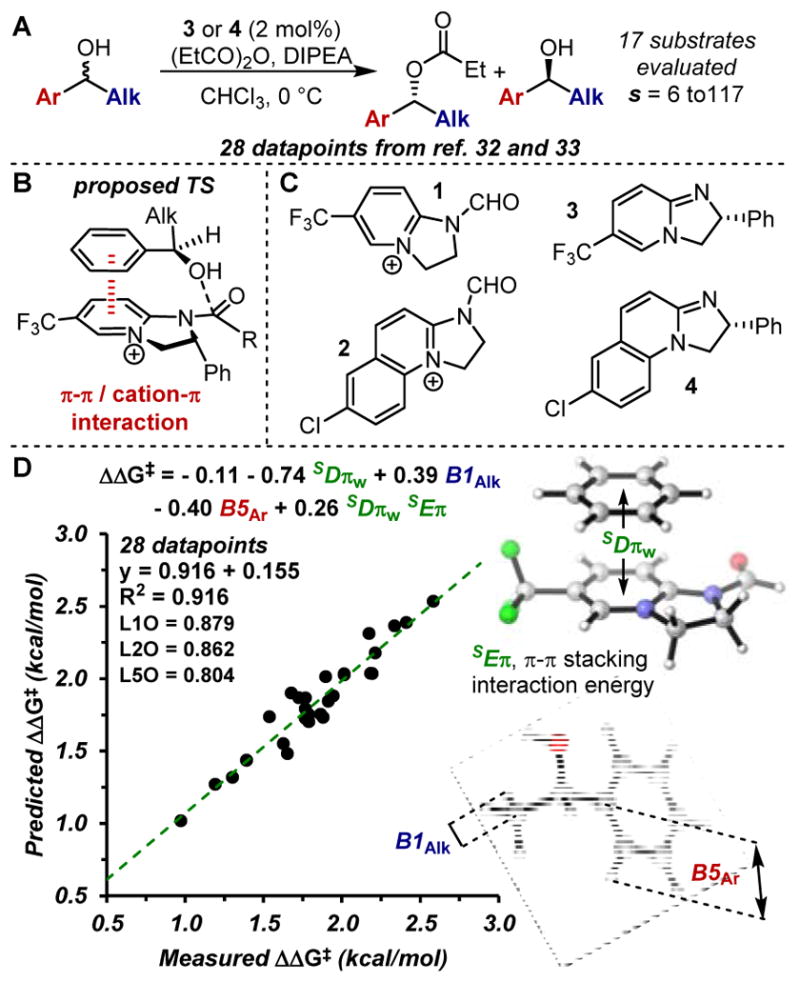
Proof-of-concept reaction system. (A) Birman’s kinetic resolution of chiral benzyl alcohols. (B) Proposed/computed transition state. (C) Simplified structures (1 and 2) used as mimic for catalysts 3 and 4. (D) Model for the Birman’s kinetic resolution.

In order to test our hypothesis, the kinetic resolution of chiral benzyl alcohols reported by Birman and coworkers was examined,¹⁵ in which stacked π-π interactions were demonstrated to be controlling elements in the computed TSs.¹⁶ Specifically, TS calculations suggest that a π-stacking interaction between aryl groups on the alcohol and catalyst is responsible for the differential reactivity of the two alcohol enantiomers (Figure 2B).¹⁶ In addition, sufficient data spanning a significant range of measured selectivity factors (s from 6 to 117, ΔΔG^‡ from 0.97 to 2.58 kcal/mol) was reported, which is required for developing statistically-sound models (see SI for details about the dataset).^15,16

Parameter collection was initiated by computing 28 unique π-π sandwich complexes between the aryl/alkenyl groups and model systems 1 and 2, which represent the cationic acylated catalysts 3 and 4 used in the reaction (Figure 2C). To simulate a π-stacking interaction, the two arenes were aligned in a parallel orientation at a defined distance, centering the interacting arene with the pyridinium ring in 1 or 2. Subsequently, the distance between the rings was optimized, resulting in the minimum energy for the stacked conformation (^SEπ) at distance ^SDπ (see Figure 2D and S1A). When additional conformers are possible, the formula in Figure 1C was applied, affording ^SEπ_w and ^SDπ_w as weighted parameters to account for the possibility of dynamic interactions.

Initial evaluation of these parameters revealed a single-parameter correlation between ^SDπ_w and the selectivity factors s, represented as ΔΔG^‡ values (R² = 0.70, see Figure S4), which supports the presence of a stacked π-π interaction in the TS. Additionally, no other single parameter evaluated revealed any statistically meaningful trends. After applying multidimensional analysis to interrogate additional effects on the reaction’s selectivity, the model reported in Figure 2D was identified (R² = 0.92), effectively describing 28 data points with three additional terms: steric Sterimol parameters B1_Alk (alkyl substituent’s minimum width),¹³ B5_Ar (aryl substituent maximum width) and the cross term ^SDπ_w^SEπ_w. Cross validation methods are consistent with a statistically sound model (see leave K out, LKO, values in plots). Examining each term’s coefficient in the model suggests that the reaction’s enantioselectivity is most influenced by the π-stacking interaction (represented by the terms ^SDπ_w and ^SDπ_w^SEπ_w) followed by steric effects. The obtained model is in excellent agreement with computations previously reported by Houk and Birman regarding the origin of the stereoselectivity in this reaction.

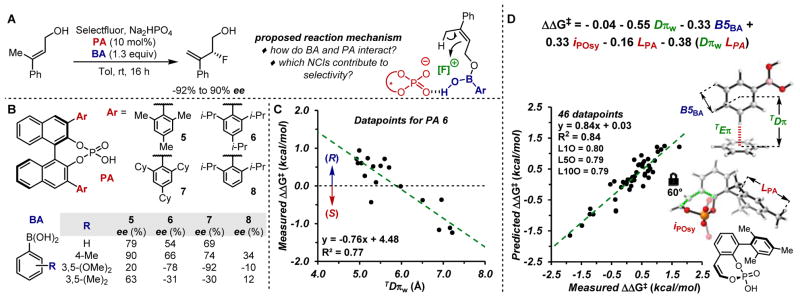
After evaluating our new π-parameters for mechanistic rationalization of a well-studied reaction, we sought to test whether they can also be applied to a system for which the specific interactions occurring in the TS have not yet been determined. Hence, the second case study for the application of these π-parameters is the enantiodivergent fluorination of allylic alcohols previously reported by our teams (Figure 3A), in which an achiral arylboronic acid (BA) in combination with a chiral phosphoric acid catalyst (PA) facilitate the enantioselective reaction.¹⁷ In this process, the allylic alcohol and the BA condense to form a mixed boronic ester,^17b which is proposed to coordinate via H-bonding with the chiral phosphate anion (Figure 3A). From this complex, the enantioselective, electrophilic fluorination occurs. Notably, the ee ranges from −92 to +90% when various combinations of PAs and BAs are applied, reflecting a ΔΔG^‡ range of 3.5 kcal/mol. Thus, this reaction is highly sensitive to NCIs involved in enantioselectivity controlling events. Despite extensive mechanistic studies that provide support for the general reaction mechanism, ^17b a clear representation of the likely NCIs responsible for enantioselectivity has not been elucidated. In this context, previous attempts to correlate all measured enantioselectivities through multilinear regression analysis were unsuccessful.

Figure 3.

Enantiodivergent fluorination of allylic alcohols. (A) Reaction scheme and general proposed mechanism. (B) Substituent effects of BAs and PAs on enantioselectivity. (C) Single-parameter correlation between the stereoselectivity obtained with PA 6 and ^TDπ_w for eighteen BAs. (D) Multivariate full-model correlating stereoselectivities from catalysts 5–8 and eighteen different BAs.

Two key observations provided a framework to initiate interrogation of this system: 1) meta-substituted BAs lead to inverted enantioselectivity compared to other substitution patterns on the BA, and 2) the ee sensitivity towards the BA substitutions is amplified when PAs 5–7, which contain substituents at the 2,6-positions, are employed (Figure 3B). On this basis, it was hypothesized that a T-shaped π-interaction may be occurring between the BA and the PA in the TS. ^17b Therefore, to define parameters, T-shaped complexes were calculated in a similar manner as previously described, using a perpendicular orientation of the probe, benzene, and the BA’s meta-positions (Figure 1B). ^TEπ and ^TDπ for the T-shaped dimers were calculated for a set of eighteen BAs, including weighting these parameters for differentially substituted arenes (^TEπ_w and ^TDπ_w). Preliminary analysis of the enantioselectivity data resulting from each BA in combination with PA 6 revealed a good correlation with a single parameter, ^TDπ_w (R² = 0.77, Figure 3C, see SI for details), which supports that T-shaped interactions are relevant in the TS.

As a next step, we sought to develop a comprehensive model by integrating different combinations of BAs and PAs (46 data points, see SI). Additional parameters to describe the PA catalysts, such as IR stretching frequencies and Sterimol values, were acquired using a simple model system (Figure 3D). The parameters include: ^TDπ_w, accounting for geometric requirements derived from the apparent presence of a π-interaction; B5_BA and L_PA, Sterimol values describing steric effects from BA and the catalyst, respectively; and, i_Posy, phosphate symmetric stretching intensity, which may represent the ability of each PA to engage in H- bond/electrostatic interactions. Since previous attempts to mathematically model this entire dataset were unsuccessful, these new NCI parameters provided the missing information for describing key influences in this complex reaction. More importantly, these results suggest that these parameters may provide a powerful platform for uncovering subtle NCIs, even when limited mechanistic/structural knowledge is available.

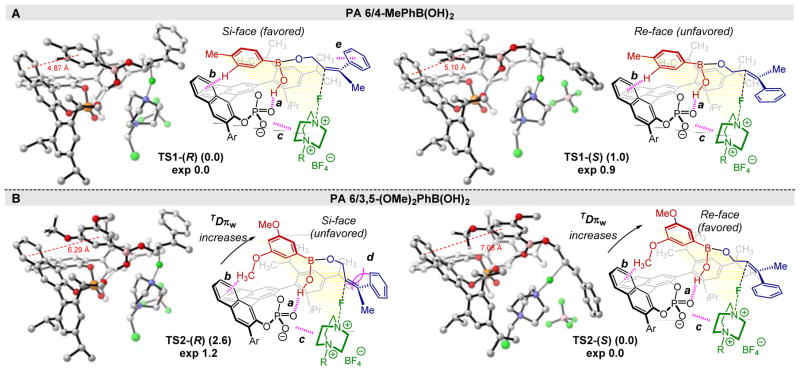
In order to further leverage this statistical physical organic strategy, a computational TS analysis for this reaction was performed at the ωB97X-D/def2-TZVPP/SMD(toluene)//ωB97X-D/6–31G(d) level of theory. PA 6 in combination with 4-methylphenyl- or 3,5-dimethoxyphenylboronic acids were selected as case studies as these groups gave divergent enantioselectivities (Figure 3B). First, a comprehensive conformational search at the TS level was performed for the PA 6/4-Me-Ph-B(OH)₂ system. Remarkably, this DFT study revealed that TSs presenting a T-shaped NCI between the aryl ring of the BA and the binaphthyl moiety of the PA catalyst are the lowest in energy.¹⁸ The favored TSs leading to the (R) and (S) products are depicted in Figure 4A with TS1-(R) leading to the major observed product (computed ΔΔG^‡ = 1.0 kcal/mol; experimental ΔΔG^‡ = 0.9 kcal/mol). Location of low-lying TSs was also performed for the PA 6/3,5-(OMe)₂-Ph-B(OH)₂ system. The analysis showed that TS2-(R) and TS2-(S) (Figure 4B) are the lowest in energy, and the formation of the (S) enantiomer as the major product is consistent with the observed results (computed ΔΔG^‡ = 2.6 kcal/mol; experimental ΔΔG^‡ = 1.2 kcal/mol). Supporting the hypothesis resulting from the parameters found in the statistical analysis, T-shaped π-interactions between the meta-substituent of the BA and the binaphthyl moiety of the catalyst are present in both systems (Figure 4A and 4B), and the computed distances between the aryl ring of the BA and the binaphthyl moiety of the catalyst are in good agreement with the calculated ^TDπ_w parameters. Additional TSs computations for the PA 6/3-OMe-Ph-B(OH)₂ system, as an example of an asymmetrically substituted BA, are consistent with these results and are reported in the SI.

Figure 4.

Structures and relative free energies (kcal/mol) of the low-lying TSs. Energies were computed at the ωB97X-D/def2-TZVPP/SMD(toluene) level of theory on the ωB97X-D/6–31G(d) geometries. Non-relevant hydrogen atoms are omitted for clarity. (A) TSs for PA 6/4-MePhB(OH)₂. (B) TSs for PA 6/3,5-(OMe)₂PhB(OH)₂.

Although the data reported provide clear support for the proposed T-shaped interaction as an important influence in the enantio-discrimination process, it is not trivial to explicitly understand its origin from the calculated TSs. Indeed, the conformations assumed by the catalyst-reagent adducts in the TSs are similar even when the BA is altered (compare TS1-(R) with TS2-(R) and TS1-(S) with TS2-(S)). Nonetheless, an advantage of merging TS calculations with the dataset analyses is the ability to harness the experimental and computational information simultaneously. For example, the interactions that stabilize the BA-PA complex are conserved in each TS, including H-bond a, electrostatics b, and π-stacking c (Figure 4A and 4B), which can be connected to the parameters i_POsy (a and b), and ^TDπ_w and B5_BA (c).

Further information can also be interpreted from the model and related back to the TSs allowing for the proposal of a stereo-chemical model (Figure 4). As an example, the term L_PA, or the length of the PA’s aryl group, appears twice in the model, which supports the significance of the para-substituent size in the enantiodetermining step. Since this parameter is also present as a cross term with ^TDπ_w, it suggests that these two terms are interrelated in the TS. Accordingly, if the BA is farther from the binaphthyl group with a longer ^TDπ_w, as is the case with 3,5-disubstituted BAs, the alkene is driven towards the PA’s aryl rings (Figure 4B). As a result, the alkene will rotate to minimize steric effects, d, between its bulkier substitution (Ph) and the para-substituent on the PA, leading to favored fluorination at the alkene’s Re-face (Figure 4B). This observation is consistent with the optimized reaction conditions previously reported, in which the best PA catalyst AdDIP (i.e., 2,6-(iPr)₂-4-Ad-Ph) contains an adamantyl (Ad) group in the para-position. ^17a Conversely, when a 3,5-unsubstituted BA is used, ^TDπ_w is shorter, situating the alkene away from the PA’s para-substituent. In this case, the alkene may rotate to position either the Me or Ph groups towards the PA with limited repulsion. This is consistent with 3,5-unsubstituted BAs generally affording lower enantioselectivity. To rationalize the inversion of stereoselection in certain examples (e.g., 4-methylphenylboronic acid), it is possible that the alkene’s Ph group engages in a CH-π interaction, e, with the para-alkyl moieties, thus stabilizing this conformation and allowing fluorination at the alkene’s Si-face (Figure 4A). Overall, combining detailed insight from the two methods provides rationalization for a diverse set of results in a complex reaction, further validating the new parameters as descriptors of NCIs occurring in the TS.

In conclusion, the need for new tools to identify and quantify NCIs in catalysis prompted us to develop new parameters for describing π-interactions: Eπ and Dπ. These easily calculated parameters have been tested in two different catalytic systems using multivariate correlations. The obtained information agreed with previously reported studies in the Birman’s kinetic resolution of benzyl alcohols by supporting the occurrence of a π-stacking interaction. These parameters also provided detailed insight into the fluorination of allylic alcohols, a complex reaction promoted by chiral anion phase transfer catalysis. Indeed, for this catalytic system, the obtained model facilitated the identification of interactions occurring in the computed TSs. Thus, this new class of parameters provides a valuable extension to developing structure-function relationships by describing weak yet significant interactions occurring in the reaction.

As shown, Eπ and Dπ used in multidimensional analysis offers a broad perspective of a reaction that can be distilled into a mathematical equation, directly relating parameters to a TS structure. Hence, this methodology offers the opportunity to validate TS analyses through a set of experimental data.

We see it as a complementary strategy to rigorous TS computations, both of which inform the nature of potential NCIs. We are currently integrating these approaches in various methods development and energy related campaigns.