Mechanisms of Cell Polarization

Abstract

Cell polarization is a key step in the migration, development, and organization of eukaryotic cells, both at the single cell and multicellular level. Research on the mechanisms that give rise to polarization of a given cell, and organization of polarity within a tissue has led to new understanding across cellular and developmental biology. In this review, we describe some of the history of theoretical and experimental aspects of the field, as well as some interesting questions and challenges for the future.

Introduction

Specifying an axis of directionality is essential for most living cells. In the repertoire of cells that move individually, including Dictyostelium amoebae, neutrophils, keratocytes, and fibroblasts, determining the cell front and back is a prerequisite for organizing the machinery that powers cell motility (Fig. 1A). This includes the actin cytoskeleton, myosin, and, in some cases, microtubules. In organized cell collectives such as epithelia, the apical and basal faces of individual cells are distinct from one another and from the lateral surfaces along which cell-cell contact is maintained (Fig. 1B). Even in plant cells, whose shapes are constrained by rigid cell walls, the axis of polarity forms with growth, and is essential for defining cell division planes, and hence, organizing the shape of the plant tissue that emerges (Fig. 1C).

Figure 1. A–C Examples of cell polarity.

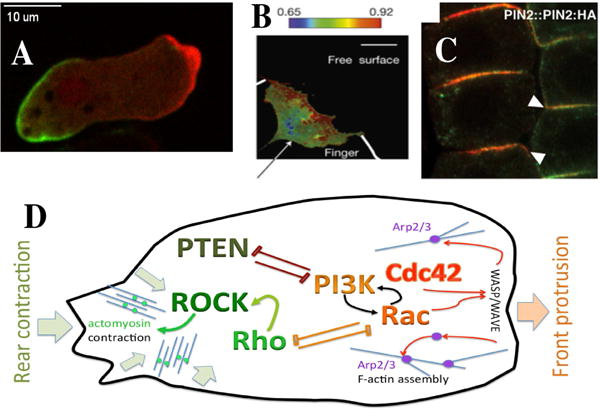
A. A polarized Dictyostelium cell moving to the right and showing an accumulation of myosin at its back and actin enrichment at its front.

B. The distribution of RhoA activity in a leader cell of an invading finger of epithelial Madin-Darby canine kidney cells displays an asymmetric distribution, with the activity being highest at the front edge [154].

C. Polar localizations of the fluorescent marker PIN2:HA at the lower side of root epidermal cells of the plant Arabidopsis thaliana. From [155]. D: A schematic sketch of proteins associated with front (in shades of red) and rear (green) of a polarized cell. The GTPases Rac and Cdc42 promote actin filament assembly (through Wave activating the branching complex Arp2/3). This leads to protrusion of the lamellipod. At the rear, the GTPase Rho activates ROCK which phosphorylates myosin light chain, leading to actomyosin contraction and retraction of the rear. Rac and Rho are often seen to be mutually antagonistic. Other proteins such as PI3K (which catalyzes the reaction PIP2–>PIP3) and PTEN (which catalyzes the reverse reaction) are also associated with the front vs rear of a polarized cell. PI3K participates in a positive feedback loop with Rac.

How cells spontaneously polarize, and how they maintain that polarity (when needed) or adapt it to a changing environment (as required) are fundamental questions in cell biology. For the past few decades, the investigation of such questions has taken place at the intersection of experimental biology, computational biology, physics, and mathematics. Cells can polarize in response to chemical, electrical, mechanical, or other physical stimuli. For example, the link between the direction of an influx of calcium ions and the polarization and direction of growth in the brown algal (fucoid) eggs was made as early as the 1970’s; e.g., [1]. A brief historical account and description of the rapid growth of cell polarization research over the past 40 years is given in [2]. More recently, the study of signaling networks that orchestrate cell polarity has emerged as a subfield of systems biology, with ever-increasing amount of data on the many molecular participants that govern that process. Here we briefly survey the evolution and current state of the field, and suggest some future promising directions.

Several overarching questions have historically focused the research on cell polarity. Among these are (1) What causes the symmetry breaking that polarizes a cell? (2) How can cell polarization be so robust for some cells, such as neutrophils, and very adaptable for others (Dictyostelium). (3) How does cell polarization fit into the broader picture of gradient sensing [3], cell motility [4–11], and chemotaxis [12–16], and more recently, planar cell polarity in tissues [17–19] and collective migration [20,21] (4) When does polarity go wrong, what cellular defects and consequent diseases arise, and how might we target such defects to find cures for the associated diseases [22–24]?

Biological observations that motivated cell polarity research

Early observations of single cells using conventional microscopy defined polarization according to cell shapes with elongated cells being more polarized than round cells. For moving cells, the migration direction is typically in the direction of the polarity axis, defined as the long-axis of the cell. Although these observations were instructive, they did not provide any data about the intracellular distributions of signaling components. This information has become available, however, due to advances in microscopy, and in particular fluorescence microscopy. Immunostaining, for example, allows the visualization of proteins in fixed cells, thus enabling the quantification of asymmetries in intracellular and membrane localizations. Even more informative, however, are methods that fuse signaling components to fluorescent probes, enabling the dynamic visualization of their spatio-temporal distribution.

These experiments have revealed that many signaling components are roughly uniformly distributed within the cytosol in unpolarized cells but have a pronounced asymmetric distribution in polarized cells. In moving cells, for example, the front is associated with high concentrations of actin while the back displays elevated myosin concentrations [25]. Other non-cytoskeleton components that show distinct localization during polarization include the phosphatidylinositol lipid PIP3 (front), along with its phosphatase and kinase (PTEN, back, and PI3K, front) [26,27]. In addition, many small GTPases display asymmetric distributions within a polarized cell. In budding yeast, Cdc42 localizes to the budding site, while in neutrophils and other migrating mammalian cells, Cdc42 is found at the front and Rho is found primarily at the back of the cell [28,29]. These distributions can be measured with high temporal and spatial precision, even under changing conditions. The emergence of such quantitative data has resulted in a surge of interest in the development of models for cell polarity establishment and maintenance, as described below.

What stimuli lead to symmetry breaking and cell polarization?

A universal mechanism for cellular polarization is chemoattraction: chemical stimuli such as Cyclic AMP (CAMP) for Dictyostelium, fMLP for neutrophils, or other chemical attractants that lead to cellular chemotaxis reorient cells and lead to their polarization. Many of the original works in the field, addressed the issue of how a weak chemical gradient of as little as 2% across a cell diameter can give rise to a macroscopic internal “map”, reviewed in [30,31]. But chemical factors are not the only type of cue that elicits polarization. Membrane tension [32] can lead to spontaneous cell polarization on a faster timescale than diffusible signals, especially in elongated cells; see [33]. In fish epidermal keratocytes, Xenopus mesendoderm cells, and Dictyostelium cells, polarization can be induced by mechanical stimuli such as the flow of fluid from a micropipette towards one edge of the cell [34,35] or forces applied locally to cadherins [36]. Electric fields are also known to induce cell polarization and migration in fish keratocytes [37] and Dictyostelium cells [38] and are responsible for cell migration during wound healing with a PI3K-dependent transduction mechanism [39]. Substrate rigidity can also result in polarization of cells, with cells moving toward stiff regions [40]. Furthermore, in plants, where cell walls are rigid, cell polarity depends on cell division planes. The plant hormone auxin is closely linked to cell division, growth, and development, and its distribution is governed by the pattern of localization of transporters (PINs) on the lateral sides of a cell. The precise signaling networks that control PIN localization are still not fully known [41]. See [42] for a computational model and [43] for an example review of work in this area. Finally, we note that some experiments suggest that Dictyostelium cells have a pre-existing polarity and continuously form pseudopods [44]. External cues can then guide these pseudopods, resulting in directed motion.

Modeling of single cell polarity — historical development as an offshoot of pattern formation theories

One of the first modeling treatments of cell polarity appeared in an early paper about biological pattern formation [45], some 20 years after the seminal pattern formation theory of Turing [46]. Relying primarily on simulations, Gierer and Meinhardt kindled the interest and curiosity of developmental biologists with their idea of lateral inhibition (local activation to amplify a small signal and long-range inhibition to prevent the activation from spreading throughout the domain unchecked) as a mechanism for pattern formation. Nearly 25 years later, in a follow-up paper [47] a model for cell polarization was revisited and sparked a revitalized interest in formulating theoretical basis to explain how polarity forms.

Meinhardt’s 1999 paper in J Cell Sci [47] was followed closely by seminal work [12,48] that investigated how cells can robustly achieve polarity even though the chemoattractant concentrations and gradient strengths can vary significantly. The basic idea in this work is that adaptation to uniform stimuli could be set up in a system where a stimulus simultaneously triggers activating and inhibitory signals. If the activator is local while the inhibitor acts globally the mechanism results in polarized cells for a wide range of gradient parameters. This local excitation and global inhibition mechanism (LEGI for short) became highly influential both theoretically and experimentally [49–52], accompanied by related models [53]. As in many pattern forming systems, cell polarity networks have both highly localized and quickly-spreading components. For instance, active forms of the protein have relatively slow spatial spread, e.g. by confinement to the membrane or to immobile cellular structures. Inhibitors, or inactive forms of the protein are assumed to be highly mobile or even global and uniform, spreading very rapidly in the cytosol. Typically, rates of diffusion of membrane versus cytoplasmic forms of the same protein (or proteins of comparable molecular weights) differ by 2–3 orders of magnitude.

The idea that cell polarization is a type of pattern formation (with a particularly simple “unimodal” pattern) led to a proliferation of models, many based on Turing-type reaction-diffusion systems of partial differential equations [3,4,54–56]. Popular among these were activator-inhibitor models known for their pattern-forming ability. The inhibitors proposed in some of the early reaction-diffusion or LEGI models have not been identified, despite much experimental effort, and are unlikely to be single agents. We should note, however, that membrane tension has also been suggested to play the role of long-range inhibitor [57].

Some, but not all models, were based on known molecular players such as the antagonists PI3K and PTEN [58,59] or small GTPases such as Cdc42, Rac, and Rho [5,56,60] in either mammalian cells or in yeast [61]. Protein modules that can act as mutually antagonistic “front-back” organizers are now known. These include Rac and Rho whose mutual antagonism can set up polarity or other cell behavior [23,62,63]. It is now accepted that activators of the cell edge cytoskeleton include Rac, or Ras, PI3K, and downstream effectors such as WASP/WAVE Arp2/3 that organize actin branching nucleation. The roles of these are clearly identified as promoting actin assembly and edge protrusion in motile cells. A schematic view of the distribution of signaling molecules in a polarized cells is shown in Fig. 1D. We should point out, however, that in some cells, the pathways directing polarity are slightly different. For example, in Dictyostelium cells, where multiple parallel pathways control directed migration [64], PI3K appears to be not essential for chemotaxis [65,66].

Recent progress in cell polarization research

(A) Progress in Experimental Methods

An important new experimental direction in the field of cell polarization is to quantify cell polarity, including spatio-temporal dynamics of signaling components, in response to carefully controlled external cues or in well-defined geometries. These cues are typically generated using microfluidics which allows the researcher to expose cells to precisely defined external cues [67–71]. These devices are particularly well-suited to generating precise and reproducible gradients of different strengths and profiles and can be used to investigate the chemotactic response of cells [16,72]. Furthermore, they can be used to rapidly change external conditions so as to study how polarity is established, reversed or maintained [67,73].

Other novel studies quantify the response of cells and cell polarity in specific geometric confinements. For example, substrates can be patterned such that cells only adhere to certain well-defined parts. Using this technique, it was found that the behavior of cells crawling on 1D stripes is much more consistent with 3D behavior than cells moving on flat, 2D substrates [74]. These patterned substrates can be used to investigate polarity questions: forcing the cells to crawl on a 1D stripe results in a strongly and consistently polarized cell. Reversal of cell polarity can then be studied by determining how cells behave when they collide “head-on”[75]. These, and other studies, have shown that contact inhibition of locomotion (CIL) plays an important role in cell-cell contacts [76,77]. The same CIL is also believed to play a significant role in the motion of monolayers and might be responsible for the response of cell clusters to chemical gradients [78,79].

Cell polarization can also be induced by geometries that force cells to move within channels with cross sections that are comparable to cell sizes [80,81]. These channel geometries were shown to induce cell polarization and resulted in persistent motion in different cell types, including Dictyostelium cells, cancer cells and human neutrophils [80–82]. In fact, geometry-induced polarity can be so persistent that neutrophils moving in U-shaped microfluidic channels can move against a gradient for extended periods of time (Fig. 2A) [83].

Fig. 2. Examples of recent experimental techniques used in studies on cell polarization.

A. Human neutrophils migrating persistently in a U-shaped microchannel containing [83]. The channel contains a gradient in chemoattractant pointing to the tip of the U and the cell is labeled with PH-Akt-GFP, a polarization marker. Throughout the cell’s trajectory, its cell polarization is persistent, even when the cell moves towards decreasing a chemoattractant concentration.

B. Light induced induction of lamellipodia in live NIH3T3 cells. A red light source was targeted to a small area and moved outwards. The laser light induces the activation of Rac, resulting in a cellular extension of approximately 30 μm.

C. The response of a Dictyostelium cell, expressing the actin marker LimEΔ-GFP (green) with phase contrast in red, to a rapid flow reversal as indicated by the white arrows [70]. The outer cell contour is shown as a white line. The quantitative data obtained from these cell reversal experiments can be used to validate models.

Another exciting new technique involves the use of light to control cellular behavior. First used to regulate neuronal spike timing [84], these optogenetic techniques can now be used to activate certain signaling components [85,86]. Importantly, the activation is achieved with high spatial and temporal resolution and is reversible. Optogenetics can be used to target a single protein, making it possible to determine how a signaling cascade is activated [87]. It can also be used to determine how cell polarity is controlled, both in single cells and in groups of cells [88–91] and promises to be an exciting new experimental tool (Fig. 2B).

(B) Progress in theoretical models and methods

The biological research in polarization has also led to a number of new mathematical findings and methods to explore typical kinds of models that arise: (well-mixed) differential equations or reaction-diffusion systems. Motivated by small GTPase biology, [92] showed that membrane-bound active GTPase with positive feedback (or mutually inhibitory Rac-Rho active forms), cytosolic inactive forms, with the total GTPase conserved in a cell can result in a rapid wave of polarization in response to a super-threshold stimulus. The wave freezes under specific conditions [93], resulting in robust polarization. An approximate bifurcation method (Local Perturbation Analysis, LPA) invented by Marée and Grieneisen [42,94], has proven to be a useful shortcut in analysis of RD systems that comprise both slow and fast rates of diffusion [95], scaling up to larger systems more conveniently than the traditional Turing stability analysis. A way to visualize a multi-parameter space was proposed by [96] and applied in the Rac-Rho cell bistability experiments described in [23].

In addition to the new analyses described above, several new computational techniques are currently pursued. In particular, methods that can describe cells as deformable objects are under development. These models are particularly well-suited if non-homogeneous intracellular regions are of importance or when there exists a feedback between shape, motility, and polarization. An important contribution to this type of research is the work of Mackenzie and coauthors who solved equations proposed by Meinhardt [47] on a moving, deforming 2D cell boundary [97]. Another technique that has been adapted to handle intra-cellular reaction-diffusion models is the cellular Potts model, [98]. In this model, cells are represented by a finite number of sites on a lattice (in 2D or 3D). Each site is assigned a “spin value” which specifies to which cell the site belongs and cell motion is implemented via a Monte Carlo update of spins which attempts to copy the spin from one lattice site to a neighboring site. This model was originally developed to describe cell sorting but has been extended to include polarity terms [99–101] as well as the effect of signaling on actin assembly and cell shape [4,5]. A recent, computationally light phenomenological example inspired by actin dynamics is [102].

Another technique uses elements from pattern formation and introduces an auxiliary field, termed “phase field”, that purely functions as a computational tool. This phase field takes on one value in the interior and another in the exterior of the cell and smoothly varies between these two values in a region that represents the cell’s boundary. A judicial coupling between the phase field and the underlying reaction-diffusion equations can then result in a model that recovers the original model in the limit of vanishing membrane thickness, the so-called sharp interface limit. A major advantage of this technique is that it does not require the explicit tracking of the membrane. For this reason, it has been used extensively in other so-called “free boundary problems”, especially in the field of pattern formation [103–106]. Studies have shown how to incorporate intra-cellular reaction diffusion as well as intra-cellular fluid flow into phase field cell models and have modeled single migratory, deformable cells [8,9,107,108]. More recent work has extended the phase field approach to motion of multiple cells [109–112]. One potential drawback of this methodology is the relatively high computational cost, since each cell requires solving its own set of equations. However, the use of GPU based computational platforms, combined with specialized algorithms, can significantly reduce these costs [109,110].

(C) Progress in linking experiments and theory

The combination of quantitative experiments and modeling can lead to new insights into the mechanisms of cell polarity. For example, experiments that mimic the periodic cAMP waves seen for DictyosteIium cells in aggregates can be generated in microfluidic devices. This allows one to determine the chemotactic response of cells and their polarity as a function of the wave period. It was found that cells have a cellular memory, i.e., they were able to maintain their polarity and ignore the so-called back of the wave, as long as the period was not more than 10 minutes [15]. These results can then be used as input to models for adaptation and memory, resulting in predictions of the topology of signaling networks. A similar approach was also carried out by Bretschneider et al who exposed Dictyostelium cells to alternating gradients of mechanical shear flow [70]. The experiments carefully quantified the spatio-temporal distributions of a fluorescent reporter for actin (Fig. 2C). The experimental findings were then tested against three different reaction-diffusion models for cell polarity. The study found that two of these models, the aforementioned models of Meinhardt and the LEGI model, were able to fit the experimental data in a satisfactory way. Thus, by quantifying the spatio-temporal responses of fluorescent reporters, these studies are able to function as model selectors.

The role of systems biology in driving cell polarization research

An interesting philosophical question is to what extent the methods of systems biology and high throughput biological observations can lead to a better understanding of cell polarity mechanisms and dynamics. Here, our review must of necessity be woefully brief, as this aspect of the research is only now beginning to take shape. To this point, most of the mechanistic modeling in the area has been built around a detailed understanding of very small networks (e.g. Rho GTPase crosstalk [113]) or simplified toy models [92,93,114] that can be fully analyzed mathematically. Such efforts can be expanded to additional layers (e.g. feedback from and to phosphoinositides [5,59]) downstream to the cytoskeleton, protrusion and contraction that generate cell shape changes and motion [5,115]. While we are beginning to study larger networks (described further on), challenges remain in developing techniques to analyze their behavior. A recent example with potential to explore the interactions of genes, mechanical forces, and multicellular interactions is the open source platform MecaGen [116].

Multicellular vs unicellular cell polarity

It is well-known that cell polarity in single migrating cells is dynamic, allowing cells to amplify external gradients and orient in complex environments; see, for example, the model by [117]. While serving a distinct function, dynamic changes in cell polarity are sometimes essential for normal development of a multicellular tissue. One example is the formation of lumens, hollow tubes of tissue consisting of one or more cell layers, as in kidney ducts and other structures. As shown in vitro by [18], such structures are initiated via cell division with the 2-cell stage having a reverse polarity; a marker such as Podocalyxin starts at the extracellular-matrix (ECM) cell surface. As the structure grows and develops, this marker is down-regulated from the “outside” and reassembled at the “interior” (lumen) cell surfaces. This reorientation involves integrins (beta1-integrin/FAK) and the antagonism of RhoA and Rac1. Defects in ECM-signaling, inhibiting beta1-integrin or disrupting the GTPase balance leads to a multicellular front-rear polarity and (aberrant) collective migration of the entire cell cluster, often associated with invasive or metastatic growth.

Collective migration plays a significant role in many normal biological processes and examples include wound healing in epithelial cell layers, specific cell groups during development. A number of papers have proposed the idea of self-generated gradient chemotaxis, wherein a cluster of cells consumes chemokine or ligand so as to form and follow that chemical gradient [118–121]. Collective migration is also a well-known aspect of tumor cell clusters during cancer metastasis. Cells within collectively migrating clusters can have different polarity states. Most notably, cells that are located at the edge of the cluster, termed leader cells, can have a larger size and more active lamellipodium than cells in the interior of the layer [122]. Leader cells are also essential for collective migration of MDCK cells [123] and Rac, PI3K, and Integrin beta 1 are upregulated in a more dramatic polar distribution in leader cells than in follower cells. In [124], the authors showed the connection between the distribution of microtubules and localization of adherens junctions in the posterior lateral line primordium of zebrafish in vivo, and explained the transition between the leader cells in front, and the more epithelial cells that form rosettes in the back.

Within collectively migrating clusters, cell-cell interaction can have a profound effect on cell polarization. Perhaps the best-studied example of this is the previously mentioned CIL, during which a cell repolarizes away from its contact points with other cells. For a review of CIL, including its molecular basis, see [125]. Other possibilities for cell-cell interactions include alignment mechanisms in which the cell’s velocity or polarity is determined by the state of its neighbors [20]. Recent studies have shown that these mechanisms can have profound impacts on the resulting migration of clusters [21,126,127].

A parallel but related realm of research in developmental biology has centered on planar cell polarity (PCP) in tissues [128]. In Drosophila wing development, protein complexes such as Frizzled-Disheveled-Flamingo (FZ-Dsh-Fmi) and Van Gogh- Prickled-Flamingo (Vang-Pk-Fmi) segregate asymmetrically to opposite sides of cells and “hold hands” across cell-cell interfaces to hard-wire polarity across neighboring cells, as reviewed in [129]. The same spontaneous emergence of asymmetry and polarity occurs in Par proteins, first identified in Caenorhabditis elegans: PAR-3 and PAR-6 concentrate at the anterior, whereas PAR-1 and PAR-2 at the posterior end as early as the single-cell stage of the embryo.

Several models have been proposed for the emergence of global organization. The polarization of PAR proteins in the C elegans embryo has been modeled in [130,131]. Similarly, PCP has been an area of active theoretical work for years. Many of the models invoke either cell-cell coupling or cell-cell comparisons, together with innate mechanisms that spawn polarization of a given cell or of the interface between neighboring cells, reviewed in [43,132]. Global signals that provide cues on the scale of many cells are proposed, but the molecular components at work in, for example, the Drosophila wing, are not yet identified. In one of the earliest models of Drosophila wing PCP [133,134], a reaction-diffusion mathematical model for the FZ-Dsh and the Vang-Pk complexes was proposed. In [43], individual cells can polarize spontaneously in absence of external bias, but cell-cell coupling organizes the spatial distribution of the polarity vectors. Another treatment using Hierarchically Colored Petri Nets was described in [135].

The molecular links between PCP and single cell polarization are now more clearly recognized. The involvement of the cytoskeleton, and segregation of actomyosin to specific lateral sides of the cells is needed for such events as cell elongation along an orthogonal axis, driving convergent extension in Drosophila, or asymmetric contractility, in C. elegans. Hence there has been recent interest in the crosstalk between Rho GTPases and PCP proteins, as reviewed in [136]. In one example, it was shown that a complex that includes Cdc42, Rac1, PAR-6 and PAR-3 is required for polarity in neurons [137]. This suggests that the lessons learned in the single and multicellular contexts will be useful in cross-fertilization and deeper understanding of polarization as a multiscale phenomenon.

Future challenges and directions in cell polarity research

It is tempting to speculate on the direction in which the field is moving. One of the challenges, related to the quest of systems-biology is to identify the full signaling pathway in specific cases. Some inroads have been made in this direction. The mutual inhibition between Rac and Rho embedded in the larger EGF-EGF receptor signaling pathway for example has been modeled using a Boolean approach [138]. See also [139] for a similar approach. A second important area is deciphering the role of mechanical forces such as membrane tension, and incorporating these into models for cell polarization. Both these areas are still in their infancy, and methods to understand these are still needed.

Another problem of interest is to what degree mechanisms need to be fine-tuned to create robust, but adaptable cell polarity. Many of the current models only work in relatively small parts of their parameter space. For example, the Meinhardt model we discussed earlier sensitively depends on some of its parameters. Likewise, building amplification into the LEGI model requires a careful fine-tuning of the parameters [15,52] as does the wave-pinning polarization mechanisms of Mori et al. [92] when captured by a single GTPase. (Robustness increases with the number of participating GTPases and feedbacks [140].) Somewhat related is the question of cell variability: how does the degree of polarization vary from cell to cell? Addressing these questions probably requires an integrated approach in which experiments and models go hand in hand.

It is also interesting to consider cell polarization in distinct geometries, for example in in 3D matrices (e.g. on collagen fibers). A recent work describes the formation of special cell appendages, regulated by a balance of Rac Arp2/3 pathway (promotes the formation of “fin-like” structures) and Rho pathways that promote formin-based actin assembly and myosin-based blebbing behavior [141]. Several modeling studies have explored the connections between the shape of a cell and the dynamics of its intracellular signaling for polarity [5,97,142–144], but these have largely focused on 2D cell projections. The computational issues associated with simulating dynamic intracellular signaling inside a deforming 3D cell are still daunting, but developments of new methods is ongoing by several groups (see, e.g. [145]), and progress has been made since the review in [143].

Now that we have data in many types of cells and conditions, it is instructive to compare between species or conditions: what is universal and what is specific? Proteins such as partitioning defective (PAR), and complexes such as Scribble, and Crumbs are responsible for polarity in epithelial cells, and appear to be universal in multicellular organisms from worms to humans. Interactions of these with the small GTPases are reviewed in [136]. Crumbs localizes to the apical domain, Scribble to the lateral and basal cell surfaces in epithelia, but in single migrating cells, all these are found at the cell front [29]. Rho GTPases and their crosstalk and cytoskeletal effectors also appear to be universal, although a variety of types of Rac but no Cdc42 occur in DictyosteIium.

We are also learning to manipulate the polarity machinery and hoping to understand how RNAi or other knockouts affect behavior. Examples of the outcomes of cells treated with RNAi include [146,147]. Some theoretical analysis of the cell shapes was provided in [62]. We have a better understanding of how cell polarity mechanisms evolved in living cells. Evolution of the family of Rho GTPases is described in [148]. Rac is the “founder”. The expression of Rho mRNA in mouse cells of various types indicates that the specialization of Rhos have led them to become expressed more specifically in particular cells and at specific times.

We expect that coupling experiments to modeling efforts will give us more insights into the topology of signaling networks. The first examples of this approach have resulted in promising results [15,149,150] and new experimental techniques, including optogenetics and microfluidics, will undoubtedly be critical. We also expect that studies in which experimental results are systematically compared to model output, as was carried out by Bretscheider et al [70], will be crucial in determining the mechanisms likely involved in cell polarity. Again, new experimental techniques will allow us to generate quantitative data required for these future studies.

We are beginning to link cell polarity and migration defects to cancer and other diseases. For example, the integrity of epithelia is coordinated by cell-cell contacts such as tight junctions and adherens junctions that form, like rivets, between adjacent cells. These are composed of large complexes of molecules that act as scaffolds for signaling, including spatial and temporal control of the activation (by GEFs) and inactivation (by GAPs) of Rho GTPases. Defects in these complexes, whether due to transcription, viral interference, or other causes can lead to disregulation, EMT, and cancer. See reviews in [22,24,151,152]. Downregulation of RhoB has been linked to changes in focal adhesion, reduced beta1 integrin, and weakening of the epithelia that drive prostate cancer, for example [153]. Further work in this direction is likely to provide better insight into factors promoting metastasis, with potential payoff in better treatment and drug targets. In short, while much progress has taken place, a great deal remains to be done.