Fusing functional signals by sparse canonical correlation analysis improves network reproducibility

Abstract

We contribute a novel multivariate strategy for computing the structure of functional networks in the brain from arterial spin labeling (ASL) MRI. Our method fuses and correlates multiple functional signals by employing an interpretable dimensionality reduction method, sparse canonical correlation analysis (SCCA). There are two key aspects of this contribution. First, we show how SCCA may be used to compute a multivariate correlation between different regions of interest (ROI). In contrast to averaging the signal over the ROI, this approach exploits the full information within the ROI. Second, we show how SCCA may simultaneously exploit both the ASL-BOLD and ASL-based cerebral blood flow (CBF) time series to produce network measurements. Our approach to fusing multiple time signals in network studies improves reproducibility over standard approaches while retaining the interpretability afforded by the classic ROI region-averaging methods. We show experimentally in test-retest data that our sparse CCA method extracts biologically plausible and stable functional network structures from ASL. We compare the ROI approach to the CCA approach while using CBF measurements alone. We then compare these results to the joint BOLD-CBF networks in a reproducibility study and in a study of functional network structure in traumatic brain injury (TBI). Our results show that the SCCA approach provides significantly more reproducible results compared to region-averaging, and in TBI the SCCA approach reveals connectivity differences not seen with the region averaging approach.

1 Introduction

Functional MRI (fMRI) is capable of measuring subject-specific and long-range correlations in brain activity (i.e. networks) as measured by changes in a direct or indirect time-series measurement of cerebral blood flow (CBF). EPI-BOLD is the standard protocol for studying network structure, however a second approach, arterial spin labeling (ASL) MRI, more directly measures CBF by tagging arterial blood and tracking changes in magnetization over time. ASL provides a quantitative measure of blood flow, which is believed to be more directly related to neuronal activity than the measure provided by EPI-BOLD [1]. One advantage of ASL is greater signal stability and reproducibility when compared to EPI-BOLD especially over the range of resting state frequencies [2]. Additionally, the ASL acquisition contains images that exhibit BOLD contrast (ASL-BOLD) [1]. Although the temporal resolution of ASL is lower than EPI-BOLD, resting state fluctuations are thought to reside well within the range of frequencies that may be captured by ASL (0.01 Hz to 0.1 Hz).

While EPI-BOLD has been used extensively to examine functional brain connectivity in large-scale brain networks, only a small number of studies have examined functional connectivity in ASL [3,4]. Two studies have compared ASL-connectivity and BOLD connectivity measured with either EPI-BOLD [5], or ASL-BOLD [6]. To our knowledge no previous work has combined the CBF and BOLD components of the ASL signal to obtain a functional connectivity measure that exploits the full information provided by this modality. The scarcity of related work may be due, in part, to the fact that most ASL sequences collect relatively fewer time frames (impacting the stability of correlations) in a given amount of scan time as well as the lack of off-the-shelf methodology for computing ASL networks. There is no work that we are aware of employing ASL-connectivity in TBI.

In this work, we contribute a new multivariate method for ASL-based network analysis. We improve upon existing approaches in two ways. First, we extend standard region-based methods with a sparse dimensionality reduction method that optimally correlates two ROIs. This is achieved by formulating the correlation between ROIs as a sparse selection optimization algorithm that finds non-uniformly weighted sub-ROIs that are most related. Second, we show how this method may jointly find these sub-ROIs by using both ASL-BOLD and CBF time series signal. Both of these advances relax some of the assumptions of standard region-based approaches while retaining the interpretability afforded by these classic approaches. In short, our contributions are: (1) We detail a new multivariate network analysis method; (2) We show how it may be used to fuse simultaneous time series measurements from multiple signal sources to estimate correlation matrices; (3) We evaluate these approaches in terms of reproducibility and applicability to studying TBI; (4) The method is freely available in a public open source toolkit [7].

2 Methods

ROI analysis for network construction

Denote the matrices that describe the ASL-BOLD or ASL-CBF time series within a whole-brain ROI as X and Y respectively. Additionally, for a given set of anatomical ROIs for which there are L regions, we denote the ASL-BOLD sub-matrix extracted from ROIⁱ as Xⁱ. Then Yⁱ will contain that same ROI's ASL-CBF measurements. The classic region-based analysis will compute $x^i=1/n{\sum }_k{x}_k^i$ which denotes averaging the $x_k^i$ columns of Xⁱ and similarly for yⁱ. From these region-averaged time-signals, a correlation matrix, ℛ, of size L × L is calculated, where ℛ(i, j) = Corr(xⁱ, x^j) with Corr denoting the Pearson's correlation.

Fusing functional signals via SCCA

Canonical correlation analysis (CCA) is a method for elucidating the relationship between two sets of measurements taken across a population [8] and is thus well-suited to multivariate neuroimaging data. Here, we show how CCA generalizes the basic ROI-based approach to network analysis described above. CCA introduces new unknown vectors, uⁱ and u^j, that act as weighted averages of Xⁱ, X^j. CCA will optimize:

$$\underset{u^i,u^j}{argmax}\mathit{\text{Corr}}(u^i{X}^i,u^j{X}^j).$$ (1)

This formulation allows for the inclusion of the full time signal in all voxels in an ROI and is “nice” in that it can be solved by singular value decomposition if the number of samples is larger than the minimum number of columns in Xⁱ or X^j. Sparse CCA extends CCA with additional constraints that allow the problem to be solved even when the input matrices are “fat” i.e. the number of columns far exceeds the number of rows, as is typically the case in functional MRI data. The SCCA formulation optimizes:

$$\begin{array}{c}\underset{u^i,u^j}{argmax}{u}^i{(X^i)}^T{X}^j{u}^j\\ \text{Subject to}\\ \sum _i{\Vert u^i\Vert }_1\le s,u^i\ge 0,\sum _i{\Vert u^j\Vert }_1\le t,u^j\ge 0,\Vert u^i{X}^i\Vert =\Vert u^j{X}^j\Vert =1,\end{array}$$

where s, t determine sparseness. Due to the non-linear (even np-hard) nature of subset selection from a large matrix, optimizing for a single canonical variate, u_i, involves a nonlinear gradient descent on the objective function above. This is one disadvantage of these methods. However, one gains robustness and the ability to exploit the full information of the input data. An additional advantage is that the formulation shown above may easily incorporate both ASL-CBF and ASL-BOLD data for simultaneous analysis. In all experiments presented here, the sparsity parameters were fixed and equal (s = t). Additionally a positivity constraint was imposed upon uⁱ and u^j.

Recall that we represent a given ROI's BOLD and ASL signal as Xⁱ and Yⁱ where each matrix is n × p (rows by columns) with n the number of acquired time points and p the number of voxels in ROIⁱ. Since both ASL-CBF and ASL-BOLD derive from the same acquisition, Xⁱ and Yⁱ will always have the same dimensions. To examine both time series measurements simultaneously, we can column-append the two matrices: Zⁱ = [[Xⁱ] [Yⁱ]]resulting in a n × 2p matrix. For clarity, X will be used in further equations with the knowledge that it could be replaced with Y or Z with no resulting changes to the algorithm.

Now note that in the standard approach to ROI-based network analysis, the correlation matrix is given by ℛ_Roi(i, j) = Corr(a(Xⁱ),a(X^j)) where a(·) indicates averaging over the ROI. The SCCA solution is trivial to use in the same manner, producing ℛ_SCCA(i, j) = SCCA(Xⁱ, X^J) = Corr(uⁱXⁱ, u^jX^j). Note that the key difference is that SCCA will optimize the canonical variates to specifically identify the sub-regions within ROIⁱ and ROI^j that are most mutually informative.

To obtain a connectivity matrix for an individual, the original ASL data and corresponding anatomical labels are required. For each labeled voxel, the ASL-CBF and ASL-BOLD times series are extracted. Motion-correction parameters are regressed out of the signals and a band pass filter is applied so that only frequencies between 0.01 Hz and 0.1 Hz are retained. This filtered time series data is then used to construct a matrix for each labeled region in the subject. For the region-averaged approach, the time-series are averaged to produce a single vector for each ROI while the SCCA method utilizes the full matrix to estimate connectivity.

3 Results

Our experimental design will establish the impact of SCCA-based network analysis on: (1) test-retest reliability of network correlation matrices; (2) how reliability changes with different signal (BOLD, CBF, concatenated BOLD-CBF) extracted from the input ASL time series; (3) the impact of the SCCA strategy on a population analysis of traumatic brain injury.

3.1 Evaluating reproducibility via test-retest data

Neuroimaging data

The cohort consists of 12 healthy young adult participants (mean age 25.5 ± 4.5, 7 female). For each subject, data was acquired at three time points. Two of these time points were acquired on the same day, in separate scanning sessions, while the third was acquired one week away from the same-day data. For each time point high resolution T1-weighted anatomic images were obtained using a 3D MPRAGE imaging sequence and the following acquisition parameters: TR = 1620 ms, TI = 950 ms, TE = 3 ms, flip angle = 15 degrees, 160 contiguous slices of 1.0 mm thickness, FOV = 192 × 256 mm², matrix = 192 × 256, 1NEX with a scan time of 6 min. The resulting voxel size was 1 mm³. Additionally, pulsed ASL (PASL) images were aquired with 80 alternating tag/control images and 2 M0 images all with 14 contiguous slices of 7.5mm thickness, FOV = 220 × 220mm², matrix = 64 × 64. Additional acquisition parameters: TI1 = 700ms, TI2 = 1700ms.

Image processing

The set of T1 images from each subjects first time point was used to construct a template using ANTs [9]. This template was brain masked and labeled with the AAL dataset [10]. A three-tissue segmentation was performed to allow the labels to be partially masked so only cortex and deep gray structures were labeled. For each time point, the T1 image was registered to the template image. Additionally, registration was used to find an intra-subject mapping between the T1 image and the M0 image that is acquired as a reference for the PASL acquisition. These transforms were composed to map the cortical labels into ASL native space for each time point. For PASL images, the M0 image served as a reference for motion-correction of all time-point volumes. Sinc interpolation was used to estimate the full time-series for both the control and tag data. The difference between control and tag was used along with relevant acquisition parameters to calculate the ASL-CBF over time, while the average of the two signals was calculated for ASL-BOLD [1].

Reproducibility testing

To examine reproducibility, functional connectivity matrices are calculated for each time point using the classic region-averaged approach and the SCCA method on: ASL-CBF, ASL-BOLD, and combined ASL-CBF and ASL-BOLD. Graph correlation [11] is used for the comparison of connectivity matrices in order to examine reproducibility between images acquired on the same day, and images acquired one week apart. The results are illustrated in figure 3. A paired, one-sided Student's t-test was used to determine when the SCCA based method produced significantly more reproducible results than the corresponding region-averaged metric. Here we list the percent improvement provided by the SCCA method along with the p-value from the t-test.

Fig.3.

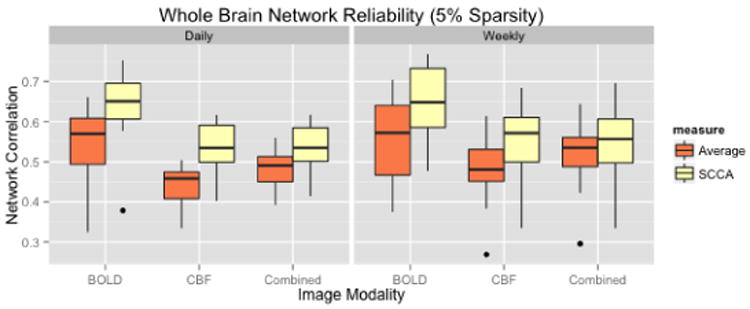
For each metric, using both region averaging (orange) and SCCA (yellow), connectivity matrices were calculated from ASL data acquired in separate acquisitions in the same day and for data acquired one week apart. Whole network correlations were then calculated to examine reliability for the daily (left) and weekly (right) data for each subject. Here we illustrate results using sparsity values of s = t = 0.05. A range of sparsity values (s = t) up to 0.25 were examined and these higher values did not produce qualitatively different results.

Daily

ASL-BOLD = 17.72% (p=5.0e-7), ASL-CBF = 23.45% (p=4.5e-7), Combined = 23.45% (p=0.0014)

Weekly

ASL-BOLD = 18.79% (p=8.1e-6), ASL-CBF = 17.97% (p=1.0e-7), Combined = 7.23% (p=1.75e-5)

The largest improvements in daily reproducibiliy occur in the CBF based functional connectivity, suggeting that in this particular case, little useful information is gained by including the ASL-BOLD signal.

3.2 Cross-sectional examination of brain connectivity in TBI

Neuroimaging data

Our cohort consists of 41 participants (mean age 30.4 ± 10.2), including 22 patients with TBI (9 females), and 18 controls (9 females). No significant difference exist between age or education in the patient or control groups. The same image T1 acquisition as described above was used for these subjects.

Image processing

Processing for this data is identical to that for the test-retest data described above. The pulsed ASL (PASL) images were acquired with 160 alternating tag/control images and 2 M0 images all with 14 contiguous slice of 7.5mm thickness, FOV = 220 × 220mm², matrix = 64 × 64. Additional acquisition parameters: TI1 = 700ms, TI2 = 1900ms.

Network differences

To identify potential effects of TBI, connectivity matrices were calculated for all subjects using all metrics. In particular, the default mode network (DMN) is of interest as this network has been shown to be affected by TBI [12] and is relevant here as the data was acquired during the resting state. Here we used the following labeled regions for the DMN: posterior cingulate gyrus, hippocampus, frontal medial orbital cortex, and the angular gyrus. This network is illustrated in figure 2. Each subject's time from injury was categorized as either: no injury, less than one year since injury, or more than one year since injury. For each metric of interest, connectivity values for intra-hemispheric connections in each hemisphere were extracted and R was used to examine the influence of diagnosis (TBI or control) on connectivity values using (in R language syntax):

Fig. 2.

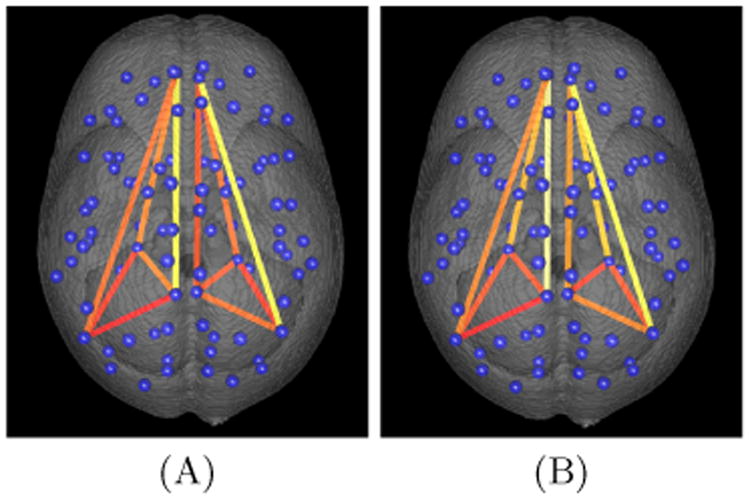
Intrahemisheric connectivity in the default mode network of an individual subject is visualized using A) ROI averaged combined CBF and BOLD and B) SCCA based combined CBF and BOLD. The centroid of all labeled regions are illustrated with blue spheres, and the connections in the DMN are illustrated with line segments. The connectivity matrix values are used along with heat-mapping to color the line segments where higher connectivity values result in “hotter” colors.

$$\mathit{\text{Conn}}~1+\mathit{\text{Diagnosis}}+\mathit{\text{Age}}+\mathit{\text{Gender}}+\mathit{\text{YearsEducation}}+\mathit{\text{InjuryTime}}$$ (2)

All p-values for diagnosis were FDR corrected and connections with q<0.1 were reported as potentially compromised connections. The region-averaging approach did not result in any reported connectivity differences between control and TBI, nor were any results reported for ASL-BOLD alone. Connectivity measured using SCCA on the ASL-CBF and the combined data both reported connectivity differences in the right hemisphere between the posterior cingulate gyrus and both the hippocampus (q = 0.084) and angular gyrus (q = 0.091).

4 Discussion

We detailed how SCCA may be used to fuse the ASL-CBF and ASL-BOLD signals to exploit both the multi-variate signal provided by ASL as well as the full information provided within each anatomical region. We demonstrated that the SCCA method provides a more repeatable measure of network connectivity than the classic region-averaged approach. However, the reproducibilty gains in combined ASL-CBF and ASL-BOLD were less than either metric examined alone. This may be a result of equally weighting the signals. As these signals have different physiological origins, an adaptive weighting method may be more appropriate and will be examined in future work. An examination of TBI suggested that the SCCA method provides a measure of connectivity that is more sensitive to disruptions in the DMN. Future work will include exploring how additional modalities, such as standard BOLD fMRI, may be incorporated into the framework described here.

There are several caveats that must be kept in mind when interpreting these findings. One important issue in connectivity studies is the possible artifacts induced by motion. While we did not find significant differences in motion parameters between groups, this confound may not be entirely ruled out, although we note that its effect should be similar across all comparisons. Regarding our BOLD findings, we note that ASL sequences are not optimized for BOLD sensitivity; in general, our findings may differ for different types of ASL or other functional MRI sequences. Finally, we did not study every frequency range and these may impact reliability in all of the studied signals. In future work, we will more carefully characterize the signal that is extracted by the SCCA approach in comparison to the ROI analysis. However, we believe that the novel findings reported in this work encourage further exploration of using SCCA to drive network analyses of the brain.

Fig. 1.

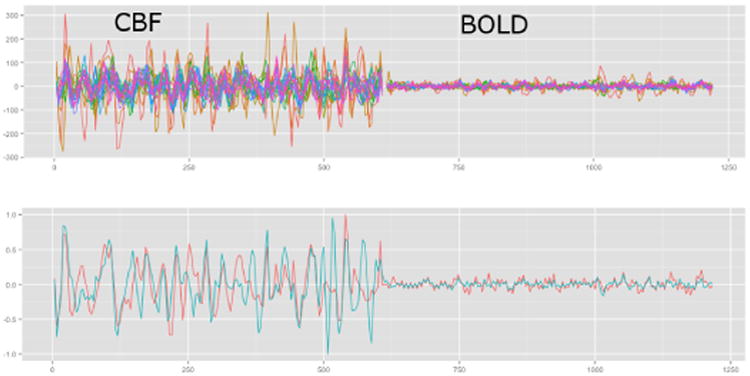
ASL signals in the cingulate gyrus of a normal individual showing ASL-CBF and ASL-BOLD in all voxels in the ROI (top). The average ASL-CBF and ASL-BOLD are illustrated on the bottom in red and the ASL-CBF and ASL-BOLD that result from using SCCA to examine connectivity with the hippocampus is shown in blue. Both signals on the bottom have been intensity normalized for visualization