Abstract
Blinded randomized controlled trials (RCT) require participants to be uncertain if they are receiving a treatment or placebo. Although uncertainty is ideal for isolating the treatment effect from all other potential effects, it is poorly suited for estimating the treatment effect under actual conditions of intended use—when individuals are certain that they are receiving a treatment. We propose an experimental design, Randomization to Randomization Probabilities (R2R), which significantly improves estimates of treatment effects under actual conditions of use by manipulating participant expectations about receiving treatment. In the R2R design, participants are first randomized to a value, π, denoting their probability of receiving treatment (vs placebo). Subjects are then told their value of π and randomized to either treatment or placebo with probabilities π and 1-π, respectively. Analysis of the treatment effect includes statistical controls for π (necessary for causal inference) and typically a π-by-treatment interaction. Random assignment of subjects to π and disclosure of its value to subjects manipulates subject expectations about receiving the treatment without deception. This method offers a better treatment effect estimate under actual conditions of use than does a conventional RCT. Design properties, guidelines for power analyses, and limitations of the approach are discussed. We illustrate the design by implementing an RCT of caffeine effects on mood and vigilance and show that some of the actual effects of caffeine differ by the expectation that one is receiving the active drug.
Keywords: study design, belief effects, efficacy bias, perceived treatment, causal inference
Randomized experiments or randomized controlled trials (RCTs) remain the most effective method for demonstrating causal effects of treatments. In a double-blind placebo controlled RCT, patients do not know whether they are receiving the active substance under study but do know that there is some chance (usually 50% for a two-group design) that they are not receiving the actual substance – thus the treatment effect is estimated when subjects are uncertain of treatment receipt. This is in marked contrast to the effects of typical interest—the effects of treatments when actually used (e.g., the drugs are actually prescribed, the food is actually consumed), and the persons receiving the treatment know unequivocally that they are receiving the treatment. Thus, the assumption that the standard double-blind RCT estimates treatment effects under actual conditions of use is incorrect, an important shortcoming given Food and Drug Administration (FDA) regulations state that new drug approvals require scientific demonstrations of the risks and benefits of the drug “under the conditions stated in the labeling” or under “conditions of use” (U.S. Food and Drug Admisistration, 2014) or in the case of a food additive, “under the conditions of its intended use” (U.S. Food and Drug Admisistration, 2004). Yet, the intended conditions of use typically do not include providing treatments to persons in a manner such that the recipients are not certain whether they are actually receiving the treatment (Colagiuri, 2010).
The present standards of RCTs, in which subjects are uncertain of receiving the treatment, exist because we are interested in isolating the treatment effect from the placebo effect (Junod, 2008). Isolating the treatment effect is important because it helps clinicians and policy-makers determine whether the beneficial effects of the treatment per se justify the expense and potential risks of treatment exposure and are not merely due to the expectancies about the treatment. Expectancies have been “defined as treatment-related outcome expectations” and are thought to be an important mechanism in explaining placebo effects (Crow et al., 1999). For example, a patient who expects a medical therapy to be beneficial to some aspect of their health may modify other aspects of their lifestyle that benefit the same health outcome. In this case, the expectancy had an effect on the outcome unrelated to the intended physiological effect of the therapy.
Subject expectancies do not just potentially affect treatment outcomes directly. Rather, subject expectancies may interact with actual treatment. If this is the case, the estimated treatment effect from a standard, blinded, placebo-controlled RCT may misestimate the effects of treatment under intended conditions of use. As described below, others have addressed this problem using variations of designs sometimes called a ‘balanced-placebo design’ (Kelemen & Kaighobadi, 2007). However, these designs involve lying to subjects, which some may judge to be ethical in some short-term experiments on healthy subjects, but is unlikely to be considered ethical in studies of treatment-seeking persons in longer term trials (Waring, 2008).
Herein, we describe a novel study design to estimate treatment effects under actual conditions of use and expectancy-by-treatment interactions without subject deception in situations where subject blinding is possible. We first discuss past research on expectancy-by-treatment interactions and alternative designs used to estimate such effects, followed by the details of our proposed study design. This will be followed by a presentation of the methods and results of a pilot study using our proposed design to examine expectation-by-caffeine effects on mood and vigilance.
Past Research on Expectancy-by-Treatment Interactions
We now provide a brief overview of past studies relevant to our proposed design. First, we describe two quantitative syntheses related to the role of the probability of receiving placebo on outcomes and discontinuation in trials of antidepressants for the treatment of major depressive disorder (MDD). Second, we describe recent RCTs which investigated the role of expectancy effects on outcomes related to the consumption of various substances (e.g., caffeine, marijuana, alcohol). This will allow us to examine probability-related inferences across and within studies, respectively, as well as demonstrate the gap that we believe our proposed new design will fill.
Meta-Analysis of RCTs
Papakostas and Fava (Papakostas & Fava, 2009) evaluated whether the probability of receiving a placebo influenced clinical outcomes in antidepressant MDD trials by pooling data from 182 randomized, double-blind, placebo-controlled clinical trials (n = 36,385). Using random-effects meta-regression they found a significant association between aspects of the study design and clinical outcomes. Specifically, they found that a greater likelihood of receiving placebo predicted a greater antidepressant effect, after adjusting for factors including publication year, study duration, sample size, and baseline depression severity. Papakostas and Fava concluded that clinical outcomes may be markedly influenced by the expectation of improvement and suggest that both modifying expectations for improvement and increasing the probability of randomizing patients to placebo might improve the ability to detect significant antidepressant treatment effects.
Malani (Malani, 2006) investigated whether the probability of treatment assignment influenced the estimated treatment effects of pharmaceuticals by looking at the results of 200 ulcer trials and 34 statin trials. These studies represented a range of treatment assignment probabilities, although most were at 0.5 or 1. The study found that expectancies affect both positive and negative effects (side effects) of a drug, such that patients who were more likely to be assigned statins tended to have both a greater reduction in low-density lipoprotein and a higher incidence of reported side effects. Malani also found that expectancy effects differed across treatment types within a medication class (perhaps due to patient expectancies generated by participating in a trial with a well-known statin brand), raising the possibility that the total effect of a drug with a small treatment effect and a large placebo effect may be greater than the total effect of a drug with a moderate treatment effect but a very small placebo effect. If patient expectancies and resulting expectancy effects are elevated by a patient’s greater confidence of receiving the treatment, the possibility of variable expectancy effects within the same class of medication has important implications for ranking the clinical value of a drug under “actual conditions” of use.
Just as a greater likelihood of receiving placebo may negatively affect participants’ expectations of improvement resulting in a larger estimated treatment effect, so may it also result in increased attrition. Tedeschini et al. (Tedeschini, Fava, Goodness, & Papakostas, 2010) evaluated the association between the probability of receiving placebo and likelihood of discontinuing treatment using pooled data from 142 clinical trials. Contrary to the hypothesis that lowered patient expectations may increase attrition, they found that receiving placebo did not predict antidepressant or placebo discontinuation rates or the risk ratio of discontinuing antidepressants versus placebo. They concluded that discontinuation rates were not influenced by receiving placebo and therefore had no effect on antidepressant-placebo comparisons.
Individual RCTs
A small but growing number of studies have attempted to estimate expectancy effects for outcomes in response to ingesting various compounds (e.g., nicotine, caffeine, marijuana, alcohol) versus placebo (Dawkins, Shahzad, Ahmed, & Edmonds, 2011; Elliman, Ash, & Green, 2010). Such studies generally use a 2 × 2 within or between subjects design in which participants are randomized into one of four conditions: drug administration (drug vs. placebo) by information provided (told receiving drug vs. told not receiving drug).
Elliman et al. (2010) used a 2 × 2 within subjects design to evaluate the effects of expectancies on mood and performance in response to ingesting caffeine vs. placebo. Twenty-five habitual coffee drinking undergraduate students were caffeine-deprived for at least 8 hours and randomized to four different testing sessions. Two of the sessions provided caffeinated coffee (200mg) and two provided decaffeinated coffee, while simultaneously providing accurate or inaccurate information regarding the caffeine content of the coffee they were to drink. After consuming the coffee and waiting for 20 minutes, participants completed the Bakan vigilance task and a short form of the Profile of Mood States. As expected, consuming caffeine enhanced performance on the vigilance task, but only among those who were accurately told that they were consuming caffeinated coffee. In the conditions in which the participant received decaffeinated coffee, expectancies had no effect on performance. The effects of the manipulations on mood were inconsistent. This same basic pattern of results (i.e., the magnitude of the effect of ingesting the compound on outcomes is contingent upon the expectancy provided to the participant) has been obtained in studies related to other substances, e.g., marijuana (Metrik et al., 2012) and salt (Liem, Miremadi, Zandstra, & Keast, 2012).
The consistent and often strong role that expectancies play in response to ingesting various compounds underscores the need to develop study designs that can better capture and disentangle expectancy effects. Developing and demonstrating a study design, ideally without including an element of deception, that successfully accomplishes this goal would have profound implications for drug trials, which seek to maximally isolate or distinguish the actual effects of the compound from expectancy effects.
The Randomization-to-Randomization (R2R) Design
The key concept of the new design stems from the realizations that we wish to (a) retain the ability to estimate treatment effects free from placebo and expectancy effects and hence wish to retain blinded, placebo-controlled designs; and (b) do so among persons who differ in how certain they are that they are actually receiving treatment. We also wish to test whether expectancy-by-treatment interactions are present and to conduct the trials without deceiving subjects. Motivation for the design comes from the realization that the conventional, blinded, placebo-controlled RCT creates problematic and uncertain expectancies because all subjects receive treatment with some probability—usually 50%. By altering the probabilities of random assignment to treatment versus placebo, we can alter expectations while maintaining a placebo-controlled, randomized design. If treatment assignment probabilities are allowed to vary from subject to subject, and subjects are made aware of those probabilities, the experimenter has presumably manipulated expectations and thus expectancies.
Further, if assignment to treatment probabilities is random with a fully known mechanism, causal inferences can be made about both the effects of assignment probability on outcomes and the treatment probability-by-treatment interaction. We are aware of one unpublished manuscript that introduced elements of this idea before us. The terminology of Ogowa and Onishi (2010) (Ogawa & Onishi, 2010) is very useful in understanding the different effects one can conceive of and, in some cases, estimate. Our methodological approach is similar to theirs, but differs on some important points as will be described below.
In brief, our design consists of the following simple steps:
Randomly assign each participant to an individual randomization probability from the open interval (0,1) from a distribution of choice (e.g., uniform, beta).
Tell each person his or her randomization probability.
Assign each person to either treatment or control on the basis of his or her individual randomization probability, without revealing the treatment assignment (i.e., maintain blinding) and conduct the remainder of the RCT as usual.
Finally, when analyzing the outcome data, include terms for treatment assignment, initial randomization probability, and a randomization probability-by-treatment assignment interaction. The fitted model can then be used to estimate treatment effects for persons whose initial randomization probabilities would be 1.0 as estimates of treatment effects under intended conditions of use.
Because subjects are randomized to a randomization probability, we refer to this design as the ‘Randomization-to-Randomization’ design (R2R, for short). We must make a distinction between ‘expectancies’ and ‘expectations’ in this design as there are subtle differences: expectations are observable quantities to which subjects are randomly assigned, while expectancies are unobservable psychological constructs. We will discuss this in more detail later, but note that the study design and analysis proposed here is principally concerned with elucidating expectation effects.
Statistical justification and notation
As described in papers delineating the conditions justifying causal inferences (Hernan & Robins, 2006; Joffe & Rosenbaum, 1999; Rosenbaum, 2002; Rosenbaum & Rubin, 1983; Rubin, 1977, 1997), we may draw causal conclusions about the effect of X on Y when either of the two following conditions is met:
Units are assigned to values of X wholly at random. This is non-controversial and is simply stating that we can draw causal inferences about the effects of assigned conditions in standard randomized experiments.
Units are assigned to values of X wholly at random conditional on some other variable, and that other variable is included as a covariate in the statistical testing and estimation model for the effect of X on Y.
Assuming a two-armed RCT with a total sample size of n, let πi, i=1,…,n, be a random variable with a range of 0 to 1 and that is randomly assigned to subjects. Let Xi be a Bernoulli distributed variable representing treatment assignment (Xi=0 for placebo control and Xi=1 for active treatment) with E(Xi)=πi for the ith subject. That is, subjects are randomly assigned to Xi=1 (treatment) with probability πi. Note that we here consider just the case of two arms; an extension of X to additional arms using a multinomial distribution would be straightforward. Further note that πi is by definition analogous to propensity scores in observational studies, as both describe the probability of being in a treatment or exposure group (Rosenbaum & Rubin, 1983).
Let Yi be a random variable that occurs and is measured after the assignment of πi and Xi (i.e., Yi is the outcome variable). Yi may or may not be influenced by Xi, by any function of πi, or by the interaction of Xi and any function of πi. Because πi is, by definition, P(Xi=1), π clearly satisfies criterion ‘b’ above as a sufficient variable to condition on to justify causal inferences. Moreover, because P(Xi=1)=E(Xi|πi)=πi, controlling for the linear effect of π is necessary and sufficient to draw causal inferences about the effects of X on Y.
For the analysis of data from an R2R design, including a treatment-by-expectation interaction, a general linear model is the simplest approach (Cohen, Cohen, West, & Aiken, 2003). Model 1 defines an example for a continuous response with ei~N(0,σ2):
| (1) |
In this model, β1 can be interpreted as the treatment effect free from placebo and expectation effects and β1+β3 can be interpreted as the treatment effect for persons nearly certain they are receiving the treatment (π≈1) (Rogosa, 1980). This treatment effect is arguably the treatment effect under “actual conditions of use”, and cannot be estimated in an unbiased way from the traditional RCT design if there is a true treatment-by-expectation interaction. We can calculate this as the difference in the expected values of a subject given treatment (Xi=1) versus placebo (Xi=0) while the subject is certain he or she is being treated (πi=1):
| (2) |
It should be noted that we are effectively making the assumption that the assigned probability π can be used directly to model a subject’s changed expectancies, such that we describe the effects of π (expectations) and expectancies interchangeably; this assumption will be discussed later.
Choices of distribution of π
In general, the randomization probability, π, can be fixed or random numbers from some distribution on the interval from 0 to 1 (in order to be a valid probability). For example, the traditional two armed RCT design with balanced allocation assigns all participants a probability of assignment to the active treatment group of 0.5 (πi=0.5 for all i=1,…,n). Note that although we may be interested in effects of treatment when subjects have full certainty that they are (π=1) or are not (π=0) being treated, assigning a subject a value of π=1 or π=0 would either break the blinding condition of this study design (if π=0,1 is used to generate a Bernoulli variable for Xi) or lead to subject deception (as in the balanced placebo design) and thus should not be done in practice. In the R2R design, participants are randomized to receive different treatment randomization probabilities that can be random draws from some discrete or continuous distribution. For example, if half of participants are given a randomization probability of 0.8 and the other half are given the probability of 0.2, we can still have a balanced random allocation but the participants will have either a high or low randomization probability. More generally, the randomization probability, πi, can be randomly selected from a distribution, such as a Beta(α,β) distribution. The flexibility of using a Beta distribution lies in that we can manipulate πi by setting the values of parameters α and β. For example, we may center πi on 0.5 (α=β>1), separate it around extreme values (α=β<1), or have it uniformly distributed between 0 and 1 (α=β=1). Note that when attempting to estimate treatment effects under “actual conditions of use,” we will explicitly be extrapolating as we are not allowing for subjects to be assigned π=1. Therefore, it may be advisable to choose a sampling distribution for π that is expected to allocate sufficient numbers of subjects to values of π near 1 to allow for reasonable estimation. The most efficient distribution for π depends on the true expectation effects; we recommend the use of simulations when designing a study to account for a variety of potential distributions and expectation effect functions.
Nonlinear expectation effects
The true effects of expectation on the outcome can be linear or nonlinear. In the R2R design, as Ogowa and Onishi (2010) note, one may wish to test for effects of nonlinear functions of π, denoted f(π), on Y. There is no reason such nonlinear functions of π cannot be included. However, because f(πi) does not equal P(Xi=1), and is not linearly related to P(Xi=1) (except in the situation in which only two unique values of π are assigned to all units), controlling for f(π) is not sufficient to ensure consistent or unbiased estimates of the effects of X on Y. In practice, it may be difficult to correctly define f(π) because the true effects of expectation for any given value of π will be unknown; an incorrectly specified f(π) is not necessarily superior to the linear modeling of π to describe the true effects of π. Based on parsimony, a linear modeling of π will be a reasonable first choice in practice but it is not immediately clear how a lack of fit may affect statistical inference. To that end, we performed a simulation study where we could observe the bias, variance, and error rates when using linear models on known linear and nonlinear expectation effects.
Simulation Study Design
We performed Monte Carlo simulations to evaluate the estimates of treatment and expectation effects under various circumstances, including both linear and nonlinear expectation effects and interactions. The analytic models used are given in Table 1, where the first three are fit to data generated as if from an R2R design whereas the fourth model considers data generated according to the models in Table 1 where the value of π is 0.5 for all subjects, as in a traditional RCT. For each combination, we evaluated the type I error rates on testing the null hypothesis of no treatment effects or of no treatment effect when π=1, using a Wald test, as described in Table 1, as well as the bias, variance, and mean squared error (MSE) of that model’s estimate of the treatment effect when the subject has full expectation (π=1) as in a clinical setting.
Table 1.
The three analytic models fit to the data generated with R2R sampling in the simulation studies
| Model Number | Formula | Omnibus Test | Test for (X|π=1) |
|---|---|---|---|
| 1 | E[y] = β0 + β1X | H0: β1 = 0 | H0: β1 = 0 |
| 2 | E[y] = β0 + β1X + β2π | H0: β1 = 0 | H0: β1 = 0 |
| 3 | E[y] = β0 + β1X + β2π + β3Xπ | H0: β1 = β3 = 0 | H0: β1 + β3 = 0 |
| 4 (RCT) | E[y|π=0.5] = β0 + β1X | H0: β1 = 0 | H0: β1 = 0 |
The simulation study considered all combinations of 30 data generating models and four analysis approaches. The 30 generating models are listed in Table 2 where the error term e had a standard normal distribution and the nonlinear expectation effects had functions
| (3) |
| (4) |
| (5) |
as seen in Figure 1, where the atan()’s domain is in radians. The specific formulae of these functions is not significant, just that for the domain [0,1] for π these functions produce different S-shaped curves pertaining to possible nonlinear relationships between π and the outcome variable, although in practice we will not know what the true curve looks like. The difference between the three curves is just in how quickly the function will produce values near its maxima as π increases; that is, the three labels (realistic, optimistic, and pessimistic) refer to how susceptible someone may be to expectation effects due to varying π.
Table 2.
The empirical statistical properties (bias, standard deviation (SD), and mean squared error (MSE)) of estimates of treatment effects when the subject was certain of treatment (X|π=1) and rejection rates of the associated hypothesis tests, for the given data generating models
| # | True Model | True X|π=1 | Fitted Model | Bias (X|π=1) | SD (X|π=1) | MSE (X|π=1) | Reject, Omnibus | Reject, X|π=1 |
|---|---|---|---|---|---|---|---|---|
| 1 | y = e | 0 | X | 0.00084 | 0.1001 | 0.0100 | 0.0502 | 0.0502 |
| X+π | 0.00081 | 0.1233 | 0.0152 | 0.0507 | 0.0507 | |||
| X+π+X*π | 0.00035 | 0.2463 | 0.0607 | 0.0504 | 0.0496 | |||
| X (RCT) | 0.00041 | 0.0998 | 0.0100 | 0.0499 | 0.0499 | |||
|
| ||||||||
| 2 | y = 0.5X + e | 0.5 | X | 0.00049 | 0.1000 | 0.0100 | 0.9987 | 0.9987 |
| X+π | 0.00060 | 0.1228 | 0.0151 | 0.9820 | 0.9820 | |||
| X+π+X*π | 0.00106 | 0.2463 | 0.0607 | 0.9600 | 0.5275 | |||
| X (RCT) | 0.00012 | 0.1001 | 0.0100 | 0.9986 | 0.9986 | |||
|
| ||||||||
| 3 | y = 0.3π + e | 0 | X | 0.10029 | 0.1007 | 0.0202 | 0.1691 | 0.1691 |
| X+π | 0.00008 | 0.1232 | 0.0152 | 0.0505 | 0.0505 | |||
| X+π+X*π | 0.00066 | 0.2465 | 0.0607 | 0.0506 | 0.0501 | |||
| X (RCT) | −0.00016 | 0.1004 | 0.0101 | 0.0504 | 0.0504 | |||
|
| ||||||||
| 4 |
y = 0.5X + 0.3π + e |
0.5 | X | 0.10034 | 0.1005 | 0.0202 | 1.0000 | 1.0000 |
| X+π | 0.00010 | 0.1230 | 0.0151 | 0.9817 | 0.9817 | |||
| X+π+X*π | −0.00007 | 0.2468 | 0.0609 | 0.9606 | 0.5266 | |||
| X (RCT) | −0.00014 | 0.0997 | 0.0099 | 0.9984 | 0.9984 | |||
|
| ||||||||
| 5 |
y = 0.5X + 0.3π + 0.2Xπ + e |
0.7 | X | 0.03443 | 0.1009 | 0.0114 | 1.0000 | 1.0000 |
| X+π | −0.09914 | 0.1233 | 0.0250 | 0.9979 | 0.9979 | |||
| X+π+X*π | −0.00010 | 0.2464 | 0.0607 | 0.9946 | 0.8086 | |||
| X (RCT) | −0.09992 | 0.1001 | 0.0200 | 1.0000 | 1.0000 | |||
|
| ||||||||
| 6 |
y = 0.5X + 0.2Xπ + e |
0.7 | X | −0.06671 | 0.1002 | 0.0145 | 1.0000 | 1.0000 |
| X+π | −0.10008 | 0.1226 | 0.0251 | 0.9979 | 0.9979 | |||
| X+π+X*π | −0.00046 | 0.2472 | 0.0611 | 0.9945 | 0.8082 | |||
| X (RCT) | −0.10028 | 0.1002 | 0.0201 | 1.0000 | 1.0000 | |||
|
| ||||||||
| 7 |
y = 0.3π + 0.2Xπ + e |
0.2 | X | 0.03272 | 0.1008 | 0.0112 | 0.6360 | 0.6360 |
| X+π | −0.10016 | 0.1234 | 0.0253 | 0.1286 | 0.1286 | |||
| X+π+X*π | −0.00100 | 0.2466 | 0.0608 | 0.1203 | 0.1273 | |||
| X (RCT) | −0.09976 | 0.1000 | 0.0199 | 0.1690 | 0.1690 | |||
|
| ||||||||
| 8 |
y = 0.2Xπ + e |
0.2 | X | −0.06667 | 0.1001 | 0.0145 | 0.2628 | 0.2628 |
| X+π | −0.10043 | 0.1231 | 0.0252 | 0.1272 | 0.1272 | |||
| X+π+X*π | 0.00048 | 0.2464 | 0.0607 | 0.1215 | 0.1279 | |||
| X (RCT) | −0.10045 | 0.1003 | 0.0201 | 0.1687 | 0.1687 | |||
|
| ||||||||
| 9 | y = f1(π) + e | 0 | X | 0.21427 | 0.1019 | 0.0563 | 0.5605 | 0.5605 |
| X+π | −0.00015 | 0.1231 | 0.0151 | 0.0497 | 0.0497 | |||
| X+π+X*π | 0.00071 | 0.2469 | 0.0610 | 0.0502 | 0.0505 | |||
| X (RCT) | −0.00013 | 0.1002 | 0.0100 | 0.0506 | 0.0506 | |||
|
| ||||||||
| 10 |
y = 0.5X + f1(π) + e |
0.5 | X | 0.21470 | 0.1012 | 0.0563 | 1.0000 | 1.0000 |
| X+π | 0.00025 | 0.1230 | 0.0151 | 0.9819 | 0.9819 | |||
| X+π+X*π | −0.00108 | 0.2464 | 0.0607 | 0.9607 | 0.5245 | |||
| X (RCT) | 0.00026 | 0.1004 | 0.0101 | 0.9987 | 0.9987 | |||
|
| ||||||||
| 11 |
y = 0.5X + f1(π) + 0.2f1(π)X + e |
0.601 | X | 0.18527 | 0.1014 | 0.0446 | 1.0000 | 1.0000 |
| X+π | −0.05061 | 0.1229 | 0.0177 | 0.9938 | 0.9938 | |||
| X+π+X*π | 0.01352 | 0.2459 | 0.0606 | 0.9850 | 0.7014 | |||
| X (RCT) | −0.05007 | 0.0997 | 0.0125 | 0.9998 | 0.9998 | |||
|
| ||||||||
| 12 |
y = 0.5X + 0.2f1(π)X + e |
0.601 | X | −0.02910 | 0.0998 | 0.0108 | 0.9999 | 0.9999 |
| X+π | −0.05019 | 0.1226 | 0.0175 | 0.9936 | 0.9936 | |||
| X+π+X*π | 0.01462 | 0.2455 | 0.0605 | 0.9849 | 0.7050 | |||
| X (RCT) | −0.05097 | 0.1000 | 0.0126 | 0.9998 | 0.9998 | |||
|
| ||||||||
| 13 |
y = f1(π) + 0.2f1(π)X + e |
0.101 | X | 0.18521 | 0.1013 | 0.0446 | 0.8029 | 0.8029 |
| X+π | −0.05043 | 0.1226 | 0.0176 | 0.0678 | 0.0678 | |||
| X+π+X*π | 0.01460 | 0.2469 | 0.0612 | 0.0693 | 0.0758 | |||
| X (RCT) | −0.05022 | 0.1002 | 0.0126 | 0.0803 | 0.0803 | |||
|
| ||||||||
| 14 |
y = 02f1(π)X + e |
0.101 | X | −0.02916 | 0.0998 | 0.0108 | 0.1095 | 0.1095 |
| X+π | −0.05055 | 0.1225 | 0.0176 | 0.0685 | 0.0685 | |||
| X+π+X*π | 0.01309 | 0.2462 | 0.0608 | 0.0688 | 0.0738 | |||
| X (RCT) | −0.05027 | 0.1000 | 0.0125 | 0.0791 | 0.0791 | |||
|
| ||||||||
| 15 | y = f2(π) + e | 0 | X | 0.17542 | 0.1014 | 0.0411 | 0.4083 | 0.4083 |
| X+π | −0.00006 | 0.1236 | 0.0153 | 0.0489 | 0.0489 | |||
| X+π+X*π | −0.25583 | 0.2482 | 0.1271 | 0.1701 | 0.1766 | |||
| X (RCT) | −0.00006 | 0.1000 | 0.0100 | 0.0504 | 0.0504 | |||
|
| ||||||||
| 16 |
y = 0.5X + f2(π) + e |
0.5 | X | 0.17587 | 0.1012 | 0.0412 | 1.0000 | 1.0000 |
| X+π | −0.00004 | 0.1236 | 0.0153 | 0.9810 | 0.9810 | |||
| X+π+X*π | −0.25506 | 0.2479 | 0.1265 | 0.9715 | 0.1694 | |||
| X (RCT) | 0.00052 | 0.1001 | 0.0100 | 0.9988 | 0.9988 | |||
|
| ||||||||
| 17 |
y = 0.5X + f2(π) + 02f2(π)X + e |
0.610 | X | 0.16782 | 0.1017 | 0.0385 | 1.0000 | 1.0000 |
| X+π | −0.01722 | 0.1236 | 0.0156 | 0.9971 | 0.9971 | |||
| X+π+i*π | −0.24525 | 0.2485 | 0.1219 | 0.9943 | 0.3161 | |||
| X (RCT) | −0.00515 | 0.1006 | 0.0101 | 1.0000 | 1.0000 | |||
|
| ||||||||
| 18 |
y = 0.5X + 02f2(π)X + e |
0.610 | X | −0.00763 | 0.1000 | 0.0101 | 1.0000 | 1.0000 |
| X+π | −0.01646 | 0.1227 | 0.0153 | 0.9977 | 0.9977 | |||
| X+π+X*π | 0.01083 | 0.2466 | 0.0609 | 0.9939 | 0.7094 | |||
| X (RCT) | −0.00516 | 0.0999 | 0.0100 | 1.0000 | 1.0000 | |||
|
| ||||||||
| 19 |
y = f2(π) + 0.2f2(π)X + e |
0.110 | X | 0.16775 | 0.1013 | 0.0384 | 0.7797 | 0.7797 |
| X+π | −0.01740 | 0.1235 | 0.0156 | 0.1161 | 0.1161 | |||
| X+π+X*π | −0.24615 | 0.2484 | 0.1223 | 0.1962 | 0.0848 | |||
| X (RCT) | −0.00530 | 0.1003 | 0.0101 | 0.1818 | 0.1818 | |||
|
| ||||||||
| 20 |
y = 0.2f2(π)X + e |
0.110 | X | −0.00793 | 0.0998 | 0.0100 | 0.1736 | 0.1736 |
| X+π | −0.01682 | 0.1230 | 0.0154 | 0.1182 | 0.1182 | |||
| X+π+X*π | 0.00985 | 0.2474 | 0.0613 | 0.0970 | 0.0781 | |||
| X (RCT) | −0.00514 | 0.1005 | 0.0101 | 0.1815 | 0.1815 | |||
|
| ||||||||
| 21 | y = f3(π) + e | 0 | X | 0.13768 | 0.1007 | 0.0291 | 0.2769 | 0.2769 |
| X+π | 0.00020 | 0.1230 | 0.0151 | 0.0495 | 0.0495 | |||
| X+π+X*π | 0.12139 | 0.2470 | 0.0757 | 0.0748 | 0.0778 | |||
| X (RCT) | 0.00013 | 0.1004 | 0.0101 | 0.0511 | 0.0511 | |||
|
| ||||||||
| 22 |
y = 0.5X + f3(π) + e |
0.5 | X | 0.13765 | 0.1009 | 0.0291 | 1.0000 | 1.0000 |
| X+π | −0.00031 | 0.1231 | 0.0152 | 0.9822 | 0.9822 | |||
| X+π+X*π | 0.12178 | 0.2462 | 0.0755 | 0.9631 | 0.7123 | |||
| X (RCT) | −0.00055 | 0.1000 | 0.0100 | 0.9988 | 0.9988 | |||
|
| ||||||||
| 23 |
y = 0.5X + f3(π) + 0.2f3(π)X + e |
0.581 | X | 0.09457 | 0.1011 | 0.0192 | 1.0000 | 1.0000 |
| X+π | −0.06127 | 0.1231 | 0.0189 | 0.9870 | 0.9870 | |||
| X+π+X*π | 0.11257 | 0.2469 | 0.0736 | 0.9760 | 0.8006 | |||
| X (RCT) | −0.06805 | 0.0999 | 0.0146 | 0.9992 | 0.9992 | |||
|
| ||||||||
| 24 |
y = 0.5X + 0.2f1(π)X + e |
0.581 | X | −0.04363 | 0.1000 | 0.0119 | 0.9997 | 0.9997 |
| X+π | −0.06154 | 0.1229 | 0.0189 | 0.9869 | 0.9869 | |||
| X+π+X*π | −0.00839 | 0.2465 | 0.0608 | 0.9720 | 0.6392 | |||
| X (RCT) | −0.06833 | 0.1003 | 0.0147 | 0.9990 | 0.9990 | |||
|
| ||||||||
| 25 |
y = f3(π) + 0.2f3(π)X + e |
0.081 | X | 0.09406 | 0.1008 | 0.0190 | 0.4072 | 0.4072 |
| X+π | −0.06145 | 0.1227 | 0.0188 | 0.0529 | 0.0529 | |||
| X+π+X*π | 0.11269 | 0.2473 | 0.0738 | 0.1053 | 0.1227 | |||
| X (RCT) | −0.06823 | 0.0999 | 0.0146 | 0.0516 | 0.0516 | |||
|
| ||||||||
| 26 |
y = 0.2f3(π)X + e |
0.081 | X | −0.04344 | 0.1000 | 0.0119 | 0.0657 | 0.0657 |
| X+π | −0.06127 | 0.1227 | 0.0188 | 0.0519 | 0.0519 | |||
| X+π+X*π | −0.00878 | 0.2461 | 0.0606 | 0.0555 | 0.0591 | |||
| X (RCT) | −0.06906 | 0.1000 | 0.0148 | 0.0507 | 0.0507 | |||
|
| ||||||||
| 27 |
y = 0.3π + 0.2f1(π)X + e |
0.101 | X | 0.07084 | 0.1007 | 0.0152 | 0.4001 | 0.4001 |
| X+π | −0.05063 | 0.1232 | 0.0177 | 0.0699 | 0.0699 | |||
| X+π+X*π | 0.01266 | 0.2460 | 0.0607 | 0.0696 | 0.0737 | |||
| X (RCT) | −0.00072 | 0.1001 | 0.0100 | 0.1699 | 0.1699 | |||
|
| ||||||||
| 28 |
y = f1(π) + 0.2Xπ + e |
0.2 | X | 0.14793 | 0.1018 | 0.0322 | 0.9265 | 0.9265 |
| X+π | −0.09929 | 0.1233 | 0.0251 | 0.1295 | 0.1295 | |||
| X+π+X*π | 0.00047 | 0.2471 | 0.0611 | 0.1236 | 0.1280 | |||
| X (RCT) | −0.14967 | 0.1000 | 0.0324 | 0.0787 | 0.0787 | |||
|
| ||||||||
| 29 |
y = 0.5X + 0.3π + 0.2f1(π)X + e |
0.601 | X | 0.07037 | 0.1003 | 0.0150 | 1.0000 | 1.0000 |
| X+π | −0.05132 | 0.1227 | 0.0177 | 0.9932 | 0.9932 | |||
| X+π+X*π | 0.01249 | 0.2465 | 0.0609 | 0.9846 | 0.6991 | |||
| X (RCT) | −0.00126 | 0.1003 | 0.0101 | 1.0000 | 1.0000 | |||
|
| ||||||||
| 30 |
y = 0.5X + f1(π) + 0.2Xπ + e |
0.7 | X | 0.14802 | 0.1011 | 0.0321 | 1.0000 | 1.0000 |
| X+π | −0.09986 | 0.1226 | 0.0250 | 0.9982 | 0.9982 | |||
| X+π+X*π | −0.00040 | 0.2460 | 0.0605 | 0.9951 | 0.8075 | |||
| X (RCT) | −0.14932 | 0.0999 | 0.0323 | 0.9998 | 0.9998 | |||
Note. The two hypothesis tests only differ for the model with the interaction term.
Figure 1.
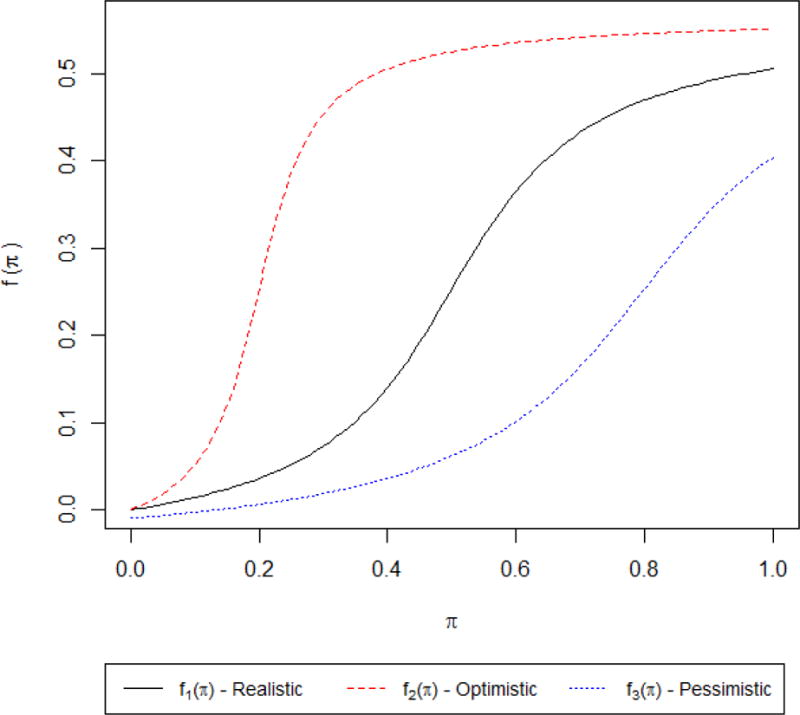
Simulated non-linearnonlinear expectationncy effects, both symmetric (realistic) and asymmetric (optimistic and pessimistic).
Despite their apparent complexity, the generating models have a distinct pattern to them. Models 1 and 2 test that the R2R design and associated analytic models preserve the Type I error rate and provide acceptable power in the absence of expectation effects. Models 3 through 8 add complexity through expectation main effects, interactions, and combinations of these terms. The next three blocks (models 9–14, 15–20, 21–26) substitute the above three nonlinear expectation effects f(π) where there was a linear π in models 3–8. Finally, models 27–30 look at combinations of linear and nonlinear expectation effects to see how the analytic models behave under unusual conditions.
Simulations were done in R 3.1.2. For each true model, we simulated 100,000 datasets sampling π from a Uniform(0,1) distribution (runif function) and e from a N(0,1) (rnorm function) for a sample of size 400. The simulation size of 100,000 allows for estimates of a Type I error with a 95% confidence interval width of 0.0003 (Burton, Altman, Royston, & Holder, 2006). The analytic models were fit with the glm function, and the tests of multiple parameters were done with the glht function in the multcomp package. The code used for the simulation is available as a supplementary file.
Simulation Study Results
The results of the simulation study are detailed in Table 2. They suggest that the Wald test preserves the nominal type I error rates as long as the linear effect of π is included in the analytical model when the true expectation effect is absent (generating model 1), linear (model 3), or nonlinear (models 9, 15, and 21). Interestingly, the addition of the linear interaction term inflates the Type I error when the expectation effects are both nonlinear and not symmetric about 0.5 (f2(π) and f3(π) in models 15 and 21, respectively) due to bias in the estimates.
The simulations also suggest that the accuracy of the estimates of treatment effects in an R2R design is mainly determined by the expectation-by-treatment interaction. If no interaction is present, linear control of π in the R2R design is sufficient to produce unbiased estimates of the treatment effect, as is the traditional RCT design. If there is a linear or nonlinear interaction, however, linear control for π and the traditional RCT design produce biased estimates. If the interaction is linear, then the use of a linear π-by-X interaction term seems to produce unbiased estimates regardless of the form of the expectation main effect. If the interaction is nonlinear, then fitting a linear interaction term may produce biased estimates if the linear approximation is sufficiently poor. Although the R2R model may provide less biased estimates of a treatment effect at full expectation in the presence of a treatment-by-expectation interaction, in all conditions its estimates came with a much greater variability (SD of roughly 0.24 vs. 0.10) and typically a larger MSE.
In summary, linear control of π and its interaction is sufficient for producing unbiased results when the true expectation effect is linear but may be biased when it is nonlinear, although this improvement comes at the cost of increased variability.
Considerations of Statistical Power
This section describes general considerations for power analyses to estimate the sample size needed to detect a “true” effect with desired probability (power) under nominal α level given the presence of an expectancy effect. Estimating the power for comparing two sample means (or proportions) in a parallel arm RCT design is conceptually and computationally simpler than in the proposed design, which involves a more complicated multiple regression model with linear or nonlinear effects of π and its interaction with X. Under some simplified assumptions, the power or sample size can be calculated analytically for multiple regression models, and such calculation has been implemented in many analytical software packages (such as SAS proc power, R package pwr, G*Power, etc.). However, simulation-based power or sample size calculation is a more flexible way to investigate many different distributions of π and to allow for non-linear effects of π. As an example of simulation-based power and sample size calculation, consider a two-armed RCT in which a total of n subjects will be equally allocated between treatment groups. For simplicity (but without loss of generality), also assume there is only a linear effect of π and its interactions, as in Eq. 1.
The procedure for simulation-based power estimation are as follows:
Use the underlying model (e.g., Eq. 1) to generate random data with specified sample sizes (n), assumed parameter values (βs) of practical importance, and assumed variance parameter (σ2).
Analyze the randomly generated data with proper methods (e.g., using SAS, R, Stata).
Test the null hypothesis H0:Lβ=0 for the vector of βs of interest (β) at nominal α level, where L is a known design matrix for general linear model hypothesis testing. For example, H0:β1+β3=0 for testing the treatment effect at π=1 in Eq. 1. A Wald F test can be used to calculate p-values.
Repeat steps 1–3 many times (e.g., 1000 times), with more replicates yielding more precise estimates.
Calculate the empirical power under the assumptions in step 1 as the proportion of observations for which the p-value is less than α.
Note that in the case where there is no treatment-by-expectancy interaction, our simulations suggest that the R2R design is less powerful than the traditional RCT design where subjects are randomized as normal with π=0.5 (see Table 1). However, when such an interaction exists the standard RCT design produces biased estimates of the treatment effect when π=1, thus comparing power of the R2R and traditional RCT designs would be invalid in such circumstances.
Overview of Pilot Study
To demonstrate the R2R design, we conducted a small trial looking at the interaction of caffeine and expectation on mood and vigilance. This specific application was chosen as it (1) had been previously demonstrated by Elliman et al. (2010) to have a caffeine-by-expectation interaction, (2) had a low monetary cost, and (3) posed minimal risk to subjects. This section describes the design and results of this trial, with an emphasis on what the R2R design allowed us to infer that a traditional RCT would not have.
Methods
Design
To implement the R2R design, π was drawn from a multinomial distribution with values of 0.1 to 0.9 by 0.1. Balance was enforced with 20 subjects per category (except for 0.5, which had 40 subjects), with randomization of the 200 total subjects done via random permutation. When assigning treatments (200 mg caffeine vs. placebo) within each category for π, balance was also enforced (e.g. 18 of the 20 subjects assigned π=0.9 were given caffeine) and randomization was done using random permutation. All personnel interacting with subjects were blinded to the pill assignment; only the statistician and pharmacy were unblinded.
Subjects were provided a brief tutorial on probability, an envelope containing their assigned value of π, and the assigned pills. Upon completion of study tasks, subjects were provided with an envelope containing the identity of their pill.
Subject Population and Recruitment
This protocol was approved by the Institutional Review Board of the University of Alabama at Birmingham (UAB) and registered at ClinicalTrials.gov (NCT02461693). Participants were recruited through flyers around the UAB campus, announcements made during undergraduate and graduate classes, and email blasts disbursed by professors of undergraduate and graduate classes. Interested persons were screened over the phone for eligibility. If eligible, participants were emailed the informed consent and asked to call study staff if they had any questions. As participants arrived at the study visit, they were given the consent form to read, individually asked if they had questions, and then signed the document.
The inclusion criteria of the study were: age≥18; willingness to take 2 caffeine or placebo pills; willingness to abstain from caffeine for 12 hours prior to study visit (8:30pm–8:30am); UAB employees or students with some college education (including current enrollment). The exclusion criteria were: uncorrected vision problems; nicotine use; use of medications for sleep, anxiety, and/or ADHD; pregnant or trying to get pregnant; lactose intolerance. Study staff learned that five subjects had violated the inclusion/exclusion criteria after randomization and participation in the study; these subjects’ data were excluded from the analysis and five additional subjects were recruited and randomly assigned the treatment and probability assignments of the excluded subjects. The flow of subjects through the study is described in the CONSORT diagram in Figure 2.
Figure 2.
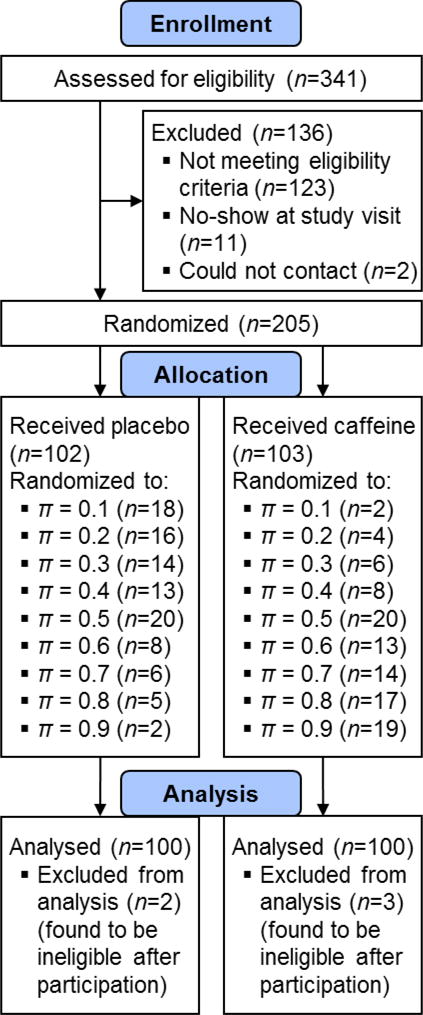
CONSORT diagram for the pilot R2R study on caffeine effects.
Outcomes
The dependent variables were measures of mood and vigilance. Mood was assessed using the Profile of Mood States (POMS) Questionnaire. The POMS is a widely used, standardized, paper-and-pencil inventory of mood states (McNair, Lorr, & Droppleman, 1971). It provides a comprehensive assessment of a wide range of mood states and captures the fundamental domains of human affect (McNair et al, 1971). It is sensitive to a wide variety of nutritional manipulations, including caffeine, as well as sleep loss and various drugs (Fine et al., 1994; Lieberman, Tharion, Shukitt-Hale, Speckman, & Tulley, 2002). It takes less than 5 minutes to complete. Volunteers rated a series of 65 mood-related adjectives with regard to how they were feeling “right now” on a scale of 0 (not at all) to 4 (extremely). The adjectives factor into six mood sub-scales: Tension-Anxiety; Depression-Dejection; Anger-Hostility; Vigor-Activity; Fatigue-Inertia; Confusion-Bewilderment and a Total Mood Disturbance score which aggregates the six subscales into a single variable. An updated version, the POMS-2, was used for this study and was administered 30 minutes after probability assignment and pill consumption.
Vigilance was assessed using the Scanning Visual Vigilance Test. This test assesses vigilance, ability to sustain attention during long, boring, continuous tasks that generate minimal cognitive load (Fine et al., 1994; Lieberman, Coffey, & Kobrick, 1998; Lieberman et al., 2002). The volunteer continuously scans a computer screen to detect an infrequent, difficult-to-detect stimulus that appears at random intervals and locations for 2 seconds. On average, a stimulus was presented once per minute. Upon detection of the stimulus, the volunteer pressed the space bar on a computer keyboard as rapidly as possible. Whether a stimulus was detected and time required for detection was recorded. Responses before or after stimulus occurrence were false alarms. The test lasted 60 minutes.
Statistical Analysis
The primary analysis of the outcome variables was done with generalized linear models of the form
| (6) |
where X is an indicator variable for whether the subject received caffeine, π is the assigned probability (modeled as a continuous linear function), and g(Y) and ε are the link function and error term, respectively, with an appropriate functional form and distribution for the outcome Y. When modeling the number of false alarms, a negative binomial distribution was assumed; when modeling the proportion of correct answers out of the 60 presented, a binomial distribution and logit link function were used; for all other variables a normal distribution was assumed. Note that when modeling the time to a correct answer, the subjects’ mean values were taken as the dependent variables and were weighted by the observed sample variance of each subject’s mean time to a correct answer to properly account for heterogeneity in both the number of correct answers and in each subject’s response time.
Inference was made using Wald tests on the interaction term (β3), and 95% confidence intervals were computed for the estimated outcome values in the two groups at various values of π. In addition, a prespecified subgroup analysis was done to estimate the effect of caffeine among only the 40 subjects assigned π=0.5, as in a traditional RCT.
One subject was missing data from the vigilance test and was excluded from the analysis. 22 subjects were missing a small portion of the adjective values from the POMS questionnaire; these values were multiple imputed (FCS, PROC MI) and Winsorized to the valid range (0–4), and combined with the observed values to compute the mood sub-scales (e.g. vigor-activity) and total mood displacement, with the imputations combined with PROC MIANALYZE. No correction was made for the testing of multiple outcomes. All calculations were done in SAS 9.4 (SAS Institute Inc., Cary, NC).
Results
Descriptive statistics for the sample demographics are given in Table 3. Note that the totals for the treatment groups are aggregated over all values of π. It could also be noted that this reveals one complexity of the R2R design, namely that it is not plainly clear how to best summarize the entire sample when subjects are randomized to a large number of unique assignments (here, 18 treatment/π combinations).
Table 3.
Sample characteristics
| Variable | Overall | Placebo | Caffeine | |||||
|---|---|---|---|---|---|---|---|---|
| Sample Size | 200 | 100 | 100 | |||||
|
| ||||||||
| Age | 31.8 (12.9) | 29.8 (11.4) | 33.8 (14.0) | |||||
|
| ||||||||
| Male | 77 (38.5%) | 39 (39%) | 38 (38%) | |||||
| Female | 123 (61.5%) | 61 (61%) | 62 (62%) | |||||
|
| ||||||||
| Hispanic | 8 (4%) | 7 (7%) | 1 (1%) | |||||
|
| ||||||||
| White | 69 (34.5%) | 30 (30%) | 39 (39%) | |||||
| Black | 89 (44.5%) | 50 (50%) | 39 (39%) | |||||
| Other | 42 (21%) | 20 (20%) | 22 (22%) | |||||
|
| ||||||||
| High School/GED | 70 (35%) | 35 (35%) | 35 (35%) | |||||
| Associate’s | 23 (11.5%) | 13 (13%) | 10 (10%) | |||||
| Bachelor’s | 66 (33%) | 31 (31%) | 35 (35%) | |||||
| Master’s | 24 (12%) | 13 (13%) | 11 (11%) | |||||
| Doctorate/Professional | 17 (8.5%) | 8 (8%) | 9 (9%) | |||||
|
| ||||||||
| Current student | 119 (60.1%) | 69 (69%) | 50 (50%) | |||||
Note. Values are Mean (SD) or Frequency (%).
To assess how the assigned value of π may have altered subject expectancies, subjects were asked 30 minutes after pill consumption about how likely they thought it was that they received a caffeine pill and which pill they believed they received (Table 4). With regard to likelihood, subjects seemed to be most sensitive to values at or across π=0.5, with most subjects correctly identifying that values less than 0.5 indicate it to be less likely than not and vice versa for values over 0.5. However, there did seem to be a hesitation to describe the likelihood as ‘very likely’ or ‘very unlikely’ at the extreme values of π (0.1, 0.2, 0.8, 0.9). This suggests that subjects may have a different thought process for interpreting very small and very large probabilities; alternatively, it may be that such a Likert scale assessment of expectancies is simply not a useful way to quantify subject expectancies. Interestingly, about 60% of subjects thought they received a placebo, despite an overall 50/50 assignment of caffeine and placebo.
Table 4.
Subject interpretations of their assigned treatment probabilities and perceptions of pill received
| Assigned Treatment Probability | Likelihood of Receiving Caffeine (n=200) | Pill Subject Thought He/She Received (n=198) | |||||
|---|---|---|---|---|---|---|---|
| Very Unlikely | Unlikely | Neither | Likely | Very Likely | Caffeine | Placebo | |
| 0.1 | 11 (55%) | 5 (25%) | 1 (5%) | 2 (10%) | 1 (5%) | 1 (5%) | 19 (95%) |
| 0.2 | 10 (50%) | 7 (35%) | 2 (10%) | 1 (5%) | 0 | 2 (10.5%) | 17 (89.5%) |
| 0.3 | 3 (15%) | 12 (60%) | 2 (10%) | 1 (5%) | 2 (10%) | 6 (30%) | 14 (70%) |
| 0.4 | 2 (10%) | 15 (75%) | 2 (10%) | 1 (5%) | 0 | 7 (35%) | 13 (65%) |
| 0.5 | 3 (7.5%) | 2 (5%) | 27 (67.5%) | 6 (15%) | 2 (5%) | 13 (32.5%) | 27 (67.5%) |
| 0.6 | 0 | 2 (10%) | 2 (10%) | 14 (70%) | 2 (10%) | 7 (36.8%) | 12 (63.2%) |
| 0.7 | 1 (5%) | 2 (10%) | 3 (15%) | 13 (65%) | 1 (5%) | 11 (55%) | 9 (45%) |
| 0.8 | 2 (10%) | 0 | 1 (5%) | 8 (40%) | 9 (45%) | 16 (80%) | 4 (20%) |
| 0.9 | 0 | 1 (5%) | 0 | 6 (30%) | 13 (65%) | 16 (80%) | 4 (20%) |
| Total | 32 (16%) | 46 (23%) | 40 (20%) | 52 (26%) | 30 (15%) | 79 (39.9%) | 119 (60.1%) |
Descriptive statistics for the outcome variables within each group are given in Table 5. Means and associated confidence intervals for the outcomes were estimated at different values of π using the model described in Eq. 6 and are given in Table 6.
Table 5.
Summary statistics for the vigilance and mood outcome measures
| Outcome | Overall | Placebo | Caffeine | |||
|---|---|---|---|---|---|---|
| n | Mean ± SE | n | Mean ± SE | n | Mean ± SE | |
| Number Correct (out of 60) | 199 | 54.6 ± 0.66 | 100 | 53.3 ± 1.00 | 99 | 55.9 ± 0.85 |
| Proportion Correct (#/60) | 199 | 0.910 ± 0.011 | 100 | 0.888 ± 0.017 | 99 | 0.932 ± 0.014 |
| Mean Time to a Correct Hit | 199 | 0.81 ± 0.02 | 100 | 0.88 ± 0.03 | 99 | 0.74 ± 0.03 |
| Number of False Alarms | 199 | 5.01 ± 0.61 | 100 | 5.80 ± 1.01 | 99 | 4.21 ± 0.67 |
| Total Mood Displacement | 177 | 8.38 ± 1.79 | 89 | 14.08 ± 2.86 | 88 | 2.63 ± 1.98 |
| Anger-Hostility | 193 | 2.37 ± 0.30 | 99 | 2.54 ± 0.46 | 94 | 2.19 ± 0.38 |
| Confusion-Bewilderment | 198 | 6.62 ± 0.35 | 99 | 7.00 ± 0.53 | 99 | 6.23 ± 0.48 |
| Depression-Dejection | 193 | 2.50 ± 0.35 | 95 | 3.15 ± 0.61 | 98 | 1.87 ± 0.35 |
| Fatigue-Inertia | 196 | 5.56 ± 0.43 | 99 | 6.65 ± 0.68 | 97 | 4.44 ± 0.49 |
| Friendliness | 199 | 13.22 ± 0.32 | 100 | 12.97 ± 0.44 | 99 | 13.47 ± 0.47 |
| Tension-Anxiety | 195 | 5.67 ± 0.37 | 97 | 5.81 ± 0.52 | 98 | 5.53 ± 0.52 |
| Vigor-Activity | 199 | 14.73 ± 0.51 | 100 | 13.13 ± 0.69 | 99 | 16.35 ± 0.73 |
Note. Values are given as Mean ± SE.
Table 6.
Estimated means and 95% confidence intervals for the outcomes given caffeine or placebo and a certain probability
| Outcome | Pill Given | Placebo | Caffeine | ||||
|---|---|---|---|---|---|---|---|
| Probability | π = 0 | π = 0.5 | π = 1 | π = 0 | π = 0.5 | π = 1 | |
| Mean Time to a Correct Hit | 0.72 (0.63,0.81) | 0.74 (0.69,0.80) | 0.77 (0.63,0.91) | 0.50 (0.40,0.60) | 0.54 (0.51,0.58) | 0.58 (0.52,0.65) | |
| Probability of a Correct Hit | 88.9% (87.2,90.5) | 88.8% (87.8,89.6) | 88.6% (85.8,90.8) | 95.3% (93.5,96.6) | 93.7% (92.9,94.4) | 91.6% (90.0,93.1) | |
| Number of False Alarms | 2.01 (1.56,2.47) | 1.66 (1.39,1.93) | 1.31 (0.62,1.99) | 1.90 (1.16,2.64) | 1.52 (1.24,1.79) | 1.14 (0.54,1.63) | |
| Total Mood Displacement | 9.6 (−0.1,19.4) | 12.5 (7.1,18.0) | 15.5 (0.8,30.1) | 12.8 (−1.9,27.4) | 6.2 (0.8,11.7) | −0.3 (−10.1,9.4) | |
| Anger-Hostility | 2.94 (1.28,4.60) | 2.38 (1.45,3.31) | 1.82 (−0.68,4.32) | 2.18 (−0.32,4.68) | 2.25 (1.32,3.18) | 2.32 (0.66,3.98) | |
| Confusion-Bewilderment | 5.98 (3.98,7.99) | 7.25 (6.12,8.37) | 8.51 (5.49,11.53) | 6.97 (3.96,9.99) | 6.43 (5.30,7.56) | 5.88 (3.88,7.89) | |
| Depression-Dejection | 2.83 (0.84,4.81) | 3.12 (2.01,4.24) | 3.42 (0.43,6.40) | 1.52 (−1.47,4.50) | 1.93 (0.81,3.04) | 2.34 (0.36,4.33) | |
| Fatigue-Inertia | 6.13 (3.75,8.50) | 6.79 (5.46,8.12) | 7.46 (3.89,11.03) | 7.10 (3.54,10.67) | 5.11 (3.77,6.44) | 3.11 (0.74,5.48) | |
| Friendliness | 13.9 (12.0,15.7) | 12.7 (11.7,13.7) | 11.5 (8.8,14.3) | 11.6 (8.9,14.4) | 13.1 (12.1,14.1) | 14.6 (12.8,16.4) | |
| Tension-Anxiety | 5.54 (3.38,7.70) | 5.90 (4.69,7.12) | 6.26 (3.01,9.51) | 4.70 (1.44,7.95) | 5.60 (4.39,6.82) | 6.51 (4.35,8.67) | |
| Vigor-Activity | 13.8 (11.1,16.6) | 12.9 (11.4,14.5) | 12.0 (7.9,16.2) | 9.7 (5.5,12.9) | 15.1 (13.5,16.6) | 20.5 (17.7,23.2) | |
The estimated treatment effects at π=1 are given in Table 7, as are the estimates from the subgroup at π=0.5. In the R2R model, we observed that there was a statistically significant interaction between the provided value of π and caffeine in their effects on the subject’s reported Vigor-Activity scale (p=0.0060). Furthermore, we noted that the R2R design estimated a significant treatment effect of 8.47 at π=1 (p=0.0009) whereas the subjects in the traditional RCT condition (π=0.5) showed a smaller non-significant effect of 2.70 (p=0.2073). The estimated treatment effect changed sign (a negative effect to a positive effect) for Anger-Hostility and Tension-Anxiety, suggesting that in some situations a failure to account for expectation may produce misleading results, though the nominal significance did not change nor was the interaction significant for these two outcomes.
Table 7.
Estimated effects of caffeine for the 40 subjects assigned π = 0.5 as in a traditional RCT, and as estimated at π = 0.5 and π = 1 by the R2R design
| Outcome | RCT, π=0.5 only | R2R, at π=0.5 | R2R, at π=1 | Trt-by-π Interaction p-value | |||
|---|---|---|---|---|---|---|---|
| (SE) | p | (SE) | p | (SE) | p | ||
| Mean Time to a Hit | −0.11 (0.06) | 0.0690 | −0.20 (0.03) | <0.0001 | −0.19 (0.08) | 0.0199 | 0.7926 |
| Probability of a Hit | 10.8 (1.3) | <0.0001 | 5.0 (0.6) | <0.0001 | 3.1 (1.5) | 0.0331 | 0.0694 |
| Number of False Alarms | −0.35 (0.31) | 0.2745 | −0.14 (0.19) | 0.4661 | −0.17 (0.43) | 0.6949 | 0.9457 |
| Total Mood Displacement | −13.61 (8.63) | 0.1148 | −6.30 (3.95) | 0.1111 | −15.77 (8.99) | 0.0793 | 0.2407 |
| Anger-Hostility | −1.92 (1.73) | 0.2688 | −0.13 (0.67) | 0.8457 | 0.50 (1.53) | 0.7444 | 0.6467 |
| Confusion-Bewilderment | −2.60 (1.70) | 0.1352 | −0.82 (0.81) | 0.3152 | −2.63 (1.85) | 0.1556 | 0.2760 |
| Depression-Dejection | −2.89 (1.66) | 0.0810 | −1.19 (0.80) | 0.1382 | −1.07 (1.83) | 0.5572 | 0.9421 |
| Fatigue-Inertia | −0.97 (2.02) | 0.6303 | −1.68 (0.96) | 0.0800 | −4.35 (2.19) | 0.0467 | 0.1748 |
| Friendliness | 2.40 (1.39) | 0.0923 | 0.41 (0.73) | 0.5798 | 3.03 (1.67) | 0.0687 | 0.0792 |
| Tension-Anxiety | −2.53 (1.86) | 0.1742 | −0.30 (0.88) | 0.7328 | 0.25 (1.99) | 0.9010 | 0.7598 |
| Vigor-Activity | 2.70 (2.10) | 0.2073 | 2.17 (1.12) | 0.0524 | 8.47 (2.55) | 0.0009 | 0.0060 |
Discussion
Expectancy effects have been observed in clinical trials and studies of the effects of ingesting various compounds (Elliman et al., 2010; Papakostas & Fava, 2009). Although empirical studies of expectancy effects have focused on clinical outcomes, such effects likely exist for multiple outcome types, including subject preferences, behaviors, or performances. Researchers from across disciplines who wish to isolate the effect of a variable will thus likely have to contend with the possible effects of π. When researchers have complete control over the information available to respondents, including the probability of receiving the treatment, expectancy effects can be estimated.
In our small pilot study of the R2R design, we were able to identify relationships between caffeine consumption, expectation, mood, and vigilance. As one might expect, subjects provided caffeine tended to have higher accuracy and faster reaction times compared to those given placebo; this effect did not seem to be modified by subject expectancies. We did find an interaction between caffeine and subject expectation in their effects on a subject’s Vigor-Activity scale, such that subjects who had greater reason to expect they were getting caffeine (those told a larger value of π) experienced significantly stronger effects of actually receiving the caffeine pill. This is similar to the study by Elliman et al. where caffeine only improved vigilance in subjects given both caffeine and a message that they were receiving caffeine. Given the results of the pilot study, it seems that such an association between caffeine and Vigor-Activity would have been missed had expectancies not been accounted for.
With regards to study execution, the R2R required only a minor increase in effort by the study staff compared to a standard RCT. Furthermore, the subjects did not express any negative feelings towards the design, which we feel is an improvement over the balanced placebo design that relies on subject deception. In fact, subjects found the novel design interesting and several were very interested in and surprised by what pill they had actually received; this response from the subjects supports the idea that it would be ethical to unblind subjects at the end of a study with the R2R design.
Although subject expectations can be manipulated using the R2R design, the mechanisms producing expectancy effects can vary greatly between applications. For example, in studies of taste preferences, individuals certain of receiving a particular treatment may feel more pressure to report a socially desirable response; subjects who are more certain that they received a high quality wine (Wansink, Payne, & North, 2007) or listened to a high quality opera may feel more pressure to report greater enjoyment of the experience, lest they reveal a lack of appreciation for things others have recognized as being of good quality. In this case, the observed expectancy effect may be best explained as a product of social desirability rather than behavioral changes that alter treatment effects. However, these expectation effects may not be so easily predicted, as in the counterintuitive finding between expectation and antidepressant discontinuation by Tedeschini et al., potentially limiting cross-study comparison of results to studies on the same topic.
Limitations
One possible objection to the adoption of experimental designs that can better estimate and adjust for expectation effects is based on tradition. Experimental designs for the analysis of treatment effects have traditionally been conducted such that all subjects have equal uncertainty about being assigned to the treatment, thus any expectancy effects would be due to the same level of uncertainty across groups—typically based on a 0.5 probability of assignment of treatment or control group. Although such designs are traditional, their generalizability to real world situations and ability to isolate the ‘true treatment effect’—effects independent from expectancy effects, also called the unknowing treatment effect (Ogawa & Onishi, 2010) – is limited. In our day-to-day lives, we are usually certain about medications taken, actions performed, and foods consumed. Thus, any researcher wishing to make an argument for the effect of some treatment in the population must consider the certainty subjects will have about being treated. Traditional RCT designs do not allow for such considerations, as all groups share some amount of uncertainty (usually the same uncertainty across groups) about their status, confounding any observed treatment effect with expectancy effects. The R2R design also requires there to be uncertainty in what intervention was given to a subject; medicinal or psychoactive compounds allow for easy blinding with a sugar pill as a control, but social or behavioral interventions may complicate or preclude the implementation of the R2R design for a study.
Another consideration of the new design is the potential power loss compared to the traditional RCT due to the multicollinearity among the independent variables from the regression model (Eq. 1). Because the value of Xi is randomly drawn from a Bernoulli distribution with the mean of πi, it is expected that as πi approaches 1, Xi has a high probability of being 1, and vice versa. Although the collinearity between π and X does not reduce the predictive power or reliability of the model as a whole, it does reduce the power for the individual predictors X, π, or their interaction. However, the sacrifice of power for any one predictor in the new design is justified if expectation or expectation-by-treatment interaction effects are of interest.
A final objection to the wider adoption of R2R designs are that they would be too complex or difficult to implement. Results from our simulations do indicate that larger sample sizes would be necessary in R2R designs in order to achieve comparable power to a traditional randomization design. While the increase in sample size requirement is not trivial, neither is it prohibitive. Ultimately, researchers need to consider the costs of increasing sample sizes (e.g., greater resources spent towards recruitment and study materials) against the costs of not accounting for expectation effects in designs. For researchers needing to account for expectation effects in their analyses—especially those who need better estimates of the effects of actual policy implementation or drug treatment, or those wishing to isolate the true effect from expectation effects–the costs of increasing sample sizes may be necessary. Also, our experience with our pilot study suggests that the added complexity of executing the R2R design (separate from increased sample size) is minimal. Reporting on the R2R design is admittedly more complex, as one should not only test for the interaction but also report on the observed or predicted treatment effect sizes at different levels of expectation (e.g. mean differences with appropriate standard errors or confidence intervals). It should be noted that if one wants to produce an even more realistic assessment by accounting for compliance effects, one could extend the R2R design to use the more complex Complier Average Causal Effect (CACE) analysis (Schochet & Chiang, 2009). Although such an extension is outside the scope of this work, it is an important future direction to be able to more accurately assess treatment and expectation effects under actual conditions of use.
As shown in our simulation study, the greatest limitation of the simple R2R design is that the use of linear terms for π and its interaction with the treatment may produce biased estimates of the treatment effect at π=1 when the expectation effects are nonlinear. If the true shape of the expectation curve can be approximated reasonably well, then the model may give reasonable estimates; unfortunately, in practice we will not know the true shape unequivocally and it is conceivable that it would be nonlinear in a given application. Spline models hold some promise and can produce good estimates of the mean outcome among subjects on treatment when π=1, but the R2R design results in a very low number of subjects on placebo with values of π near 1 with which to inform the spline model, which may result in estimates with high variability for the same sample size. Beyond linear splines, possible adjustments to the design and analysis include using polynomial splines, altering the sampling distribution of π to provide better coverage of the data, or utilizing a type of sampling weights for the observations based on the value of π. Such investigations to optimize the performance of the R2R design under nonlinear expectancies are outside the scope of this paper, but remain an essential area of future research for the design.
As mentioned earlier, we have made the assumption that our manipulation of the expectation π is interchangeable with the changed expectancies of subjects. Given the randomization of π, we feel that it is reasonable to infer that effects of π on the outcome are acting through (and only through, if blinding is maintained) unobserved expectancies. We do acknowledge, however, that such a ‘black box’ assumption is limited and not particularly satisfying for those who want to better understand the intricacies of expectancy effects. Beyond treating the relationship between π and the outcome of interest as nonlinear, it is reasonable to consider a more nuanced model. It would be very reasonable to consider subject expectancies as a latent variable, such that π can affect expectancies and those expectancies can influence the outcome. Furthermore, both of those relationships could, in practice, be linear or nonlinear. Although we have attempted to gain some insight to these expectancies (see Table 4), it is unclear how one could best operationalize this construct. Further research into how to best use latent variable analyses in R2R designs could provide great insight into the underlying mechanisms of subject expectancies.
To conclude, the standard placebo-controlled randomized trial estimates unbiased treatment effects, but does so for conditions that do not well represent the intended conditions of actual use because they estimate effects among persons who cannot reasonably be certain that they are receiving the intervention. If the known likelihood that one is receiving the intervention influences the intervention’s effects, and the effects under intended conditions of use are of interest, alternative designs are needed. R2R is one such design, though more work remains to refine the analysis of it.
Supplementary Material
In blinded randomized controlled trials (RCT), participants are uncertain whether they are receiving treatment or placebo. Although uncertainty is required to isolate the treatment effect from all other potential effects, it is poorly suited to estimate the treatment effect under actual conditions of intended use because under actual conditions of intended use, individuals know that they are receiving a treatment. We propose an experimental design, Randomization to Randomization Probabilities (R2R), to improve estimates of treatment effects under actual conditions of use by manipulating participant expectations about receiving treatment. In the R2R design, participants are first randomized to a probability of receiving treatment (vs placebo). Subjects are then told their probability and are subsequently randomized to either treatment or placebo with that probability. By influencing subject expectations and incorporating this into the analysis, we better approximate actual conditions of use. The R2R design does this without deceiving subjects thereby providing a more ethical alternative to the balanced placebo design. We illustrate the R2R design with an RCT evaluating the effects of caffeine on mood and vigilance, showing that some of the effects of caffeine differ by the expectation that one received caffeine. We believe the R2R design can be used to better estimate treatment effects by more closely resembling the actual conditions in which treatments are delivered and received.
Acknowledgments
This study is supported in part by NIH grants P30DK056336, T32DK062710, R25DK099080, and R25HL124208. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or any other organization. The authors thank Drs. Joseph C. Cappelleri and Rositsa B. Dimova for their helpful comments on an early draft of the manuscript, and Dr. Taraneh Soleymani for her help in carrying out the pilot study. The work has been presented in part at Experimental Biology (April 2016) and the University of Alabama at Birmingham School of Public Health Research Day (April 2016).
Footnotes
Supplementary Materials
The R code used in the simulation is provided in an additional file.
Contributor Information
Brandon J. George, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL
Peng Li, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL; Department of Biostatistics, University of Alabama at Birmingham, Birmingham, AL.
Harris R. Lieberman, Department of Health Behavior, University of Alabama at Birmingham, Birmingham, AL
Greg Pavela, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL; Department of Health Behavior, University of Alabama at Birmingham, Birmingham, AL.
Andrew W. Brown, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL
Kevin R. Fontaine, Department of Health Behavior, University of Alabama at Birmingham, Birmingham, AL
Madeline M. Jeansonne, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL
Gareth R. Dutton, Department of Medicine, University of Alabama at Birmingham, Birmingham, AL
Adeniyi J. Idigo, Office of Energetics, University of Alabama at Birmingham, Birmingham, AL
Mariel A. Parman, Department of Health Behavior, University of Alabama at Birmingham, Birmingham, AL
Donald B. Rubin, Department of Statistics, Harvard University, Cambridge, MA
David B. Allison, Department of Biostatistics, University of Alabama at Birmingham, Birmingham, AL
References
- Burton A, Altman DG, Royston P, Holder RL. The design of simulation studies in medical statistics. Statistics in Medicine. 2006;25(24):4279–4292. doi: 10.1002/sim.2673. [DOI] [PubMed] [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. 3rd. Mahwah, NJ: Erlbaum; 2003. [Google Scholar]
- Colagiuri B. Participant expectancies in double-blind randomized placebo-controlled trials: potential limitations to trial validity. Clinical Trials. 2010;7(3):246–255. doi: 10.1177/1740774510367916. [DOI] [PubMed] [Google Scholar]
- Crow R, Gage H, Hampson S, Hart J, Kimber A, Thomas H. The role of expectancies in the placebo effect and their use in the delivery of health care: a systematic review. Health Technol Assess. 1999;3(3):1–96. [PubMed] [Google Scholar]
- Dawkins L, Shahzad FZ, Ahmed SS, Edmonds CJ. Expectation of having consumed caffeine can improve performance and mood. Appetite. 2011;57(3):597–600. doi: 10.1016/j.appet.2011.07.011. [DOI] [PubMed] [Google Scholar]
- Elliman NA, Ash J, Green MW. Pre-existent expectancy effects in the relationship between caffeine and performance. Appetite. 2010;55(2):355–358. doi: 10.1016/j.appet.2010.03.016. [DOI] [PubMed] [Google Scholar]
- Fine BJ, Kobrick JL, Lieberman HR, Riley RH, Marlowe B, Tharion WJ. Effects of caffeine or diphenhydramine on visual vigilance. Psychopharmacology (Berl) 1994;114:233–238. doi: 10.1007/BF02244842. [DOI] [PubMed] [Google Scholar]
- Hernan MA, Robins JM. Estimating causal effects from epidemiological data. J Epidemiol Community Health. 2006;60(7):578–586. doi: 10.1136/jech.2004.029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe MM, Rosenbaum PR. Invited commentary: propensity scores. Am J Epidemiol. 1999;150(4):327–333. doi: 10.1093/oxfordjournals.aje.a010011. [DOI] [PubMed] [Google Scholar]
- Junod SW. FDA and Clinical Drug Trials: A Short History. In: Davies M, Kerimani F, editors. A Quick Guide to Clinical Trials. Washington: Bioplan Inc.; 2008. [Google Scholar]
- Kelemen WL, Kaighobadi F. Expectancy and pharmacology influence the subjective effects of nicotine in a balanced-placebo design. Exp Clin Psychopharmacol. 2007;15(1):93–101. doi: 10.1037/1064-1297.15.1.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman HR, Coffey BP, Kobrick J. A vigilance task sensitive to the effects of stimulants, hypnotics and environmental stress-the Scanning Visual Vigilance test. Behav Res Meth Instr. 1998;30:416–422. [Google Scholar]
- Lieberman HR, Tharion WJ, Shukitt-Hale B, Speckman KL, Tulley R. Effects of caffeine, sleep loss and stress on cognitive performance and mood during US Navy SEAL training. Psychopharmacology (Berl) 2002;164:250–261. doi: 10.1007/s00213-002-1217-9. [DOI] [PubMed] [Google Scholar]
- Liem DG, Miremadi F, Zandstra EH, Keast RS. Health labelling can influence taste perception and use of table salt for reduced-sodium products. Public Health Nutr. 2012;15(12):2340–2347. doi: 10.1017/S136898001200064X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malani A. Identifying Placebo Effects with Data from Clinical Trials. Journal of Political Economy. 2006;114(2):236–256. [Google Scholar]
- McNair DM, Lorr M, Droppleman LF. Profile of Mood States Manual. San Diego: Educational and Industrial Testing Service; 1971. [Google Scholar]
- Metrik J, Kahler CW, Reynolds B, McGeary JE, Monti PM, Haney M, Rohsenow DJ. Balanced placebo design with marijuana: pharmacological and expectancy effects on impulsivity and risk taking. Psychopharmacology (Berl) 2012;223(4):489–499. doi: 10.1007/s00213-012-2740-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Onishi K. Placebo and Belief Effects: Optimal Design for Randomized Trials. 2010 Retrieved from http://faculty.wcas.northwestern.edu/~sro850/BeliefEffects.pdf.
- Papakostas GI, Fava M. Does the probability of receiving placebo influence clinical trial outcome? A meta-regression of double-blind, randomized clinical trials in MDD. Eur Neuropsychopharmacol. 2009;19(1):34–40. doi: 10.1016/j.euroneuro.2008.08.009. [DOI] [PubMed] [Google Scholar]
- Rogosa D. Comparing Nonparallel Regression Lines. Psychological Bulletin. 1980;88(2):307–321. [Google Scholar]
- Rosenbaum PR. Covariance Adjustment in Randomized Experiments and Observational Studies. Stat Sci. 2002;17(3):286–327. [Google Scholar]
- Rosenbaum PR, Rubin DB. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- Rubin DB. Assignment to Treatment Group on the Basis of a Covariate. Journal of Educational Statistics. 1977;2(1):1–26. [Google Scholar]
- Rubin DB. Estimating causal effects from large data sets using propensity scores. Ann Intern Med. 1997;127(8):757–763. doi: 10.7326/0003-4819-127-8_part_2-199710151-00064. [DOI] [PubMed] [Google Scholar]
- Schochet PZ, Chiang H. Estimation and Identification of the Complier Average Causal Effect Parameter in Education RCTs. Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education; 2009. [Google Scholar]
- Tedeschini E, Fava M, Goodness TM, Papakostas GI. Relationship between probability of receiving placebo and probability of prematurely discontinuing treatment in double-blind, randomized clinical trials for MDD: a meta-analysis. Eur Neuropsychopharmacol. 2010;20(8):562–567. doi: 10.1016/j.euroneuro.2010.02.004. [DOI] [PubMed] [Google Scholar]
- U.S. Food and Drug Admisistration. Guidance for Industry: Frequently Asked Questions About GRAS. 2004 4/14/2015. Retrieved from http://www.fda.gov/Food/GuidanceRegulation/GuidanceDocumentsRegulatoryInformation/IngredientsAdditivesGRASPackaging/ucm061846.htm.
- U.S. Food and Drug Admisistration. Code of Federal Regulations Title 21. 2014 8/21/2015. Retrieved from http://www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfcfr/CFRSearch.cfm?CFRPart=314&showFR=1&subpartNode=21:5.0.1.1.4.2.
- Wansink B, Payne CR, North J. Fine as North Dakota wine: sensory expectations and the intake of companion foods. Physiology & behavior. 2007;90(5):712–716. doi: 10.1016/j.physbeh.2006.12.010. [DOI] [PubMed] [Google Scholar]
- Waring DR. The antidepressant debate and the balanced placebo design: An ethical analysis. International Journal of Law and Psychiatry. 2008;31:453–462. doi: 10.1016/j.ijlp.2008.09.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


