Cardiovascular Event Prediction by Machine Learning: The Multi-Ethnic Study of Atherosclerosis

Abstract

Rationale

Machine learning may be useful to characterize cardiovascular risk, predict outcomes and identify biomarkers in population studies.

Objective

To test the ability of random survival forests (RF), a machine learning technique, to predict six cardiovascular outcomes in comparison to standard cardiovascular risk scores.

Methods and Results

We included participants from the Multi-Ethnic Study of Atherosclerosis (MESA). Baseline measurements were used to predict cardiovascular outcomes over 12 years of follow-up. MESA was designed to study progression of subclinical disease to cardiovascular events where participants were initially free of CV disease. All 6814 participants from MESA, aged 45 to 84 years, from 4 ethnicities, and 6 centers across USA were included. 735 variables from imaging and non-invasive tests, questionnaires and biomarker panels were obtained. We used the RF technique to identify the top 20 predictors of each outcome. Imaging, electrocardiography and serum biomarkers featured heavily on the top-20 lists as opposed to traditional CV risk factors. Age was the most important predictor for all-cause mortality. Fasting glucose levels and carotid ultrasonography measures were important predictors of stroke. Coronary artery calcium score was the most important predictor of coronary heart disease and all atherosclerotic cardiovascular disease combined outcomes. Left ventricular structure and function, and cardiac troponin-T were among the top predictors for incident heart failure. Creatinine, age and ankle brachial index were among the top predictors of atrial fibrillation. Tissue necrosis factor-α and interleukin-2 soluble receptors, and N-terminal pro-Brain Natriuretic Peptide levels were important across all outcomes. The RF technique performed better than established risk scores with increased prediction accuracy (decreased Brier score by 10–25%).

Conclusions

Machine learning in conjunction with deep phenotyping improve prediction accuracy in cardiovascular event prediction in an initially asymptomatic population. These methods may lead to greater insights regarding subclinical disease markers without apriori assumptions of causality.

Clinical Trial Registration

Multi-Ethnic Study of Atherosclerosis (MESA) http://mesa-nhlbi.org/.

ClinicalTrials.gov Identifier

NCT00005487

INTRODUCTION

Event prediction has been the cornerstone of cardiovascular epidemiology as exemplified by the Framingham study and other prospective studies that function as pillars for much of what comprises current cardiovascular medicine.¹ A fundamental goal of such efforts has been event prediction over relatively long periods of time such as ten years or a lifetime. These efforts have allowed us to characterize sub-clinical disease processes and target key risk factors for modification (e.g. smoking cessation, statin therapy, blood pressure control).² Epidemiological studies used to derive such predictive models frequently contain hundreds or thousands of variables. It is in this context that machine learning methods might be useful as a means to identify the best predictors of outcomes from among millions of phenotypic data points.

The Cox-PHM is often limited for data mining purposes due to correlation between variables, nonlinearity of variables (including potential complex interactions among them), as well as the possibility of over-fitting. On the other hand, machine learning methods, such as Random Survival Forests (RF), use a non-parametric decision tree approach to overcome these issues.³ The purpose of this study was to (a) compare machine learning approaches to Cox-PHM and traditional risk scores for cardiovascular event prediction; and (b) identify the important predictors for each of six cardiovascular clinical outcomes in a large epidemiologic study.

METHODS

The design of the MESA study have been described previously.⁴ Briefly, MESA is a prospective, population-based observational cohort study of 6814 men and women representing four racial/ethnic groups, aged 45–84 years and free of clinical cardiovascular disease at enrollment. As part of the baseline examination (2000–2002), study participants were recruited at six field centers in the United States. Institutional review boards of all field centers approved the study protocol and all participants gave informed consent. Information regarding assessment of markers within MESA has been described previously,⁴ a detailed description is provided in the supplement and a list of markers is shown in Table 1. We included markers from questionnaires, demographics, traditional risk factors, anthropometry, medication use, biochemistry, MRI of the heart and aorta, coronary computed tomography, carotid ultrasound, ECG exams, and ABI.

Table 1.

A list of the markers that were used for prediction in this study.

Traditional Risk Factors, Demographics, Anthropometry, Site

Age, gender, race, body mass index, body surface area, waist-to-hip ratio, systolic blood pressure, diastolic blood pressure, pulse pressure, diabetes, smoking status, pack years, high density lipoprotein cholesterol, low density lipoprotein cholesterol, total cholesterol, triglycerides, heart rate, creatinine, site, waist circumference, Hip circumference, fasting glucose

Medication use

All hypertension, Angiotensin Converting Enzyme, Angiotensin-II Receptor Blockers, lipid-control, statins, beta-blockers, calcium channel blockers

Atherosclerotic markers – computed tomography, carotid ultrasonography

Coronary artery calcium score, ankle-brachial index, common and internal carotid artery intima media thickness, maximum carotid stenosis

Questionnaire

Family history of heart attacks, Alcohol use, Number of drinks per week, emphysema, asthma, arthritis, Cancer, liver disease, education level, economic status/income, exercise metabolic equivalents

Magnetic Resonance Imaging (MRI) markers

Left ventricular (LV) mass, LV End-diastolic volume, LV End-systolic volume, LV Ejection fraction, LV mass-volume ratio, LV stroke volume, LV sphericity index at end-diastole and end-systole, LV cardiac output, LV end-diastolic wall thickness, LV end-systolic wall thickness, ascending aortic distensibility, descending aortic distensibility, pulse wave velocity, maximum ascending aortic area, maximum descending aortic area, aortic arch distance, Maximum left atrial (LA) volume, Minimum LA volume, Maximum LA strain, Total LA ejection fraction, Passive LA ejection fraction, Active LA ejection fraction, Right ventricular (RV) mass, RV End-diastolic volume, RV End-systolic volume, RV Ejection fraction, RV stroke volume.

Lab Biomarkers

Interleukin-2 soluble receptor, Plasmin-Antiplasmin Complex, D-dimer, Factor viii, N-Terminal pro-Brain Natriuretic Peptide, cardiac troponin T, C-reactive protein, Interleukin-6, fibrinogen, homocysteine, Tissue necrosis factor-a soluble receptor

Electrocardiographic (ECG) main

PR duration, QRS duration, QT duration, P-axis, QRS axis, T-axis, Minnesota codes, ECG-LV hypertrophy by cornell voltage and novacode, heart rate variability short-term and overall components, Cornell voltage

ECG all

P, P’, Q, R, R’, S, S’, T and T’ wave duration, amplitude, area, and intrinsicoid; Middle and End of ST segment amplitudes; Amplitude at the point of 60 msecs from J-point; STJ amplitude; total QRS area, balance, deflection balance, intrinsicoid; for each of the leads (AVL, AVR, AVF, I, II, III, V1, V2, V3, V4, V5, V6).

Outcomes

All-cause death, stroke, all cardiovascular disease (CVD), coronary heart disease (CHD), atrial fibrillation (AF) and heart failure (HF) events adjudicated as part of MESA were used as end-points (details in Supplement). A telephone interviewer contacted each participant (or representative) every six–nine months to inquire about all interim hospital admissions, outpatient diagnoses, and deaths. Two physicians reviewed all medical records for independent end-point classification and assignment of event dates. Stroke was defined as rapid onset of a documented focal neurologic deficit (vascular causes) lasting 24 hours or until death, or if < 24 hours, when there was a clinically relevant brain lesion. Criteria for CHD included any of myocardial infarction, resuscitated cardiac arrest, definite angina, probable angina followed by revascularization and CHD death. CVD outcomes represented a composite of CVD death, stroke, and CHD. Criteria for incident HF as an end-point included symptomatic HF diagnosed by a physician for a patient receiving medical treatment for HF and 1) pulmonary edema/congestion, and/or 2) dilated ventricle or poor LV function, or evidence of LV diastolic dysfunction. Criteria for incident AF as an end-point required in-hospital AF diagnosis according to ICD9 codes.

Statistical analysis

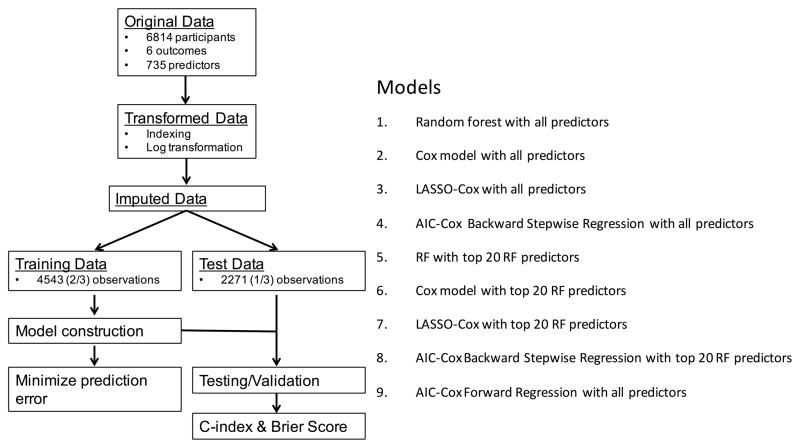
Figure 1 shows the statistical analysis procedures followed in this study. Data transformation, indexing and imputation (details in Supplement) was performed as necessary to generate data points to predict six outcomes over the follow-up period. 66·6% of the dataset was randomly selected from the overall group of participants for training; the remaining 33·3% were used for testing/validation. The training dataset was used for model construction using different approaches and optimized to reduce prediction error. These models were then tried on the test dataset to examine model performance and identify the best predictors.

Figure 1. A flowchart describing the general framework of the study.

Models were built using the training dataset, and the test dataset was used for computing the C-index and the Brier Score shown in Table 4.

Models tested

We tested nine different models in our analysis. The first model used the random survival forest (RF) algorithm on all available variables.³ RF is an ensemble tree method for analysis of right-censored data. Details of the RF implementation are provided in the supplement. In short, trees are grown by binary recursive splitting of data. At each split, a candidate variable that maximizes the difference in cumulative hazard between the daughter nodes (and the cut-off that identifies this maximum difference) is chosen. The splitting stops at the terminal nodes when the data at hand can no longer be split such that each terminal node has at least one unique outcome. For each tree, the cumulative hazard rate of a case is determined based on the terminal node that contains it. An ensemble hazard function (and survival probability) is estimated by averaging over all trees in a forest.

The Akaike Information Criterion⁵ for Cox regression with backward stepwise (AIC-BW Cox) elimination and the AIC-Cox with forward stepwise (AIC-FW Cox) regression, as well as the least absolute shrinkage and selection operator for Cox regression (LASSO-Cox), were tested in addition to the Cox-PHM. LASSSO-Cox minimizes the log partial likelihood subject to the sum of the absolute values of the parameters being bounded by a constant. It shrinks coefficients and produces some coefficients that are zero, allowing efficient variable selection.⁶

While RF can be used instead of Cox regression analysis for risk prediction, it can also be used as an efficient variable selection technique. For variable selection using RF, the variables were ranked by the mean of the minimal depth of the maximal subtree (highest point in the tree of a variable) over the entire forest (averaged over 1000 trees). Variables appearing higher on the tree have a higher rank. The top-20 ranked variables were then used again with RF, AIC-FWCox, AIC-BW-Cox, LASSO-Cox and Cox-PHM models.

Performance evaluation

We assessed the performance of each prediction model to discriminate outcomes on the test dataset using Harrell’s concordance index (C-index),⁷ and the accuracy of prediction (mean squared distance between the predicted probabilities and actual outcomes) using the Brier score (BS).⁸ Higher C-index and lower BS indicate better prediction performance. C-index and BS for nested models generated using subsets of predictors (chosen based on increasing variable importance) were calculated to assess problems of overfitting. We also compared the results of RF techniques to published risk scores.^9–11 When the models failed to converge, no results were reported and this was considered the worst possible outcome.

Data analysis was performed using R software, using publically available libraries for Cox-PHM,¹² Lasso-Cox,⁶ AIC-Cox,⁵ and RF methods.¹³

RESULTS

A total of 6814 participants were included. The average age was 62 years with 53% women, 28% African-American, 38% Caucasian, 12% Chinese-American and 22% Hispanic. 13% of the participants were diabetic, 45% classified as hypertensive based on JNC VI criteria, and 50% were current or former smokers. Over a median of 11·2 years (IQR :10·6 – 11·7), MESA identified 831 all-cause deaths, 710 cardiovascular events (CVD) including 498 CHD events among which 229 were non-fatal myocardial infarctions, 200 strokes, 259 cases of incident HF and 317 incident AF events (Table 2).

Table 2.

General characteristics of the MESA sample at baseline, 2000–2002.

Variable	Value
Age (in years)	62·15 (10·23)
Gender (% female)	52·85
Race
% African-American	27·78
% Caucasian	38·48
% Chinese-American	11·78
% Hispanic	21·95
Body Mass index (kg/m2)	28·34 (5·48)
Diabetes
% Impaired Fasting Glucose	13·83
% Treated	10·01
% Untreated	2·64
Systolic Blood Pressure (mm Hg))	126·59 (21·48)
Use of Hypertension Medication (%)	37·23
Heart Rate (bpm)	63·13 (9·66)
Smoking status
% current	13·06
% former	36·62
Total Cholesterol (mg/dL)	194·16 (35·73)
HDL cholesterol (mg/dL)	50·96 (14·83)
Lipid Medication use (%)	16·15
Heart Failure, n (%)	259 (3·8)
All Cardiovascular Disease, n (%)	710 (10·4)
Coronary Heart Disease, n (%)	498 (7·3)
Atrial Fibrillation, n (%)	317 (4·7)
All-cause Death, n (%)	831 (12·2)
Stroke, n (%)	200 (2·9)

Predictors by outcomes

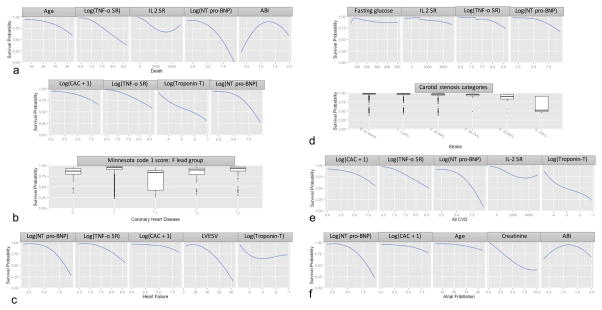
Table 3 shows the top-20 predictors using RF for each of the outcomes ordered by the minimal depth of maximal subtree. These were the predictors used for the RF-20, Cox-20, Lasso-20, and AIC-20 models. Figure 2 shows Lowess plots of the 12-year survival probability calculated from the RF method over the range of values for the top-5 variables.

Table 3.

The top-20 ranked variables by the variable importance from the random survival forest method for each of the outcomes of interest. The relative variable importance (RVI) of each variable can be assessed using the normalized minimal depth of the maximal subtree (which can be seen in Figure 3). The normalized RVI values vary from 0 (most important) to 1 (least important).

Rank	Death	RVI	Stroke	RVI
1	Age	0·00	Fasting glucose	0·00
2	Tissue Necrosis Factor-α soluble receptor	0·07	Interleukin-2 soluble receptor	0·09
3	Interleukin-2 soluble receptor	0·09	Maximum carotid stenosis	0·11
4	N-Terminal pro-Brain Natriuretic Peptide	0·16	Tissue Necrosis Factor-α soluble receptor	0·13
5	Ankle-Brachial Index	0·21	N-Terminal pro-Brain Natriuretic Peptide	0·16
6	Coronary Artery Calcium score	0·25	Internal carotid intima media thickness	0·18
7	Common carotid intima media thickness	0·26	Systolic blood pressure	0·24
8	Internal carotid intima media thickness	0·32	Pulse pressure	0·28
9	Descending aortic distensibility	0·33	Descending aortic distensibility	0·32
10	Plasmin-Antiplasmin Complex	0·35	Ankle-Brachial Index	0·32
11	Cardiac Troponin-T	0·37	Coronary Artery Calcium score	0·32
12	D-dimer	0·37	R Amplitude in Lead V2	0·32
13	Maximum ascending aortic area	0·38	R Amplitude in Lead V6	0·35
14	Ascending aortic distensibility	0·39	Minnesota code 1 score: F lead group	0·35
15	Homocysteine	0·39	Ascending aortic distensibility	0·37
16	Thoracic aorta arch length	0·41	Age	0·38
17	R Amplitude in Lead V	0·41	Cardiac output	0·39
18	Interleukin-6	0·41	JT Duration	0·40
19	Economic status/income	0·42	LV mass-volume ratio	0·40
20	Maximum descending aortic area	0·42	End-diastolic septal anterior wall thickness	0·41

Rank	Coronary Heart Disease	RVI	All CVD	RVI
1	Coronary Artery Calcium score	0·00	Coronary Artery Calcium score	0·00
2	Tissue Necrosis Factor-α soluble receptor	0·28	Tissue Necrosis Factor-α soluble receptor	0·24
3	Cardiac Troponin-T	0·31	N-Terminal pro-Brain Natriuretic Peptide	0·25
4	N-Terminal pro-Brain Natriuretic Peptide	0·35	Interleukin-2 soluble receptor	0·28
5	Minnesota code 1 score: F lead group	0·36	Cardiac Troponin-T	0·35
6	Ankle-Brachial Index	0·37	Ankle-Brachial Index	0·40
7	Common carotid intima media thickness	0·44	Common carotid intima media thickness	0·41
8	Interleukin-2 soluble receptor	0·48	Pulse pressure	0·41
9	Pack years of smoking	0·50	Maximum ascending aortic area	0·42
10	Internal carotid intima media thickness	0·50	Internal carotid intima media thickness	0·42
11	Factor VIII	0·50	Age	0·42
12	End-systolic mid-ventricular septal wall thickness	0·52	R Amplitude in Lead V4	0·44
13	Maximum descending aortic area	0·53	Systolic blood pressure	0·44
14	End-systolic mid-ventricular antero-septal wall thickness	0·54	Factor VIII	0·46
15	Maximum ascending aortic area	0·54	Ascending aortic distensibility	0·47
16	S Amplitude in Lead AVR	0·55	Waist-to-hip ratio	0·47
17	End-diastolic basal septal wall thickness	0·55	Minnesota code 1 score: F lead group	0·48
18	Left ventricular ejection fraction	0·56	End-diastolic basal septal wall thickness	0·48
19	Pulse pressure	0·56	Plasmin-Antiplasmin Complex	0·49
20	Descending aortic distensibility	0·56	End-diastolic basal inferior wall thickness	0·49

Rank	Heart Failure	RVI	Atrial Fibrillation	RVI
1	N-Terminal pro-Brain Natriuretic Peptide	0·00	N-Terminal pro-Brain Natriuretic Peptide	0·00
2	Tissue Necrosis Factor-α soluble receptor	0·07	Coronary Artery Calcium score	0·23
3	Coronary Artery Calcium score	0·07	Age	0·27
4	End-systolic left ventricular volume	0·10	Creatinine	0·31
5	Cardiac Troponin-T	0·20	Ankle-Brachial Index	0·36
6	End-diastolic left ventricular volume	0·21	Interleukin-2 soluble receptor	0·39
7	Left ventricular ejection fraction	0·24	Tissue Necrosis Factor-α soluble receptor	0·41
8	QTC INTERVAL	0·32	Common carotid intima media thickness	0·45
9	QT Index	0·34	R Amplitude in Lead V4	0·53
10	Interleukin-2 soluble receptor	0·36	STJ Amplitude in Lead V5	0·53
11	Waist-to-hip ratio	0·38	Internal carotid intima media thickness	0·55
12	Ankle-Brachial Index	0·42	Pulse pressure	0·55
13	PR INTERVAL	0·45	Estimate of overall heart rate variability	0·56
14	Creatinine	0·45	End-systolic basal lateral wall thickness	0·56
15	Pulse pressure	0·46	End-systolic mid-ventricular anterior wall thickness	0·56
16	End-diastolic left ventricular mass	0·47	Heart Rate	0·57
17	Estimate of overall heart rate variability	0·51	QRS AXIS (degrees)	0·57
18	T Amplitude in Lead V1	0·51	Cardiac Troponin-T	0·57
19	Minnesota code 1 score: V lead group	0·51	Total left atrial ejection fraction	0·57
20	Minnesota code 1 score: F lead group	0·52	Pack-years of smoking	0·58

Figure 2. Plots showing Lowess curves (for continuous variables) and box plots (for categorical variables) of the survival probability vs variable values for the top-5 predictors for each of the outcomes at 12 years.

The y-axis represents survival probability calculated from the RF-20 algorithm (range: 0 to 1). The x-axis spans the range (or categories) of the variable of interest. Abbreviations: NT pro-BNP = N-terminal pro-Brain Natriuretic peptide, TNF-α SR = tissue necrosis factor- α soluble receptor, IL2 SR = interleukin-2 soluble receptor, CAC = coronary artery calcium score, LVESV = left ventricle end-systolic volume. Units for each variable: NT pro-BNP – pg/ml, TNF-α SR – pg/ml, IL2 SR – pg/ml, CAC – Agatston’s units, cardiac troponin T – ng/ml, ABI – ratio, age – years, fasting glucose – mg/dl.

Increasing age, perhaps reflecting duration of risk exposure, was the most important predictor of all-cause death. Inflammation and immune response measured by increased interleukin-6, fibrinogen, homocysteine, TNF-α SR and IL2 SR levels; and abnormal hemostasis measured by increased D-Dimer, plasmin-antiplasmin complex and factor VIII levels were among the top 20 markers of all-cause death underlining the role of inflammation and thrombosis as common pathways for chronic diseases leading to death. Similarly, cardiac stress measured by increased NT pro-BNP levels, and myocyte damage by increased cardiac troponin T levels were among the top predictive markers of death reflecting the role of cardiac failure on mortality. In addition to biomarkers that featured so prominently, low and high values of ABI, increased carotid IMT, increased CAC score, aortic dimension and distensibility also showed lower survival probability, indicating the importance of atherosclerosis and vascular abnormalities to mortality in the general population. Importantly also, economic status/income was among the top 20 markers of all-cause death in MESA highlighting the potential power of inequality as a mortality risk factor even when one considers the theoretical distance between such a risk factor and death in the accepted causation chain for most chronic degenerative diseases.

Increased fasting glucose levels were the most important risk factor for stroke, while high blood pressure, a known stroke risk, and age also featured in the top-20 list. Measures of atherosclerosis (with carotid stenosis being most important) and inflammation were also top-5 predictors of stroke.

Expectedly, a composite of atherosclerosis measures (low and high ABI, increased carotid IMT, decreased aortic distensibility) were among the most important predictors of CHD which represents a subset of CVD events, with CAC being by far the most important, reflecting the specific influence of coronary atherosclerosis. Increased LV regional wall thickness (myocardial hypertrophy), decreased ejection fraction (myocardial function) and increased aortic cross-sectional area (aortic dilatation), as well as biomarkers of abnormal hemostasis, inflammation, myocardial stress and damage featured among the other top predictors of CHD. Importantly, ECG LV hypertrophy as well as major Q-wave and repolarization abnormalities were markers of CHD and CVD events in MESA. Additionally, among traditional risk factors, pack years of smoking and pulse pressure were among the top predictors for CHD, while systolic blood pressure and age were among the top predictors for CVD.

For incident HF as the endpoint, cardiac chamber stress (increased LV volume, and increased NT-proBNP levels), and decreased LV function from MRI were the most important markers. LV hypertrophy on ECG, a lengthened QT interval indicating increased risk for tachyarrythmias, increased creatinine levels, increased vascular stiffness, atherosclerosis as measured by CAC and ABI, and inflammation were also among the top predictors for HF. Increased pulse pressure and increased waist-to-hip ratio were also among the top risk factors for incident HF reflecting the role of obesity and hypertension on incident HF development.

For incident AF as the endpoint, inflammation, higher levels of creatinine, atherosclerosis (CAC and ABI), and repolarization abnormalities were the most important markers. Decreased LA function, and increased age and pulse pressure were also among the top risk factors for AF development.

Predictors across outcomes

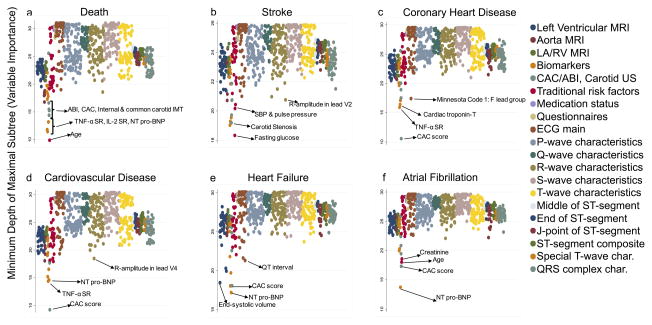
In general, variables from imaging markers, ABI, and serum biomarkers were of intermediate-to-high prediction importance while questionnaires and medication exposures were of lower importance. Components of ECG related to ST segments were of intermediate importance while other ECG indices ranged from low to intermediate prediction importance. As illustrated in Online Figure III, just the first five-six variables listed by the RF algorithm produced C-indices greater than 0·75 for CVD, CHD, incident HF and AF prediction reflecting the importance of NT-proBNP (HF and AF) and CAC (CHD and CVD). Prediction of all-cause mortality and stroke with a C-index greater than 0·75 required a larger group of variables.

Comparison of prediction models

Table 4 shows the C-index and the Brier score (BS) for the eight tested models using the test datasets. The standard Cox, Lasso-Cox and AIC-Cox methods failed to converge when all the 735 variables were included, and hence BS and C-index could not be calculated. As shown in Online Figure III, using the nested models, less than 20 variables were necessary to obtain a stable and high C-index for the RF method. Addition of more variables into the model beyond 30 resulted in minimal improvement of the C-index, if any. Figure 3 shows variable importance measured using the minimum depth of the maximal subtree, for each of the 735 variables used in analysis. Lower values correspond to greater prediction importance.

Table 4.

The number of variables and the performance (Concordance-index and Brier score) for each of the models tested as well as for the risk scores at the end of follow-up.

	DTH	STRK	CHD	CVD	HF	AF
Number of variables
RSF with all covariates	735	735	735	735	735	735
RSF with top 20 covariates	20	20	20	20	20	20
AIC-Cox with Forward Selection	13	9	5	6	5	6
Cox with top 20 RSF covariates	20	20	20	20	20	20
Lasso Cox with top 20 RSF covariates	19	17	19	19	10	15
AIC Cox Backward Selection with top 20 RSF covariates	16	12	13	13	11	12
Concordance-index @ 12 years
RSF with all covariates	0·86	0·77	0·81	0·81	0·84	0·82
RSF with top 20 covariates	0·84	0·75	0·80	0·80	0·84	0·75
AIC-Cox with Forward Selection	0·78	0·70	0·74	0·74	0·78	0·79
Cox with top 20 RSF covariates	0·80	0·66	0·75	0·76	0·81	0·78
Lasso Cox with top 20 RSF covariates	0·80	0·67	0·75	0·76	0·82	0·78
AIC Cox Backward Selection with top 20 RSF covariates	0·80	0·68	0·75	0·76	0·80	0·78
Brier Score @ 12 years
RSF with all covariates	0·083	0·031	0·067	0·083	0·035	0·039
RSF with top 20 covariates	0·076	0·030	0·065	0·079	0·033	0·038
AIC-Cox with Forward Selection	0·088	0·032	0·069	0·087	0·035	0·045
Cox with top 20 RSF covariates	0·086	0·031	0·070	0·087	0·035	0·037
Lasso Cox with top 20 RSF covariates	0·086	0·031	0·070	0·087	0·033	0·038
AIC Cox Backward Selection with top 20 RSF covariates	0·086	0·031	0·069	0·087	0·035	0·038

HF: heart failure, CVD: all cardiovascular disease, CHD: coronary heart disease, AF: atrial fibrillation, DTH: death, STRK: stroke, RSF: random survival forest, LASSO: least absolute shrinkage and selection operator, AIC: Akaike Information Criteria.

Figure 3. Plots showing the variable importance for each of the 735 variables used in analysis.

The color of the dots represents the category or type of measurement. The legend on the right provides the phenotype category ordered from left-to-right on the individual plots. The variable importance is measured using the minimum depth of the maximal subtree, with lower values representing greater importance of corresponding variable. Abbreviations: NT pro-BNP = N-terminal pro-Brain Natriuretic peptide, TNF-α SR = tissue necrosis factor- α soluble receptor, IL2 SR = interleukin-2 soluble receptor, CAC = coronary artery calcium score, ABI = ankle-brachial index, IMT = intima media thickness, SBP = systolic blood pressure.

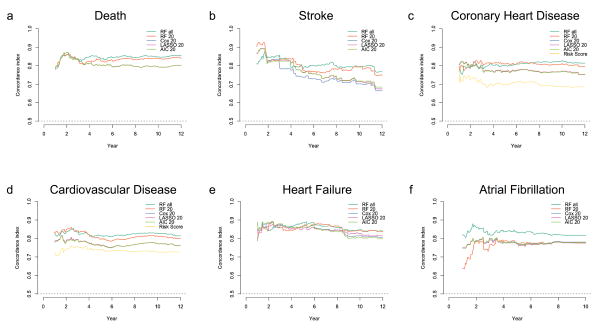
For all outcomes of interest, the RF model with all 735 covariates showed a very high C-index and low BS. The RF-20 model was comparable and even outperformed the RF model with all covariates in some cases. Both the RF models outperformed the AIC-FWCox across all endpoints with higher C-index and lower BS. The use of RF for variable selection with top 20 (RF-20) covariates and subsequent application of Lasso-Cox and AIC-BWCox resulted in fewer variables selected into the final models for most of the outcomes. The C-indices from these standard Cox, Lasso-Cox and AIC-BWCox models were high and the BS low in general, and very similar to that of the RF-20 model. Figures 4a–4f show the C-index values over time for all the models (models that did not converge are not shown). In general, the C-index values were higher for prediction of short-term as compared to long-term events.

Figure 4. The concordance index for each of the models tested over time.

The full models (models with all 735 variables) did not converge for the LASSO-Cox, AIC-Cox and the Cox PHM models, and hence are not shown here. The prediction ability of conventional risk scores for heart failure (MESA HF risk score), cardiovascular disease (AHA/ASCVD risk score) and coronary heart disease (Framingham CHD risk score) are also shown (yellow curve). In general, the C-index for all variables decreased over time.

The models from machine learning that included biomarkers and measures of sub-clinical disease were, as expected, better than the AHA/ASCVD (C-index: 0·73, BS: 0·11) and the Framingham (C-index: 0·73, BS: 0·089) risk scores for incident CVD prediction (see Table 4). The performance of the RF-20 model for incident CHD prediction was better than the Framingham CHD risk score (C-index: 0·69, BS: 0·072) with a higher C-index and lower BS.

When comparing the population-specific risk scores, the RSF-20 model from machine learning that included biomarkers and measures of sub-clinical disease was better than the MESA CHD Risk score (C-index: 0·79, BS: 0·074) for incident CHD prediction¹⁴ (see Table 4). The performance of the RF-20 model for incident CHF prediction was better than the MESA-HF¹⁵ risk score (C-index: 0·80, BS: 0·038) with a higher C-index and lower BS.

DISCUSSION

The results of this study suggest that machine learning methods are well-suited for meaningful risk prediction in extensively phenotyped large-scale epidemiological studies. The RF based method of risk prediction provided better event prediction over standard risk scores. RF based methods of variable selection followed by Cox regression methods also allowed for improved prediction of outcomes, without problems of overfitting and non-convergence while accounting for nonlinearities. The results also suggest the importance of deep phenotyping using subclinical markers defined by imaging, electrocardiographic and blood biochemistry, as revealed by their prominent presence on the lists of top-20 predictors, for cardiovascular disease event prediction.

This work is unique by demonstrating patterns of predictors that vary for specific disease outcomes. While age, inflammation, cardiac stress and vascular disease dominate the prediction of death in the MESA study, impaired glucose metabolism and hypertension lead in the prediction of stroke and sub-clinical atherosclerosis markers occupy center stage in forecasting overall cardiovascular events be they limited to the heart (CHD) or involving the systemic circulation. For incident heart failure and atrial fibrillation, a combination of markers reflecting increased cardiac chamber stress coupled with electric dysregulation are at the forefront of potential outcome determinants.

Another important pattern of findings from this investigation was the underrepresentation of certain traditional CV risk factors such as gender, race/ethnicity, and therapy exposure (medication use) among the top predictors of disease outcome. Important exceptions to such trend were the presence of socioeconomic status as one of the top predictors of death and the role of hypertension as a top predictor of stroke, CVD, CHD as well as incident HF and AF. The lower than expected representation of traditional risk factors may stem from the fact that because fundamental to the genesis, maintenance and progression of CV diseases, they are intrinsic components of other phenotypes, particularly sub-clinical phenotypes that are more distal to disease initiation but closer to adverse outcomes. Even though some of these risk factors did not feature in the top 20, they remain crucial to medical practice, particularly, disease prevention.

Machine learning and deep phenotyping

The application and use of machine learning tools for CVD are still controversial.¹⁰ This is so, even as there has been an increasing use of imaging tests, ECG exams and lab tests in recent years.¹⁶ In most cases, even when multiple markers are acquired, not all are used for diagnosis.¹⁷ For example, regional function measures from imaging, large portions of biomarker panels or ECG signals are frequently ignored by many clinicians. As we move into the age of precision medicine, understanding the utility of phenotypic data and methods to analyze already acquired information is of paramount importance. Machine learning methods, and RF particularly, have been used before for CVD risk prediction.^18–27 In this study, we were able to use deeply phenotyped data to predict outcomes in a population study that accounts for time to event.²⁸ The added advantage is that these methods can be extended and refined, regularly, with new data. They also account for non-linearity in relationships (Figure 2), for example, both high and low values of ABI (as previously shown) were predictive of incidence of CVD.

This work also confirms the influence of certain markers and risk factors on CV events. From this analysis, the importance of markers, heretofore underestimated, such as TNF-α SR and IL2 SR, come to fore with machine learning. In this regard, machine learning opens the possibility of discovering new relationships that are not hypothesis driven and without prior assumptions. Identifying effective disease markers and discovering unknown mechanisms may be of benefit for effective screening strategies, and suggest specific targets for risk reduction. Yet another advantage of this technique is the ability to recognize the best predictors within a domain (questionnaires, imaging, etc), as well as their importance with respect to predictors from other domains. This approach to biomarker identification may be of particular benefit in intermediate risk groups where underlying subclinical risk is not apparent in traditional CV risk factors.

Methodological considerations

In this study, We used the minimum depth of the maximal subtree as the main measure of variable importance because of prior research that showed inherent advantages to using this over permutation testing²⁹. While there are other methods to do the same, the change in Gini index, for example, they may not utilize survival data and hence may not be the best method in the case of survival analysis as ours. However, we provide the top-10 variables from both the Gini index (12-year cut-off) and permutation testing in the Supplement.

While deep phenotyping might help in biomarker discovery, it is seen from Online Figure III, that far fewer than the measured variables are necessary for obtaining a high C-index. To this end, RF methods may help in identifying important variables. We have shown the top-20 variables, as well as the C-index and BS using just the top-20 models. It is plausible that the optimal number of variables is less than 20. However, formal methods need to be developed with consideration to cost, appropriateness, ease of access, and reproducibility of measurements for a more judicious approach to variable selection for event prediction.

MESA, designed to study progression of subclinical disease to manifest symptoms and outcomes, was performed in a middle-aged population free of CV disease at baseline. Therefore, results may not generalize to other study populations. We did not include genetic data; the identification of the phenome-genome interaction and assessment of their combined prediction ability may potentially improve our findings.³⁰ While phenomorphing (longitudinal covariate data) and risk prediction is of interest, it is out of the scope of this study. While this study identifies top predictors as a method of “biomarker discovery”, further work is required including validation in other populations, as the training and test datasets were drawn from within the MESA study population.

Conclusion

In an extensively phenotyped population free of CV disease at baseline, using random forests, we show efficient cardiovascular risk prediction for specific outcomes including death, stroke, CV events, incident heart failure and atrial fibrillation. Inflammation, subclinical atherosclerosis, myocardial damage, and cardiac chamber stress were among the most important predictors across all outcomes. We provide a framework for “big data” applications to obtain meaningful risk prediction, biomarker identification, and generate data-driven hypotheses.

NOVELTY AND SIGNIFICANCE.

What Is Known?

• Machine learning techniques, such as the random survival techniques, may be an effective statistical methodology for handling biomedical data of increased volume, velocity, and variety, under the curse of dimensionality.

• These methods do not require a priori assumptions regarding causality and may thus be suitable for defining the role of novel biomarkers in cardiovascular disease prediction.

What New Information Does This Article Contribute?

• Machine learning methods are better suited for meaningful risk prediction in extensively phenotyped large-scale epidemiological studies than regular Cox proportional Hazards models or risk scores.

• Random survival forests may be an effective machine learning strategy for incident cardiovascular event prediction and risk stratification in large populations with large phenotypic datasets.

There is a lack of studies using machine-learning techniques with deep phenotyping (multiple evaluations of different aspects of a specific disease process) for cardiovascular event prediction. We examined the ability of combining deep phenotyping with machine learning for cardiovascular event prediction in the Multi-Ethnic Study of Atherosclerosis (MESA). The random survival forests based method of risk prediction yielded an entirely unexpected perspective on event prediction of specific outcomes such as death, stroke, cardiovascular events, incident heart failure and atrial fibrillation, with superior predictive power and improved accuracy than established risk scores. The results also suggest the importance of subclinical disease markers determined by imaging, electrocardiography and blood tests, as revealed by their prominent presence on the lists of the top-20 phenotyping predictors for the selected outcomes. This strategy could yield insights about specific use of variables for specific event prediction and guiding strategies to prevent cardiovascular disease outcomes. Potentially, these techniques could be applied retrospectively to analyze large phenotyping datasets for identifying disease mechanisms, and as a means of hypothesis generation, without prior assumptions.

Nonstandard Abbreviations and Acronyms

ABI

ankle-brachial index

AF

atrial fibrillation

AIC

Akaike Information Criterion

CAC

coronary artery calcium score

CHD

coronary heart disease

Cox-PHM

Cox Proportional Hazard regression model

CVD

cardiovascular disease

ECG

electrocardiography

HF

heart failure

IL2 SR

interleukin-2 soluble receptor

IMT

intima media thickness

IQR

interquartile range

JNC

Joint National Committee

LA

left atrium

LASSO

least absolute shrinkage and selection operator

LV

left ventricle

MESA

Multi-Ethnic Study of Atherosclerosis

MRI

magnetic resonance imaging

NT pro-BNP

N-terminal pro-Brain Natriuretic peptide

RF

Random Survival Forests

RV

right ventricle

SBP

systolic blood pressure

TNF-α SR

tissue necrosis factor-α soluble receptor