Estimating the Economic Value of Information for Screening in Disseminating and Targeting Effective School-based Preventive Interventions: An Illustrative Example

Abstract

When candidates for school-based preventive interventions are heterogeneous in their risk of poor outcomes, an intervention’s expected economic net benefits (ENB) may be maximized by targeting candidates for whom the intervention is most likely to yield benefits, such as those at high risk of poor outcomes. Although increasing amounts of information about candidates may facilitate more accurate targeting, collecting information can be costly. We present an illustrative example to show how cost-benefit analysis results from effective intervention demonstrations can help us to assess whether improved targeting accuracy justifies the cost of collecting additional information needed to make this improvement.

The potential value of investment in early interventions is often conveyed in the context of cost-benefit analysis (CBA). In a CBA, the criterion for determining whether an investment is worthwhile is the monetized value of the intervention’s expected beneficial effects minus its costs. This difference is the intervention’s expected net benefit (ENB).

For an intervention aimed at preventing poor outcomes, one factor that may affect the ENB or cost of the intervention is the risk of poor outcomes for each intervention candidate. When candidates are heterogeneous in this risk, an intervention’s ENB may be maximized by targeting candidates for whom the intervention is most likely to yield a benefit, such as those at high risk of poor outcomes (Karoly et al., 1998; Salkever et al., 2008).

In practice, targeting is accomplished by using measures (screening information) that are correlated with the level of expected benefits of the program for each candidate to identify candidates for whom the net benefits of the intervention are expected to be positive. Although many different elements of screening information could be useful for intervention targeting, the additional cost of collecting additional screening information must be factored when deciding how much screening information to use in creating a targeting approach. Consequently, improvements in the ability to accurately target interventions resulting from additional screening information must be weighed against the costs of collecting additional screening information.

Several recent papers have addressed the issue of the value of screening information in the context of intervention programs to prevent adolescent violence. Petras, Chilcoat, Leaf, Ialongo, & Kellam (2004) tested the ability of an instrument for assessing aggressive behavior (TOCA-R), in elementary school grades, to predict later violent behavior of adolescent males. They compared predictions from TOCA-R assessments at 6 different time points in the elementary grades, and found that the earliest assessment (fall of 1^st grade) was the best single time point for minimizing false positives (i.e., individuals who were predicted to have later violent behavior but actually were not subsequently observed to have such behavior), while the next to last assessment (spring of 4^th grade; the last assessment was spring of 5^th grade) was best for minimizing false negatives (i.e., individuals who were predicted to not have later violent behavior but were actually observed to have such behavior). When both types of errors were weighted equally, the assessment in the spring of 3^rd grade was found to be the best single time point predictor. Since the performance of the assessment varied systematically over time, the authors suggested that assessments at multiple time points “promise the highest utility in preventing youth violence” (Petras et al., 2004, p 88).

In a subsequent paper, Petras et al. (2005) used a similar approach and data to test predictions of juvenile court convictions involving violent behavior by adolescent females. In this case, the aggression rating in the spring of 5^th grade was the best single predictor regardless of the relative weights assigned to false positives versus false negatives. The predictive powers of the authors’ models, however, were relatively low, due in part to the much lower rate of violent juvenile court convictions for females (compared to males). The authors also suggested that this reinforces their previous suggestion that predictive models using assessments at multiple time points should be considered.

In follow-up work, Petras et al. (2013) have implemented their suggestion of using TOCA-R assessments at multiple time points. They also extended their definition of the violent behavior dependent variable to include 1) incarceration for a violent offense in young adulthood and 2) “a diagnosis of Antisocial Personality based on the young adult’s self-report of antisocial behavior.” Assessments at six time points were included in their statistical models for males. Assuming equal weights for false positives and false negatives, results indicated more accurate predictions when the first five ratings (fall of 1^st to spring of 4^th grade) were used compared with the results using the single best rating (spring of 5^th grade). Analogous results for females were not presented because three of the six assessments (fall of 1^st grade, spring of 2^nd grade, and spring of 4^th grade) were not significant at the 0.05 two-tailed level in preliminary bivariate logistic regressions. The authors concluded that assessments at multiple time points, prior to 5^th grade, for males were valuable but that “policy makers will need to weigh the burden and costs of repeated screenings against the potential decrease in effectiveness of the intervention if it is delayed.” Petras et al. (2013).

Another recent paper addressed a related situation concerning the use of single vs. multiple sources of screening information during kindergarten and 1^st grade for predicting the occurrence of 5^th grade behavior problems relating to externalizing behavior (Hill, Lochman, Cole, & Greenberg, 2004). This paper separately addressed two issues: 1) the predictive ability of various screening options, and 2) the “utility” of four different decision rules (defined in terms of expected social costs), under one of the screening options, for selecting children for an intervention. The screening options considered were teacher TOCA-R ratings alone vs. TOCA-R plus additional parent ratings from the Child Problem Behavior Scale, and for each of these two options the use of kindergarten ratings only vs. 1^st grade ratings only vs. combined kindergarten and 1^st grade ratings. In terms of predicting 5^th grade outcomes, they concluded that teacher-plus-parent 1^st grade ratings performed about as well as teacher-plus parent ratings for both 1^st grade and kindergarten. They did not, however, contrast the different screening strategies in terms of “utility”.

Finally, there is a substantial amount of literature on the expected value of perfect information (EVPI) in the context of cost-effectiveness and medical decision analyses; for example, Felli & Hazen (1998) and Meltzer (2001). In contrast with the aforementioned studies by Petras et al. (2004, 2005, 2013) and Hill et al. (2004), which focus on risk predictions at an individual level, research on the EVPT has generally addressed the issue of quantifying uncertainty and valuing additional information in decision models.

In the present paper, we extend the argument developed by Petras et al. (2004, 2005, 2013) and Hill et al. (2004) by illustrating an approach to place a dollar value on the added net benefits of additional screening information for targeting. This dollar value can be directly compared with the estimated costs of obtaining such additional screening information, to determine whether or not efforts to obtain this information are economically justified.

Methods

General Framework of Analyst’s Decision Problem for the Hypothetical Program Example

In the program example used below to illustrate our approach, we consider a hypothetical scenario in which a school is planning the implementation of a 6^th grade intervention which has been previously subjected to CBA and which has been shown to be efficacious at preventing: (1) arrest before the age of 16, and (2) adult incarceration. We consider an analyst who is tasked with targeting the intervention to the subset of intervention candidates who, based on screening information, are most likely to maximize the ENB of the intervention. Before the analyst can target the intervention, however, they must decide what specific screening information they will use to accomplish the targeting. This circumstance gives rise to two questions: (1) what set of screening information will result in the most accurate targeting, and (2) is the cost of obtaining this screening information less than the incremental increase in the intervention’s ENB that results from more accurate targeting?

We can describe the decision problem facing the analyst more formally. Let us define the following abbreviations:

• ENB(0) = expected net benefits with no targeting;

• ENB(j) = expected net benefits (excluding consideration of targeting costs) with the jth targeting regime, j = 1, 2, ….., n-1, n (with n possible regimes);

• TC(j) = costs of screening information with the jth targeting regime; and

• ENB*(j) = ENB(j) - TC(j), where ENB*(j) is expected net benefits (including consideration of targeting costs) with the jth targeting regime.

Thus, we can define Ω(j) = ENB*(j)-ENB(0) as representing the net value of the information required to implement targeting regime j relative to not targeting at all. The problem for the analyst is select the one of the n possible targeting regimes that makes ENB*(j), and therefore Ω(j), as large as possible. Of course, if the maximum ENB*(j) is less than ENB(0), then it is better to not target at all.

If for all screening regimes (j=1,…, n), all relevant screening information could be obtained at a nominal cost, TC(j) for any regime j will be approximately equal to zero so that any screening information items that increase ENB would be worthwhile using. This situation might be approximated by schools that routinely collect many relevant information items on all students. If, however, the analyst knows that one or more of the elements of screening information requires a non-trivial investment for measurement (e.g., hiring staff to field an in-person survey to teachers, students, and/or parents), they may wish to compare between ENB when using that costly screening information vs. ENB without use of that information. This note illustrates how this comparison might be carried out.

Specific Analytical Inputs for Our Specific Hypothetical Example

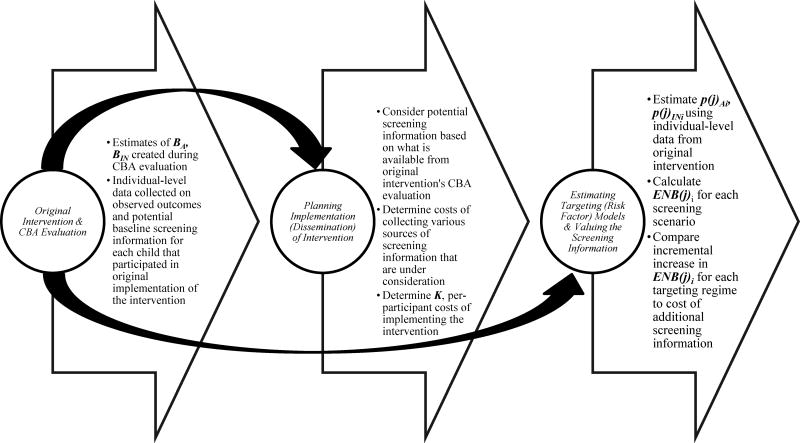
The process of estimating the economic value of screening information, as depicted in Figure 1, originates with several analytical inputs that would be derived from various sources, including the original CBA evaluation of the intervention that the school is seeking to disseminate. Table 1 summarizes these inputs and each is discussed in detail below.

Figure 1.

Process to Estimate the Economic Value of Screening Information

ENB(j)_i = (p(j)_Ai x $910) + (p(j)_INi x $10,577) − $3,561

ENB(j)_i, expected net benefit for participant i for jth targeting regime; p(j)_Ai, estimated risk of arrest before the age of 16 participant i for jth targeting regime; p(j)_INi estimated risk of incarceration as an adult for participant i for jth targeting regime; B_A, the monetized average per-person expected economic benefits of preventing arrest before the age of 16; B_IN, the monetized average per-person expected economic benefits of preventing adult incarceration; K is per-participant cost of implementing the intervention for jth targeting regime

Table 1.

Required Analytical Inputs to Estimate the Economic Value of Screening Information

Analytical Input	Source	Purpose
Costs of collecting various sources of screening information Screening information must have been previously collected for children that participated in the original implementation of the intervention that the school is seeking to disseminate	Assumed to be known for dissemination	For comparison against increases in expected net benefits of the intervention that are realized when using the various sources of screening information for targeting
BA, BIN BA and BIN represent the monetized average per-person expected economic benefits of preventing arrest before the age of 16 and preventing adult incarceration, respectively	Original CBA evaluation of the intervention that the school is seeking to disseminate or economic literature	Estimation of expected net benefit of the intervention for each participant
K The per-participant cost of implementing the intervention	Assumed to be known for dissemination	Estimation of expected net benefit of the intervention for each participant
Individual-level data on observed outcomes and potential baseline screening information for each child that participated in the original implementation of the intervention that the school is seeking to disseminate	Original CBA evaluation of the intervention that the school is seeking to disseminate	To develop regression analyses (targeting models) which relate the screening information to the outcomes and are used to create a participant-level predicted probability of the outcomes
p(j)Ai, p(j)INi p(j)Ai and p(j)INi represent the i’th participant’s estimated risk of arrest before the age of 16 and their estimated risk of adult incarceration from the jth targeting regime, respectively	Targeting models	Estimation of expected net benefit of the intervention for each participant

The inputs required for selecting the best targeting strategy involve the following: (1) a specific menu of targeting options and the corresponding costs of obtaining the screening information for implementing each option; (2) information about the cost of each undesirable outcome which the intervention seeks to prevent; (3) information about the cost of the intervention; (4) information—for each intervention participant—on the probabilities of experiencing each of the undesirable outcomes in the absence of the intervention; and (5) information—for each intervention participant—on the expected impact of the intervention in reducing these probabilities.

In our hypothetical example, there are two undesirable behavioral outcomes for any participant: arrest before age 16 and incarceration as an adult. We assume the analyst has reason to believe (1) that the pool of potential participants is heterogeneous and (2) that the addition of information on aggressive disruptive behavior will enable more accurate targeting of the intervention to the candidates for whom the benefits are likely to be the greatest. (More specific assumptions about heterogeneity are explained below.)

In particular, we assume that our analyst is considering potentially targeting the intervention based on one or more of the following elements of behavior-related screening information: (1) whether or not the candidate was subjected to disciplinary removals in the 5^th grade (collected at the end of the 5^th grade school year); (2) a professionally-fielded survey of teacher ratings of each candidate’s aggressive disruptive behavior in the 5^th grade (collected at the end of the 5^th grade school year); and (3) a professionally-fielded survey of teacher ratings of each candidate’s aggressive disruptive behavior in the 3^rd grade (collected at the end of the 3^rd grade school year), which would necessitate that the collection of information for the intervention begins three years before the actual implementation of the intervention.

We further assume that information on 5^th grade disciplinary actions (item 1) will be inexpensive to obtain and thus would be the minimum amount of screening information on which targeting may be accomplished. In contrast, however, professionally-fielded surveys (items 2 and 3) would presumably entail non-trivial amounts of time and expense to collect. For the purposes of our example, we assume that the information on aggressive disruptive behavior will cost $125 per participant to collect and process for the 5^th grade and $125 per participant to collect and process for the 3^rd grade.

Using CBA Evaluation Results for Targeting

Since the value of information derives from its potential to increase ENB for the program via targeting, it is useful to begin by describing the situation when student participants are not heterogeneous and therefore targeting is not useful. In this case, the expression for the ENB with no targeting becomes

$$\text{ENB}(0)=[{\mathrm{V}}_{\mathrm{A}}\times {\mathrm{p}}_{\mathrm{A}}\times {\mathrm{\delta }}_{\mathrm{A}}+{\mathrm{V}}_{\text{IN}}\times {\mathrm{p}}_{\text{IN}}\times {\mathrm{\delta }}_{\text{IN}}-\mathrm{K}]\times \mathrm{N},$$ (1)

where V_A and V_IN are the dollar value of each prevented arrest and the dollar value of each prevented incarceration respectively, where p_A and p_IN are the probabilities (for each participant) of an arrest and an incarceration respectively, where δ_A and δ_IN are the intervention effects of fractional reductions in p_A and p_IN, K is the intervention cost per participant, and where N is the total number of participants with no targeting.

Alternatively, assuming V_A, δ_A,V_IN and δ_IN are the same for all participants, we can define B_A = (V_A x δ_A) as the program’s dollar benefit per expected arrest in the absence of the program and B_IN = (V_IN x δ_IN) as the program’s dollar benefit per expected incarceration in the absence of the program. Then the expected benefit for the overall program with N participants becomes

$$\text{ENB}(0)=[{\mathrm{B}}_{\mathrm{A}}\times {\mathrm{p}}_{\mathrm{A}}+{\mathrm{B}}_{\text{IN}}\times {\mathrm{p}}_{\text{IN}}-\mathrm{K}]\times \mathrm{N},$$ (1a)

If instead we assume (1) that there are variations among students in the undesirable outcome probabilities p_Ai and p_INI, but maintain the assumptions (2) that at the individual student level, K, B_A, and B_IN are the same for every student and (3) that there is no targeting, the expressions for ENB(0) in (1) and (1a) above remain the same but p_A and p_IN are now equal to the mean values of the probabilities p_Ai and p_INi averaged across all N participants. Note, however, that these assumptions imply a simple pattern of heterogeneity in program impacts. Specifically they imply that for any individual student, the expected program impacts in reducing the probabilities of teen arrest and adult incarceration are strictly proportional to the values of p_Ai and p_INI for that student. We shall use these assumptions in the analysis with our hypothetical example.

With these assumption, for the ith student,

$$\text{ENB}{(0)}_{\mathrm{i}}=[{\mathrm{B}}_{\mathrm{A}}\times {\mathrm{p}}_{\text{Ai}}+{\mathrm{B}}_{\text{IN}}\times {\mathrm{p}}_{\text{INi}}-\mathrm{K}],$$ (2)

so for the intervention for all students,

$$\text{ENB}(0)=\mathrm{\sum }\text{ENB}{(0)}_{\mathrm{i}}\text{for}\mathrm{i}=1,\dots ,\text{N.}$$ (2a)

Obviously ENB(0)_i will be > 0 for students with high probabilities of undesirable outcomes but may be < 0 for some students with low probabilities of these outcomes. This implies that targeting the program to those students for whom ENB(0)_i > 0 will increase ENB over the value observed for ENB(0).

Given our assumptions, the key magnitudes on which to focus in targeting the program are the values of the p_Ai’s and p_INi’s. The ability to accurately assess these probabilities is the basis for targeting to be useful, and if having more information on individual students can improve our assessments of the p_Ai’s and p_INi’s, that information may be valuable for increasing ENB of the program. Since more information on risk factors will alter and (hopefully) improve our estimates of the outcome probabilities for each potential participant, it will also alter the targeting decision based on the rule that any student with ENB(j)_i > 0 (where j is the targeting regime) should be included in the program. We reflect this correspondence between the screening information, the targeting regime, and the risk probability estimates by replacing the the p_Ai’s and p_INi’s with the corresponding p(j)_Ai’s and p(j)_INi’s (indexed to the jth targeting regime) in our formulas. Thus, we restate the analyst’s problem in selecting a screening information plan and a corresponding targeting strategy as choosing the largest value of ENB*(j) where

• ENB(j) = Σ[B_A x p(j)_Ai + B_IN x p(j)_INi - K] (for values > 0 only);

• and ENB*(j) = Σ ENB(j)_I (when >0) – TC(j).

Thus, if targeting regime j uses additional information compared to no targeting, then (as noted above) the value of that information (relative to no targeting) is just Ω (j) = ENB*(j)-ENB(0).

As a practical matter, the analyst in our simple example obviously needs to access key elements of information in order to find and implement her optimal targeting scheme. Some of these elements can be reasonably assumed to be provided by the original economic evaluation of the intervention program: V_A, V_IN, δ_A, δ_IN, B_A, B_IN, and K. We recognize, however, that if the circumstances in which the first economic evaluation of the intervention was carried out differed in important respects from those in which the analyst is projecting to replicate the intervention, some revisions in these magnitudes may be needed. In particular, it is important to consider the comparability of the populations of potential participants in the first economic evaluation compared with the population in the relevant venue for the analyst. An important indicator is the overall expected rates of undesirable outcomes in the absence of interventions so it may be useful for the analyst to attempt to secure comparative data for that purpose (since corresponding rates from the first economic evaluation have presumably been reported). Of course, the best situation would be where detailed individual-level data from the first economic evaluation are available to the analyst both for comparison purposes and (if not reported in the first evaluation) to examine possible patterns of heterogeneous program impact.

For our hypothetical example, we use the estimates for B_A, B_IN, and K from a previous exposition of the target efficiency framework (Salkever et al., 2008; these estimates were originally derived from a CBA of the Elmira Prenatal/Early Infancy Project, as reported in Karoly et al. (1998), pp. 132–35.). According to that earlier analysis, the value of preventing an arrest before the age of 16 (B_A) was estimated to be $910, the value of preventing adult incarceration (B_IN) was estimated to be $10,577, and the intervention cost (K) was estimated to be $3,561.

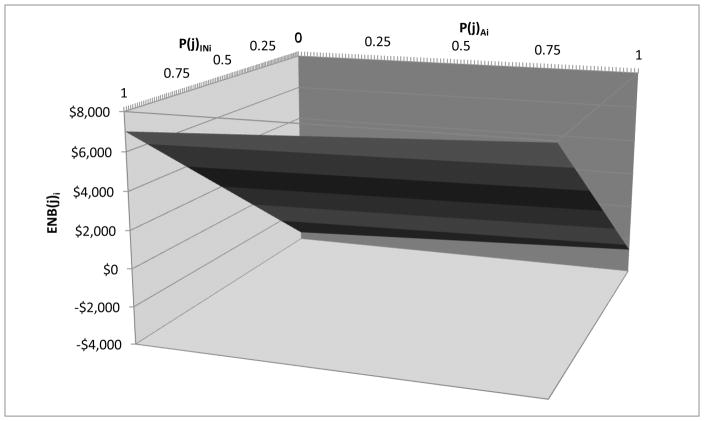
Thus, for example, using information from the jth targeting regime, a participant for whom p(j)_Ai is 0.75 and p(j)_INi is 0.50, ENB(j)_i would equal 0.75 x $910 + 0.25 x $10,577 − $3,561, or $2,410 (see also Appendix Figure 1 for a graphical depiction of the possible ENB(j)i values based on different p(j)_Ai and p(j)_INi). If the analyst only selects participants for whom ENB(j)_i > 0, the total ENB(j) of the program with targeting regime j, under the conditions of ‘target efficiency’ (Salkever et al., 2008) is Σ_i ENB(j)_i summed across all participants i where: [(p(j)_Ai x B_A) + (p(j)_INi x B_IN) - K] > $0.

Appendix Figure 1.

Plot of Expected Net Benefits by Predicted Arrest and Incarceration Risks

ENB(j)_i = (p(j)_Ai x $910) + (p(j)_INi x $10,577) − $3,561

ENB(j)_i, expected net benefit for participant i for jth targeting regime; p(j)_Ai, estimated risk of arrest before the age of 16 participant i for jth targeting regime; p(j)_INi estimated risk of incarceration as an adult for participant i for jth targeting regime

Estimating Targeting (Risk Factor) Models

Once our analyst has chosen the elements of feasible screening information for which they wish to estimate the intervention’s economic value, the next step is to estimate values for the p(j)_Ai’s and p(j)_INi’s targeting models for each of the j feasible targeting regimes, using individual-level data for children that participated in the original implementation of the intervention that the school is seeking to disseminate. The data used for these targeting models are observed dichotomous outcomes (in our specific example, whether the child was ultimately arrested before the age of 16 and whether the child was ultimately incarcerated as an adult) and the elements of screening information for which the analyst wishes to estimate the economic value.

The analyst will fit a series targeting models, one model each for the j potential sets of screening information of interest. For each j, this yields each original participant’s estimated risks of arrest before the age of 16 (p(j)_Ai) and their estimated risks of adult incarceration (p(j)_INi) based on the specified sets of screening information for that regime. In our specific example, the analyst will fit separate logistic regression models in which the outcomes are modeled as a function of: (Model set for j=1) 5th grade disciplinary removals; (Model set for j=2) 5th grade disciplinary removals + 5th grade aggressive disruptive behavior; (Model set for j=3) 5th grade disciplinary removals + 5th grade aggressive disruptive behavior + 3rd grade aggressive disruptive behavior. From each set of models, each participant’s aforementioned estimated risks p(j)_Ai are p(j)_INi are equal to the predicted probability of the model’s outcome, derived from the model’s beta and constant coefficients. Our analyst therefore obtains a total of 3 different estimates of p(j)_Ai and 3 different estimates of p(j)_INi, for j=1, 2, or 3.

Valuing the Screening Information

Thus far, the analyst has: (1) identified potential elements of screening information that were actually measured for the children that participated in the original implementation of the intervention that the school is seeking to disseminate; (2) obtained estimates of the cost of collecting these elements of screening information in the context of the implementation (dissemination) of the intervention; (3) obtained estimates B_A, B_IN, and K from the original CBA evaluation of the intervention that the school is seeking to disseminate or from the economic literature; and (4) obtained estimates of p(j)_Ai and p(j)_INi from logistic regression models which treated the outcomes as a function of the j sets of screening information of interest. These analytical inputs allow for calculation of ENB(j)_i for j=1, 2, or 3 for each original participant.

The additional screening information included in Model sets j=2 and j=3 should facilitate more accurate targeting of the intervention when compared with Model set 1. By calculating the total ENB(j), j=1, 2, or 3 of the intervention under the conditions of target efficiency (i.e., Σ_i ENB(j)_i summed across all participants i where: [(p(j)_Ai x B_A) + (p(j)_INi x B_IN) - K] > $0) that are yielded when using the three different targeting model sets, and by dividing the between-model set differences in these values by the number of candidates that would have been included in the intervention under target efficiency for each model, the analyst can calculate whether the per-candidate gain in ENB is greater than the per-candidate cost to collect information on 5^th grade aggressive disruptive and 3^rd grade aggressive disruptive behavior ($125 per screened candidate). If targeting the original intervention based on the additional screening information could have enabled gains in ENB that exceed the cost of collecting the additional screening information, the analyst may conclude that such information may be similarly valuable in the context of the intervention dissemination.

Data

To illustrate an application of the approach described above, we use data from an actual randomized study of an early childhood intervention – the Prevention Intervention Research Center’s (PIRC) Baltimore intervention trials – which took place in the Baltimore, Maryland public school system during the 1985–1986 and 1986–1987 school years Petras et al., 2004, 2005, 2013). We use data for male control group subjects for estimating our targeting models, since outcomes of interest were rarely observed for females and since observed intervention group outcomes were potentially affected by the interventions in these trials. The PIRC cohort data were linked to incarceration and juvenile arrest data, our outcomes of interest. Data on incarceration came from administrative records for the State of Maryland Department of Corrections; study subjects were approximately 26 years old at the time these data were collected. Data on juvenile arrests were self-reported from a follow-up interview of study subjects at age 20. All other data on the study subjects, including teacher and school information, were drawn from the PIRC website (http://www.jhsph.edu/prevention/Data/index, originally accessed on October 5, 2011). From this dataset we also had information on the three elements of screening information that are of interest to our hypothetical analyst: whether or not the candidate was subjected to disciplinary removals in the 5^th grade, teacher ratings of each candidate’s aggressive disruptive behavior in the 5^th grade, and teacher ratings of each candidate’s aggressive disruptive behavior in the 3^rd grade. We followed the overall approach outlined above, the results of which we discuss in the next section.

Results

Sample Characteristics

Descriptive information on the 344 participants used to fit the targeting models is shown in Table 2. Overall, 25.3% of the participants were ultimately arrested before the age of 16, 17.2% were ultimately incarcerated as an adult, and 8.1% were subjected to disciplinary removals in the 5^th grade. The univariate distributions of the 5^th grade and 3^rd grade aggressive disruptive behavior were nearly identical with respect to their mean and median values.

Table 2.

Sample Characteristics, N = 344

	Arrested before the age of 16	Incarcerated as an adult	5th grade disciplinary removals	5th grade aggressive disruptive behavior	3rd grade aggressive disruptive behavior
Mean/%	25.3%	17.2%	8.1%	2.38	2.37
SD	-	-	-	1.16	1.22
Minimum	0	0	0	1.00	1.00
Median	0	0	0	2.09	2.09
Maximum	1	1	1	5.73	6.00
N of observations	344	344	344	344	344

SD, standard deviation

Targeting Models

Results of the targeting models are presented in Table 3. The results show that in Model set j=1, 5^th grade disciplinary removals were not a statistically significant predictor of arrest before the age of 16 but were a statistically significant predictor of incarceration as an adult. In Model set j=2, the addition of 5^th grade aggressive disruptive behavior increased the models’ C-statistic, a measure of predictive/discriminant accuracy, and pseudo R-squared values several-fold, and this element of screening information was a statistically significant predictor of both arrest before age of 16 and incarceration as an adult. In Model set j=3, the addition of 3^rd grade aggressive disruptive behavior marginally increased the models’ C-statistic and pseudo R-squared values, and this element of screening information was also a statistically significant predictor of both arrest before age of 16 and incarceration as an adult.

Table 3.

Targeting Models

	Arrested before the age of 16 5th grade disciplinary removals			Incarcerated as an adult
	Coefficient (95% Confidence Interval), 2-tailed P
	Model set j=1	Model set j=2	Model set j=3	Model set j=1	Model set j=2	Model set j=3
5th grade disciplinary removals	0.545 (−0.270 to 1.359), P=0.190	0.083 (−0.780 to 0.946), P=0.851	−0.052 (−0.937 to 0.832), P=0.908	1.457 (0.647 to 2.267), P<0.001	0.944 (0.069 to 1.819), P=0.034	0.823 (−0.074 to 1.719), P=0.072
5th grade aggressive disruptive behavior	-	0.510 (0.294 to 0.726), P<0.001	0.323 (0.068 to 0.579), P=0.013	-	0.710 (0.458 to 0.962), P<0.001	0.524 (0.233 to 0.815), P<0.001
3rd grade aggressive disruptive behavior	-	-	0.332 (0.089 to 0.574), P=0.007	-	-	0.354 (0.077 to 0.631), P=0.012
Constant	−1.133 (−1.389 to −0.876), P<0.001	−2.385 (−3.002 to −1.767), P<0.001	−2.744 (−3.434 to −2.054), P<0.001	−1.745 (−2.054 to −1.435), P<0.001	−3.603 (−4.404 to −2.803), P<0.001	−4.044 (−4.953 to −3.135), P=0.000
N of observations	344	344	344	344	344	344
C-statistic	0.522	0.667	0.686	0.574	0.757	0.78
Pseudo R-squared	0.0042	0.0613	0.0798	0.0358	0.1390	0.1589

Estimated Economic Value of Screening Information

The results of the final analysis used to estimate the economic value of screening information are shown in Table 4. In the absence of targeting (i.e., enrolling all 344 individuals at a cost of $3,561 per participant [total cost of $1,224,984], preventing 87 participants from experiencing arrest before age of 16 [87*$910, total B_A = $79,170], and preventing 59 participants from experiencing incarceration as an adult [59*$10,577, total B_IN = $624,043]), the total ENB(j) of the intervention is negative (−$521,771).

Table 4.

Expected Net Benefits of Intervention for Targeting Regimes

Screening Information/Targeting Regime	Total ENB(j) Under Target Efficiencya	N of Participants Selected for Interventionc	Incremental Per-Participant ENB Gain from Additional Screening Informationd
Model set j=1: 5th grade disciplinary removals	$36,316	28	Reference
Model set j=2: 5th grade disciplinary removals + 5th grade aggressive disruptive behavior	$96,218	58	$1,033 vs. Model 1
Model set j=3: 5th grade disciplinary removals + 5th grade aggressive disruptive behavior + 3rd grade aggressive disruptive behavior	$104,998	61	$1,126 vs. reference $144 vs. Model 2

^aFor the jth targeting regime, target efficiency is achieved if the administrator only selects participants for whom ENB(j)i > 0; the total ENB of the program under the conditions of target efficiency is Σi ENB(j)i summed across all participants i where: [(p(j)_Ai x $910) + (p(j)_INi x $10,577) − $3,561] > $0

As expected, with the increases in predictive accuracy that we observed in the targeting models, the addition of screening information increased the total ENB(j) under target efficiency. Using only the basic targeting information for Model set j=1, the total ENB(j) under target efficiency increased by $558,087 (i.e., from −$521,771 to $36,316). The total ENB(j) under target efficiency also increased from $36,316 for Model set j=1 (5^th grade disciplinary removals) to $96,218 for Model set j=2 (5^th grade disciplinary removals + 5^th grade aggressive disruptive behavior). However, the total ENB(j) under target efficiency increases only modestly thereafter, to $104,998, when incorporating the additional information on 3^rd grade aggressive disruptive behavior into Model set j=3.

When the ENB(j) gains are expressed on a per-participant unit, comparing results from j=2 with j=1, it is evident that the collection of the 5^th grade aggressive disruptive behavior screening information is economically justified because the $1,033 per-participant gain in ENB among 58 participants enrolled ($59,914 total [$1,033 x 58 selected participants]) exceeds the estimated cost of $125 per candidate to collect the screening information ($43,000 total, [$125 x 344 candidates]). Comparing results for j=3 with j= 2, however, the $144 per-participant gain in ENB(j) among 61 participants enrolled ($8,784 total, [$144 x 61 selected participants]) does not exceed the estimated cost of $125 per candidate to collect the 3^rd grade aggressive disruptive behavior screening information (another $43,000).

Discussion

We presented a hypothetical example to illustrate an approach to estimating the increased value, in terms of ENB, of collecting additional information for screening and targeting in early-intervention programs. In our estimates for a hypothetical program potentially enrolling up to 344 subjects, additional screening of children for aggression at a single time point (5th grade) nearly tripled the ENB(j) of the program with targeted selection (from $36,316 to $96,218, or $174 per candidate screened). Addition of 3^rd grade information, which constituted a multiple time point approach, resulted in only modest gains in the ENB(j) of the program (from $96,218 to 104,998, or $26 per candidate screened). These estimates imply that in this illustrative example the 5^th grade screening of children for aggression was economically justified based on the assumption that it could be carried out for $125 per candidate.

While we obviously cannot draw substantive conclusions from the results of this simple example, we do suggest that it illustrates a general approach to assessing the economic value of screening information in the context of disseminating or replicating a preventive intervention that has been shown to have some level of efficacy. Note that for an analyst to apply this general method in a real-world situation, she requires relevant information, and/or reasonable assumptions, about several aspects of the intervention’s effectiveness. These include the dollar valuation of each prevented undesirable outcome (V_A,V_IN in our example), the average per person attributable risk of each undesirable outcome (p_A and p_IN in our example), and the fraction of each undesirable outcome prevented by the intervention (δ_A and δ_IN in our example). The initial CBA evaluations of the original intervention demonstrations should provide estimates of these magnitudes, though in some cases these evaluations will be incomplete and other data sources or assumptions will be required for targeting replications of the intervention and for deciding on the amount of screening information to be collected. It would also be most helpful from the analyst’s perspective if these CBA evaluations were conducted for demonstrations of the intervention with target populations and resource environments similar to those in which replications of the intervention is being considered. If the populations differ, there would be considerable uncertainty regarding the generalizability of the results to the population in which the intervention is being considered.

Results from prior CBA evaluations of the intervention may also be good sources for information on the costs of replicating the intervention and the relationship of intervention cost to the number of subjects included in the intervention (i.e., economies or diseconomies of scale). In our illustrative example we assumed that cost per participant is constant regardless of subject characteristics or the number of participants in the program (i.e., constant-returns to scale). It is possible that for a given intervention, an increase in the number of participants could decrease overall per-participant costs if the resources needed to implement the intervention (e.g. teachers) could be shared across participants (i.e., economies of scale). The opposite could be the case (i.e., diseconomies of scale), if there are additional incremental costs associated with accommodating larger groups of participants.

Heterogeneity of subjects (in expected costs and benefits of being included in the intervention) is at the heart of the rationale for screening and for targeting an intervention based on screening. Since our example is only illustrative, we make several strong simplifying assumptions about such heterogeneity. First, we assume that benefits for preventing each type of undesirable outcome are proportional to the attributable risk (absent the intervention) of that outcome occurring. (CBA studies that examine heterogeneity in effectiveness may in fact find a more complex link between heterogeneity in subjects’ attributable risk and the level of risk reduction achieved via the intervention.)

Second, we assume homogeneity in intervention costs across all subjects. Even in the absence of economies or diseconomies of scale, this assumption may be inaccurate because of heterogeneity in the service needs and/or risks of adverse outcomes among the subjects. A recent example of the latter is the Fast Track intervention. (Here again, detailed results on intervention costs from a CBA evaluation may provide valuable evidence for either our simplifying assumption or specifying alternate assumptions about cost behavior.)

The uncertainty around the assumptions upon which the demonstrated approach is based could be handled through one- or multiple-way sensitivity analyses that vary the values of intervention benefits, intervention costs, costs of collecting the screening information, and predicted probabilities used in the ENB equation. For example, one could use the boundaries of the 95% confidence intervals around the beta coefficients in the logistic regressions to create alternative p(j)_Ai and p(j)_INi.

One other piece information needed for our hypothetical administrator should also be noted: the detailed information on empirical risk factor models that enables additional screening data to be used to improved assessments of attributable risk for each potential intervention participant. The source for this information could be the original CBA study that first documented the intervention’s effectiveness; but it might also be available from unrelated epidemiologic studies of populations similar to the population to be served by the intervention under consideration. In practice, reports of CBA interventions rarely provide this level of detailed information or access to individual-level data; availability of such data – assuming it is appropriately de-identified and protected for privacy – through an online appendix or approval process would be necessary to facilitate widespread use of the approach described here.

It is also reasonable to expect that the analyst’s information needs would be greater in more realistic applications that relaxes some of our other simplifying assumptions. For example, instead of measuring effectiveness as prevention of only two types of discrete undesirable outcomes, she may want to measure effectiveness in multiple dimensions some of which are measured by continuous rather than discrete indicators (e.g., years of education complete, future earnings, etc.). CBA results that model interaction effects of risk factors (identified by screening) on these multiple dimensions may not be readily available.

Finally, to better understand the circumstances under which the economic benefits of screening information and targeting may be positive, it is helpful to specify the circumstances under which they will in fact be of no benefit. Three such scenarios can be suggested: 1) when the intervention does not produce positive net benefits for any potential participants, 2) when the intervention produces positive net benefits for all potential participants and there are no limits on the resources available to implement the intervention, and 3) when the intervention produces the same positive net benefits (i.e., no heterogeneity) for all potential participants but there are limits on the resources available to implement the intervention. In the first case, there is no justification for the intervention. In the second, the best policy is universal implementation of the intervention to all available potential participants. In the third, we can randomly select the participants or groups of participants, without using any screening information, until available resources are used up.

In all other situations, screening information will have positive economic benefits, and the problem then is to calibrate these benefits and compare them to the costs of obtaining this information. There may, of course, be situations where individual-level selection based on screening is constrained. For example, if the intervention is classroom-based and can only be delivered to the full class rather than to individual students or small groups of students, individual-level screening information on all students only has benefits because it can help us select the classes (made up of the individual students) in which the expected net benefit of the intervention is largest.

In situations where individual-level selection is feasible, detailed information may be especially important in finding strategies for disseminating high-cost interventions that may have positive expected net benefits for high-risk children even though their expected net benefits are negative when targeting is less precise. An example is the Fast Track program. The Fast Track intervention (Conduct Problems Prevention Research Group, 1999; CPRC 1999) was a multi-component intervention targeted to the prevention of aggression in young children. The intervention included both a universal component and a component in which participants were subjected to a multiple-gating procedure whereby they were selected and ranked according to a severity-of-risk screen score. The intervention was also expensive, costing approximately $58,000 per child (Foster, 2010). Based on analysis of program cost-effectiveness acceptability curves, it was demonstrated 1) that the overall intervention was not economically justified at likely levels of policymakers’ monetary valuations for the key outcomes when including all selected participants, but 2) that it was far more likely to be economically justifiable when targeted to the subset of participants who were the most at risk (Foster & Jones, 2007).

Conclusion

Recent studies have illustrated how additional screening information can improve predictive accuracy in identifying young children at high risk of undesirable adolescent and adult outcomes such as arrest and incarceration. This increase in predictive accuracy is desirable to more accurately target these children for early preventive interventions to avoid these outcomes. Since additional screening entails costs as well as benefits, this note uses a simple example to illustrate how the economic benefits of additional screening can be computed as the increased dollars of expected net benefits from an intervention program. This allows us to measure the economic value of additional screening information as the increased dollars of expected net benefits minus the costs of the additional screening itself; a positive result for this calculation indicates that additional screening is economically justified. Finally, we briefly noted the directions in which our simple example could be extended to relax the simplified assumptions made in our exposition, and we commented on the potential value of this general approach in promoting more targeted replications of high-cost, effective preventive interventions.