Identification of immune correlates of protection in Shigella infection by application of machine learning

Abstract

Background

Immunologic correlates of protection are important in vaccine development because they give insight into mechanisms of protection, assist in the identification of promising vaccine candidates, and serve as endpoints in bridging clinical vaccine studies. Our goal is the development of a methodology to identify immunologic correlates of protection using the Shigella challenge as a model.

Methods

The proposed methodology utilizes the Random Forests (RF) machine learning algorithm as well as Classification and Regression Trees (CART) to detect immune markers that predict protection, identify interactions between variables, and define optimal cutoffs. Logistic regression modeling is applied to estimate the probability of protection and the confidence interval (CI) for such a probability is computed by bootstrapping the logistic regression models.

Results

The results demonstrate that the combination of Classification and Regression Trees and Random Forests complements the standard logistic regression and uncovers subtle immune interactions. Specific levels of immunoglobulin IgG antibody in blood on the day of challenge predicted protection in 75% (95% CI 67–86). Of those subjects that did not have blood IgG at or above a defined threshold, 100% were protected if they had IgA antibody secreting cells above a defined threshold. Comparison with the results obtained by applying only logistic regression modeling with standard Akaike Information Criterion for model selection shows the usefulness of the proposed method.

Conclusion

Given the complexity of the immune system, the use of machine learning methods may enhance traditional statistical approaches. When applied together, they offer a novel way to quantify important immune correlates of protection that may help the development of vaccines.

Graphical abstract

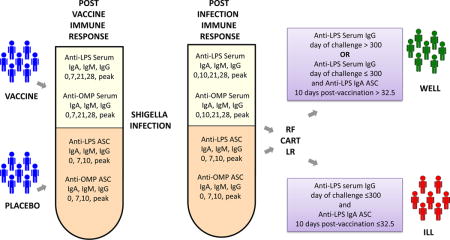
1. Introduction

Immunologic correlates of protection are important in vaccine development for 1) providing insight into mechanisms of protection, 2) assisting in identifying promising vaccine candidates, and 3) providing endpoints in bridging clinical vaccine studies [1–3]. Identification of immune correlates in humans can only be accomplished through clinical studies that measure immunologic predictive variables as well as clinical efficacy outcomes. These include large efficacy trials that assess naturally occurring disease outcomes after vaccination, challenge studies that expose the vaccinees to disease-causing pathogens, and carefully designed case-control studies that compare immune responses in naturally infected subjects and uninfected control subjects (or subjects with infection who do not have disease). Establishing immune correlates of protection early in the clinical development process is expected to expedite the selection and development of promising vaccine candidates.

Our objective is to develop a methodology for the identification of immune correlates of protection in early clinical studies, using the center for vaccine development (CVD) Shigella challenge dataset as a proof of principle.

Prior related work uses classical statistical modeling by fitting logistic regression (LR) or scaled logit models to the clinical outcome [4–11]. This enables the estimation of the probability of protection for given immune responses by inverting the logit transform. One of its drawbacks is that predictors enter into the model in an additive way and, as a result, the model cannot handle interactions that might be playing an important role in protection unless they are incorporated into model equation manually on the basis of prior knowledge. Another shortcoming is that it doesn’t generate cutoff values which define the correlates of protection. The aforementioned drawbacks can be overcome by looking for multiple immune markers simultaneously using a data driven approach based on machine learning procedures, which are well suited to predict outcomes from complex sets of variables and outperform standard models [12–14].

In this paper we propose a new method for defining immune correlates of protection and apply it to Shigella infection. The method combines Classification and Regression Trees (CART) and Random Forests (RF) with the simplicity of the standard linear LR model to obtain immune variables or combinations of them, as well as optimal cutoffs that differentiate who is likely to be protected upon exposure to an infectious agent and who is not.

Unlike prior approaches, the novel contribution of the proposed method is concerned with the use of RF for variable selection together with CART for the detection of immune interactions: RF ranking of variable importance identifies a subset of immune predictors that better predict the outcome; they are the inputs of a CART model that generates cutoffs and interactions from which the probability of protection is estimated using LR. Confidence intervals (CI) for such probability are derived accordingly by bootstrapping LR models. This procedure will be called the combined modeling approach.

The paper is organized as follows: Section 2 provides the background covering the machine learning and statistical techniques used in the paper. Section 3 is a section of methods that includes data collection methods and the proposed combined modeling approach. An application of the approach to the Shillega dataset is carried out in Section 4, which contains the results of the combined modeling approach as well as comparison with the output obtained by application of LR with standard Akaike Information Criterion for model selection. Finally, we provide a summarized discussion and some concluding remarks in Section 5.

2. Background

2.1. Classification and Regression Trees

CART is a nonparametric data driven method for classification and regression [15]. Tree models have been largely applied to find variable interactions having a high predictive strength with a clinical output [16–21].

CART generates a binary tree structure in which child nodes represent a binary partition obtained by splitting the parent nodes; the splits are generated by assessing the impurity of the outcome Y at parent and descendant nodes using measures like Gini and Entropy [15]. The algorithm looks for the splitting point that maximizes the impurity decrease: Δi(t) = i(t) − p_L i(t_L) − p_R i(t_R), with i(t), i(t_L) and i(t_R) the impurities at the parent node and at its left and right descendants, and p_L and p_R the proportion of cases at the descendants.

CART models are grown in a recursive way until a large tree structure is obtained. Then, an automated pruning of the resulting tree structure is carried out by removing uninformative branches in order to avoid overfitting. The resulting tree is the tradeoff between model complexity and predictive accuracy. For further details about CART tuning controls and some other technical insights see the pioneer monograph by Breiman et al. [15].

2.2. Random Forests for classification

RF is an ensemble of trees [22]; its learning mechanism arises from the idea of aggregating CART predictions. The algorithm involves two sources of randomization: the bootstrap resampling to get the trees of the ensemble and the random selection of the eligible set of inputs for splitting the nodes of the trees, an idea brought from the random subspace method [23]. RF is a powerful classifier which has been applied within different domains, including studies that involve small sample high-dimensional data [24–30]. Its predictive strength along with some of the utilities generated by RF output [22, 31], has made RF a widely applied algorithm.

RF learning mechanism can be summarized as follows: ntree bootstrap samples are drawn from the data to grow T₁, T₂, …, T_ntree unpruned trees. In order to find the splitting variable at each node, a semi-randomized variable selection is undertaken by looking for the best cutoff value among a subset of mtry eligible predictors selected at random. In a classification setting the prediction of a new instance is carried out by majority voting of the predictions made by all the trees in the forest. The misclassification error is estimated by RF using the out of bag procedure [22].

Additionally, RF assigns a score to each predictor; the score accounts for the relevance the predictor has for classifying the outcome, so the algorithm generates a ranking of variable relevance that allows to identify the most predictive variables. Since RF is built on the aggregation of decision trees, which can detect variable interactions, the selection method will rank a variable on the basis of its individual association with the outcome as well as on the strength of the interaction it may have with other variables to predict the outcome. This is one of its main advantages with respect to Correlation based Feature Selection and other filter methods [32], that only assess the individual effect of each predictor on the clinical outcome.

The main usefulness of RF variable importance ranking is that it allows to remove variables that do not contribute to classifying the outcome and identify variables that do. A widely used importance measure, implemented in randomForest R package [31], is the accuracy based measure of relevance (ac.rel), which essentially quantifies how much the predictor is missed when classifying the outcome variable [22].

Along this work we have set the following values for the previous RF controls: ntree = 1000 and mtry = default, which is roughly the square root of the number of predictors as suggested by Breiman [22].

2.3. Logistic regression modeling

LR is a standard parametric modeling approach used in biostatistics and in vaccine and immunologic studies [4, 6, 9, 10, 12, 33–35]. LR rests on the traditional linear model with the logit for the posterior probability of illness being modeled by a linear combination of the immune predictors:

$$\log \frac{P(Y=1|\mathbf{X})}{P(Y=0|\mathbf{X})}={\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+\cdots {\alpha }_p{X}_p.$$ (1)

The coefficients in (1) are usually fitted by maximum likelihood using the iteratively reweighted least squares method. Upon inversion of the logit transform, one can estimate the posterior probability of protection for specified levels of the immune response, ensuring estimates in the interval [0, 1]. More important for our goals, and quite interesting from the immunologic standpoint, is the fact that LR can also be used to generate CIs for the probability of protection by bootstrapping the model in (1) applying the nonparametric bootstrap percentile method [36, 37].

3. Methods

3.1. Subjects

We analyzed data from clinical trials conducted at the CVD between 1992 and 1993 (Table 1). This dataset is valuable in that it contains immunologic variables as well as clinical efficacy outcomes from Shigella challenge studies.

Table 1.

Study design of Shigella experiments.

Study	Sample size	Exposure 1	Immune analysis	Exposure 2	Immune analysis	Exposure 3	Immune analysis
A	29	2 × 109 CFU EcSf2a-2	Post vaccination	1 × 103 CFU 2457T	Post challenge
B	11	7 × 108 CFU EcSf2a-2	Post vaccination	1 × 103 CFU 2457T	Post challenge
B	8	Placebo		1 × 103 CFU 2457T	Post challenge
B+C	5	7 × 108 CFU EcSf2a-2	Post vaccination	1 × 103 CFU 2457T	Post challenge	1.4 × 103 CFU 2457T	Post challenge
B+C	6	Placebo		1 × 103 CFU 2457T	Post challenge and post “vaccination”	1.4 × 103 CFU 2457T	Post challenge
C	12					1.4 × 103 CFU 2457T	Post challenge
C	7					1.4 × 102 CFU 2457T	Post challenge

Shigella is a bacteria that causes diarrhea and dysentery after ingestion of contaminated food or water. Shigella flexneri 2a is an important disease-causing serotype that has been chosen as a target for vaccine development. Although Shigella flexneri 2a is a dangerous bacterial pathogen that can cause severe disease and even death if not properly treated, if properly treated it can be cured without sequelae. This allows for the conduct of challenge trials in which volunteers ingest the vaccine or placebo and subsequently ingest a disease-causing strain of Shigella flexneri 2a to determine if the vaccine protects from infection. EcSf2a-2 is a Shigella vaccine candidate composed of an Escherichia coli bacteria that expresses Shigella flexneri 2a antigen lipopolysaccharide (LPS).

Three trials were designed to test whether the EcSf2a-2 vaccine protects against Shigella challenge with a disease-causing Shigella flexneri 2a strain approximately one month after vaccination. In trial A [38], 29 volunteers received three doses of 2 × 10⁹ colony forming units (CFU) of EcSf2a-2 (days 0, 3 and 6) prior to challenge. In trial B [39], 16 volunteers received four doses of 7 × 10⁸ CFU of EcSf2a-2 (days 0, 3, 14 and 17), and along with 14 unvaccinated control subjects were challenged. In trial C [40], five vaccinees and six placebo recipients who had all been challenged were brought back one month after the challenge for an additional challenge with the same strain. Additionally, we assessed the dose response of the wild type strain in unexposed, never vaccinated or challenged, volunteers.

It is important to note that assessing immunologic predictive variables in the context of two doses of vaccine as well as a challenge strain is experimentally comparable to assessing immunologic predictive variables in efficacy trials where the dose of naturally occurring inoculum is variable, as well as case-control studies where both the dose of the naturally occurring disease-causing inoculum and the dose of the naturally occurring “ vaccinating ” inoculum are variable. Thus, combining three clinical trials with varying inocula that influence predictive as well as outcome variables is conceptually similar to naturally occurring infection and resultant protection.

3.2. Immune markers and clinical outcome

Anti-LPS and anti-outer membrane protein (OMP) serum IgM, IgA and IgG antibodies on days 0, 7, 21, 28 and peak after the first dose of vaccine and on days 0, 10, 21, 28 and peak after challenge, as well as IgM, IgA and IgG antibody secreting cell (ASC) responses on days 0, 7, 10 and peak after vaccine or challenge, were assessed as described in the original manuscripts [38–40] and included in the analysis. Post-vaccination immune markers were assessed after initial exposure to Shigella immunization, and post-challenge with wild-type Shigella immune markers were assessed after challenge (Table 1). A total of 108 inumune features were measured. The outcome “ ill ” includes fever (defined by an oral temperature > 100°F), and diarrhea (having two or more loose stools > 200 milliliters total within 48 hours or one loose stool > 300 milliliters).

3.3. Combined RF + CART + LR modeling

The combined modeling approach integrates RF and CART with LR modeling to achieve three goals: 1) identifying immune biomarkers correlated to the clinical outcome, 2) the discovery of interactions among the immune predictors that better explain the clinical outcome as well as obtaining cutoffs that optimally define the immune correlates of protection and 3) the estimation of the probability of protection using LR.

3.3.1. Variable selection with RF

The stability of methods for variable selection has become a hot topic in the literature [41–45]. Here we adopt the strategy by Boulesteix [42] who proposed the aggregation of ranked immune marker lists obtained from successive runs of RF on different resamples in order to control the instability of a single ranking. The procedure can be summarized as follows:

RF average variable importance score

Set the number B of bootstrap samples

Step 1. For k = 1 to B

Draw a bootstrap sample from the data, run RF and generate the ranking of variable importance.

Let ac.reli,k be the importance assigned to the ith immune predictor in the kth RF run.

Step 2. For each immune predictor, compute its average score $ac.re{l}_i=\frac{{\displaystyle {\sum }_{k=1}^{B}ac.re{l}_{i,k}}}{B}$

Step 3. Sort the ac.relis to generate the ranking of average importance scores

Another way of constructing ac.rel_i measures is to get them scaled so that they range in the interval [0, 100]. The scaled scores are given by

$$\mathit{scale}.ac.re{l}_i=100\times \frac{ac.re{l}_i-{min}_{i=1,\dots ,p}ac.re{l}_i}{{max}_{i=1,\dots ,p}ac.re{l}_i-{min}_{i=1,\dots ,p}ac.re{l}_i},i=1,\dots ,p.$$ (2)

Once the ranking of scaled scores is obtained, the top ranked predictors may be determined with pre-set values such as for example an average score greater than 70. It is also possible to determine them based on the screeplot of scores that allows to visualize the steepest decay in the scores.

3.3.2. Variable interaction modeling with CART

RF selection provides a subset with the relevant predictors, ${\left\{X_{i_j}\right\}}_{j=1}^H$, that are used as inputs to grow a CART structure whose terminal nodes represent a partition of the data in subsets ${\left\{{ℛ}_i\right\}}_{i=1}^J$ described by a set of binary rules. The partition can be mathematically described by a set of indicator functions: for each observation, the indicator I(ℛ_i) takes values 1 or 0 depending on whether the observations meets the the rules for ℛ_i or not. A large tree reveals complex interactions among predictors rather than individual effects. The researcher can also merge subsets from ${\left\{{ℛ}_i\right\}}_{i=1}^J$ to reduce its complexity.

In addition, it is well-known that trees are biased towards the generation of splits in variables with missing values, which is our case. To handle this issue, Salford Systems CART® 6.0 allows penalization of the missingness of predictors [46]; the penalty is obtained multiplying the impurity by

$$f=a\cdot {(\mathit{proportion}.\mathit{not}.\mathit{missing}.\mathit{cases})}^b$$ (3)

with a, b > 0 controlling the amount of penalty. Note that a = 1 and b = 0 implies no penalty. In addition, for a given a, the closer b gets to zero the smaller the penalty becomes. In our data several trials showed that a = 1, b = 0.5 were good choices that maximize the performance of the tree.

The remaining CART controls were chosen to optimize tree performance: priors = EQUAL, splitting rule = GINI, and parent node minimum cases = 10, terminal node minimum cases = 5. These settings are used to get all the trees of this paper.

3.3.3. LR estimation of the probability of protection

Suppose that M indicator variables I(ℛ_i): i = 1, 2, …, M are obtained by CART seeker stage. In the last step of the combined modeling approach they are taken as predictors to fit the LR model:

$$\log \frac{P(Y=1|I({ℛ}_1),\dots ,I({ℛ}_M))}{P(Y=0|I({ℛ}_1),\dots ,I({ℛ}_M))}={\alpha }_0+{\alpha }_{1}I({ℛ}_1)+{\alpha }_{2}I({ℛ}_2)+\cdots {\alpha }_{M}I({ℛ}_M).$$ (4)

Once the model in (4) has been fitted, inversion of the logit transform yields an estimate $\widehat{p}$ of the probability P (Y = 1|I(ℛ₁), …, I(ℛ_M)). For a given confidence level, we can obtain the bootstrap CI for such a probability by application of the nonparametric bootstrap percentile method [36, 37]. The method requires to draw R bootstrap resamples from the dataset.

Fig. 1 contains a workflow diagram describing the proposed combined modeling method.

Fig. 1.

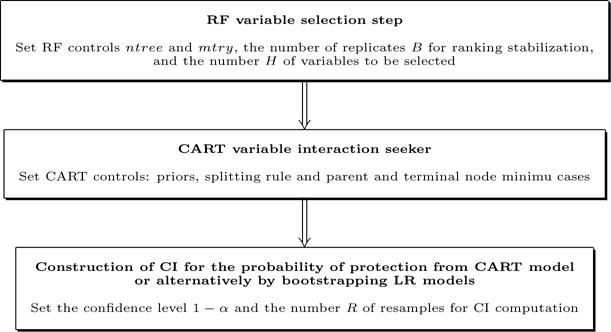
Scheme of the modeling procedure.

4. Results

Commercial Salford Systems CART® 6.0, along with R 3.0.2 own code — which can be provided by the authors upon request—were utilized on post-vaccination and post-challenge responses to identify important correlates, cutoff values, and probabilities of not getting ill.

4.1. Variable selection with RF

RF selection deployed on the entire set of immune variables identified post-challenge ASC responses as highly predictive such that effects of the remaining predictors were overwhelmed. In order to avoid this masking phenomenon, RF selection is carried out independently in four biologically relevant blocks having their own idiosyncrasy: 1) post-vaccination ASC, 2) post-vaccination serum, 3) post-challenge ASC and finally 4) post-challenge serum. The barplots in Fig. 2 show the top five immune markers, given by score (2), for each block. Variables with score above 70% are defined as relevant (threshold corresponding to a decay of at least 30 points in score (2), which is the maximum decay observed for all the barplots of Fig. 2). The adopted criterion follows the rationale behind the use of the screeplot, a display of the decay of a score, which enables the visual location of the point where the maximum decay is attained. Hence, the following are retained: anti-LPS IgA ASC on day 10 as well as anti-LPS IgG on day 0 and 7 from the post-vaccination blocks; and anti-LPS IgM and IgA ASC on day 7 as well as anti-LPS IgA peak and day 10 from the post-challenge variables. These findings suggest that post-vaccination cells making IgA as well as antibodies against IgG may be the dominant predictors of protection, whereas post-challenge cells making IgM and IgA as well as IgA antibodies may be the dominant predictors of protection.

Fig. 2.

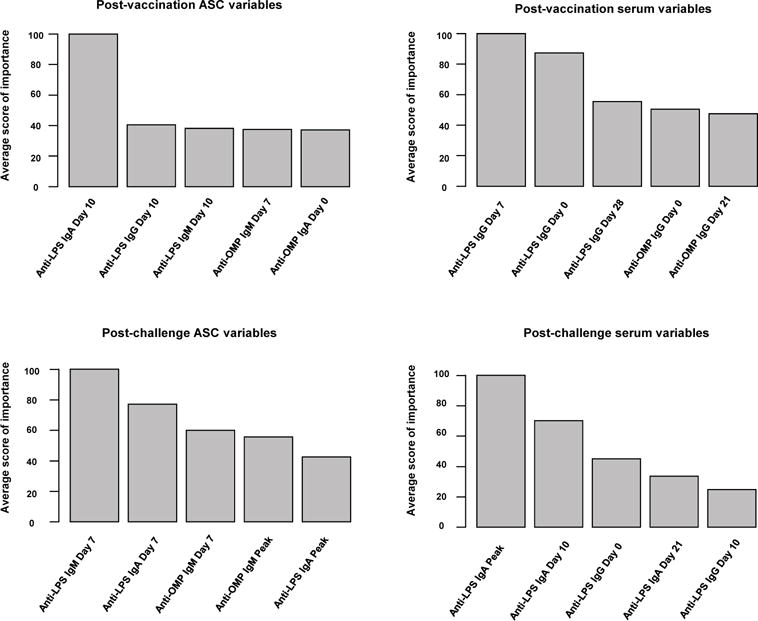
RF rankings for the average score of variable importance.

An exploratory tree grown with the most relevant predictors shows that anti-LPS ASC IgA and IgM at day 7 after challenge accurately classifies the outcome (see Fig. 3). The highly predictive post-challenge immune responses are not practical to measure in a natural infection environment as they occur after the event of interest; but they may be informative. In order to account for their effects the best post-challenge ASC split, given by the condition “ Day 7 post challenge anti-LPS IgM ASC less than 2.50 ”, is replaced by the post-vaccination variables that best predicts it. These are found using RF with the indicator I(Day 7 post challenge anti-LPS IgM ASC ≤ 2.50), that represents the best split, as the outcome variable and the post-vaccination variables as predictors. Score (2) is computed and the top ranked variables are used in place of the best post-challenge marker.

Fig. 3.

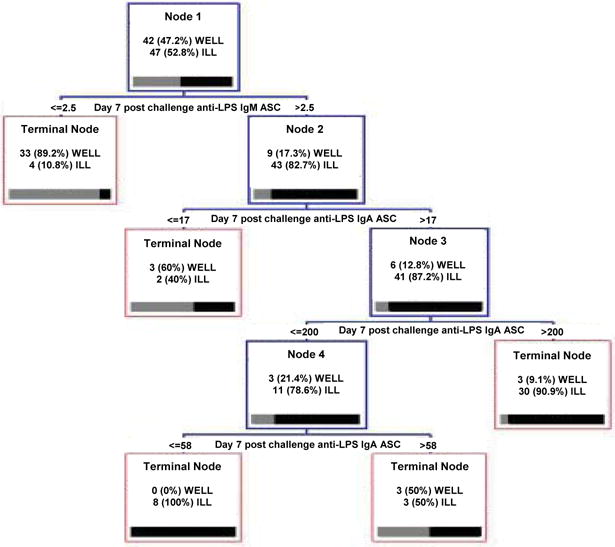
Exploratory CART obtained from the top ranked post-vaccination and post-challenge selected immune predictors.

When the post-vaccination variables are ranked in accordance to (2), we observe seven relevant variables with scores above 70: anti-LPS IgA ASC day 10 at the top, and also anti-LPS IgG serum on day 0, anti-OMP IgM ASC on day 7, anti-LPS IgG and IgA ASC on day 7, anti-OMP IgA ASC on day 7 and anti-LPS IgM serum peak. They are retained as they will potentially highlight the immune interactions that better explain the clinical outcome.

4.2. CART modeling stage

At this stage, a tree is grown with the most influential post-vaccination ASC and serum variables, and the most relevant post-vaccination variables that predict the condition “ Day 7 post challenge anti-LPS IgM ASC ≤ 2.50 ” (third and fourth columns of Table 2). We also include all the immune markers on the day of challenge (first two columns of Table 2) because of practical reasons, as they indicate most accurately the state of the immune response at the time of infection. The results are depicted by the top tree of Fig. 4: the performance of the tree model is carried out by the 10-fold cross validation method, which is a reasonable alternative to account for the bias-variance tradeoff in small data sets as ours [47]. The method gives an error close to 39% with terminal nodes 1, 3 and 4 capturing nearly 81% of the ill status and 28.5% of false positives (FP), as provided by CART® 6.0 ROC curve. After merging terminal nodes, we get a tree with four terminal nodes, as shown by the bottom tree of Fig. 4, leading to a 33% error rate with terminal nodes 1 and 2 catching 85% of the ill class and a FP rate about 36%. Hence, we get a simpler tree with a very small loss in the FP rate.

Table 2.

Immune predictors selected by RF and used to get CART model.

Post-challenge secreting cells	Post-challenge serum	Post-vaccination secreting cells	Post-vaccination serum
Anti-LPS IgA Day 0	Anti-LPS IgA Day 0	Anti-LPS IgA Day 7
Anti-LPS IgG Day 0	Anti-LPS IgG Day 0	Anti-LPS IgA Day 10	Anti-LPS IgG Day 0
Anti-LPS IgM Day 0	Anti-LPS IgM Day 0	Anti-LPS IgG Day 7	Anti-LPS IgG Day 7
Anti-OMP IgA Day 0	Anti-OMP IgA Day 0	Anti-OMP IgA Day 7	Anti-LPS IgM Peak
Anti-OMP IgG Day 0	Anti-OMP IgG Day 0	Anti-OMP IgM Day 7
Anti-OMP IgM Day 0	Anti-OMP IgM Day 0

Fig. 4.

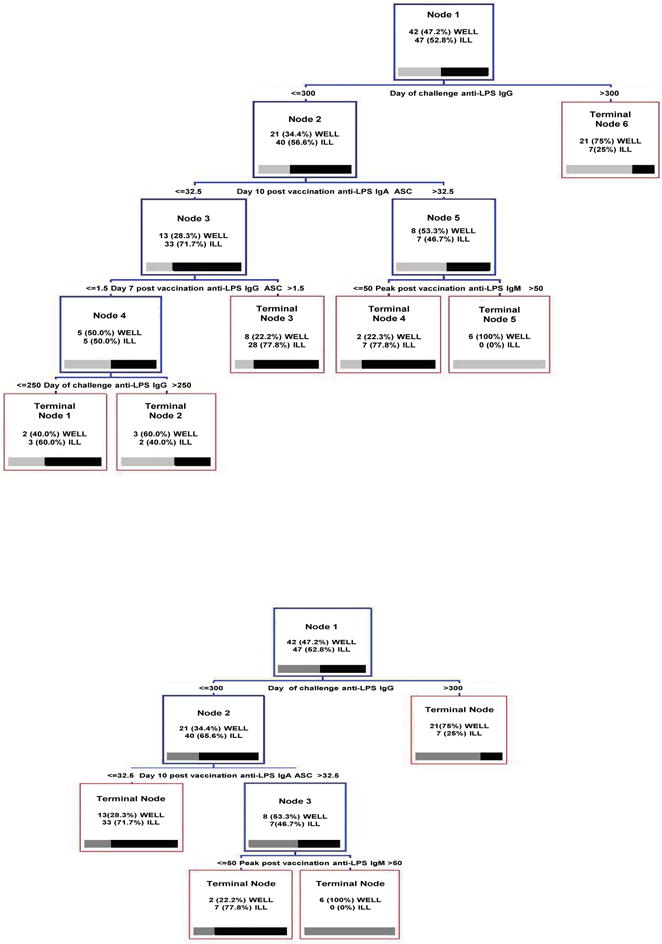
Trees obtained using the post-vaccination relevant predictors and post-challenge variables on the day of challenge: initial tree (top) and pruned tree (bottom)

4.3. LR modeling stage

LR along with the bootstrap method allows to get CIs for the probability $\widehat{p}$ of the status well. Table 3 shows the results when anti-LPS IgG serum on the day of challenge is the only predictor, when anti-LPS IgG serum on the day of challenge and anti-LPS IgA ASC on day 10 enter in (1), and when the splitting variables enter as predictors through their indicators as in (4).

Table 3.

Estimates and CI for the probability of protection.

Immune marker predictors	$\widehat{p}$	LR bootstrap CI for p
Anti-LPS IgG serum on the day of challenge	0.51	(0.44, 0.60)
Anti-LPS IgG serum on the day of challenge + anti-LPS IgA ASC day 10 post-vaccination	0.71	(0.60, 0.83)
Anti-LPS IgG serum on the day of challenge > 300 cutoff	0.75	(0.67, 0.86)
Interaction Anti-LPS IgG serum on the day of challenge ≤ 300 and anti-LPS IgA ASC day 10 post-vaccination > 32.5	1.00	—

To calculate the CIs we take R = 5000 and a 95% confidence level. The estimate $\widehat{p}$ is computed with values of the immune response set at the levels: anti-LPS IgG on the day of challenge at 300.1 in the models with this single predictor, and at 300 for anti-LPS IgG on the day of challenge and 32.51 anti-LPS IgA ASC day 10 post-vaccination in the models with both predictors. The results show that protection increases for tree models that generate cutoffs and interactions, achieving 75% and 100% protection, which demonstrates that the combination of immune markers outperforms single markers when looking for correlates of protection.

Note that the CI of the last row is not available. This happens because the 5 cases that meet the splitting rules are well individuals. This fact is not obvious from the bottom tree of Fig. 4 which has ill and well individuals at internal node 3, but can be explained by the way CART deals with missing values (NAs): node 2 contains 35 NAs for anti-LPS IgA ASC day 10 post-vaccination; CART internally classifies them using a surrogate split that resembles the primary split. In this case, the best surrogate is found for anti-LPS IgA day of challenge and the surrogate sends 10 cases to node number 3 (3 well and 7 ill). Unlike CART, the LR skips NAs using only fully informed observations, which explains the 100% protection.

4.4. Comparison with LR using the AIC criterion for model selection

Akaike Information Criterion (AIC) [48] with LR is used for model selection in the same way RF rankings helped in the identification of relevant variables. The functions of the R package bestglm [49] were employed for the implementation. The analysis is carried out for post-vaccination ASC and serum immune predictors separately yielding the variables in Table 4; Post-challenge variables on the day of challenge were also incorporated to the selection.

Table 4.

List of immune predictors selected by LR using AIC for model selection.

Post-cha. secreting cells	Post-cha. serum	Post-vac. serum LPS	Post-vac. serum OMP	Post-vac. secreting cells
		Anti-LPS IgA Day 0
		Anti-LPS IgA Day 7	Anti-OMP IgA Day 10
Anti-LPS IgA Day 0	Anti-LPS IgA Day 0	Anti-LPS IgA Peak	Anti-OMP IgA Day 21
Anti-LPS IgG Day 0	Anti-LPS IgG Day 0	Anti-LPS IgG Day 7	Anti-OMP IgA Day 28
Anti-LPS IgM Day 0	Anti-LPS IgM Day 0	Anti-LPS IgG Day 21	Anti-OMP IgG Day 0	Anti-OMP IgA Day 0
Anti-OMP IgA Day 0	Anti-OMP IgA Day 0	Anti-LPS IgG Peak	Anti-OMP IgG Day 10
Anti-OMP IgG Day 0	Anti-OMP IgG Day 0	Anti-LPS IgM Day 0	Anti-OMP IgG Peak
Anti-OMP IgM Day 0	Anti-OMP IgM Day 0	Anti-LPS IgM Day 21	Anti-OMP IgM Day 0
		Anti-LPS IgM Day 28	Anti-OMP IgM Day 10
		Anti-LPS IgM Peak

Finally, LR models with the most significant variable and with the two most significant immune variables are fit, and probabilities of protection and CIs are calculated accordingly at the median levels of the immune response (Table 5). General omparison with Table 3 shows that lower probabilities of protection are obtained from the classical LR with AIC method than from LR with RF+CART variable selection. This fact demonstrates that the combination of machine learning with traditional methods like LR may complement the latter to uncover interactions in data generated by complex biological mechanisms.

Table 5.

Estimates and CI for the probability of protection (immune predictors obtained using LR with AIC criterion).

Immune marker predictors	$\widehat{p}$	LR bootstrap CI for p
Anti-LPS IgM Peak serum post vaccination	0.53	(0.46, 0.63)
Anti-LPS IgM Peak serum post vaccination + anti-OMP IgG serum day 0 post vaccination	0.52	(0.42, 0.62)

5. Discussion

The combined modeling approach offers the addition of data driven machine learning methods and classical statistical modeling for assessing a complex dataset for predictive variables such as immune correlates of protection. The approach serves to identify important biomarkers, provide cutoffs, and highlight interactions that allow prediction of protection. The results demonstrate the increased predictive capacity of assessing multiple immune correlates rather than focusing on a single immune correlate. Comparison with the results obtained by classical LR with AIC highlights the usefulness of the proposed method to model the complexity of the immune system.

Low post-challenge IgM ASC and IgA ASCs in peripheral blood were the strongest predictors. Mechanistically this may be expected, as low ASCs in peripheral blood post-challenge have been described in volunteers protected from Shigella infection [40] and hypothesized to be low in peripheral blood because they are present at the gut in subjects who are protected.

During infection, components of the pathogen such as Shigella LPS and OMP bind receptors of B and T cells. B cells become ASCs and make antibodies, while T helper cells assist B cells, and T cytotoxic cells kill infected host cells that antibodies cannot access [50]. ASCs initially make antibodies called immunoglobulin IgM and then switch to make antibodies called IgG or IgA. While IgG antibodies circulate in the blood, IgA antibodies are actively secreted through mucous membranes, which cover the respiratory and the gastrointestinal tracks where most pathogens invade [51]. High IgM ASCs and low IgA ASCs would therefore be expected in the blood of subjects not previously exposed (and therefore not protected), while low IgM ASCs and high IgA ASCs would be expected in the blood of subjects that were previously exposed (and are protected).

Post-vaccination, serum anti-LPS IgG on the day of challenge was identified as important, as was anti-LPS IgA ASC 10 days post-vaccination. This was further quantified: individuals who have a post-vaccination anti-LPS IgG titer > 300 were 75% (95% CI 67 – 86) likely to be protected, and individuals that did not have serum IgG but had an increase in ASCs that makes IgA accounted for the remainder needed achieve 100% protection. Our findings are consistent with the redundant nature of the immune response, and demonstrate that two immune correlates of protection predict protection better than one immune correlate.

Limitations of our approach include the need for immunological data combined with clinical efficacy data. This information is difficult to obtain and in our case we combined data from three similar studies. Although there may be differences in ways immune or clinical parameters were measured as well as biases introduced in one study versus the others, the combination of studies resembles the variability found in natural infection. In addition, all estimates of protection need validation by future independent studies, which may utilize classification to handle a binary outcome, well versus ill, as well as regression if the outcome is defined as a spectrum of well versus ill. Another limitation, which also opens the door for future research, is concerned with the choice of RF parameters: they were set at their defaults as recommended by Breiman [22]; additional specific domain studies oriented to parameter optimization such as particle swarm optimization, genetic algorithm, and other stochastic optimization methods may shed light on the settings of parameters and enhance the performance of the proposed approach.

In summary, immune biomarkers that predict protection are important to vaccine development and yet difficult to identify, especially early in the product development pathway. The immune system is complex and redundant and each individual may be protected by different means. This complexity requires multiple ways of assessing predictive biomarkers, one of which is offered by the proposed combined modeling approach. We have applied this approach to identify predictive immune correlates including post-vaccination serum IgG as well as IgA ASC. Future work will focus on challenge studies with other pathogens including cholera for which similar datasets exist, as well as efficacy trials and case-control designs. The application of the proposed approach may help vaccinologists identify promising vaccine candidates in an effort to develop new and improved vaccines.

Highlights.

• Immune correlates of protection are important to vaccine development

• CART and random forests machine learning methods are presented in a combined approach as complements to traditional logistic regression that may provide insight into mechanisms of protection

• Application to the Shigella dataset reveals interesting immune interactions and immune correlates