Improved Magnetic Resonance Fingerprinting Reconstruction with Low-Rank and Subspace Modeling

Abstract

Purpose

This article introduces a constrained imaging method based on low-rank and subspace modeling to improve the accuracy and speed of MR Fingerprinting (MRF).

Theory and Methods

A new model-based imaging method is developed for MRF to reconstruct high-quality time-series images and accurate tissue parameter maps (e.g., T₁, T₂, and spin density maps). Specifically, the proposed method exploits low-rank approximations of MRF time-series images, and further enforces temporal subspace constraints to capture magnetization dynamics. This allows the time-series image reconstruction problem to be formulated as a simple linear least-squares problem, which enables efficient computation. After image reconstruction, tissue parameter maps are estimated via dictionary-based pattern matching, as in the conventional approach.

Results

The effectiveness of the proposed method was evaluated with in vivo experiments. Compared with the conventional MRF reconstruction, the proposed method reconstructs time-series images with significantly reduced aliasing artifacts and noise contamination. Although the conventional approach exhibits some robustness to these corruptions, the improved time-series reconstruction in turn provides more accurate tissue parameter maps. The improvement is pronounced especially when the acquisition time becomes short.

Conclusions

The proposed method significantly improves the accuracy of MRF, and also reduces data acquisition time.

Introduction

MR Fingerprinting (MRF) (1) is a recently introduced quantitative MRI framework. It features a novel data acquisition and image reconstruction paradigm to enable simultaneous quantitative measurements of multiple MR tissue parameters (e.g., T₁, T₂, and spin density). In data acquisition, MRF employs a series of time-varying quasi-random acquisition parameters (e.g., flip angles and repetition times) to probe the spin system. Additionally, it performs a highly-undersampled, variable-density spiral acquisition that varies over time to collect k-space data. Together, this produces significant spatial and temporal incoherence. For image reconstruction, MRF utilizes a two-step procedure. First, a gridding reconstruction and coil combination is performed to reconstruct time-series images from highly-undersampled data. Second, the estimation of tissue parameters is accomplished by pattern matching to a pre-computed dictionary on a voxel-by-voxel basis. The spatiotemporal incoherence ensures tissue parameter maps are minimally corrupted by aliasing artifacts through pattern matching. The conventional approach above is simple and computationally efficient, but sub-optimal from a statistical estimation perspective (2,3). In practice, it often requires a relatively long acquisition train (or acquisition time) to ensure good accuracy. This can result in clinically uncomfortable acquisition time for imaging applications that require broad volumetric coverage (4).

To reduce data acquisition time while improving accuracy, a number of iterative reconstruction methods have recently been proposed (2, 3, 5–8). In particular, principled statistical reconstruction methods (2, 3, 5, 6), which model imaging physics, image priors and noise statistics, have been developed to reconstruct MR tissue parameters directly from highly-undersampled, noisy k-space data. These methods lead to improved estimation performance and/or reduced acquisition time. Moreover, they provide useful theoretical insight into the conventional approach. It has been shown analytically in (2, 3) that the conventional approach is equivalent to the first iteration of the maximum likelihood (ML) reconstruction. In spite of the theoretical insight and empirical success, these methods result in challenging nonconvex optimization problems, which require specialized algorithms and initializations (3).

In this work, we introduce an alternative model-based reconstruction method for MRF based on low-rank and subspace modeling. This builds on the previous low-rank reconstruction methods for dynamic MRI (9–11) and conventional MR relaxometry (12–17). Here the proposed method enforces an explicit low-rank constraint to capture strong spatiotemporal correlation within MRF time-series images. Further, it predetermines the temporal subspace of the low-rank model from an ensemble of magnetization evolutions (obtained from Bloch simulations). The proposed model results in a simple linear least-squares formulation, allowing efficient computation. Similar to the conventional approach, it employs a two-step procedure. However, rather than using artifact-corrupted time-series images, it integrates low-rank and subspace modeling with the sensitivity encoding (SENSE) based parallel imaging to reconstruct high-quality time-series images. This in turn provides improved accuracy of tissue parameter maps. The effectiveness of the proposed method was evaluated by comparing to tissue parameter maps generated from in vivo “gold-standard” time-series data, as well as the conventional approach and ML reconstruction.

Recently, a number of low-rank reconstruction methods have been proposed for MRF (5,18–21), including a preliminary account of this work presented in (18). Note that the proposed method has key differences from other low-rank MRF reconstruction methods. Specifically, the proposed method enforces an explicit low-rank constraint via matrix factorization, and further imposes a temporal subspace constraint to model magnetization dynamics. This is different from (5, 19) in which the low-rank constraint is enforced implicitly via a surrogate function (e.g., the nuclear norm (22)). As demonstrated in (11, 23, 24), the explicit rank constraint often leads to better reconstruction performance and more efficient computation over the implicit counterpart. In (20), an iterative algorithm based on the projection onto convex set was described to solve a low-rank reconstruction problem for MRF. Compared with (20), the proposed method rigorously formulates the image reconstruction problem as an optimization problem and naturally integrates with the SENSE-based parallel imaging model. In (21), although an explicit low-rank constraint was also used for image reconstruction, it does not incorporate any subspace constraint. Moreover, the reconstruction algorithm in (21) involves the singular value decomposition at each iteration, which can be computationally expensive.

Theory

In MR Fingerprinting, the contrast-weighted image I_m(x) can be expressed as (2, 3):

$$I_m(\mathbf{x})={\varphi }_m(T_1(\mathbf{x}),T_2(\mathbf{x}))\rho (\mathbf{x}),$$ [1]

for m = 1, … ,M. Here, m is a time index, T₁(x), T₂(x), and ρ(x) respectively denote the two primary relaxation times and the spin density, and ϕ_m(·) denotes the contrast-weighting function that is determined by magnetization dynamics. The imaging equation for MRF can be written as

$$d_{m,c}(\mathbf{k})=\int {\mathbf{S}}_c(\mathbf{x})I_m(\mathbf{x})exp(-i2\pi \mathbf{k}·\mathbf{x})d\mathbf{x}+n_{m,c}(\mathbf{k}),$$ [2]

for c = 1, … ,N_c, where d_m,c(k) denotes the measured k-space data associated with I_m(x) from the cth receiver coil, S_c the coil sensitivity for the cth receiver coil, and n_m,c the measurement noise. The goal of MRF reconstruction is to determine {T₁(x), T₂(x), ρ(x)} from highly-undersampled and noisy measurements {d_m,c(k)}.

To address this problem, statistical reconstruction methods (2, 3, 5, 6) form the following data model:

$$d_{m,c}(\mathbf{k})=\int {\mathbf{S}}_c(\mathbf{x}){\varphi }_m(T_1(\mathbf{x}),T_2(\mathbf{x}))\rho (\mathbf{x})exp(-i2\pi \mathbf{k}·\mathbf{x})d\mathbf{x}+n_{m,c}(\mathbf{k}),$$ [3]

by combining Eq. [1] with Eq. [2]. Given the noise statistics of n_m,c (i.e., complex Gaussian noise), unknown MR tissue parameters can be estimated directly from {d_m,c(k)} with a maximum likelihood criterion (2, 3). Improved estimation performance can be attained by incorporating an image prior model, e.g., low-rank model (5) or structured sparsity model (6), into a penalized maximum likelihood formalism. Although statistical reconstruction yields improved accuracy over the conventional approach (1), they all face solving a challenging nonlinear and nonconvex optimization problem due to the data model in Eq. [3]. To bypass such difficulty, we introduce an alternative reconstruction method. Rather than performing direct parameter reconstruction from measured data, the proposed method follows a two-step procedure: we first reconstruct ${\{I_m(\mathbf{x})\}}_{m=1}^M$ with a low-rank and subspace model-based reconstruction, and then estimate MR tissue parameter maps from time-series images on a voxel-by-voxel basis. Here the proposed time-series reconstruction employs a simple convex formulation (i.e., a least-squares formulation), which significantly simplifies computation.

For simplicity, we consider a discrete image model, in which the MRF time-series images ${\{I_m(\mathbf{x})\}}_{m=1}^M$ can be completely represented by the following Casorati matrix (9):

$$\mathbf{C}=\left[\begin{array}{ccc}{I}_1({\mathbf{x}}_1)& \dots & I_M({\mathbf{x}}_1)\\ ⋮& \ddots & ⋮\\ I_1({\mathbf{x}}_N)& \dots & I_M({\mathbf{x}}_N)\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{I}}_1& \cdots & {\mathbf{I}}_M\end{array}\right]\in {ℂ}^{N\times M},$$ [4]

where the first and second directions of C respectively denote the spatial and temporal dimensions, and I_m ∈ ℂ^N contains the values of I_m(x) on a grid at N spatial locations. Accordingly, the imaging equation in Eq. [2] can be rewritten as

$${\mathbf{d}}_{m,c}={\mathbf{F}}_m{\mathbf{S}}_c{\mathbf{I}}_m+{\mathbf{n}}_{m,c},$$ [5]

where d_m,c ∈ ℂ^P_m contains the measured data for I_m from cth coil, F_m ∈ ℂ^P_m×N denotes the undersampled Fourier encoding matrix, S_c ∈ ℂ^N×N is a diagonal matrix containing the coil sensitivities for the cth coil, and n_c ∈ ℂ^P_m is the noise vector. With more compact matrix notation, we have

$${\mathbf{d}}_c=\mathrm{\Omega }(\mathbf{F}{\mathbf{S}}_c\mathbf{C})+{\mathbf{n}}_c,$$ [6]

for c = 1, … ,N_c, where d_c ∈ ℂ^P contains all the measured data from the cth coil, F ∈ ℂ^N_p×N denotes the fully-sampled Fourier encoding matrix, Ω(·) : ℂ^N_p×M → ℂ^P is a linear operator that undersamples the k-space and then concatenates the measured data into a vector, and $P={\sum }_{m=1}^M{P}_m$ denotes the total number of measurements from the cth coil. Given that k-space is sampled far below the Nyquist rate in MRF, direct inversion of the data (e.g., with a gridding reconstruction) creates significant aliasing artifacts to time-series images. Although, with the incoherent signal excitation and acquisition, the conventional MRF reconstruction manages to produce artifact-free tissue parameter maps with a simple pattern-matching strategy, its performance is often heavily dependent on the length of a data acquisition train. Distinct from the conventional approach, here we utilize a low-rank and subspace model to reconstruct high-quality time-series images, from which we estimate MR tissue parameters. We will demonstrate that improved time-series images leads to better accuracy in tissue parameter estimation.

More specifically, we enforce a low-rank constraint on the Casorati matrix C, i.e., rank(C) ≤ L, to capture strong spatiotemporal correlation within MRF time-series images. Under this constraint, the matrix C only has L(M+N−L) degrees of freedom, which can be much less than the total number of entries of C, thus enabling the reconstruction of C from sub-Nyquist measurements. Mathematically, rank constraint can be enforced in a number of ways. For example, it can be replaced by a surrogate function (e.g., the nuclear norm (22), the Schatten p-norm (22), and the log-determinant function (25)). Alternatively, it can be imposed explicitly via matrix factorization (9,10,25), i.e., C = UV, where U ∈ ℂ^N×L and V ∈ ℂ^L×M. Note that the rows of U and columns of V respectively span the spatial and temporal subspaces of the Casorati matrix. For many imaging problems, the value of L is known a priori, or can be properly determined before image reconstruction. In such cases, the use of an explicit rank constraint can lead to better reconstruction performance and more efficient computation (11). Here we adopt this type of low-rank constraint, and the selection of L for MRF will be discussed later with concrete examples. Accordingly, the image reconstruction problem can be formulated as a low-rank matrix recovery problem (26), for which a number of numerical algorithms can be applied (e.g., (23, 24, 27, 28)).

Rather than directly solving a generic low-rank matrix recovery problem, we further incorporate a temporal subspace constraint (9, 11–13, 15, 17, 29) to simplify the image reconstruction problem. Specifically, in the context of MRF, a dictionary D ∈ ℂ^K×M can be constructed using Bloch simulations, which contains all possible signal evolutions. Ignoring the modeling error and quantization error in dictionary construction, the temporal subspace of C should be contained by the principal temporal subspace of D. As a consequence, we can pre-estimate V from D using the singular value decomposition. Note that with the subspace constraint, a “stronger” low-rank constraint is imposed by the proposed method. Mathematically, with a pre-estimated V̂, the image reconstruction problem reduces from a general low-rank matrix recovery problem to the following linear least-squares problem:

$$\widehat{\mathbf{U}}=arg\underset{\mathbf{U}}{min}\sum _{c=1}^{N_c}{\Vert {\mathbf{d}}_c-\mathrm{\Omega }(\mathbf{F}{\mathbf{S}}_c\mathbf{U}\widehat{\mathbf{V}})\Vert }_2^2,$$ [7]

which can be efficiently solved by a number of iterative numerical solvers (e.g., the conjugate gradient algorithm). Upon solving Eq. [7], we can form the Casorati matrix by Ĉ = ÛV̂. Then MR tissue parameter maps can be estimated on a voxel-by-voxel basis by pattern matching with the dictionary as in the conventional approach.

Methods

Data Acquisition

We performed in vivo MRF experiments to evaluate the performance of the proposed method for neuroimaging. Specifically, the experiments were conducted on a 3T Siemens Tim Trio scanner (Siemens Medical Solutions, Erlangen, Germany) equipped with a 32-channel receiver coil. A healthy volunteer was scanned with the approval from the Institutional Review Board. The inversion recovery fast imaging with steady state precession (IR-FISP) MRF pulse sequence was used in the experiments, which is immune to main magnetic field inhomogeneity (30). For this imaging sequence, the unknown tissue parameters include T₁, T₂, and spin density. We acquired k-space data using the spiral trajectory and data acquisition parameters (i.e., flip angles and repetition times (TR)) used in (30). A single spiral interleave was collected for each TR (or time point), and a set of fully-sampled data consists of 48 spiral interleaves. Other relevant imaging parameters were: field-of-view (FOV) = 300 × 300 mm², matrix size = 256 × 256, and slice thickness = 5 mm.

We acquired two imaging slices with the acquisition lengths M = 900 and 1400 time points, respectively. For each slice, we performed a standard MRF acquisition as described above. Similar to (3,30,31), we also collected a set of fully-sampled data for each slice to generate “gold-standard” data sets, from which we estimated T₁, T₂, and spin density maps as our references. More specifically, upon performing an MRF acquisition, we rotated the spiral trajectory at each time point, and proceeded with another acquisition. Here a single MRF acquisition was repeated 48 times. By grouping the data from all the acquisitions, we generated a set of fully-sampled spiral data for each time point. Note that a short delay (i.e., 10 sec) was given between consecutive acquisitions to ensure the recovery of magnetization to thermal equilibrium, and that the subject was informed to stay still during the acquisition process. As an example, the standard MRF acquisition for a single imaging slice with M = 900 took 11.8 sec, while the associated fully-sampled acquisition took 17.3 min.

In addition to the MRF experiments, we performed calibration scans using a vendor-provided gradient echo (GRE) sequence to estimate the coil sensitivities maps (32). Moreover, we measured the actual spiral trajectory experienced by the spins using a specialized pulse sequence (33), which avoids the effects of trajectory distortion caused by various acquisition imperfections (e.g., eddy currents and gradient timing delays).

Model Evaluation

We first evaluated the representational power of the proposed low-rank and subspace model in the “gold-standard” data which was fully sampled. The goal is to understand how the proposed model affects the accuracy of MR tissue parameter maps. Regarding the low-rank model evaluation, we formed the Casorati matrix C from the time-series images reconstructed from the fully-sampled data, and calculated its singular value spectrum. Furthermore, we calculated Eckart-Young approximations of C with different ranks using the singular value decomposition. Note that the rank-L Eckart-Young approximation Ĉ provides the best rank-L approximation of C in terms of minimizing the Frobenius norm of the approximation error, i.e., ||C − Ĉ ||_F. For each Ĉ, we estimated the associated tissue parameter maps with the same signal evolution dictionary as the one in (30). Specifically, the dictionary contains 18838 entries of signal evolutions constructed based on the following parameter discretization scheme: the possible T₁ values were set within [20, 3000] ms, with an increment of 10 ms; the possible T₂ values were set within [10, 300] ms, with an increment of 5 ms. Here we ignore transmission radiofrequency (RF) field inhomogeneity (i.e., $B_1^{+}$ inhomogeneity) in the dictionary construction (more discussion on the $B_1^{+}$ effect is in the Discussion section).

Regarding the evaluation of the subspace model, we extracted the dominant temporal subspaces of the dictionary D, and projected each row of C onto these subspaces to obtain low-rank approximations. More specifically, assuming that the rows of Ṽ ∈ ℂ^L×M span the dominant L-dimensional temporal subspace of D, the rank-L approximation of C, under the subspace model, can be expressed as C̃ = C(Ṽ^HṼ) ∈ ℂ^N×M. For each C̃, we estimated the corresponding tissue parameter maps.

To assess the accuracy of reconstructed parameter maps, we used the following two metrics: (i) overall normalized root-mean-square error (NRMSE) = ||θ − θ̂||₂/||θ||₂, where θ and θ̂ respectively denote the tissue parameters obtained from the fully-sampled reference and reconstruction; (ii) voxelwise error = |θ_n − θ̂_n|/θ_n, where θ_n and θ̂_n respectively denote the tissue parameters at the nth voxel obtained from the reference and reconstruction. Here, the regions associated with the background, skull, scalp, and cerebrospinal fluid are excluded in calculating the overall NRMSE.

Image Reconstruction

In order to test the proposed model in clinically relevant data, we assessed the performance of the proposed method for image reconstruction with standard MRF acquisitions with a 48× acceleration. As described before, we pre-estimated the sensitivity maps and the temporal subspace, and then solved Eq. [7] to determine the spatial subspace. According to the model evaluation above and the number of measurements acquired, we empirically selected the rank L = 8 to ensure the good reconstruction performance (more discussion on rank selection can be found in the Discussion section). After reconstruction, we estimated tissue parameter maps using the pattern matching strategy as in the conventional approach. Here the same signal evolution dictionary as before was used for pattern matching.

We compared the performance of the proposed method to the “gold-standard” reference data. Similarly, we computed the NMRSE and error maps of the conventional MRF reconstruction (1) and the ML reconstruction (3). Moreover, to evaluate the robustness of the methods with shorten acquisition lengths, we retrospectively took the k-space data associated with the first 700 TRs from the MRF acquisition with M = 1400, and manually formed a truncated MRF acquisition with M = 700. We compared the reconstruction performance at M = 700 with the one at M = 1400 for the first imaging slice. Finally, we performed a comparison of the proposed method with the conventional approach and the ML reconstruction for the second imaging slice with M = 900.

The above three reconstruction methods were implemented on a Linux workstation with 24 Intel Xeon E5-2643, 3.40 GHz processors and 128 GB RAM using Matlab 2014b. Generally, the runtime of the above image reconstruction methods depends on the length of data acquisition. As a concrete example, for M = 700, the computation time of the conventional approach, ML reconstruction, and proposed method are 2 min, 36 min, and 22 min, respectively. Here note that the ML reconstruction involves solving a nonconvex optimization problem, for which the reconstruction performance and runtime depend on the specific algorithm and initialization. Following (3), we solved the ML reconstruction by the alternating direction method of multipliers, and initialized it with the gridding reconstruction. For the proposed method, it is solved by the pre-conditioned conjugate gradient algorithm (a set of sample code can be accessed at https://sites.google.com/site/zhaoboresearch/software

Results

We show representative results from the in vivo MRF experiments to illustrate the performance of the proposed method.

Model Evaluation

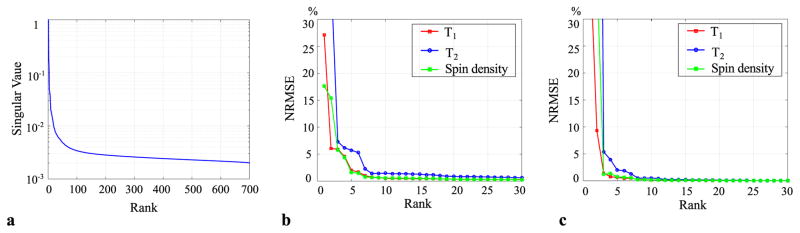
Figure 1 shows the results of the low-rank and subspace model evaluation. Here we aim to illustrate the model representational power with fully-sampled data. This provides benchmarks for image reconstruction with undersampled MRF acquisitions. Figure 1a plots the singular value spectrum of the Casorati matrix associated with the time-series images with M = 700. As expected, the singular values decay rapidly due to strong spatiotemporal correlation within the time-series images. Figure 1b plots the overall NRMSE of T₁, T₂, and spin density maps from the Eckart-Young approximations with the rank L ranging from 1 to 30. As can be seen, with a relatively small rank value (e.g., L = 6 ~10), the low-rank approximations are able to provide very accurate T₁, T₂, and spin density maps (i.e., NRMSE < 1%).

Fig. 1.

Low-rank approximations of a Casorati matrix associated with a set of in vivo MRF time-series images with M = 700. a: Normalized singular value spectrum of the Casorati matrix. b: NRMSE of MR tissue parameters estimated from the Eckart-Yong approximations with different ranks. c: NRMSE of MR tissue parameters estimated from the proposed low-rank and subspace models with different ranks.

Figure 1c plots the overall NRMSE of T₁, T₂, and spin density maps estimated from the proposed low-rank and subspace model. Interestingly, the proposed model provides even more accurate parameter maps than the Eckart-Young low-rank approximation. This is likely due to the fact that the Eckart-Young approximations are optimal in terms of minimizing the approximation errors, but the Eckart-Young subspaces, which are estimated from in vivo time-series images, are susceptible to noise perturbation. In contrast, the subspaces extracted from the dictionary are noise free, which turns out to provide better accuracy. In the Supporting Material of the paper, Supporting Figure S1 shows the T₁, T₂, and spin density maps from the reference and the proposed model with L = 8, together with the associated voxelwise error maps. Consistent with the NRMSE plot shown in Figure 1c, the proposed model yields accurate tissue parameter maps. Qualitatively, the edge structure of these parameter maps is well preserved, which is highly desirable.

Image Reconstruction

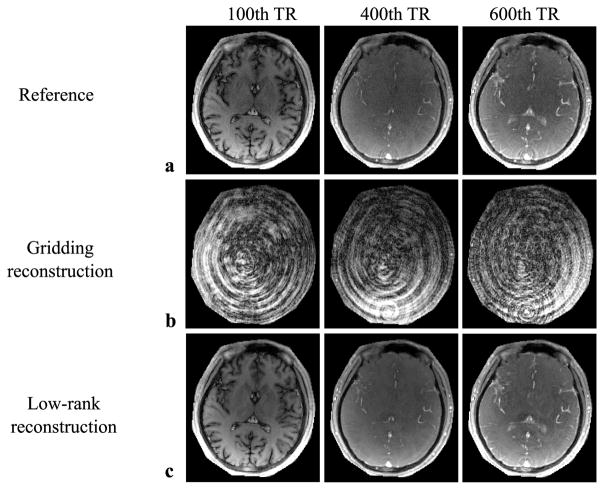
Figure 2 shows the example time-series images obtained from the gridding reconstruction (employed by the conventional approach) and the proposed method with L = 8. Here the data are from the MRF acquisition with M = 700. For comparison, we also show the corresponding time-series images reconstructed from the fully-sampled data. Clearly, with the low-rank and subspace model, the proposed method produces much higher-quality time-series images than the gridding reconstruction.

Fig. 2.

Representative MRF time-series images from the reference (reconstructed with a set of fully-sampled data), as well as the gridding reconstruction and the proposed low-rank reconstruction (both reconstructed with a 48× accelerated spiral acquisition). a: Time-series images from the reference. b: Time-series images from the gridding reconstruction. c: Time-series images from the proposed low-rank reconstruction. Here the regions associated with the background are set to be zero. As can be seen, the proposed method reconstructs high-quality time-series images from highly-undersampled data, whereas the gridding reconstruction suffers from severe aliasing artifacts.

Supporting Figure S2 in the Supporting Material illustrates the subsequent pattern matching with the time-series images obtained from the fully-sampled data, the gridding reconstruction, and the proposed method. The plots show the intensity from a white-matter voxel. Although, with the spatiotemporal incoherence, the conventional approach manages to produce tissue parameters with reasonable accuracy, the high-quality time-series images reconstructed by the proposed method is able to provide estimates closer to the “gold-standard” data.

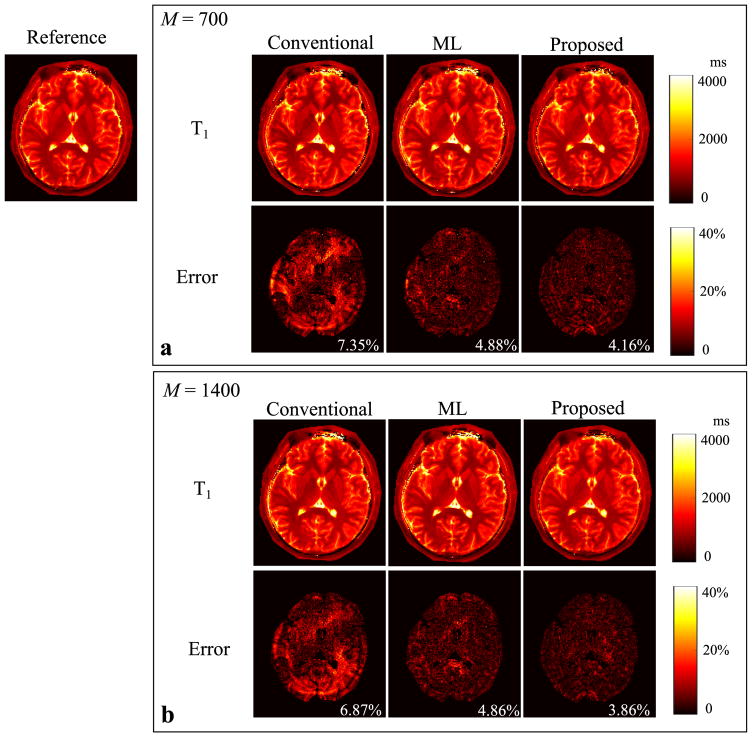
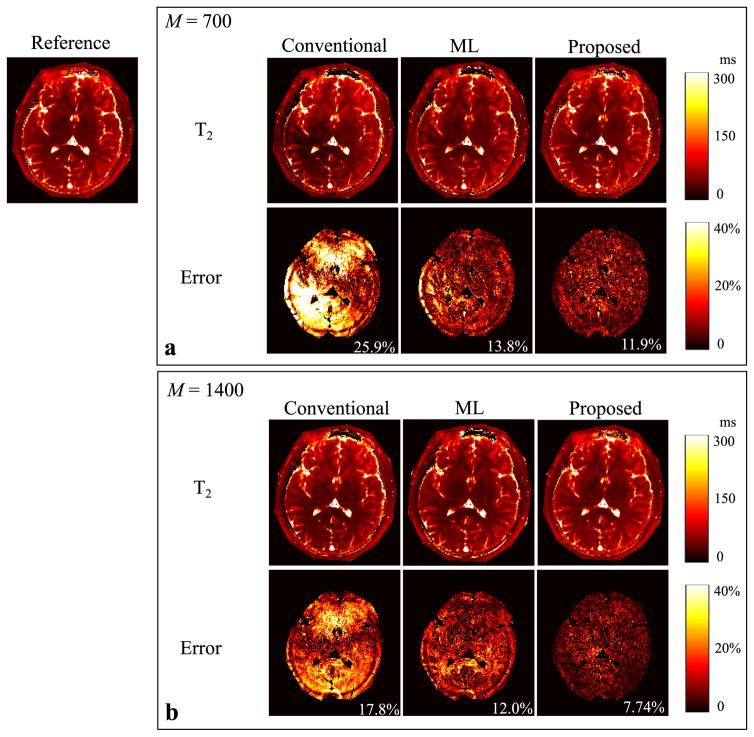
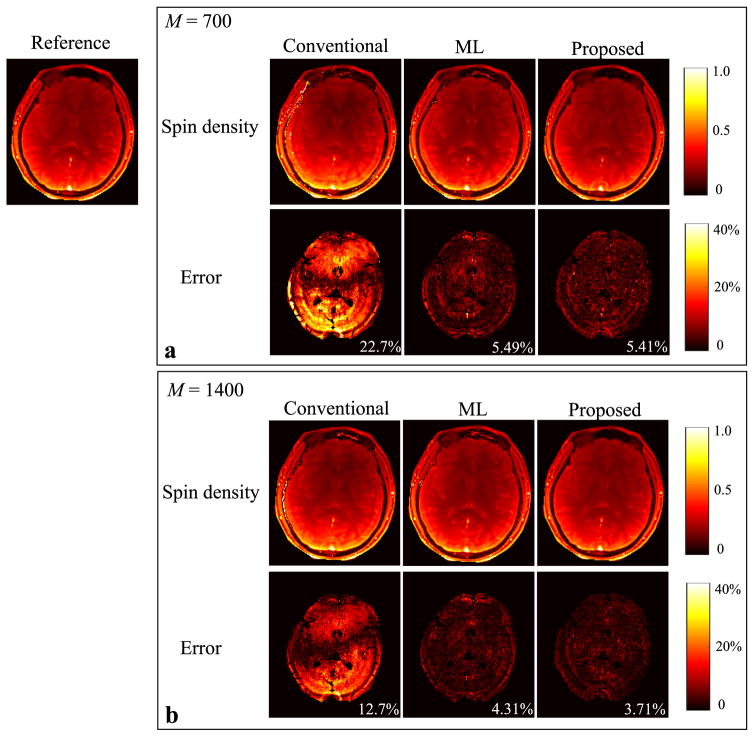
Figure 3 shows the reconstructed T₁ maps from the conventional approach, the ML reconstruction, and the proposed method with the two acquisition lengths, i.e., M = 700 and 1400. The error maps were computed by comparing to the reference from the “gold-standard” fully-sampled acquisition. Similarly, we show the reconstruction results for the T₂ maps and spin density maps in Figure 4 and Figure 5, respectively. As can be seen, all three reconstruction methods yield improved performance as the acquisition length doubles. But the proposed method outperforms the conventional approach and the ML reconstruction at both acquisition lengths. In particular, the proposed method with M = 700 provides even more accurate tissue parameter maps than the conventional approach with M = 1400.

Fig. 3.

Reconstructed T₁ maps for the slice 1 from the conventional MRF reconstruction, the ML reconstruction, and the proposed method (L = 8) with two acquisition lengths (i.e., M = 700 and 1400). a: Reconstructed T₁ maps and corresponding error maps from the acquisition length M = 700. b: Reconstructed T₁ maps and corresponding error maps from the acquisition length M = 1400. Note that the overall NRMSE is labeled at the lower right corner of each error map, and that the regions associated with the background, skull, scalp, and CSF are not included into the NRMSE calculation, and are set to be zero in each error map.

Fig. 4.

Reconstructed T₂ maps for the slice 1 from the conventional MRF reconstruction, the ML reconstruction, and the proposed method (L = 8) with two acquisition lengths (i.e., M = 700 and 1400). a: Reconstructed T₂ maps and corresponding error maps from the acquisition length M = 700. b: Reconstructed T₂ maps and corresponding error maps from the acquisition length M = 1400. Note that the overall NRMSE is labeled at the lower right corner of each error map, and that the regions associated with the background, skull, scalp, and CSF are not included into the NRMSE calculation, and are set to be zero in each error map.

Fig. 5.

Reconstructed spin density maps for the slice 1 from the conventional MRF reconstruction, the ML reconstruction, and the proposed method (L = 8) with two acquisition lengths (i.e., M = 700 and 1400). a: Reconstructed spin density maps and corresponding error maps from the acquisition length M = 700. b: Reconstructed spin density maps and corresponding error maps from the acquisition length M = 1400. Note that the overall NRMSE is labeled at the lower right corner of each error map, and that the regions associated with the background, skull, scalp, and CSF are not included into the NRMSE calculation, and are set to be zero in each error map.

Supporting Figure S3 in the Supporting Material shows the reconstructed tissue parameter maps associated with the slice 2 with the acquisition length M = 900. Similar to the results for the slice 1, the proposed method leads to significant improvement of accuracy over the conventional approach. Here with the low-rank and subspace model, the proposed method also provides better accuracy than the ML reconstruction.

Discussion

We have demonstrated the effectiveness of the proposed method in terms of improving the reconstruction accuracy and/or reducing data acquisition time for MRF. The proposed method utilizes the low-rank and subspace model to enable accurate MRF parameter estimates from highly-undersampled data. Note that it is fundamentally different from the recent work in (34), which employs the low-rank and subspace model to reduce the dimensionality of the dictionary and thus speeds up the pattern matching for the conventional MRF reconstruction. Here we leverage the low-dimensional model to solve an ill-posed inverse problem for high-quality time-series image reconstruction. More specifically, for the work in (34), the reconstruction accuracy is similar to that of the conventional approach, while the computational efficiency is improved. In contrast, the proposed method provides much better accuracy over the conventional approach.

The proposed method requires selection of a proper rank value, which involves a fundamental trade-off between the model representational power and the amount of measurements collected. On one hand, as shown in Figure 1, a higher rank generally leads to a better representation of time-series images as well as more accurate tissue parameter maps. On the other hand, it requires collecting a larger number of measurements (i.e., longer acquisition time). A necessary (but not sufficient) condition for a well-posed least-squares problem in Eq. [7] is LN < PN_c. In practice, due to temporal undersampling and correlated multicoil measurements, when the number of unknowns approaches the number of measurements, the conditioning of the inverse problem becomes worse, which can incur severe noise amplification. An effective means of addressing this trade-off is to incorporate additional regularization to improve the conditioning of the problem. For example, our early work (15,18) has demonstrated the effectiveness of enforcing a joint sparsity constraint on time-series images, although this constraint can result in a more complex optimization problem.

In this paper, we evaluated the performance of the proposed method with in vivo experiments in which the “gold standard” data were acquired from fully-sampled MRF experiments. Besides the experimental validation, we also carried out systematic simulation studies with a numerical brain phantom (the ground truth T₁, T₂, and spin density maps are shown in Supporting Figure S4). The simulation results can be found at the Supporting Material of the paper (see Supporting Figure S5 and Supporting Figure S6). Simply put, the proposed method leads to improved accuracy over the conventional MRF reconstruction and the ML reconstruction in the simulations, which is consistent with the in vivo results shown in the paper.

Over the past few years, the low-rank and subspace model-based imaging paradigm (9) has been successfully applied to a variety of imaging applications, including cardiac imaging (11, 35, 36), phase-contrast flow imaging (37, 38), speech imaging (39), functional MRI (40), spectroscopic imaging (41), and parameter mapping (12, 13, 15, 17, 42). Our contribution here is to utilize the low-dimensional subspace structure of magnetization dynamics to enable reconstruction of high-quality MRF time-series images from highly-undersampled data. Rather than estimating a temporal subspace from some physically-acquired training data, the proposed method determines the subspace structure directly from the magnetization evolution dictionary (obtained from Bloch simulations), alleviating the burden of acquiring additional training data. As demonstrated in this work, this subspace estimation scheme works well for neuroimaging applications, where physiological motion often does not dominate. Nonetheless, this may have potential limitations. Specifically, such a scheme relies on the assumption that an accurate dictionary for spin dynamics is known a priori. It may be too stringent for certain quantitative imaging application (e.g., applying MRF to cardiac imaging (43) or fetal imaging (44)), in which the subspace structure cannot be not fully described by the spin-dynamics alone. In such scenarios, acquiring training data, e.g., with a navigator approach (9, 11, 15, 35), can be beneficial in terms of effectively capturing physiological motion (e.g., heart beating or breathing motion). Alternatively, we could also perform simultaneous estimation of spatial subspace and temporal subspace from all the measurements in an iterative manner using advanced algorithms (e.g., (10, 23, 25)). It is worthwhile to systematically explore these extensions in future work.

In this work, we have not considered $B_1^{+}$ inhomogeneity for neuroimaging applications at 3T. Nonetheless, for body imaging (45) or ultrahigh field imaging applications (46, 47), $B_1^{+}$ inhomogeneity can be significantly more severe, which should be properly compensated. Given that the proposed method is based on a two-step procedure as the conventional approach, the existing $B_1^{+}$ inhomogeneity compensation schemes for MRF (30, 45, 47) can be applied after the proposed time-series image reconstruction. Here note that modeling $B_1^{+}$ inhomogeneity can lead to an expanded signal evolution dictionary, which may require a higher-dimensional temporal subspace (or a larger rank) for image reconstruction to ensure good accuracy.

Recently, there has been active research in developing model-based imaging methods to accelerate conventional MR relaxometry (e.g., (12–17, 48–56)). In this respect, the distinction between MRF and these accelerated parameter mapping methods can become blurred, and the existing model-based relaxometry methods could potentially be applied to accelerate MRF. Nonetheless, MRF experiments have a number of unique characteristics that are different from conventional MR relaxometry (e.g., randomized acquisitions). The effectiveness of applying these methods to MRF should be evaluated on a method-by-method basis.

Conclusions

This paper presents a model-based reconstruction method for MRF. It effectively integrates the low-rank and subspace modeling with parallel imaging to reconstruct high-quality time-series images from highly-undersampled MRF acquisitions. These improved time-series image reconstructions are shown to enhance the accuracy of resulting tissue parameter maps. The proposed method employs a simple least-squares reconstruction formulation, allowing for efficient computation. Given its simplicity and effectiveness in enabling reduced acquisition times, we expect that the proposed method will have a practical impact on rapid quantitative MRI with MRF.