Quantifying the influence of measured and unmeasured individual differences on demography

Summary

1. Demographic rates can vary not only with measured individual characters like age, sex and mass but also with unmeasured individual variables like behaviour, genes and health.

2. Predictions from population models that include measured individual characteristics often differ from models that exclude them. Similarly, unmeasured individual differences have the potential to impact predictions from population models. However, unmeasured individual differences are rarely included in population models.

3. We construct stage-and-age structured models (where stage is mass) of a roe deer population, which are parameterized from statistical functions that either include, or ignore, unmeasured individual differences.

4. We found that mass and age structures substantially impacted model parameters describing population dynamics, as did temporal environmental variation, while unmeasured individual differences impacted parameters describing population dynamics to a much smaller extent once individual heterogeneity related to mass and age has been included in the model. We discuss how our assumptions (unmeasured individual differences only in mean trait values) could have influenced our findings and under what circumstances unmeasured individual differences could have had a larger impact on population dynamics.

5. There are two reasons explaining the relative small influence of unmeasured individual differences on population dynamics in roe deer. First, individual body mass and age both capture a large amount of individual differences in roe deer. Second, in large populations of long-lived animals, the average quality of individuals (independent of age and mass) within the population is unlikely to show substantial variation over time, unless rapid evolution is occurring. So even though a population consisting of high quality individuals would have much higher population growth rate than a population consisting of low quality individuals, the probability of observing a population consisting only of high quality individuals is small.

Graphical abstract

Introduction

The effects of among- and within-individual variation can markedly influence population dynamics, particularly in mammals (Benton, Plaistow & Coulson, 2006; Caswell, 2001). Most previous studies of factors generating individual variation in survival and reproduction have focused on size/mass, sex and age (Caswell, 2001). Age and mass both influence population growth when survival and reproductive rates vary substantially between small and large individuals, or between those that are young, prime-aged and elderly (Eberhardt, 1985; Gaillard et al., 2000b; Caswell, 2001). Most studies have focused on these attributes because they are both important for population dynamics (Albon et al., 2000; Gaillard et al., 2000b; Caswell, 2001) and often easy to measure. However, among the myriads of characters that are left unmeasured in most studies, some are known to influence survival and/or reproductive rates (e.g., behaviour (Reid et al., 2004), genes of known and unknown function (Peripato et al., 2002), disease state (Jolles, Cooper & Levin, 2005)) and thus might be important for modeling population dynamics.

Age or stage structure can shape population dynamics when the age or mass structure of the population fluctuates in response to environmental variation caused by climatic conditions or intra- or inter-specific competition (Coulson et al., 2001). The same logic applies to unmeasured individual differences: changes in the proportion of high quality individuals within the population in response to variation in environmental conditions or population density will cause the distribution of unmeasured individual differences to change, which should alter population dynamics. Although unmeasured individual differences influence numerous life history traits, little is known about their impact on population dynamics (but see Rees et al. (1999) on plants, Caswell (2011)). Nonetheless there is growing evidence that unmeasured characters have the potential to affect demography (Vindenes, Engen & Sæther, 2008; Kendall et al., 2011). For example, individuals differ in their expected survival and reproduction as a function of their susceptibility to stochastic factors (Kendall & Fox, 2003), with individual stochasticity strongly shaping the distribution of individual lifetime reproductive success in birds (see Tuljapurkar, Steiner & Orzack (2009) on swans, Cygnus olor and Steiner, Tuljapurkar & Orzack (2010) on kittiwakes, Rissa tridactyla).

Individual differences in performance that cannot be easily attributed to a specific measured character (Lewis et al., 2006; Stopher et al., 2008; Aubry et al., 2009; Knape et al., 2011) are widely studied in ecology and evolution via the use of generalized linear mixed effect models. The use of these models supports the existence of individual heterogeneity in reproductive traits (van de Pol & Verhulst, 2006) and survival (Cam et al., 2002) that can mask life history trade-offs (van Noordwijk & de Jong, 1986), including senescence (Nussey et al., 2008). Assumptions about unmeasured individual differences vary among studies but they all aim to capture individual differences that are not accounted for by measured fixed effects such as age or mass. The influence of unmeasured characters (whether genetic, phenotypic, morphological or something else) on a life history is captured by models that include individual identity as a random effect. Such random effects have been used to estimate latent individual quality and have been interpreted as heterogeneity in individual frailty (Link, Cooch & Cam, 2002; Vaupel, Manton & Stallard, 1979) but they can also be generated by stochastic factors. For instance, individuals with the same latent quality are likely to have different fates in response to random events and thereby display different trajectories of reproduction and/or survival (dynamic heterogeneity sensu Tuljapurkar, Steiner & Orzack 2009; Caswell 2011).

The influence of unmeasured individual differences on population growth can be estimated in two ways (Coulson, 2012). First, one can compare predictions from population models parameterized with estimates obtained from statistical analyses that do, and do not, correct for unmeasured individual differences. Second, the magnitude of unmeasured individual differences in demographic performance can explicitly be incorporated into models (Rees et al., 1999; Ellner & Rees, 2006; Lindberg, Sedinger & Lebreton, 2013) to compare populations of high or low quality. We used both approaches to construct Integral Projection Models (IPMs) for a population of roe deer. IPMs provide a useful tool to study the consequences of individual variation on demography (Vindenes, Engen & Sæther, 2008) because they offer a process-oriented way to study the dynamics of continuous character distributions (Easterling, Ellner & Dixon, 2000; Ellner & Rees, 2006). IPMs are straightforward to parameterize using generalized linear mixed effect models (Ellner & Rees, 2006; Jacquemyn, Brys & Jongejans, 2010; Coulson, 2012) and perturbation analyses can be used to explore how sensitive model predictions are to model parameters (Caswell, 1978; Rose, Rees & Grubb, 2002; Coulson, Tuljapurkar & Childs, 2010).

We compared the influence of age and mass, measured characters, with the additional (in models already including measured characters) influence of unmeasured random individual differences on the dynamics of a population of roe deer (Gaillard et al., 1998b, 2000a). Considering the influence of individual heterogeneity on demographic rates (Nussey et al., 2008) and on demographic stochasticity and population dynamics (Kendall et al., 2011), we expect individual differences to impact population growth rate, net reproductive rate and generation time as well as demographic structure. Nevertheless, given the large amount of variation in body mass (Nussey et al., 2011) and age (Coulson et al., 2001) observed in populations of large herbivores, we expected that variation in body mass and age would impact population dynamics more than other (unmeasured) individual differences.

Materials and methods

Study population and data collection

The studied population of roe deer inhabits an enclosed area of 1,360 ha in the Trois Fontaines forest in North-eastern France (48°43’N, 2°61’W). Over the study period, population size was controlled to be around 250 individuals older than 1 year of age by yearly removals (Gaillard et al., 1993), except between 2001–2005 when an experimental manipulation of density was performed and population size peaked at 450 individuals. The roe deer is a long-lived and iteroparous species, with most females (>95%, Gaillard et al. 1998b) aged two years or older giving birth every year in May to either a single or twin fawns. The maximum known age at death of females was eighteen years, with a mean lifespan of 8.5 years. The demographic rates of roe deer are largely influenced by age (Gaillard et al., 1993, 1998a). Newborn fawns are characterized by a low survival and a rapid growth, prime-aged individuals show a high and constant survival, body mass and reproductive rates, and demographic rates decrease among old individuals from 8 years of age. Reproductive patterns are also influenced by individual body mass (Hamel et al., 2009a). The population is not subject to systematic predation by large predators or by hunting, and the few animals killed by humans were right-censored.

The roe deer population has been intensively monitored since 1975 by the Office National de la Chasse et de la Faune Sauvage (Gaillard et al., 1993). Most roe deer are marked with both numbered ear tags and leather collars. Each year, between 120–300 roe deer are caught between December and March. Individuals captured for the first time are sexed and marked and all captured individuals are weighed to the nearest 100g. The age and sex of all individuals considered here are accurately known because they were captured within their first year of life either as newborn (Delorme, Gaillard & Jullien, 1988) or as 8 months old during winter captures when age is determined by the tooth eruption sequence (Flerov, 1952). When possible, the identity of the mother of a fawn is assigned by direct observations of lactating behaviour or by the identification of an escaping female in the vicinity of the fawn.

Estimation of demographic rates

We start by defining a as age, t as time and z as the continuous measured character, body mass. IPMs model the dynamics of a distribution of a continuous character over time (Easterling, Ellner & Dixon, 2000; Ellner & Rees, 2006). IPMs include four functions (the demographic rates) that fully describe changes in the character distribution between two consecutive time steps (year). These are: i) the association between the character and survival (S(a, t, z)), ii) the association between the character and recruitment (M(a, t, z)), iii) the probability of expressing a given character value at time t + 1 given the character value at time t conditional on survival (Growth, G(a, t, z′|z)), and iv) the probability of producing an offspring with a given character value at time t + 1 given the parental character value at time t conditional on reproduction (Inheritance, D(a, t, z′|z)). Following standard terminology in IPM literature (Coulson et al., 2011; Coulson, 2012), we defined inheritance as the part of the trait that is transmitted from mothers to offspring, whatever the mechanism of transmission. The distribution of body mass n(a + 1, t + 1, z′) in the population at time t + 1 depends on the distribution of body mass n(a, t, z) at time t and on the four functions. Then:

$$n(1,t+1,z\prime )={\sum }_a\int \mathit{\text{dzD}}(a,t,z\prime |z)M(a,t,z)n(a,t,z)$$

$$n(a+1,t+1,z\prime )=\int \mathit{\text{dzG}}(a,t,z\prime |z)S(a,t,z)n(a,t,z),a\ge 1$$

Vital functions are integrated over a range larger than observed body mass values. The continuous IPM can be approximated as a high dimensional discrete matrix A (see Appendix S1) (Easterling, Ellner & Dixon, 2000).

We restricted the analyses to females because the required data for males (father-fawn affiliation in particular) were lacking. We thus modelled the distribution of female body mass only. To parameterize IPMs, we estimated the four functions using regression models that included year as a random effect to correct for yearly variation of each demographic rate, body mass as a fixed covariate, age class as a fixed factor and an individual random effect in models including the influence of unmeasured individual differences. Body mass is a good predictor of individual quality in roe deer (Hamel et al., 2009b) with statistically significant positive effects in all IPM functions (see Table S3). Both survival and reproduction of roe deer are strongly age-structured. As in most species of large herbivores studied so far (Gaillard et al., 2000b), demographic performance of roe deer females first increases from yearling to prime-aged adults (from 2 to 8 years of age, Gaillard et al. 1993), and then decreases as a result of senescence (in a two-step process in roe deer survival, a first between 8 and 11 years of age and a second after 11 years of age, Festa-Bianchet, Gaillard & Côté 2003). Thus, the most complex age model included 4 different classes (1, 2–7, 8–11, 12+). Unmeasured individual differences can be corrected for in statistical models using generalized linear mixed effect models with individual identity as a random effect on the overall intercept (Nussey et al., 2008). For instance, the estimated variance of unmeasured individual differences for recruitment represents the amount of individual differences that is unrelated to age and body mass if these are fitted as fixed effects in expected recruitment.

The recruitment function adds new individuals to the population and in our case, gives the number of offspring a female of a given age and body mass has weaned successfully (i.e., that survived until 8 months of age) The recruitment function, i.e. the number of offspring successfully weaned by mothers of body mass z and age a was decomposed into two functions: the probability of successfully weaning at least one fawn (realized fertility, F(a, t, z)), and the probability of producing twins conditional on successful reproduction (twinning rate, ϕ(a, t, z)). The parameters in the functions F(a, t, z) and ϕ(a, t, z) were estimated using a generalized linear mixed model with a binomial error structure linking realized fertility or twinning rate to body mass, age, year (Y ) and individual identity (I, when including unmeasured individual effect in the model) using the lme4 package in R. For the realized fertility function for instance,

$$F(a,t,z)=\frac{e^{{\alpha }_F(a,t)+{\beta }_F\ast z(t)+{\epsilon }_{Y,F}+{\epsilon }_{I,F}}}{1+e^{{\alpha }_F(a,t)+{\beta }_F\ast z(t)+{\epsilon }_{Y,F}+{\epsilon }_{I,F}}},{\epsilon }_{Y,F}~N(0,s_{Y,F}^2),{\epsilon }_{I,F}~N(0,s_{I,F}^2)$$

where α and β are the intercept and the slope of the model, and, $s_Y^2$ and $s_I^2$ are the variances of the random effect of year (Y) and individual identity (I), respectively.

Regressions were performed on 805 potential breeding events of 233 females for realized fertility (Fig. 1 D) and on 588 effective breeding attempts of 212 females for twinning rate (Fig. 1 E). The recruitment function for a female of body mass z, age class a, at time t was then F(a, t, z)*(1+ϕ(a, t, z))/2. We divided the recruitment by 2 because we used a female-based model. We then assumed a balanced sex ratio at recruitment (i.e. 8 months of age). In the absence of between-sex differences in fawn survival in roe deer (Gaillard et al., 1997), this measure provides a reliable estimate of the number of daughters recruited by females.

Figure 1.

Growth (A), inheritance (B), survival (C), realized fertility (D) and twinning rate (E) functions used to build the three age-class IPM (Model 6, Tables 1 and S1): yearling (dark grey dotted lines), prime-aged (2–7 y.o., black solid lines) and senescent (>7 y.o., grey dashed lines) females. For the growth (inheritance) function, at each female body mass at t corresponds a normal distribution of female (offspring) body mass at t+1. The mean transitions from female body mass at t to female (offspring) body mass at t + 1 are presented. (A–B) Each point represents an individual. (C–D) The size of points are proportional to the number of observed individual values for a given body mass.

The survival function removes individuals from the distribution through mortality by linking individual probability of surviving to body mass. The exact age of death was known for all females in the data set used to estimate the survival function. We consequently did not need to correct for the confounding effects of imperfect detection on survival estimates (Gimenez et al., 2008). For the survival function, random effects cannot reliably estimate heterogeneity in survival because a given individual must only die once. To assess the amount of unmeasured individual differences in the survival function we used a frailty model. We tested for individual heterogeneity in the survival function using a parametric model with a logit link, including continuous effects of body mass and age but excluded the effect of year to minimize the number of parameters to estimate. We modeled individual frailty as a normally distributed random effect with one degree of freedom, using the functions frailty and survreg of the package "survival" (Therneau, 2014) in R. We found no significant effect of unmeasured individual differences on the survival function. To avoid missing any heterogeneity in frailty in the population which can have important effect on population dynamics (Vaupel & Yashin, 1985), we investigated potential model convergence problems. To do so, we used a generalized linear mixed model and the package MCMCglmm to model the survival between two time steps with a two-level (0,1) multinomial distribution and including fixed effects of body mass and age classes, and random effects of both unmeasured individual differences and year. Using this Bayesian framework, we investigated the robustness of parameter estimates with varying prior distributions and numbers of iterations. As with the frailty survival model, we found no influence of unmeasured individual differences on survival. Consequently, we used the parameters estimated from a generalized linear mixed model with both discrete age classes and continuous body mass as fixed effects, and a random effect of year to parameterize the S(a, t, z) function of our IPM based on 398 episodes of survival for 99 females (Fig. 1C). The parameterization of the survival function is therefore similar to the fertility and the twinning rate functions, but excluding individual random effect.

$$S(a,t,z)=\frac{e^{{\alpha }_S(a,t)+{\beta }_S\ast z(t)+{\epsilon }_{Y,S}}}{1+e^{{\alpha }_S(a,t)+{\beta }_S\ast z(t)+{\epsilon }_{Y,S}}},{\epsilon }_{Y,S}~N(0,s_{Y,S}^2)$$

The growth function transforms mass within the distribution by giving the transition probability between mass at t and at t+1 and the inheritance function determines the mass of the new recruits in the population as a function of the mass and the age of their mother. The growth G(a, t, z′|z) and inheritance D(a, t, z′|z) functions were assumed to be normal probability density functions with means μ_Gro(a, t, z) and μ_Inh(a, t, z) and variances ${\sigma }_{\mathit{\text{Gro}}}^2(a,t,z)$ and ${\sigma }_{\mathit{\text{Inh}}}^2(a,t,z)$, respectively. For growth (inheritance), each body mass (maternal body mass) z at t predicts a normal distribution of body masses (offspring body mass) z′ at t + 1:

$$G(a,t,z\prime |z)=\frac{1}{\sqrt{2\pi }{\sigma }_{\mathit{\text{Gro}}}(a,t,z)}{e}^{-\frac{{(z\prime -{\mu }_{\mathit{\text{Gro}}}(a,t,z))}^2}{2{\sigma }_{\mathit{\text{Gro}}}^2(a,t,z)}}$$

$$D(a,t,z\prime |z)=\frac{1}{\sqrt{2\pi }{\sigma }_{\mathit{\text{Inh}}}(a,t,z)}{e}^{-\frac{{(z\prime -{\mu }_{\mathit{\text{Inh}}}(a,t,z))}^2}{2{\sigma }_{\mathit{\text{Inh}}}^2(a,t,z)}}$$

The growth function was estimated using 488 measures of body mass for 233 females (Fig. 1 A). As we expected that relationship between two successive body masses should change with age class (i.e. a yearling must grow faster than any prime-aged individual), we performed two models including or not an interaction between age and body mass. We found no evidence of such an interaction between body mass and age (Likelihood ratio test: χ² = 2.140, df = 2, P = 0.343). As a consequence, the mean of the growth function, μ_G(a, t, z) was estimated from the linear mixed model between body mass z′ at time t + 1 and body mass z, age a at time t, and year and individual identity (when included) as random effects. The variance ${\sigma }_G^2(a,t,z)$ was estimated with a the linear mixed regression using the squared residuals of the previous relationships (see Coulson 2012; Rees, Childs & Ellner 2014 for further details). As the model for the variance of the growth function was never investigated in roe deer, we selected the best model that described the data using the Akaike Information Criterion. We fitted four models: a model including an effect of age and body mass, a model including an effect of age, a model including an effect of body mass and an intercept only model. The variance of the growth function was best fitted by a model with an effect of age (all ΔAIC > 3).

$${\mu }_G(a,t,z)={\alpha }_{{\mu }_G}(a,t)+{\beta }_{{\mu }_G}(a)\ast z(t)+{\epsilon }_{Y,{\mu }_G}+{\epsilon }_{I,{\mu }_G},$$

$$\text{with }{\epsilon }_{Y,{\mu }_G}~N(0,s_{Y,{\mu }_G}^2),{\epsilon }_{I,{\mu }_G}~N(0,s_{I,{\mu }_G}^2).$$

$${\sigma }_G^2(a,t)={\alpha }_{{\sigma }_G^2}(a,t)+{\epsilon }_{Y,{\sigma }_G^2}+{\epsilon }_{I,{\sigma }_G^2},$$

$$\text{with }{\epsilon }_{Y,{\sigma }_G^2}~N(0,s_{Y,{\sigma }_G^2}^2),{\epsilon }_{I,{\sigma }_G^2}~N(0,s_{I,{\sigma }_G^2}^2).$$

The inheritance function was defined similarly to the growth function. The regression between mother and offspring body mass was performed on 109 offspring from 64 mothers and an additive effect of sex was included in the model to keep only the intercept linking mothers to female fawns (Fig. 1 B, Table S1). By visual inspection, we could suspect that offspring body mass deviates from a Gaussian distribution. However, a Kolmogorov-Smirnov test did not lead us to reject the hypothesis that the distribution followed a Gaussian distribution (Inheritance: D = 0.087, P = 0.379). The variance of the inheritance function was best fitted using a model with an intercept only (all ΔAIC > 1).

We recorded the parameters (intercepts, slope and variances of the random effects) of each function to parameterize IPMs. We created 200 body mass classes between 1 and 44kg, the heaviest female roe deer recorded being 32kg. The matrices contained 12 ages (with similar survival, growth, reproduction and inheritance within a given age class). The last age-class pooled together all females older than 12 years (senescent females). Consequently, our matrix A had 2400 (12 × 200) columns and rows (see Appendix S1). The outputs of the IPM were the parameters describing the population dynamics: the population growth rate, the net reproductive rate and the generation time. These parameters were estimates that were averaged over years as we used year as a random effect to parameterize the functions and build an IPM that does not vary over years. All statistical analyses were performed with the software R using code (see Appendix S2) based on Easterling, Ellner & Dixon (2000) and Coulson, Tuljapurkar & Childs (2010).

IPM model: modelling unmeasured individual differences

The first analysis that can be done to investigate the influence of unmeasured individual differences on population growth involves constructing IPMs using statistical functions identified from generalized linear mixed models with, and then without, individual identity included as a random intercept. For example, the recruitment function could take two forms:

• without unmeasured individual differences:

  $$M_0(a,t,z)=f({\alpha }_0(a,t)+{\beta }_0\ast z(t)+{\epsilon }_Y)\text{ with }{\epsilon }_Y~N(0,s_Y^2),$$

  where α(a, t) is the intercept β, the slope linking recruitment to body mass and $s_Y^2$ is the variance of the random effect of year of the recruitment function. f represents a link function.
• including unmeasured individual differences:

  $$M_I(a,t,z)=f({\alpha }_I(a,t)+{\beta }_I\ast z(t)+{\epsilon }_Y+{\epsilon }_I)\text{ with }{\epsilon }_I~N(0,s_I^2),$$

  where $s_I^2$ is the variance of the random effect of individual identity on the intercept of the recruitment function.

The second analysis that can be performed is a perturbation analysis by adding P_I to the intercept of one of the four functions, corresponding to a change in the average of the unmeasured trait(s) among individuals within the population. For instance, the recruitment function becomes:

$$M_I(a,t,z)=f({\alpha }_I(a,t)+{\beta }_I\ast z(t)+{\epsilon }_Y+P_I+{\epsilon }_I)$$

The influence of unmeasured individual differences on population dynamics can be assessed by comparing situations in which P_I represents a hypothetical population consisting of high (P_I > 0) or low (P_I < 0) average quality of individuals within the population (Coulson, 2012).

When applied to recruitment, these perturbations will impact the first rows of the matrix A (see Appendix S1) where each entry can be defined by a line corresponding to the age a’ and mass z’ and a column corresponding to the age a and mass z:

$$A(a\prime =1,z\prime ,a,z)=D_I(a,t,z\prime |z,P_I=0)M_I(a,t,z,P_I\ne 0).$$

Similarly, when the inheritance function is perturbed, each entry becomes:

$$A(a\prime =1,z\prime ,a,z)=D_I(a,t,z\prime |z,P_I\ne 0)M_I(a,t,z,P_I=0).$$

When the growth or the survival functions are perturbed, all entries of the matrix for which a′ > 1 will be perturbed. We can perturb each function independently, or we can perturb all functions simultaneously. These perturbations assume populations consisting of individuals with an average value of performance P_I.

Analysis

First, we investigated the effects of body mass and age structure on population dynamics without modelling unmeasured individual differences. All models included year as a random effect on the intercept to account for yearly variations in demographic rates. We built four different matrix models containing different age structures and excluding any relationship between the different functions and body mass (see Table 1). The most complex age-structured model included four age classes as described in this population (Gaillard et al., 1998a): yearlings (i.e., one-year-old females, that do not breed in roe deer, Gaillard et al. 1992), prime-aged adults (2–7 y.o.), old (8–11 y.o.) and senescent females (>11 y.o. with reduced survival and reproductive performance). Then, we simplified this model to investigate the influence of age-structure on population dynamics. The third model contained three age classes: yearlings, prime-aged adults (2–7 y.o.) and senescent females (>7 y.o.). The second model contained only two age classes: yearlings and adult females (>1 y.o.). The simplest model had no age structure. We recorded the parameter estimates for each statistical model (Table S1). We examined the effects of age structure by comparing survival and recruitment, population growth rate, net reproductive rate and generation time with the most complex model.

Table 1.

Influence of the age and body mass structures and individual differences on parameters describing population dynamics.

	Model	log(λ)	R0	Tc	Sur	Rec	LE
1	Yr + no age	0.121	2.289	2.974	0.751	0.570	1.012
2	Yr + 2 age classes	0.056	1.738	4.270	0.758	0.380	3.813
3	Yr + 3 age classes	0.075	2.023	4.071	0.800	0.389	4.231
4	Yr + 4 age classes	0.076	2.042	4.104	0.801	0.389	4.275
5	Yr + 3 age classes + body mass	0.053	1.749	4.540	0.766	0.365	4.152
6	Yr + 3 age classes + body mass +ID	0.054	1.763	4.540	0.767	0.365	4.165

ID: unmeasured individual differences, Sur: survival, Rec: recruitment, LE: life expectancy at 8 months of age

For the following analyses, we selected the most parsimonious age-structured model: the model with the minimum number of age classes that gave the same parameters describing the population dynamics as our most complex model describing reliably (based on previous detailed analyses of age-dependent demography in the focal population, e.g. Festa-Bianchet, Gaillard & Côté 2003; Gaillard et al. 2013) the demographic rates of our population. Then, we investigated the influence of the body mass structure by comparing a matrix model (including the most parsimonious age structure) and an IPM including the influence of body mass in addition to the influence of age. From this IPM, we estimated the asymptotic population growth rate (λ), the reproductive values and the stable age-size distribution, the net reproductive rate (R₀) and the cohort generation time (T_c) and compared it to the result of the matrix model. We also estimated mean body mass and mean survival and recruitment rates across all ages and body masses from this IPM (Coulson, Tuljapurkar & Childs, 2010; Coulson, 2012).

We next performed an elasticity analysis using the body mass- and age-structured IPM without modelling unmeasured individual differences to identify the body mass class that most influences the population growth rate. Elasticity measures the proportional change in predicted population growth rate (λ) generated by a proportional perturbation of the matrix entries. We calculated elasticities at the level of the matrix entries (Caswell, 2001). Then we summed elasticities over body mass classes to obtain elasticities for each age class.

Second, we used IPMs to model unmeasured individual differences (model 6, Table 1, R code is provided in Appendix S2). As described in the section on modelling unmeasured individual differences, we first compared the parameters describing the population dynamics estimated from an IPM including only age and mass-structure to the ones estimated from an IPM that also included unmeasured individual differences. Second, to look at the relative influence of unmeasured individual differences in each function, we performed a perturbation analysis and compared the dynamics of populations characterized by a median average individual quality (P_I = 0 in all functions), a high average individuals quality for this given function (P_I = 0 in all functions except that with P_I = Q_I) or a low average individual quality for this given function (P_I = 0 in all functions except that with P_I = −Q_I). For instance, the influence of unmeasured individual differences in the realized fertility function was investigated by setting P_I = 0 in the growth, twinning rate, survival and inheritance functions and successively P_I = Q_I,F and P_I = −Q_I,F in the realized fertility function. We estimated Q_I,F by simulating the individual intercept representing the average individual quality value in realized fertility of populations of 250 individuals using a normal distribution with mean 0 and standard deviation s_I,F (standard deviation of the component for unmeasured individual difference estimated from the generalized linear model of realized fertility). Q_I,F was the third quartile (and so −Q_I,F was the first quartile) of the distribution of the average individual quality values of 500,000 simulated populations. It is not realistic to consider that a population with a high average individual quality will be constituted only by high quality individuals because in any population there is always a distribution of individual quality. The question is thus how much the average quality of individuals within a population varies across environmental conditions. This is especially important to compare reliably the influence of individual heterogeneity with that of environmental heterogeneity in population dynamics. As a consequence, we needed to take into account how often a “good population” occurs. We repeated this analysis for each function separately. Then, we investigated how two populations either of high (with P_I = Q_I) or low (with P_I = −Q_I) average individual quality (i.e. high or low performance for all demographic rates) differed in terms of population growth rate, net recruitment rate, and generation time.

Finally, we compared the perturbations generated by unmeasured individual differences to those generated by yearly variation in environmental conditions, by adding an average value of year quality P_Y to the intercept. P_Y was successively set to P_Y = Q_Y (favorable year) and P_Y = −Q_Y (unfavorable year) with P_I = 0 in both cases. We simulated a distribution of 500,000 years using a normal distribution of mean 0 and standard deviation s_Y (standard deviation of the component for year, different for each function). Q_Y was the third quartile of this distribution. As for unmeasured individual differences, we altered the intercept (and not the slope) in each function successively and then in all functions at the same time.

Results

Effects of age and size structure

The parameters describing the population dynamics were similar for models incorporating either three or four age classes in models of survival, growth, recruitment and inheritance (log(λ₄) = 0.076 vs. log(λ₃) = 0.075, R₀₄ = 2.042 vs. R₀₃ = 2.023 and T_c4 = 4.104 vs. T_c3 = 4.071 for four and three age classes respectively, Table 1, models 4 and 3). While models with one or two classes of older females provided similar results, the model without any senescence (model 2, Table 1), and even more the model lacking a yearling class (i.e., model with no age, 1), led to markedly different results compared to the model with three age-classes. When using two age-classes (yearling vs. adult females, model 2), log(λ) and R₀ decreased by 25% and 14%, respectively, whereas T_c increased by 5% (Table 1) compared with a model including three age classes, likely because of a shorter life expectancy (by 5 months) in a model with only two age classes (Table 1). In a model without any effect of age (model 1), all individuals can potentially reproduce, so the mean recruitment increased by 46% compared to a model with three age-classes, leading R₀ and log(λ) to increase (13% and 61%, respectively, Table 1). We therefore selected the model with three age classes for the following analyses.

To investigate the influence of the body mass structure on population dynamics, we compared the model with three age classes (model 3, Table 1) to an IPM including body mass in addition to age (model 5). The third model excluding the effect of body mass over-estimated both the population growth rate (Table 2, log(λ₃) = 0.075 vs. log(λ₅) = 0.053 for model 5) and the net reproductive rate (R₀₃ = 2.023 vs. R₀₅ = 1.749) and under-estimated the generation time (T_c3 = 4.071 vs. T_c5 = 4.540) compared to the IPM including the influence of individual body mass (model 5). This high population growth rate was a consequence of an over-estimation of recruitment (0.389 vs. 0.365) due to the non-linear relationship between body mass and the realized fertility (Fig. 1 D.).

The elasticity analysis performed on model 5 (including body mass and age) revealed that survival among prime-aged females had the highest potential impact on the population growth rate (e_Spa = 0.51, Fig. S1 A.). Relative perturbations in survival among yearlings and recruitment among prime-aged females also had substantial potential impact on λ₅ (e_Sy = 0.24 and e_Rpa = 0.23, respectively). However, survival and recruitment among senescent females only weakly influenced λ₅ (e_Ssen and e_Rsen < 0.02). Among prime-aged females, the elasticities were highest for survival and recruitment of 23kg (Fig. S1 B.) and 23.5kg females, respectively.

Influence of unmeasured individual differences

We built IPMs including unmeasured individual differences in addition to body mass and age. The variance of the random intercept of individual identity was estimated to be zero in the mean of the growth function, with age explaining most of the observed differences among individual growth rates (the effect of individual identity explained 62%, 33% and 0% of the variation of individual growth in a model including no age and no body mass, mass but no age and body mass and three age classes, respectively). No heterogeneity was detected in the survival function. Using a frailty model, we found no detectable individual heterogeneity in the survival function (χ² = 1.57, df = 1, P = 0.210). Using a generalized linear mixed model and the MCMCglmm package, we found estimates of the fixed effects similar to the ones found using a frailty model or a generalized linear mixed model (using the lme4 package). However, the variance of the individual random effect was highly variable among the different runs, a twofold variation from 0.07 to 0.15 with very large confidence intervals at 95%: [0.0002 0.5], compared to those obtained for fixed parameters. We thus parameterized our IPMs using the results of the generalized linear mixed model (from the lme4 package), excluding the random individual effect. We analysed the influence of unmeasured individual differences on population dynamics only in realized fertility, twinning rate and inheritance functions.

Changes in slope of body mass were high when comparing models including or not unmeasured individual differences (6% to 23% of difference) for realized fertility, twinning rate and inheritance functions. However, variations in population growth rate, net reproductive rate and generation time were small when unmeasured individual differences were corrected for in the statistical analyses used to identify the functions for the IPMs (Table 1, models 5 and 6). The reproductive value as a function of body mass remained similar in models with and without unmeasured individual differences (Fig. 2 B), whereas the stable age-size distribution differed between these two models (Fig. 2 A). The distribution of yearling body mass (first “hump”) can be clearly distinguished from the distribution of adult body mass when including unmeasured individual differences (model 6 and 5, Fig. 2 A).

Figure 2.

Stable body mass distributions (A) and reproductive values (B) modelled using three age-classes and including (model 6, Table 1, solid lines) or not (model 5, Table 1, dashed line) unmeasured individual differences.

Because unmeasured individual differences affected parameter estimation, we explored its potential impact on population dynamics by using the variance components estimated from the generalized linear mixed effect models to construct populations characterized by low, mean and high average quality of individuals (model 6 with P_I = −Q_I, P_I = 0 or P = Q_I) in each function separately, and then in all functions at the same time (except the survival and mean of the growth functions in both cases). In all cases, populations consisting of high versus low average individual quality exhibited small changes in parameters describing population dynamics (Fig. 3). The population growth rate (on a logarithmic scale) and the net reproductive rate decreased by 6.3% and 3.2%, respectively and the generation time increased by 0.6% from a high (P_I = Q_I) to a low (P_I = −Q_I) performance population, on average (model 6 with (P_I ≠ 0 in all functions). Such differences were mostly (60%) driven by changes in mean recruitment. The realized fertility function contributed slightly more to changes in parameters describing population dynamics than the twinning rate function (34% and 26%, respectively). The presence of positive co-variation among individual intercepts across functions had almost no effect on model parameters describing population dynamics (Fig. 3).

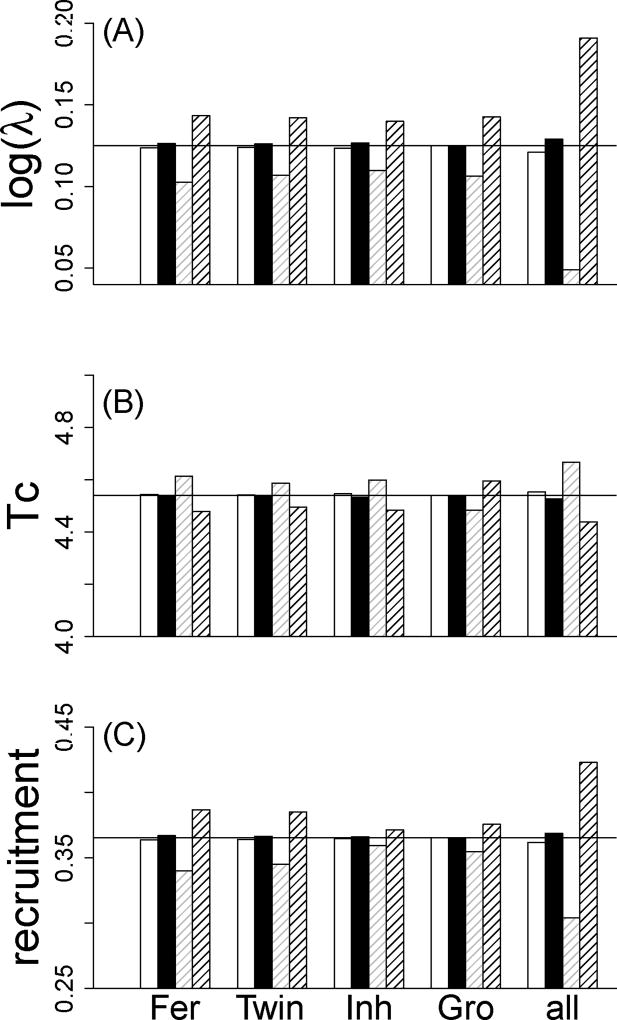
Figure 3.

Influence of unmeasured individual differences compared to the influence of variation in environmental conditions on three parameters describing population dynamics: the population growth rate (log(λ), A), the cohort generation time (T_c, B) and the mean recruitment rate (C). Two populations of different (high (black) and low (white)) average performance were compared to two populations facing contrasting (favorable (black hatched) and unfavorable (grey hatched)) years using the model 6 (Table 1). Median parameters are represented by a black solid line. Each function was successively perturbed (Realized fertility, Twinning rate, Inheritance and Growth) before being all perturbed at same time (all).

The perturbation of growth rate produced by variation in year quality was higher than that produced by variation in unmeasured individual differences. The population growth rate (on a logarithmic scale) and the net reproductive rate decreased by 74% and 46%, respectively and the generation time increased by 5% between favorable and unfavorable years when environmental conditions affected all functions (Fig. 3). As for unmeasured individual differences, the recruitment function was the target of changes in environmental conditions. When only realized fertility or twinning rate was affected, the population growth rate (on a logarithmic scale) decreased by 28% and 25%, respectively between favorable and unfavorable years (when survival, inheritance or growth were affected, log(λ) decreased by 0%, 21% and 25% respectively).

Discussion

Although the recruitment and inheritance functions were clearly influenced by unmeasured individual differences (modeled as random effects on the intercept of these functions), the parameters describing the population dynamics from our models were not. The age-structure, size-structure and yearly variation all affected the population dynamics to a much larger extent than unmeasured individual differences modeled as an individual random effect in the different functions of the IPM.

Let us replace individual random effects with an important but most often unmeasured life-history trait, birth date. Birth date is a typical trait that is strongly linked to individual quality because individual fitness is higher for early-born than for late-born individuals (Plard et al., 2015). However, the influence of birth date on population dynamics is much lower than the influence of environmental variations in roe deer because the distribution of individual birth dates does not change over years (Plard et al., 2014a), whereas climate change has strong negative influence on the population growth rate (Gaillard et al., 2013). By including birth date in addition to body mass and age in the different functions of the IPMs (Table S2 for the estimates of the different models of demographic rates including birth date or not on a smaller dataset including only individuals with known birth date), the estimated intercepts and slope of these functions do not change much compared to results obtained when using individual random effects. There are two reasons for this: first, birth date is a normally distributed trait in roe deer (Plard et al., 2013) and should be correctly modeled using random individual effects. Second and more importantly, most of the influence of birth date on future reproductive abilities and on fitness is mediated through body mass (Plard et al., 2015). Indeed early-born females have a higher fitness than late-born females because they reach a higher body mass as adults. Heterogeneity in body mass should approximately reflect heterogeneity in individual birth date and adding birth date in a model of population dynamics using body mass does not substantially change the parameters describing the population dynamics.

In other words, the influence of heterogeneity created by some unmeasured variables (that can be important for each specific demographic rate) on population dynamics can be negligible if the individual differences in some measured variables (body mass and age) already capture a large part of the individual heterogeneity existing in the population or if the individual distribution of this unmeasured trait does not change much with time. Our results support two previous studies that included unmeasured individual differences in IPMs. In the Soay sheep, Ovis aries, when accounting for body mass, correcting for random effects of individual identity had less influence on the population dynamics than correcting for population density (Coulson, 2012). Likewise, Rees et al. (1999) found that unmeasured individual variation (modeled as an individual random effect on the intercept) in growth and mortality rates had only small impacts on the population dynamics of a plant species, Onopordum illyricum.

Unmeasured individual differences have been reported to be a major source of variation to consider when estimating survival and reproductive parameters. Moreover, the failure to account for unmeasured individual differences can lead to biased estimates of demographic variability and the parameters describing population dynamics (Clark, 2003; Kendall et al., 2011). Recently Vindenes & Langangen (2015) developed an IPM including fixed individual differences suggesting that individual heterogeneity has the potential to influence population dynamics. They, however, had no data to estimate empirically the parameter (alpha) through which individual differences influenced the survival function (they chose a random range for alpha) and so did not provide empirical evidence. Our findings indicate that in the case of roe deer, individual heterogeneity plays only a minor role in population dynamics once individual differences associated with age and body mass are accounted for, but also support Vindenes and Langangen’s view that individual differences can be important to the evolution of populations in variable environments and to eco-evolutionary dynamics.

In our analysis, unmeasured individual differences influenced both the recruitment and the inheritance functions but not the mean of the growth and the survival functions. Despite the fact that heterogeneity in survival can be an important cause of variation in population dynamics (Kendall et al., 2011), previous studies have reported little variation in population growth rate even after correcting for individual heterogeneity in survival and growth (Rees et al., 1999; Coulson, 2012). Nevertheless, the weak influence of unmeasured individual differences in survival could be due to an underestimation of the variance component of our model caused by our relatively low sample size (n = 99). Thus, we considered a hypothetical case where unmeasured individual differences influence survival to a greater extent to assess the potential impact of individual heterogeneity in survival on population dynamics (see Fig. S2). In this case, unmeasured individual differences in survival did influence the population dynamics. However, variation in environmental conditions had still a larger influence on population dynamics than unmeasured individual differences in both reproduction and survival (Fig. S2). As a consequence, species showing large individual differences in survival are expected to be more influenced by individual heterogeneity than our study species. In long-lived species, such as roe deer, adult survival displays little variation and has been described as representing a case of environmental canalization (Gaillard & Yoccoz, 2003). Consequently, in species showing this kind of demographic tactic, individual differences independent of age and mass are expected to have little impact on population dynamics.

The recruitment of individuals with a median mass remained similar in models that either corrected (or not) for unmeasured individual differences. As expected, light (heavy) individuals recruited fewer (more) offspring in models including unmeasured individual differences than in models excluding them. Including unmeasured individual variation mainly impacted very light and very heavy individuals (it was the same in Coulson (2012) for Soay sheep). Population growth rate was weakly sensitive to extreme individuals as revealed by the elasticity analysis. Females weighing around 22–24 kg had the largest impact on population growth. Including unmeasured individual differences in recruitment only had a small influence on individuals with median mass and consequently only little influenced population growth rate.

Nevertheless, our study made two assumptions that, if not fulfilled, could have contributed to decrease the influence of unmeasured individual differences on population dynamics. First, we assumed that individual random effects reliably capture individual heterogeneity caused by unmeasured traits. This is not necessarily the case. For instance, when individual differences in the unmeasured trait follows a multinomial distribution (e.g. by displaying different groups of individuals according to their fixed quality), then individual random effects (which assume a normal distribution of individual differences) could not reliably capture such individual heterogeneity and would fail to model correctly the influence of unmeasured individual differences. However, this is not expected to occur in roe deer for which other characters known to influence individual quality follow a Gaussian distribution (like birth date in roe deer, see above). Second, we only included random effects of individual differences on the intercept of the function, but not on their slope. Krishnakumar et al. (unpublished results) have shown that random effects associated with slopes have a much larger and more non-linear influence on the parameters that describe population dynamics (the generation time, the net reproductive rate and the asymptotic population growth rate) than random effects associated with intercepts. Thus, unlike random effects associated with intercepts, random effects associated with slopes do not produce the same proportional change for lighter and heavier individuals. As a result, we can expect that unmeasured individual differences are not likely to produce a major impact on model output except if these unmeasured differences interact with the measured trait when influencing the different demographic rates. Moreover, the impact of unmeasured individual differences should be more important in small populations or in populations during the process of colonization (Vindenes, Engen & Sæther, 2008) as the probability to have a population consisting mostly of low or high quality individuals increases in small populations.

Individual differences in demographic rates of large herbivores mostly result from differences in body mass, with heavier individuals living longer and having higher annual reproductive success than light individuals (Gaillard et al., 2000b). Therefore, measured individual differences in body mass and age shape most observed variation in individual fitness (Plard et al., 2014b). A model including heterogeneity in body mass and age should thus capture a large proportion of individual heterogeneity within a population of large herbivore such as roe deer. Unmeasured individual differences in other traits are likely to be correlated to differences in body mass at a given age (leading to the concept of individual quality, Wilson & Nussey 2010) or to be relatively small and have only a weak effect on population dynamics. While for some species, age-dependent models can be advantageously replaced with mass-dependent models because reproduction and survival are mostly related to body mass (Sauer & Slade, 1987; Gamelon et al., 2012), the distribution of body mass alone does not allow to estimate a reliable individual age of first reproduction in roe deer. Age variation therefore matters, especially because, as recruitment continuously increases with body mass, yearlings are allowed to give birth before the observed age of first reproduction in roe deer (2 y.o.). Not accounting for this constraint leads to erroneous metrics of population dynamics when age structure is not explicitly included in models.

In conclusion, our study demonstrates that individual heterogeneity in age and mass generates crucial sources of individual variation that influence the dynamics of a population. On the other hand, unmeasured individual differences are important for many things, but not necessarily for all things, in this population. In a long-lived species like roe deer, the individuals constituting the population remain similar from one year to the next (with a generation time of about 4 years, about 25% of individuals are replaced each year). As individual quality is highly repeatable (e.g. Plard et al. 2013), temporal variation in average individual quality in a population of a long-lived species like roe deer should be dampened, explaining why we report only a minor influence of individual heterogeneity on population dynamics compared to the impact of age-structure and yearly variation.