Significance
How planarians reproduce by ripping themselves into a head and a tail piece, which subsequently regenerate into two new worms, is a centuries-old biomechanics problem. Michael Faraday contemplated how this feat can be achieved in the 1800s, but it remained unanswered because it is experimentally difficult to observe planarians “doing it.” We recorded Dugesia japonica planarians in the act and developed a physical model that captures pivotal steps of their reproduction dynamics. The model reproduces experimental time scales and rupture stresses without fit parameters. The key to rupture is a local reduction of the animal’s cross-sectional area, which greatly amplifies the stresses exerted by the planarian’s musculature and enables rupture at substrate stresses in the pascal range.
Keywords: planarians, biomechanics, fission, rupture, traction forces
Abstract
Asexual freshwater planarians reproduce by tearing themselves into two pieces by a process called binary fission. The resulting head and tail pieces regenerate within about a week, forming two new worms. Understanding this process of ripping oneself into two parts poses a challenging biomechanical problem. Because planarians stop “doing it” at the slightest disturbance, this remained a centuries-old puzzle. We focus on Dugesia japonica fission and show that it proceeds in three stages: a local constriction (“waist formation”), pulsation—which increases waist longitudinal stresses—and transverse rupture. We developed a linear mechanical model with a planarian represented by a thin shell. The model fully captures the pulsation dynamics leading to rupture and reproduces empirical time scales and stresses. It asserts that fission execution is a mechanical process. Furthermore, we show that the location of waist formation, and thus fission, is determined by physical constraints. Together, our results demonstrate that where and how a planarian rips itself apart during asexual reproduction can be fully explained through biomechanics.
Michael Faraday and his contemporaries were intrigued by the observation that asexual freshwater planarians, squishy worms a few millimeters in length, reproduced by tearing themselves into a head and tail offspring, in a process called binary fission (1). How was it possible for these animals to generate the forces necessary to rip themselves using only their own musculature and substrate traction? The question has remained unanswered to this day, because it is experimentally difficult to study the fission process in sufficient detail to figure out how it works. Planarian fission is fast, violent, and irregular. No induction mechanism has been identified, although decapitation has been shown to increase fission probability (2–4). Furthermore, planarians are photophobic (5), fission occurs primarily in the dark (4, 6), and even slight disturbances cause it to stop, complicating real-time imaging of the process. Finally, in the planarian species most commonly used in stem cell research, fission occurs on average approximately once per month per worm (7) and only lasts from a few minutes to tens of minutes (this study). All these factors make fission dynamics hard to study and rendered it a neglected area of planarian research (8, 9), although fission and regeneration are intimately linked (2, 3).
The most comprehensive study of fission that we have found in the literature is the 1922 thesis (in French) of Vandel on asexual reproduction of several European Dugesia species (10). Vandel described fission as spontaneous and fast, varying in duration from seconds to minutes, and regulated but not triggered by environmental factors. He noted that the fission plane is highly variable along the head–tail axis. Furthermore, by observing two consecutive fissions of the same animal, the first occurring close to the head and the second almost at the center, Vandel concluded that it was “impossible to formulate rigorous conclusions. One must limit oneself to giving the general trends and looks of this phenomenon without trying to explain all the observed exceptions” [author translation] (10). Because where along the body axis a planarian divides affects the fitness and reproductive behaviors of its offspring (7, 11–13), understanding how fission location is regulated is an important question to be answered. Regarding the division process, Vandel described fission as a mechanical process, whereby the anterior and posterior parts act independently, with the anterior part rhythmically pulsing and the posterior part largely adhering to the substrate.
Here we focus on the biomechanics of fission in the asexual planarian Dugesia japonica. Using time-lapse video recording, statistical analysis, and mathematical modeling, we show that Vandel was right in interpreting fission as a mechanical process, but wrong in declaring the fission location unpredictable. We dealt with the experimental challenges elaborated on above by decapitating specimens to increase fission frequency and recording events over the course of months to obtain data of the necessary quality for quantitative shape analysis. These imaging data were complemented by traction force experiments using special substrates, which were sufficiently soft and stable to allow for these kinds of long-term experiments.
The analysis of 22 fissions made it possible to identify three key stages shared among all events we observed in this species: a local constriction (“waist formation”), pulsation—which increases waist longitudinal stresses—and transverse rupture. As soft-bodied animals, planarians exhibit these body shape changes through the action of perpendicularly oriented, antagonistic muscle groups on weakly compressible internal fluids and tissues, which make up what is called a hydrostatic skeleton (see reviews in refs. 14 and 15). Waist formation is key to successful rupture, because it enhances the longitudinal stresses at a given longitudinal tension force exerted by the planarian’s musculature by an order of magnitude.
We found fission to be distinctively different from the three known gaits of planarian locomotion, which are gliding, peristalsis, and scrunching (16). Thus, fission poses a novel biomechanics scenario and the existing models that describe these planarian gaits are inadequate to describe fission dynamics.
Following D’Arcy W. Thompson’s thesis that “in the representation of form and in the comparisons of kindred forms … we discern the magnitude and the direction of the forces which have sufficed to convert the one form into the other” (17), we used the analysis of planarian body shapes to develop an enhanced readability thin-cylindrical-shell model, which fully captures pulsation dynamics leading to rupture and reproduces empirical time scales and stresses. Importantly, the model only uses experimental data and parameters from the literature as inputs. This implies that rupture is a purely mechanical process that can be fully accounted for by physical mechanisms without requiring any additional biological explanations.
Besides solving this centuries-old mystery about the biomechanics of planarian reproduction, this study highlights the power of a practical approach, combining quantitative image analysis and a simple physical model, for gaining insights into a complex biological phenomenon which is not accessible to controlled experimentation and perturbations.
Results
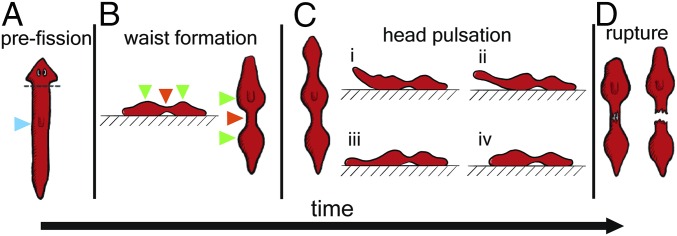
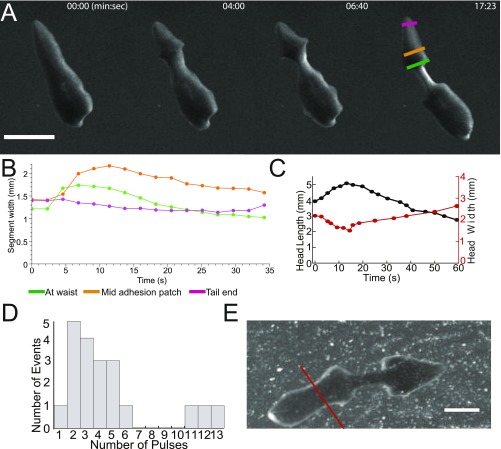
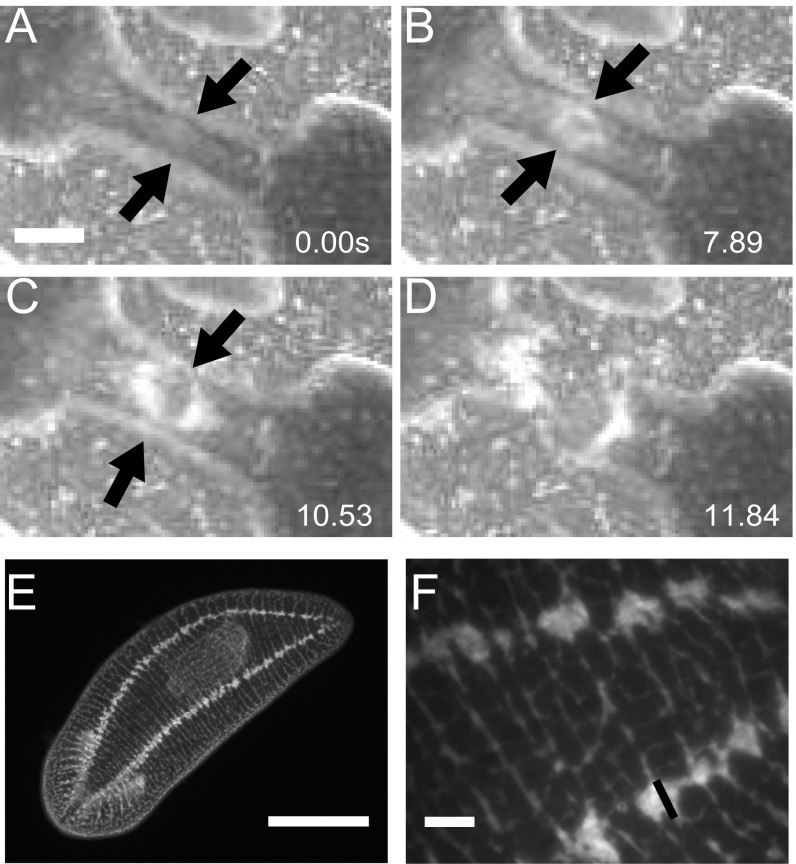
Months of continuous recording of decapitated D. japonica allowed us to capture a sufficient number of fission events occurring in open space for a quantitative study of fission dynamics. Decapitation promotes fission (2–4) without altering its dynamics (Movies S1 and S2) and was thus used as a means to increase the number of events. Qualitative analysis of these time-lapse movies indicated that D. japonica fission occurs as a sequence of three distinct stages: waist formation, pulsation, and rupture (Fig. 1 and Movie S2). Fission relies on the animal’s thin (10 µm) subepidermal muscle network (14), which consists of longitudinal (parallel to the head–tail axis), circular (perpendicular to the head–tail axis), and diagonal muscles (Fig. S1).
Fig. 1.
Cartoon of D. japonica fission. (A) Unperturbed planarian before fission. The pharynx is marked by the blue arrowhead. To increase the fission rate (3), we amputate as indicated by the gray line. (B) Waist formation. Tissue movement causes local narrowing (orange arrowhead) and formation of wide contact regions at the head and tail (green arrowheads). The waist is not in contact with the surface. (C) The head lifts off the substrate during pulsation and then readheres and slides back against the surface. (D) Rupture.
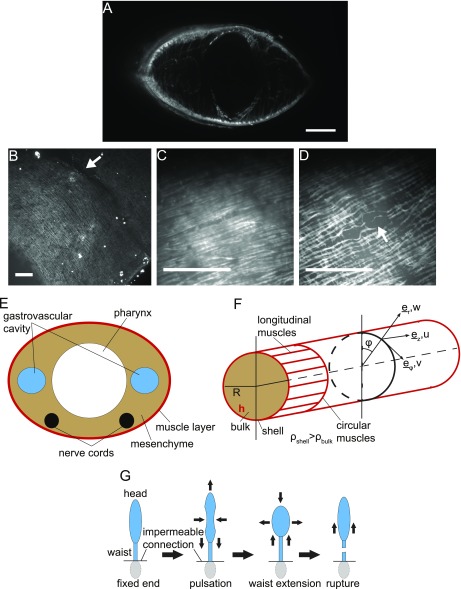
Fig. S1.
Muscle structure and modeling. (A) Cross-section of a worm’s musculature showing the subepidermal layer, outline of the pharynx, and diagonal fibers. (B) Before rupture, large-scale defects can be seen in the musculature in the waist zone, indicated by a white arrow. (C and D) High magnification of the musculature architecture of worm undergoing fission (C) a distance away from the waist and (D) in the waist region. White arrow in B and D indicates defects in the muscle network. (Scale bars: 200 µm in A and 50 µm in B–D.) (E) Schematic cross-sectional area of planarian indicating major anatomical features. (F) Cross-section of simplified worm as a cylindrical shell as used in the model. (G) Model predictions for head pulsations and rupture.
Given the muscles’ anatomical orientation, the vertico-lateral narrowing which leads to the formation of a waist is mediated by local contractions of circular muscles. Narrowing causes the waist region to lose contact with the substrate, while the body mass is actively redistributed toward the head and tail, leading to the formation of broad regions of contact with the substrate (Fig. 1B).
Next, the pulsation stage starts, as the planarian lifts its head (whenever we use the term “head,” we refer to the region anterior to the waist. The true head was amputated in our experiments as indicated in Fig. 1A and described in Materials and Methods) from the substrate (Fig. 1C), and “flesh waves,” axially propagating lateral indentations of the worm head, are produced by contractions of circular muscle fibers. It appears that the generation of these waves is facilitated by the lack of contact (and, hence, of friction) between the lifted head and the substrate. As the planarian body is nearly incompressible (hydrostatic skeleton), these radial contractions produce longitudinal head extension and stresses in the waist. To return to its original shape the planarian then contracts its longitudinal muscles. Stresses in the waist are largest during the relaxation phase (contraction) of the head. When the longitudinal stress in the waist exceeds a critical value, rupture occurs (Fig. 1D) and the worm flesh rips into head and tail pieces, concluding the fission. The two offspring regenerate into whole planarians in roughly a week.
As the cartoon (Fig. 1) illustrates, fission dynamics are fairly complex. We first discuss where the waist forms. Then, we show how body shape analysis allows construction of a simple physical model that explains how pulsation can lead to rupture and estimate the magnitude of the rupture stresses.
Location of Waist Formation.
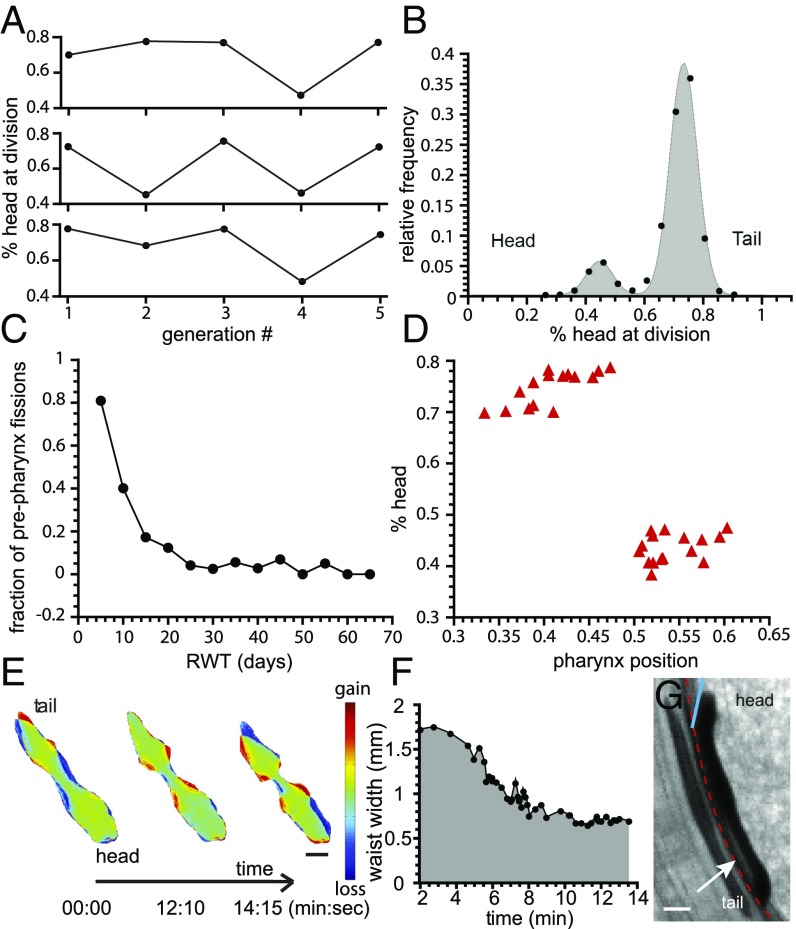
Vandel (10) observed that an individual planarian divided at different locations when followed through consecutive fissions, which led him to the conclusion that the fission plane cannot be predicted. Because he did not study D. japonica, we checked whether this observation held equally true in this species. Indeed, as illustrated by the examples in Fig. 2A, the fission location varies and it is seemingly impossible to predict where an individual planarian fissions (note that the dynamics of these fission events were not recorded).
Fig. 2.
Waist formation. (A) The waist position along the head–tail axis is not conserved across generations for a single planarian line. (B) Frequency of occurrence of waist position, expressed as percentage head at division (n = 1,335). (C) Quantification of the fraction of prepharynx fissions as a function of RWT. (D) Quantification of percentage head at division as a function of relative pharynx position shows that the latter predicts fission position. (E) Color-coded maps of worm footprint, showing a representative sequence of waist formation in an amputated planarian. Colors indicate the change in the mass per unit area, with green corresponding to no change, blue to loss, and red to gain of mass. (Scale bar: 1 mm.) (F) The width of the waist region versus time in E. (G) Side view image of a planarian undergoing fission. The dashed red line outlines the Petri dish wall. The white arrow highlights a gap between the waist of the worm and the substrate. The blue line indicates the angle by which the planarian lifts its head before pulsation. (Scale bar: 1 mm.)
We then took advantage of a unique large-scale dataset on the birth and division sizes, growth curves, and time between fissions (reproductive waiting time, RWT) we had accumulated on D. japonica (18) and applied statistical analysis to assay whether those data would provide further insight. We found an asymmetric double-Gaussian distribution for the waist location based on imaging n = 1,335 specimens within 3 d after fission (Fig. 2B and Materials and Methods). Of note, the area of low fission probability between the peaks, as determined by manual inspection of a subpopulation of n = 40 specimens, coincides with the location of the pharynx, which is a powerful muscle used to ingest food (19). Thus, planarians divide neither at a pole nor at the pharynx but have a nonzero probability of dividing anywhere else along the head–tail axis, with the majority of events happening posterior to the pharynx. This distribution of waist position also explains why planarian fission is generally reported in the literature as occurring posterior to the pharynx (20–22).
Whether a planarian divides pre- or postpharynx has a significant effect on its offspring, because it determines birth size and thus offspring survival and reproductive success (7). We therefore binarized the data in Fig. 2B into pre- (%H < 0.56) versus postpharynx (%H ≥ 0.56) fissions and correlated it with other known quantities about the properties and history of these worms. While the following arguments hold true for all D. japonica, we only discuss individuals originating from a head offspring below, because prepharynx fissions are negligible for planarians that originate from tails (<<1%).
We found a strong correlation between a planarian’s RWT and fission location (Fig. 2C), whereas the planarian’s size at division had no effect (Fig. S2). Nearly all prepharynx fissions resulted from worms with short RWTs (<2 wk; Fig. 2C). Upon inspection of the physical characteristics of these planarians, we found that we can predict where (either pre- or postpharyngeally) an individual D. japonica will divide through quantification of its relative pharynx position (Fig. 2D). Fission occurs anterior to the pharynx when the pharynx is located relatively closer to the tail (Fig. 2D). This is frequently the case for animals with short RWTs (Fig. S2). A comparison of pharynx positions at birth and at division of pre- and postpharyngeal dividers shows that the former have not repositioned their pharynx sufficiently to allow for a postpharyngeal fission. Because repositioning takes time, this can explain why we primarily observe prepharynx divisions in rapid dividers.
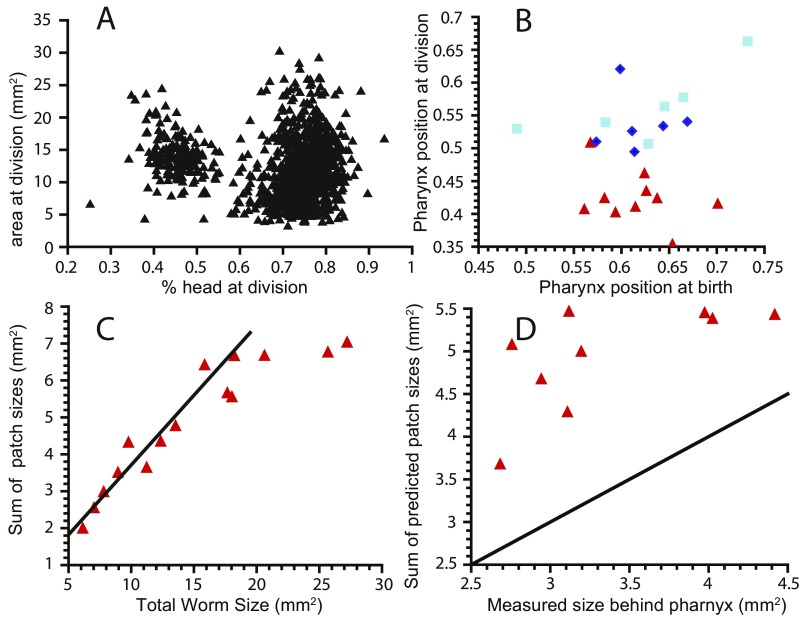
Fig. S2.
Position of fission plane. (A) Area at division does not affect the distribution of fission position between prepharynx (low percentage head at division) and postpharynx (high percentage head at division). (B) Comparison of pharynx positions at birth and at division for worms that divide postpharynx (red triangles) which have low relative pharynx position at division (i.e., the pharynx is closer to the head). Worms that divide postpharynx either after less than 14 d (dark blue diamonds) or more than 14 d (light blue squares) both have the pharynx close to the tail (>0.5). (C) The total size of the contact area with the substrate scales linearly with total worm size (linear fit shown as black line), which allows us in D to predict the required contact area for worms that divide prepharynx and show that this predicted size exceeds the available tail size postpharynx. The black line is a y = x guide for the eye.
We can explain why pharynx position matters with biomechanical arguments. To pull itself apart, a planarian needs to form two sufficiently large contact regions (adhesion patches) with the substrate. If the pharynx is located close to the tail end, the posterior part of the animal is too small to accommodate the adhesion patches and fission occurs anterior to the pharynx (Fig. S2). Because the size of these patches scales with worm size (Fig. S2), absolute worm size does not matter.
To summarize, our statistical analysis shows that it is possible to predict whether a particular D. japonica planarian will fission pre- or postpharynx, solely through quantification of its relative pharynx position.
Mechanism of Waist Formation.
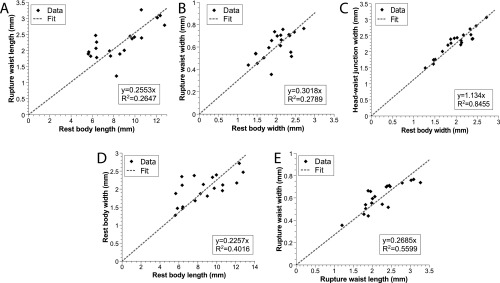
Waist formation, which is a local narrowing in the vertical and lateral directions, is achieved by contractions of circular muscles. Peristaltic contractions move mass from the waist region toward the head and tail (Fig. 2 E and F, Fig. S3 A and B, and Movie S3). As a result of this mass redistribution, the area of contact with the substrate on either side of the waist increases, whereas the waist part of the worm body detaches from the substrate (Fig. 2G and Movie S4). Waist formation is critical for successful fission. It has the physiological benefit of preventing gut spillage during the subsequent rupture. Not less importantly, for a given longitudinal tension force, the reduction in the worm cross-section in the waist region leads to a proportional amplification of the longitudinal tensile stress. That said, the waist diameter is anatomically constrained and scales with the initial width of the worm (Fig. S4 and SI Text). This scaling indicates the existence of a mechanism preventing the formation of waists that are too narrow. Experimentally, we found that the ratio of cross-sections of the head, , and of the waist, , is limited by ∼14, suggesting that the tensile stress at the waist can be amplified by a factor of up to ∼14, compared with the characteristic traction stress in the head (or the tail) (Fig. S4 and SI Text).
Fig. S3.
Waist formation and pulsations. (A) Representative sequence of waist formation. (Scale bar: 3 mm.) (B) Material transfer out of the waist into the tail adhesion patch. Colors correspond to colors in A. (C) Head length and head width as a function of time for a single fission event. Due to conservation of volume, head width and head length are anticorrelated. (D) Distribution of number of pulses per fission event. (E) The kymographs of pulsation (Fig. 3B in the main text) was computed along the red line shown here. (Scale bar: 2 mm.)
Fig. S4.
Rupture. (A) The waist length at rupture represents a constant fraction of the worm’s rest length. (B) The same holds true for the waist width with respect to the worm’s rest width. (C) During waist formation, the radial expansion of the head pieces occurs by a constant factor. (D) Before rupture, worms do tend to have a conserved ratio of rest width to length. (E) At rupture, waist length and width also correlate together.
Pulsations.
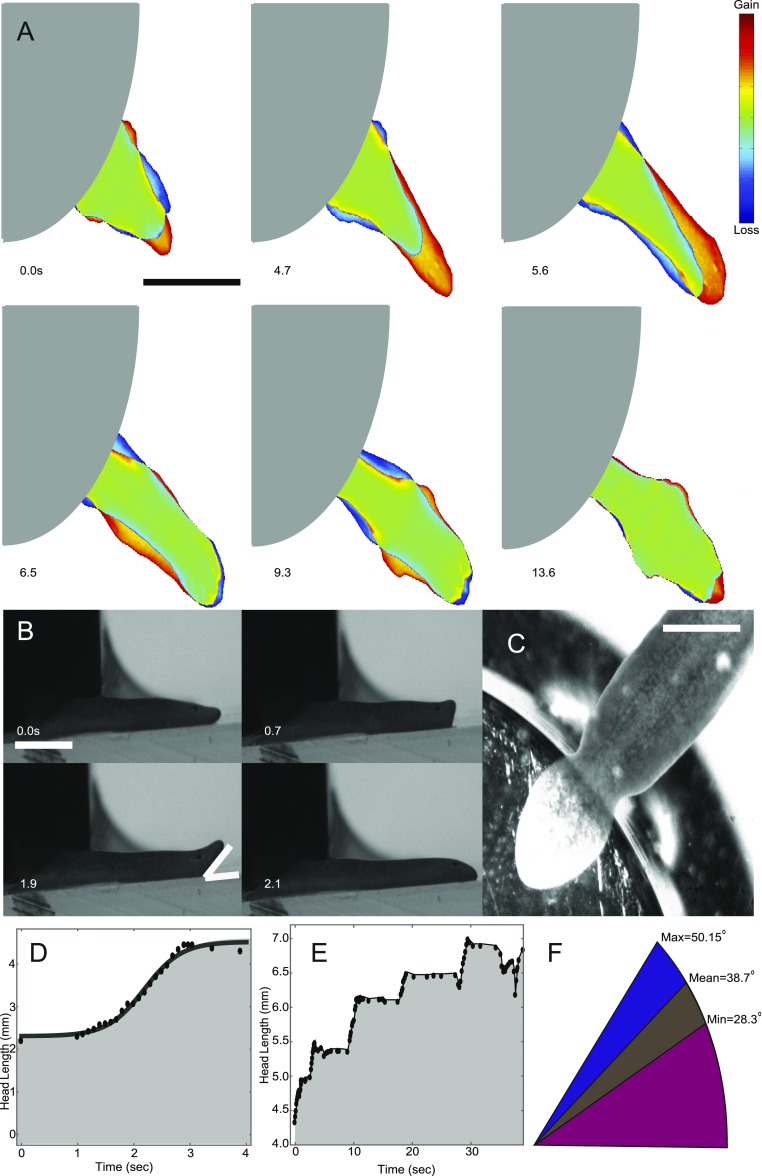
Once the waist is formed, pulsations begin, that is, the planarian executes multiple longitudinal extensions and contractions of the head and/or tail parts of its body (Fig. 3 A–C, Fig. S3 C and D, and Movies S5 and S6). On average, head pulses occur more frequently than tail pulses (89 head pulses versus 19 tail pulses total for n = 22 fissions), suggesting that head pulses are critical for generating tensile stresses causing the rupture in the waist region. Notably, head and tail pulses were asynchronous and we never observed a “tug-of-war” between them.
Fig. 3.
Pulsation. (A) Representative sequence of head pulsation of an amputated planarian. Color coding is the same as in Fig. 2. (Scale bar: 3 mm.) (B) Kymograph showing multiple head pulses. (Vertical scale bar: 20 s; horizontal scale bar: 1 mm.) (C). Head length as a function of time during a series of head pulsations. (D) Head extension is logistic and fast, whereas (E) head contraction is linear and slow. (F and G) Head and waist lengths are anticorrelated. (F) Consecutive images of a planarian with its head and waist lengths shown by red and blue lines, respectively. (Scale bar: 3 mm.) (G) Time dependences of head length and waist length of the planarian from the images in F.
At the beginning of each head pulse, the anterior of the head detaches from the substrate (Fig. 2G, Fig. S5, and Movies S4 and S7). The detachment allows the head to break out of the mucus layer (Figs. S5 and S6 and SI Text), minimizing friction with the substrate during head extension. Circular muscle contractions then elongate the head (Fig. 3D and Fig. S3). This is a necessity of the planarian’s hydrostatic skeleton: If a worm elongates, while both its width and height decrease, it can only be a result of contraction of the circular muscles. The head reattaches to the substrate and slowly contracts. Head contraction is achieved by shortening of the worm’s longitudinal muscles and resisted by friction with the substrate (Fig. 3E). These different dynamics are clearly seen in Fig. 3 D and E), where head length during pulsation increases logistically (S shape in Fig. 3D) but decreases linearly with time. Importantly, head and waist dynamics are anticorrelated. As the head extends, the waist gets compressed and buckles (Movies S5 and S6). As the head contracts, the waist region gets stretched (Fig. 3 F and G).
Fig. S5.
Planarian crushing experiments. (A) Representative sequence of head pulses for a planarian whose tail is held underneath a 5-g weight. (Scale bar: 3 mm.) (B) Representative side-view sequence of a planarian lifting its head during pulsation. (Scale bar: 1 mm.) (C) Worm underneath weight as viewed from the bottom. (Scale bar: 1 mm.) (D) Head length as a function of time for a pulsation event, exhibiting logistic growth like during fission, but at a faster rate. (E) Head length as a function of time for multiple pulses. (F) Mean angle and range of angles observed for head lifting in weight experiments.
Fig. S6.
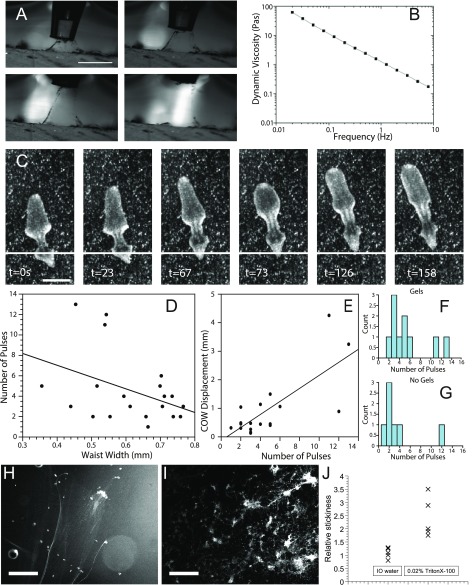
Role of adhesion in fission. (A) Representative sequence showing attachment of mucus to the end of a pipette tip. Mucus is being stretched as the tip is lifted up until it breaks. (Scale bar: 1 mm.) (B) Mucus viscosity for various frequencies of stimuli. Both axes are measured on a logarithmic scale. (C) Sequence showing worm slippage during pulsation phase of fission. Horizontal line indicates position of tail adhesion patch at t = 0 s. (Scale bar: 2 mm.) (D) Relationship between waist width and number of pulses. Because the waist width scales with the total size of the worm (Fig. S3B), this relationship shows that the number of pulses is negatively correlated with size of the worm. (E) Relationship between the number of pulses and the center of waist (COW) displacement, which indicates slippage plays a role in the number of pulses necessary to fission. (F) Distribution of number of pulses per fission event for events happening on soft gels. (G) Distribution of number of pulses per fission event for events happening on plastic Petri dishes. (H) Mucus staining of a gliding worm showing a faint trail. (I) Mucus staining of a worm treated with 0.025% Triton X-100 showing a large increase in mucus secretion (Materials and Methods). (Scale bar: 1 mm in H and I.) (J) Quantification of relative stickiness in IO water and Triton X-100.
The maintenance of proper adhesion with the substrate is crucial during this stage. We observed some animals slipping during pulsation (Fig. S6) and interpret this as resulting from weak adhesion with the substrate, leading to poor stress transmission to the waist. In accordance with this interpretation, animals that slip execute more pulsations before rupture. Interestingly, the number of pulses was weakly anticorrelated with a planarian’s size, suggesting that the absolute size matters for successful fission (Fig. S6). In other situations where substrate adhesion is critical, we and others have shown that an increase in mucus secretion is key (16, 23). To directly prove the link between a planarian’s mucus secretion and adhesion, we treated planarians with Triton X-100, which increased mucus secretion (Fig. S6). Using a custom aspiration setup, we then quantified the aspiration force required to detach worms from their substrate. Triton X-100–exposed planarians required larger aspiration forces than control planarians (Fig. S6). Based on these data, we postulate that substrate adhesion during fission is mediated through the increased presence of mucus.
Rupture.
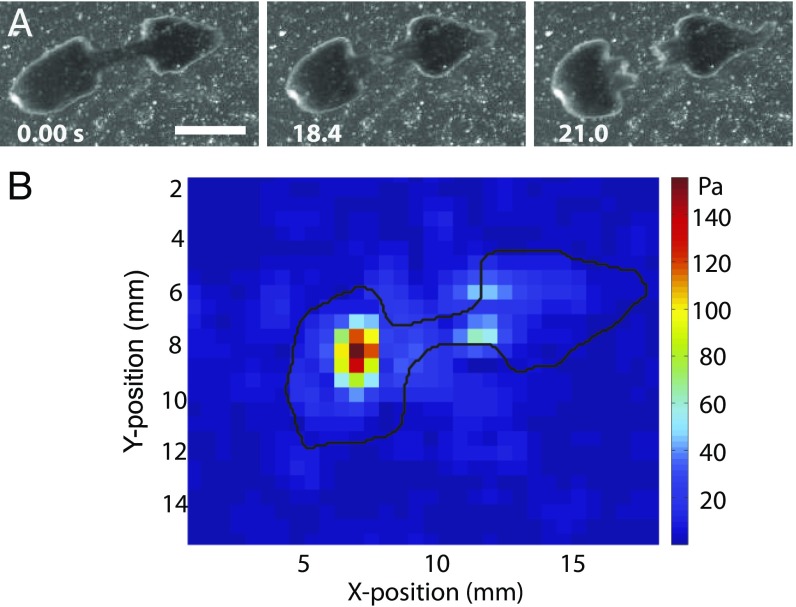
The ultimate and key step in fission is successful rupture (Fig. 4A). Rupture occurs when the stress in the waist, induced by contraction of the head, exceeds a critical threshold (Fig. S4E). In most cases (20/22 fissions; Materials and Methods and Movie S8), rupture is nucleated at the center of the waist region. We measured the stresses exerted on the substrate during fission using traction force measurements (Fig. 4B). To this end, we fabricated thick (∼5 mm), soft (Young’s modulus E = 1.2 kPa) silicone gel substrates with 30- to 45-μm-diameter beads imbedded in an ∼70-μm-thick surface layer as the tracer particles (SI Materials and Methods). A map of displacements of the beads from their zero-stress locations (when the substrate was not deformed by the worm) was generated and converted into a map of traction stresses using previously published algorithms (24) (SI Materials and Methods). The stresses were on the order of 100 Pa (Fig. 4B).
Fig. 4.
Rupture. (A) Image sequence of a worm rupturing. (Scale bar: 2 mm.) (B) Color-coded map of the substrate traction stresses produced by a D. japonica (contour in black) a short time before rupture.
Projection of the stresses on the axis of the worm (direction along the waist) was then integrated over the areas of the head and of the tail, providing the pair of opposing traction forces that stretch the waist. The stretching force before rupture was a few hundred micronewtons and, when divided by the cross-sectional area of the waist, it provided an estimate of ∼2,000 Pa for the tensile stress in the waist immediately before rupture. Once rupture is completed, the two offspring move independently and regenerate into new full worms within about a week.
A comparison of the fission dynamics of events on soft polydimethylsiloxane gels versus plastic Petri dishes revealed no significant differences in terms of the number of pulses (Fig. S6), suggesting that the interaction with the mucus dominates substrate effects on fission.
It is evident from this quantitative analysis that fission dynamics have little in common with normal planarian locomotion via cilia-based gliding, which does not involve body shape changes (16). There are some similarities between fission and the two muscle-based planarian gaits, peristalsis and scrunching (16, 23), insofar as all involve body elongation–contraction cycles and require good contact with the substrate for successful execution. However, fission pulsation dynamics are different from those observed in peristalsis or scrunching, which either show no asymmetry or relatively longer elongation periods, respectively. Finally, waist formation is a unique feature of fission. Because of these differences, existing models for these gaits fail to reproduce the observed fission dynamics.
Therefore, we developed a linear mechanical model with the planarian head represented by a thin, cylindrical, elastic shell (corresponding to the thin musculature network) filled with a viscous liquid (corresponding to coarse-grained, squishy internal tissue). The same model could be applied to the tail part on the other side of the waist, but we focus on the head because tail pulsations do not occur in all fission events. Although the deformations during fission are large, this linear thin-shell model allows us to capture pulsation and rupture dynamics using only physical arguments and scaling estimates.
Physical Model.
We treat the head as a uniform, long, thin, cylindrical, elastic shell of cross-sectional radius R, Young’s modulus E, and shell thickness h which encloses material of density ρ (Fig. S1). Although planarians, being flatworms, have elliptical cross-sectional areas, the simplification to circular cross-sectional areas has a negligible effect on the results (SI Text). We assume that the head is connected to the waist by an impermeable junction, through which no matter crosses on the time scale of pulsations (Fig. S1). This assumption is reasonable, as the data show no material transfer once the waist has been established (Movies S4 and S5). The long-thin approximation applies, since while .
A thin, cylindrical, elastic shell supports three modes of waves: longitudinal, flexural, and torsional. The last ones can be ignored as there is no indication that the planarian twists during pulsation. Longitudinal wave displacements on an elastic cylinder are predominantly axial while flexural (F)-waves support primarily radial (lateral) displacements. These two modes are linearly coupled at finite Poisson ratio (Eqs. S1–S3).
The experimentally observed flesh waves correspond to F-waves. They are initiated by contractions of circular muscles in the head part anterior to the substrate contact region, causing local changes in the radius. The head anterior is detached from the substrate during extension and therefore has no friction with it. The deformation propagates longitudinally at the group velocity of F-waves. As the wave progresses anteriorly the head extends forward due to volume conservation. Simultaneously, the wave propagates in the head posterior toward the waist region and because the head–waist connection is impermeable the waist region experiences a compression and buckles. Thus, qualitatively, the model predicts the observed anticorrelation of head and waist length during head extension. Furthermore, we can compare the F-wave group velocity with the observed flesh pulse speed (SI Text for calculations). Using only experimentally measured values of the parameters, we calculate that the F-wave propagates at . This is in excellent agreement with the observed flesh pulse speed of . Our model thus properly captures the dynamics of head extension during pulsations.
Regarding the head contraction phase, the main difference to extension is that the head anterior is now in contact with the substrate and thus friction needs to be taken into account. Head contraction dynamics are determined by this competition between muscular relaxation and friction with the substrate as inertial forces can be neglected. The balance of these two forces defines a relaxation time scale (SI Text):
| [1] |
All values in Eq. 1 were experimentally determined, with the height of the mucus layer, the mucus viscosity, the surface area of contact with the substrate, E the elastic modulus of the shell, the head volume, and the length of the head (Table S1). Using these values gives , which is in reasonable agreement with the experimental value of the relaxation time .
Table S1.
Experimental values and estimates that are referenced throughout the text
| Quantity | Value | Source |
| Duration of total fission process | 17.8 ± 10.1 min (n = 17) | Measured duration between initiation of waist formation and rupture |
| Young’s modulus of worm shell (E) | 500 Pa | 16 |
| Planarian shell thickness (hshell) | 10 µm | 14 |
| Mucus layer thickness (hmucus) | 10 µm | 16 |
| Planarian waist radius (RWaist) | 0.31 ± 0.06 mm (n = 22) | Half the measured width of the waist region |
| Planarian head radius (R) | 1.2 ± 0.1 mm (n = 22) | Half the measured width of the head piece before pulsation begins |
| Planarian density (ρ) | 1,000 kg/m3 | See description of density measurement in Materials and Methods |
| Planarian head volume (VH) | 22 ± 11 mm3 (n = 22) | Assuming a cylindrical worm, , where R and L are the measured worm head radius and length, respectively |
| Planarian–substrate contact area (Acontact) | 8.7 ± 3.3 mm2 (n = 22) | Measured manually as the area of the worm head profile when imaged from above |
| Mucus viscosity (η) | 65 Pa·s | See Fig. S6B and description of mucus rheology in Materials and Methods |
| Stress amplification factor | 14 ± 3 (n = 22) | Assuming both cylindrical head and waist, we have |
| Pulse extension velocity | 1.1 ± 0.4 mm/s (n = 16) | Using values from logistic fits of extension described in Materials and Methods |
| Contraction duration | 44 ± 20 s (n = 18) | Measured duration of the linear contraction phase of pulsation |
| Maximum longitudinal strain (ε) | 0.43 ± 0.15 (n = 16) | Using values from logistic fits of extension described in Materials and Methods, |
| Traction stress on substrate (σ) | 100 Pa | Measured from traction force experiments; value reflects the order of magnitude of measured stresses |
| Radial contraction | 0.27 ± 0.13 mm (n = 16) | Difference between maximum and minimum radius in the head during pulsation |
This table describes the characteristic values of relevant experimental parameters. The Source column lists either the relevant reference from the literature or the method of calculation and/or measurement. Entries in the Value column that stem from experiment are average values and accompanied by ±SD.
Taken together, pulsation time scales are well captured by the linear model, both during elongation and contraction phases, although it is too simple to reproduce the trajectory of pulsations (logistic during elongation and linear during contraction). Head extension is quick, whereas head contraction is slow and thus allows for the buildup of stresses in the waist required for rupture. The model correctly predicts that head extension and waist extension are anticorrelated (Fig. S1), consistent with experimental observations (Fig. 3 F and G). During head extension, the waist appears shorter, because it bends vertically (Fig. 3 F and G and Movies S4 and S5), whereas during head contraction the waist is extended (Fig. 3 F and G) and thus under increased longitudinal stresses. Once these stresses exceed the tissue’s yield, rupture occurs. We estimate this critical stress necessary for rupture (SI Text) using a linear approach and experimentally determined parameters only (Table S1) and obtain , which is in reasonable agreement with our traction force measurements.
Magnitude of Rupture Stresses.
The rupture stresses we found are in the kilopascal range, which is orders of magnitude lower than stresses previously reported for rupture of tissues in other animals (25, 26). It is possible that biological processes preceding or accompanying waist formation weaken the waist and lower the required rupture stresses. The idea of a predefined “fission zone,” with metabolic, cellular, or structural differences compared with the rest of the worm, was already suggested over 50 years ago by Child (27) and Tokin (reviewed in refs. 2 and 28). Hori and Kishida (3) performed structural analysis of the postpharyngeal region and observed “presumptive changes in preparation for fissioning” in some, but not all, of the samples. Because these samples were fixed planarians without a waist, it is impossible to tell if fission would have occurred in the studied region. Thus, experimental evidence demonstrating the existence of a fission zone is absent. Our data on the distribution of the waist location argue against a permanent fission zone but allow for the possibility that the animal locally prepares for fission before each event (e.g., via enzymatic digestion of extracellular matrix components by metalloproteinases, which have been shown to play a role in planarian tissue homeostasis and regeneration) (29, 30).
To test whether such weakening of the fission zone was necessary, we measured the stresses needed to rip a nondividing planarian apart by applying suction to both ends of a planarian using pipette tips connected to a peristaltic pump (Fig. 5A and Materials and Methods). In this experiment (Fig. 5B), a waist was not formed and the time to rupture was much shorter (seconds compared with minutes in fission), rendering biochemically induced structural changes unlikely. However, this pulling experiment yielded stresses comparable to those obtained in our traction force measurements, with values ranging between 7.0 kPa and 13.1 kPa. Additionally, we quantified where the worms ruptured and contrasted these measurements with the fission data (Fig. 5C). As expected, pulled planarians could tear anywhere along the head–tail axis, including at locations which are “forbidden” zones in fission, such as the very anterior or posterior regions of the animal.
Fig. 5.
Magnitude of rupture stresses. (A) Schematic of the planarian pulling experiment. (B) Representative image of a pulled planarian. (B, i) right before and (B, ii) right after rupture. (C) Distributions of rupture planes in fission (black circles, n = 22) and pulling (gray triangles, n = 16) experiments.
We also estimated the stresses required to crush a planarian by adding a small weight onto its trunk region (Fig. S5 and SI Text). Worms were crushed by a 5-g weight with a contact area of 8.9 mm2, thus exerting a stress of σ = F/A = 5.6 kPa. The results of these both tests indicate that stresses of a few kilopascals are sufficient to rupture a planarian.
Together, these data show that rupture during fission can be achieved through the planarian’s mechanical properties and the physical mechanisms of pulsations and does not require enzymatic weakening. The planarian’s “trick” of progressive necking is key to successful fission. Once rupture is initiated at these relatively low stresses of a few kilopascals, the cross-sectional area of the waist decreases further and the internal stresses increase accordingly. We found that the nerve cords break last during fission (Fig. S7). Because their diameter is only 50 µm (Fig. S7), this implies stresses in the megapascal range, similar to what has been reported as the tensile strength limit for nerve tissues in other organisms (25, 31).
Fig. S7.
Nerve cords break last. (A) Worm waist prefission; arrows indicate nerve cords at the edge of the worm. (Scale bar: 1 mm.) (B) Beginning of rupture; black arrows indicate nerve cords remaining on the edges of the worm. (C) After initial rupture in the center of the waist has almost completely nucleated outward; black arrows indicate that the nerve cords have not broken, and are some of the last tissue to break. (D) Worm has completely ruptured. (E) Full worm picture of antibody staining against synapsin showing two nerve cords that run along either side of the planarian. (Scale bar: 1 mm.) (F) Zoomed-in picture of E showing nerve cord width is roughly 50 µm. (Scale bar: 100 µm.)
SI Materials and Methods
Planarian Maintenance.
Specimens of clonal asexual D. japonica were used for all fission experiments. Planarians were stored in Tupperware containers in the dark in a temperature-controlled Panasonic incubator at 20 °C in planarian water (36) or instant ocean water (37). Planarians were fed organic beef or chicken liver from a local butcher three times a week to increase growth rates and the chance of fission (11). Worms were cleaned 2 h after feeding and starved for 1 wk before being used for experiments. Since planarians do not need a brain to fission, specimens were decapitated to increase the likelihood of fission in the presence of light (34). Cuts were performed with a clean razor blade perpendicular to the head–tail axis and as close to the head as possible. We did not detect any effects of the cuts on fission dynamics. Moreover, wound healing is quick (a few hours) compared with when fission first occurred, which was at least one but often several days after worms were amputated. Thus, planarians depicted in the movies, except for the weight experiments and Movie S1, do not have a head. Animals used for observation ranged between 0.5 and 1.2 cm in length after decapitation.
Fission Recording and Data Analysis.
The substrate and planarians were imaged from 20 cm below with a FireWire A641f CCD camera (Basler AG) recording continuously at 0.8–3 frames per s (fps) using a custom-written MATLAB (MathWorks) script. The water was replaced completely and the gel surface washed at least once a week with planarian water. Planarians were exchanged either after successful fission or after 2 wk without reproducing. For each fission event, the corresponding image sequence showing only the animal engaged in fission was isolated and cropped using ImageJ (NIH). All image analysis was done using ImageJ or MATLAB. Worm areas, contact areas with the substrate (adhesion regions), and tail areas postpharynx were manually measured in ImageJ. Head and tail adhesion regions as well as their sum were found to scale linearly with worm size (Fig. S2). Linear fits of these measurements in MATLAB were then used to predict the total adhesion region size of a planarian based on its total size. The predicted sizes were then compared with the available tail areas postpharynx in individuals that divided prepharynx.
Kymograph and Fission Color Sequences.
The kymograph shown in Fig. 3B was generated in ImageJ by plotting the pixel intensity of the red line shown in Fig. S3E for each image in the sequence and plotting lines for consecutive images from top to bottom. Sharp lines in kymographs correspond to moving sharp features (such as edges), and the slope of the line is proportional to the velocity of the feature. Artificial color sequences of fission events to emphasize body shape changes were obtained through inversion of the raw images, manual masking of the planarians at two consecutive time points, and subsequent subtraction of the resulting two images. The background is shown in white while colors correspond to differences in gray levels between the two time points. Positive differences correspond to gain of material while negative ones correspond to loss.
Single-Worm Statistical Data.
Planarians were kept as individuals in separate Petri dishes, 100 mm in diameter and 20 mm in height (Fisher Scientific), containing 25 mL of planarian water. They were fed organic liver once per week, cleaned twice per week, and checked for divisions three times per week (7). Fissions were tracked using the SAPling database and barcode system (35). Planarians were imaged at birth with a Leica S6D stereo microscope (Leica Microsystems) using a Basler A601f CCD camera equipped with Pylon viewer software (Basler AG). Planarian outlines were obtained using boundary detection in ImageJ and MATLAB. From these, the area at division was obtained by summing the areas of the head and tail offspring. The percentage of head at division was obtained by dividing the size of the head offspring at birth by the area at division of the parent worm. The pharynx position was measured as its relative position along the length of the worm either at birth or before division. Overall, our dataset represents 1,335 fission events with information on the worm identity at birth (head or tail), its ancestry, its area at birth and at division, and its RWT. Pharynx positions were only measured manually on a subset of these worms.
Through visual inspection we found that a cutoff at 56% of head at division binarized the data into pre- and postpharynx fission events. From this binarization we computed the fraction of prepharynx fissions as a function of RWTs.
Gel Preparation and Traction Force Measurements.
Deformable gel substrates were prepared from CY 52-276 silicone gel (Dow Corning), by mixing the A and B components of the gel at a ratio of 1.2:1. The two components were thoroughly mixed in a 50-mL test tube over a period of 5 min using an overhead stirrer. The mixture was then degassed by centrifuging the test tube at ∼400 × g for 3 min. The gel prepolymer was poured into 60-mm Petri dishes to form ∼5-mm layers which were baked for 15 min on a 95 °C hot plate to initiate cross-linking of the gel, making it sufficiently solid to withstand spin coating with a thin layer of the gel prepolymer. As the Petri dishes baked, glass tracer particles (30- to 45-μm glass beads, purchased from Amazon as “Green Glow in the Dark Pigment Powder”) were mixed with an aliquot of the gel prepolymer at a mass ratio of 1:12. The suspension of the bead in the prepolymer was deposited onto surfaces of the prebaked gel in the 60-mm Petri dishes and the dishes were spun on a spin coater at 1,200 rpm for 20 s, producing ∼70-µm-thick layers of the bead suspension. Finally, the Petri dishes were covered, flipped upside down to make the beads move toward the gel surface, and baked overnight in an 80 °C oven. The Young’s modulus of the silicone gel was measured at 1.2 kPa using a recently developed gel rheometer (38). The substrate and planarians were imaged using the same method described above. The observed bead motion was measured using custom-written scripts in MATLAB and converted into traction stresses using the scripts previously published and distributed in ref. 24.
Planarian Pulling.
Worms in planarian water were subjected to external stresses using a peristaltic pump (Cole Parmer). The inlet was split forked into two and capped with nested plastic pipette tips (TipOne; USA Scientific) to decrease the cross-sectional area over which the force by the pump was being applied. The inner diameter of the pipette tip (P10) was 0.48 mm and chosen empirically to allow for an individual planarian, comparable in size to the specimen used in fission experiments, to be sucked a considerable amount into the pipette tip.
The tips were positioned at the anterior and posterior ends of the planarian, and the pump’s revolutions per minute (rpm) were slowly increased until the worm was ripped apart. The rpm necessary to rip a planarian varied little between individuals. Pulling experiments were imaged from above using a Leica S6D Stereo Microscope and a Basler A611f CCD camera with Pylon viewer software. Upper and lower bounds for the stress applied to the planarian were calculated using the peristaltic pump to lift chrome steel beads. The pump was able to lift n = 5 beads of mass kg at the rpm necessary to rip a planarian, giving us a lower bound for the applied stress, and was unable to lift n = 5 beads of mass kg at the rpm necessary to rip a planarian, giving us an upper bound for the applied stress. The beads that were tested were of masses kg, kg, kg, kg, kg, and kg, giving us a range of kg. Only the kg and kg masses could be lifted at rpm necessary to rip a planarian. The stress was calculated using Newton’s second law on the bead, , where p is the pressure of the pump, A is the cross-sectional area of the pipette tip, is the mass of the bead, g is gravitational acceleration, is the density of water, and r is the radius of the bead. This yielded a lower-bound stress of 7.0 kPa and an upper-bound stress of 13.1 kPa.
Mucus Pulling Experiments.
Experiments were performed using a horizontally mounted Leica stereo S8APO microscope, equipped with a Point Gray Flea USB 3 camera (Point Gray) mounted on a ring stand (Fisher Scientific). Image sequences were captured using a custom MATLAB script. Backlighting was provided using a G-2001 cold LED panel (GEPE). To generate mucus, planarians were cut on a clean glass slide (Fisher Scientific). The slide was then mounted on a glass panel for imaging. An M-152 micromanipulator (Narshige) with a 200-mL pipette tip (Fisher Scientific) attached to the end was moved into the mucus until some mucus got stuck to its tip. Video recording was started and the tip was lifted until the mucus film was stretched to its maximum length and ruptured. Mucus lengths were obtained in ImageJ and MATLAB by measuring length of mucus in the last frame before rupture occurred.
Planarian Crushing.
For top-view movies, a 5-g weight (Troemner) was put onto the tail region of a planarian and the worm was imaged using a Leica S6D stereo microscope and a Basler A601f CCD camera with Pylon viewer software. For side-view and bottom-view movies, the same 5-g weight was put onto the tail region of the planarian and imaged using a Leica stereo S8AP0 microscope and a Point-Gray camera controlled by MATLAB. Images were analyzed using ImageJ and MATLAB and head length was measured as defined in Fig. S8.
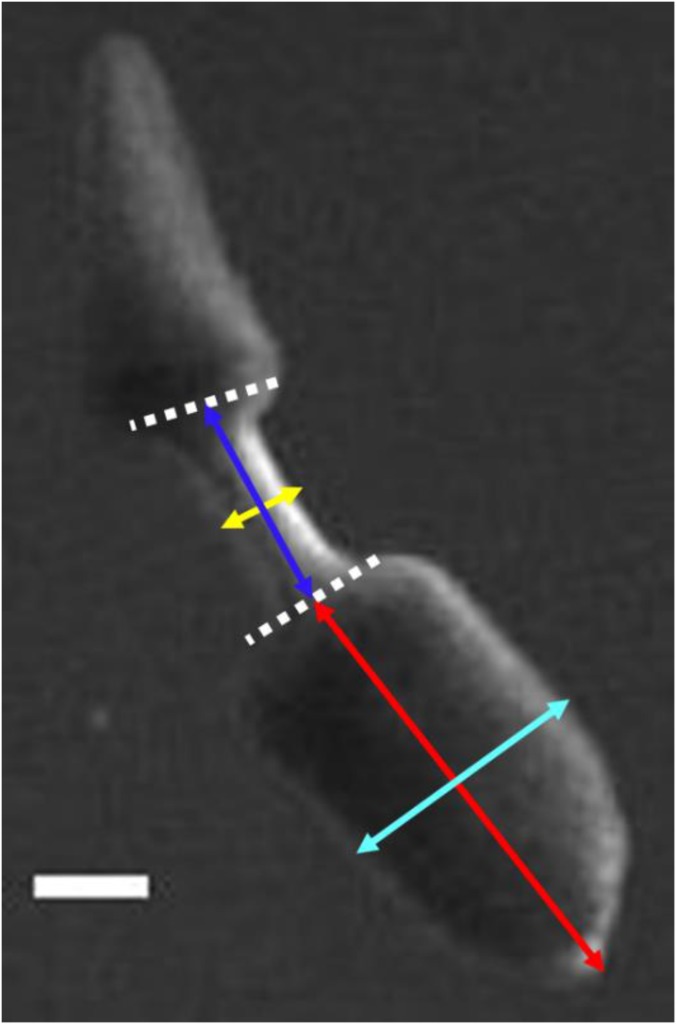
Fig. S8.
Definition of morphometric parameters. White dashed lines mark the boundaries of the waist region. The blue arrow defines the waist length as the distance between the respective midpoints of the white dashed lines. The yellow arrow defines the waist width as the distance across the middle of the waist, which is also the thinnest part of the waist region. The red arrow defines the head length as the distance between the tip of the head and the midpoint of the head/waist boundary. The cyan arrow defines the head width as the distance across the middle of the head piece. (Scale bar: 2 mm.)
Planarian Density.
To determine an approximate value for the typical density of D. japonica, 10 planarians were imaged individually from above using the Leica S6D stereo microscope and a Basler A601f CCD camera with Pylon viewer software. The worms were then weighed all together on an AE 200 (Mettler Toledo) scale. To calculate the density, the total mass recorded was then divided by the total volume of the worms, which was estimated by assuming the worm was an ellipsoid. The worm length and width were measured from the top-view images in ImageJ, and the worm height was assumed to scale with worm width as shown in ref. 36.
Antibody Staining.
Asexual Schmidtea mediterranea planarians were used for antibody staining because of their smaller size at fission (7). Antibody staining was performed using standard protocols (39). For nervous system staining, randomly selected S. mediterranea were used. S. mediterranea observed to undergo waist formation in preparation of fission were fixed before rupture for the muscle staining experiments. Since fission cannot be controlled, it was unknown at which state during fission fixation was performed. Specimen were fixed in 4% paraformaldehyde in 1× PBS for 20 min and bleached overnight in 100% methanol supplemented with 6% hydrogen peroxide. They were incubated overnight at 4 °C with either an antimuscle or antisynapsin antibody raised in mouse from the Developmental Studies Hybridoma Bank (clone 6G10-C7 for antimuscle and clone 3C11 for antisynapsin) diluted 1:500 in antibody blocking buffer consisting of PBS supplemented with 0.3% Triton-X (Sigma Scientific), 0.1% Tween-20 (Sigma Scientific), 1% FBS (Sigma Scientific), and 0.1% DMSO (Sigma Scientific). After 4–6 h of washes, worms were incubated overnight at 4 °C with an Alexa488-conjugated anti-mouse secondary antibody (Thermo Fisher) diluted 1:500 in antibody blocking buffer. Specimens were imaged using an inverted IX81 spinning disk confocal microscope (Olympus Corporation) controlled by Slidebook software (Intelligent Imaging Innovations).
Mucus Rheology Measurements.
Mucus was scraped off of planarians by repeatedly stroking them on their dorsal side with a soft plastic pipette tip. Mucus rheology was measured by placing the fresh mucus sample into an Anton Paar MCR301 rotational rheometer (Anton Paar) with a plate diameter of 2.5 cm and a gap width of 50 µm between plates. Measurements of shear stress were made in response to oscillatory deformations with equally logarithmically spaced frequencies from 0.02 Hz to 9 Hz (Fig. S5). From shear stress τ, and shear deformation γ, the complex viscosity η was computed using . During fission, the “oscillatory stimulus” is the contraction phase of pulsation, which happens at about 0.023 Hz, so the mucus viscosity during fission is about 65 Pa·s.
Stickiness Experiments and Mucus Visualization.
To determine the substrate adhesion (“stickiness”) of planarians, we placed individual D. japonica planarians into a 3D-printed plastic arena (150 mm × 100 mm × 16 mm), filled with 30 mL of ionized (IO) water, and allowed it to acclimate. The arena was printed using white PLA filament (MatterHackers) on a LulzBot Taz 6 (LulzBot). A water flow was briefly introduced to the planarian from a distance of ∼25 mm. The flow rate was increased in discrete steps until the planarian was fully displaced. The flow was sourced by a 3D-printed reservoir (82.5 mm × 82.5 mm × 35 mm) attached to 5-mm-diameter silicon tubing, which was clamped onto a custom-built system with an automated variable-height shaft. Flow measurements were made with an Arduino UNO board (Arduino) and a Hall sensor (Amazon), connected in series with the tubing. Flow rate was controlled by varying the height difference between the reservoir and the arena. Each worm was measured twice. The initial experiment was conducted in IO water, then the planarian was incubated and allowed to rest for 1 min in either IO water or in IO water supplemented with detergent (0.02% Triton X-100). After incubation the same worm was measured again in IO water. Of note, measurements of untreated and treated worms were alternated and we did not observe any trends in stickiness over time. We report the relative stickiness as the ratio of the second measurement to the first one. To visualize mucus secretion induced by detergent exposure, planarians were treated with 0.025% Triton X-100 for 10 min. The longer incubation time was chosen to ensure that gliding trails could be visualized (16). For mucus staining, they were allowed to move on no. 1 coverslips. The staining was performed with fluorescein-conjugated VVA lectin as previously reported (16). Images were acquired on an Olympus IX81 inverted microscope. To visualize mucus trails, the exposure time had to be 2.5 times longer for control worms than for Triton X-100–treated planarians. In addition, image treatment was necessary to enhance contrast. Both demonstrate the larger amount of mucus secreted after treatment with Triton X-100.
SI Text
Morphometric Relationships in the Waist.
We found that that the waist diameter is anatomically constrained and that it scales with the initial width of the worm. One possibility is that actin fibers forming the circular muscles that contract during waist formation possess a nonlinear force–elongation relationship, as observed in the medicinal leech (40). The force required to contract the worm width by >70% (Fig. S4B) could be too large because of this nonlinearity. In addition, contraction of the circular muscles forces the longitudinal fibers closer together. It is conceivable that, at some degree of contraction, these fibers start resisting further compression and thus further reduction of diameter of the waist.
To understand what sets the ratio of head and waist cross-sectional areas and thus determines the amplification factor of stresses in the waist region, we measured total body length, total body width, waist length, waist width, head piece length, head piece width, tail piece length, and tail piece width of the 22 recorded fission events. We refer to these quantities as , , , , , , , and , respectively. We use B to denote width to avoid notation confusion between width and waist.
We found that and at the moment of rupture scaled linearly with, respectively, and (Fig. S4 A and B) (i.e., longer, wider worms also form longer and wider waists) (see main text).
Furthermore, we observed that does not change during the formation of the waist, and thus
Because the head and tail pieces expand radially by the same factor relative to (Fig. S3C) and scales linearly with , we can define two constants:
Combined with the incompressibility condition
these constraints imply that the ratio of to is set by
Inserting the experimental values of α and β from Fig. S4 B and C sets the waist length to be a factor 0.263 times the original length, which agrees with the data in Fig. S4A.
Finally, since we also observed that and scale linearly (Fig. S4D), it logically follows that and also scale together, as shown in Fig. S4E.
Planarian Crushing Experiments.
Because fission events are rare and cannot be induced on command, it is experimentally difficult to capture events at high spatial and temporal resolution. Therefore, we tried to mimic fission by pinning the tail region of a planarian down using a small weight and recording how it broke free. Although this scenario is not similar to fission biologically, it does provide additional insight into different aspects of fission dynamics at high spatial and temporal resolution. The weight experiments helped confirm that the planarian lifts its head during the pulsing phase. Side-view imaging allowed us to quantify the angle and the height at which the head is lifted (Fig. S6 and Movie S7). The height of head lifting is about 1 mm, consistent with our mucus pulling measurements, in which we were able to stretch planarian mucus to a length of about 1 mm before breakage (Fig. S5). We thus conclude that the worm lifts its head to break free from the mucus to minimize drag during head extension.
In agreement with this picture, head elongation in the weight experiments followed the same logistic time course observed in fission, albeit at a significantly faster pace (Fig. S6). In this situation, we rarely observed multiple pulses, which is likely due to the fact that the worms were able to partially pull themselves out from underneath the weight before tearing. Occasionally, a narrowing would be visible close to the edge of the weight, vaguely resembling a waist region. However, the worm was always crushed by the weight and did not fission. Overall, these experiments demonstrate that head lifting during extensions is a key component of the fission process and is presumably used to reduce frictional drag and thus achieve higher strains for a given stress.
Model of Fission Dynamics.
The dynamics of fission and its different steps poses questions as to the elastodynamics of planarians. Specifically,
-
i)
What are the physical ingredients controlling flesh waves/pulsations? Can the space–time response be calculated and/or characterized?
-
ii)
What determines the planarian’s relaxation time, after pulsation?
-
iii)
Can the radial impulse observed experimentally be shown to be consistent with the axial stresses in the waist when fission occurs?
To answer these questions, we use a linear approximation for tractability and model the worm (anterior) as a uniform, thin, cylindrical, elastic shell. The thin elastic shell model is justified by the anatomy of the worm, which can be coarse-grained into bulk material of density encompassed by a muscle network of thickness h (Fig. S1). Our model assumes that the stiffness is set by the muscle network/shell rather than the worm’s interior (i.e., that the elastic modulus of the shell is significantly higher than that of the mesenchymal tissue). We use an experimentally estimated mean value for since is not available. Consistent with this approach, geometric nonlinearities are not treated.
The constitutive equations for such a thin shell using Donnell’s linear theory are (41)
| [S1] |
| [S2] |
| [S3] |
Here refer to longitudinal (i.e., axial), azimuthal, and radial (flexural) perturbations of the shell (Fig. S1), R is the radius of the head, ν is the Poisson ratio, β is given by , is the pressure, and cs is the speed of sound where E is the Young’s modulus of the worm and is the mean density of the worm. The basic waves are coupled by finite Poisson ratio.
We then make assumptions that simplify these equations. First, azimuthal perturbations are ignored, as there is no evidence for the role of twisting in fission dynamics. Second, loading is ignored () because the planarian shell is—in contrast to nematodes (42)—not pressurized. In addition, acoustic coupling is irrelevant, that is, effective speeds are strongly subsonic as the speed of sound in the worm is 0.7 m/s and worm density is similar to that of water (SI Materials and Methods). Under these assumptions, the model supports two types of linear responses (and waves) corresponding to flexural and longitudinal perturbations, captured by the following simplified equations:
By assuming a wave solution to these equations of the form we can derive the dispersion relation for these traveling waves.
Pure radial bending (i.e., flexural) waves have a dispersion relation , where is the axial wavenumber. The shell curvature ensures that the wave frequency exceeds the dissipative damping rate for the worm.
Pure longitudinal waves have . As pulsations are dominantly radial, the characteristic velocity of an initially localized pulse is set by the flexural wave group velocity, which can be calculated as
Taking yields a pulse velocity , which agrees well with the observed pulse velocity of (Table S1). Since the response to pulsation is an axially propagating radial perturbation, the local treatment given here is consistent with experimental observations.
Using the same model assumptions, we then ask whether we can reproduce the time scale of length relaxation during pulsation. Slippage is determined by the competition between the axial elastic restoring force on the worm and friction of the worm with its substrate. We calculate the time scale for contraction using Newton’s second law on the head piece with mass . Thus, for axial displacement , we have
| [S4] |
where is the elastic longitudinal restoring force with an effective spring constant , with the Young’s modulus, the length of the head, and the volume of the head. The form of follows from the axial restoring force one gets by linear longitudinal elastic forces. The friction coefficient is set by viscous drag on the mucus layer. , the friction force, is given by , where is the mucus viscosity, is the area of contact of the worm with the substrate, is the depth in the mucus layer, and is the thickness of the mucus layer. Taking yields .
We can substitute this into Eq. S4 and get
As slip times are long compared with longitudinal inertial time scales, inertia is neglected (), so frictional drag balances axial forces and we can write
and obtain for the inverse slip time. Using our experimental values of , , , , , and , we thus find , which is in reasonable agreement with the empirical mean value of 44 s.
As we show in the main text (Fig. 3 F and G), the tension in the waist is increased during this relaxation/head contraction phase of pulsation. Once the stresses reach a critical threshold, the waist starts to rupture. To estimate the magnitude of these rupture stresses, we again take a linear approach. Taking the deformations of the head to be volume-preserving (because of incompressibility), a radial contraction δR < 0 induces an axial extension . This extension implies an axial strain and an axial stress . The latter implies a force on the waist during the relaxation phase of pulsation wave, in agreement with the experimental data (Fig. 3 F and G). Thus, the stress in the waist is . Because of the differences in cross-sectional areas of head and waist region , the longitudinal stress in the waist exceeds the longitudinal stress in the head by a large factor (∼14). We estimate this critical stress necessary for rupture using experimentally determined parameters only (Table S1) and obtain , which is in reasonable agreement with our data from independent traction force measurements.
Effect of Circular Cross-Sections.
The cylindrical model assumes that the cross-sectional area of the head and waist are circular. This simplification of the animal’s cross-sectional geometry, which in reality is more elliptical than circular (Fig. S1), has only minor effects on the results. Circular cross-sections appear in four aspects of the theoretical description:
-
i)
The cross-sectional areas affect the stress amplification factor, which is central to our interpretation of the data. To estimate the cross-sectional areas of head and waist, we used ratios of R2 instead of actual cross-sections. From side-view imaging, we find that the ratios of waist height to head height are on the order of three to four (manual measurement), yielding a cross-section ratio of 11.2–13.9, which is comparable to our estimate of 14.
-
ii)
Assuming that planarian width and height correlate (as shown in ref. 36), the head extension velocity is unaffected if we use circular instead of elliptical cross-sectional areas.
-
iii)
During the contraction phase, the head is more circular in cross-section than normal. Thus, while using a circular cross-sectional area leads to an overestimation of the volume, using the elliptical cross-sectional area of an unperturbed worm leads to an underestimation thereof. The head volume enters in the estimation of the contraction time scale as 1/V. Therefore, the circular cross-section leads to a smaller contraction time than using the elliptical one (82 s versus 109 s). The “true” value lies between these estimates.
-
iv)
The cross-sectional geometry enters in the Hooke’s law estimation of rupture stresses. We assume a certain elongation based on the radial contraction. Using the measured cross-sectional area ratio from the side-view movies of the head and waist (11.2–13.9), we obtain an estimate for the stress in the waist of 2.5–3.1 kPa, which is comparable to our originally reported value (3 kPa) based on a circular cross-section.
In summary, using a circular instead of an elliptical cross-section has a small effect on the contraction time, a negligible effect on the stress estimate, and no effect on the amplification factor and the head extension velocity. Furthermore, it does not affect the qualitative prediction of the model that head and waist extension are anticorrelated.
Discussion and Conclusions
As an active, living biomaterial, D. japonica planarians are able to coordinate and execute their own dissection. Our results demonstrate how they can develop sufficiently large tensile stresses to tear themselves apart. Because D. japonica are soft and squishy (32)—with an elastic modulus 1,000 times smaller than that of nematodes (16, 33)—they are able to tear themselves apart using only substrate adhesion and their own musculature. The self-inflicted rupture is facilitated by the formation of a narrow waist, where tensile stresses are amplified due to reduced cross-sectional area. Friction with the substrate, the mucus rheology, and the planarian’s elastic modulus are key parameters in determining the dynamics of the contraction phase and, ultimately, rupture. The planarian only needs to exert sufficiently large stresses to break the weakest structures. Once tearing is initiated, the waist cross-sectional area decreases further and tensile stresses are greatly amplified, resulting in stresses able to break stronger anatomical features such as the muscles or nerve cords. From a biomechanical standpoint one could argue that planarians fission because they are soft and thus can do it. However, that’s only one part of the story. Planarians fission because they have stem cells which allow them to regenerate the missing structures after the act. Fission is the sole mode of reproduction of the asexual planarians studied here, which poses the question of how this species creates population diversity. Where a planarian divides affects the fitness and reproductive behaviors of its offspring (7, 11–13). Therefore, understanding how fission location is regulated is an important evolutionary question to be answered.
We showed that the waist and thus the fission location is determined through the relative position of the pharynx. Animals with short RWTs have less time to reposition their pharynx following the previous fission and thus mechanically cannot divide postpharyngeally, frequently resulting in large tails. What causes some animals to divide rapidly, whereas other comparably sized animals take a long time, remains unknown. However, now that we can predict where an individual will divide, we can start to dissect whether molecular differences exist between pre- and postpharynx dividers, which could provide insights into the mechanisms controlling RWT and, if existent, a fission trigger.
Finally, going beyond planarian reproduction, this study shows how one can gain insights into complex animal behaviors that are difficult to access experimentally, simply by “watching.” Quantitative image analysis allows for the construction of simple physical models which can then be tested against the empirical data, potentially revealing new regulatory mechanisms.
Materials and Methods
Planarian Maintenance, Fission Experiments, and Analysis.
Specimens of clonal asexual D. japonica were used for all fission experiments. Since planarians do not need a brain to fission, specimens were decapitated to increase the likelihood of fission in the presence of light (34). Details on planarian maintenance, fission experiments, and analysis are provided in SI Materials and Methods.
Single-Worm Statistical Data.
Fissions were tracked using the SAPling database and barcode system (35) and planarian head and tail sizes were quantified as described in detail in SI Materials and Methods.
Traction Force Measurements.
Traction forces were measured using custom gel substrates as described in detail in SI Materials and Methods.
Planarian Pulling.
Planarians were subjected to external stresses using a peristaltic pump (Cole Parmer). Upper and lower bounds for the stress applied to the planarian were calculated using the peristaltic pump to lift chrome steel beads. Details are provided in SI Materials and Methods.
Supplementary Material
Acknowledgments
We thank the group of A. Ott for mucus rheology experiments; R. Schwarz, J. Talbot, and B. Lincoln for help with fission experiments; W. Shi for help with the drawings; and D. Kleinfeld, W. Kristan, J. Posakony, M. Vergassola, and D. Hagstrom for discussions and comments on the manuscript. This work was supported by the Burroughs Wellcome Fund Career Awards at the Scientific Interface and NSF CAREER Grant 1555109 (to E.-M.S.C.), NSF Grant PHY 1205921 (to E.R. and A.G.), US Department of Energy Grant FG02-04ER54738 and the Center for Momentum Transport and Flow Organization (P.H.D.), and a Hellman undergraduate research scholarship (to K.J.K.). The 6G10-C7 antibody developed by R. Zayas and the 3c11 antibody developed by E. Buchner were obtained from the Developmental Studies Hybridoma Bank, created by the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the NIH and maintained at the Department of Biology, University of Iowa.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1700762114/-/DCSupplemental.
References
- 1.Hirshfeld AW. The Electric Life of Michael Faraday. 1st Ed Walker Books; London: 2006. [Google Scholar]
- 2.Brondsted HV. Planarian regeneration. Biol Rev Camb Philos Soc. 1955;30:65–126. [Google Scholar]
- 3.Hori I, Kishida Y. A fine structural study of regeneration after fission in the planarian Dugesia japonica. Hydrobiologia. 1998;383:131–136. [Google Scholar]
- 4.Morita M, Best JB. Effects of photoperiods and melatonin on planarian asexual reproduction. J Exp Zool. 1984;231:273–282. [Google Scholar]
- 5.Paskin TR, Jellies J, Bacher J, Beane WS. Planarian phototactic assay reveals differential behavioral responses based on wavelength. PLoS One. 2014;9:e114708. doi: 10.1371/journal.pone.0114708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Azuma K, Shinozawa T. Rhodopsin-like proteins in planarian eye and auricle: Detection and functional analysis. J Exp Biol. 1998;201:1263–1271. doi: 10.1242/jeb.201.9.1263. [DOI] [PubMed] [Google Scholar]
- 7.Carter JA, Lind CH, Truong MP, Collins E-MS. To each his own. J Stat Phys. 2015;161:250–272. [Google Scholar]
- 8.Nentwig MR. Comparative morphological studies of head development after decapitation and after fission in the planarian Dugesia dorotocephala. Trans Am Microsc Soc. 1978;97:297–310. [PubMed] [Google Scholar]
- 9.Hori I, Kishida Y. Further observation on the early regenerates after fission in the planarian Dugesia japonica. Belg J Zool. 2001;131(Suppl 1):117–121. [Google Scholar]
- 10.Vandel A. Recherches expérimentales sur les modes de reproduction des planaires triclades paludicoles. 1st Ed Edition du Bulletin biologique de la France et de la Belgique; Paris: 1922. [Google Scholar]
- 11.Dunkel J, Talbot J, Schötz E-M. Memory and obesity affect the population dynamics of asexual freshwater planarians. Phys Biol. 2011;8:026003. doi: 10.1088/1478-3975/8/2/026003. [DOI] [PubMed] [Google Scholar]
- 12.Quinodoz S, Thomas MA, Dunkel J, Schötz E-M. The more the merrier? J Stat Phys. 2011;142:1324–1336. [Google Scholar]
- 13.Thomas MA, Quinodoz S, Schötz E-M. Size matters! J Stat Phys. 2012;148:664–676. [Google Scholar]
- 14.Cebrià F. Planarian body-wall muscle: Regeneration and function beyond a simple skeletal support. Front Cell Dev Biol. 2016;4:8. doi: 10.3389/fcell.2016.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kier WM. The diversity of hydrostatic skeletons. J Exp Biol. 2012;215:1247–1257. doi: 10.1242/jeb.056549. [DOI] [PubMed] [Google Scholar]
- 16.Cochet-Escartin O, Mickolajczyk KJ, Collins E-MS. Scrunching: A novel escape gait in planarians. Phys Biol. 2015;12:056010. doi: 10.1088/1478-3975/12/5/056010. [DOI] [PubMed] [Google Scholar]
- 17.Thompson DW. On Growth and Form: The Complete Revised Edition. Dover Publications; Mineola, NY: 1992. [Google Scholar]
- 18.Yang X, Kaj KJ, Schwab DJ, Collins ES. Coordination of size-control, reproduction and generational memory in freshwater planarians. Phys Biol. 2017;14:036003. doi: 10.1088/1478-3975/aa70c4. [DOI] [PubMed] [Google Scholar]
- 19.Orii H, Ito H, Watanabe K. Anatomy of the planarian Dugesia japonica I. The muscular system revealed by antisera against myosin heavy chains. Zoolog Sci. 2002;19:1123–1131. doi: 10.2108/zsj.19.1123. [DOI] [PubMed] [Google Scholar]
- 20.Child CM. The relation between regulation and fission in planaria. Biol Bull. 1906;11:113–123. [Google Scholar]
- 21.Mead RW. Proportioning and regeneration in fissioned and unfissioned individuals of the planarian Dugesia tigrina. J Exp Zool. 1985;235:45–54. [Google Scholar]
- 22.Sheĭman IM, Sedel’nikov ZV, Shkutin MF, Kreshchenko ND. [Asexual reproduction of planarians: Metric studies] Ontogenez. 2006;37:130–135. [PubMed] [Google Scholar]
- 23.Glazer AM, et al. The Zn finger protein Iguana impacts Hedgehog signaling by promoting ciliogenesis. Dev Biol. 2010;337:148–156. doi: 10.1016/j.ydbio.2009.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Style RW, et al. Traction force microscopy in physics and biology. Soft Matter. 2014;10:4047–4055. doi: 10.1039/c4sm00264d. [DOI] [PubMed] [Google Scholar]
- 25.Kwan MK, Wall EJ, Massie J, Garfin SR. Strain, stress and stretch of peripheral nerve. Rabbit experiments in vitro and in vivo. Acta Orthop Scand. 1992;63:267–272. doi: 10.3109/17453679209154780. [DOI] [PubMed] [Google Scholar]
- 26.Muiznieks LD, Keeley FW. Molecular assembly and mechanical properties of the extracellular matrix: A fibrous protein perspective. Biochim Biophys Acta Mol Basis Dis. 2013;1832:866–875. doi: 10.1016/j.bbadis.2012.11.022. [DOI] [PubMed] [Google Scholar]
- 27.Child CM. Studies on the dynamics of morphogenesis and inheritance in experimental reproduction. II. Physiological dominance of anterior over posterior regions in the regulation of Planaria dorotocephala. J Exp Zool. 1911;11:187–220. [Google Scholar]
- 28.Krichinskaya EB. Asexual reproduction, regeneration, and somatic embryogenesis in the planarian Dugesia tigrina (Turbellaria) Hydrobiologia. 1986;132:195–200. [Google Scholar]
- 29.Isolani ME, et al. Planarians as a model to assess in vivo the role of matrix metalloproteinase genes during homeostasis and regeneration. PLoS One. 2013;8:e55649. doi: 10.1371/journal.pone.0055649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sawada T, Oofusa K, Yoshizato K. Characterization of a collagenolytic enzyme released from wounded planarians Dugesia japonica. Wound Repair Regen. 1999;7:458–466. doi: 10.1046/j.1524-475x.1999.00458.x. [DOI] [PubMed] [Google Scholar]
- 31.Topp KS, Boyd BS. Structure and biomechanics of peripheral nerves: Nerve responses to physical stresses and implications for physical therapist practice. Phys Ther. 2006;86:92–109. doi: 10.1093/ptj/86.1.92. [DOI] [PubMed] [Google Scholar]
- 32.Dexter JP, Tamme MB, Lind CH, Collins E-MS. On-chip immobilization of planarians for in vivo imaging. Sci Rep. 2014;4:6388. doi: 10.1038/srep06388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Backholm M, Ryu WS, Dalnoki-Veress K. Viscoelastic properties of the nematode Caenorhabditis elegans, a self-similar, shear-thinning worm. Proc Natl Acad Sci USA. 2013;110:4528–4533. doi: 10.1073/pnas.1219965110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Best JB, Abelein M, Kreutzer E, Pigon A. Cephalic mechanism for social control of fissioning in planarians: III. Central nervous system centers of facilitation and inhibition. J Comp Physiol Psychol. 1975;89:923–932. doi: 10.1037/h0077164. [DOI] [PubMed] [Google Scholar]
- 35.Thomas MA, Schötz E-M. SAPling: A Scan-Add-Print barcoding database system to label and track asexual organisms. J Exp Biol. 2011;214:3518–3523. doi: 10.1242/jeb.059048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hagstrom D, Cochet-Escartin O, Zhang S, Khuu C, Collins E-MS. Freshwater planarians as an alternative animal model for neurotoxicology. Toxicol Sci. 2015;147:270–285. doi: 10.1093/toxsci/kfv129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.King RS, Newmark PA. In situ hybridization protocol for enhanced detection of gene expression in the planarian Schmidtea mediterranea. BMC Dev Biol. 2013;13:8. doi: 10.1186/1471-213X-13-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gutierrez E, Groisman A. Measurements of elastic moduli of silicone gel substrates with a microfluidic device. PLoS One. 2011;6:e25534. doi: 10.1371/journal.pone.0025534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ross KG, et al. Novel monoclonal antibodies to study tissue regeneration in planarians. BMC Dev Biol. 2015;15:2. doi: 10.1186/s12861-014-0050-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wilson RJ, Skierczynski BA, Meyer JK, Skalak R, Kristan WB., Jr Mapping motor neuron activity to overt behavior in the leech. I. Passive biomechanical properties of the body wall. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1996;178:637–654. doi: 10.1007/BF00227377. [DOI] [PubMed] [Google Scholar]
- 41.Junger MC, Feit D. Sound, Structures, and Their Interaction. 2nd Ed MIT Press; Cambridge, MA: 1986. [Google Scholar]
- 42.Gilpin W, Uppaluri S, Brangwynne CP. Worms under pressure: Bulk mechanical properties of C. elegans are independent of the cuticle. Biophys J. 2015;108:1887–1898. doi: 10.1016/j.bpj.2015.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.