Cell volume change through water efflux impacts cell stiffness and stem cell fate

Significance

Cell volume is thought to be a well-controlled cellular characteristic, increasing as a cell grows, while macromolecular density is maintained. We report that cell volume can also change in response to external physical cues, leading to water influx/efflux, which causes significant changes in subcellular macromolecular density. This is observed when cells spread out on a substrate: Cells reduce their volume and increase their molecular crowding due to an accompanying water efflux. Exploring this phenomenon further, we removed water from mesenchymal stem cells through osmotic pressure and found this was sufficient to alter their differentiation pathway. Based on these results, we suggest cells chart different differentiation and behavioral pathways by sensing/altering their cytoplasmic volume and density through changes in water influx/efflux.

Abstract

Cells alter their mechanical properties in response to their local microenvironment; this plays a role in determining cell function and can even influence stem cell fate. Here, we identify a robust and unified relationship between cell stiffness and cell volume. As a cell spreads on a substrate, its volume decreases, while its stiffness concomitantly increases. We find that both cortical and cytoplasmic cell stiffness scale with volume for numerous perturbations, including varying substrate stiffness, cell spread area, and external osmotic pressure. The reduction of cell volume is a result of water efflux, which leads to a corresponding increase in intracellular molecular crowding. Furthermore, we find that changes in cell volume, and hence stiffness, alter stem-cell differentiation, regardless of the method by which these are induced. These observations reveal a surprising, previously unidentified relationship between cell stiffness and cell volume that strongly influences cell biology.

Cell volume is a highly regulated property that affects myriad functions (1, 2). It changes over the course of the cell life cycle, increasing as the cell plasma membrane grows and the amount of protein, DNA, and other intracellular material increases (3). However, it can also change on a much more rapid time scale, as, for example, on cell migration through confined spaces (4, 5); in this case, the volume change is a result of water transport out of the cell. This causes increased concentration of intracellular material and molecular crowding, having numerous important consequences (6, 7). Alternately, the volume of a cell can be directly changed through application of an external osmotic pressure. This forces water out of the cell, which also decreases cell volume, increases the concentration of intracellular material, and intensifies molecular crowding. Application of an external osmotic pressure to reduce cell volume also has other pronounced manifestations: For example, it leads to a significant change in cell mechanics, resulting in an increase in stiffness (8); it also impacts folding and transport of proteins (9), as well as condensation of chromatin (10). These dramatic effects of osmotic-induced volume change on cell behavior raise the question of whether cells ever change their volume through water efflux under isotonic conditions, perhaps to modulate their mechanics and behavior through changes in molecular crowding.

Here, we demonstrate that when cells are cultured under the same isotonic conditions, but under stiffer extracellular environments, they reduce their cell volume through water efflux out of the cell, and this has a large and significant impact on cell mechanics and cell physiology. Specifically, as a cell spreads out on a stiff substrate, its volume decreases, and the cell behaves in a similar manner to that observed for cells under external osmotic pressure: Both the cortical and cytoplasmic stiffness increase as the volume decreases; the nuclear volume also decreases as cell volume decreases. Moreover, stem-cell differentiation is also strongly impacted by cell volume changes. These results suggest that cells in different environments can change their volume through water efflux. This leads to changes in molecular crowding and impacts the mechanics, physiology, and behavior of the cell, having far-reaching consequences on cell fate.

Results

Bulk and Shear Moduli of Cells Increase as Cell Volume Decreases Under External Osmotic Compression.

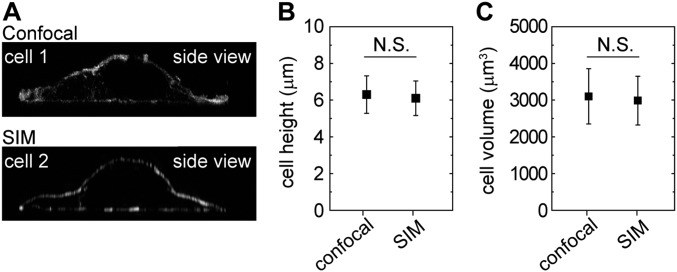
To directly probe the consequences of changes in cell volume, we control the external osmotic pressure through the addition of 300-Da polyethylene glycol (PEG 300) (8, 11). We measure the cell volume by fluorescently labeling the cytoplasm and cell surface and use confocal microscopy to identify the boundaries of the cell in 3D (12, 13). The measured volumes have been shown to be consistent with those measured by atomic force microscopy (AFM) (8). We further validate our confocal measurements by comparing them to those made by using high-resolution structured illumination microscopy (SIM) on the same sample; the measured cell volumes are consistent for both techniques, indicating a measurement uncertainty of <10% (Fig. S1). Because cell volume naturally changes during the cell cycle, we make all our observations after starving cells overnight; however, measurements made under standard culture conditions exhibit the same behavior, albeit with increased variability.

Fig. S1.

Comparison of 3D cell morphology measurements with confocal microscopy and super-resolution SIM. (A) Side views of two representative MEF cells imaged with confocal and SIM are shown. Cells are fixed, with actin filaments stained with phalloidin–Alexa Fluor 488. (B and C) When we image the same sample using confocal and SIM separately, the measured cell height (B) and volume (C) are consistent for both techniques; no statistically significant difference is found for cell height and volume measurements between the two techniques. N.S., not significant.

To explore the dependence of cell volume on external osmotic pressure, we culture A7 cells on glass substrates and add increasing concentrations of PEG 300 to the medium; PEG 300 does not penetrate the cell membrane and thus increases the external osmotic pressure. Since the osmotic pressure imbalance across the cell cortex is negligible (14), the external osmotic pressure must be matched by the internal osmotic pressure, which is controlled by the concentration of ions and small proteins. Thus, to compensate for the increase of external osmotic pressure, the cell must increase its internal osmolyte concentration either by ion influx or water efflux. We find that the cell volume decreases with increasing external osmotic pressure (Fig. S2). This must be due to water efflux, because the cell volume recovers its original value upon removal of the external osmotic pressure. Cells eventually reach a minimum volume under extreme osmotic compression (Fig. S2); this reflects the volume of the total intracellular material, as well as any osmotically inactive water required to hydrate ions and proteins. This behavior is reminiscent of an ideal gas system with an excluded volume, where the pressure is purely entropic in origin. Indeed, the relationship between osmotic pressure P and cell volume V is consistent with P = Nk_BT/(V − V_min), where N is the number of intracellular osmolytes, k_B is the Boltzmann constant, T is the absolute temperature, and V_min is the minimum volume (8). To confirm that the decrease in cell volume is due to water efflux, we use the Bradford assay to measure the total protein content per cell before and after osmotic compression and find no significant difference (SI Materials and Methods).

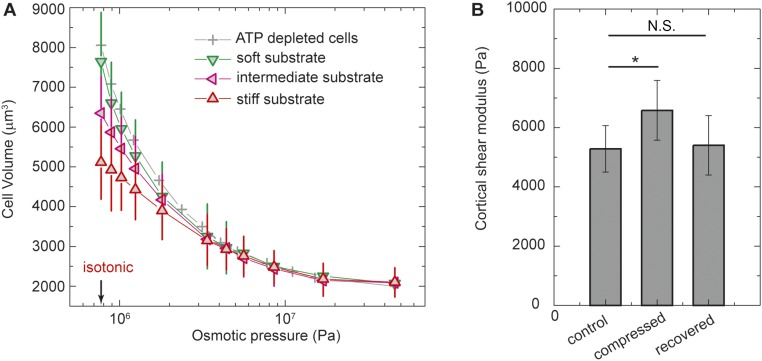
Fig. S2.

Dependence of cell volume and cortical modulus on the applied external osmotic pressure. (A) A7 cells either growing on collagen-coated PA gels with different stiffness or being depleted of ATP on glass are compressed by increasing amounts of PEG 300 polymers to apply external osmotic pressure to extract-free water out of cells. The volume of cells decreases with increasing osmotic pressure and reaches a minimum size at extreme osmotic pressure; the minimum volume does not depend on substrate stiffness. (B) Cortical shear modulus of A7 cells measured by using OMTC before application of osmotic compression, 10 min after osmotic compression (with 5% PEG 300), and 10 min after the osmotic compression is removed. The cortical shear modulus increases after the application of osmotic compression and reduces back to approximately the same value after removal of the osmotic compression. n > 200. *P < 0.01. N.S., not significant.

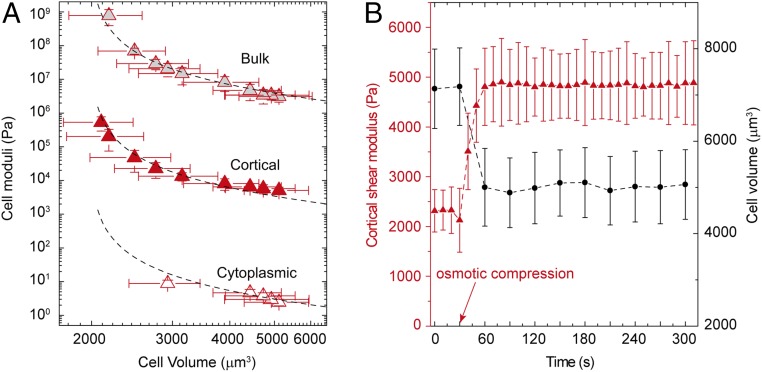
As cell volume decreases, it becomes increasingly difficult to remove additional water and further shrink the cell because the concentration of intracellular ions and other materials increases. The resistance of water leaving a cell is the osmotic bulk modulus and is defined as B = −VdP/dV ∼ −V∆P/∆V. By varying the osmotic pressure and measuring the resultant volume of A7 cells cultured on a glass substrate, we measure B and find that it increases as cell volume decreases, as shown by the points at the top in Fig. 1A. Using the expression for the volume dependence of P, we can predict the behavior of the bulk modulus, B = Nk_BTV/(V − V_min)². This functional form provides an excellent fit to the data, as shown by the dashed line through the points at the top in Fig. 1A. The value of V_min determined by the fit is 2,053 ± 30 µm³; this agrees with the minimum volume measured when the cells are exposed to extreme osmotic compression to remove all osmotically active water, ∼2,100 µm³. The fit also provides a value for N, and this gives a concentration of ∼200 mM, which is consistent with the known salt concentration within a cell (15). The excellent fitting with a constant N suggests that the total amounts of ions and proteins remain approximately constant during osmotic compression. While the osmotic pressure balance is largely controlled by ion concentration, the concentration of large proteins and organelles also increases as free water leaves the cell. It is the volume of these proteins and organelles (including the nucleus) that predominantly determines V_min. Moreover, as the cell approaches its minimum volume, molecular crowding must increase within the cell, and this might lead to additional changes in cell behavior.

Fig. 1.

Mechanical properties of A7 cells on glass as a function of cell volume under external osmotic pressures. (A) Osmotic bulk modulus (gray triangles), cortical shear modulus (red triangles), and cytoplasmic shear modulus (open triangles) increase as cell volume is decreased upon external osmotic compression. The dashed line through gray triangles represents the least-squares fit using the functional form, B = Nk_BTV/(V − V_min)² (R² = 0.99). Dashed lines through the cortical and cytoplasmic moduli are exactly the same fit, simply scaled by a factor of 500 and 100,000, respectively. (B) Cortical shear modulus of a single A7 cell, measured by OMTC, increases immediately after the application of an osmotic compression with 0.26 M PEG 300; this is concurrent with a decrease in cell volume after osmotic compression.

Among many cell properties, cortical stiffness has been shown to depend on volume through molecular crowding as cells are osmotically compressed (8). To measure changes in cortical stiffness, we use optical magnetic twisting cytometry (OMTC) to determine the cortical shear modulus, G, of A7 cells, as shown in Fig. S3 (8, 16, 17); the results obtained with OMTC are in quantitative agreement with those obtained by using AFM (18, 19). The cortical shear modulus and the volume both change rapidly, but simultaneously, as the external osmotic pressure is increased, as shown in Fig. 1B; moreover, the cortical shear modulus recovers its initial value immediately upon removal of the external osmotic pressure (Fig. S2B). Interestingly, the cell cortical stiffness has the same trend as the bulk modulus and is described by exactly the same functional form as shown by the points and dashed line, respectively, in the middle of Fig. 1A. The value of V_min obtained by fitting the functional form to the data, 2,004 ± 41 µm³, agrees well with that obtained from the fit to the bulk modulus. However, the value of the shear modulus is consistently three orders of magnitude less than that of the bulk modulus. The similar dependence of the shear and bulk moduli on cell volume implies that molecular crowding has the dominant effect on both.

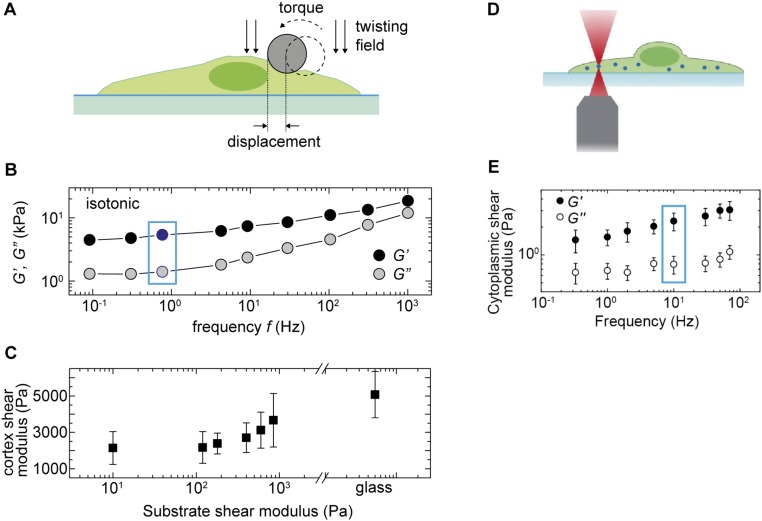
Fig. S3.

Cell cortical stiffness and cytoplasmic stiffness measured with OMTC and optical tweezers, respectively, under different conditions. (A) Schematic illustration of the OMTC measurement (17). A magnetic field introduces a torque that causes the 4.5-µm ferromagnetic bead to rotate and to deform the cell cortex to which it is bound. (B) A representative measurement of A7 cell cortex mechanics in isotonic medium using OMTC. The cell cortex exhibits power-law rheology behavior across four orders of magnitude in frequency. A noticeable plateau in both G′ and G′′ also exists at low frequency. For convenience and consistency, we use cortex modulus measurement at 0.75 Hz (indicated by the blue box) across all different microenvironmental conditions. (C) Cell cortical stiffness (G′) increases with substrate stiffness, consistent with previous measurement using other methods. (D) Schematic illustration of the cytoplasmic stiffness measurement using optical tweezers. (E) A representative measurement of cytoplasmic mechanics in A7 cells. The cell cytoplasm exhibits power-law rheology behavior across three orders of magnitude in frequency. For convenience and consistency, we use cortex modulus measurement at 10 Hz (indicated by the blue box) across all different microenvironmental conditions.

The major contribution of the shear modulus of the cell comes from the cortical stiffness. However, the cell is a highly heterogeneous structure, and the interior is much softer; the cytoplasm of the cell is a weak elastic gel with a shear modulus that is three orders of magnitude lower than that of the cortex (17, 20). To measure cytoplasmic stiffness, we microinject PEG-coated polystyrene beads into A7 cells and use laser tweezers to determine the cytoplasmic shear modulus, as shown in Fig. S3 (Materials and Methods). The intracellular shear modulus increases as cell volume decreases, following an identical trend as both the cortical shear and bulk moduli, as shown by the lower points in Fig. 1A. The cytoplasmic shear modulus clearly increases as the cell volume is further decreased, but its value is too large to be measured with the laser tweezers. Over the range accessible, the cytoplasmic shear modulus behavior has the same functional form as do the other two moduli, as shown by the dashed line at the bottom of Fig. 1A; however, its value is a further three orders of magnitude less than that of the cortical shear modulus.

Cells Reduce Their Volume When Cultured on Stiffer Substrates.

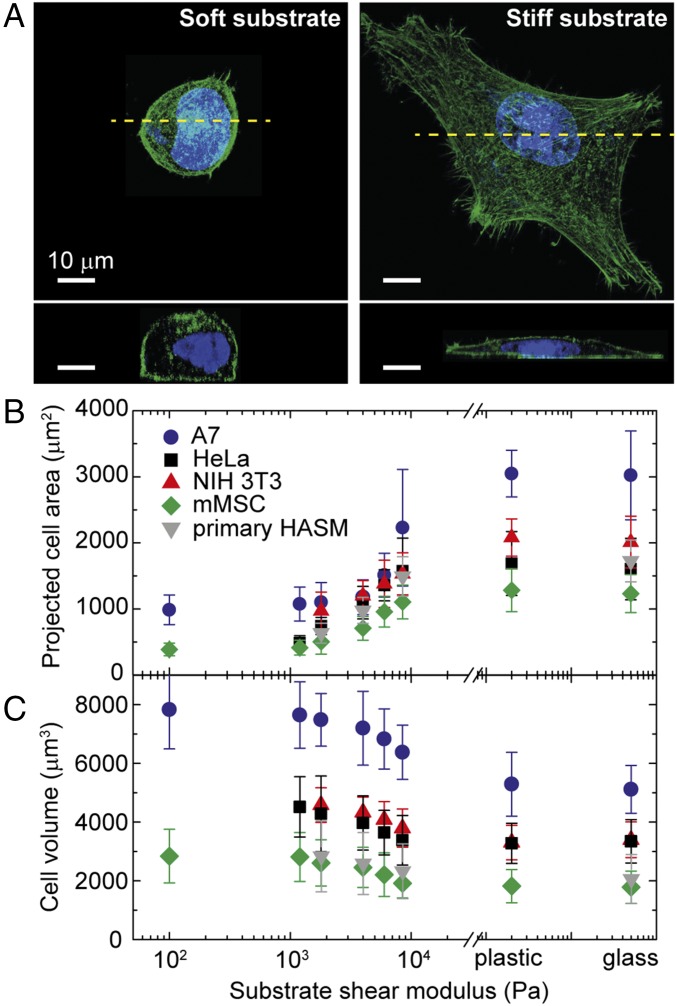
Cortical stiffness is a key physical property of cell mechanics, and its value typically decreases as the stiffness of the substrate on which the cells are grown decreases (21). Cell morphology can vary markedly with substrate stiffness, and this could also impact molecular crowding, even under isotonic conditions. To investigate this possibility, we culture A7 cells on 100-µm-thick polyacrylamide (PA) gels coated with collagen I; by varying gel composition, we tune the shear modulus of the gels from 0.1 to 10 kPa, matching the physiological elasticities of natural tissues (Table S1). To probe cell morphology, we measure the cell spread area; it increases significantly for cells cultured on stiffer substrates (21–24), as shown by the confocal images in Fig. 2A, Upper, and as summarized in Fig. 2B. Surprisingly, however, cell volume is not conserved: As substrate rigidity increases, cell volume decreases. On the most rigid substrates, the volume decrease is as much as ∼40% compared with cells grown on the softest substrates where their volume is a maximum, as shown in Fig. 2C. Other mammalian cell types, including HeLa, NIH 3T3, mouse mesenchymal stem cell (mMSCs), and primary human airway smooth muscle cells, show similar behavior (Fig. 2C). This confirms the generality of the dependence of cell volume on substrate stiffness. Thus, even without changes in external osmotic pressure, the cell volume can change.

Table S1.

Composition and shear modulus of PA gels in our experiment

Acrylamide (%)	Bis, %	Shear modulus, Pa
3	0.04	100
3	0.06	200
5	0.1	1,200
7.5	0.05	1,800
7.5	0.15	4,000
7.5	0.2	6,000
7.5	0.3	8,500
7.5	0.5	10,000

Fig. 2.

Morphology and volume of adherent cells change with increasing substrate stiffness. (A) Top and side views of fixed A7 cells on a stiff (shear modulus of 10 kPa) and a soft (shear modulus of 1,200 Pa) PA gel substrate coated with collagen I. The actin cortex (green) and nucleus (blue) are labeled. (B) The projected cell area increases with increasing substrate stiffness. (C) Cell volume markedly decreases with increasing substrate stiffness. Error bars represent the SD (n > 200 individual cells). HASM, human airway smooth muscle.

Table S2.

Changing substrate stiffness

Substrate shear modulus, Pa	Cell volume, μm3	Cortex shear modulus, Pa
100	7,833	2,141
1,200	7,646	2,167
1,800	7,482	2,386
4,000	7,197	2,705
6,000	6,829	3,121
8,500	6,377	3,661
Glass	5,116	5,072

Table S3.

Changing adhesive pattern size on glass

Island area, μm2	Cell volume, μm3	Cortex shear modulus, Pa
707	7,758	2,101
1,256	7,213	2,493
1,590	6,965	3,310
1,963	6,411	3,795
Unpatterned	5,328	4,863

Table S4.

Applying osmotic pressure on a soft substrate, with shear modulus 1,200 Pa

[PEG], %	Osmotic pressure, Pa	Cell volume, μm3	Cortex shear modulus, Pa
0	773,000	7,646	2,167
2.6	1.02414E6	5,955	3,011
5	1.24451E6	5,277	3,799
10	1.80668E6	4,257	5,971
20	3.38506E6	3,252	11,049

Table S5.

Applying osmotic pressure on a glass substrate

[PEG], %	Osmotic pressure, Pa	Cell volume, μm3	Cortex shear modulus, Pa
0	773,000	5,116	5,072
2.6	1.02414E6	4,729	5,754
5	1.24451E6	4,425	6,496
10	1.80668E6	3,898	8,126
20	3.38506E6	3,147	13,422

Table S6.

Applying osmotic pressure on a glass substrate with 1,256-μm² patterns

[PEG], %	Osmotic pressure, Pa	Cell volume, μm3	Cortex shear modulus, Pa
0	773,000	7,401	2,539
1	890,490	6,748	2,579
2.6	1.02414E6	6,223	3,547
5	1.24451E6	5,518	3,895
10	1.80668E6	4,437	7,210
20	3.38506E6	3,502	12,916

Restricting Spread Area Increases Cell Volume.

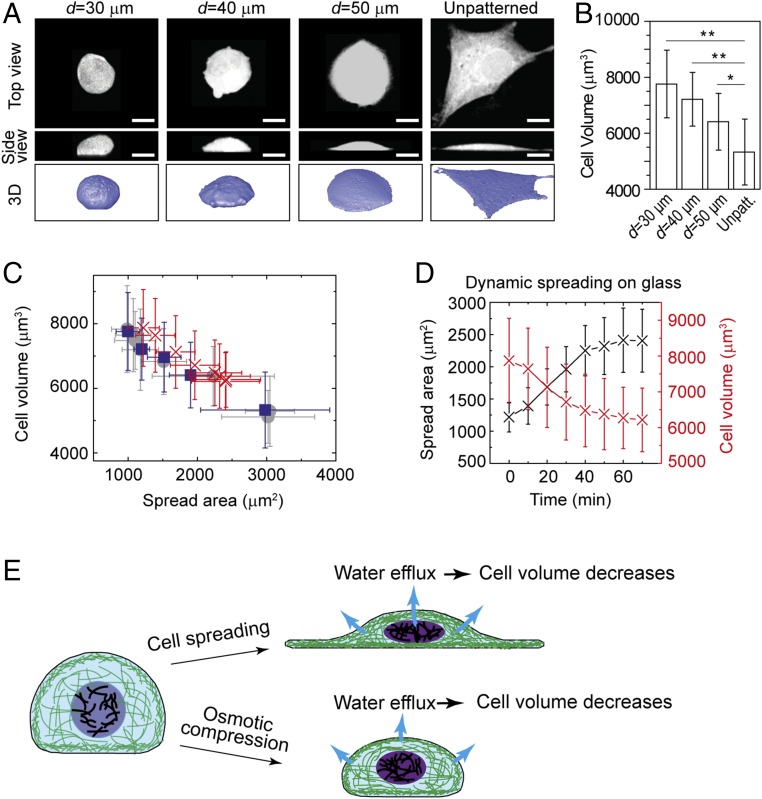
To further explore the nature of the change in cell volume with substrate stiffness, we investigate the role of spread area. We culture A7 cells on a glass substrate, but control the spread area by restricting their adhesion. We micropattern collagen “islands” of varying size on a glass substrate to limit the adhesion area of the cells (25). Interestingly, we find that cells with limited spread area have a larger height compared with cells with unrestricted spread area (Fig. 3A). Moreover, the cell volume also increases as the spread area decreases, as shown in Fig. 3B. The same effect is observed when we grow cells on micropatterned softer substrates: If the cell spread area is restricted to be less than that of a freely spreading cell on the substrate, the volume increases. Remarkably, cell volume exhibits the same dependence on spread area regardless of how the area is attained, either through controlling the adhesive area on a stiff substrate or through varying substrate stiffness, as shown by the comparison of the blue and gray points in Fig. 3C.

Fig. 3.

Cell volume of A7 cells increases when the cell spread area is decreased by growing cells on micropatterned collagen islands. Error bars represent the SD. *P < 0.05; **P < 0.01. (A) Shown are 3D images of A7 cells on micropatterned islands of different sizes on glass. Cells are labeled with cell tracker green. (Scale bars, 20 μm.) (B) Cell volume decreases with increasing cell spread area on glass. (C) Cell volume plotted as a function of the projected area, for cells on substrates with different stiffnesses (gray circles; n > 200), cells on a glass substrate but with different available spread area (blue squares; n > 200), and a dynamically spreading cell (red crosses; n = 3). (D) Variation of cell spread area and volume as a single cell dynamically attaches on a stiff substrate (n = 3). (E) Schematic illustration of cell volume decrease through water efflux, as cells spread out or are osmotically compressed.

Cell Volume Reduction Is Due to Intracellular Water Efflux.

To determine whether the reduction in cell volume under isotonic conditions is due to changes in protein content or to water efflux, we monitor a single trypsinized cell as it spreads on a rigid substrate. The cell changes from its initial rounded state to a fully spread state in ∼20 min. During this time period, the cell volume decreases concomitantly with increasing spread area, as shown in Fig. 3D. The relationship between volume and spread area is identical to that of cells cultured on confined areas or on substrates of varying rigidities, as shown by the red × symbols in Fig. 3C. Water can leave the cell within a minute (8, 26), while changes in amount of intracellular materials due to growth can typically take hours for mammalian cells (3, 27). Thus, these results suggest that volume reduction under isotonic conditions is most likely controlled through water exchange, albeit at isotonic osmotic pressure.

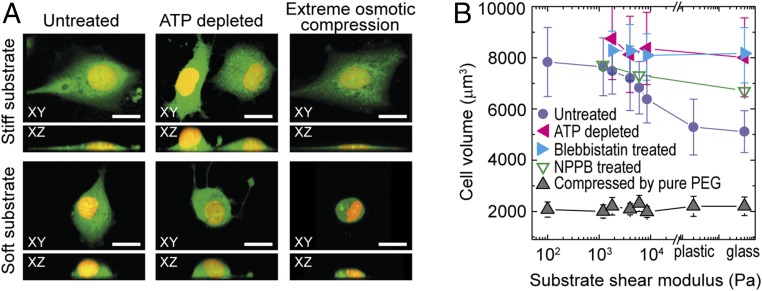
To confirm that cell volume variation upon spreading is due to water efflux and not protein loss, we measure the total protein content per cell for cells cultured on both stiff and soft substrates and find no significant difference (SI Materials and Methods). Consistent with this, when we apply extreme osmotic pressure to cells by exchanging culture medium with pure PEG, thereby extracting all osmotically active water from the cells, we find that the resultant minimum volume, V_min, is independent of substrate stiffness (Fig. 4). Since V_min approximately reflects the amount of intracellular material and bound water that is osmotically inactive (8), these data support the view that variation of cell volume results from exchange of free intracellular water.

Fig. 4.

Cell morphology and volume under drug treatment and osmotic compression. (A) The 3D morphology of control cells and cells with ATP depletion and under extreme osmotic compression, on stiff and soft substrates. Cytoplasm (green) and nucleus (yellow) are labeled. (Scale bars: 20 μm.) (B) Cells without active contraction (blebbistatin-treated and ATP-depleted) and under extreme osmotic compression do not exhibit a volume dependence with substrate stiffness; cells with choloride channels-inhibited (NPPB treated) exhibit a weaker volume dependence with substrate stiffness. The control data of A7 cells is same as in Fig. 2C. Error bars represent the SD (n > 200 individual cells).

Ion Channels and the Actomyosin Cytoskeleton Play a Role in Cell Volume Reduction During Spreading.

The efflux of water during cell spreading under isotonic conditions must have a different origin than the efflux of water during osmotic compression. In both cases, the osmotic pressure is balanced across the cell membrane. Under osmotic compression, the total amount of material, including ions and proteins, remains approximately constant; the internal osmotic pressure increases as a result of increasing intracellular osmolyte concentration through water efflux. During cell spreading, cell volume reduction occurs under isotonic conditions; for water to leave the cell, the total amount of osmolytes must change. Since the amount of protein per cell remains constant, it is instead likely the reduction of osmolytes for cells on stiff substrates is due to the exchange of ions with the surroundings. During cell spreading, cytoskeletal tension increases, and this has been tied to the increase of ion channel activity (28–30). To test the role of ion channel activity on cell volume variation, we inhibit chloride ion channels by 0.1 mM 5-nitro-2-(3-phenylpropylamino)-benzoic acid (NPPB) after cells fully spread. The decrease in cell volume with increasing substrate stiffness is significantly suppressed when ion channels are blocked, as shown by the green open triangles in Fig. 4B. This indicates that cell volume reduction under isotonic conditions requires the activity of ion channels to change the total amount of internal osmolytes and hence ensure that the osmotic pressure remains balanced.

To further test if active cell processes play a role in the reduction of cell volume, we treat cells with 10 µM blebbistatin to inhibit myosin II motor activity and thus directly reduce cytoskeletal tension. Blebbistatin treatment prevents cells from decreasing their volume on stiff substrates, as shown by the blue triangles in Fig. 4B. The same increase in volume is observed when we inhibit general motor activity by depleting ATP using 2 mM sodium azide and 10 mM 2-deoxyglucose, as shown by the pink triangles in Fig. 4B. These results further demonstrate that active cellular processes are involved in volume decrease under isotonic conditions and that cells must actively control the osmolyte concentration using ion channels to affect water efflux and change their volume.

Cell Moduli Demonstrate a Universal Dependence on Cell Volume.

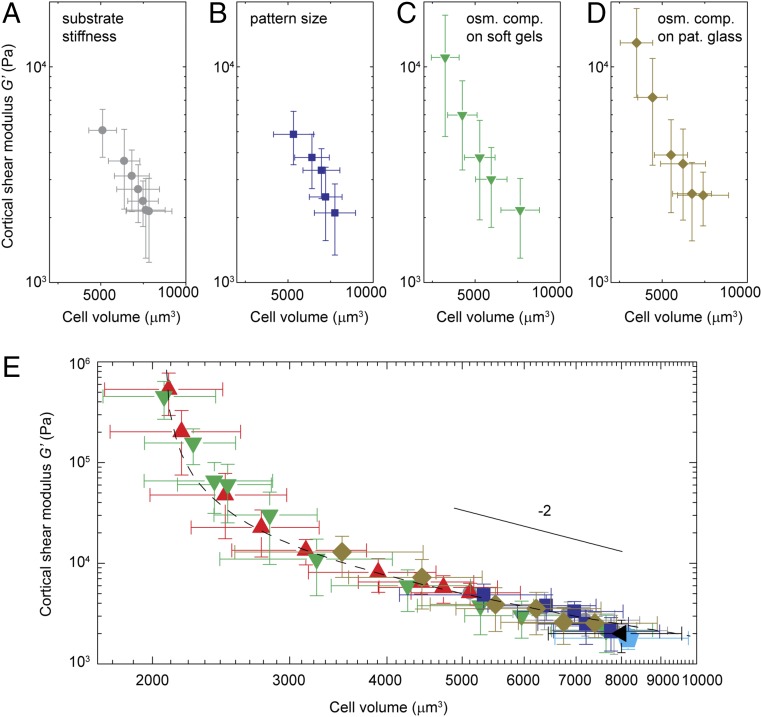
Cell cortical stiffness increases with substrate stiffness as the cells increase their spread area under isotonic conditions; cell cortical stiffness also increases as we change the spread area for fixed substrate stiffness. However, cell stiffness also increases for fixed substrate stiffness and fixed spread area when the osmotic pressure is increased, thereby decreasing cell volume. We therefore hypothesize that cell volume change is the common descriptor underlying the cell stiffness change observed in all these cases. To investigate this hypothesis, we plot cortical stiffness as a function of volume: Cell stiffness decreases with increasing volume as cells are grown on softer substrates (Fig. 5A). Cell stiffness decreases in a similar fashion with increasing volume as cells are grown on a substrate with fixed stiffness, but with varying adhesive areas (Fig. 5B). Similarly, cell stiffness increases as cells grown on a soft substrate are compressed by an external osmotic pressure (Fig. 5C) and when cells grown on a stiff substrate and a highly constrained area are compressed through osmotic pressure (Fig. 5D). Remarkably, when we plot all these data on a single graph (Fig. 5E), they all overlay and exhibit a universal dependency between cell stiffness and cell volume across all perturbations. Thus, cell volume change is indeed a common descriptor of cell stiffness change. The data shown here are all obtained for a single cell type, A7; however, similar scaling behavior between cell stiffness and cell volume is observed for each cell type, although they are shifted in amplitude and volume (Fig. S4).

Fig. 5.

Relationship of cell cortical stiffness and cell volume. (A–D) Dependence of cell cortex shear modulus of A7 cells on their volume, under different conditions, including cells cultured on substrates of varying stiffnesses (A), on a stiff substrate with micropatterns of varying sizes (B), on a soft substrate with a shear modulus of 100 Pa with addition of increasing amount of osmotic pressure (C), and on a glass substrate with small micropatterns limiting cell spreading and with the addition of osmotic pressures (D). (E) Cell cortical shear modulus scales with cell volume, as shown for cells growing on substrates of varying stiffness (gray circles), on a glass substrate with restricted available spread area using micropatterns (blue squares), on a soft substrate with osmotic compression (shear modulus of 100 Pa, green upside down triangles), on an unpatterned (red triangles) and a micropatterned glass substrate (yellow diamonds) with osmotic compression, and on a glass substrate with 10 μM blebbistatin treatment (cyan pentagon) or depleted of ATP (black triangle). Solid line shows the power-law fitting of the data, scales as V⁻². Dashed line shows fitting to G ∝ k_BTV/(V − V_min)² Error bars represent the SD (n > 200 individual cells). osm. comp., osmotic compression; pat., patterned.

Fig. S4.

Dependence of cell cortical stiffness on cell volume observed for other cell types and in 2D monolayers. (A) Cortical shear modulus and cell volume of Eker rat uterine leiomyoma cells (ELT3) are measured for cells cultured under different conditions, such as on substrates of varying stiffness (filled symbols) and on glass under increasing osmotic pressure (open symbols). Similar scaling behavior is observed for ELT3 and A7 cells, yet it is shifted in both the cortical shear modulus and volume between the cell types. (B) Cortical shear modulus and cell volume of MCF10A cells growing in a 2D monolayer at varying densities. MCF10A human breast cells are seeded at varying densities and therefore grow into a 2D monolayer with different cell densities. Cell volume and cortical stiffness of cells are measured at different cell densities, as plotted in B, Inset. Similar scaling behavior between cortical stiffness and cell volume is observed for MCF10A cells in 2D monolayers with different densities, as is observed for isolated cells under different cell culture conditions.

Interestingly, if we restrict the data to those cell volumes physiologically accessible without application of external osmotic pressure, where cells solely respond to either changes in substrate stiffness or spread area, the behavior is consistent with G ∝ 1/V², as shown by the solid line in Fig. 5E. Intriguingly, this is very similar to the behavior of biopolymer networks reconstituted from either actin or vimentin, where the shear modulus is approximately proportional to the square of the concentration (31–34). This would be expected if the change in the shear modulus is due solely to the water exchange responsible for the volume change. If the data for all measured volumes are included, the full behavior is well described by G ∝ k_BTV/(V − V_min)², as shown by the dashed line in Fig. 5E_. While there is no model that predicts this behavior for the shear modulus, it is nevertheless identical in functional form to the behavior of the bulk modulus over the same range of volumes, B ∝ k_BTV/(V − V_min)². This functional form for the bulk modulus is a direct consequence of the measured P–V relationship of the cell, which reflects the effects of increased molecular crowding as water is drawn from the cell. Thus, our results suggest that a similar crowding phenomenon is also responsible for the change in the cortical shear modulus under various perturbations that we tested here. Similarly, both osmotic bulk modulus and cytoplasmic shear modulus across multiple perturbations are also observed to be universally dependent on cell volume (Fig. S5), as they do under osmotic compression shown in Fig. 1A.

Fig. S5.

Universal dependence of osmotic bulk modulus, cortical shear modulus, and cytoplasmic modulus on volume of A7 cells. Osmotic bulk modulus (top), cortical shear modulus (middle), and cytoplasmic shear modulus (bottom) increase in a universal fashion as cell volume is decreased upon various perturbations. In the top, up, left, and down triangles represent measurements with cells cultured on substrates with high, intermediate, and low stiffness, respectively. Gray plus symbols represent ATP-depleted cells. Symbols in the middle are described in Fig. 5. In the bottom, cytoplasmic stiffness in cells cultured on substrates of varying stiffness (gray circles), on a soft substrate with osmotic compression (shear modulus of 100 Pa; green upside-down triangles), on a unpatterned glass substrate (red triangles) with osmotic compression, and on a glass substrate with 10 μM blebbistatin treatment (cyan pentagon) or depleted of ATP (black triangle). The solid lines are the same functional form used in Fig. 1. Error bars represent the SD (n > 200 individual cells for the bulk modulus calculation and for OMTC measurement; n > 5 for optical tweezers measurement).

To explore the generality of the correlation between cell stiffness and cell volume, we also include the data with actomyosin contraction inhibited through addition of blebbistatin; we find that cortical stiffness and volume remain exactly on the same functional curve, as shown by the cyan pentagon in Fig. 5E. Similarly, when ATP is completely depleted, the data exhibit the same behavior, as shown by the black triangle in Fig. 5E. Interestingly, not only for isolated cells, similar behavior is also observed for cells in a 2D monolayer. We grow epithelia MCF10-A cells into a monolayer, but with different cell densities, and measure the corresponding cell volume and cortical shear modulus; we find that cell volume decreases as the density of cells increases (Fig. S4B). Cell volume and stiffness again remain correlated: As cell density increases, cell volume decreases, and cortical stiffness increases in a fashion consistent with a 1/V² dependence. These results imply that cell volume plays role in determining cell mechanics, even for cells in confluent layers.

Nuclear Volume Tracks Cell Volume.

The nuclear envelope, like the cell membrane, is selectively permeable and allows water exchange; therefore, we wonder if water efflux from the cell extends to the nucleus. To test this, we fluorescently label cell nuclei and use 3D confocal microscopy to measure their volume. We find that cell nuclear volume tracks cell volume both for cells grown under isotonic conditions on different substrates and also for cells whose volume is changed through external osmotic pressure (12), as shown in Fig. 6. This suggests that the cell nucleus also becomes more crowded as cell volume decreases, and this has a direct consequence on the degree of motion within the nucleus. To illustrate this, we measure fluctuating motion of GFP-tagged histone H2B, which is widely used to report on positional fluctuations of chromatin (35, 36); we calculate their mean-squared displacement and find a marked reduction in the level of fluctuations as molecular crowding is increased through an external osmotic pressure (9, 20, 37) (Fig. 6B).

Fig. 6.

Cell nuclear volume and nuclear dynamics change with cell volume. (A) Nucleus volume always directly tracks cell volume, decreasing proportionally with increasing substrate stiffness, spread area, and osmotic pressure; the ratio between nuclear volume and cell volume remains approximately constant for each tested cell type. (B) Mean square displacement of GFP-tagged Histone in MCF-10A cell nuclei, reflecting positional fluctuation of chromatin, significantly reduces under external osmotic compression through application of 0.1 M PEG 300. osm. comp., osmotic compression; sub., substrate.

Stem-Cell Fate Can Be Directed by Changing Cell Volume.

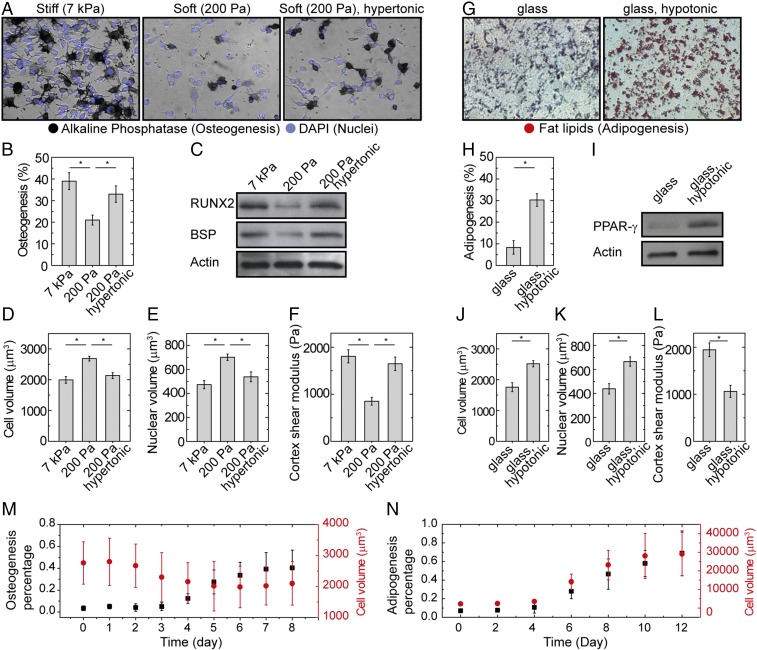
Of the many properties of cells that vary with cell stiffness (38), cell spread area (39), and substrate stiffness (40), one of the most consequential is stem-cell differentiation. We therefore investigate the impact of cell volume on stem-cell differentiation, since cell volume is intrinsically related to cell stiffness, as well as the other parameters like molecular crowding. To do so, we externally impose changes in cell volume through osmotic compression; this results in changes of cell stiffness, but not spread area or substrate properties. Moreover, we confirm that this does not change the tension within the cell, as measured by the traction force microscopy (TFM) (ref. 41; Fig. S6). We grow mMSCs on two different PA gel substrates, one a stiff substrate with a shear modulus of 7 kPa and the other a soft substrate with a shear modulus of 0.2 kPa. On a soft substrate, cells typically have a larger volume than cells on a stiff substrate; thus, we apply additional osmotic pressure by adding 0.1 M PEG 300 (+100 mOsm) to the medium so that the volume of cells grown on the soft gel matches that of the cells grown on the stiff gel (Fig. 7 D and E). We find that when volumes are matched, cell stiffnesses are also matched (Fig. 7F). We expose the cells to bipotential differentiation medium that is supportive of both osteogenic and adipogenic fates (SI Materials and Methods). After 1 wk of culture, we observe substantially increased osteogenic differentiation, as indicated by alkaline phosphatase (ALP) activity on the rigid substrate, compared with unperturbed cells on soft substrate, as expected (40). Unexpectedly, osmotically compressed cells grown on the soft substrate also exhibit enhanced ALP activity, suggesting preferential osteogenic differentiation (Fig. 7 A and B). This is confirmed by Western analysis of the expression of osteogenic biomarkers runt-related transcription factor 2 (RUNX2) and bone sialoprotein (BSP), as shown in Fig. 7C.

Fig. S6.

Cell morphology, traction force, and substrate properties under osmotic compression. (A–C) Cell morphology (Upper) and traction stress intensity map (Lower) of mMSCs on a stiff gel, a soft gel, and a soft gel with osmotic compression. mMSCs are cultured on a collagen I-coated PA gel, with 500-nm fluorescent beads previously mixed in the gel substrate for visualizing traction displacement applied by cells. Cells on a stiff gel have larger spreading area and stronger traction stresses than those cultured on a soft gel. However, when we compress cells with osmotic pressure on a soft gel, while the height of the cell dramatically decreases, cell spreading area and traction stress does not significantly change. The cytoplasm and nucleus are labeled with cell tracker and DRAQ-5. (D) Frequency dependent shear moduli of a soft PA gel substrate measured by OMTC, in isotonic medium (black symbols), and in medium with additional osmotic pressure by adding 0.1 M PEG 300 (red symbols). This result shows that PA gel is indeed an elastic gel with G′ (filled symbols) greater than G′′ (open symbols); moreover, the osmotic pressure we apply to compress cells does not significantly affect the mechanical property of the PA gel substrate.

Fig. 7.

Cell volume affects differentiation of mMSCs. (A–F) Osteogenesis. (A) In situ staining of mMSC for ALP (black) and nucleus (DAPI, blue) after 1 wk of culture in the presence of combined osteogenic and adipogenic chemical supplements shows increased osteogenesis on the stiff substrate (shear modulus of 7 kPa) and the soft substrate (shear modulus of 200 Pa) with osmotic compression (with 0.1 M PEG 300, additionally to the medium), compared with the control on soft substrate without additional osmotic pressure. (B) Mean percentages of mMSC osteogenesis. Error bars, SEM (n = 3 samples). *P < 0.05. (C) Western analysis of osteogenic protein expression (RUNX2 and BSP) in mMSCs after 3 d of culture. (C–F) Cell volume (D), nucleus volume (E), and cortex shear modulus (F) measured with confocal microscopy and OMTC, for three experimental conditions (n > 50 individual cells). *P < 0.05. (G–L) Adipogenesis. (G) In situ staining of mMSC for fat lipids (red) after 2 wk of culture in the presence of combined osteogenic and adipogenic chemical supplements shows enhanced adipogenesis on stiff substrate with application of hypotonic pressure (with the addition of 30% DI water), compared with the control. (H) Mean percentages of mMSC adipogenesis. Error bars, SEM (n = 3 samples). *P < 0.05. (I) Western analysis of adipogenesis protein expression (PPAR-γ) in mMSCs after 1 wk of culture. (J–L) Cell volume (J), nucleus volume (K), and cortex shear modulus (L) measured with confocal microscopy and OMTC, for three experimental conditions (n > 50 individual cells). *P < 0.05. (M) mMSCs are exposed to osteogenesis medium for 10 d. The ratio of cells expressing high level of ALP, as measured by using Fast Blue staining, as described in SI Materials and Methods, is counted in three independent samples fixed each day. Volume of cells is observed each day as well. As the ratio of differentiated cells increases, cell volume decreases correspondingly (n = 3 samples; error bars represent SD). (N) mMSCs are exposed to adipogenesis medium for 2 wk. The ratio of cells with clear fat lipid accumulation, as visualized by ORO staining, as described in SI Materials and Methods, is counted in three independent samples fixed every 2 d. Volume of cells is measured at the same time as well. As the ratio of differentiated cells increases, cell volume increases correspondingly (n = 3 samples; error bars represent SD). (Magnification: A and G, 400×.)

As a contrapositive test, we use hypotonic conditions (−80 mOsm) to swell cells grown on a stiff substrate, such that both cell volume and nuclear volume match those of cells grown on a soft substrate (Fig. 7 J and K). We again find that when volumes are matched, cell stiffnesses are matched (Fig. 7L). In this case, we observe substantial adipogenic differentiation as shown by in situ staining of neutral lipid accumulation [Oil Red O (ORO)] and the expression of adipogenic biomarker peroxisome proliferator-activated receptor gamma (PPAR-γ) (Fig. 7 G–I). The results indicate that we can influence stem-cell differentiation either toward osteogenic or adipogenic fates by changing their volume; this suggests that the intranuclear and possibly intracellular crowding affects stem-cell fate.

Stem-Cell Fate Affects Cell Volume.

In the absence of strong chemical cues, physical properties such as substrate stiffness or external osmotic pressure affect stem-cell differentiation. However, chemical signals can often override these physical cues. While we have shown that physical signals change cell volume, we wonder if chemical cues also change cell volume during differentiation. Thus, we grow mMSCs on a soft PA gel, which would bias the cells toward adipogenic differentiation; however, we add supplements (β-glycerol phosphate, ascorbic acid, and dexamethasone) to the medium (details in Materials and Methods) to direct the cells toward osteogenic differentiation. The mMSCs undergo osteogenic differentiation under these conditions. Interestingly, we find that cell volume decreases during this process and, surprisingly, even precedes osteogenic differentiation, as shown in Fig. 7M. Conversely, we find that cell volume increases when we chemically induce adipogenesis using dexamethasone alone for mMSCs cultured on stiff substrates, as shown in Fig. 7N. These results suggest that cell volume and stem-cell differentiation are strongly correlated.

SI Materials and Methods

Fabrication of PA Gel Substrate.

Variably compliant PA gels are made according to the procedure described by Pelham and Wang (24), on 35-mm glass-bottom culture dishes (MatTek), with a no. 1 coverslip on the bottom. Briefly, the glass is aminosilanized to enable PA attachment. Gel stiffness is varied over two orders of magnitude by controlling the concentration of the cross-linker bis-acrylamide (Bio-Rad) and the monomer acrylamide (Bio-Rad) concentrations; gels are mainly made of 7.5% acrylamide, but gels with shear modulus <2,000 Pa are made of 3% acrylamide gels (Table S1). For TFM measurements, a small volume (<1%) of 500-nm red fluorescent latex particles (Invitrogen) is added to the solution to act as a marker of gel deformation. Polymerization is initiated by the addition of ammonium persulfate and n,n,n′,n′-tetramethylethylenediamine; after polymerization is started, a controlled volume is added to the glass-bottom dishes. During polymerization, the gel is covered with a second unmodified coverslip and inverted to create a flat gel surface. After polymerization is complete, the top coverslip is removed, and collagen I (Vitrogen; Cohesion Tech) at a concentration of 0.1 mg/mL in solution is chemically cross-linked to the gel surface by using the sulfo-SANPAH (Pierce Biotechnology) activation method. Collagen attachment and uniformity are confirmed by using fluorescent collagen (Elastin Products). As we have shown (55), comparing known amounts of fluorescent collagen dried on aminosilanized coverslips with gel surfaces allows calibration of the collagen surface density and is found to be ∼250–650 ng/cm² for the gels used in this study (56). Gel thickness is controlled to be 70–100 µm and is confirmed by confocal microscopy. The elastic shear modulus G′ of macroscopic samples of the PA gels are characterized mainly by using a rheometer (AR-G2; TA Instruments); for in situ characterization, we also use OMTC in the same sample when we measure cell cortical stiffness.

Cell Culture and Pharmacological Interventions.

We use different cell lines and primary cells to demonstrate the robustness of our observation. A7 cells (57) (gift from Tom Stossel laboratory at Harvard Medical School, Boston) are cultured in DMEM with 2% FBS, 8% newborn calf serum (Invitrogen), 10 mM Hepes buffer, and 100 unit/mL penicillin/streptomycin at 37 °C and 5% CO₂. HeLa, NIH 3T3, and MEF cells (ATCC) are cultured in DMEM with 10% FBS (Invitrogen) and 100 units/mL penicillin/streptomycin at 37 °C and 5% CO₂. Culture of stem cells is described below. Cells are allowed to spread on substrates for several hours (>4 h), then are synchronized by starvation in serum-free medium overnight before volume imaging and stiffness measurement. Confocal imaging and OMTC measurements are performed in serum-free medium at 37 °C and 5% CO₂. For both cell volume measurement and OMTC, we measure >200 cells under each condition.

Cells are synchronized to avoid cell size growth and volume change due to natural variations during the cell cycle. Volume of unsynchronized A7 cells in regular culture medium is also measured for comparison. Surprisingly, we do not observe a difference in the average cell volume of 200 individual cells between synchronized and unsynchronized cells; the SD of the volume of unsynchronized cells (∼30–40% of the cell volume) is, indeed, larger than that of synchronized cells (∼20–30% of the cell volume).

To assess the contribution of the cortical acto-myosin contractile system to changing cell volume, blebbistatin (Toronto Research Chemicals), a specific inhibitor of myosin II activity that keeps myosin II in a weakly bound state to actin (58), is dissolved in DMSO and added to cell medium to a 10 µM final concentration for 30 min in an incubator. To inhibit the general motor activity, ATP depletion is achieved by treating cells with 2 mM sodium azide (NaN₃) and 10 mM deoxyglucose in PBS for 1 h.

To inhibit chloride ion channels in cells, we allow A7 cells to fully spread on PA gel substrates overnight, then add 0.1 mM NPPB into cell culture medium for 1 h.

Cell Labeling and Immunofluorescence.

Cells for confocal imaging are plated on glass coverslips or PA gel substrates at a density of 20 cells per mm² and allowed to adhere overnight. Live cells are fluorescently labeled according to the manufacturer’s instructions, with CellTracker Red CMTPX, Orange CMTMR, Green CMFDA (Invitrogen), CellMask plasma membrane stains (Invitrogen), and DRAQ5 (Cell Signaling Technology) to label cytoplasm, membrane, and cell nucleus, respectively. The cells are imaged and sectioned at 0.15-μm intervals by using excitation from a 633- or 543-nm HeNe laser or the 488-nm line of an argon ion laser using a 63×, 1.2-NA water immersion objective on a laser-scanning confocal microscope (TCS SP5; Leica). To label the actin cortex and acquire a secondary measure of the cell boundary and cell size, we also fix cells and label their actin structures using phalloidin. For fixation, the cells are rinsed with PBS, followed by a wash in 4% paraformaldehyde (Polysciences) in PBS for 10 min, permeabilized with 0.1% Triton X-100 in PBS for 5 min, and blocked with 1% BSA in PBS for 1 h. To visualize the actin structure, the fixed cells are incubated with 1 mg/mL Alexa 488 phalloidin (Invitrogen) and 1% BSA in PBS for 30 min, then washed in PBS. The cells are subsequently incubated with 1 µM DRAQ5 in PBS for 5 min in the dark to label cell nuclei. After a final wash, cells are then covered with mounting medium and stored at 4 °C overnight before observation by laser confocal microscopy.

Bradford Assay.

Samples are subjected to a modified Bradford assay to estimate total protein as per manufacturer’s instructions (BCA; Thermo Scientific Inc.). A standard curve is created with known amounts of BSA. Absorbance is measured at 560 nm with a microplate reader (Synergy HT and KC4 software; Bio-Tek Instruments). Measurements are performed overnight after seeding cells at a desired number concentration. Osmotic compression is added on the cells 10 min before measurement. More than three independent measurements are done for each condition. Total protein mass has been found to be 420 ± 87 pg per cell (mean ± SD, n = 4) while cultured on glass substrate under isotonic condition, 395 ± 69 pg per cell (mean ± SD, n = 3) while cultured on glass substrate but under 0.1 M PEG 300 osmotic compression in addition to cell culture medium, and 403 ± 72 pg per cell (mean ± SD, n = 3) while cultured on 1 kPa PAA gel substrate. There is no statistically significant difference between any two of these conditions.

Fabrication of Micropatterned Islands.

The fabrication of micropatterned islands coated with collagen I is achieved following existing microcontact printing protocols (25, 59). Briefly, 0.1 mg/mL collagen I solution is dried on a flexible stamp made of polydimethylsiloxane (PDMS) containing a structure of the desired pattern; the PDMS stamps are fabricated by using soft lithography (60). For patterning on a glass surface, a new glass coverslip (no. 1 coverslip from VWR) is transiently burnt by using a flame to clean and oxidize its surface. For patterning on a PA gel surface, a thin gel (∼100 µm in thickness) with flat surface is left open to air in a clean hood for 15 min until it is partially dry. After surface preparation, the PDMS stamp with dried collagen protein on the surface is gently pressed onto the substrate; the collagen proteins then quickly absorb to certain substrate regions that are in direct contact with the PDMS stamp. To confirm protein transfer and that the pattern matches that of our design, we tested our procedure using fluorescent collagen. To inhibit cell adhesion to areas without collagen, the printed surface of the substrate is then covered with poly(l-lysine)-g-poly(ethylene glycol) solution (surface solutions) for 1 h at room temperature. The microprinted substrates are then stored at 4 °C before use.

For growing cells on micropatterned substrates, cells are detached by using trypsin–EDTA and then collected by centrifugation and resuspended in cell culture medium at 50,000 cells/mL. The cell solution is then added on top of the micropatterned substrate at a density of ∼10,000 cells per cm². The substrate covered with cells is then placed in a tissue culture incubator for 15–30 min to allow cells to attach onto the micropatterned islands. Unattached cells are removed from the substrate with a gentle wash with warm culture medium. We then add enough medium to the substrate with cells attached to fully cover the substrate and let cells fully spread on the micropatterned islands in a tissue culture incubator; most micropatterned islands have individual cells spreading to a defined size confined by the island, as we designed (Fig. 3).

The 3D Volume Measurement (Including SIM).

Stained cells are observed by using a 63×/1.2-NA water-immersion lens on a Leica TSC SP5. Image processing is carried out by using AMIRA software (Version 5.3.3; Visage Imaging). Cells that we observe are randomly selected. Optical cross-sections are recorded at 0.15-μm z-axis intervals to show intracellular, nuclear, and cortical fluorescence. x–y pixel size is chosen to be comparable to z-axis interval to achieve better voxel resolution and better deconvolution result. By using a theoretically calculated point spread function, a stack of gray-level images (8 bits) was subjected to deconvolution before 3D visualization. The 3D visualization was carried out by using ImageJ and AMIRA software.

The volume is calculated by counting voxel number, after thresholding the stack. The threshold is chosen as the fluorescent intensity on the bottom interface of the cell which can be identified from the reflection signal, which is confirmed as the intensity defining the boundary on the x–y plane fluorescent intensity map. The confocal measurement has been previously compared with AFM; results from two techniques agree.

To further confirm our measurement precision, we compare the 3D morphology, height, and volume of a fixed cell grown on a glass substrate measured by confocal microscopy to those measured by super-resolution SIM (Zeiss) (Fig. S1); super-resolution 3D SIM requires a significantly longer processing time, but gives a much higher resolution in all dimensions. Here, we use a voxel size of 40 × 40 × 110 nm. The cell height and volume measurements from confocal and SIM do not show statistical difference, as shown by the side view of cells and data in Fig. S1. This comparison confirms that our 3D confocal imaging approach is more than sufficient to make accurate measurements of different cell size parameters.

Osmotic Stress.

Hyperosmotic stress is applied by adding PEG 300 to isotonic culture medium. The relation between molarity and osmolality for solutions of PEG in water is taken from previous measurements. The actual osmotic pressure applied to cells is calculated by adding the osmotic pressure due to PEG to that of isotonic solution (300 mOsm) and is further confirmed through a selective measurement by using a microosmometer (model 3300; Advanced Instruments, Inc.). Cells are allowed to equilibrate in PEG solution for 10 min at 37 °C and 5% CO₂, before we perform the imaging or OMTC measurements. The cell size and mechanics achieve equilibration within 2 min after adding PEG based on previous studies (8). We further confirm with confocal imaging that the decrease of cell size is predominantly due to a change in cell height. Surprisingly, the cell size decreases within 20 s and maintains the small volume for hours, as shown in Fig. 1B and Movie S1.

Cortical Stiffness Measurements.

The mechanical properties of the cell cortex are probed by using OMTC, which is a high-throughput tool for measuring adherent cell mechanics with high temporal and spatial resolution (16, 48, 49). For these measurements, cells are plated on collagen I-coated substrates at a density of ∼10–20 cells per mm² and allowed to adhere for a few hours before being switched to serum-free medium and incubated overnight. The 4.5-μm ferromagnetic beads (produced as described in ref. 61) coated with poly-l-lysine (4 kDa) are incubated with the cells for 20 min to achieve strong coupling to the cell surface; poly-l-lysine binds to the cells nonspecifically and tightly, but does not induce active remodeling of the cytoskeleton (8). Unbound beads are removed by gentle washing, leaving a few beads attached to each cell. The dish is mounted on a heated microscope stage to maintain 37 °C. Beads are magnetized by a strong, horizontal magnetic field and then twisted by an oscillatory vertical magnetic field at frequencies of f = 0.1–1,000 Hz and amplitudes of ∼25–50 Gauss. The motions of hundreds of beads in a field of view are recorded with a CCD camera (C4742-95–12ERG; Hamamatsu) mounted on an inverted microscope (DM IRE2; Leica) with a 10× objective, and the beads’ positions are determined in real time with >10 nm accuracy by means of an intensity-weighted center-of-mass algorithm. A schematic illustration is shown in Fig. S3A. The ratio between the torque and bead motion thus defines an apparent stiffness for a cell, which has the unit Pascals per nanometer. A series of geometric factors, based on finite element models that take into account the cell thickness and bead–cell coupling, can be used to convert the apparent stiffness into shear modulus of the cell, as discussed (16, 48, 49). The bead–cell contact geometry is characterized by confocal fluorescence microscopy of labeled live cells; beads are embedded ∼30% deep in cells after 20-min embedding, regardless of the substrate; the same geometric factors are used. Previous measurements of cortical stiffness using OMTC agree with values obtained by other methods, such as AFM (50). Frequency-dependent shear moduli of A7 cells in isotonic medium are shown in Fig. S3B. We note that there is a gentle increase in cortex modulus with frequency, reported before as power-law rheology; nevertheless, a low-frequency plateau in both elastic and loss modulus exists. For convenience, in this work, we use cortex shear modulus measured at a fixed frequency, 0.75 Hz, for comparison under different microenvironmental conditions.

Cytoplasmic Material Properties Measured Using Optical Tweezers.

To directly measure the micromechanical properties of the cytoplasm, we perform active microrheology measurements using optical tweezers to impose a sinusoidal oscillation as a function of frequency, ω, on a 500-nm-diameter probe particle within a cell, as illustrated in Fig. S3D. To optically trap a bead, a beam from a variable-power Nd:YAG solid-state laser (4 W, 1,064 nm; Spectra Physics) is steered through a series of Keplerian beam expanders to overfill the back aperture of a 100× 1.3-NA microscope objective (Nikon S-fluor; Nikon). To steer the beam and manipulate the trapped bead, two acousto-optic deflectors are used (NEOS Technologies). By using a custom-written Labview program (National Instruments), the acousto-optic deflectors are manipulated to control the beam in the plane of the microscope glass slide. For detection, the bead is centered on a high-resolution position detection quadrant detector (MBPS; Spectral Applied Research) and illuminated by using brightfield illumination from a 75-W Xe lamp. The linear region of the detector is calibrated by trapping a bead identical to those used in the cells in water and moving it across the detector by using the acousto-optic deflectors in known step sizes. The trap stiffness is calibrated from the mean-squared Brownian motion of a trapped bead in water at various laser power settings by using the principle of energy equipartition as described (62).

Once calibrated, the laser trap is used to optically trap and manipulate intracellular beads. A laser power corresponding to a trap stiffness of ∼0.05 pN/nm is used. Trapped beads are oscillated across a frequency range of 0.3–70 Hz by using the acousto-optic deflectors, and the laser position and bead displacement are recorded simultaneously, from which the elastic and viscous shear moduli are determined. By measuring the resultant displacement of the bead, x(ω), subjected to an applied sinusoidal trap oscillation with a force F at frequency ω, we extract the effective spring constant, K(ω) = F(ω)/x(ω), for the intracellular environment (17, 20). The complex shear modulus G = G′ + iG′′ is related to the spring constant through a generalization of the Stokes relation K = 3πGd. Thus, we can determine the full frequency-dependent modulus of the cytoplasm. The measured cytoplasmic modulus is ∼1–10 Pa, much lower than that measured on the actin cortex (17); presumably, this reflects the more densely cross-linked actin structure in the cell cortex, whereas the beads probe the cytoplasm, which is much more dilute and hence lower in elasticity. We note that the measured elastic modulus G′ is significantly larger than the loss modulus G′′ over the frequency range from 0.3 to 70 Hz, in several cell types, as we reported (17, 20). The data plotted in the lower part of Fig. 1 and Fig. S5 are G′ measured at 10 Hz under different conditions.

Stem Cell Culture and Differentiation.

The clonally derived murine bone marrow (mMSC) line originally from BALB/c mice (D1s) are purchased from American Type Cell Culture and are maintained in standard DMEM and supplemented with 10% FBS and 1% penicillin/streptomycin (Invitrogen). They are cultured at no more than 80% confluency at no greater than passage 25 in serum-supplemented DMEM. For experiments, cells are trypsinized and plated on collagen I coated soft and stiff substrates at a density of 20 cells per mm². We then let cells fully attach and spread for 1 h, before applying osmotic pressure and adding bipotential differentiation medium. In the compression sample, we also add 0.1 M PEG 300 (100 mOsm) to the medium so that the volume and stiffness of cells on the soft gel match those of the cells grown on the stiff gel, as measured with confocal and OMTC. Similarly, in the swelling sample on glass, after plating cells, we apply hypotonic pressure by adding 30% deionized water into culture medium. To induce differentiation (51), mMSC cultures are supplemented with 10 mM β-glycerol phosphate (Sigma), 50 μg/mL ascorbic acid (Sigma), and 0.1 μM dexamethasone (Sigma), as dexamethasone alone has demonstrated ability to induce adipogenesis of D1 in vitro (52). Culture medium with additional osmotic pressures and supplements are exchanged every 3 d.

To chemically trigger stem cell differentiation without changing osmotic pressure in the medium, D1 cells are cultured in regular medium supplemented with 10 mM β-glycerol phosphate (Sigma), 50 μg/mL ascorbic acid (Sigma), and 0.1 μM dexamethasone (Sigma) toward osteogenesis and cultured in regular medium supplemented with 0.1 μM dexamethasone along toward adipogenesis.

Western analysis of MSC lineage specification.

For Western blots, after 3 d (osteogenesis, as shown in Fig. 7 A–F) or 1 wk (adipogenesis, as shown in Fig. 7 G–L) of culture, cells are lysed in RIPA buffer (Sigma-Aldrich) with Complete Mini protease inhibitor (Roche). Lysates are centrifuged at 16,000 × g at 4 °C for 20 min, and total protein is estimated with a Bradfrod assay (BCA; Thermo Scientific Inc.), as per the manufacturer’s instructions. Protein lysates are separated in precast Tris–glycine or –acetate gels and transferred onto nitrocellulose membranes (both Invitrogen). Blots are incubated with primary antibodies at 4 °C overnight. Following washes, blots are incubated with appropriate species-specific secondary antibodies (Jackson Immunoresearch Laboratories), and chemiluminescence (Thermo Scientific Inc.) is detected by films (Kodak MR; Sigma-Aldrich). Images of Western blots are quantified by using ImageJ software. Actin bands are scanned to normalize for loading differences between samples. Antibodies we use for immunoblotting are mouse anti-RUNX2 antibody, mouse anti-BSP antibody, and mouse anti–PPAR-γ antibody (Abcam), mouse anti-actin antibody (Chemicon), and goat anti-mouse secondary antibody (Jackson Immunoresearch Laboratories).

Immunostaining.

After 1 wk (osteogenesis, as shown in Fig. 7 A–F) or 2 wk (adipogenesis, as shown in Fig. 7 G–L) of culture, cells are fixed with 4% paraformaldehyde and 0.1% Triton X-100 in PBS. For osteogenesis examination, ALP activity (osteogensis biomarker) is visualized by Fast Blue staining (200 μg/mL NAMP combined with 200 μg/mL Fast Blue salt) in alkaline buffer (100 mM Tris⋅HCl, 100 mM NaCl, 0.1% Tween-20, and 50 mM MgCl₂, pH 8.2), as shown in Fig. 7A. For adipogenesis examination, fat lipid accumulation (a functional marker for adipogenesis) is visualized by ORO (600 μg/mL in isopropyl alcohol for 2 h at 25 °C) staining, as shown in Fig. 7G. Nuclei are visualized with 2.7 mM DAPI in PBS. After staining, cells are equilibrated back to neutral pH by using PBS. The densities of ALP-expressing cells and ORO-positive cells are calculated by counting the number of cells in more than three randomly selected fields (10× magnification) and normalizing to the total number of cells detected by DAPI staining in each individual sample.

TFM.

Cell contractility is measured by using the TFM technique according to described methods (41, 53, 54). mMSCs are plated sparsely and grown on collagen I-coated PA gel substrates of two different stiffnesses used for differentiation. The dish is mounted on a heated microscope stage to maintain 37 °C. A phase-contrast image is taken to record cell shape, and a fluorescence image of the particles embedded in the gel just below the cell’s basal surface is taken to record gel deformation induced by cell contraction. After the cell is detached from the gel by using trypsin–EDTA, a second fluorescence image of the particles in the unstressed gel is taken. It has been confirmed that addition of trypsin–EDTA does not induce a background expansion or contraction of the gel (55). Images are from using a Leica SP5 confocal microscope with an image size of 512 × 512 pixels and a pixel size of 160 nm. Displacement fields due to cell tractions are determined by using an image correlation method (54), and tractions are determined by means of the Fourier transform traction cytometry technique (41), using a Matlab software package kindly provided by Rama Krishnan and James Butler at Harvard Medical School, Boston. Approximately 10 cells are measured for each condition.

Cytoplasmic and Intranuclear Movement.

To measure cytoplasmic movement, we microinject inert tracer particles into the cell, then track their movement over time in cells. Fluorescent carboxylate-modified polystyrene spherical particles (200 nm; Molecular Probes) are rendered inert by grafting short amine-terminated methoxy-poly(ethylene glycol) to the surface of carboxylated microspheres. PEG-coated particles are stored at 4 °C and used within 2 wk. Microinjection is performed by using a glass needle and a FemtoJet microinjector (Eppendorf) mounted on a bright-field microscope. Approximately 50 cells are injected per dish; each cell is injected up to 50 tracer particles to eliminate the interference to cell function. Cells are then allowed to recover in culture medium for 6 h and imaged on a confocal microscope at 37 °C and 5% CO₂. Organelles and injected tracer particles are imaged with bright-field or confocal microscopy using a 63×/1.2-NA water immersion lens on a Leica TSC SP5. Please refer to SI Materials and Methods for more details.

The trajectories of the fluorescent particles are recorded every 100 ms for ∼1 min. The images are processed with particle tracking software written by J. Crocker, D. Grier, and E. Weeks, in IDL. Particle centers are found in each image with an accuracy of 22 nm.

To track intranuclear movement, we transfect cells with histone H2B-GFP, then image the nuclear structure at a 50-ms interval for 30 s. Similar analysis using particle tracking algorithm is then performed to calculate the structure fluctuation inside the nucleus.

Measurement of Osmotic Bulk Modulus.

We determine the osmotic bulk modulus of the cells from their pressure–volume relationship. To measure the relationship between cell volume and external pressure, we grow cells in suspension and also on collagen-coated substrates with different stiffness. We premix PEG 300 into isotonic cell culture medium to apply additional osmotic pressure. Cells are labeled with cell tracker to enable the volume quantification by using confocal microscopy, as shown in Fig. 4A. After the addition of medium with PEG, cell volume suddenly decreases to an equilibrate value within 10 s and maintains this steady state for at least 2 h in our experiment, as shown in Fig. 1B. To confirm that cells achieve a steady state, we remove the additional osmotic pressure by exchanging back to isotonic medium and find that cell volume returns to its initial value instantly; as we cycle the osmotic pressure, cells always maintain at the same volume under a certain pressure. The relationship between applied osmotic pressure P and average cell volume V is plotted in Fig. S2; as external osmotic pressure increases, cell volume decreases. This P–V relationship allows us to directly calculate the bulk modulus of living cells, as B = −VdP/dV, which is shown in the upper portion of Fig. 1A and Fig. S5.

Comparison Between Actomyosin Contraction and Osmotic Pressure.

The mechanism that drives intracellular water content change remains unclear. Our results suggest that actomyosin contraction is involved; however, it is unlikely that actonmyosin is able to mechanically change the volume of the cell, as wringing a sponge, because the forces generated by the cytoskeleton are too weak to withstand an osmotic pressure mismatch between the interior and exterior of the cell in the absence of osmolite change (∼MPa, ref. 8).

The contractile stress generated by actomyosin cortex is on the order of 1 kPa, as measured by TFM shown in Fig. S6, and as discussed (42). Under physiological condition, the osmotic pressure inside the cell approximately equals the osmotic pressure in the cell medium, which is ∼300 mOsm (Π₀ = ∼0.8 MPa) (8). If we assume no osmolite exchange across cell membrane, shrink of cell volume would immediately lead to an increase in the intracellular osmotic pressure; osmotic pressure is linearly proportional to the osmolarity, as Π = CRT/V, where C represents amount of osmolite, R, the gas constant, T, the temperature, and V, the volume of the cell. For example, we observe a cell volume reduction of ∼40% during cell spreading; assuming no osmolite exchange, C remains constant; thus, the intracellular osmotic pressure becomes Π = CRT/(1–40%)V = ∼1.67 CRT/V = 1.67 Π₀. Therefore, the osmotic pressure difference between the interior and exterior of the cell is ∼1.67Π₀ − Π₀ = ∼0.5 MPa, which is almost three orders of magnitude greater than the contractile stress generated by actomyosin contractility. By comparing these two quantities, it is impossible for actomysoin contractility to mechanically change the volume of the cell and balance the osmotic pressure difference resulted.

Discussion

The data presented here establish the critical importance of cell volume and molecular crowding in determining cell properties, including cell stiffness and intracellular dynamics. Unlike a growing and dividing cell, where volume change is associated with an increase of intracellular protein and other materials, we show that changes in cell volume can alternately be directly associated with changes in intracellular water content while levels of proteins and other materials remain constant: Upon increase of substrate stiffness or cell spread area, cells respond by decreasing their water content and hence increasing their stiffness. While actomyosin contractility is essential for this adaptation, cell contraction itself cannot mechanically change cell volume: The stress generated by the cytoskeleton is too weak (42) (∼1–10 kPa, as shown in Fig. S6) to withstand or induce any osmotic pressure difference since pressures are on the order of megapascals (8); therefore, cytoskeletal forces cannot squeeze water out of cells. Instead, it is most likely that contractile tension of the cytoskeleton increases activity of ion channels, which, in turn, affects intercellular water content and hence cell volume (28, 29); this is consistent with our finding that cell volume change is suppressed as we inhibit the activity of specific ion channels and ATP-dependent processes. Surprisingly, both the cortical shear modulus and the cell bulk modulus exhibit exactly the same functional form with cell volume, as shown by Fig. S5. The origin of this behavior for the bulk modulus can be understood as a consequence of molecular crowding; however, the underlying origin of the behavior for the cortical shear modulus is unclear, although the behavior in the physiologically accessible volumes is consistent with the concentration dependence of reconstituted networks, and hence with water content.

Our results also indicate that changing protein concentration has major implications for cell physiology, typified by the effect cell volume change has on stem-cell differentiation. Changes in intracellular water content will change intracellular molecular crowding and cellular dynamics (Fig. 6 and Fig. S7). This will undoubtedly cause significant variations in many internal physiological processes, such as protein folding and binding kinetics (7, 43–45), structural rearrangements and transport phenomena (8, 9, 44), and protein expression patterns (2, 6, 46). Moreover, similar effects extend into the nucleus since the volume of the cell nucleus decreases as cell volume decreases (Fig. 6A). This will change the intranuclear molecular crowding, and possibly lamin concentration, which has been suggested to affect chromatin structure, mobility, and therefore transcription and gene expression patterns (10, 47). Thus, cell volume and cell nuclear volume, which are defined features of the cell, may change in physiological conditions such as under tissue compression and osmotic variance in the body, therefore significantly impacting myriad cellular processes, such as signaling, protein dynamics, and even stem-cell differentiation.

Fig. S7.

Mean square displacement of 200-nm-diameter latex beads in the cytoplasm of A7 cells cultured at different conditions, including varying substrate stiffness and under varying osmotic compressions. The movement of these beads increases as cell volume increases, suggesting that an increase in the degree of molecular crowding in cells hinders intracellular movement.

Materials and Methods

Cell Culture and Pharmacological Interventions.

Cell culture protocol and pharmacological interventions are described in SI Materials and Methods. Cells are synchronized to avoid cell size growth and volume change during cell cycle.

Cell Labeling and Immunofluorescence.

Cells for confocal imaging are plated at a density of 20 cells per mm². Live cells are fluorescently labeled with CellTracker, CellMask plasma membrane stains (Invitrogen), and DRAQ5 (Cell Signaling Technology) to label cytoplasm, membrane, and cell nucleus, respectively. The cells are imaged and sectioned at 0.15-μm intervals by using excitation from a 633- or 543-nm laser or a 488-nm line of an argon laser and a 63×, 1.2-NA water immersion objective on a laser scanning confocal microscope (TCS SP5; Leica). To label actin cortex and get a better resolution of cell boundary and cell size, living cells cultured on substrates are fixed, and their actin structures are labeled by using phalloidin.

Fabrication of PA Gel Substrate and Micropatterned Islands.

The fabrication of PA gel substrates with different stiffness and micropatterned islands follows standard procedures (24) and is described in SI Materials and Methods.

The 3D Volume Measurement.

Stained cells are observed by using a 63×/1.2-NA water immersion lens on a Leica TSC SP5. Cells that we observe are randomly selected. Optical cross-sections are recorded at 0.15-μm z-axis intervals to show intracellular, nuclear, and cortical fluorescence. By using theoretical point spread function, a stack of gray-level images (8 bits) are subjected to deconvolution before 3D visualization. The 3D visualization is carried out by using ImageJ and AMIRA software. The volume is calculated by counting voxel number, after thresholding the stack. The confocal measurement has been previously compared with AFM; results from two techniques agree. More details are in SI Materials and Methods.

Super-resolution SIM imaging of fixed cells is performed on a microscope (ELYRA SIM; Carl Zeiss) with an Apochromat 63×/1.4-NA oil objective lens (Fig. S1). We use a voxel size of 40 × 40 × 110 nm; the cell height and cell volume measurements from confocal and SIM do not show statistical difference, as shown in Fig. S1.

Osmotic Compression.

Hyperosmotic stress is applied by adding PEG 300 to isotonic culture medium. Cells are then allowed to equilibrate in PEG solution for 10 min at 37 °C and 5% CO₂, before measurements. The cell size decreases within 20 s and maintains the small volume for hours, as shown in Movie S1.

Cortical Stiffness Measurements.

The mechanical properties of the cell cortex are probed by using OMTC, which is a high-throughput tool for measuring adherent cell mechanics with high temporal and spatial resolution (16, 48, 49). Measurements are done at 37 °C. Measurements of cortical stiffness using OMTC agree with values obtained by other methods such as AFM (50). Frequency-dependent shear moduli of A7 cells in isotonic medium are shown in Fig. S3. For convenience, in this work, we use cortex shear modulus measured at a fixed frequency, 0.75 Hz, for comparison under different microenvironmental conditions. More details are in SI Materials and Methods.

Cytoplasmic Material Properties Measured Using Optical Tweezers.

To directly measure the micromechanical properties of the cytoplasm, we perform active microrheology measurements using optical tweezers to impose a sinusoidal oscillation on a 500-nm-diameter probe particle microinjected in a cell, as described (17, 20). The trap stiffness we use is calibrated as 0.05 pN/nm. Trapped beads are oscillated across a frequency range of 0.3–70 Hz; the frequency-dependent shear modulus of the cytoplasm is shown in Fig. S3. The data plotted in the lower part of Fig. 1A and Fig. S5 are G′ measured at 10 Hz under different conditions. More details are in SI Materials and Methods.

Stem Cell Culture and Differentiation.

The clonally derived murine bone marrow mesenchymal stem cell line originally from BALB/c mice (D1s) are purchased from American Type Cell Culture and are maintained in standard DMEM and supplemented with 10% FBS and 1% penicillin/streptomycin. They are cultured at no more than 80% confluency at no greater than passage 25 in serum-supplemented DMEM. For experiments, cells are trypsinized and plated on collagen I-coated soft and stiff substrates at a density of 20 cells per mm². We then let cells fully attach and spread for 1 h, before applying osmotic pressure and adding bipotential differentiation medium. In the compression sample, we add 0.1 M PEG 300 (100 mOsm) to the medium, so that the volume and stiffness of cells on the soft gel match those of the cells grown on the stiff gel, as measured with confocal and OMTC. Similarly, in the swelling sample on glass, after plating cells, we apply hypotonic pressure by adding 30% deionized water into culture medium. To induce differentiation (51), mMSC cultures are supplemented with 10 mM β-glycerol phosphate (Sigma), 50 μg/mL ascorbic acid (Sigma), and 0.1 μM dexamethasone (Sigma), as dexamethasone alone has demonstrated the ability to induce adipogenesis of D1 in vitro (52). Culture medium with additional osmotic pressures and supplements are exchanged every 3 d.

Western Analysis of MSC Lineage Specification.

For Western blots, after 3 d (osteogenesis, as shown in Fig. 7 A–F) or 1 wk (adipogenesis, as shown in Fig. 7 G–L) of culture, cells are lysed in RIPA buffer (Sigma-Aldrich) with Complete Mini protease inhibitor (Roche). Lysates are centrifuged at 16,000 × g at 4 °C for 20 min, and total protein is estimated with a Bradford assay (BCA; Thermo Scientific Inc.). Protein lysates are separated in precast Tris–glycine or –acetate gels and transferred onto nitrocellulose membranes (both Invitrogen). Blots are incubated with primary antibodies at 4 °C overnight. Following washes, blots are incubated with appropriate species-specific secondary antibodies (Jackson ImmunoResearch Laboratories) and chemiluminescence (Thermo Scientific Inc.) is detected by films (Kodak MR; Sigma-Aldrich). Images of Western blots are quantified by using ImageJ software. Actin bands are scanned to normalize for loading differences between samples. Antibodies we use for immunoblotting are mouse anti-RUNX2 antibody, mouse anti-BSP antibody, and mouse anti–PPAR-γ antibody (Abcam), mouse anti-actin antibody (Chemicon), and goat anti-mouse secondary antibody (Jackson Immunoresearch Laboratories).

Immunostaining.

After 1 wk (osteogenesis, as shown in Fig. 7 A–F) or 2 wk (adipogenesis, as shown in Fig. 7 G–L) of culture, cells are fixed with 4% paraformaldehyde and 0.1% Triton X-100 in PBS. For osteogenesis examination, ALP activity is visualized by Fast Blue staining [200 μg/mL naphtol-AS-MX-phosphate (NAMP) combined with 200 μg /mL Fast Blue salt] in alkaline buffer (100 mM Tris⋅HCl, 100 mM NaCl, 0.1% Tween-20, and 50 mM MgCl₂, pH 8.2), as shown in Fig. 7A. For adipogenesis examination, fat lipid accumulation is visualized by ORO (600 μg/mL in isopropyl alcohol for 2 h at 25 °C) staining, as shown in Fig. 7G. Nuclei are visualized with 2.7 mM DAPI in PBS. The density of ALP-expressing cells and ORO-positive cells are calculated by counting the number of cells in more than three randomly selected fields (10× magnification), and normalizing to the total number of cells detected by DAPI staining, in each individual sample.

TFM.

Cell contractility is measured using the TFM technique according to described methods (41, 53, 54). More details are in SI Materials and Methods.