Time-resolved measurements of an ion channel conformational change driven by a membrane phase transition

Significance

Membranes act as a host matrix to many different biomolecules, such as membrane proteins. As highly dynamic structures, membranes have many modes of fluctuation accessible under physiological conditions. By inducing a phase transition that thins a membrane with a temperature jump and monitoring the response of a model ion channel, we are able to track in a time-resolved manner how this protein responds to fast structural changes in the membrane.

Abstract

Using temperature-jump infrared spectroscopy, we are able to trigger a gel-to-fluid phase transition in lipid vesicles and monitor in real time how a membrane protein responds to structural changes in the membrane. The melting of lipid domains in 1,2-dimyristoyl-sn-glycero-3-phosphocholine vesicles is observed to occur in as fast as 50 ns, with a temperature dependence characteristic of critical slowing. Gramicidin D (gD) added to the membrane responds primarily to the change in thickness of the membrane on a timescale coincident with the membrane melting. Using structure-based spectral modeling, we assign the conformational changes to compression and rotation of a partially dissociated gD dimer. Free energy calculations indicate that the high rate is a result of near-barrierless diffusion on a protein energy landscape that is radically reshaped by membrane thinning. The structural changes associated with the phase transition are similar to the fluctuation modes of fluid phase membranes, highlighting the importance of understanding the dynamic nature of the membrane environment around proteins.

The remarkable functions of integral membrane proteins are intimately tied to their membrane environment. Mechanosensitive ion channels are sensitive to changes in the lateral pressure profile of membranes (1), while several membrane-embedded enzymes have been shown to have membrane thickness-dependent activities (2). In these examples, the interaction between individual lipids and the protein is weak, but the collective effect of the membrane is significant enough to alter the function of the protein. The membrane is not a static scaffold, but a dynamic, fluctuating environment that exerts time-varying forces on membrane proteins. Membrane fluctuations spanning length scales from angstroms to micrometers operate on timescales ranging from picoseconds to greater than milliseconds (3–5). However, the role of this dynamic environment on the behavior of membrane proteins is unclear, as a result of a limited repertoire of experiments that monitor the fast time-dependent interactions.

We report on the use of infrared (IR) spectroscopy in combination with a rapid temperature jump (T-jump) to monitor membrane protein conformational changes induced by rapid membrane thinning. Time-resolved IR spectroscopy is a label-free reporter of the structure and dynamics of membranes and proteins using vibrations native to the system (3, 6). However, picosecond vibrational lifetimes limit the observable time window in these experiments. T-jump relaxation experiments offer a route to extending this window; a rapid perturbation shifts the equilibrium of the system, and a probe is used to monitor the relaxation of the system to this new equilibrium (7).

We demonstrate that a fast T-jump (10 °C in <10 ns) is able to induce and track a phase transition in lipid vesicles. Incorporating the protein gramicidin D (gD) into the membrane (Fig. 1A) provides a way to study the effect of phase transitions on membrane proteins. Using the structural changes in the lipid as a “secondary” perturbation, we are able to determine that the conformational response of gD to changes in the bilayer thickness occurs on nanosecond to microsecond timescales. Structural modeling of the IR spectrum of gD (8) allows us to assign conformational changes arising from structural changes in the membrane. These experiments provide insight into the mechanism of lipid phase transitions and how proteins respond to changes in their environment. This adds a new dimension to coupling between proteins and their membrane environment; not only is the average environment important but the time-dependent behavior of the lipid must be considered.

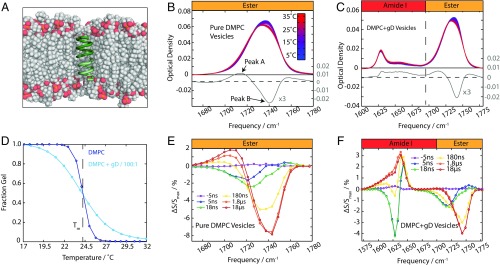
Fig. 1.

Monitoring the phase transition with IR spectroscopy. (A) gD embedded in a DMPC bilayer. Note the mismatch in between the length of gD and the bilayer thickness. (B) Temperature-dependent FTIR spectra of pure DMPC vesicles. The difference spectrum (T₂ − T₁, T₂ = T_m + 5 °C, T₂ = T_m − 5 °C) is shown in gray. (C) FTIR spectra of DMPC + gD vesicles. The difference spectrum is the same as in B. (D) Melting curves for DMPC and DMPC + gD vesicles. (E) Transient spectral response of pure DMPC vesicles in the ester region (T_i = 19 °C to T_f = 30 °C). (F) Transient spectral response of DMPC gD vesicles in the amide I and ester regions (T_i = 19 °C to T_f = 30 °C).

Results

Observing the Melting of Lipid Vesicles with IR Spectroscopy.

The temperature-dependent FTIR spectra of 120-nm, large, unilamellar 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) vesicles (Fig. 1B) reveal that the ester carbonyl stretching band is composed of two overlapping peaks, assigned previously to an ester hydrogen-bonded to water and a free ester group (3, 9). The hydrogen-bonded ester groups are centered at 1,728 cm⁻¹, while the non–hydrogen-bonded esters absorb at ∼1,743 cm⁻¹ (labeled peak A and peak B, respectively). As membranes undergo the phase transition from the gel phase to the fluid phase, the bilayer thickness decreases and the area per lipid headgroup (APL) increases (10, 11), resulting in greater water penetration into the ester region of the lipids. The FTIR data show a gain of peak A and a loss of peak B as the temperature increases for both pure DMPC vesicles (Fig. 1B) and vesicles containing a 100:1 mixture of DMPC and gD (Fig. 1C).

The behavior of gD in the membrane can be probed with the amide I carbonyl vibration (1,600- to 1,700-cm⁻¹ region; Fig. 1C). This spectrum is sensitive to the structure of the protein as a result of coupling between amide carbonyls that form delocalized modes (12). The amide I spectrum of gD has been described previously (8), which showed the intense mode at 1,630 cm⁻¹ (η_∥ mode) arises from a vibration delocalized over the helix. The thermal response of the amide I peak in Fig. 1C shows a blue shift of η_∥ and a net increase in intensity. The blue shift of amide I vibrations with temperature arises from the weakening of hydrogen bonds within the protein (13). A decrease in intensity typically accompanies a temperature rise, since the transition dipole moment of the amide I mode decreases with weaker hydrogen bonds (14). This is counter to the trend observed here.

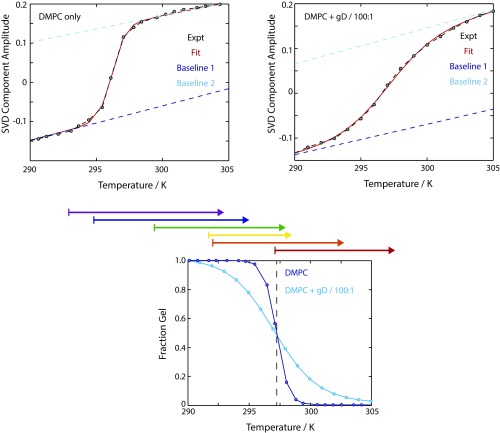
Melting curves for the transition are derived from the ester region of the FTIR spectra by performing a singular value decomposition on the 1,680- to 1,780-cm⁻¹ region (Fig. 1D and Fig. S1). The melting curves with and without gD differ little in melting temperature, T_m, but have a very different slope at T_m, indicating that gD lowers the enthalpy of melting $(\mathrm{\Delta }{H}_m)$ (15). To compare with calorimetric data, we fit a two-state model to these curves, yielding these parameters for pure DMPC vesicles: $\mathrm{\Delta }{H}_m$ = 1,405 kJ⋅mol⁻¹ and T_m = 24 °C, while for the 100:1 DMPC/gD vesicles, $\mathrm{\Delta }{H}_m$ = 409 kJ⋅mol⁻¹ and T_m = 24 °C. In both cases $\mathrm{\Delta }{C}_p$ < 1 J⋅mol⁻¹⋅K⁻¹, in good agreement with calorimetry (16, 17). The large enthalpies arise from the cooperative nature of the transition; many lipids transition from the gel to the fluid phase simultaneously (17). The broader transition of the gD-containing vesicles is reflected in the lower effective enthalpy of this transition, although it is unclear whether this reflects a decrease in the effective cooperative unit when gD is added or the per-lipid enthalpy is decreased on the addition of gD.

Fig. S1.

Melting curves obtained from the ester carbonyl region (1,690–1,780 cm⁻¹) of pure DMPC vesicles (Left) and gD-containing vesicles (Right). Experimental data are plotted as black dashed lines, and the fit is modeled as a solid red line. Baselines are also shown. (Bottom) Comparison of the extracted gel fraction as a function of temperature for the two systems. Above this panel, arrows illustrate the T-jump ranges from T_i to T_f that are discussed in the main text. Expt., experiment.

Tracking the Fast Kinetics of Lipid Vesicles Melting.

In addition to tracking the temperature dependence of the lipid phase transition, the ester carbonyl stretch can be used to study the kinetics of the phase transition. An intense 10-ns optical pulse excites solvent vibrations, which relax on a subnanosecond timescale to increase the sample temperature from an initial temperature (T_i) to a final temperature (T_f) ∼10 °C higher (18). The elevated temperature persists until it dissipates due to thermal diffusion [solvent relaxation timescale (τ_sol) = 2 ms]. The response of the membrane to this change in temperature (T-jump) is monitored with a time-delayed heterodyned dispersed vibrational echo (HDVE) pulse sequence. HDVE uses three noncollinear, 100-fs mid-IR pulses resonant with the carbonyl vibrations to generate a signal. This transient-HDVE approach yields vibrational “snapshots” of the system after time delays varying from nanoseconds to milliseconds. These data are presented as a transient-HDVE difference spectrum: the change in the amplitude HDVE spectrum at T_i after a T-jump time delay, τ: $\mathrm{\Delta }S\left(\omega ,\tau \right)=\left|S\left(\omega ,\tau \right)\right|-\left|S{\left(\omega \right)}_{eq}\right|$. Further details of the HDVE experiment are provided in Vesicle Composition Dependence of Spectral Response and in studies by Chung et al. (18) and Khalil et al. (19).

Fig. 1 E and F shows the transient spectrum $\mathrm{\Delta }S\left(\omega ,\tau \right)$ for pure DMPC and DMPC + gD vesicles for time delays between 5 ns and 18 μs following a jump to T_f = 30 °C. The τ = 5-ns difference spectrum (dark blue) shows a loss of intensity at 1,720 cm⁻¹ and a slight gain at higher frequencies. This arises from weakening of water/ester hydrogen bonds within the lipid due to the increase in temperature. The response at times longer than 1 μs shows the same shape as the FTIR difference spectrum (Fig. 1A): a loss of peak B and gain of peak A.

Addition of gD to the DMPC vesicles yields a similar response from the ester group, while the magnitude of the amide I response from gD is equal in magnitude to the ester response. At early times (τ < 100 ns) the amide response blue-shifts, as expected from hydrogen bond weakening (HBW). At later times (τ > 1 μs), the gD amide I band shows a net increase in oscillator strength. This change is the opposite of a thermal weakening of hydrogen bonds, and indicates a protein conformational change that increases the number or strength of hydrogen bonds in the system. The increase in oscillator strength is more striking in the transient data than the FTIRs because of the different scaling of the signal with transition dipole moment (μ⁴ vs. μ²). (The spectral response of gD was also studied at lower protein/lipid concentrations, and consistent responses were observed, as shown in Supporting Information.)

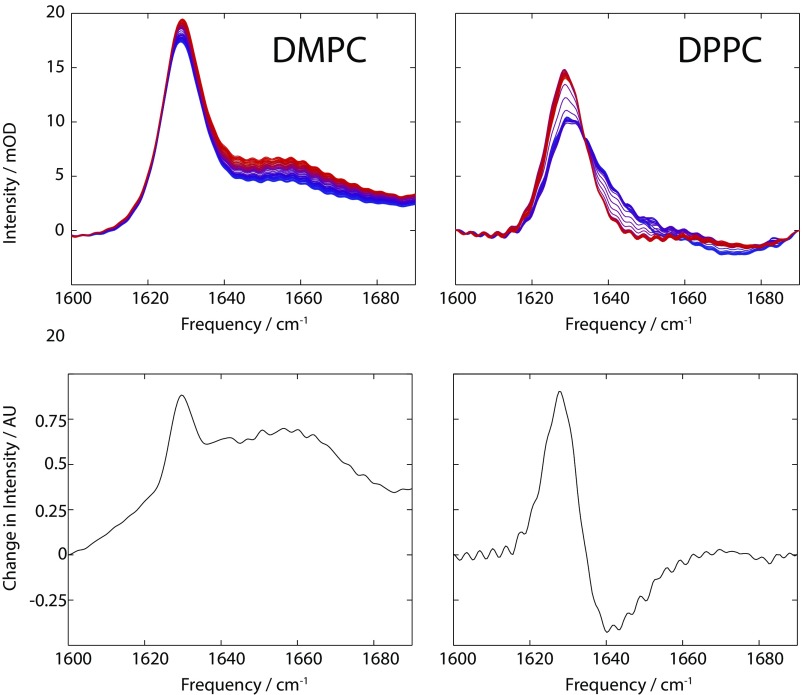
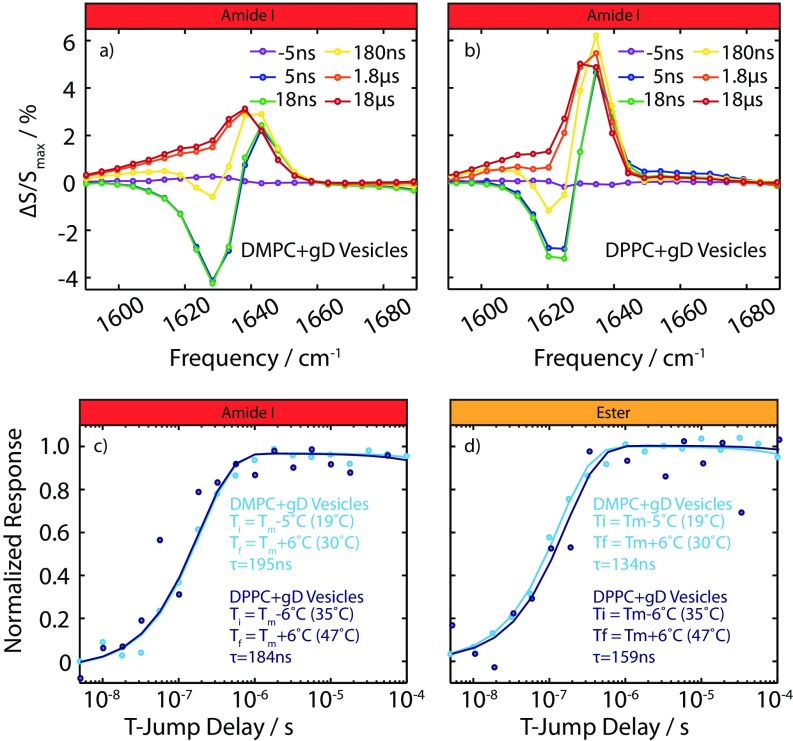
To test whether the transient amide I response of gD is correlated with the thinning of the membrane, we varied the lipid environment of gD from DMPC to 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC). On melting, the hydrocarbon thickness of DMPC changes from 30.3 Å (gel) (11) to 25.4 Å (fluid) (10), while for DPPC, the thickness changes from 34.4 Å (20) to 27.9 Å (21). The magnitude of the response from gD almost doubles in the thicker DPPC bilayer; however, the timescale of the ester response and amide I response is essentially unchanged by the change in lipid (Figs. S2 and S3). This demonstrates that the bilayer thickness is a key coordinate governing the protein conformational change. A similar effect is observed in the FTIR measurements (shown in Fig. S2); both have thermal difference spectra that are a superposition of the HBW of the amide I vibration and the protein conformational change response. In DPPC, the difference spectrum shows the conformational change more clearly, while in DMPC, the HBW response dominates.

Fig. S2.

(Upper) Amide I temperature-dependent FTIR spectra for DMPC (Left) and DPPC (Right). mOD, milli-optical density. (Lower) singular value decomposition-derived difference spectra. AU, arbitrary unit.

Fig. S3.

Bilayer thickness and gD kinetics. (A) Amide I spectral response for DMPC + gD vesicles (following T_i = 19 °C to T_f = 30 °C). (B) Amide I spectral response for DPPC + gD vesicle (T_i = 35 °C to T_f = 47 °C). (C) Kinetic trace of the amide I response for DMPC + gD and DPPC + gD vesicles at 1,630 cm⁻¹. (D) Kinetic trace of the ester response for the DMPC + gD and DPPC + gD vesicles at 1,743 cm⁻¹.

Temperature Dependence of Relaxation Rates.

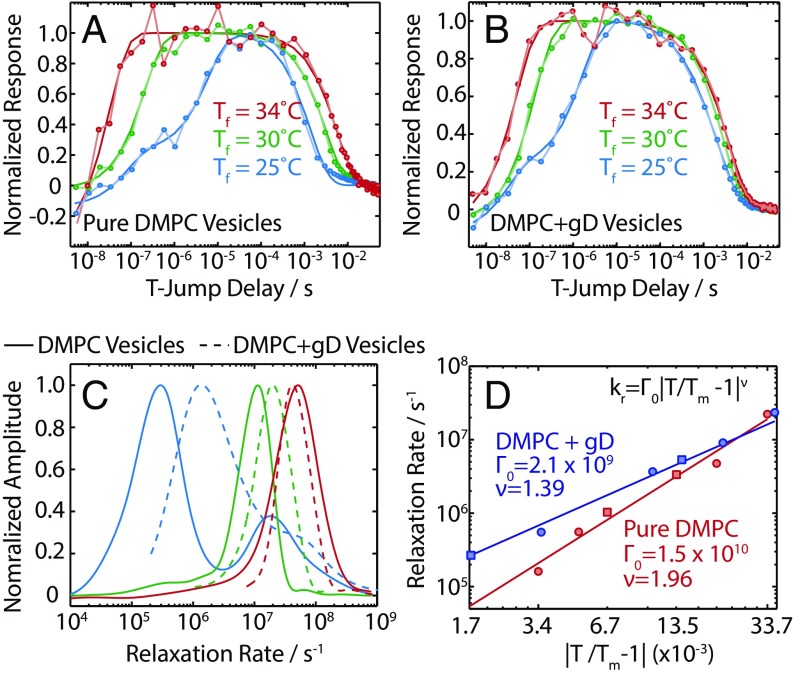
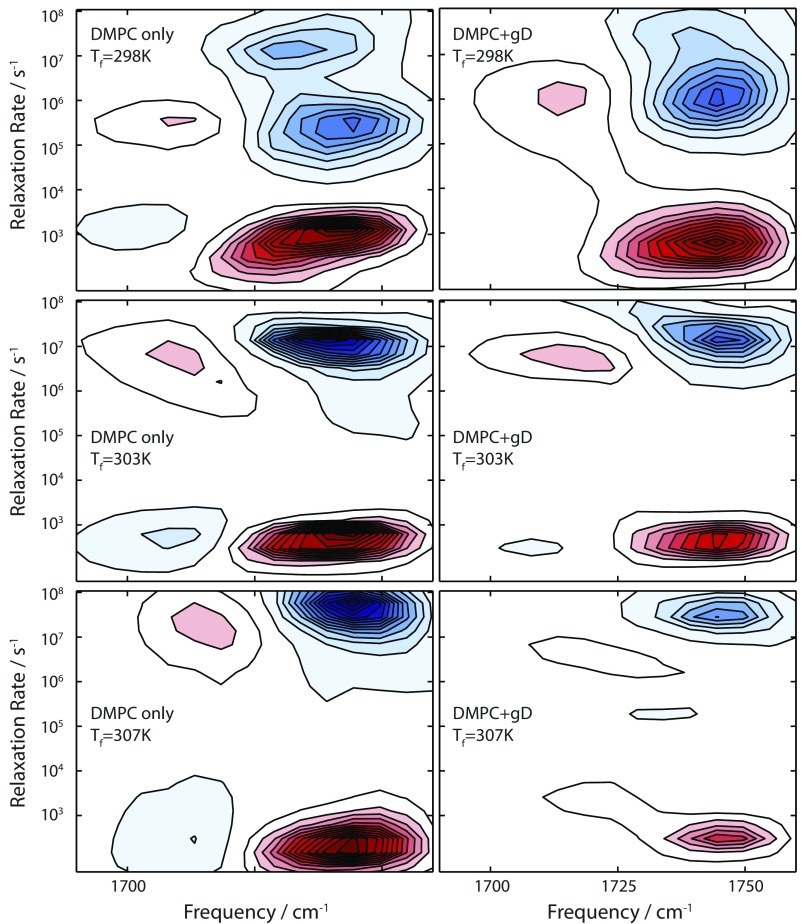
The transient spectral response of the lipid vesicles demonstrates that the hydration levels of the lipid are changing in response to the T-jump, but more insight can be obtained by examining the temperature dependence of these kinetics. Fig. 2 A and B shows the kinetics for peak B of the ester groups for DMPC vesicles with and without gD over a 9 °C range above T_m: T_f = T_m + 1,6,10 °C. Previous experiments on lipid vesicles, using a variety of probes, have found evidence of multiple relaxation timescales, and a dependence on the particular probe used (6, 22–25). To address this uncertainty about the dynamics present, how they may depend on vibrational frequency, and which functional form is appropriate to describe the kinetics, we first used a maximum entropy (MaxEnt) method to determine the inverse Laplace transform (ILT) of the kinetic traces and obtain the underlying distribution of rates as a function, shown in Fig. S4 (26). This provides a minimally biased distribution of rates for each detection frequency.

Fig. 2.

(A) Normalized kinetic traces for the loss of peak B (1,743 cm⁻¹) for pure DMPC vesicles. (B) Normalized kinetic traces for the loss of peak B for DMPC + gD vesicles. (C) Rate distributions for the kinetic traces shown in A and B determined with the MaxEnt-ILT method. (D) Temperature dependence of τ_PT, and fit to a critical slowing model for pure DMPC and DMPC + gD vesicles. Squares indicate points where T_f < T_m, and circles indicate points where T_f > T_m.

Fig. S4.

Rate distributions obtained from MaxEnt-ILT of T-jump data for DMPC-only vesicles (Left) and DMPC + gD vesicles (Right) at a variety of final temperatures.

The rate distributions for the kinetics in Fig. 2 A and B are shown in Fig. 2C. For pure DMPC at T_f = 25 °C, 1 °C above T_m, two distinct rates are present at 10⁵ s⁻¹ and 10⁷ s⁻¹. At T_f = T_m + 10 °C, the rates have sped up over two orders of magnitude: The slowest rate is 10⁸ s⁻¹, and the fastest rate exceeds our experimental window of observation. The rate spectrum is used to determine the appropriate functional form for the kinetics (mono- or biexponential relaxation), and we fit the kinetic traces to obtain timescales. Fits are illustrated in Fig. 2 A and B, and the timescales are listed in Tables S1 and S2. We label the fast component (<100 ns) of the bimodal rate distribution τ_fast, the slower component as τ_PT (50 ns to 10 μs), and the timescale associated with relaxation back to equilibrium at T_i as τ_relax.

Table S1.

Variation of melting rates of pure DMPC vesicles as a function of final temperature obtained from exponential fits to the relaxation signals at 1,743 cm⁻¹

Tf, °C	τPT, ns	τrelax, ms
19	301	τSol (≤2 ms)
22	970	τSol
25	6,200	τSol
25.5	1,830	τSol
30	207	3.08
34	45	5.43

τ_Sol refers to relaxation time equal to or faster than the solvent thermal equilibration time of 2 ms.

Table S2.

Variation of melting rates of 100:1 DMPC/gD vesicles as a function of final temperature obtained from exponential fits to the relaxation signals at 1,743 cm⁻¹

Tf, °C	τPT, ns	τrelax, ms
21	245	τSol (≤2 ms)
23.5	3,440	τSol
25	1,700	τSol
28	190	τSol
30	134	2.86
34	51	3.60

The temperature dependence of τ_PT is non-Arrhenius, showing a minimum in rate around T_m. The corresponding relaxation rates (Fig. 2D) follow the power law dependence (25):

$$k_{PT}\left(T\right)={\mathrm{\Gamma }}_0{\left|\frac{T}{T_m}-1\right|}^{\nu }.$$

This phenomenon is critical slowing, and is indicative of a phase transition (27). This is observed both in pure DMPC vesicles and DMPC + gD vesicles. The presence of gD in the sample increases the rate of the phase transition; at 1 °C from the T_m, the rate of the transition is ∼3.5-fold faster. Previous transient studies have also reported timescales consistent with critical behavior (6, 24).

At the high temperatures (T_f = 30 °C and 34 °C), τ_relax increases (Fig. 2 A and B), an effect that is especially pronounced in pure DMPC vesicles. The relaxation of the heated solvent back to equilibrium can be tracked by the change in linear absorption of the D₂O solvent, which yields a decay time τ_sol ∼ 2 ms (18). The relaxation of the ester response at T_f = 30 °C and 34 °C lags behind this (τ_relax = 3 ms and 5.4 ms), indicating the presence of a millisecond timescale.

Discussion

Structural Changes in DMPC.

Membrane phase transitions are extremely complex. Light scattering (22), fluorescence (23), and IR spectroscopy (6) experiments have all revealed different elements of the process (summarized in Table S3). The timescales reported range from nanoseconds to greater than milliseconds, revealing that the transition is a multistage process. This complexity is perhaps unsurprising, given the collective nature of the process and the many structural changes associated with it. In the fluid phase, the membrane thins as the acyl chains become more disordered, increasing APL results in lateral expansion of the membrane, and vesicles change shape and size. It is therefore important to consider which elements of the transition our experiments report on, and which structural changes are responsible for the change in the amide I band. The ester carbonyl stretch in DMPC reports on the populations of hydrogen-bonded and non–hydrogen-bonded esters. The phase transition alters these populations, but it is not the sole mechanism by which these populations may change. However, the power-law temperature dependence of τ_PT indicates the phase transition is responsible (25). Critical slowing arises from the divergence of the correlation length of fluctuations at T_m. The observation of critical behavior in our experiments is a clear indication of a cooperative process. Thus, the change in hydrogen bond populations arises from a concerted change of many lipids.

Table S3.

Summary of previous transient experiments that addressed the timescale of the main phase transition in lipid vesicles

Perturbation	Probe	Timescales observed	Refs.	Lipid
T-jump	C-D Stretch vibration	0.1–10 μs	(6)	DPPC vesicles
T-jump	Turbidity	0.02–20 ms	(24)	DPPC vesicles
T-jump	Fluorescence	Sub-20 μs, 1–10 ms	(23)	DPPC vesicles
T-jump	Fluorescence	Microseconds	(22)	DMPC vesicles
T-jump	Turbidity	10 μs, 100–1,000 μs, ms	(22)	DMPC vesicles, fast-timescale minor component
Pressure	Ultrasound	ns, 10 ns, 0.001–1 ms	(25)	DMPC vesicles

Taken together, the change in hydration, the cooperative nature of the process, and the agreement between the timescales measured here and those determined for kinking in the acyl chain (6) suggest a “local melting” description for the melting of the vesicle. This refers to domains of the membrane undergoing a transition to the fluid phase (described by APL, acyl chain disorder, and membrane thickness), but global changes in vesicle shape and curvature are not yet complete. This model is bolstered by the observation that the lipid phase-dependent insertion of a peptide into a membrane could be observed on a submillisecond timescale after a T-jump across the T_m (28).

Characterization of the processes associated with τ_fast and τ_relax is more challenging since they are at the limits of experimental detection. However, they are consistent with the description of the phase transition as a multistep process. Speculatively, we may consider the similarity in timescales measured by turbidity change (22) to our millisecond component. These experiments are sensitive to size and shape changes of the vesicles. These changes will be intimately tied to the diffusion of water across the fluid phase membrane on a millisecond timescale (29) to accommodate the greater surface area. The ester carbonyl stretch will not be directly sensitive to this process. However, the vesicle cannot relax back to the initial configuration until this water has been expelled.

Conformational Changes in gD.

The response of the amide I region can provide detailed structural information on the changes occurring in the protein during the phase transition due to the delocalized nature of the amide I vibrations. The variation in magnitude of the amide I response in DMPC vs. DPPC demonstrates that bilayer thickness is a key reaction coordinate. Changes in bilayer thickness alter the monomer/dimer equilibrium of gD; conductance measurements show that the channel lifetime decreases in thicker bilayers (30, 31). This effect arises because gD is too small to span the hydrophobic region of most membranes. This mismatch leads to a trade-off between the energy required to deform the membrane and the energy required to disrupt hydrogen bonds in gD.

To determine the nature of this structural distortion in gD, a robust analysis of the spectral response is needed to isolate the spectrum of protein conformational changes from other contributions, such as HBW. We used two methods to separate these contributions using their distinct temporal behaviors. In the first method, we fit the response of each frequency between 1,600 cm⁻¹ and 1,680 cm⁻¹ and plotted the amplitude of the τ_PT component. The second method uses the MaxEnt-ILT method to extract the spectral response associated with the rate λ_PT. Both methods yield a consistent spectrum associated with the protein distortion spectrum, as shown in Fig. 3A.

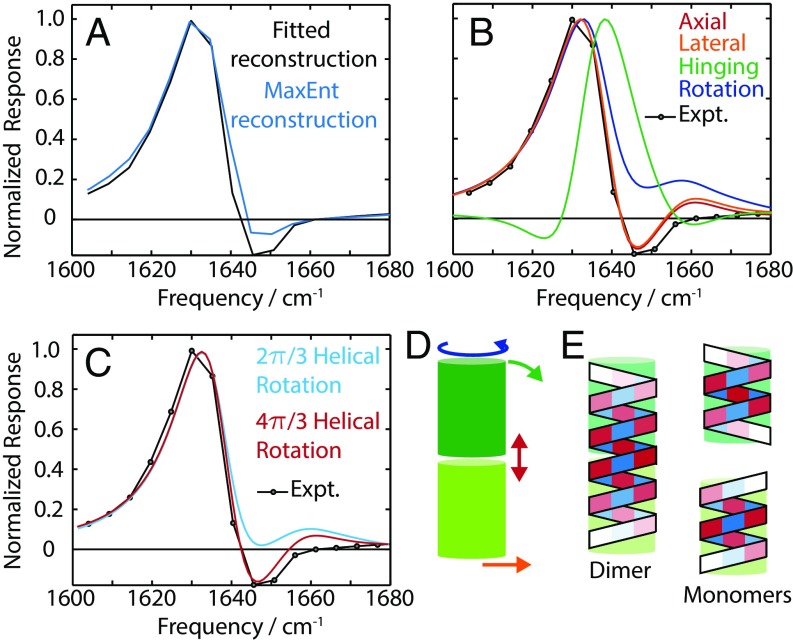
Fig. 3.

(A) Protein-distortion spectrum determined from the experimental data by either fitting or MaxEnt-ILT. (B) Comparison of calculated spectra for the rigid-body distortion model and experiment. (C) Comparison between calculated spectra for the twisting distortion model and experiment (Expt.). (D) Schematic of the different distortion types. (E) Illustration of the amplitude and phase of the η_|| vibrational mode for dimer and monomers.

The dominant features in the protein distortion spectrum are a frequency red shift and gain in intensity; that is, a structural change in gD occurs which lowers the frequency of the h_II mode and increases its intensity. The spectral model of gD in the study by Stevenson and Tokmakoff (8) shows that the frequency of this mode decreases as the vibration becomes more delocalized. In the absence of secondary structure changes, this delocalization is realized by bringing amide carbonyls into closer proximity and is assisted by formation of hydrogen bonds between amide groups [increasing their transition dipole moment by up to 10% (32)]. This suggests that the interfacial contacts of the gD monomers are initially broken, lacking hydrogen bonds at the interface, and as the membrane becomes thinner, these contacts are restored. These states are labeled the partially dissociated dimer, D*, and the fully associated dimer, D.

To determine the nature of D*, we consider rigid-body distortions of gD and calculate the associated spectral change. We focus on rigid-body motions, rather than distortions of the monomer units, for several reasons. First, compression of the helix requires the hydrogen bonds between each rung to compress by ∼1 Å. Second, functional studies have demonstrated that a monomer–dimer transition can occur in cases of hydrophobic mismatch. Finally, simulations of the gD dissociation found no evidence of distortion of the monomers (33).

Using the structure of gD in micelles (Protein Data Bank ID code 1JNO) (34), we initially consider four rigid body motions of the monomers (shown in Fig. 3D): axial and lateral displacements, rotation, and “hinging” of the monomer unit. Of these motions, only axial and lateral displacements give satisfactory agreement with the experimental response. The dependence of the population of D* on the bilayer thickness suggests that the axial distortion is responsible for the spectral response we observe. However, the description of the monomer units as cylinders neglects specific local interactions, particularly, the interfacial hydrogen bonds. The distorted structure is initially present in the equilibrated sample, suggesting there may be some energetic stabilization of the structure. A combination of axial separation and rotation allows some interfacial hydrogen bonds in the separated states. This combined motion has been suggested as the reaction coordinate for full dissociation of the gD dimer in simulations (35).

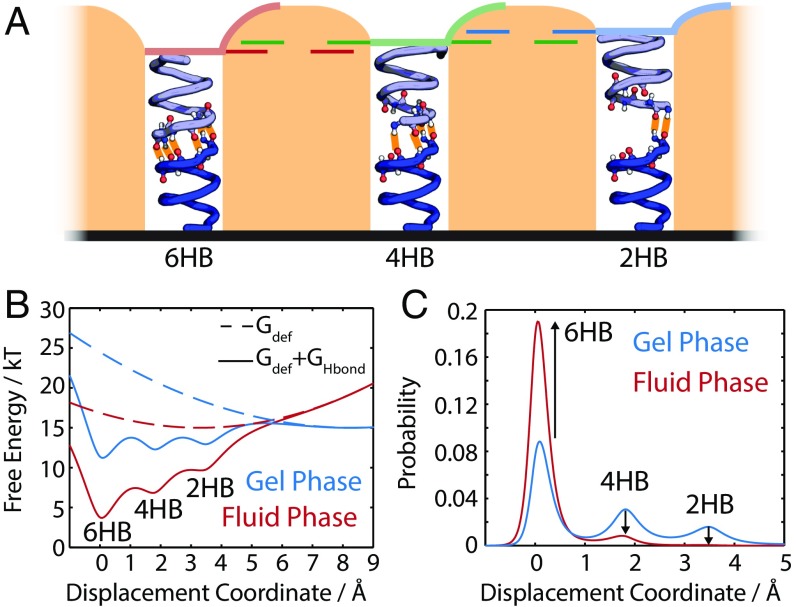
The stereochemistry of gD allows for six, four, two, or zero hydrogen bonds at the interface. We consider the four and two hydrogen-bond states (4HB and 2HB) (Fig. 4) as candidates for D*, and find that the spectral change calculated for the transition from the 2HB state to the 6HB state most closely resembles the experimental data (Fig. 3C). However, multiple conformations may coexist, resulting in superposition of responses. We conclude that some population of gD is initially in the distorted dimer state, D*, which undergoes a transition to the dimer structure, D, during the phase transition. This conclusion rests on the following observations:

• i)Axial, lateral, and screw displacement responses are consistent with the experimental data.
• ii)The response magnitude increases in thicker bilayers. Axial and screw displacements are most sensitive to this coordinate.
• iii)The distorted structure is populated in the gel phase. The preservation of hydrogen bonds with the screw distortion will stabilize this structure relative to the axially distorted structure.

Fig. 4.

(A) Cartoon of the three proposed structures with 6HB, 4HB, and 2HB formed at the monomer interface. Changes in the length of the protein are highlighted. (B) Calculated free energy surfaces for two membrane thicknesses corresponding to gel and fluid phase DMPC membranes. (C) Populations of each of these configurations for thicknesses corresponding to gel and fluid phase DMPC membranes.

This model is an extension to the mismatch models used to explain gD conduction changes with membrane thickness (36). Fluorescence-electrophysiology experiments suggested that there may be an intermediate distorted dimer structure (37). The timescale of changes in the amide I response (0.1–10 μs) precludes a true monomer-to-dimer transition since lateral diffusion of gD is too slow (38). The 4HB/2HB distorted structures have been discussed before as a candidate for the transition state in the monomer–dimer transition; our results suggest that this structure is also populated at equilibrium (39). Although other motions [e.g., rotation of the monomers to an interfacial mode, similar to the behavior of other small membrane proteins (40)] may be consistent with our spectroscopic data, these motions may be discounted because of the rapid timescale observed and the extremely hydrophobic nature of gD. The experiments presented here add a new dimension to the mismatch picture of membrane–protein interactions: Small changes in mismatch can result in structural distortions of integral membrane proteins.

Mechanical Coupling Between gD and Lipid Membranes.

The spectral response of gD provides insight into which structures are present and how fast the conformational changes occur, but it does not directly offer a microscopic explanation. Within experimental error, gD responds on the same timescale as DMPC, indicating that the gD conformational change and membrane thinning are concerted. The speed of the D* → D transition is perhaps surprising, as the multi-angstrom axial compression and the rupture and formation of hydrogen bonds and other contacts are expected to impose a significant energetic barrier. This view, however, assumes that the T-jump minimally perturbs the energy landscape that describes the dynamics of the system (i.e., that the Boltzmann-weighted populations and the rates present differ little from T_i to T_f). However, if the T-jump reshapes the energy landscape, barrier-free, diffusion-limited [or “downhill” (41, 42)] dynamics may be observed. The lateral diffusion constant of gD in DMPC, although not strictly applicable to the structural change of interest here, provides an estimate of <30 ns as the timescale for diffusion-limited compression of gD by $\langle x^2\rangle =4\AA$.

To test this picture, we constructed a model for the energy landscape along the gD distortion coordinate, building on the work of Nielsen et al. (43). We model gD as two cylinders held together by hydrogen bonds within a membrane of variable thickness. The effect of hydrophobic mismatch is included via the membrane deformation free energy. The 6HB, 4HB, and 2HB configurations are stabilized using Morse potentials stabilized by 4 k_BT per pair of hydrogen bonds. (These expressions are reproduced in Timescales of the Ester Response.) Fig. 4 shows the energy surfaces for the system and corresponding populations of the 6HB, 4HB, and 2HB states calculated with the thickness for the gel and fluid phases of DMPC. Membrane thinning significantly reshapes the energy landscape, almost completely alleviating the hydrophobic mismatch. The populations of the 6HB, 4HB, and 2HB configurations are consistent with our earlier assignment. In the fluid phase, the populations of 4HB and 2HB decrease significantly, while the population of the 6HB state increases. The significant reshaping of the energy landscapes across the phase transition indicates that the concept of diffusion-limited conformational changes to gD in response to changes in membrane thickness is plausible.

The conditions in our experiment may seem extreme in comparison to the environment that membrane proteins respond to at thermal equilibrium. However, neutron spin echo experiments have shown that large-amplitude (0.5 nm) thickness fluctuations occur in membranes (5, 44), while NMR measurements have demonstrated that bilayers are highly dynamic environments, with significant collective fluctuations (4, 45). The similarity of the thickness fluctuation amplitudes reported by the neutron spin echo experiments and the thickness change induced by our T-jump, in combination with the correlated motion of gD and membrane thinning, suggest that the structure of gD in the fluid phase may undergo large-amplitude fluctuations within the membrane. Because gD is a small protein, we do not expect the precise details of its response to be replicated in larger proteins. However, it serves to illustrate the importance of membrane fluctuations to the structure and function of membrane proteins. Although the structural changes observed here are subtle, similar conformational changes have been proposed as a mechanism for gating activity in gD (37). Another intriguing possibility is that mixtures of lipids and/or small molecules may alter the behavior of membrane proteins by altering the magnitude of thickness fluctuations rather than the average thickness itself (5). The role of membrane fluctuations on membrane proteins is still poorly understood; however, given that structural fluctuations in potassium channels are believed to be involved in ion selectivity and gating (46–48), it seems plausible that fluctuations in the membrane environment may be translated into functional changes via protein/lipid mechanical coupling.

The experiments presented here also demonstrate the potential of T-jump experiments of membranes proteins to induce rapid environmental changes. Previous experiments have studied the transient conduction (49) of potassium ion channels in response to T-jumps. Using the structural changes in membrane may provide a new route to studying systems such as mechanosensitive ion channels.

Conclusions

Transient IR spectroscopy is able track the progress of a phase transition in membranes and the effect of that phase transition on a model membrane protein. The experiments presented here reveal that the melting of lipid domains can occur on a 0.1- to 10-μs timescale, consistent with other IR experiments (6) and simulations (50). Global shape changes observed by turbidity experiments occur on a millisecond timescale (22), indicating a multistep mechanism to the gel-to-fluid transformation in vesicles. Local melting induced by the T-jump changes the thickness of the membrane, altering the hydrophobic mismatch between gD and the DMPC bilayer and inducing a conformational change in gD. Our model indicates this conformational change is a rotation and compression of the monomers relative to each other, which changes the number of interfacial hydrogen bonds. This transition proceeds very rapidly, with the protein response tracking the change in bilayer thickness. The high rate observed arises from the highly nonequilibrium state created by the compression of the membrane, which allows an almost barrierless transition between protein conformations. Although gD is a small model protein, it has been successfully used over many years to demonstrate key principles for membrane proteins. In the present case, we believe that the sensitivity of gD to the membrane environment may highlight a more general principle: Membrane proteins respond not only to the average structure of their membrane environment but can also respond dynamically to fluctuations in this environment.

Materials and Methods

Sample Preparation.

DMPC and DPPC were purchased from Avanti Polar Lipids. Samples were dissolved in chloroform in a glass vial, dried under N₂, and then placed under vacuum overnight to remove residual solvent. Samples were rehydrated in D₂O (50 mM sodium phosphate buffer) to a concentration of 20 mM. Samples were held at 10 °C above the lipid T_m for 1 h before vortexing and sonication to ensure a homogeneous sample. Samples were extruded through a 100-nm membrane to form large unilamellar vesicles. The vesicles were characterized with light scattering, yielding an average vesicle diameter of 120 nm.

The gD was purchased from Alfa Aesar, and was first dissolved in MeOD (Cambridge Isotopes) to exchange the labile amide protons for deuterons. The gD is a mixture of gramicidins A, B, and C, which differ by a single point mutation at position 12 [which is either a Trp (A), Phe (B), or Tyr (C)]. The exchanged gD was added to the lipid/chloroform mixture before drying under nitrogen at a 100:1 lipid/protein molar ratio. A 100:1 ratio was used to provide as large a lipid/protein ratio as possible, while still providing sufficient signal from the amide I vibration of the protein. Additional concentration data are presented in Fig. S5.

Fig. S5.

Protein response extracted from the MaxEnt-ILT rate spectrum for the 100:1 (blue) and 1,000:1 (red) DMPC/gD vesicle samples. AU, arbitrary unit.

IR Spectroscopy.

All samples for IR spectroscopy were sandwiched between two CaF₂ windows separated by a 50-μm Teflon spacer and mounted in a brass sample cell. Temperature was controlled by a circulating chiller connected to a brass sample holder. The temperature was monitored by a thermocouple attached directly to the sample cell. FTIR spectra were collected on a Bruker Vertex spectrometer. Buffer background spectra were collected and subtracted to remove the solvent contribution to the spectra.

HDVE spectra were collected as outlined elsewhere (18, 19). Briefly, mid-IR pulses 100 fs in duration were used in a home-built interferometer to generate three pulse replicas, which were overlapped in a sample to generate the vibrational echo signal. This signal was then overlapped with a final pulse for heterodyne detection on a HgCdTe array detector. The scaling of the transition dipole of the vibration (μ⁴) suppressed the solvent signal, so no buffer spectra subtraction was required. The T-jump pulse was generated from a neodymium-doped yttrium aluminium garnet–pumped optical parametric oscillator tuned to an output wavelength of 1.9 μm. Sub–10-ns pulses with an energy of 10 mJ were focused to a diameter of 300 μm in the sample. The final temperature of the T-jump (typically T_i + 10 °C) was determined from the change in the transmission of the broad D₂O bend–libration combination band centered at 1,550 cm⁻¹.

Two-State Thermodynamics Model for Melting

A two-state model for the gel-to-fluid transition of lipid vesicles can be fit to the temperature-dependent FTIR to extract thermodynamic parameters (51). If we consider the transition $G\rightleftarrows F$, the gel fraction may be written as

$${\theta }_g=\frac{1}{1+K_{eq}},$$

where

$$K_{eq}=\exp \left(-\frac{\mathrm{\Delta }G°}{RT}\right)$$

and

$$\mathrm{\Delta }G°\left(T\right)=\mathrm{\Delta }H°\left(1-\frac{T}{T_m}\right)+\mathrm{\Delta }{C}_p\left(T-T_m-T\ln \left(\frac{T}{T_m}\right)\right),$$

where $K_{eq}$ is the equilibrium constant, $\mathrm{\Delta }G°\left(T\right)$ is the temperature-dependent Gibb’s free energy, $\mathrm{\Delta }H°$ is the enthalpy of the transition, $\mathrm{\Delta }{C}_p$ is the change in heat capacity between the gel and fluid phases, and $T_m$ is the melting temperature. Calorimetric measurements on DMPC vesicles suggest that the heat capacity before and after the transition is essentially the same, and we expect that $\mathrm{\Delta }{C}_p$ will be zero. Nonetheless, we include it in our expression as a test of the quality of the data and fit.

The melting curve obtained from the temperature-dependent FTIR ($I$) of the ester carbonyl stretching vibration is modeled as

$$I={\theta }_g{f}_g+{\theta }_f{f}_f,$$

where $f_i=a_{i}T+b_i$. This accounts for sloping baselines in the data, which arise from the temperature dependence of the ester vibrations (e.g., changes in dipole strength with temperature, frequency shifts due to changes in H-bond strength with temperature).

Experimental data and fits are shown in Fig. S1. Note that the baselines for the gel and fluid phases are similar, and are similar between pure DMPC and DMPC + gD datasets. This is consistent with the assignment of these sloping baselines as arising from “nonspecific” temperature dependences of the ester carbonyl vibrations.

DPPC gD FTIR Spectra

The amide I FTIR spectra for gD-containing DMPC and DPPC vesicles are shown in Fig. S2. The DPPC difference spectrum shows a line shape more similar to the microsecond transient amide I signal, while the DMPC difference spectrum is more reminiscent of the nanosecond transient response. This is consistent with the thickness-dependent model presented in the main text, which predicts that the thicker DPPC bilayer should contain a greater population of the distorted gD structure.

Note, however, that the transient spectra are only sensitive to changes on a submillisecond timescale, which is too slow for effects such as true monomer–dimer transitions to play a role. The FTIR spectra are collected are at equilibrium, and thus are not restricted in this manner. There may also be some contribution to the difference spectra of DPPC from these other processes.

Comparison of Transient Spectra for DMPC and DPPC Bilayers

HDVE.

HDVE spectroscopy is a third-order nonlinear spectroscopic technique (18, 19, 52). Three mid-IR pulses, resonant with the ester and amide I modes, interact with the sample. The first pulse creates a coherence between the vibrational ground state and one quantum of excitation of one of the vibrational modes. The second interaction creates either a population state of this vibration, or a coherence between two different modes. The third interaction creates a coherence between this population state and either the second excited state or the ground state before the signal is emitted with a wavevector: $k_s=-k_1+k_2+k_3$. In the experiments in the main text, the time delay between interaction 1 and interaction 2 is set to zero, while the delay between interaction 2 and interaction 3 is kept constant at 150 fs. Thus, the signal emitted contains similar information to a vibrational pump-probe experiment.

One of the primary advantages of the HDVE experiment is that the D₂O background signal is suppressed because the HDVE experiment signal is proportional to ${\mu }_i^4$, where ${\mu }_i$ is the transition dipole moment of the ith oscillator. D₂O has a high concentration (>55 M), resulting in notable linear absorption; however, the nonlinear signal is negligible as a result of the very small transition dipole moment in the region of interest.

HDVE spectra are complex valued spectra, and contain oppositely signed resonances from the fundamental $\nu =0\to 1$ vibrational transitions and also $\nu =1\to 2$ double-excitation transitions. To simplify the analysis and comparison with FTIR spectra, we consider only the amplitude (absolute value), which results in spectra that are completely positive. Thus, negative features in the transient spectra can be associated with losses and positive features can be associated with gains. To generate the amplitude HDVE, we use the Kramers–Kronig relation to generate the complex-values HDVE response and calculate the absolute value of this response (52).

gD FTIR-HDVE Spectral Comparison.

The FTIR difference spectrum of gD and the transient HDVE spectrum presented in Fig. 1 show many corresponding features, but one notable difference between the two spectra is the presence (absence) of a broad feature centered at ∼1,650 cm⁻¹ in the FTIR (HDVE) spectrum. Although the analysis in the main text does not focus on this peak, a discussion of its possible origins is included here for completeness.

The simplest explanation is that it is an artifact from the D₂O background subtraction; in the FTIR measurements, background absorption from the D₂O bend–libration combination band is present. At each temperature, a spectrum of the protein/lipid sample and of a D₂O sample was collected, which were later subtracted. While this is generally an effective procedure, low-intensity broad artifactual features may occasionally be observed in the difference spectrum.

An alternative explanation is that the feature is real, and does indeed arise from the protein. Previous 2D IR studies of gD (8) noted that peaks in this region of the FTIR are suppressed in the 2D IR signals (equivalent to the HDVE signals reported here). This arises because these peaks are composed of many weak transitions; the higher order dipole scaling (μ⁴ vs. μ²) in HDVE experiments causes these modes to be less visible than the intense peak at 1,630 cm⁻¹. Changes in the intensity of these weak modes may fall below the detection limits of the transient experiment.

A third explanation is that the timescales associated with these changes are beyond the observable time window of the experiment. If, for example, this peak corresponded to the complete dissociation and unfolding of gD (which would be expected to yield a peak centered at ∼1,650 cm⁻¹, which is associated with the “random coil” configuration), then this process would be unlikely to occur within the 2-ms experimental window. The FTIR difference spectra are not subject to these temporal restrictions, as the sample is allowed to equilibrate at each temperature for several minutes. Each of these explanations would paint a different picture of the underlying process.

Timescales of the Ester Response

Multiple Timescales in Lipid Melting.

As discussed in the main text, there is clear evidence of multiple timescales in the T-jump data. In the context of the wider literature on this subject, this is not a surprising result. Some notable transient experiments that address the main phase transition in simple lipid vesicles are summarized in Table S1.

The long (millisecond) timescale identified in the main text is of particular interest. The very different timescales of the growth of the transient signal and the relaxation (0.1–10 μs vs. >2 ms) make it clear that a simple two-state kinetic scheme cannot describe the full melting process. Interpretation of this millisecond timescale is hampered by the thermal relaxation of the sample. Since it is slower than τ_sol, this timescale effect of this timescale is a lag time between the solvent relaxation and the relaxation of the ester response. While deconvolution of the signals is mathematically possible, it is an ill-posed problem, highly susceptible to noise in the data. This means we are constrained to stating that the lag between the solvent and relaxation and ester relaxation is consistent with the presence of a millisecond (>2 ms, <50 ms) timescale in the system. Similar trends are observed in the DMPC/gD samples, although the lag behind the solvent relaxation is shorter. A speed-up in the millisecond dynamics of lipid vesicles on addition of gD has been observed in turbidity measurements (22), suggesting that the millisecond timescales observed here may arise from the same physical process.

It is also useful to consider what insight the milliseconds dynamics described in Table S1 may provide into the origins of the millisecond timescale. The IR-probed T-jump experiments in the study by Nagarajan et al. (6) discussed in the main text are most similar in concept, execution, and results to our experiment. However, a small-amplitude (<20%), microsecond response was observed in the turbidity experiments in the study by Genz and Holzwarth (22). This may simply arise from a small population of rapidly melting vesicles in the sample. However, the amplitude of the turbidity change is proportional not only to change in the concentration of a particular species but also to change in the scattering cross-section of that species. The assignment of the 0.1- to 10-μs timescale as local melting and thinning of the bilayer could perhaps give rise to a small change in the scattering cross-section of the lipid membranes, and thus may be responsible for this microsecond timescale. As a final note, the earlier discussion about temperature-dependent energy landscapes has an important role in comparing T-jump data: Many of the earlier T-jump experiments used small changes in temperature (typically 1–2 K), which means we should not expect quantitative agreement between the timescales; the initially prepared states will be subject to different driving forces from the reshaping of the energy landscape.

MaxEnt Regularization for ILTs.

The problem of ILTs and regularization strategies have been discussed in great detail in many studies (26, 53, 54). The ILT will transform the time-domain experimental data to rate space. This is desirable as it requires no assumptions about the number of rates or their functional form, other than that they may be expressed as a sum of terms of the form $\exp \left(-{\lambda }_{i}t\right)$. However, the ILT is an ill-posed problem; in the presence of even a small amount of noise, the ILT result will change dramatically. This class of problem can be addressed by the application of regularization methods that introduce some constraint based on the expected rate distribution. One regularization method is a MaxEnt constraint that includes an entropy term $S=-{\displaystyle {\sum }_i{x}_i\left(\ln \left(x_i/X_i\right)-1\right)}$, where $x_i$ is the discretized rate distribution and $X_i$ is the prior that contains what is already known about the system. This is set to a flat uniform distribution of low amplitude ($X_i\approx 1\times {10}^{-5}$).

The ILT is performed by determining the rate distribution that minimizes the function

$$F=\eta {\chi }^2-S,$$

where

$${\chi }^2=\frac{1}{N}{\displaystyle \sum _i^N\frac{{\left(I_{expt}\left(t_k\right)-I_{calc}\left(t_k\right)\right)}^2}{{\sigma }_k^2}}$$

and ${\sigma }_k^2$ is the variance of the noise in the experiment. This term is estimated from the negative-time transient data (i.e., when the probe arrives before the T-jump pulse). Since this response should be zero, this provides a convenient estimate for the noise. The parameter $\eta$ acts to constrain the value of ${\chi }^2$.

The rate distributions presented were calculated by choosing an initial value of $\eta ={\sigma }_k^2$, and minimizing $F$ using a Newton–Raphson scheme. The value of $\eta$ was increased, and the previous minimized solution was used as the initial guess for the minimization of the new $F$. This was repeated until ${\chi }^2=2$. A value of ${\chi }^2$ greater than unity was chosen to minimize the possibility of spurious features in the rate distribution, at the expense of possibly broader peaks in the distribution. However, since the shape and relative widths of the distributions are not the focus of the analysis in the main text, this does not present a problem.

Calculated rate distributions as a function of detection frequency for the DMPC only and DMPC + gD samples are shown in Fig. S4.

Vesicle Composition Dependence of Spectral Response.

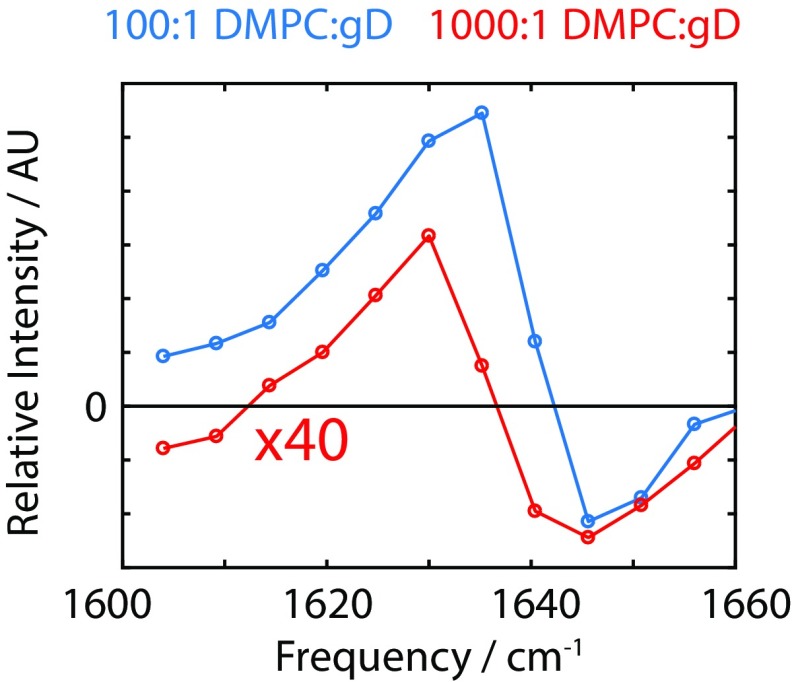
The transient-HDVE data were collected for two protein–lipid compositions: 100:1 DMPC/gD and 1,000:1 DMPC/gD. The transient spectral response is consistent in both cases, as shown in Fig. S5. In both cases, the response shows a characteristic increase in intensity at lower frequencies, and a slight decrease in intensity at higher frequencies.

The intensity of the 1,000:1 DMPC/gD response is smaller than would be expected from concentration arguments alone (10-fold expected vs. ∼45-fold observed). This is a reflection of the small protein signal in the 1,000:1 experiment; the response from the DMPC ester group at higher frequencies has a sufficiently long tail that the 1,000:1 protein response cannot be easily isolated. Thus, we do not expect the magnitudes to be quantitative. However, the similarity in line shape of the transient response is consistent with the distorted dimer structure proposed in the main text.

gD: Spectral Modeling.

The calculation of the IR spectra of gD conformers is similar to that presented by Stevenson and Tokmakoff (8). Amide I spectral calculations require two components: a Hamiltonian of the amide I manifold and a matrix of the transition dipole moments. It is most convenient to construct this in the site basis (i.e., the basis of the individual amide units). To construct the Hamiltonian, a site energy is assigned to the diagonal elements. Stevenson and Tokmakoff (8) demonstrated that considering uniform site energies is sufficient to capture the vibrations of gD. The coupling between amide units (the off-diagonal elements of the Hamiltonian) is calculated numerically from the expression

$$J_{ij}=A\left(\frac{{\mu }_i\cdot {\mu }_j}{{\left|R_{ij}\right|}^5}-3\frac{\left({\mu }_i\cdot r_{ij}\right)\left({\mu }_j\cdot r_{ij}\right)}{{\left|R_{ij}\right|}^3}\right),$$

where ${\mu }_i$ is the transition dipole moment of oscillator $i$, $r_{ij}$ is the unit vector connecting oscillators $i$ and $j$, and $R_{ij}$ is the distance between oscillators $i$ and $j$. To calculate these couplings, a simple structural model of gD is generated, and some uniform displacement or rotation of one monomer unit is then applied. The new structure is used to determine $r_{ij}$ and $R_{ij}$. The value of ${\mu }_i$ is calculated from this structure by using the fixed relation of the transition dipole moments to the carbonyl bond vector [following the work by Moore and Krimm (56), the transition dipole moment is 20° rotated from the CO bond axis; this has significant implications for which modes are IR-active in amide I spectra].

The third-order nonlinear signal is calculated numerically using the method outlined by Reppert and Tokmakoff (55), using in-house software (available at https://github.com/mreppert/g_spec). The spectra presented in the main text are shown as the [aHDVE(no distortion) − aHDVE(distortion)] so that they may be compared directly with experiment.

gD: Membrane Mechanical Coupling Model.

The model described in the main text is a modification of the model presented by Andersen and coworkers (43). In this model, the free energy of bilayer deformation is described by the surface integral:

$$\mathrm{\Delta }{G}_{def}={\displaystyle \underset{\text{Ω}}{\int }\frac{1}{2}\left\{\frac{K_a}{d_0^2}{u}^2+K_c{\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)}^2+\alpha \left[{\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial u}{\partial y}\right)}^2\right]\right\}d\text{Ω}},$$

where $u\left(x,y\right)$ is the local monolayer perturbation, $d_0$ is the equilibrium bilayer thickness, $K_a$ is the elastic deformation modulus, $K_c$ is the splay-distortion modulus, and $\alpha$ is the interfacial tension. Conceptually, this free energy is composed of three contributions: the compression-expansion (CE) energy (first term), the splay-distortion (SD) energy (second term), and the surface tension (final term). The CE energy can be thought of as describing the bilayer as a set of springs: Displacement from the equilibrium thickness is subject to a harmonic restoring potential. The SD energy arises from necessary changes in packing and lipid–lipid interactions because of the curvature of the deformation profile around the protein.

Determining the minimum free energy conformation of the lipid requires that

$$K_c{\nabla }^{4}u-\alpha {\nabla }^{2}u+\left(\frac{K_a}{d_0^2}\right)u=0.$$

Assuming radial symmetry, the deformation profile may be expressed in terms of modified zero-order Bessel functions of the second kind, ${\mathcal{K}}_0\left(k_{\pm }r\right)$, where

$$k_{\pm }^2=\frac{1}{2}\left(\frac{\alpha }{K_c}\pm \sqrt{\frac{{\alpha }^2}{K_c^2}-\frac{4K_a}{d_0^2{K}_c}}\right).$$

The expression for the deformation profile is

$$u\left(r\right)=A_{+}{\mathcal{K}}_0\left(k_{+}r\right)+A_{-}{\mathcal{K}}_0\left(k_{-}r\right),$$

where

$$A_{+}=\frac{k_{-}{\mathcal{K}}_1\left(k_{-}r\right)u_0+{\mathcal{K}}_0\left(k_{-}{r}_0\right)s}{k_{-}{\mathcal{K}}_0\left(k_{+}{r}_0\right){\mathcal{K}}_1\left(k_{-}{r}_0\right)-k_{+}{\mathcal{K}}_0\left(k_{-}{r}_0\right){\mathcal{K}}_1\left(k_{+}{r}_0\right)}$$

and

$$A_{-}=\frac{-k_{-}{\mathcal{K}}_1\left(k_{-}r\right)u_0-{\mathcal{K}}_0\left(k_{+}{r}_0\right)s}{k_{-}{\mathcal{K}}_0\left(k_{+}{r}_0\right){\mathcal{K}}_1\left(k_{-}{r}_0\right)-k_{+}{\mathcal{K}}_0\left(k_{-}{r}_0\right){\mathcal{K}}_1\left(k_{+}{r}_0\right)}.$$

${\mathcal{K}}_1$ is the modified first-order Bessel function of the second kind, $r_0$ is the radius of the protein causing the deformation, and $s$ is determined from the boundary conditions ${\frac{\partial u}{\partial r}|}_{r_0}=s$. The thickness of the bilayer around the protein is $u\left(r_0\right)=u_0$. This expression for the deformation profile then returns the expression for the deformation free energy:

$$\mathrm{\Delta }{G}_{def}=-\pi r_0{K}_c\left[s\left(A_{+}{k}_{+}^2{\mathcal{K}}_0\left(k_{+}{r}_0\right)+A_{-}{k}_{-}^2{\mathcal{K}}_0\left(k_{-}{r}_0\right)\right)+u_0\left(A_{+}{k}_{+}^3{\mathcal{K}}_1\left(k_{+}{r}_0\right)+A_{-}{k}_{-}^3{\mathcal{K}}_1\left(k_{-}{r}_0\right)\right)+\gamma u_{0}s\right].$$

Parameters for the membrane are given in the study by Nielsen et al. (43). The key variables for this work are the equilibrium thickness, $d_0$, and the thickness of the protein, $u_0$. The $d_0$ term varies with the phase of the lipid, and so introduces temperature dependence into this model.

The modification introduced into this model in the main text is to consider $u_0$ as a variable, not a static term. This is introduced to include the effect of conformational changes in gD. The gD deformations are considered to be rigid-body motions of the monomer units. The main interaction is taken to be the hydrogen bond interactions between the monomer units, which are modeled as a Morse potential:

$$G_{Hbond}={\displaystyle \sum _{i=1}^3{\epsilon }_i\left({\left[1-\exp \left(-a_i\left(r-r_i\right)\right)\right]}^2-1\right)}.$$

Each of the terms in the sum represents one of the three plausible hydrogen bond configurations (6HB, 4HB, and 2HB). The well depths and separations are estimated from coarse-grained simulations (35). We stress here that this model is not intended to be quantitative, but rather illustrative.