Molecular origin of the weak susceptibility of kinesin velocity to loads and its relation to the collective behavior of kinesins

Significance

Successful functioning of biological systems depends on efficient cellular transport supported by several classes of active biological molecules known as motor proteins. Although they have been intensively studied using various experimental methods, their molecular properties remain not fully understood. We developed a theoretical approach by using structure-based molecular dynamics simulations. It allowed us to understand at the molecular level the effect of external forces on kinesin motor proteins. It is shown that a force-regulated coupling between the neck linker and the ATP binding site of a kinesin accounts for experimentally observed weak susceptibility to loads. Our framework helps us to rationalize the low cooperativity among kinesins. The presented method is a powerful tool in clarifying microscopic features of motor proteins.

Abstract

Motor proteins are active enzymatic molecules that support important cellular processes by transforming chemical energy into mechanical work. Although the structures and chemomechanical cycles of motor proteins have been extensively investigated, the sensitivity of a motor’s velocity in response to a force is not well-understood. For kinesin, velocity is weakly influenced by a small to midrange external force (weak susceptibility) but is steeply reduced by a large force. Here, we utilize a structure-based molecular dynamic simulation to study the molecular origin of the weak susceptibility for a single kinesin. We show that the key step in controlling the velocity of a single kinesin under an external force is the ATP release from the microtubule-bound head. Only under large loading forces can the motor head release ATP at a fast rate, which significantly reduces the velocity of kinesin. It underpins the weak susceptibility that the velocity will not change at small to midrange forces. The molecular origin of this velocity reduction is that the neck linker of a kinesin only detaches from the motor head when pulled by a large force. This prompts the ATP binding site to adopt an open state, favoring ATP release and reducing the velocity. Furthermore, we show that two load-bearing kinesins are incapable of equally sharing the load unless they are very close to each other. As a consequence of the weak susceptibility, the trailing kinesin faces the challenge of catching up to the leading one, which accounts for experimentally observed weak cooperativity of kinesins motors.

Motor proteins or biological molecular motors are active enzymatic molecules that help control the internal organization of cells by driving the movements of vesicles and organelles along cytoskeletal filaments (1, 2). The molecular structures (3–9), chemomechanical cycles (10–12), and regulation mechanisms (13–20) of these critical mechanical enzymes have been studied extensively to resolve how these proteins convert the free energy available from ATP hydrolysis into mechanical motion. A number of precision biophysical techniques have been developed to characterize the motor step sizes, unloaded velocities, stalling forces, and processivity, since these properties are crucial to understand how motors transport their cargo and are often used to distinguish the different classes of motors expressed in cells. However, the slope of single-motor force–velocity relationships (dv/dF), which has also been referred to as the susceptibility of the motor velocity to load, χ_vel (F), has also been shown to be critical to motor mechanics, particularly when motors function collectively. Theoretical analyses showed that χ_vel (F) can be a key determinant of the active contractility in actomyosin networks (21) as well as in the collective force generation by multiple motor proteins overcoming an opposing force in a viscous cellular milieu (22–24). In both cases, χ_vel (F) defines how rapidly a system of coupled motors can adapt its filament-bound configuration to balance the forces between its constituent motors.

χ_vel (F) is a complex parameter that can vary considerably depending on the motor type and across different loading regimes. Previous single-molecule analyses have shown that the kinesin motor velocity changes sluggishly at low loads [i.e., χ_vel (F) is low below the single-kinesin stalling force] (25). In contrast, the velocities of single myosin and dynein motors decrease much more rapidly at low loads, yielding a stronger χ_vel (F) in the same loading regime (26, 27). Herein, we pinpointed the molecular origin of the weak χ_vel (F) for kinesins by analyzing the impact of loading forces on the transition rates in the chemomechanical cycle. Using structure-based molecular dynamics simulations, we identified the ATP release rate as the key reason for the weak susceptibility of kinesin velocity to the small loading forces (Fig. 1A). We discovered that the contact formation between the neck linker and the motor head is coupled to the dynamics of the open or the closed state of the ATP binding site through a preserved coevolving network formed by α6, β1/β6, and switch I/II within the motor head. Such coupling is only activated at large loading forces, leading to the weak χ_vel (F) to small loading forces.

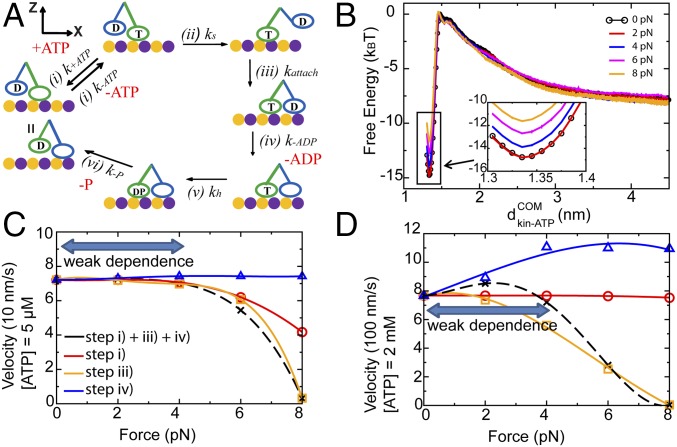
Fig. 1.

The chemomechanical cycle of a single double-headed kinesin under an external force. (A) A schematic diagram of the chemomechanical cycle of a single double-headed kinesin on an MT. T represents an ATP-bound motor head. D represents an ADP-bound motor head. DP represents an ADP$\cdot$P-bound motor head; k represents the reaction rate of each step in a cycle. (B) The free energy profile of binding/unbinding between the ATP and the leading head (LH) in step i at 300 K with external loading forces of F = 0, 2, 4, 6, and 8 pN separately. $d_{kin-ATP}^{COM}$ represents the distance between the center of mass of ATP and that of the LH. The free energy profile in the bound state ($d_{kin-ATP}^{COM}$ = 1.34 nm) is zoomed in and shown in Inset. (C and D) Numerically calculated velocity of single kinesin as a function of external loading forces at (C) 5 μM ATP and (D) 2 mM ATP. The black dashed lines represent the calculated velocity when steps i, iii, and iv are all force-dependent. The profile shows a weak dependence on small forces. The red solid lines represent the calculation assuming that only step i is force-dependent. For other steps, we assume that they are force-independent. The orange solid lines represent the calculation assuming that only step iii is force-dependent. The blue solid lines represent the calculation assuming that only step iv is force-dependent. Steps i (ATP release) and iii (attachment) cause a slow decrease in the velocity under loading forces. They serve as important steps to resist small forces. Error bars are shown in B.

Finally, building on this framework, we further examined how the χ_vel (F) of a single kinesin influences the cooperativity of multiple kinesin proteins. To this end, we developed a quantitative relationship between the force partitioning and the spatial arrangement between two kinesins on their filament using an atomistic structure of kinesins docking on the microtubule (MT) and molecular dynamic simulations. The force partitioning can be directly measured from our ab initio simulations. We found that the leading kinesin takes more than 90% of the overall load when the distance between two kinesins is larger than 48 nm. With the weak susceptibility, χ_vel (F), it is difficult for the trailing kinesin to catch up with the leading one. Therefore, the uneven force partitioning remains and leads to the low cooperativity between two kinesins. Our study provides a structural basis of χ_vel (F), which is critical to fully understand the collective behavior of multiple motors and facilitate potential protein engineering for high-efficiency motors.

Results and Discussion

Determine the Key Chemical Steps That Account for the Weak Susceptibility of Kinesin Velocity to External Loads.

Experimental studies show that the overall velocity of a kinesin slowly decreases under loading forces unless the forces approach the stalling force (25). We interrogated the impact of loading forces on the reaction rate for each chemical step of the chemomechanical cycle (Fig. 1A) to identify the key chemical steps that account for weak susceptibility of kinesin velocity to external loads, χ_vel (F). The chemomechanical cycle starts from a process when the leading head of a kinesin on a MT binds an ATP, while the ADP-bound trailing head detaches from the MT (Fig. 1A, step i). In the next chemical step, the ADP-bound trailing head swings from the back to the front of the ATP-bound leading head (Fig. 1A, step ii). The new ADP-bound leading head steps on the MT (Fig. 1A, step iii) and releases ADP (Fig. 1A, step iv). Finally, the cycle ends with the hydrolysis of ATP at the ATP-bound trailing head followed by the release of phosphate (Fig. 1A, steps v and vi). The structures of kinesins are known for steps i, iii, and iv in particular, which allows us to evaluate the changes in the free energy landscape under force by means of molecular dynamics simulations. The velocity of a single kinesin can be calculated from the simplified Michaelis–Menten framework presented below in Eqs. 1–3 (details of derivations are in Michaelis–Menten Representation of the Kinesin Cycle):

$$V=\delta \frac{k_{cat}^{eff}\left[S\right]}{K_M^{eff}+\left[S\right]}$$ [1]

$$k_{cat}^{eff}={\left(\frac{1}{k_s}+\frac{1}{k_{attach}}+\frac{1}{k_{-ADP}}+\frac{1}{k_h}+\frac{1}{k_{-p}}\right)}^{-1}$$ [2]

$$K_M^{eff}=\frac{k_{cat}^{eff}}{k_s}\left(\frac{k_s+k_{-ATP}}{k_{+ATP}}\right).$$ [3]

k_ATP, k_−ATP, k_s, k_attach, k_−ADP, k_h, and k_−p are the rates of the chemical reaction for the key steps in Fig. 1A. [S] is the concentration of ATP. δ is the step size of kinesin: 8 nm.

In the following, utilizing high-resolution structures of kinesin obtained in previous experiments (3, 4), we created a structure-based coarse-grained model to derive the free energy surfaces along chosen reaction coordinates for several chemical steps in the chemomechanical cycle of a single kinesin (steps i, iii, and iv in Fig. 1A). Those free energy surfaces were found to be modulated by external forces differently. Next, the kinetic rates as a function of external forces were calculated from the free energy surfaces. In this way, we were able to determine the key chemical steps in the cycle that account for the low χ_vel (F) of a single kinesin. As detailed below, those chemical steps are ATP release (step i) and attachment (step iii) (Fig. 1A). We will further explain the relationship of χ_vel (F) that characterizes the gait of a single kinesin and the cooperativity between two kinesins in later sections.

Step i.

The reaction coordinate was chosen to be the distance between the center of mass of ATP and that of the leading head of the kinesin, $d_{kin-ATP}^{COM}$ (Fig. 1B). The free energy barrier of ATP release is defined by the free energy between the ATP-bound state ($d_{kin-ATP}^{COM}$ = 1.34 nm) and the transition state ($d_{kin-ATP}^{COM}$ = 1.46 nm), ΔG_r. We found that the difference between ΔG_r at F = 2 pN and that at F = 0 is less than 0.1 k_BT, indicating that ATP release is barely affected by a small loading force. ΔG_r slowly increases with loading force. At a large force of 8 pN, ΔG_r decreases by 3 k_BT compared with the case at F = 0, indicating a significant increase in the rate of ATP release under large external loading forces. Based on Eqs. 1 and 3, an increase in the rate of ATP release decreases the velocity of a single kinesin. The negligible change in ΔG_r at 2 pN as well as the slow increase in ΔG_r from 2 to 8 pN imply a weak χ_vel (F) at small loading forces.

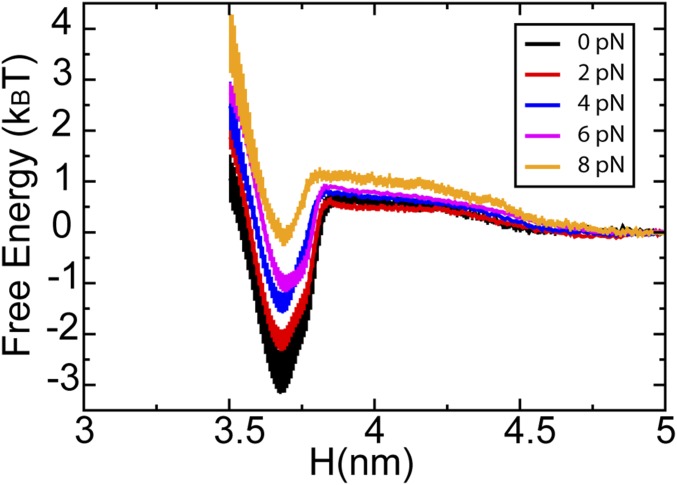
Step iii.

The reaction coordinate was chosen to be the distance between the center of mass of the leading head and that of the MT along the normal to the MT at F = 0 pN and F = 8 pN (Fig. S1). The free energy barrier of attachment increases at F = 8 pN compared with that at F = 0. This increase corresponds to a lowered attaching rate under loading forces and thus, contributes to the smaller velocity of kinesin from Eqs. 1–3.

Fig. S1.

The free energy profile of the LH of a single load-bearing kinesin docking to the MT under various loading forces ranging from 0 to 8 pN. H represents the distance between the center of the mass of the LH and that of the MT in the Z direction (Fig. S7).

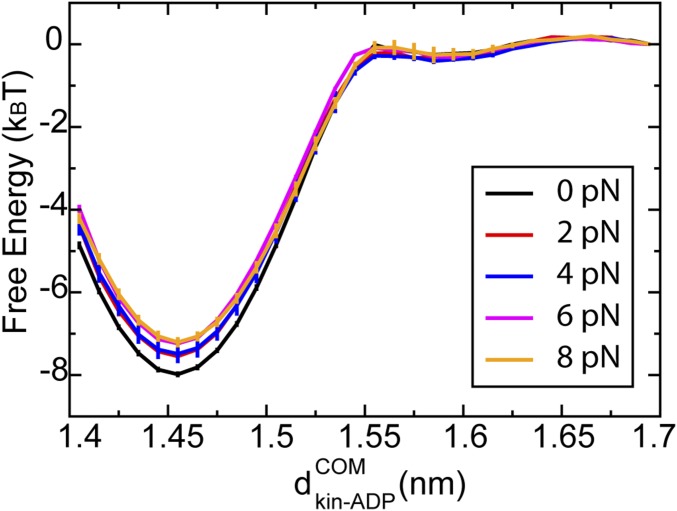
Step iv.

The reaction coordinate was chosen to be the distance between the center of mass of ADP and that of the leading head of the kinesin, $d_{kin-ADP}^{COM}$ (Fig. S2). Under an external loading force of 8 pN, the free energy barrier of ADP release decreases. The overall velocity of a kinesin grows with an increase in the rate of ADP release under an external loading force.

Fig. S2.

The free energy profile of ADP release from the LH of a single load-bearing kinesin under various loading forces ranging from 0 to 8 pN; $d_{kin-ADP}^{COM}$ represents the distance between the center of mass of ADP and that of LH of the kinesin.

We examined whether our model could reproduce the weak χ_vel (F) observed in the experiment (25) at small loading forces. The rate of a certain chemical step can be calculated by the mean first passage time method (28) (details are in Calculate the Force–Velocity Curve from Simulation Data) by Eqs. 4 and 5:

$$k\left(F\right)={\left({\displaystyle \underset{X_0}{\overset{X_1}{\int }}dX{\displaystyle \underset{0}{\overset{X}{\int }}\frac{dX\prime e^{\frac{G\left(X,F\right)-G\left(X\prime ,F\right)}{k_{B}T}}}{D\left(X\right)}}}\right)}^{-1}$$ [4]

$$D\left(X\right)=\frac{1}{2}\frac{d\langle X^2\rangle }{dt}.$$ [5]

X is the reaction coordinate. D is the diffusion coefficient along the reaction coordinate. G (X, F) is the free energy under an external loading force F. Steps i, iii, and iv are all force-dependent chemical steps (Fig. 1B and Figs. S1 and S2). The velocity of a single kinesin under external loading forces can be calculated by substituting the rates of those steps obtained in Eqs. 4 and 5 to the expression of the velocity in Eqs. 1–3 at both a low concentration (5 μM) (black curve in Fig. 1C) and a high concentration (2 mM) (black curve in Fig. 1D) of ATP. The predicted velocities reproduce the weak χ_vel (F) at small loading forces observed in the experiment (25), indicating that our model qualitatively captures the unique response of a single kinesin to external loading forces, despite neglecting the force dependence in steps ii, v, and vi. Step ii was not investigated, because it was shown experimentally (29) that the stepping of an ADP-bound trailing head is on the order of several microseconds under F = 5 pN, whereas the other steps in the chemomechanical cycle are of the order of milliseconds (30). Thus, the time spent in step ii is too short to influence the velocity of a single kinesin at moderate loading forces. Although backward stepping is a possibility at a large force of 8 pN (29), accounting for this possibility is beyond the scope of our study. Steps v and vi were also neglected. Without the crystal structure for a kinesin with both ADP and phosphate, it is difficult to realistically apply our structure-based model for these steps. We assumed that these steps are less affected by external loading forces. As mentioned above, even with this approximation, we can still qualitatively reproduce the weak χ_vel (F) from simulation data. The details of these two steps will be investigated in future works. For Fig. 1D, there is a slight increase in the kinesin velocity from 767 nm/s at F = 0 to 852 nm/s at F = 2 pN. This is because the increase in velocity from step iv is slightly larger than the decrease of velocity from other steps at a lower force according to our simulations. This minor increase is small in comparison with the overall changes of the velocity in Fig. 1D. Thus, this slight increase does not influence the main conclusion of this work.

To dictate the key chemical steps accounting for the weak χ_vel (F), we decomposed the overall response to loading forces into three individual steps. The velocity was recalculated by assuming that only step i is force-dependent (red curves in Fig. 1 C and D), that only step iii is force-dependent (orange curves in Fig. 1 C and D), or that only step iv is force-dependent (blue curves in Fig. 1 C and D). The results indicate that both steps i and iii lead to a slow decrease in the velocity of a single kinesin under external loading forces, while step iv causes an increase in the velocity. We concluded that steps i (ATP release) and iii (attachment) are the key steps that determine the weak χ_vel (F) for a single kinesin. At a low concentration of ATP, step iv (ADP release) does not affect the velocity of kinesin (Fig. 1C, blue line). However, at a high concentration of ATP, step iv might be important to maintain the overall velocity of kinesin, because it counteracts the impact from other steps (Fig. 1D, blue line). In the next section, we will discuss the molecular origin of these observations.

Molecular Origin of the Weak Susceptibility of Kinesin Velocity to External Loads.

It is easy to understand why step iii does not introduce a sensitive response of the velocity of a single kinesin to external loading forces. In the absence of forces, the attachment rate constant is 11 μM⁻¹ s⁻¹ (11). For a single head-bound state, the effective MT concentration can be ∼1 mM (11), which leads to an attachment rate of 11,000 s⁻¹. This value is orders of magnitude faster than other steps. As a result, the velocity is much less affected by this step unless the force is sufficiently large to decrease the rate of this step, such that it is comparable with that of other steps. Fig. 1 C and D shows that, only when F > 4 pN (the rate decreases to 264 s⁻¹), this step begins to influence the velocity of kinesin.

For step i, it can be argued that, at high concentrations of ATP, when the ATP binding rate is much faster than the ATP release rate, the weak χ_vel (F) might be caused by the fact that external loading forces largely affect the ATP release rate rather than the ATP binding rate as shown in Fig. 1B. Nevertheless, experiments show that this weak χ_vel (F) exists at both high (2 mM) and low (5 μM) concentrations of ATP (25). It is reasonable to speculate that such a weak χ_vel (F) also comes from structural changes in the kinesin molecule itself.

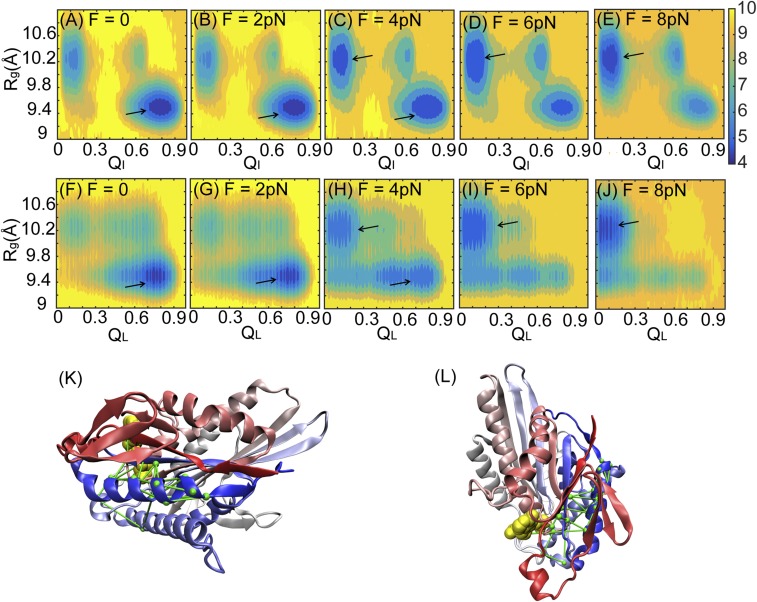
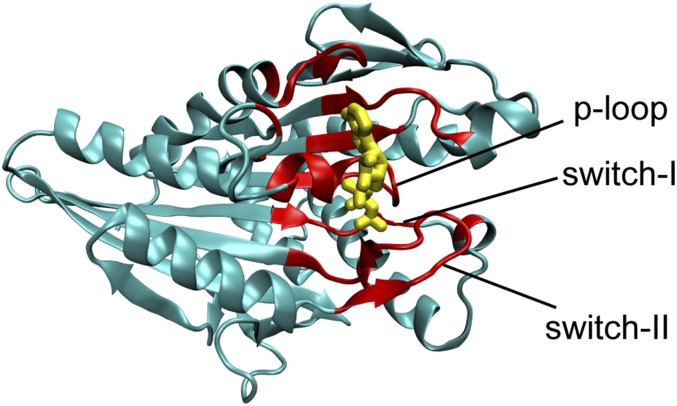
We note that the fraction of native contact formations between ATP and kinesin in its ATP-bound state (Q_I; Q_I ranges from zero to one) is a useful parameter to distinguish key conformations in response to ATP release under forces. Below, we relate the impact of forces exerted on the neck linker at one side of the motor head to the opposite side, where it releases ATP in two steps. First, we plotted a 2D potential of mean force (PMF) as a function of the radius of gyration (R_g) of the ATP binding pocket and Q_I (Fig. 2 A–E). The ATP binding pocket includes kinesin residues within 10 Å of the ATP surface (shown in Fig. S3). At F = 0 pN (Fig. 2A) and F = 2 pN (Fig. 2B), the closed state dominantly populates at R_g = 9.4 Å and Q_I = 0.8. At F = 8 pN, the open state is mostly populated at R_g = 10.2 Å and Q_I = 0.1 (Fig. 2E). The presence of a large force favors a structurally open state of the ATP binding pocket, which weakens the contacts between ATP and the motor head.

Fig. 2.

Conformational changes of a single double-headed kinesin under an external force. (A–E) 2D free energy as a function of the radius of gyration of the ATP binding pocket, R_g, and the fraction of native contact formation between a single kinesin and ATP, Q_I, at loading forces of F = 0, 2, 4, 6, and 8 pN separately. (F–J) 2D free energy as a function of R_g and the fraction of native contact formation between the leading head and the connecting neck linker, Q_L, at loading forces of F = 0, 2, 4, 6, and 8 pN separately. The free energy is colored in units of k_BT at T = 300 K. Black arrows point to the basin of the low free energy from each panel. (K and L) Structure of a motor head and its connecting neck linker with a network of lines from the DCA. The kinesin motor head is colored from red (N terminus) to blue (C terminus) and shown from the front view (K) and the top view (L). ATP is colored in yellow.

Fig. S3.

Illustration of the ATP binding pocket defined in the simulation. The motor head is colored in cyan, and ATP is colored in yellow. The ATP binding pocket is defined as beads within 10 Å around the ATP surface, which are colored in red.

Second, we plotted the PMF as a function of the R_g of the ATP binding pocket and the fraction of native contact formation between the neck linker and motor head, Q_L (ranging from zero to one; Q_L = 1 is when the neck linker completely binds to the motor head). In the absence of loading forces (Fig. 2F), the dominant basin is Q_L = 0.7, and R_g = 9.4 Å (closed state), indicating that the contact formation between the neck linker and the motor head of a single kinesin noncompetitively inhibits the ATP release by favoring the closed state of the motor head. It is in accordance with an experimental study showing that both the neck linker and ATP bind to a motor head (31). This coupling between the neck linker and the ATP binding site was also observed by other research groups (32, 33). In this work, we further identified how this coupling was regulated by external loading forces. At a small force of 2 pN (Fig. 2G), the dominant basin is the same as that at F = 0, indicating that a small force is insufficient to initiate the structural changes that propagate from the neck linker to the ATP binding site. At a large force of 8 pN (Fig. 2J), Q_L peaks at 0.1, and R_g reaches an open state of 10.2 Å that favors the release of ATP, indicating that the detachment of the neck linker from motor head could lead to a switch from the “closed” to the “open” state.

Such structural coupling between the neck linker and the ATP binding pocket prompted us to investigate the allosteric intramolecular network. Direct coupling analysis (34) (DCA), a statistical inference framework used to infer direct coevolutionary couplings among residue pairs in multiple sequence alignments, was applied to probe a network of highly coevolutionary tendencies beginning from the neck linker to the ATP binding site. We identified the network through α6, β1/β6, and switch I/II, as shown by green lines in Fig. 2 K and L. This DCA generalizes the correlated motion that is possibly preserved throughout evolution across the kinesin family.

This intramolecular allostery also exists for the ADP release process, thus explaining the increase in the rate of ADP release, as shown in Fig. S2. In addition, our finding provides a plausible molecular explanation for experimental observations (35), showing that ADP release is controlled by the direction of the loading force. When the direction of the force is opposite to the motion of kinesin, ADP release is favored, because the force disrupts the contact formation between the neck linker and the motor head. When the loading force and kinesin motion are in the same direction, ADP release is hindered, because the attachment of the neck linker to the motor head is favored. Our results seem to disagree with another experimental investigation (36) claiming that external loading forces decrease the rate of ADP release. We noted that the step of ADP release in their kinetic model is equivalent to the combined process of steps iii and iv in our study. Given that the velocity of a kinesin can either decrease in step iii or increase in step iv under external force, it is possible that the velocity decreases under force when both steps iii and iv are considered in our model.

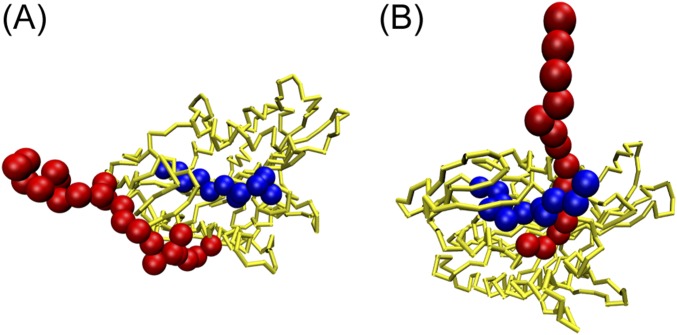
The contact formation between the neck linker and the motor head, which inhibits ATP release, was identified to account for such a weak χ_vel (F) to small forces. However, because the position of a disordered neck linker (36) with respect to the motor head is not known, one may speculate about the robustness of our major result. To test this hypothesis, we placed the disordered neck linker outside the N terminus of the motor head (Fig. S4A). We ran another simulation with a different position of the neck linker by placing it between the N terminus and the main body of a motor head (Fig. S4B), which was the arrangement in a previous computational study (13). We found that, under an external loading force, the structure of the motor head switches from the “closed state” to the “open state,” regardless of the relative position of the disordered neck linker with respect to the motor head. In addition, we calculated the structural differences between the closed and open states for both cases (neck linker is “inside” in Fig. S5A, and neck linker is “outside” in Fig. S5B). The findings in Fig. S5 A and B are very similar (Fig. S5C). Therefore, it can be concluded that our results do not depend on the position of the neck linker.

Fig. S4.

Different relative positions of a disordered neck linker with respect to a motor head. The neck linker is colored in red. The N terminus of the motor head is colored in blue, and the rest part is colored in yellow. (A) In this work, the neck linker was placed outside the N terminus of the motor head. (B) In the prior work (13), the neck linker was modeled between the N terminus and the rest part of the motor head.

Fig. S5.

Difference contact map between the open state (R_g of the ATP binding pocket is 10.2 Å) and the closed state (R_g of the ATP binding pocket is 9.4 Å). (A) The neck linker is between the N terminus and the rest part of the motor head as shown in Fig. S4A, and (B) the neck linker is outside the N terminus of the motor head as shown in Fig. S4B. (C) The difference between A and B. It shows that the differences between A and B are very small.

Geometric Constraints Cause Uneven Force Partitioning Between Two Load-Bearing Kinesins.

We further examined how the weak susceptibility of kinesin velocity to external loads, χ_vel (F), influences the cooperativity of multiple kinesin proteins. The influence was examined by first analyzing the load balancing between two kinesins from coarse-grained molecular simulations (details are in Coarse-Grained Model and Hamiltonian). A previous well-known analytical model on the cooperativity of multiple motors was developed by Lipowsky and coworkers (37, 38). Using a mean-field assumption, it was suggested that every motor protein equally shares the loading force from a cargo, implying that the performance of motors grows with the number of motors. However, this mean-field view was challenged by several recent experiments (22–24), which found that two interacting kinesins produce a force much less than expected for a cooperative team.

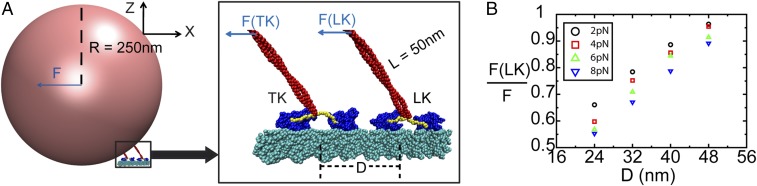
We applied an external force F on the cargo in the −X direction (Fig. 3A) and found that the partitioned force on the leading kinesin under F, F(LK)/F, grows with the separation between the two kinesins, D (Fig. 3B). As the distance D approaches 48 nm, the leading kinesin shoulders almost the entire external loading force, such that the performance of the two kinesins is essentially represented by one kinesin.

Fig. 3.

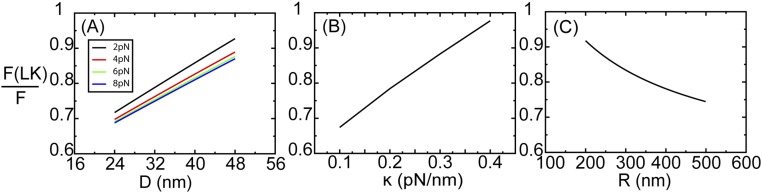
Force partitioning between two load-bearing kinesins. (A) Illustration of two load-bearing kinesins attaching to an MT and jointly carrying a cargo with a radius of 250 nm. The stalk length of each kinesin is 50 nm. The cargo is pulled by an external force in the –X direction. Right is the zoomed structure of two kinesins and the MT. The MT is colored cyan. The cargo is colored pink. The motor heads are colored blue. The neck linkers are colored yellow. The stalks are colored red. The separation between two kinesins is D. The external force F is partitioned between the leading kinesin, F(LK), and the trailing kinesin, F(TK). (B) Result of the force partitioning, F(LK)/F, plotted against D at varying external forces from coarse-grained molecular simulations. This graph shows that the leading kinesin takes the majority of the overall loading forces.

At an external loading force of 8 pN, F(LK)/F reaches 0.9 at D = 48 nm, implying that the leading kinesin takes up to 7.2 pN by itself. This force is close to the experimentally measured detaching force of 6–8 pN for a single kinesin (23). This finding is probably the main reason why the detaching force of two kinesins is similar to that of one kinesin according to recent experimental measurements (23). Our coarse-grained model allows the elastic deformation of a kinesin under external forces. Because of such deformation, F(LK)/F at an external load force of 2 pN is 15% greater than that at an external force of 8 pN (Fig. 3B), indicating that the cooperativity of two kinesins at F = 8 pN is greater than that at F = 2 pN. This finding agrees with the experimental observation that the cooperativity of kinesins grows with loading force (22).

This uneven partitioning of forces on the two kinesins was illustrated by a simple geometric constraint (details are explained in Numerical Calculations on the Force Partitioning of Two Load-Bearing Kinesins). The distance between a cargo and each of the two kinesins was modeled to follow a simple Hook’s law. The leading kinesin is farther from the center of the cargo than the trailing kinesin. Numerically, the outcome that F(LK)/F differs by the loading forces (Fig. S6A) agrees with our simulations (Fig. 3B). F(LK)/F grows with the stiffness of a motor protein (Fig. S6B) and inversely grows with the size of the cargo (Fig. S6C). Both calculations agree with other theoretical investigations of the cooperativity of kinesin motor proteins (24, 39).

Fig. S6.

(A) The numerical calculations of the force partitioning on the LK, F(LK), under several external loading forces, F, as a function of the distance between two kinesins, D. For B and C, F is set to 8 pN, and D is set to 48 nm. We plot F(LK)/F as a function of (B) the stiffness of kinesin, κ, and (C) the radius of the cargo, R.

The Weak Susceptibility of Kinesin Velocity to External Loads Affects the Cooperativity with Another Motor Protein.

Because of the geometrical constraints, the partitioning of forces between two load-bearing motors depends on their separation (D). For example, the leading kinesin shares the most load at D = 48 nm. The two kinesins share a rather balanced load at D = 24 nm, implying better cooperativity than in the former condition (Fig. 3B). Thus, the relative movement between the two motors under an external loading force, which determines their separation, becomes the key factor that dictates the cooperativity between two motors. Before we discuss the cooperation between any two interacting motors, we must quantify the relation of their separation D under external loading forces from the force–velocity profile of a single motor.

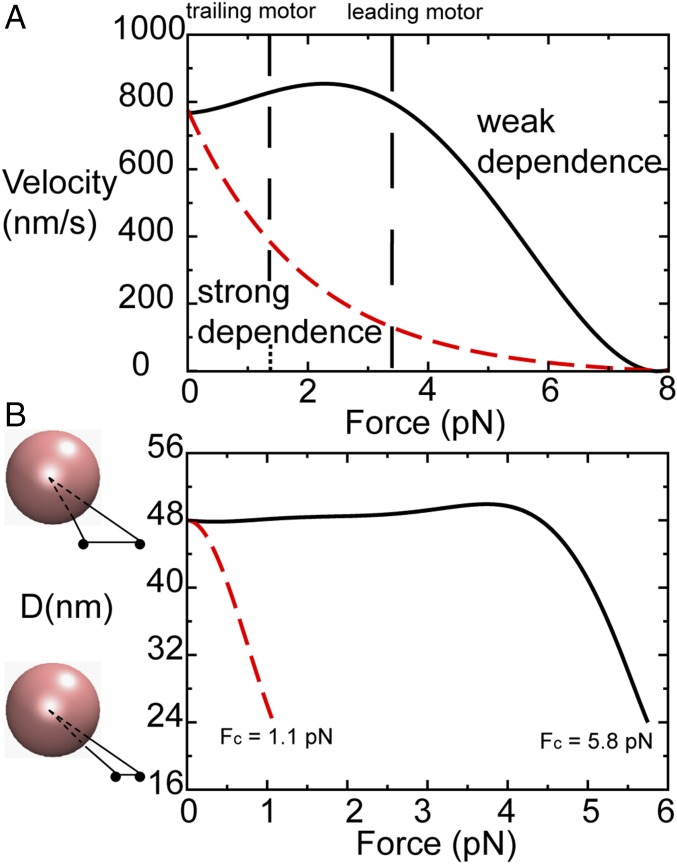
A motor protein’s velocity decreases with external force (25–27) as illustrated in Fig. 4A. There are two types of curves that characterize the gait of a single motor under external forces. For a motor protein with a weak χ_vel (F), such as kinesins, the gait follows the upper curve (black in Fig. 4A), such that the velocity changes slowly at small forces, as shown in experiments (25). In contrast, for other motor proteins with a strong χ_vel (F), such as myosins and dyneins, the velocity sharply diminishes at low external loads (26, 27), following the lower curve (red in Fig. 4A). Because this work only focuses on kinesin, we used the computed force–velocity curve of kinesin (black in Fig. 1D) to represent the weak χ_vel (F) (black in Fig. 4A) and used an illustrative curve to represent the strong χ_vel (F) (red in Fig. 4A).

Fig. 4.

Numerical calculations on the distance between two load-bearing motor proteins as a function of loading force. (A) Two force–velocity relationships for motor proteins. The black solid curve is the numerically calculated force–velocity relationship for a single kinesin, as shown in Fig. 1D. This relationship represents the weak susceptibility of kinesin velocity to external loads. In contrast, the red dashed line shows a strong susceptibility. The vertical dashed lines correspond to the forces and velocities experienced by the leading motor and trailing motor in a two-motor load-sharing system. (B) Distance between two load-bearing motor proteins, D, as a function of the external loading force, F, calculated from the curves in A, with the computing procedure given in Numerical Calculations on the Distance Between Two Load-Bearing Motor Proteins as a Function of Loading Force. F_c denotes the total force on the two interacting kinesins in a triangular configuration when the two are at the smallest separation on an MT, reaching a possibly highest cooperativity. For the black curve (weak susceptibility), F_c is 5.8 pN. For the red curve (strong susceptibility), F_c is 1.1 pN.

Given that each forward step of 8 nm for a motor protein occurs in milliseconds, it is prohibitive for us to perform structure-based molecular dynamic simulations on the head-over-head motion of two motor heads. Thus, we modeled a static optical trap experiment and computed D as a function of F by combining computer simulations and numerical calculations, as shown in Fig. 4B (details of the method are in Numerical Calculations on the Distance Between Two Load-Bearing Motor Proteins as a Function of Loading Force). We denote F_c as the total force on the two interacting kinesins in a triangular configuration when the two are the closest on an MT at D = 24 nm, reaching a possibly highest cooperativity. We showed that, for motor proteins that follow the “upper curve” in the force–velocity relationship (Fig. 4A, black), F_c is 5.8 pN. In contrast, for motor proteins that follow the “lower curve” in the force–velocity relationship (Fig. 4A, red curve), F_c is 1.1 pN. One can ask about the role of F_c for a single motor in the cooperativity between two motors. Since the detachment rate of the motors from the MT increases exponentially with external forces, a high F_c indicates a high probability for the leading motor to detach from the MT before the trailing kinesin catches up with the leading motor; the cooperativity between two motors is low. For the motors that follow the lower curve in the force–velocity profile, their motion is highly cooperative as shown for myosins (40) and dyneins (27) in previous experimental studies.

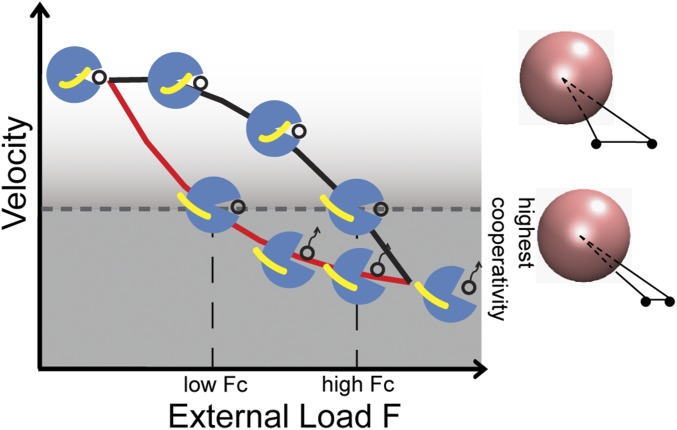
Our model is able to explain the recent experimental observations in the system of two kinesins carrying a cargo that primarily uses one kinesin for transportation (23). From a structural perspective, we provide snapshots of an intramolecular allostery between the neck linker and the ATP binding pocket of a single kinesin mediated by forces that dictates the weak χ_vel (F) to small forces (Fig. 5, black curve). We can test the validity of our predictions by suggesting a structural mutation on the interface between the neck linker and the motor head that would allow a kinesin to follow the lower curve in Fig. 5 (red curve). We would expect an increase in cooperativity between two interacting mutant kinesins.

Fig. 5.

A schematic force–velocity diagram with cartoons showing the spatial arrangement between the neck linker (yellow) and the motor head of a leading kinesin (blue spheres). The black open circles represent ATP. The upper black curve denotes the motion of a WT kinesin with a neck linker that detaches from the motor head at a force close to the stall force. The lower red curve denotes the motion of a kinesin mutant with a neck linker that detaches from the motor head at a force much lower than the stall force. F_c is the total force on the two interacting kinesins in a triangular configuration when the two are at the smallest separation on an MT, reaching a possibly highest cooperativity. Two WT kinesins reach this highest cooperativity at a higher external load than the two mutants.

The biological importance of χ_vel (F) was further manifested in a group of collaborating protein motors. In bidirectional transportation with frequent reversals (41, 42), kinesins and dyneins moving in opposite directions are required to jointly drive a cargo (38, 43). When there are multiple copies of dyneins against multiple copies of kinesins, the odds of winning for dyneins grow when they work in teams. The distinctive gait of a motor protein with varying force–velocity dependence facilitates frequent reversals of the moving direction when they work in teams (41, 42).

Coarse-Grained Model and Hamiltonian

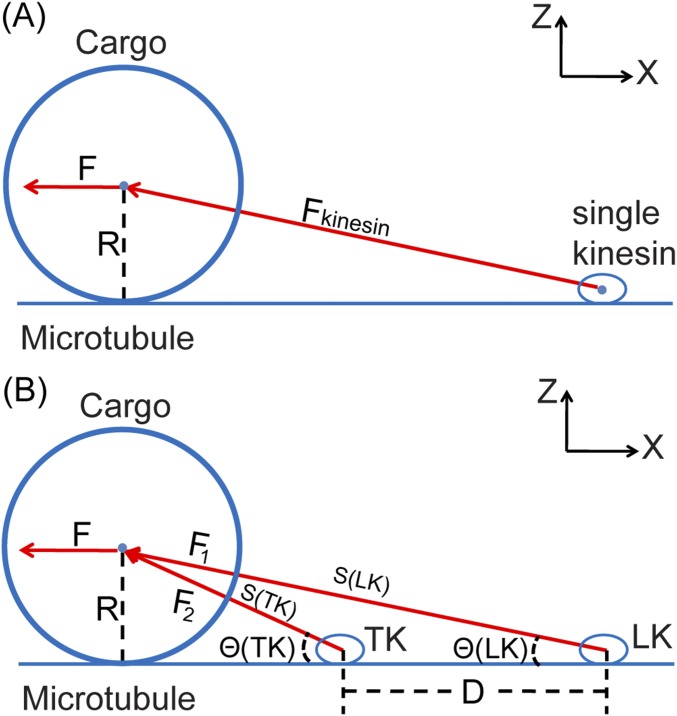
We developed two sets of coarse-grained models: a single load-bearing motor and two load-bearing motors. The system of the singe load-bearing motor includes a 16-nm MT and a single double-headed kinesin that carries a cargo. This kinesin binds to the MT on the surface (as shown in Fig. S7A). The system of the two load-bearing motors includes two 16-nm MTs and two double-headed kinesins that jointly carry a cargo. Each kinesin binds to an MT on the surface. The distance between the center of mass of the two load-bearing motors is D (as shown in Fig. 3A).

Fig. S7.

Illustration of (A) a single load-bearing kinesin that carries a cargo on the MT and (B) an LK and a TK jointly sharing an external load from a cargo on the MT. R is the radius of the cargo. F is the external loading force pointing to the –X direction. For A, F_kinesin is the force exerted by the single kinesin on the center of mass of the cargo. For B, F₁ is the force exerted by the LK on the cargo. F₂ is the force exerted by the TK on the cargo. θ(LK) is the angle between F₁ and F. θ(TK) is the angle between F₂ and F. D is the distance between the two kinesins. S(LK) is the distance between the center of the cargo and the LK. S(TK) is the distance between the center of the cargo and the TK.

To create the initial structure of a double-headed kinesin, first, a single-headed kinesin structure that docks on the MT was taken from the Protein Data Bank (PDB; ID code 3J8Y). This single-headed kinesin contains a motor head (residues 5–322) and part of the neck linker (residues 323–334). However, the rest of the neck linker (residues 335 and 336) and the whole stalk (residues 337–669) are still missing. We then created a double-headed kinesin by aligning the second kinesin in tandem to the first kinesin on the MT. Next, we used other crystal structures available in the PDB to create the complete structure of the neck linker and the stalk. We built the structure of the neck linker and the initial segment of the stalk (residues 323–368) by superposing our model with another ADP-bound kinesin (PDB ID code 3KIN).We built the rest of the 50-nm stalk that is a coiled coil dimer from the dimerization domain of cortexillin I (PDB ID code 1D7M) by following the procedure developed by Zhang and Thirumalai (45). Each coil extends from residue 369 to residue 669.

We used the SMOG server (46) to generate the Cα only model (44) for kinesins and the MT. The cargo that connects to the kinesin was represented by a hard sphere with a radius of 250 nm. This size matches with the sampling preparation in the experiment from Diehl and coworkers (23) that used a small segment of elastin to connect the stalk and cargo. In our coarse-grained model, the elastin was simplified to one bead. The interaction between this bead and the last bead of the stalk of kinesin satisfies the worm-like chain model that is parameterized from the experiments (23) to reproduce the elasticity of the system.

The Hamiltonian of the system follows the model developed by Zhang and Thirumalai (45) with several extensive modifications to fit the experiment (23) (see below). The structure of the MT was spatially fixed, but the rest of the system was not. The Hamiltonian of the system is

$$H=V_{bond}+V_{DH}+V_{optical}+V_{elastin}+V_{nb}.$$

V_bond is the bonding energy represented by a finite extensible nonlinear elastic (FENE) potential from the abovementioned work (45):

$$V_{bond}={\displaystyle \sum _{i,j}k\times R^2\times \log \left(1-\frac{{\left(r_{ij}-{r_{ij}}^0\right)}^2}{R^2}\right)}.$$

The spring constant k was set to $3.75\times {10}^4$ kJ/mol per nanometer². The finite extensibility b was set to 0.2 nm; r_ij is the distance between two adjacent beads i and j within the kinesin. FENE potential also exists between the elastin bead and the cargo bead.

V_DH represents the electrostatic interactions between any two charged beads within kinesin as well as those between kinesins and MT. Its form also followed the above mentioned work (45):

$$V_{DH}={\displaystyle \sum _{i,j}\frac{q_i{q}_j}{4\pi \epsilon {\epsilon }_0{r}_{ij}}{e}^{-\kappa r_{ij}}}.$$

In the equation, r_ij is the distance between two charged beads i and j. There are four types of charged amino acids: Arg $\Rightarrow$ +1e, Lys $\Rightarrow$ +1e, Glu $\Rightarrow$ −1e, and Asp $\Rightarrow$ −1e. The relative dielectric constant ε was set to 80 to mimic the aqueous environment. The debye length κ⁻¹ was set to 1 nm (corresponding to anionic strength of 0.1 M).

V_optical mimics the confining effect on the cargo from the optical tweezers. Our V_optical differs from the previous work (45) by placing the potential in the X and Y directions according to the experimental setup (23). V_optical was modeled as

$$V_{optical}=k_x{\left(x-x_0\right)}^2+k_y{\left(y-y_0\right)}^2.$$

In the equation, x and y are the coordinates of the cargo in the X and Y directions. In our system, the X direction is along the main axis of MT, and the Z direction is normal to the surface (Fig. S7). The spring constants, k_x and k_y, were set to 0.039 kJ/mol per nanometer²; x₀ and y₀ are the coordinates of the center of the optical trap. In the simulation, y₀ is the projection of the center of mass of MT in the Y direction. To mimic an experimental procedure (23), we modified x₀ to change the magnitude of the external loads.

V_elastin represents the interaction between the elastin bead and last bead of the stalk of kinesin (23). V_elastin was represented by

$$V_{elastin}=\frac{k_{B}T}{P}\left[\frac{r^2}{2L}-\frac{r}{4}-\frac{L^2}{4\left(r-L\right)}-\frac{r^3}{4L^2}\right].$$

Its derived force F_elastin was represented by a widely known worm-like chain model formula (51):

$$F_{elastin}=-\frac{d{V}_{elastin}}{dr}=-\frac{k_{B}T}{P}\left[0.25{\left(1-\frac{r}{L}\right)}^{-2}-0.25+\frac{r}{L}-0.75{\left(\frac{r}{L}\right)}^2\right].$$

In the equation, r is the distance between the elastin bead and the last bead of the stalk of kinesin. The persistent length P was set to 0.1 nm, and contour length L was set to 115 nm. These parameters were fitted, so that the elasticity of the system could match with the experiment (23). For the system having two load-bearing kinesins, the distance between the elastin bead connecting to the leading kinesin (LK) and that connecting to the trailing kinesin (TK) was constrained to 50 nm by a harmonic potential with the spring constant $3.75\times {10}^4$ kJ/mol per nanometer² to match with the experiment (23).

V_nb represents the nonpeptide bond interactions for any two beads i and j $\left(\left|i-j\right|>2\right)$ within two kinesins: those between kinesins and MT and those between a single kinesin and ATP (ADP). We modified three chemical states of kinesins by varying V_nb to represent the ATP-bound (PDB ID code 3J8Y, a cryo-EM structure), the ADP-bound (PDB ID code 3KIN, a crystal structure), and the φ state without any nucleotide (PDB ID code 3J8X, a cryo-EM structure).

We developed V_nb to investigate the force partitioning between the two load-bearing kinesins in Force Partitioning Between Two Load-Bearing Kinesins. Next, we modified V_nb to investigate the binding of ATP (ADP) for a single load-bearing kinesin in ATP Binding for a Single Load-Bearing Kinesin and ADP Release for a Single Load-Bearing Kinesin by adopting a dual basin structure-based (SB) model. This dual basin SB model was only applied to the motor head of a kinesin that allowed the sampling of the ATP-bound (ADP-bound) state and the φ state.

Force Partitioning Between Two Load-Bearing Kinesins.

We used a single-basin SB model for this scenario. The leading heads (LHs) of each kinesin are in the φ state. The trailing heads (THs) of each kinesin are in the ATP-bound state. Both kinesins tightly bind to the MT by making the same number of physical contacts. For each kinesin, the contacts between the LH and MT or between the TH and MT were taken from different crystal structures (PDB ID codes 3J8X and 3J8Y):

$$V_{nb}={\displaystyle \sum _{i,j}\epsilon \left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{\epsilon }{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\hspace{0.17em}{\mathrm{\Delta }}_{ij}+{\displaystyle \sum _{i,j}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}\right)}.$$

${\mathrm{\Delta }}_{ij}$ is a notation to distinguish the native and the nonnative contacts. The definition of a native contact formation followed a previous study (52), where the cutoff was set to 1.0 nm. If $i,j\in LH$ in the φ state (3J8X), then ${\mathrm{\Delta }}_{ij}=1$ when residues i and j form a native contact; otherwise, ${\mathrm{\Delta }}_{ij}=0$. If $i,j\in TH$ in the ATP-bound state (3J8Y), then ${\mathrm{\Delta }}_{ij}=1$ when residues i and j form a native contact; otherwise, ${\mathrm{\Delta }}_{ij}=0$.

The SD of a Gaussian function, σ, was set to 0.03 nm. The van der Waals radius of a bead, σ_rep, was set to 0.38 nm. The solvent-mediated interaction, ε, was set to 1.875 kJ/mol. The coefficient to scale the repulsion between nonnative contacts, ε_rep, was set to 1.875 kJ/mol as well.

ATP Binding for a Single Load-Bearing Kinesin.

This scenario refers to step i in the chemomechanical cycle (Fig. 1A). We used a single-basin SB model to represent the system with the exception of LH. For LH, we used a dual basin SB model to sample both the φ state (3J8X) and the ATP-bound state (3J8Y), where LH tightly bound to the MT by making the same number of physical contacts found in each corresponding crystal structures. We used a single-basin SB model to represent the ADP-bound state of TH that detached from the MT. For ATP, we used a similar model from previous coarse-grained simulations on proteins with ligands (53, 54) by representing each heavy atom of ATP as one bead. Any bond between two ATP beads was constrained by a strong harmonic potential with the spring constant $3.75\times {10}^4$ kJ/mol per nanometer².

For TH, V_nb with a single-basin SB model is

$$V_{nb}={\displaystyle \sum _{i,j\in kine\sin }\epsilon \left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{\epsilon }{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\hspace{0.17em}{\mathrm{\Delta }}_{ij}+{\displaystyle \sum _{i,j\in kine\sin }{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}\right)}.$$

${\mathrm{\Delta }}_{ij}=1$ if residues i and j form a native contact in the ADP-bound structure (3KIN); otherwise, ${\mathrm{\Delta }}_{ij}=0$.

For LH, V_nb with a dual basin SB model is

$$\begin{array}{l}{V}_{nb}={\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}{\epsilon }_1\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_1}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}\cdot \left(1-{\mathrm{\Delta }}_{ij}^{\prime }\right)\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}{\epsilon }_2\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_2}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}^{\prime }\cdot \left(1-{\mathrm{\Delta }}_{ij}\right)\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}\epsilon \left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^{0\prime }\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{\epsilon }{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}\cdot {\mathrm{\Delta }}_{ij}^{\prime }\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}\right)}\cdot \left(1-{\mathrm{\Delta }}_{ij}^{\prime }\right)\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in ATP\end{array}}{\epsilon }_{ATP}\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_{ATP}}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}{\mathrm{\Delta }}_{ij}^{″}\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in ATP\end{array}}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}^{″}\right)}.\end{array}$$

${\mathrm{\Delta }}_{ij}$, ${\mathrm{\Delta }}_{ij}^{\prime }$, and ${\mathrm{\Delta }}_{ij}^{″}$ are notations to distinguish the native and nonnative contacts as follows. ${\mathrm{\Delta }}_{ij}=1$ if residues i and j form a native contact in the φ state (3J8X); otherwise, ${\mathrm{\Delta }}_{ij}=0$. ${\mathrm{\Delta }}_{ij}^{\prime }=1$ if residues i and j form a native contact within the kinesin or between the kinesin and MT in the ATP-bound state (3J8Y); otherwise ${\mathrm{\Delta }}_{ij}^{\prime }=0$. ${\mathrm{\Delta }}_{ij}^{″}=1$ if residues i and j form an interfacial native contact between the kinesin and ATP in the ATP-bound state (3J8Y); otherwise, ${\mathrm{\Delta }}_{ij}^{″}=0$.

ε₁ represents the solvent-mediated interactions of the native contacts in the φ state (3J8X) but not in the ATP-bound state (3J8Y; i.e., ${\mathrm{\Delta }}_{ij}=1$, ${\mathrm{\Delta }}_{ij}^{\prime }=0$). ε₂ represents the solvent-mediated interactions of the native contacts within the kinesin or between the kinesin and MT in the ATP-bound state but not in the φ state (i.e., ${\mathrm{\Delta }}_{ij}=0$, ${\mathrm{\Delta }}_{ij}^{\prime }=1$). ε represents the solvent-mediated interactions of the native contacts in both the φ state and ATP-bound state (i.e., ${\mathrm{\Delta }}_{ij}=1$, ${\mathrm{\Delta }}_{ij}^{\prime }=1$). The coefficient to scale the repulsion between nonnative contacts, ε_rep, can be found in Calculating the Free Energy of the Binding Between ATP (ADP) and the LH of a Single Load-Bearing Kinesin. ε_ATP represents the solvent-mediated interactions of the native contacts between the kinesin and ATP molecule in the ATP-bound state (i.e., ${\mathrm{\Delta }}_{ij}^{″}=1$). ε₁ = 1.0ε, ε₂ = 0.54ε, and ε_ATP = 0.12ε.

ADP Release for a Single Load-Bearing Kinesin.

This scenario refers to steps iii and iv in the chemomechanical cycle (Fig. 1A). We used a single-basin SB model to represent the system of a single load-bearing kinesin with the exception of LH. For LH, we used a dual basin SB model to sample both the φ state (3J8X) and ADP-bound state (3KIN). LH binds to MT by making the same number of physical contacts found in the φ state. For TH, we used a single-basin SB model for representing the ATP-bound state that binds to MT by making the same number of physical contacts found in the ATP-bound structure (3J8Y). Each heavy atom of ADP was modeled as a single bead. Any bond between two ADP beads was constrained by a strong harmonic potential with the spring constant $3.75\times {10}^4$ kJ/mol per nanometer².

For TH, V_nb with a single-basin SB model is

$$V_{nb}={\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}\epsilon \left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{\epsilon }{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}{\mathrm{\Delta }}_{ij}+{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}\right)}.$$

${\mathrm{\Delta }}_{ij}=1$ if residues i and j form a native contact in the ATP-bound state (3J8Y); otherwise, ${\mathrm{\Delta }}_{ij}=0$.

For LH, V_nb with a dual basin SB model is

$$\begin{array}{l}{V}_{nb}={\displaystyle \sum _{i,j\in kine\sin }{\epsilon }_1\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_1}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}\cdot \left(1-{\mathrm{\Delta }}_{ij}^{\prime }\right)\\ +{\displaystyle \sum _{i,j\in kine\sin }{\epsilon }_2\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_2}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}^{\prime }\cdot \left(1-{\mathrm{\Delta }}_{ij}\right)\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in MT\end{array}}{\epsilon }_M\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_M}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}^{\prime }\cdot \left(1-{\mathrm{\Delta }}_{ij}\right)\\ +{\displaystyle \sum _{i,j\in kine\sin }\epsilon \left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^{0\text{'}}\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{\epsilon }{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}\cdot {\mathrm{\Delta }}_{ij}\cdot {\mathrm{\Delta }}_{ij}^{\prime }\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in kine\sin ,MT\end{array}}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}\right)}\cdot \left(1-{\mathrm{\Delta }}_{ij}^{\prime }\right)\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in ADP\end{array}}{\epsilon }_{ADP}\left[\left(1-e^{-\frac{{\left(r_{ij}-r_{ij}^0\right)}^2}{2{\sigma }^2}}\right)\times \left(1+\frac{1}{{\epsilon }_{ADP}}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\right)-1\right]}{\mathrm{\Delta }}_{ij}^{″}\\ +{\displaystyle \sum _{\begin{array}{l}i\in kine\sin \\ j\in ADP\end{array}}{\epsilon }_{rep}{\left(\frac{{\sigma }_{rep}}{r_{ij}}\right)}^{12}\left(1-{\mathrm{\Delta }}_{ij}^{″}\right)}.\end{array}$$

${\mathrm{\Delta }}_{ij}$, ${\mathrm{\Delta }}_{ij}^{\prime }$, and ${\mathrm{\Delta }}_{ij}^{″}$ are notations to distinguish the native and nonnative contacts as follows. ${\mathrm{\Delta }}_{ij}=1$ if residues i and j form a native contact within the kinesin in the ADP-bound state (3KIN); otherwise, ${\mathrm{\Delta }}_{ij}=0$. ${\mathrm{\Delta }}_{ij}^{\prime }=1$ if residues i and j form a native contact in the φ state (3J8X); otherwise, ${\mathrm{\Delta }}_{ij}^{\prime }=0$. ${\mathrm{\Delta }}_{ij}^{″}=1$ if residues i and j form an interfacial native contact between the kinesin and ADP in the ADP-bound state (3KIN); otherwise, ${\mathrm{\Delta }}_{ij}^{″}=0$.

ε₁ represents the solvent-mediated interactions of the native contacts within the kinesin in the ADP-bound state (3KIN) but not in the φ state (3J8X; i.e., ${\mathrm{\Delta }}_{ij}=1$, ${\mathrm{\Delta }}_{ij}^{\prime }=0$). ε₂ represents the solvent-mediated interactions of the native contacts within the kinesin in the φ state but not in the ADP-bound state (i.e., ${\mathrm{\Delta }}_{ij}=0$, ${\mathrm{\Delta }}_{ij}^{\prime }=1$). ε_M represents the solvent-mediated interactions of the native contacts between the kinesin and MT in the φ state (i.e., ${\mathrm{\Delta }}_{ij}=0$, ${\mathrm{\Delta }}_{ij}^{\prime }=1$). ε represents the solvent-mediated interactions of the native contacts within the kinesin in both the φ state and ADP-bound state (i.e., ${\mathrm{\Delta }}_{ij}=1$, ${\mathrm{\Delta }}_{ij}^{\prime }=1$). ε_rep can be found in Calculating the Free Energy of the Binding Between ATP (ADP) and the LH of a Single Load-Bearing Kinesin. ε_ADP represents the solvent-mediated interactions of the native contacts between the kinesin and ADP molecule in the ADP-bound state (i.e., ${\mathrm{\Delta }}_{ij}^{″}=1$). ε₁ = 0.92ε, ε₂ = 1.0ε, ε_M = 0.5ε, and ε_ADP = 0.16ε.

Michaelis–Menten Representation of the Kinesin Cycle

We assumed that there is a strong coupling between ATP turnover rate of kinesin and kinesin stepping on an MT. Each chemical step in the chemomechanical cycle of kinesin was assumed to be irreversible, except ATP binding and releasing (Fig. 1, step i). Consider the following scheme:

$$0\begin{array}{c}{k}_{ATP}\left[S\right]\\ \leftrightarrow \\ k_{-ATP}\end{array}1\stackrel{k_s}{\to }2\stackrel{k_{attach}}{\to }3\stackrel{k_{ADP}}{\to }4\stackrel{k_h}{\to }5\stackrel{k_{-P}}{\to }6.$$

Assume that F_i(t) is the probability for the system to reach state 6 if, at time t = 0, the system is in state i. This function is governed by the backward master equations:

$$\frac{d{F}_0\left(t\right)}{dt}=k_{ATP}\left[S\right]F_1\left(t\right)-k_{ATP}\left[S\right]F_0\left(t\right)$$ [S1]

$$\frac{d{F}_1\left(t\right)}{dt}=k_s{F}_2\left(t\right)+k_{-ATP}{F}_0\left(t\right)-\left(k_s+k_{-ATP}\right)F_1\left(t\right)$$ [S2]

$$\frac{d{F}_2\left(t\right)}{dt}=k_{attach}\left(F_3\left(t\right)-F_2\left(t\right)\right)$$ [S3]

$$\frac{d{F}_3\left(t\right)}{dt}=k_{ADP}\left(F_4\left(t\right)-F_3\left(t\right)\right)$$ [S4]

$$\frac{d{F}_4\left(t\right)}{dt}=k_h\left(F_5\left(t\right)-F_4\left(t\right)\right)$$ [S5]

$$\frac{d{F}_5\left(t\right)}{dt}=k_{-P}\left(F_6\left(t\right)-F_5\left(t\right)\right)$$ [S6]

$$F_6\left(t\right)=\delta \left(t\right).$$ [S7]

We further defined

$$\stackrel{\sim }{F_i\left(s\right)}={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}{F}_i\left(t\right)dt}.$$ [S8]

Then, the mean first passage time from state 0 to state 6 is

$$\tau ={\displaystyle \underset{0}{\overset{\infty }{\int }}t{F}_0\left(t\right)dt}=-{\stackrel{\sim }{\frac{d{F}_i\left(s\right)}{ds}}|}_{s=0}.$$ [S9]

The rate is

$$k=\frac{1}{\tau }.$$ [S10]

The velocity of kinesin $V=k\cdot \delta$, while $\delta$ is the step size of kinesin: 8 nm. This expression of V (Eqs. 1–3) was derived by solving Eqs. S1–S10.

Calculate the Force–Velocity Curve from Simulation Data

For each step in the chemomechanical cycle of single kinesin, we first obtained the free energy landscape under various loading forces through coarse-grained simulations. Next, we calculated the rate using the following equations:

$$k\left(F\right)={\left({\displaystyle \underset{X_0}{\overset{X_1}{\int }}dX{\displaystyle \underset{0}{\overset{X}{\int }}\frac{dX\prime e^{\lambda \frac{G\left(X,F\right)-G\left(X\prime ,F\right)}{k_{B}T}}}{D\left(X\right)}}}\right)}^{-1}$$

$$D\left(X\right)=\frac{1}{2}\frac{d\langle X^2\rangle }{dt}.$$

X is the reaction coordinate. D is the diffusion coefficient along the reaction coordinate, which in our case, can be calculated by the Stokes–Einstein relationship. G is the calculated free energy (Fig. 1B and Figs. S1 and S2). In the absence of forces, the activation barrier computed from the simulations, ∆G^‡, is 15 k_BT for ATP release (step i), 0.5 k_BT for attachment (step iii), and 8 k_BT for ADP release (step iv). Although our SB coarse-grained model is able to get the appropriate qualitative behavior for each chemical step in the chemomechanical cycle of kinesin, it is well-known that the homogenous SB model used in our work quantitatively underestimates activation barriers and the roughness in the free energy landscape. Thus, the computed rates are always faster than the experimental values. To resolve this issue, we chose to apply an empirical scaling factor λ on the free energy measured in simulation (G → λ·G), so that the computed rate matches with the experimental value at zero force. With a force at 2, 4, 6, or 8 pN, we kept these determined λ values unchanged. Without this correction to the barrier, we cannot get the force–velocity curve observed in previous experiments. The computed velocity of kinesin in the presence of a force was determined by the following equations:

$$V\left(F\right)=\delta \frac{k_{cat}^{eff}\left(F\right)\left[S\right]}{K_M^{eff}\left(F\right)+\left[S\right]}$$

$$k_{cat}^{eff}\left(F\right)={\left(\frac{1}{k_s}+\frac{1}{k_{attach}\left(F\right)}+\frac{1}{k_{-ADP}\left(F\right)}+\frac{1}{k_h}+\frac{1}{k_{-p}}\right)}^{-1}$$

$$K_M^{eff}\left(F\right)=\frac{k_{cat}^{eff}\left(F\right)}{k_{step}}\left(\frac{k_s+k_{-ATP}\left(F\right)}{k_{+ATP}}\right).$$

k_ATP, k_−ATP, k_s, k_attach, k_−ADP, k_h, and k_−p are the rates of chemical reaction in Fig. 1A. [S] is the concentration of ATP. δ is the step size: 8 nm. For our analytical calculations, k_s = 10,000/s, k_ATP = 2/μM per second, and k_h⁻¹ + k_−p⁻¹ = 150⁻¹ (55).

The free energies after the scaling (λ·G) are in the same order of magnitude as the free energies before scaling (G). Our model allowed us to comprehensively analyze the dynamics in the system with external loading forces. Our method was also validated by two observations: (i) the experimentally observed weak susceptibility of single kinesins is reproduced in our model, and (ii) our calculations produce the same stall force as in experiments.

Numerical Calculations on the Force Partitioning of Two Load-Bearing Kinesins

We qualitatively explained the uneven force partitioning of two load-bearing kinesins by arguing the geometrical arrangement of an LK and a TK. We provided a simplified illustration in Fig. S7B. R of 250 nm is the radius of the cargo. F is the external loading force pointing to the –X direction. D is the distance between two kinesins. F₁ is the force exerted by LK on the cargo along a stiff stalk. F₂ is the force exerted by TK on the cargo along a stiff stalk. θ(LK) is the angle between F₁ and F. θ(TK) is the angle between F₂ and F.

The distance between the center of cargo and LK, X_L, satisfies

$$X_L=\frac{R}{\sin \theta \left(LK\right)}.$$ [S11]

LK can be modeled as an elastic spring with the stiffness of κ and the equilibrium length of l_1. Then, the force exerted by the LK is

$$F_1=\mathrm{\kappa }\times \left(\frac{R}{\sin \theta \left(LK\right)-l_1-R}\right).$$ [S12]

Similarly, the force exerted by the TK is

$$F_2=\mathrm{\kappa }\times \left(\frac{R}{\sin \theta \left(TK\right)-l_2-R}\right).$$ [S13]

The geometrical arrangement of the system requires

$$R\times \left(\cot \theta \left(LK\right)-\cot \theta \left(TK\right)\right)=D.$$ [S14]

The system is pulled by an external loading force F pointing to the –X direction. F(LK) and F(TK) are the projections of F₁ and F₂ in the X direction for LK and TK, respectively. Therefore, the balance of forces requires

$$F\left(LK\right)=F_1\cos \theta \left(LK\right)$$ [S15]

$$F\left(TK\right)=F_2\cos \theta \left(TK\right)$$ [S16]

$$F=F\left(LK\right)+F\left(TK\right).$$ [S17]

For any given D and F, we numerically solved the values of F(TK) and F(LK) with Eqs. S12–S17. The choice of the constants l₁, l₂, and κ will not affect the result qualitatively. The numerical solution is shown in Fig. S6A.

Numerical Calculations on the Distance Between Two Load-Bearing Motor Proteins as a Function of Loading Force

We modeled the motion of two load-bearing motor proteins in a static optical trapping experiment by gradually increasing the external loading force on the cargo, F, from zero. The distance between two motor proteins, D, is shown in Fig. S7B. We set the D to be 48 nm in our investigation as the initial value for the numerical analysis.

The force partitioned on the leading motor in the X direction (the direction of the main axis of MT) as F(LK) and that on the trailing motor as F(TK). Because of the geometrical constraint, the uneven force partitioning, F(LK) and F(TK), is represented by

$$F\left(LK\right)=\gamma \times F$$ [S18]

$$F\left(TK\right)=\left(1-\gamma \right)\times F.$$ [S19]

γ is the force partitioning on the leading motor. We obtained γ by fitting F(LK)/F in Fig. 3B as a function of D and F using an empirical expression with the correlation coefficient, R = 0.993:

$$\gamma =0.0135\times D+0.339-\left(F-2\right)\times 0.0175.$$ [S20]

We then obtained F(LK) and F(TK) in Eqs. S18 and S19 using γ in Eq. S20. Next, using the force–velocity relationship of the trailing and leading motors from Fig. 4A, we derived the expressions of the velocity of the TK, V(TK), and the velocity of the LK, V(LK), as a function of F.

We modeled a stepwise increment of the external loading force over time by assuming that F, V(TK), and V(LK) remain unchanged during a time interval τ. The stepwise increment of force is ΔF of 0.001 pN. We computed τ from a simple relation between the displacement and the velocity by satisfying the equation below:

$$\tau =\frac{X\left(F+\mathrm{\Delta }F\right)}{V\left(F+\mathrm{\Delta }F\right)}-\frac{X\left(F\right)}{V\left(F\right)}.$$ [S21]

X(F) or X(F + ΔF) was the displacement of the cargo as a function of the loading force F or F + ΔF, respectively. V(F) or V(F + ΔF) was the velocity of the cargo as a function of the loading force F or F + ΔF, respectively, which was derived from the force–velocity relationship in Fig. 4A.

The difference in V(TK) and V(LK) [V(TK) > V(LK)] at a given F during the time interval τ provided the updated distance of D′ from D:

$$D\prime =D-\tau \times \left(V\left(TK\right)-V\left(LK\right)\right).$$ [S22]

As a result, D as a function of F was numerically computed using Eqs. S18–S22.

Conclusion

We delineate the weak susceptibility of kinesin velocity to external loads by showing that only under large loading forces can the motor head release ATP at a fast rate; thus, the velocity of kinesin significantly reduces. The molecular origin of the weak susceptibility is the intramolecular coupling between the neck linker and ATP binding site of kinesin, which only activates under large forces. This coupling is preserved by a network of coevolving amino acids that form α6, β1/β6, and switch I/II within the motor head. For two load-bearing kinesins, the leading kinesin takes more than 90% of an overall load when their separation is larger than 48 nm. Because of the weak susceptibility, it is unfavorable for the trailing kinesin to catch up with the leading one, contributing a low cooperativity between two kinesins.

Methods

We used the C_α-only structure-based model (44) to represent two sets of coarse-grained models, a single load-bearing motor and two load-bearing motors. The system of the singe load-bearing motor includes a 16-nm MT and a single double-headed kinesin that carries a cargo. This kinesin binds to the MT on the surface (as shown in Fig. S7A). The system of the two load-bearing motors includes two 16-nm MTs and two double-headed kinesins that jointly carry a cargo. Each kinesin binds to an MT on the surface (as shown in Fig. 3A). The Hamiltonian of the system follows a previous work (45) with several modifications. The details of the Hamiltonian can be found in Coarse-Grained Model and Hamiltonian. The model was created by using the web server SMOG (46).

We used the Langevin equations of motion for the coarse-grained molecular simulations. An in-house version of Gromacs4.5 (47, 48) was developed, where the nonbonded interactions were represented by a Gaussian formula. The Langevin equations of motion were integrated in the low friction limit with a damping coefficient of 1.0 ${{\tau }_L}^{-1}$ (49). The integration time step is ${10}^{-3}{\tau }_L$, where ${\tau }_L={\left(m{\sigma }^2/\epsilon \right)}^{0.5}$; m is the mass of a C_α bead, ε is the solvent-mediated interaction, and σ is the van der Waals radius of a C_α bead. We collected over 50,000 statistically significant conformations for data convergence. Thermodynamic properties and errors from the samples were computed with the weighted histogram analysis method (50).

Calculating the Free Energy of the Binding Between ATP (ADP) and the LH of a Single Load-Bearing Kinesin

The umbrella sampling method was used for obtaining the free energy profile of the binding between ATP and LH of a single load-bearing kinesin. The reaction coordinate was chosen to be the distance between the center of mass of ATP and that of the LH of kinesin, $d_{kin-ATP}^{COM}$. The bin size is 0.05 nm for $d_{kin-ATP}^{COM}$ ranging from 1.3 to 1.7 nm, and it is 0.1 nm for $d_{kin-ATP}^{COM}$ ranging from 1.7 to 9.0 nm. The spring constant for the harmonic potential used in the umbrella sampling method was set to $2.0\times {10}^4$ kJ/mol per nanometer².

This method was also used to obtain the free energy profile of ADP release from LH of a single load-bearing kinesin. There are two steps for ADP release, shown by steps iii and iv in Fig. 1A. In step iii, the reaction coordinate, H, was chosen to be the distance between the center of mass of LH and that of the MT in the Z direction, ranging from 3.5 to 5.0 nm. We set the bin size to 0.1 nm. In step iv, the reaction coordinate was chosen to be the distance between the center of mass of ADP molecule and that of LH of kinesin, $d_{kin-ADP}^{COM}$, ranging from 1.4 to 1.7 nm with a bin size of 0.05 nm.