Significance
Water is vital to our everyday life, but its structure at a molecular level is still not fully understood from either experiment or theory. The latter is hampered by our inability to construct a purely predictive, first principles model. The difficulty in modeling water lies in capturing the delicate interplay among the many strong and weak forces that govern its behavior and phase diagram. Herein, molecular simulations with a recently proposed nonempirical quantum mechanical approach (the SCAN density functional) yield an excellent description of the structural, electronic, and dynamic properties of liquid water. SCAN (strongly constrained and appropriately normed)-based approaches, which describe diverse types of bonds in materials on an equal, accurate footing, will likely enable efficient and reliable modeling of aqueous phase chemistry.
Keywords: water, ab initio theory, hydrogen bonding, density functional theory, molecular dynamics
Abstract
Water is of the utmost importance for life and technology. However, a genuinely predictive ab initio model of water has eluded scientists. We demonstrate that a fully ab initio approach, relying on the strongly constrained and appropriately normed (SCAN) density functional, provides such a description of water. SCAN accurately describes the balance among covalent bonds, hydrogen bonds, and van der Waals interactions that dictates the structure and dynamics of liquid water. Notably, SCAN captures the density difference between water and ice Ih at ambient conditions, as well as many important structural, electronic, and dynamic properties of liquid water. These successful predictions of the versatile SCAN functional open the gates to study complex processes in aqueous phase chemistry and the interactions of water with other materials in an efficient, accurate, and predictive, ab initio manner.
Water is arguably the most important molecule for life and is involved in almost all biological processes. Without water, life, as we know it, would not exist, earning water the pseudonym “matrix of life,” among others (1). Despite the apparent simplicity of an O molecule, water in the condensed phase displays a variety of anomalous properties that originate from its complex structure. In an ideal arrangement, water molecules form a tetrahedral network of hydrogen (H) bonds with each vertex being occupied by a water molecule. This tetrahedral network is realized in the solid phase ice Ih, but thermal fluctuations disrupt the H-bond network in the liquid state, with the network fluctuating on picosecond to nanosecond timescales. Due to the complexity of the H-bond network and its competition with thermal fluctuations, a precise molecular-level understanding of the structure of liquid water remains elusive. Major challenges lie in unambiguously capturing the atomic-scale fluctuations in water experimentally. Current approaches such as time-resolved spectroscopy (2, 3) and diffraction measurements (4, 5) may be able to resolve changes on picosecond timescales but rely on interpretation through models, which often cannot describe all of the details of liquid water with quantitative accuracy. Not surprisingly, the nature of the H-bond network in liquid water continues to be at the center of scientific debate, and advances in both experiment and theory are needed, especially with regard to quantitative modeling of aqueous phase chemistry.
Ab initio molecular dynamics (AIMD) simulation (6) is an ideal approach for modeling the condensed phases of water across the phase diagram and aqueous phase chemistry using quantum mechanical principles (7–11), although for some applications, such as the study of liquid vapor phase equilibria (12), Monte Carlo methods are better suited. In particular, Kohn-Sham density functional theory (DFT) (13)—used to model the system in its electronic ground state—provides an efficient framework that enables the simulation of the length and timescales needed to converge many statistical mechanical averages in disordered, liquid state systems. The DFT formalism is exact for the electronic ground-state energy and density, but in practice approximations must be adopted to describe many-body effects, included in the exchange-correlation (XC) functional. XC functionals can be conceptually arranged, by accuracy and computational efficiency, according to Jacob’s ladder (14), with the simplest local density approximation (LDA) (15, 16) on the bottom rung of the ladder, followed by generalized gradient approximations (GGAs) (17–19), meta-GGAs, hybrid functionals (20, 21), and so on.
The past three decades have witnessed widespread successes of DFT in elucidating and predicting properties of materials. However, water still presents a major challenge, with many DFT-based simulations yielding results that are not even qualitatively consistent with experimental measurements. The H-bonds formed between gas-phase water clusters were first treated within the LDA (22, 23), which overestimates H-bond strengths and yields interwater distances that are too close. This overbinding is largely corrected by GGA-level functionals, which became a class of popular functionals to study liquid water within the last two decades (10). Despite the improvements over LDA that are provided by GGAs, H-bond strengths are overestimated and, consequently, the dynamical properties predicted by GGAs are generally much too slow. Worse still, GGAs predict that ice sinks in water—that is, water has a lower density than ice (11, 24–26). These disagreements remain even after considering hybrid functionals (11) and accounting for nuclear quantum effects (NQEs) (27), illustrating that the deficiencies are a manifestation of errors within the underlying GGA to the XC functional.
The difficulty in modeling liquid water with DFT arises from the delicate nature of the H-bond network. An H bond is a directional attractive force between the oxygen of one molecule and the protons of another. While mainly electrostatic in nature, H-bonds also exhibit a nonnegligible covalency. Notably, a covalent O–H bond binds one order of magnitude stronger than an H bond in water. Therefore, a slightly misbalanced covalent bond inevitably incurs a nonnegligible error in the predicted H-bond strength. Moreover, water molecules interact with each other through van der Waals (vdW) dispersion forces at larger distances, which are nondirectional and in general weaker than H bonds by roughly an order of magnitude. Thus, one needs to capture the balance among interactions whose magnitudes vary by orders of magnitude in water.
The short-ranged portion of the vdW interactions has been captured by local and semilocal XC functionals. In contrast, the intermediate- and long-ranged parts of the vdW interactions have not been captured by any general-purpose GGA. Recent studies have identified vdW interactions as an important determinant of water structure; vdW interactions often lead to more disordered water structures, more accurate water densities, and improved dynamic properties (11, 24–26, 28–30). Thus, the H-bond network of liquid water is produced by a delicate competition among covalent bonds, H bonds, and vdW interactions, and describing this complex interplay of interactions continues to be a highly challenging task. In this regard, nonempirical, general purpose XC functionals that describe all types of interactions on an equal footing are imperative but still largely absent in the literature.
To address the above issues, we performed AIMD simulations of liquid water in the isothermal-isobaric ensemble (31), using the strongly constrained and appropriately normed (SCAN) meta-GGA functional (32). SCAN is inherently nonempirical, developed by satisfying all 17 known exact constraints on semilocal XC functionals. Thus, the results obtained from SCAN are purely predictive and do not rely on training data. SCAN was shown to predict the energetics of gas-phase water hexamers and ice phases with quantitative accuracy, while other XC functionals, even with vdW corrections, were unable to make even qualitative predictions (33). This suggests that SCAN possesses the ingredients necessary to describe liquid water. Indeed, we demonstrate that SCAN predicts structural, electronic, and dynamic properties of liquid water in excellent agreement with experimental measurements. In particular, due to its ability to describe vdW interactions on intermediate length scales, SCAN yields the correct density ordering between liquid water and ice, correctly predicting that ice floats on liquid water. The dynamics of liquid water are also improved to near quantitative agreement with experiments. We expect the computationally efficient and accurate SCAN functional to serve as a major quantum mechanics-based tool for studying chemical processes in aqueous media.
Molecular and Electronic Structure of Liquid Water
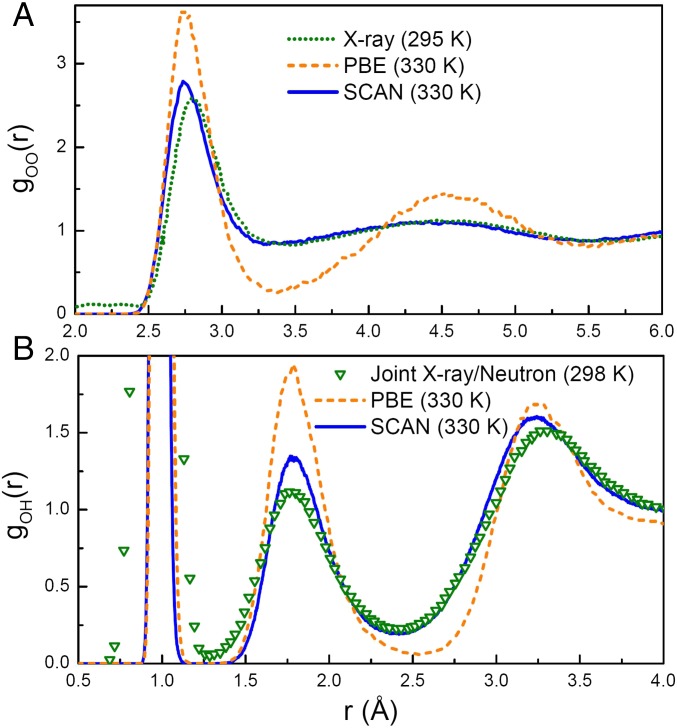
The pair structure of liquid water can be measured by X-ray diffraction (4, 5) and neutron diffraction experiments (4), from which structural information is contained in the resulting radial distribution functions (RDFs). We compare the RDFs obtained from AIMD simulations with SCAN and the Perdew–Burke–Ernzerhof (PBE) (19) GGA, as well as the experimental data. Here we compare two fully ab initio density functionals, without an empirical dispersion (D) correction to either. While such a correction improves PBE for solids and liquids (34), it slightly worsens PBE’s unacceptable overbinding of molecules, and thus PBE-D is not recommended for reactions in solvents. Fig. 1 A and B shows the oxygen–oxygen and oxygen–hydrogen RDFs, goo(r) and goh(r), respectively. SCAN dramatically improves almost all features in goo(r) and goh(r), producing a pair structure in much better agreement with experimental measurements than PBE.
Fig. 1.
RDFs (A) goo(r) and (B) goh(r) of liquid water predicted by PBE and SCAN at 330 K, as well as that from X-ray diffraction experiments (5) for goo(r) and joint X-ray/neutron diffraction experiments (4) for goh(r). An elevated temperature of 30 K was used in AIMD simulations to mimic NQEs (35).
The first peak of goh(r) contains all correlations within the covalent O–H bonds. SCAN enhances the covalency of water molecules, shortening the covalent bond length to 0.977 Å [first maximum in goh(r)], in comparison with the 0.989 Å from PBE. The shorter O–H bond length indicates that the oxygen and protons bind more strongly. Consequently, the protons of water molecules are less easily donated to form H bonds.
Correlations between H-bonded neighbors are contained in the first peak of goo(r) and the second peak of goh(r). As evidenced by Fig. 1, SCAN captures these correlations with high accuracy due to its ability to describe H-bonding. The region between the first and second peaks of goo(r) predominantly consists of non–H-bonded water molecules that occupy the interstitial space between H-bonded neighbors; the increased number of water molecules in the interstitial regions is due to vdW interactions, as discussed further below. Subsequent coordination shells are also captured by SCAN, evidenced by the good agreement between the second and third peaks in goo(r). We emphasize that the near perfect agreement between the SCAN goo(r) and experiment is nontrivial, because the structure of water is a manifestation of the delicate interplay among covalent bonds, H bonds, and vdW interactions.
The strength of directional H bonds is largely determined by the electronic structure of water molecules. The electronic density of states (DOS) of liquid water, averaged over trajectories, is shown in Fig. 2A and compared with the DOS measured by full valence band photoemission spectroscopy (43). The four peaks of the DOS are assigned to the , , , and orbitals based on the spatial symmetries of the water molecule. The simulated DOS are aligned at the position of the orbital peak (44). The energy difference between the peak predicted by PBE and experiment is 2.3 eV. SCAN substantially lowers this energy difference to 0.9 eV, providing a much better description of the strongly bound orbital than the GGA-level description provided by PBE. Note that the strongly bound orbital is mainly composed of the characteristic orbital and is close to the oxygen atom.
Fig. 2.
(A) DOS of liquid water, averaged over SCAN and PBE trajectories, as well as from photoemission spectroscopy (43). The peaks are labeled according to the symmetric orbitals of a water molecule with symmetry. Data are aligned (44) to the peak of the experimental (EXP) data. (B) Distributions of the centers of maximally localized Wannier functions (MLWFs) with respect to the oxygen position for lone and bonding electron pairs. Inset shows a representative snapshot of the MLWFs of a water molecule; lone and bonding pair MLWFs are colored green and blue, respectively.
The above four orbitals are related to the two lone electron pairs and two bonding electron pairs of a water molecule; the lone electron pairs are closely connected to the and orbitals, while the bonding electron pairs have a strong relation to the and orbitals. Therefore, the improved DOS by SCAN implies that the lone and bonding electron pairs are better captured than those from PBE. We examine the lone and bonding electron pairs on an equal footing through MLWFs (45), which are generated from a unitary transformation of the occupied Kohn–Sham eigenstates. Fig. 2B shows the distributions of the centers of the MLWFs. The lone electron pairs are closer to the oxygen atom in the SCAN description of water than PBE, while the bonding electron pairs only differ slightly between the two XC functionals. The smaller distance between lone electron pairs and oxygen in SCAN leads to a less negative environment around the lone electron pairs and explains the lower energy of the orbital in comparison with that of PBE. Meanwhile, the nearly unchanged description of bonded electron pairs in the two functionals is consistent with the observation that and states are also similar. Consequently, electrostatic attractions between oxygen nuclei and protons of neighboring water molecules are weaker in SCAN than PBE, weakening the directional H-bond strength.
In addition to improving the intermolecular structure, the reduced H-bond strength in SCAN also improves the intramolecular structure of water. The shorter distance between the lone electron pairs and the oxygen nucleus weakens the capability to accept H bonds and water molecules become less polarizable. The reduction in polarizability is expected to improve other electronic properties of liquid water, moving them in closer agreement with experimental measurements. Indeed, the dipole moment of liquid water, computed via MLWFs, is reduced by SCAN. Table 1 shows that D with PBE, while reduces to 2.97 D with SCAN, in better agreement with experimental measurements of 2.9 0.6 D (38). This improvement indicates that the important dipole–dipole interactions in liquid water are better described by SCAN.
Table 1.
Properties of water (330 K) and ice Ih (273 K) predicted by SCAN and PBE functionals in the isobaric-isothermal ensemble
| Method | (g/mL) | (g/mL) | (g/mL) | (D) | (D) | (eV) | (/ps) | (ps) | ||
| SCAN | 1.050 0.027 | 0.964 0.023 | 0.086 0.035 | 1.089 0.038 | 2.97 0.29 | 3.29 0.21 | 4.92 0.14 | 0.68 0.18 | 0.190 0.025 | 2.9 0.4 |
| PBE | 0.850 0.016 | 0.936 0.013 | −0.086 0.021 | 0.908 0.021 | 3.12 0.28 | 3.35 0.21 | 4.43 0.13 | 0.83 0.11 | 0.018 0.002 | 7.1 0.5 |
| EXP | 0.99656 (36) | 0.9167 (37) | 0.080 | 1.087 | 2.9 0.6 (38) | 8.7 0.6 (42) | 0.593 (4) | 0.187 (39) | 2.4 (40) |
Densities of water () and ice Ih (), density difference (), density ratio , dipole moments of water () and ice Ih (), band gap (), tetrahedral order parameter (q), diffusion coefficient (D), and rotational correlation time (). The temperatures for experimental data (EXP) , , , D, and are 300 (36), 273 (37), 298 (38), 298 (39), and 300 K (40), respectively. The experimental q value (4) was obtained by combining X-ray diffraction at 296 K and neutron diffraction data at 298 K in a structural model using empirical potential structural refinement. No experimental data of are found, but an induction model gave rise to 3.09 D for (41). Experimental data for q, D, and are for D2O chosen for consistency with the masses used in simulations for the dynamic properties. Error bars correspond to 1 SD.
We also estimate the band gap of water, , by averaging over eight randomly selected configurations from the trajectories. SCAN and PBE predict and 4.43 eV, respectively. While SCAN improves by about 0.5 eV, it differs significantly from the experimental value of 8.7 eV (42). We attribute this discrepancy to the well-known underestimation of band gaps by GGAs and meta-GGAs.
The SCAN functional can describe the intermediate-ranged vdW interactions (33), which shift the first minimum and the second maximum of (r) toward the first peak, with respect to that of PBE (without vdW interactions), as shown in Fig. 1A. Water molecules beyond the first coordination shell experience nondirectional attractions from surrounding water molecules in SCAN and are pulled into the interstitial spaces between H-bonded waters by these vdW forces. Consequently, the peak position of the second coordination shell shifts inward toward the central oxygen, and the population of interstitial waters increases, illustrated by the increase in the height of the first minimum in (r). Thus, the inclusion of nondirectional vdW interactions on intermediate length-scales leads to a more disordered and highly packed water structure.
From the increased packing, one expects the density of liquid water predicted by SCAN to be larger than that from PBE. Moreover, the dominant effect of vdW interactions is to provide cohesive interactions between molecules in condensed phases. Within the vdW picture of liquids, this leads to a cohesive pressure of magnitude , which “squeezes” water molecules closer together (29); is the vdW constant and a measure of the strength of these attractive interactions, and is the density of liquid water. Indeed, the SCAN functional predicts to be significantly higher than that predicted by PBE, as shown in Table 1 and Fig. S1.
Fig. S1.
Density fluctuations of liquid water and ice Ih as obtained from both SCAN and PBE trajectories using the isobaric-isothermal ensemble (NpT). A relatively shorter trajectory was generated for ice Ih because its density of solid phase converges quickly. The PBE functional incorrectly predicts that ice Ih (green line) is denser than water (orange line), while the SCAN functional successfully captures the larger density of water (blue line) than that of ice Ih (pink line). The black dashed and dotted lines represent the approximate experimental values of water density at ambient conditions (300 K) and ice density at 273 K under ambient pressure. An additional 30 K was applied to water to mimic the NQE (35). The averaged densities are listed Table 1.
Another problem of paramount importance is that solid water, ice Ih, floats on liquid water near ambient conditions. This is probably the most widely known anomalous property of water. However, almost all DFT-based approaches, except some of those relying on empirical parameters, predict a solid phase that is denser than the liquid. In this regard, we also carried out AIMD simulations of ice Ih containing 96 water molecules at 273 K. SCAN predicts a that is larger than the density of ice Ih (), Table 1 and Fig. S1, while for PBE, .
The water density from SCAN is larger than that determined experimentally, which is a significant improvement over the 15%, 25%, and 39% underestimation by the PBE, BLYP (17, 18, 24), and PBE0 (11) functionals, respectively. Compared with PBE, SCAN increases and by 21% and 3%, respectively. The 21% increase of by SCAN is vital in correcting the density ordering between the two phases by other functionals. Indeed, the experimental density difference between liquid water and ice Ih, , is correctly predicted by SCAN as 0.086 g/mL, while the opposite sign is predicted by PBE. SCAN also correctly predicts , in agreement with the experimental value of , and in contrast to the 0.908 ratio via PBE. Note that the water density obtained by PBE is slightly lower than the results of previous studies, and we discuss the difference in Bulk Densities.
Tetrahedral Structure of the H-Bond Network
With the translational order encoded in RDFs well captured by SCAN, we now focus on the tetrahedral orientational ordering of liquid water induced by the H-bond network. An ideal tetrahedral H-bonding structure shown in Fig. 3A Inset is formed because a water molecule can possess four optimal H bonds: two accepting and two donating. Thermal fluctuations break and reform H bonds, causing the tetrahedral structures in liquid water to be distorted or broken by entropic effects. This, combined with the increased packing due to vdW interactions, leads to an average number of H bonds per molecule slightly less than four in liquid water.
Fig. 3.
(A) Distributions of the number of hydrogen bonds in liquid water from SCAN and PBE. Inset illustrates an ideal tetrahedral H-bonding structure. Oxygen and hydrogen atoms are respectively depicted in red and white; H bonds are shown with dashed lines. (B and C) Bond angle distributions from (B) PBE and (C) SCAN. is decomposed into contributions arising from waters with a fixed number of HBs (2, 1, and 0) between a central oxygen and its two nearest neighbors. The experimental of O is inferred from experiments (4), and the area of is normalized to unity. (D and E) Free energies () as a function of and the oxygen–oxygen distance from (D) PBE and (E) SCAN. The free energy minimum is identified by the red circle and referenced to zero. The direction of change of the free energy minimum with increasing is shown with a red arrow. The cutoff distance used for computing the free energies is the same as that for and is shown with a dashed red line.
To illustrate the impact of SCAN on the H-bond network, distributions of the number of H bonds per molecule are presented in Fig. 3A. The percentage of water molecules participating in four H bonds drops from 72% in PBE to 56% in SCAN. This suggests that H bonds are weaker with SCAN than with PBE. SCAN predicts an average of 3.61 H bonds per molecule, smaller than the 3.77 obtained from PBE. This reduction in the number of H bonds is consistent with the influences of the underlying SCAN functional on liquid water: Directional H bonds are weakened and more easily broken by thermal fluctuations. The increased disorder is further stabilized by the inclusion of the intermediate-ranged vdW interactions naturally arising in SCAN.
The reduction of H bonds produced by SCAN disrupts the tetrahedral structure of liquid water. To quantify the amount of tetrahedral order, we adopt the tetrahedral order parameter (9). A perfect tetrahedral local environment corresponds to , and decreases as the local structure becomes less tetrahedral. Following experimental work (4), we evaluate using a cutoff radius that yields an average coordination number of 4. The resulting cutoffs are 3.15 and 3.45 Å for SCAN and PBE, respectively, with SCAN in better agreement with the cutoff of 3.18 Å inferred from the experiment (4). Despite the high first peak in the PBE (r), the shorter cutoff from SCAN suggests a more compact first coordination shell, consistent with the higher density of liquid water it predicts. PBE results in an overly tetrahedral liquid (Table 1). SCAN, however, yields in better agreement with experiments on heavy water (4), suggesting that SCAN provides a more accurate structural description of the fluctuating H-bond network.
Three-body correlations in water can be quantified by the bond angle distribution , where is the angle formed by an oxygen of a water molecule and two of its oxygen neighbors; neighbors are defined using the same cutoff as above (4). The PBE in Fig. 3B displays a high peak centered around the tetrahedral angle, 109.5 °, and is a much narrower distribution than that from the experiment. This indicates that PBE overestimates the tetrahedral character of the liquid, consistent with the above described overstructuring. In stark contrast, the SCAN is in excellent agreement with the experiment, with almost exactly the same widths and intensities of the two peaks close to 109.5 ° and 55 ° (Fig. 3C).
The peak located near 109.5 ° arises from tetrahedral structures. The peak at is related to broken H bonds and interstitial, non–H-bonded water, and major differences between SCAN and PBE are observed in this region of the distribution. We decompose into three contributions according to the number of H bonds a water molecule formed within a water triplet. The of triplets formed with 2, 1, and 0 H bonds are plotted in Fig. 3 B and C. Triplets involving 2 H bonds dominate the PBE , while triplets with broken (0 or 1) H bonds contribute much less. In contrast, triplets with less than 2 H bonds contribute significantly to the predicted by SCAN, especially near .
The free energy as a function of and the distance between neighboring oxygen atoms in the triplet reveals additional insights, as shown in Fig. 3 D and E. As expected, the minimum free energy corresponds to tetrahedral-like structures with and Å. In contrast to PBE, SCAN predicts a significant fraction of triplets with far from , indicating that the SCAN liquid is more disordered. The free energies suggest that water molecules in the first coordination shell experience a smaller free energy barrier to adopt a broad range of -values with SCAN than with PBE.
Importantly, there are substantial differences between the two functionals in describing the dependence of the free energy on . With PBE, as is increased away from the free energy minimum, hardly moves from 109.5 °, as depicted by the red arrow in Fig. 3D. This is consistent with the overstructuring of water by PBE and implies that is weakly influenced by fluctuations of the first coordination shell. In contrast, SCAN produces a stronger correlation between and , such that the free energy is lowered at larger by decreasing , illustrated by the red arrow in Fig. 3E. This is consistent with the higher population of non–H-bonded, interstitial waters in the SCAN prediction. These nontetrahedrally oriented water molecules contribute significantly to below and highlight the reduced tetrahedrality of the SCAN H-bond network.
Dynamics
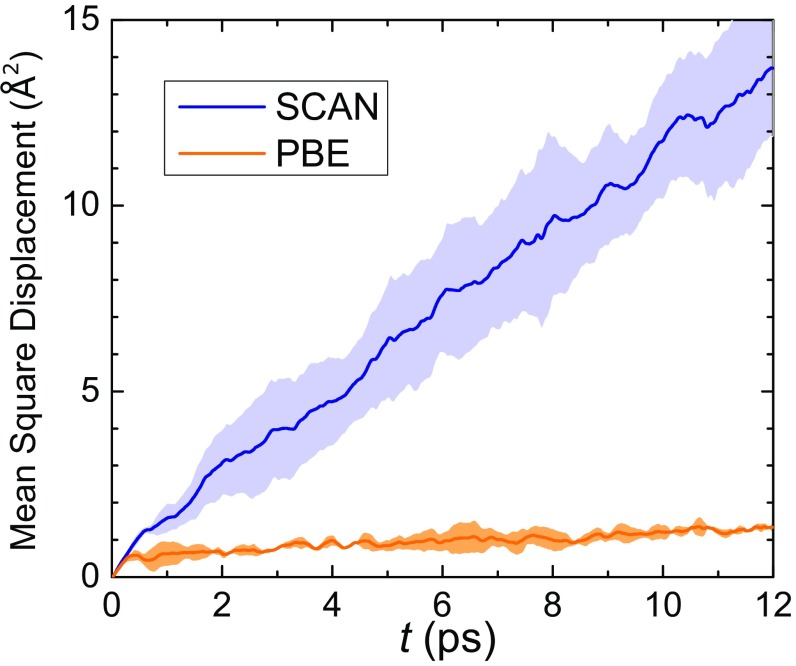
Changes in the H-bond energy alter the delicate enthalpy–entropy balance in liquid water that dictates its dynamic properties; for example, breakage and formation of H bonds through thermal fluctuations controls diffusion. Thus, stronger H bonds tilt the enthalpy–entropy balance toward energetic contributions, reducing the tendency to break H bonds and consequently lowering the diffusion coefficient . We estimate from the long-time limit of the mean squared displacement (MSD), averaged over the oxygen and hydrogen atoms (see MSDs). Indeed, the value of PBE is an order of magnitude smaller than that of experiment, while SCAN improves the estimate of to near agreement with the experiment, see Table 1 and Fig. S2.
Fig. S2.
MSDs for the SCAN and PBE systems consisting of 64 water molecules. Shaded regions indicate one SE.
H-bond dynamics are more directly probed via the second-order rotational correlation function of the O–H bond vector , , where is a second-order Legendre polynomial. The integral of yields the rotational correlation time of the O–H bond; correlation functions and details surrounding computation are given in Rotational Time Correlation Functions. SCAN predicts a value of in agreement with nuclear magnetic resonance spectroscopy (40), Table 1 and Fig. S3, while rotational dynamics are slowed in the PBE system. The mechanism for rotational relaxation of the O–H bond vector is associated with breaking an H bond. In PBE, H bonds are too strong, significantly hindering this pathway. SCAN appropriately predicts the weight of these pathways for rotational relaxation due to its accurate description of H bonding.
Fig. S3.
Second-order rotational time correlation functions, , for the O–H bond vector of water as described by SCAN and PBE. B is the same as A, but zoomed in on the region from 0 to 0.5 ps.
Conclusions and Outlook
The SCAN density functional provides a genuinely predictive ab initio model of liquid water. Importantly, SCAN is a long-awaited XC functional that can correctly predict liquid water that is denser than ice at ambient conditions. SCAN excellently describes covalent and H bonds due to an improved description of electronic structure and captures intermediate-ranged vdW interactions that further improve the structure and thermodynamics of liquid water. These vdW forces can play a critical and active role at interfaces—for example, underlying drying transitions (28, 29, 46), instilling confidence that SCAN will enable predictive modeling of heterogeneous chemical environments.
However, there are still improvements to be made regarding the water structure. SCAN predicts a slightly overstructured first peak of goo(r). Previous studies have attributed the overstructuring to self-interaction errors (16), which can be mitigated by including a fraction of exact exchange in hybrid functionals. Moreover, the first peak in goh(r) is too narrow, and the error is dominated by the lack of NQEs of hydrogen (35). The widths and intensities of peaks in the computed DOS are also, respectively, narrower and higher than those in the experimental DOS. In fact, DFT is not rigorous for photoemission spectra and does not include lifetime broadening; NQEs, however, can additionally broaden the DOS, bringing the resulting widths and intensities in closer agreement with the experiment (44). NQEs can be accounted for within the Feynman discretized path-integral approach (27, 35, 44).
In conclusion, the SCAN XC functional within DFT shows promising predictive power and will likely enable confident ab initio predictions for complex systems at the forefront of physics, chemistry, biology, and materials science (47).
Materials and Methods
We performed Car–Parrinello molecular dynamics (6) in Quantum ESPRESSO (48). We used the Hamann–Schlüter–Chiang–Vanderbilt pseudopotentials (49) generated using PBE. The valence electrons, including the electron of H and the electrons of O, were treated explicitly. The energy cutoff was 130 Ry. Simulations were performed in the isothermal-isobaric ensemble (constant NpT) by using the Parrinello–Rahman barostat (31) and a single Nosé–Hoover thermostat (50) with a frequency of 60 THz to maintain a constant pressure () and temperature (), respectively. K for liquid water and 273 K for ice Ih; the 30 K increase above ambient conditions in the former mimics NQEs on the liquid structure (35). We adopted a cubic cell with = 64 water molecules. The fictitious mass of the electrons was set to 100 au, and the corresponding mass preconditioning with a kinetic energy cutoff of 25 Ry was used to all Fourier components of wavefunctions (51). The deuterium mass was used instead of hydrogen to enable the use of a timestep of 2 au; dynamics were compared with O instead of O. SCAN and PBE trajectories for water were 30.0 and 20.0 ps in length, respectively. Corresponding trajectories for ice Ih were 11.1 and 13.8 ps, respectively. The first 5 ps of each trajectory was used for equilibration and the remainder used for analysis. We used a standard geometric criterion for hydrogen bonding; covalently bonded O–H are associated with an O–H distance of less than 1.24 Å, and H bonds have an O–O distance less than 3.5 Å and a angle less than (52). Additional details are in Computational Details.
Computational Details
The NpT algorithm was implemented in the Quantum ESPRESSO (48) package. In our water simulations, all of the plane waves with kinetic energies below 150 Ry were included, and we followed ref. 53 to maintain a constant plane wave kinetic energy cutoff of Ry for a fluctuating cell by adding a smooth step function with height Ry and width Ry to the plane wave kinetic factor as , where erf is the error function. The reference cells were chosen to be cubes with side lengths of 14.3345 Å and 12.6579 Å for PBE- and SCAN-based AIMD simulations, respectively.
We ran parallel AIMD simulations using both SCAN (32) and PBE (19) XC functionals on 216 computer cores and recorded the wall times of 100 MD steps. The system was bulk liquid water consisting of 64 water molecules as used in this work. Both simulations were carried out on nodes with 2 × Intel Ivy Bridge @ 2.4 GHz and up to 64 GB RAM. We obtained 6.44 and 3.89 s per step for SCAN and PBE functionals, respectively, with SCAN being only 1.66 times more costly than PBE. Therefore, we conclude the cost of using the SCAN functional in studying liquid water is not dramatically more expensive than that of using the PBE functional and can be considered on the same level.
Bulk Densities
Bulk densities as a function of time are shown in Fig. S1 for the SCAN and PBE descriptions of liquid water and ice Ih. The ice Ih phase remained solid throughout and did not transform to the liquid phase in the AIMD trajectories. The averaged densities are listed in Table 1 with the error bars corresponding to 1 SD. With PBE the dynamics of ambient liquid water is very sluggish, and we find that at 330 K the mean density of liquid water (0.85 g/mL as shown in Table 1) computed with PBE can vary within 0.01 g/mL (as estimated by another independent run of more than 60 ps by members of R.C.’s group with PBE and all of the same parameters) depending on the initial configuration and trajectory length. Since PBE liquid density is well below PBE ice Ih density, we did not try to reduce the statistical uncertainty in the PBE liquid density. In addition, a recent study found structural, dynamical, and electronic properties of liquid water as obtained by AIMD simulations using CP2K/Quickstep (54) and Quantum ESPRESSO packages compared well (55), with the latter equilibrium density 0.02 g/mL lower and first-peak 0.1 higher than corresponding CP2K values. These differences are comparable to the statistical uncertainties. Therefore, the small difference in the PBE liquid density found here—0.85 versus 0.865 to 0.887 g/mL by ref. 24—as well as the slightly higher first-peak—3.61 versus 3.36 to 3.54 (24)—is attributed to both statistical uncertainties and numerical differences of these approaches. The densities clearly fluctuate around an average value for each trajectory, illustrating equilibration of the trajectories. Moreover, the fact that water is denser than ice Ih in the SCAN prediction is clearly observed, while the opposite is found for PBE. Finally, we note that fluctuations in the density of water are larger in the SCAN trajectory than in the PBE trajectory. This indicates that water is more compressible in the SCAN description than PBE, which produces a more rigid and ordered liquid structure.
vdW Interactions in SCAN and PBE
As discussed extensively in the main text, an accurate description of water and ice from first principles is challenging because the H-bond network of water arises from a delicate balance of strong intramolecular covalent bonds, weak intermolecular H bonds, and even weaker vdW interactions. GGA functionals exhibit delocalization problems, and the intermediate- and long-ranged vdW attraction is strongly underestimated. To be specific, the exchange energy density obtained from GGA is much more negative than LDA in regions with a large reduced density gradient. Therefore, the attractive vdW interactions between water molecules are missing in GGAs, which results in more ordered water molecules and a lower bulk density. The SCAN functional captures this delicate balance between covalent bonds, H bonds, and vdW interactions in water, which is critical in accurately describing the water density.
By including a dimensionless variable in the kinetic energy density, SCAN can reduce to different GGAs by recognizing covalent single bonds when , slowly varying densities when , and noncovalent bonds when . It was recently demonstrated that SCAN captures the intermediate-ranged vdW interactions for a variety of materials (33). To further illustrate this point, we applied the Tkatchenko–Scheffler (TS) vdW scheme (56) to both the PBE and SCAN functionals. The TS scheme determines the “turn-on” radius for atom pairs based on the XC functional used, and a larger TS scaling parameter implies that a larger radius is adopted to turn on the vdW interactions. The scaling parameters were obtained by fitting to the S22 molecular database. We find that in both water and ice structures, the scaling parameters are 0.94 and 1.17 for the PBE and SCAN functionals, respectively. The 24.5% larger scaling parameter in SCAN demonstrates that it captures the vdW interactions out to significantly larger distances than PBE.
MSDs
The MSDs computed from SCAN and PBE trajectories are shown in Fig. S2, where the center-of-mass positions of water molecules were used to compute MSDs. Each trajectory was divided into sections to compute the MSDs, each 12 ps in length and separated by 3.0 ps. We chose five and three sections for SCAN and PBE trajectories, respectively. Next, a linear fitting of the long-time, linear region of the MSDs was performed to obtain the values. Finally, the obtained values were averaged, and the result is listed in Table 1; the slope of the linear region is equal to . Clearly, water diffuses much faster in the SCAN description than PBE, due to the weaker H bonds predicted by the SCAN functional. The computed from SCAN and PBE are 0.190 and 0.018 , respectively. The diffusion coefficient from PBE is close to the 0.020 reported in a previous work (9). However, we note that correlations may exist in divided sections and affect the accuracy of computed diffusion coefficients (57, 58). More accurate diffusion coefficients require longer simulation times, and we leave this investigation for future work.
Rotational Time Correlation Functions
The second-order rotational correlation function for the O–H bond vector was calculated according to , where is a second-order Legendre polynomial. These time correlation functions as predicted for water by PBE and SCAN are shown in Fig. S3. Clearly, SCAN results in significantly faster rotational dynamics, evidenced by the much faster decay of the SCAN than that of PBE. As discussed in the main text, this is because SCAN results in weaker and more physical hydrogen bonding interactions than PBE.
The short-time behavior of is shown in Fig. S3B. We find that the initial short-time decay (50 fs) of is identical in the two models. This initial decay is due to rapid inertial, librational motions of water that do not require hydrogen bond breakage. Thus, in both models, hydrogen bonds are still intact on this short timescale, and no major differences between SCAN and PBE are found. However, the oscillation in occurs at different times in the two models. A larger oscillation is found in PBE, which occurs before the slight oscillation in the SCAN .
Finally, to estimate the rotational correlation time of the O–H bond, we must integrate . To do so, we first note that the long time decay of is well described by an exponential. Thus, we fit to an exponential at long times (after the initial change in slope associated with librations). The fitted exponential is then used to describe the decay of for times longer than 7 and 9 ps in PBE and SCAN, respectively. We then numerically integrate this composite to obtain , which are listed in Table 1 of the main text.
Validation of SCAN in Different Packages
To further validate our results using the SCAN functional for liquid water, we ran AIMD simulations on a cell of 32 water molecules for 20 ps by using both VASP (59) and Quantum ESPRESSO (48) packages. The cell was chosen to be a cube of side length 9.877 Å. We adopted the NVT ensemble with the Nosé–Hoover thermostat, and the temperature was set to 330 K. We used the mass of deuterium instead of hydrogen to speed up the convergence. In VASP, we used projector-augmented-wave (PAW) potentials with configurations of [O]22 and [H]1. In particular, we chose the hard PAW potentials for oxygen and hydrogen atoms and set the energy cutoff to 1,200 eV to converge our results. The Born–Oppenheimer molecular dynamics was performed with a time step of 0.5 fs. In Quantum ESPRESSO, we carried out Car–Parrinello molecular dynamics (6), and the settings were chosen to be the same as described in the main text.
In Fig. S4, the oxygen–oxygen RDFs are shown for the above two calculations. We find both electronic structure packages yield almost the same features. In particular, the first peaks from both packages are almost identical. The results suggest that the properties of liquid water as predicted by the SCAN functional are reliable and are reproducible with converged basis set and electron dynamics.
Fig. S4.
Oxygen–oxygen RDFs for 32 water molecules in condensed phase as obtained from the SCAN functional implemented in Vienna Ab initio Simulation Package (VASP) and Quantum ESPRESSO electronic structure packages.
RDF
We plot in Fig. S5 the zoomed-in first peak of RDF from both PBE- and SCAN-based AIMD simulations. The first peak position represents the length of O–H covalent bond and we can see that SCAN predicts a slightly shorter covalent bond (0.977 Å) than that from PBE (0.989 Å).
Fig. S5.
Zoomed-in RDF (as shown in Fig. 1B) as obtained from SCAN- and PBE-based AIMD simulations.
Acknowledgments
This work was supported by US Department of Energy (DOE) SciDac Grant DE-SC0008726. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by Office of Science of the US DOE Contract DE-AC02-05CH11231. R.C.R., Z.S., and J.P.P. were supported as part of the Center for the Computational Design of Functional Layered Materials, an Energy Frontier Research Center funded by US DOE, Office of Science, Basic Energy Sciences Award DE-SC0012575. M.F.C.A. is partially supported by the CNPq–Brazil. X.W. is partially supported by National Science Foundation (NSF), DMR Award DMR-1552287.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1712499114/-/DCSupplemental.
References
- 1.Ball P. Water as an active constituent in cell biology. Chem Rev. 2008;108:74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 2.Fecko CJ, Eaves JD, Loparo JJ, Tokmakoff A, Geissler PL. Ultrafast hydrogen-bond dynamics in the infrared spectroscopy of water. Science. 2003;301:1698–1702. doi: 10.1126/science.1087251. [DOI] [PubMed] [Google Scholar]
- 3.Wernet P, et al. The structure of the first coordination shell in liquid water. Science. 2004;304:995–999. doi: 10.1126/science.1096205. [DOI] [PubMed] [Google Scholar]
- 4.Soper A, Benmore C. Quantum differences between heavy and light water. Phys Rev Lett. 2008;101:065502. doi: 10.1103/PhysRevLett.101.065502. [DOI] [PubMed] [Google Scholar]
- 5.Skinner LB, et al. Benchmark oxygen-oxygen pair-distribution function of ambient water from x-ray diffraction measurements with a wide Q-range. J Chem Phys. 2013;138:074506. doi: 10.1063/1.4790861. [DOI] [PubMed] [Google Scholar]
- 6.Car R, Parrinello M. Unified approach for molecular dynamics and density-functional theory. Phys Rev Lett. 1985;55:2471–2474. doi: 10.1103/PhysRevLett.55.2471. [DOI] [PubMed] [Google Scholar]
- 7.Kuhne TD, Krack M, Parrinello M. Static and dynamical properties of liquid water from first principles by a novel Car-Parrinello-like approach. J Chem Theor Comput. 2009;5:235–241. doi: 10.1021/ct800417q. [DOI] [PubMed] [Google Scholar]
- 8.Santra B, et al. On the accuracy of van der Waals inclusive density-functional theory exchange-correlation functionals for ice at ambient and high pressures. J Chem Phys. 2013;139:154702. doi: 10.1063/1.4824481. [DOI] [PubMed] [Google Scholar]
- 9.DiStasio RA., Jr Santra B, Li Z, Wu X, Car R. The individual and collective effects of exact exchange and dispersion interactions on the ab initio structure of liquid water. J Chem Phys. 2014;141:084502. doi: 10.1063/1.4893377. [DOI] [PubMed] [Google Scholar]
- 10.Gillan MJ, Alfè D, Michaelides A. Perspective: How good is DFT for water? J Chem Phys. 2016;144:130901. doi: 10.1063/1.4944633. [DOI] [PubMed] [Google Scholar]
- 11.Gaiduk AP, Gygi F, Galli G. Density and compressibility of liquid water and ice from first-principles simulations with hybrid functionals. J Phys Chem Lett. 2015;6:2902–2908. doi: 10.1021/acs.jpclett.5b00901. [DOI] [PubMed] [Google Scholar]
- 12.McGrath MJ, et al. Simulating fluid-phase equilibria of water from first principles. J Phys Chem A. 2006;110:640–646. doi: 10.1021/jp0535947. [DOI] [PubMed] [Google Scholar]
- 13.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965;140:A1133–A1138. [Google Scholar]
- 14.Perdew JP, Schmidt K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. In: Van Doren V, Van Alsenoy C, Geerlings P, editors. AIP Conference Proceedings. Vol 577. AIP; Melville, NY: 2001. pp. 1–20. [Google Scholar]
- 15.Ceperley DM, Alder B. Ground state of the electron gas by a stochastic method. Phys Rev Lett. 1980;45:566–569. [Google Scholar]
- 16.Perdew JP, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems. Phys Rev B. 1981;23:5048–5079. [Google Scholar]
- 17.Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 18.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 19.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 20.Perdew JP, Ernzerhof M, Burke K. Rationale for mixing exact exchange with density functional approximations. J Chem Phys. 1996;105:9982–9985. [Google Scholar]
- 21.Adamo C, Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J Chem Phys. 1999;110:6158–6170. [Google Scholar]
- 22.Laasonen K, Csajka F, Parrinello M. Water dimer properties in the gradient-corrected density functional theory. Chem Phys Lett. 1992;194:172–174. [Google Scholar]
- 23.Laasonen K, Parrinello M, Car R, Lee C, Vanderbilt D. Structures of small water clusters using gradient-corrected density functional theory. Chem Phys Lett. 1993;207:208–213. [Google Scholar]
- 24.Schmidt J, et al. Isobaric-isothermal molecular dynamics simulations utilizing density functional theory: An assessment of the structure and density of water at near-ambient conditions. J Phys Chem B. 2009;113:11959–11964. doi: 10.1021/jp901990u. [DOI] [PubMed] [Google Scholar]
- 25.Wang J, Román-Pérez G, Soler JM, Artacho E, Fernández-Serra MV. Density, structure, and dynamics of water: The effect of van der Waals interactions. J Chem Phys. 2011;134:024516. doi: 10.1063/1.3521268. [DOI] [PubMed] [Google Scholar]
- 26.Miceli G, de Gironcoli S, Pasquarello A. Isobaric first-principles molecular dynamics of liquid water with nonlocal van der Waals interactions. J Chem Phys. 2015;142:034501. doi: 10.1063/1.4905333. [DOI] [PubMed] [Google Scholar]
- 27.Ceriotti M, Cuny J, Parrinello M, Manolopoulos DE. Nuclear quantum effects and hydrogen bond fluctuations in water. Proc Natl Acad Sci USA. 2013;110:15591–15596. doi: 10.1073/pnas.1308560110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Baer MD, et al. Re-examining the properties of the aqueous vapor-liquid interface using dispersion corrected density functional theory. J Chem Phys. 2011;135:124712. doi: 10.1063/1.3633239. [DOI] [PubMed] [Google Scholar]
- 29.Remsing RC, Rodgers JM, Weeks JD. Deconstructing classical water models at interfaces and in bulk. J Stat Phys. 2011;145:313–334. [Google Scholar]
- 30.Del Ben M, Hutter J, VandeVondele J. Probing the structural and dynamical properties of liquid water with models including non-local electron correlation. J Chem Phys. 2015;143:054506. doi: 10.1063/1.4927325. [DOI] [PubMed] [Google Scholar]
- 31.Parrinello M, Rahman A. Crystal structure and pair potentials: A molecular-dynamics study. Phys Rev Lett. 1980;45:1196–1199. [Google Scholar]
- 32.Sun J, Ruzsinszky A, Perdew JP. Strongly constrained and appropriately normed semilocal density functional. Phys Rev Lett. 2015;115:036402. doi: 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
- 33.Sun J, et al. Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional. Nat Chem. 2016;8:831–836. doi: 10.1038/nchem.2535. [DOI] [PubMed] [Google Scholar]
- 34.Bankura A, Karmakar A, Carnevale V, Chandra A, Klein ML. Structure, dynamics, and spectral diffusion of water from first-principles molecular dynamics. J Phys Chem C. 2014;118:29401–29411. [Google Scholar]
- 35.Morrone JA, Car R. Nuclear quantum effects in water. Phys Rev Lett. 2008;101:017801. doi: 10.1103/PhysRevLett.101.017801. [DOI] [PubMed] [Google Scholar]
- 36.Linstrom PJ, Mallard W. 2001. NIST Chemistry Webbook; NIST Standard Reference Database No. 69 (National Institute of Standards and Technology, Gaithersburg, MD)
- 37.Haynes WM. CRC Handbook of Chemistry and Physics. 86th Ed CRC; Boca Raton, FL: 2005. [Google Scholar]
- 38.Badyal Y, et al. Electron distribution in water. J Chem Phys. 2000;112:9206–9208. [Google Scholar]
- 39.Mills R. Self-diffusion in normal and heavy water in the range 1-45. deg. J Phys Chem. 1973;77:685–688. [Google Scholar]
- 40.Ropp J, Lawrence C, Farrar T, Skinner J. Rotational motion in liquid water is anisotropic: A nuclear magnetic resonance and molecular dynamics simulation study. J Am Chem Soc. 2001;123:8047–8052. doi: 10.1021/ja010312h. [DOI] [PubMed] [Google Scholar]
- 41.Batista ER, Xantheas SS, Jónsson H. Molecular multipole moments of water molecules in ice Ih. J Chem Phys. 1998;109:4546–4551. [Google Scholar]
- 42.Bernas A, Ferradini C, Jay-Gerin JP. On the electronic structure of liquid water: Facts and reflections. Chem Phys. 1997;222:151–160. [Google Scholar]
- 43.Winter B, et al. Full valence band photoemission from liquid water using EUV synchrotron radiation. J Phys Chem A. 2004;108:2625–2632. [Google Scholar]
- 44.Chen W, Ambrosio F, Miceli G, Pasquarello A. Ab initio electronic structure of liquid water. Phys Rev Lett. 2016;117:186401. doi: 10.1103/PhysRevLett.117.186401. [DOI] [PubMed] [Google Scholar]
- 45.Marzari N, Mostofi AA, Yates JR, Souza I, Vanderbilt D. Maximally localized Wannier functions: Theory and applications. Rev Mod Phys. 2012;84:1419–1475. [Google Scholar]
- 46.Remsing RC, Weeks JD. Dissecting hydrophobic hydration and association. J Phys Chem B. 2013;117:15479–15491. doi: 10.1021/jp4053067. [DOI] [PubMed] [Google Scholar]
- 47.Dong H, Fiorin G, Carnevale V, Treptow W, Klein ML. Pore waters regulate ion permeation in a calcium release-activated calcium channel. Proc Natl Acad Sci USA. 2013;110:17332–17337. doi: 10.1073/pnas.1316969110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Giannozzi P, et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J Phys Condens Matter. 2009;21:395502. doi: 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
- 49.Hamann D, Schlüter M, Chiang C. Norm-conserving pseudopotentials. Phys Rev Lett. 1979;43:1494–1497. [Google Scholar]
- 50.Martyna GJ, Klein ML, Tuckerman M. Nosé-Hoover chains: The canonical ensemble via continuous dynamics. J Chem Phys. 1992;97:2635–2643. [Google Scholar]
- 51.Tassone F, Mauri F, Car R. Acceleration schemes for ab initio molecular-dynamics simulations and electronic-structure calculations. Phys Rev B. 1994;50:10561–10573. doi: 10.1103/physrevb.50.10561. [DOI] [PubMed] [Google Scholar]
- 52.Luzar A, Chandler D. Hydrogen-bond kinetics in liquid water. Nature. 1996;379:55–57. [Google Scholar]
- 53.Bernasconi M, et al. First-principle-constant pressure molecular dynamics. J Phys Chem Solid. 1995;56:501–505. [Google Scholar]
- 54.Vandevondele J, et al. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput Phys Commun. 2005;167:103–128. [Google Scholar]
- 55.Miceli G, Hutter J, Pasquarello A. Liquid water through density-functional molecular dynamics: Plane-wave vs atomic-orbital basis sets. J Chem Theor Comput. 2016;12:3456–3462. doi: 10.1021/acs.jctc.6b00271. [DOI] [PubMed] [Google Scholar]
- 56.Tkatchenko A, Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys Rev Lett. 2009;102:073005. doi: 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
- 57.Kuo IFW, et al. Liquid water from first principles: Investigation of different sampling approaches. J Phys Chem B. 2004;108:12990–12998. [Google Scholar]
- 58.Kuo IFW, Mundy CJ, McGrath MJ, Siepmann JI. Time-dependent properties of liquid water: A comparison of Car-Parrinello and Born-Oppenheimer molecular dynamics simulations. J Chem Theor Comput. 2006;2:1274–1281. doi: 10.1021/ct6001913. [DOI] [PubMed] [Google Scholar]
- 59.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]