Designing Thin, Ultrastretchable Electronics with Stacked Circuits and Elastomeric Encapsulation Materials

Abstract

Many recently developed soft, skin-like electronics with high performance circuits and low modulus encapsulation materials can accommodate large bending, stretching, and twisting deformations. Their compliant mechanics also allows for intimate, nonintrusive integration to the curvilinear surfaces of soft biological tissues. By introducing a stacked circuit construct, the functional density of these systems can be greatly improved, yet their desirable mechanics may be compromised due to the increased overall thickness. To address this issue, the results presented here establish design guidelines for optimizing the deformable properties of stretchable electronics with stacked circuit layers. The effects of three contributing factors (i.e., the silicone inter-layer, the composite encapsulation, and the deformable interconnects) on the stretchability of a multilayer system are explored in detail via combined experimental observation, finite element modeling, and theoretical analysis. Finally, an electronic module with optimized design is demonstrated. This highly deformable system can be repetitively folded, twisted, or stretched without observable influences to its electrical functionality. The ultrasoft, thin nature of the module makes it suitable for conformal biointegration.

1. Introduction

Periodic bilayer or multilayer structures can be formed by stacking together two or more layers with identical or similar structures. Such architectures are abundant in nature, with examples ranging from simple, micro/nanolevel lipid bilayer constructs^[1] to complex systems like xylems^[2,3] and butterfly wing patterns.^[4–6] Systems with multiple overlapping layers have also been widely used in engineered devices for various purposes, including strengthening mechanics,^[7–9] saving space,^[10,11] and providing special optical, electrical, and magnetic effects.^[4,12–15] Recently, soft, skin-like electronic devices that allow for extreme level of bending, twisting, and elongation with unaffected electrical functionality have captured widespread research and commercial attention.^[16] Reported devices range from epidermal/in vivo health monitors,^[17–24] to artificial electronic skins,^[25–34] to wearable power-supply or light-emitting diode (LED) modules,^[35–40] and to fully implantable optogenetics platforms.^[41] Many of those systems build upon an “island-bridge” mechanics design, which combines high-performance electronic components (i.e., islands), deformable interconnects (i.e., bridges), and rubber-like silicone encapsulation materials. Stretchable electronics with two layers of stacked circuit layouts have also been developed. For instance, Zhang et al. measured core-body temperature using two sets of heat flux sensors vertically separated by a silicone matrix.^[42] Here, the two overlapping sensors provide a differential temperature reading necessary for thermal characterization. Recently, Lee et al. proposed a skin-mountable power management device with high functional density and reduced planar dimensions (Figure 1).^[39] This outcome was achieved by using a bilayer circuit construct, where chip-scale batteries and an array of solar cells stacked above them were separated by insulating, rubber-like materials. However, examples like these are rare in the literature and stretchable electronics with even more layers of overlapping circuits remain unexplored. One challenge is that stacking may easily double or even triple the overall thickness, resulting in bulkier, stiffer devices that cannot be conformably integrated with soft, curvilinear surfaces. This change in mechanical behaviors is undesirable, especially for epidermal or implanted bioelectronics applications that require intimate, biocompatible integration with surfaces of soft tissues. In this paper, we present a detailed study of stretchable electronics with a bilayer circuit construct, and a set of guidelines for optimizing their deformable properties. We analyze three key design factors contributing to stretchability of multilayer systems, namely, interlayer mechanics, encapsulation design, and buckling/ post-buckling physics of interconnects through finite element analysis (FEA), experimental measurements, and simple analytic models. The results lead to the demonstration of a thin, ultrasoft, high areal-coverage electronic module with bilayer layout, with the ability to accommodate repetitive folding, 180° twisting, and more than 40% elongation without any degradation in electrical performance. Such devices can also be folded into temporary configurations with as many as six stacked circuit layers, with some retention of system stretchability.

Figure 1.

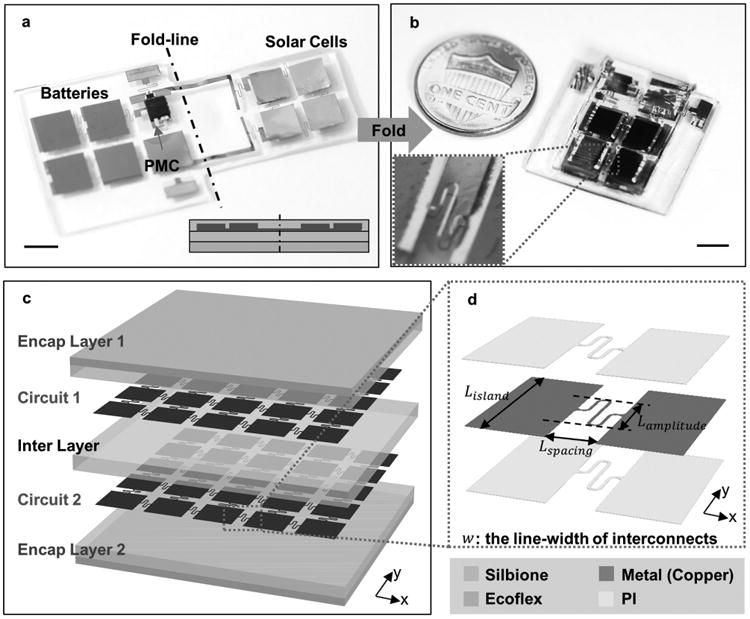
Optical images and schematic illustrations for stretchable electronics with bilayer circuit layout. a) A skin-mountable power management system prior to folding integration. The inset shows a schematic cross-sectional profile of the device. (Scale bar: 500 μm). b) Optical image of the device after “folding-style” integration, in comparison with a one-cent coin. The inset shows a magnified view of the two stacked, well-aligned interconnects. (Scale bar: 500 μm). c) Exploded-view illustration of the typical construct of electronics with stacked circuit layers. d) Magnified illustration of a unit cell of a circuit in (c), featuring the conductive metal layer and polyimide clads.

2. Results and Discussion

Figure 1a illustrates the skin-mountable power management system developed by Lee et al. before the final integration step. The 2 × 2 solar cell array, a similar shaped battery array, power management chips, straight connecting wires, and serpentine-shaped interconnects reside on a composite substrate made of a skin-like elastomer (modulus of ≈60 kPa, Ecoflex 00–30, Smooth-on) and an ultralow modulus silicone adhesive (modulus of ≈3 kPa, Silbione RT Gel 4717 A/B, Bluestar Silicones). The entire circuit is covered by the same silicone adhesive on top. In the final integration step, the right half of the device (defined by the fold line) is held in position, while the left half is rotated, aligned, and eventually pressed against the other half, analogous to a typical Japanese origami process. Due to the highly adhesive and compliant nature of the ultrasoft silicone, the gap between the two interfaces in contact closes spontaneously to eliminate any remaining air gaps. The strain induced by the folding step is accommodated by the deformation near the folding site, and does not affect the overall stretchability of the system. Figure 1b shows the device after this “folding-style” integration, where the lateral dimension is reduced by 50% in comparison to that in Figure 1a. Since the solar cells reside above batteries, their exposure to light remains unobstructed. The inset in Figure 1b highlights the good vertical alignment among the component islands and interconnects achieved by the folding step. Figure S1a–e of the Supporting Information and the Experimental Section describe the fabrication procedures in detail. A stacked construct in stretchable electronics can also be obtained via direct, layer-by-layer fabrication, as outlined in Figure S1f–j and in the Experimental Section. Both approaches yield the basic geometrical structure schematically illustrated in Figure 1c. Two circuit layers with well-aligned patterns are mechanically and electrically separated by a soft silicone inter-layer (e.g., Silbione) and encapsulated from top and bottom by opposing bilayer composite (e.g., Silbione/Ecoflex). This process places the circuit layers in an immediate surrounding matrix made of ultrasoft material. Previous studies demonstrate that this layout is favorable for the overall deformability of the device because the mechanical constraint from matrix is minimized.^[20,39] In an application requiring high areal coverage η₀ of functional components in a single circuit layer, the circuit layer patterns can be generated by repetition of the unit cell shown in Figure 1d in two in-plane directions. The unit cell consists of two functional components (islands) with side length L_island separated by a distance L_spacing and connected by a serpentine-shaped interconnect with amplitude L_amplitude and width w. From the definition of areal coverage η₀ = [L_island/(L_island + L_spacing)]², we can easily determine that L_spacing/L_island ≤ 0.3 is required for η₀ of ≈60% or higher. The small spacing in comparison to the size of islands places demanding requirements on the interconnect pattern design and necessitates a systematic understanding of buckling mechanics, as elaborated on in following paragraphs. In the cross-section of one circuit layer, conductive metal parts (e.g., copper, E ≈ 119 GPa) are sandwiched by two polyimide clads (PI, E ≈ 2.5 GPa) for electrical insulation. For multilayer electronics with N identical or similar circuit layers, an effective areal coverage η_eff can be defined as η_eff = N · η₀.

The elastic stretchability of an electronic device ε_{elastic − device} (see Note 1 in the Supporting Information for details) with island-bridge design can be related to the elastic stretchability of the interconnect ε_{elastic − ict} (defined by the yield strain of metal, ≈0.3%) as

$${\epsilon }_{\text{elastic}-\text{device}}={\epsilon }_{\text{elastic}-\text{ict}}\cdot (1-\sqrt{{\eta }_0})$$ (1)

This result suggests that when high areal coverage is required, the deformable mechanics of interconnects must be fully exploited to provide adequate system-level stretchability. Optimization relies upon analyzing the respective contributions of the three constituents in the structure, namely, the interlayer, the encapsulation, and the circuit patterns. We take a representative cell size L_island = 5 mm employed by Lee et al. to illustrate. To identify the effects of the Silbione interlayer of different thicknesses, we adopt the cross-section shown in the inset of Figure 2a. We use unit cell patterns in both circuit layers and fix the key dimensions as L_spacing = 1.5 mm, L_amplitude = 2.2 mm, and w = 100 μm. In both top and bottom composite encapsulations, the thicknesses of the Silbione and Ecoflex are set as t_Silbione = 300 μm and t_Ecoflex = 200 μm, respectively. The interlayer defines the vertical separation between the two layers of circuits filled by Silbione, with thickness t_inter While it is desirable to have circuit layers perfectly overlapping, mismatch between patterns in the upper and lower layers may occur, due to misalignment in fabrication processes or dissimilar circuit patterns in the two layers (see Note 2 and Figure S2 in the Supporting Information for details). This mismatch can significantly change the stretchability of the two circuits involved by affecting interlayer mechanics. Here, we look into three typical scenarios with in-plane pattern mismatch, namely x-directed, y-directed, and mirrored misalignments in addition to the case with perfectly aligned patterns. We start by setting the interlayer thickness t_inter as 400 μm, a sufficiently large value used by Lee et al.^[39] 3D FEA and experimental measurement are used to study the deformation and elastic stretchability of the pair of interconnects under each of the four alignment conditions. The results in Figure 2a show that, as expected, the interconnect pair with perfect alignment yields the highest elastic stretchability (ε_{lastic − ict} = 150%), which is even slightly higher than the elastic stretchability of a similarly encapsulated monolayer interconnect (ε_{elastic − ict} = 148%, Figure S3, Supporting Information). FEA results and experimental images shown in Figure 2b both indicate that the initially aligned interconnects (top row) remain aligned throughout the elongation (bottom row), whereby interconnect segments in the upper or lower layer buckle in synchrony. As the interconnects deform, typically by out-of-plane buckling and in-plane bending, they induce significant deformation in the surrounding silicone matrix. The deformed matrix, in return, mechanically constrains further deformation of the interconnects. When the two interconnects are perfectly aligned, mechanical constraints from the matrix are minimized. This behavior contributes to the high elastic stretchability of both interconnects. A sufficient thickness of the interlayer is required in order to minimize the mechanical constraints, as shown in Figure 2a. The elastic stretchability of interconnects remains almost constant as the interlayer thickness t_inter decreases, until the thickness reaches a critical minimum value t_{inter − crit} ≈ 150 μm (the last solid marker in the curve, Figure 2a). These results set the optimal interlayer design for stretchable electronics with stacked circuits, where a thin overall construct is desirable. Further thinning the interlayer below t_{inter − crit} will enhance the interference between the two interconnects via the thin separating medium and cause slightly decreased stretchability.

Figure 2.

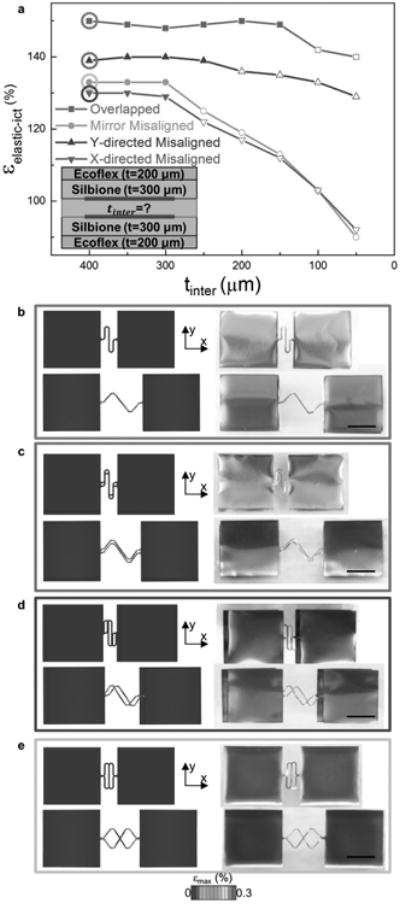
Design optimization of silicone interlayer between interconnects, guided by numerical and experimental results. a) The elastic stretchability of interconnects versus the interlayer thickness, for interconnect pairs with and without misalignments. b–e) FEA and optical images of initial (top) and deformed (bottom) interconnects, when the two interconnects involved are vertically overlapped (b), misaligned by 300 μm in y direction (c), misaligned by 300 μm in x direction (d), and mirrored (e). The deformed interconnects were all stretched toward their elastic stretchabilities. The color in FEA images denotes the maximum principal strain in metal. (Scale bars: 250 μm).

Cases with pattern misalignments, however, are much more complex. With the interlayer thickness set as 400 μm, we find that the interconnect pair supports higher elastic stretchability when the misalignment is y-directed (Figure 2c, ε_{elastic – ict} = 139%) rather than x-directed (Figure 2d, ε_{elastic − ict} = 130%) or mirrored (Figure 2e, ε_{elastic − ict} = 133%). This difference can be attributed to the different, additional constraints imposed by the interlayer due to pattern misalignment. When two interconnects with y-directed misalignment are adequately elongated (Figure 2c), they do not share overlapped regions anymore and behave almost like two independent interconnects with only lateral interaction. Since no severe deformation in the interlayer is required to accommodate this interaction, the additional constraints from the strained interlayer are also relatively small, so that the interconnects maintain acceptable stretchability. Similar to the previous case, the elastic stretchability of interconnects with y-directed misalignment is not very sensitive to interlayer thickness either, as shown in Figure 2a. On the other hand, two interconnects with x-directed or mirrored misalignment always share one or more overlapped sites. In close proximity with these sites, the two interconnects buckle and bend in distinct ways (Figure 2c,d), so that the interlayer must undergo severe deformation in order to accommodate their vertical and lateral interaction. In return, the interlayer significantly constrains the motion of the interconnects, leading to low stretchability. It is noteworthy that unlike lateral interaction, vertical interaction between the two interconnects can be greatly enhanced when the thickness of the interlayer medium decreases. As a result, the stretchabilities of interconnect pairs with x-directed or mirrored misalignment are quite sensitive to reductions in interlayer thickness. When the interlayer is thinner than t_{inter − crit} 300 μm (much larger than that of perfectly aligned interconnects), interconnect elastic stretchability decreases significantly. Therefore, alignment of circuit layers is important in order to achieve desirable stretchable mechanics with the thin interlayer design.

To optimize the design of the composite encapsulation, we use the cross-sectional structure shown in the inset of Figure 3a. A single-layer unit cell test circuit is bonded to a composite substrate layer consisting of Silbione and Ecoflex, both 300 μm thick, before being encapsulated on top by a superstrate with various designs. The relatively “bulky” substrate provides an almost semi-infinite condition at the bottom, so that contributions to interconnect stretchability from the encapsulation layer on top can be studied specifically. We alter the encapsulation layer's effective stiffness and the amount of mechanical constraint it imposes to the deformable circuit by tuning the thicknesses of Ecoflex or Silbione constituent, or both. Both FEA and experimental observation were used in the study, with remarkable agreement in deformation features from these two approaches for each case analyzed. Figure 3a and Figure S4 (Supporting Information) show that the elastic stretchability of the interconnects can change as much as ≈60% for Silbione thicknesses in the range of 100–300 μm, and Ecoflex thicknesses of 10–300 μm. For optimal encapsulation (defined by providing maximized interconnect stretchability), both Silbione and Ecoflex layers should be thin. Figure 3b and Figure S5a (Supporting Information) demonstrate the deformed unit cell with thin Silbione (t_Silbione = 100 μm), thin Ecoflex (t_Ecoflex = 10 μm) encapsulation at its limit of elastic stretchability (168%). Both FEA prediction and experimental observation show comparable deformation characteristics with less strained, flat mid-line segments lying in plane and higher strained adjacent arc regions buckling upward. The soft, compliant nature of Silbione enables significant out-of-plane buckling in the arc regions. This buckling partially relieves excessive strain localization in the metal, so that a maximum level of elongation can be accommodated before plastic yielding. However, the desirable high stretchability cannot be maintained when using only thin Ecoflex or Silbione layers individually. A thick Silbione layer (e.g., ≈300 μm) imposes increased constraints on the deforming interconnects, even if the Ecoflex constituent is thin. Figure 3c and Figure S5b (Supporting Information) suggest that although replacing a moderately thin Silbione layer with a thick one is not sufficient to qualitatively affect the buckling characteristics, it still leads to a slightly reduced ε_{elastic − ict} of ≈160%. A worse scenario occurs when using the thin Silbione (t_Silbione = 100 μm), thick Ecoflex (t_Ecoflex = 200 μm) encapsulation strategy, as shown in Figure 3d and Figure S5c (Supporting Information). We can clearly observe a qualitative change in the deformation mode. In the new mode, the lack of out-of-plane buckling (for relieving localized strain) causes a significant decrease of the interconnect elastic stretchability, to only 110%. The severely reduced out-of-plane displacement follows from the increased thickness, and consequent rigidity of the higher modulus Ecoflex. Instead of a thin, compliant film with negligible mechanical effects, a bulky, stiff Ecoflex layer can dominate the mechanics of the composite encapsulation. Via the comparatively thin Silbione layer underneath, this “stiff” Ecoflex layer suppresses the buckling behavior of the interconnects. The influences of Ecoflex are further amplified by the comparatively thin Silbione medium, which places the stiff Ecoflex layer into close proximity to the interconnects. In fact, an encapsulation structure with thin Silbione, thick Ecoflex layers yields even lower stretchability than one where both constituents are thick (e.g., t_Silbione = 300 μm and t_Ecoflex = 200 μm). Therefore, keeping both constituting layers thin in the composite encapsulation construct yields the best stretchable mechanics, in addition to the desirable minimum device thickness.

Figure 3.

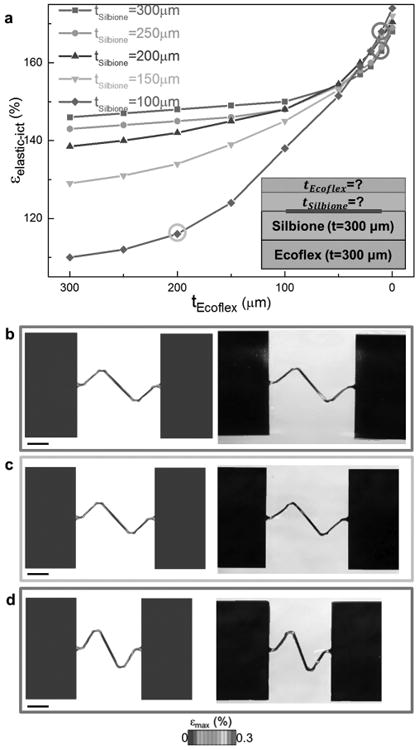
Design optimization of composite encapsulation, guided by numerical and experimental results. a) Elastic stretchability of interconnect with different thicknesses of core (Silbione) and shell (Ecoflex) constituents in the encapsulation. b–d) FEA and optical images of deformed interconnects with three representative encapsulation strategies. The combination “thin Silbione, thin Ecoflex” (b) provides better stretchability than “thick Silbione, thin Ecoflex” (c) or “thin Silbione, thick Ecoflex” (d). The deformed interconnects were all stretched toward their elastic stretchabilities. The color in FEA images denotes the maximum principal strain in metal. (Scale bars: 100 μm).

In the above discussions, excellent agreement to experimental images validates the 3D FEA models and establishes their utility as an effective tool for interconnect design optimization. Specifically, 3D FEA models provide information on (i) the buckling patterns of the interconnects, (ii) the elastic stretchability limits, and (iii) strain distributions in each material and the locations of plastic yielding. To obtain the optimized interconnect geometry at a given areal coverage (e.g., η₀ = 59.2%), we search the interconnect amplitude to locate the maximum elastic stretchability ε_{elastic − ict}, while fixing the size of islands (L_island = 5 mm), the spacing among them (L_spacing = 1.5 mm), and the width (w = 100 μm) of serpentine interconnects. Since previous studies demonstrated the role of PI thickness in affecting the mechanics of stretchable circuits,^[43–45] we perform the search for circuit layers with medium (t_PI = 4.8 μm), thick (t_PI = 7.5 μm), and thin (t_PI = 2.1 μm) PI clads while maintaining the thickness of conductive metal (t_metal = 0.5 μm). In all FEA models, a single circuit layer (PI/Cu/PI) resides on a relatively thick composite substrate (t_Silbione = t_Silbione = 300 μm) prior to encapsulation by a superstrate of optimized design (t_Silbione = 100 μm, t_Silbione = 10 μm). Figure 4a shows the elastic stretchability of interconnects with L_amplitude ranging from 2 to 4 mm. It is clear that the three curves corresponding to different PI thicknesses display distinct trends. When the thickness of PI clads is 4.8 μm, elastic stretchability of the interconnects increases rapidly and almost linearly from 154% to 204% as the amplitudes increase from 2 to 2.6 mm. Beyond 2.6 mm, further increment in amplitude causes a much slower increase in ε_{elastic − ict}, which reaches a plateau at 216% when L_amplitude = 3.6 mm. For interconnects with thin PI clads (t_PI = 2.1 μm), elastic stretchability increases relatively slowly from 112% to 134% when L_amplitude increases from 2 to 4 mm. The values of ε_{elastic − ict} are much lower than those obtained when PI clads are of medium thickness. Contrary to these two cases, the elastic stretchability of interconnects with thick PI clads (t_PI = 7.5 μm) shows almost a reversed trend. When their amplitudes are small (e.g., L_amplitude = 2 mm), these interconnects exhibit high elastic stretchability (ε_{elastic − ict} = 184%), which compares favorably with their counterparts with the same amplitude and PI clads of medium thickness. However, as the interconnect amplitude increases, their elastic stretchability continuously decreases. When the amplitude is 4 mm, the resulting interconnect elastic stretchability is only 145%. This value is only about two thirds of that obtained from interconnects with medium-thickness PI clads (ε_{elastic − ict} = 215%).

Figure 4.

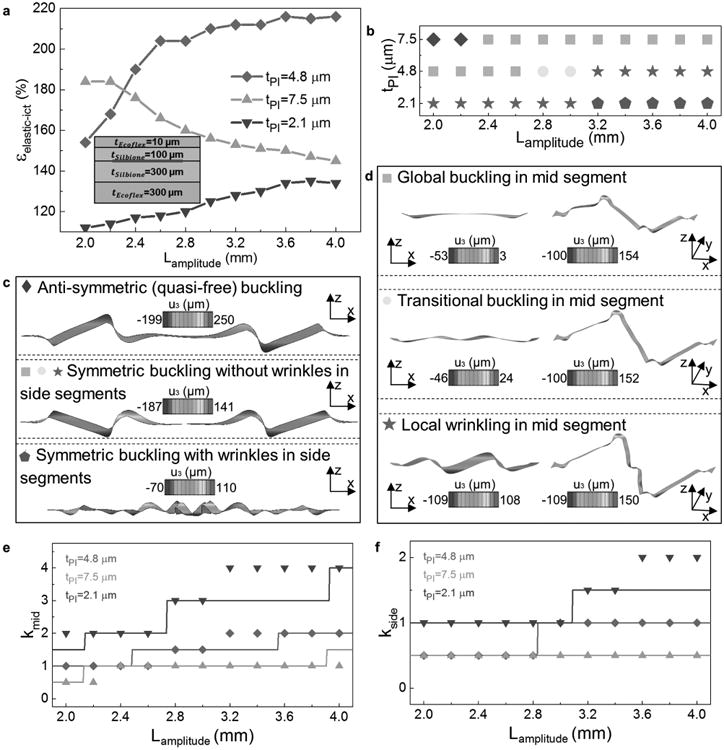
Buckling mechanics of interconnects with different structures. a,b) Elastic stretchability (a) and buckling mode (b) for interconnects with eleven representative amplitudes and three representative PI clad thicknesses. The markers corresponding to each mode are: Mode I (◆), Mode II (■), Mode III (●), Mode IV (★), and Mode V (☖). c,d) FEA images of the five characteristic buckling modes of interconnects. The color denotes out-of-plane displacement u₃ in the metal layer of interconnects. In (d), images in the left column are magnified side views of the middle segments for interconnects in the right column. e,f) The number of ripples formed in the middle (e) and the side (f) segments of interconnects, as calculated analytically (solid lines) and predicted by FEA (scattered dots).

These seemingly contradictory results can be interpreted by the distinct buckling mechanics of the interconnects. Figure 4b–d of the Supporting Information shows the various buckling modes of interconnects in each case, extracted from FEA models. For interconnects with small amplitude, thick PI clads (e.g., L_amplitude = 2 mm and t_PI = 7.5 μm) with consequently high stiffness, twisting is more energetically favorable than bending of the segments.^[46] Therefore, an “antisymmetric” buckling mode, dominated by segment twisting, will occur. As shown in Figure 4c (top panel), the four curved parts of the interconnect move vertically up and down, respectively, and the out-of-plane displacement u₃ is antisymmetric about the center. Both the long, straight segment in the middle and the two shorter straight segments at the side undergo mostly twisting, with no observable wrinkle formation. Since such interconnects are very stiff in relation to the substrate and superstrate, the mechanical resistance from the surrounding materials become insignificant. These interconnects deform in a manner similar to free-standing or free-floating ones (Figure S6, Supporting Information), with curved parts, typically the site of failure, accommodating most of the applied load by large out-of-plane motion to circumvent excessive strain localization. Therefore, interconnects buckling antisymmetrically show desirable, high elastic stretchabilities. However, antisymmetric buckling cannot be sustained by interconnects with larger amplitude, or thinner PI clads. For these interconnects, constituting the much larger portion in our discussion, “symmetric” buckling modes takes place. Symmetric buckling involves all the curved parts moving upward, so that their out-of-plane displacement u₃ is symmetric about the center. Since segment bending is more energetically favorable in comparison with twisting, global buckling or local wrinkle patterns will form in the initially flat straight segments. Here, global buckling means the straight segment buckles out-of-plane and forms ONE complete “wave” shape, as shown by Figure 4d (top panel). In contrast, local wrinkling (Figure 4d, bottom panel) suggests that two or more periodic “ripples” form in the straight segment. In some cases, transitional buckling, illustrated by Figure 4d (middle panel) may also occur. This means that the one “wave” has bifurcated, but has not formed two complete periodic “ripples.” Since a straight wire must be evidently longer than the wavelength in order to induce wrinkling patterns, the longer mid segment is more likely to form buckles and wrinkles than the shorter side segments in the same interconnect.^[45] Based on whether wrinkles form in the side segments, we divide symmetric buckling into two categories, as illustrated by Figure 4c (middle and bottom panels). Symmetrically buckled interconnects without wrinkles in the side segments can be further placed into three sub-categories, depending on whether global buckling (Figure 4d, top panel), transitional buckling (Figure 4d, middle panel) or local wrinkling (Figure 4d, bottom panel) occurs in the mid-segment. We characterize the aforementioned modes of buckling by the number of periodic buckling/wrinkling ripples formed in the middle (k^mode_mid) and side (k^mode_side) straight segments. While the counted numbers of ripples are usually integers, we assign 0.5 to antisymmetrical buckling and 1.5 to transitional buckling in order to complete the system in a physically meaningful way. The five different modes discussed above appear in Table 1, together with their k^mode values.

Table 1.

Criteria for determining buckling modes of interconnect.

Mode #	kmodeside	kmodemid	Description
I (◆)	0.5	0.5	Antisymmetric buckling
II (■)	0.5 or 1	1	Symmetric buckling without wrinkles in the side segments and global buckling in the mid segment
III (●)	0.5 or 1	1.5	Symmetric buckling without wrinkles in the side segments and transitional buckling in the mid segment
IV (★)	0.5 or 1	2, 3, …	Symmetric buckling without wrinkles in the side segments and local wrinkles in the mid segments
V (☖)	1.5, 2, 3, …	2, 3, …	Symmetric buckling with wrinkles in the side segments

The systematic classification of symmetric buckling allows us to understand the results shown in Figure 4a. For interconnects with thick PI clads (t_PI = 7.5 μm), increasing their amplitudes makes them gradually deviate from the antisymmetric mode (Mode I). When buckling symmetrically (Mode II), these interconnects are too stiff to render the formation of wrinkles in the mid or side segments. Without wrinkles to release stored energy, strain in the metal layer accumulates at the sites of the bent curved wires and compromises the stretchable mechanics of the interconnect, as shown in Figure S7a,b of the Supporting Information. As L_amplitude continues to increase, interconnects gradually lose all the desirable mechanics of antisymmetric buckling and have decreasing elastic stretchability. For interconnects with medium PI clads (t_PI = 4.8 μm), the interconnects buckle symmetrically (Mode II) when the amplitudes are small (L_amplitude ≤2.6 mm), without wrinkles forming in straight segments. In this range, the elastic stretchability of the interconnects is mostly determined by length of the serpentine. Therefore, increasing L_amplitude effectively promotes ε_{elastic − ict}. Beyond ≈2.6 mm, increasing L_amplitude renders the formation of transitional buckles (Mode III) or local wrinkles (Mode IV) in the mid segment, while none are observed in the side segments. Wrinkling (in the mid segment) supersedes serpentine length and becomes the dominant influence for stretchability. The elastic stretchability of the interconnect increases much more slowly, and eventually stabilizes when a plateau is reached. When the PI clads of interconnects are thin (t_PI = 2.1 μm), wrinkling always occur in the mid segment (Mode IV). As the amplitude increases, and consequently the lengths of the side segments, wrinkles start to form in the side segments as well (Mode V). Increasing the amplitude promotes elastic stretchability of the interconnects by encouraging the occurrence of wrinkles, which help to release the localized strain in the curved parts (Figure S7c,d, Supporting Information). However, for the interconnects with thin PI pads, microwrinkles form at the edges of the curved wires. These microwrinkles have very small radii of curvature ≈10 μm, which leads to a large local strain in the metal and, therefore, a low elastic stretchabilty for the interconnects (Figure S7e, Supporting Information). When L_amplitude is large, even though ε_{elastic − ict} has increased to 135%, this value is still inferior by comparison. In summary, for a given areal coverage (η₀ = 59.2%), a high elastic stretchability ε_{elastic − ict} 215%, or equivalently ε_{elastic − device} 49.6% can be obtained when the amplitudes of the interconnects are large (L_amplitude ≥ 3.6 mm) and the PI clads are of medium thickness (t_PI = 4.8 μm).

The analyses above demonstrate that the designs of the interconnect can be optimized via the study of their detailed buckling mechanics. Therefore, identifying the exact mode of buckling is the critical first step toward finding the stretchability of a proposed design. Here, we use a simple analytical model to predict the pattern of buckle/wrinkle formation in the straight segments in the interconnect by considering only the effects of the compliant, immediate substrate material (i.e., Silbione). The relatively thin composite superstrate (t_Silbione = 100 μm and t_Ecoflex = 10 μm) and the stiffer layer in the substrate (i.e., Ecoflex) are neglected because they play subordinate roles in determining the buckling mechanics of interconnects. In the study of Jiang et al., a stiff thin film bonded onto a prestrained elastomeric substrate, releasing the prestrain ε_pre results in a compressive strain ε_comp = ε_pre/(1 + ε_pre) in the film to induce buckle/wrinkle formation.^[47] The wavelength of wrinkles (or buckles) is given by

$$\lambda =2\pi t_{\mathrm{f}}{\left(\frac{{\overline{E}}_{\mathrm{f}}}{3{\overline{E}}_{\mathrm{s}}}\right)}^{\frac{1}{3}}{(1+{\epsilon }_{\text{pre}})}^{-1}{[1+\frac{5}{32}{\epsilon }_{\text{pre}}(1+{\epsilon }_{\text{pre}})]}^{-1/3}$$ (2)

where t_f is the thickness of the film, Ē = E/(1–ν^[2]) denote the plane-strain modulus (E is the Young's modulus and ν is the Poisson ratio) and the subscripts “f” and “s” refer to the film and its immediate substrate, respectively. For our serpentine-shaped interconnects bonded onto the top surface of composite substrate, the straight segments undergo compression due to the Poisson effect when the spacing between two islands is elongated by ε_appl. In the analytical model, the applied strain ε_appl should take values comparable to the elastic stretchability of the interconnects ε_{elastic − ict} to obtain the buckling mode of interest. Since the elastomeric substrate is nearly incompressible (i.e., ν = 0.5),^[45,47] the compressive strain along the direction of straight segments can also be expressed as ε_comp = 1 − (1 + ε_appl)^−1/2 (see Note 3 in the Supporting Information for details). Therefore, an equivalent prestrain in the substrate is be given by

$${\epsilon }_{\text{pre}}=\sqrt{1+{\epsilon }_{\text{appl}}}-1$$ (3)

Since the “film” in the current context is a trilayer interconnect with conductive metal (e.g., copper) clad by two equally thick PI layers (t_metal = 0.5 μm, Ē_metal =134.55 GPa and t_PI is 2.1 μm, 4.8 μm, or 7.5 μm, Ē_PI =2.83 GPa), the thickness and equivalent plane-strain modulus of the film can be expressed as

$$\begin{array}{c}{t}_{\mathrm{f}}=2t_{\text{PI}}+t_{\text{metal}}\\ {\overline{E}}_{\mathrm{f}}={\overline{E}}_{\text{PI}}+({\overline{E}}_{\text{metal}}-{\overline{E}}_{\text{PI}}){\left(\frac{t_{\text{metal}}}{2t_{\text{PI}}+t_{\text{metal}}}\right)}^3\end{array}$$ (4)

The thickness and properties of the substrate are also defined by using the values of Silbione layer in the composite (i.e., t_s = 300 μm, E_s = 3 kPa, and $\overline{E_{\mathrm{s}}}=3.99\text{kPa}$). By substituting Equations (3) and (4) into Equation (2), we can express the buckling wavelength as

$$\lambda =2\pi {[\frac{{\overline{E}}_{\text{PI}}}{{\overline{E}}_{\mathrm{s}}}{(2t_{\text{PI}}+t_{\text{metal}})}^3+\frac{{\overline{E}}_{\text{metal}}-{\overline{E}}_{\text{PI}}}{3{\overline{E}}_{\mathrm{s}}}{t}_{\text{metal}}^3]}^{\frac{1}{3}}g({\epsilon }_{\text{appl}})$$ (5)

where $g({\epsilon }_{\text{appl}})={[1+\frac{5}{32}(1+{\epsilon }_{\text{appl}}-\sqrt{1+{\epsilon }_{\text{appl}}})]}^{-1/3}/\sqrt{1+{\epsilon }_{\text{appl}}}$ is a function only related to the applied strain. Equation (5) explicitly shows that the buckling (or wrinkling) wavelength increases with the thickness of the PI clads. For instance, when the thicknesses of PI are 2.1, 4.8, and 7.5 μm, paired with the applied strains 125%, 200%, and 160%, respectively, the wavelengths of the wrinkles obtained from Equation (5) are 1193, 2134, and 3358 μm. For interconnects with thinner PI clads, wavelengths are smaller so that more periodic ripples can fit into straight segments of the same length. Therefore, wrinkles are more likely to form. The number of periodic ripples in a certain straight segment k^analytic can be calculated as

$$\begin{array}{c}{k}_{\text{mid}}^{\text{analytic}}=┌\frac{L_{\text{amplitude}}-2R}{\lambda }┐\\ k_{\text{side}}^{\text{analytic}}=┌\frac{\frac{1}{2}{L}_{\text{amplitude}}-2R}{\lambda }┐\end{array}$$ (6)

where R is the radius of ½ and ¼ circular curve segments, and the subscripts “mid” and “side” represent the longer middle segments and the shorter side segments, respectively (Figure S8, Supporting Information). The superscript “analytic” suggests that this number is obtained analytically, and the symbol ┌┐ is used here to denote rounding up to the nearest k^mode's in Table 1. This type of rounding is adopted in order to achieve more accurate prediction of buckling modes, through counterbalancing the slight overestimation of wavelength by Equation (5). As an example, for a representative interconnect with large amplitude (L_amplitude = 3.6 mm) and medium PI clads (t_PI = 4.8 μm), we calculate its numbers of ripples as $k_{\text{side}}^{\text{analytic}}=2$ and $k_{\text{mid}}^{\text{analytic}}=1$. Table 1 suggests that Mode IV will occur, where wrinkles are only expected to form in the mid-segment of this symmetrically buckled interconnect. This prediction based on analytic criteria matches precisely with the mode obtained from FEA models. Figure 4e,f shows the number of ripples in the mid (Figure 4e) and side (Figure 4f) segments, as predicted by FEA (scattered dot figures) and calculated following Equations (2)–(6) (solid lines). The good agreement in the prediction of buckling modes with FEA models for the majority of cases (27 out of 33, Table S1 and Note 4, Supporting Information) validates these proposed criteria.

The areal coverage of component islands η₀ is another important design consideration for stretchable electronics. Usually, there exists a compromise between maximized fill-factor of functional components and the desirable deformable mechanics of the device. To find the effect of areal coverage, we use FEA models to study the elastic stretchability of unit cells with different spacings between islands. The size of the islands (L_island = 5 mm) and the cross-sectional design of the circuit (t_metal = 0.5 μm and t_PI = 4.8 μm), substrate (t_Ecoflex = 300 μm and t_Silbione = 300 μm), and superstrate (t_Ecoflex = 10 μm and t_Silbione = 100 μm) are all kept the same. When spacing values are 1.5 mm, 1.25 mm, and 1 mm, the resulting areal coverage η₀'s are 59.2%, 64.0%, and 69.4%, respectively. For unit cells with different η₀'s, we let the amplitude of interconnects L_amplitude vary in the range of 2–4 mm to obtain the corresponding, optimized device-level elastic stretchability ε_{elastic − device}. The results, plotted in Figure 5a, show that for each of the three cases, stretchabilities are enhanced when increasing the amplitude of interconnects, before a plateau is reached. Beyond this value, further increasing the amplitude does not significantly change the stretchability values. When the distributions of islands are sparse (L_spacing = 1.5 mm), medium (L_spacing = 1.25 mm), and dense (L_spacing = 1 mm), the optimized elastic stretchabilities are ≈50%, ≈40%, and ≈33%, respectively. Out of the three spacing values, we consider L_spacing = 1.25 mm to be optimal, as it simultaneously offers high areal coverage (η₀ = 64%) and sufficient elastic stretchability (≈40%, about 1.5 times that of human skin), both improved from previously reported devices.^[20,39] The buckling modes of the interconnects in each case obtained from finite element analysis are plotted in Figure 5b. As expected, wrinkles start to form in the mid segment when L_amplitude increases, so that the buckling mode transforms from Mode II, to Mode III, and then to Mode IV. No wrinkles are observed in the side segments. Figure 5c shows that the change of buckling mode is accompanied by a transition in the weakest site. Shorter interconnects (with small amplitudes) tend to fail at the ½ circular wires joining the mid segments, while longer ones (with large amplitudes) encounter plastic deformation first at the ¼ circular wires near the islands. A likely explanation is that the formation of wrinkles in the mid segments releases excessive local strains in the interconnects, so that plastic yielding is postponed until yielding takes place at the connection sites with islands. Interestingly, the transitions of both buckling modes and weakest sites occur at smaller L_amplitude for circuits with denser island distributions. The detailed cause and mechanism will be investigated in the future.

Figure 5.

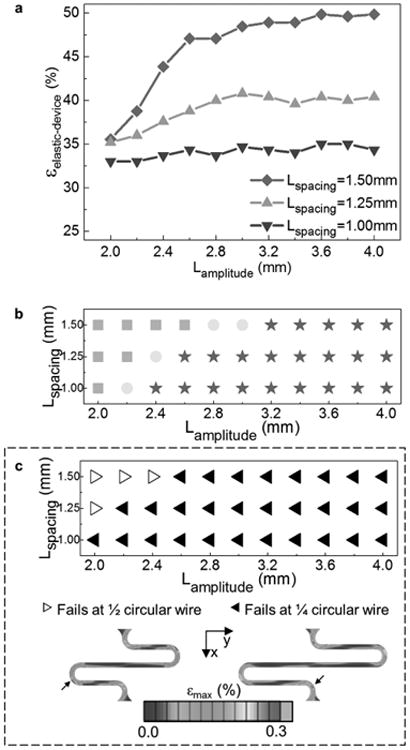
a) Elastic stretchability, b) buckling patterns, and c) sites of failure for device with coarse (L_spacing = 1.5 mm), medium (L_spacing = 1.25 mm), and dense (L_spacing = 1 mm) distribution of component islands and different interconnect amplitudes. The scale in (c) denotes the maximum principal strain in metal.

Now, we demonstrate a representative electronic module with optimized design, featuring ultrasoft, thin construction and very high areal coverage of functional components. This device can be compliantly wrapped on a human index finger (Figure 6a) or a stirring rod (Figure 6b). In the device, the upper and lower circuit layers are separated by an inter medium with minimum critical thickness (150 μm) and encapsulated from both sides by thin composite encapsulations (t_Silbione = 100 μm and t_Ecoflex = 10 μm). The resulting overall thickness of the device is only ≈370 μm, almost one-fourth of previously reported devices.^[39,42] In each circuit layer, 36 square electronic “islands” with side length L_island = 5 mm are densely distributed in a 4 × 9 matrix, with the spacing among islands set as L_spacing = 1.25 mm. The areal coverage η₀ of a single circuit layer is 64%. Based upon the investigation of serpentine buckling mechanics, we set the amplitude of the interconnect L_amplitude to 3 mm, and the thickness of each PI/Cu/PI circuit to 4.8/0.5/4.8 μm. In addition to doubled effective areal coverage (η_eff = 128%), Figure 6c demonstrates that stacking two circuit layers with good alignment yields a device with uncompromised stretchable mechanics. FEA results show the elastic stretchability of the device as ≈42%, which is much higher than that of human skin (≈20%–30%). Even with maximum tensile deformation, the electrical properties of the interconnect networks remain invariable, as supported by a lack of measurable change in the resistance (Figure 6d). Besides stretching, the module can also sustain large repetitive twisting deformation. The FEA model in Figure 6e shows that the maximum principal strains in the metal are much below 0.3% when the device is twisted up to 90°, proving that the deformation is elastic and reversible. Further increasing the twist angle leads to instability where the structure wrinkles inward, yet the change in electrical resistance of the device is less than 1% even at 180° of twisting. The module can be folded twice (about two axes, in opposite directions) to form a recoverable shape with as many as six stacked circuit layers (Figure 6f and Figure S9, Supporting Information). At the folding site, the strain in metal remains below the yield strain, despite the large levels of deformation in the elastomers. The invariance in resistance of the circuit also supports that the deformation is reversible. Here, the excessive load associated with folding is accommodated by the buckling of interconnects in both circuit layers. It is noteworthy that the temporary six-layer structure can still sustain some level of elastic uniaxial elongation (Figure 6g and Figure S10, Supporting Information), yet the exact elastic stretchability is more difficult to predict due to the complex geometry and boundaries. Our FEA model analyzes a worst-case scenario, assuming adjacent encapsulation layers are perfectly tied together. Although this model greatly overestimates mechanical constraints and thus underestimates device elastic stretchability, the obtained value (23%) is still sufficient for most skin-mountable or implantable bioelectronics applications.

Figure 6.

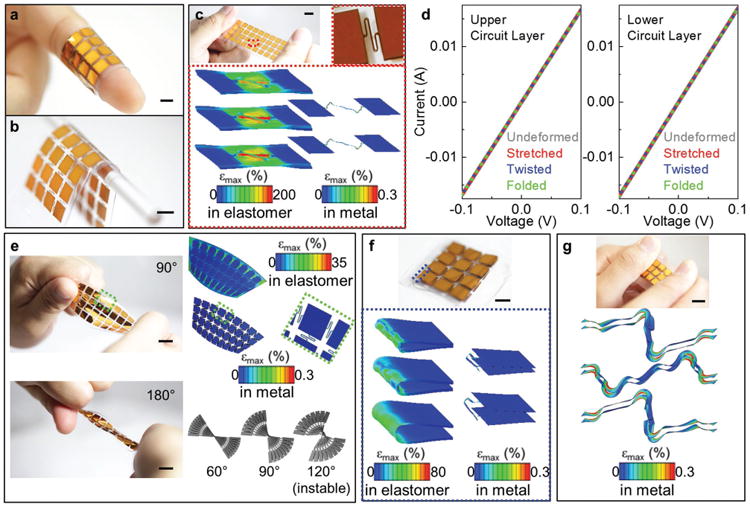
Mechanics and performance of a representative, structurally optimized electronic module with bilayer circuit construct. a,b) Optical images of the device compliantly wrapped around (a) an index finger and (b) a stirring rod. (Scale bar: 500 μm). c) Optical image and FEA results of the device in a uniaxially stretched configuration. (Scale bar: 1 cm). In FEA model, the unit cell (magnified in the optical image) is elongated by 42%. Left column: deformed composite superstrate (top), inter layer (middle), and composite substrate (bottom). Right column: deformed upper (top) and lower (bottom) circuit layer. d) Current–voltage curves measured from the serpentine interconnects under different deformations (undeformed, stretched, twisted, folded). e) Optical images and FEA results of the device in a twisted configuration. In experiment, the device was twisted by 90° (top left) and 180° (bottom left). Structural instability was observed at 180° twisting. (Scale bar: 1 mm.) FEA results show the global deformation of elastomer (1st row) and circuit layers (2nd row, left), and highlight the local site with most severe deformation (2nd row, right). FEA images in the 3rd row show the side view of the circuits before (60° and 90°) and after (120°) the onset of structural instability. f) Optical image and FEA results of the device in a temporarily folded configuration. (Scale bar: 500 μm). FEA models the local site with most significant deformation. Left column: deformed composite superstrate (top), interlayer (middle), and composite substrate (bottom). Right column: deformed upper (top) and lower (bottom) circuit layer. g) Optical image and FEA results for stretching a folded device. (Scale bar: 1 mm). FEA results show a set of deformed serpentine interconnects in the device (elongated by 23%) in a worst-case scenario. Top: upper and lower circuits in the 1st device layer. Medium: lower and upper circuits in the 2nd device layer. Bottom: upper and lower circuits in the 3rd device layer. In all FEA results, color denotes maximum principal strain in metal or in elastomer.

3. Conclusions

This work presents systematic guidelines for designing stretchable electronics with stacked bilayer circuits. The effects of all constituent layers of a device on its stretchability, namely, the ultralow modulus interlayer, the composite encapsulation, and the interconnect structures, have been examined via combined FEA and experiments. Studies of interconnect buckling mechanics suggest that the exact mode of buckling plays a key role in deciding how much elongation the interconnects can accommodate before the onset of plastic yielding. Effective, simple analytic criteria are proposed to predict the buckling mode of the interconnect by calculating the number of periodic wrinkles in its straight segments. The resulting electronic module, combining all the optimized design parameters in discussion, is remarkably stretchable, highly twistable, and reversibly foldable, despite having a high areal coverage of nondeformable, functional components. The greatly reduced overall thickness makes the module much more compliant in comparison to previously reported electronics with stacked circuit designs, making it applicable for conformal, nonintrusive mounting to biological tissues with complex surface structures. The stacking strategy proposed in this work may also benefit the design of stretchable electronic modules with other interconnect motifs.

4. Experimental Section

Electronics Preparation

A≈100 μm-thick polydimethylsiloxane (PDMS, Sylgard 184) spin-coated on a glass slide and cured on a hotplate at 180 °C for 30 min served as a temporary substrate for circuit fabrication. Placing this substrate in an ultraviolet/ozone generator for 4 min created a hydrophilic surface on the PDMS. A polyimide (PI, HD MicroSystems, 4.8 μm) layer spin-coated on top of the PDMS substrate and prebaked on a hot plate at 150 °C for 5 min and hard-baked in the vacuum oven at 250 °C for 60 min formed the base layer of the device. A 500 nm thick layer of Cu deposited with an electron beam evaporator (e-beam evaporator, AJA) served as the active metallization. Photolithography (AZ P4620, AZ 400 K) and etching (Type CE-100) defined patterns of electrodes and interconnects in this layer. Another PI (4.8 μm) layer coated on the Cu followed by deposition of SiO₂ (50 nm) by plasma-enhanced chemical vapor deposition (Plasma-Therm) served as an etching mask. Photolithography and reactive ion etching of the SiO₂ (RIE, Plasma-Therm, 20 sccm CF₄, 100 W, 50 mT) and PI (RIE, March, 20 sccm O₂, 150 W, 195 mT) and then the PI defined features to match the geometry of the underlying Cu traces. Immersion in buffered oxide etchant removed the remaining SiO₂. A water-soluble tape (Aquasol, USA) facilitated transfer of the resulting stack to a stretchable substrate.

Bilayer Circuits Using Folding Integration

Mixing a base and curing agent for a shell (Ecoflex, Smooth-on inc., E∼60 kPa) at a weight ratio of 1:2 and then spin casting at 250 rpm for 3 min and curing at room temperature yielded a soft, stretchable substrate with thickness of ≈300 μm. A core material (Silbione 4717, Bluestar, E ≈ 3 kPa) also mixed in a 1:2 (A:B) weight ratio spin-coated at 300 rpm for 6 min on top of this substrate defined the based layer of the soft core for the devices. After transfer printing the electrode/interconnect stack and bonding the components, another layer of core material (≈200 μm) was coated on the system. Folding of the system yielded a stacked structure of arrays of solar cells (top)/power management circuit-battery array (bottom) after partial curing of core material.

Direct Preparation of Electronics with Bilayer Circuits

The shell (≈10 μm) and core (≈100 μm) layers were spin-coated on a silicon wafer. The first electronics were transfer printed on the core/shell substrate and with additional core (≈150 μm) material spin-coated on the system. After alignment/transfer printing of the second electronics along with the first electronics, additional layers of core/shell were applied to encapsulate the system and complete the fabrication.

Evaluation of Electronic Performance

A DC sourcemeter (model 2400, Keithley) allowed measurement of the current–voltage characteristics under biaxial stretching to confirm the mechanical stability of the contact pads and interconnects.