Hidden heritability due to heterogeneity across seven populations

Abstract

Meta-analyses of genome-wide association studies (GWAS), which dominate genetic discovery are based on data from diverse historical time periods and populations. Genetic scores derived from GWAS explain only a fraction of the heritability estimates obtained from whole-genome studies on single populations, known as the ‘hidden heritability’ puzzle. Using seven sampling populations (N=35,062), we test whether hidden heritability is attributed to heterogeneity across sampling populations and time, showing that estimates are substantially smaller from across compared to within populations. We show that the hidden heritability varies substantially: from zero (height), to 20% for BMI, 37% for education, 40% for age at first birth and up to 75% for number of children. Simulations demonstrate that our results more likely reflect heterogeneity in phenotypic measurement or gene-environment interaction than genetic heterogeneity. These findings have substantial implications for genetic discovery, suggesting that large homogenous datasets are required for behavioural phenotypes and that gene-environment interaction may be a central challenge for genetic discovery.

Introduction

Meta-analyses of genome-wide association studies (GWAS), which dominate genetic discovery are based on diverse data sources that span vast historical time periods and populations.¹ The proportion of phenotypic variance accounted for by single-nucleotide polymorphisms (SNPs) that reach genome-wide significance, and the polygenic scores constructed from all SNPs using GWA study results, however, represent only a fraction of heritability estimates derived from twin and other whole-genome studies.^2,3

To understand this disparity, it is essential to explain three central ways to measure heritability (see Box 1 for detailed definitions). First, narrow-sense heritability stems from family-based studies and often twin research (h²_family) and produces the highest heritability estimates. These studies demonstrated a genetic basis for anthropometric traits such as height and body mass index (BMI), but also behavioral phenotypes such as educational attainment and human reproductive behavior (i.e., number of children, age at first birth).^4–6A recent meta-analysis of twin studies from 1958-2012⁴ estimated, for instance, heritability for educational attainment as 52% (N=24,484 twin pairs) and 31% for reproductive traits (N=28,819 twin pairs).

Box 1. Definitions of heritability.

Heritability

Heritability is the proportion of the phenotypic variance accounted for by genetic effects and narrow sense heritability refers to the additive genetic variance component (for discussion also see 5,48). There are several ways to estimate heritability. First, the highest and prominent estimates are derived from family-based studies (h²_family), such as twin studies, where, typically, the genetic resemblance between relatives is mapped to phenotypic similarity, taking unique- and shared-environment effects into account. Under several assumptions, estimates of h²_family ought to reflect only additive-genetic effects. A second method is the proportion accounted for by genetic variants known to be robustly associated with the phenotype of interest, derived from a GWAS (genome-wide association study) (h²_GWAS). This measure tends to produce the lowest levels. Finally, there is the proportion of phenotypic variance jointly accounted for by all variants on standard GWAS chips. This is sometimes referred to as the SNP- or chip-based heritability (h²_SNP). Typically, h²_SNP is substantially larger than h²_GWAS and provides an ‘upper level estimate’ of the genetic effects that could be identified with a well-powered GWAS. The h²_GWAS increases in tandem with GWAS sample sizes and is expected to approach h²_SNP asymptotically under the assumption that the phenotype of interest is homogeneous in its genetic architecture across different environments.

Missing heritability

The gap between the h²_family and h²_GWAS is referred to as ‘missing heritability’.² Potential reasons for missing heritability are for example non-additive genetic effects (although empirical evidence on this is scarce), ⁸,¹³ large effects of rare variants, ¹⁵ and potentially inflated estimates from twin studies due to shared environmental factors. ¹⁷ The missing heritability is commonly defined as the sum of the still-missing and hidden heritability, which we define below.¹⁶

Still-missing heritability

Yang and colleagues ⁹ argued that most genetic effects are too small to be reliably detected in GWAS of current sample sizes which is why they proposed the whole-genome restricted maximum likelihood estimation performed by GCTA software. ⁴⁹ Studies applying these whole-genome methods typically produce estimates that lie between twin studies and polygenic scores h²_GWAS < h²_SNP < h²_family. The discrepancy h²_SNP < h²_family has been referred to as ‘still-missing heritability’.³ A stylized fact is that for many traits the still-missing heritability is roughly equal to h²_SNP.⁵⁰ It is generally assumed that by genotyping rarer and structural variants, the still-missing heritability will decrease, as the denser arrays will increase h²_SNP.

Hidden heritability

Since we expect to be able to almost fully capture h²_SNP in the long run, the discrepancy between h²_SNP and h²_GWAS is sometimes referred to as ‘hidden heritability’.¹⁶ The current study is mainly interested in the question of how h²_SNP changes, depending on whether we examine differences within or between populations. Here we focus on hidden heritability as the genetic variation due to heterogeneity that cannot possibly be explained by SNP associations based on meta-analyses of multiple populations. Since h²_GWAS is usually inferred from meta-analyses that include multiple populations, heterogeneity in genetic effects on a phenotype between these populations could deflate h²_GWAS and would also deflate h²_SNP – which is typically obtained within single populations. Within a single design we therefore demonstrate how one estimate of h² depends upon population heterogeneity. Missing heritability is thus commonly defined as the sum of the still-missing and hidden heritability.¹⁶ As indicated, the hidden portion will decrease as sample sizes grow and the still-missing portion will decrease with denser forms of genotyping.

GWAS heritability estimates (h²_GWAS) estimate the proportion of phenotypic variance accounted for by genetic variants known to be robustly associated with the phenotype of interest and produce the lowest estimates. The polygenic score from a recent meta-GWAS of educational attainment with over 300,000 participants explains around 4% of the variance⁷ with another GWAS for age at first birth explaining only 1%.⁸

Yang and colleagues argued that most genetic effects are too small to be reliably detected in GWAS of current sample sizes and proposed an alternative approach: whole-genome restricted maximum likelihood estimation (GREML) performed by GCTA software.^9,10 This third measure is often referred to as SNP- or chip-based heritability (denoted by h²_SNP), and is the proportion of phenotypic variance explained by additive genetic variance jointly estimated from all common variants on standard GWAS chips. These estimates are typically between h²_family and h²_GWAS estimates. Contrary to the low h²_GWAS estimates of between 1–4% for these phenotypes, the SNP-heritability has been estimated as 22% for educational attainment, 15% for age at first birth and 10% for number of children.^11,12

This stark discrepancy in heritability estimates has spawned debates about ‘missing heritability’ (the difference between h²_GWAS and h²_family) and ‘hidden heritability’ (difference between h²_GWAS and h²_SNP ) (for full definitions see Box 1 ³).^2,13–16 ‘Missing heritability’ has been linked to fundamental differences in study designs between family and whole-genome studies², non-additive genetic effects^13,14 and inflated estimates from twin studies due to shared environmental factors ¹⁷. Empirical evidence for either of these reasons is scarce. A recent investigation on height and BMI, however, demonstrates that the inclusion of rare genetic variants can increase the heritability estimate based on whole-genome methods.¹⁵ The underlying reason for the discrepancy of ‘hidden heritability’ between h²_SNP versus h²_GWAS estimates are less well understood.¹⁸

Here, we interrogate the common assumption underlying GWA studies’ meta-analyses, that genetic effects are ‘universal’ across environments. The large GWAS meta-analyses required to detect SNP associations consist of a wide array of samples across historical periods and countries, representing heterogeneous populations subject to diverse environmental influences. Heterogeneity across environments can emerge for different reasons such as differences in population structure, genotype or phenotype measurement, heterogeneous imputation quality across sampling populations or sensitivity of the phenotype to environmental change. Demographic research has shown that education and reproductive behavior are strongly modified by environmental changes such as female educational expansion or the introduction of effective contraception.¹⁹ If genetic effects are not universal but rather heterogeneous across populations, heritability estimates from GWAS meta-analyses should produce weaker signals and we would witness a reduction in both the discovery rate and the variance explained from SNPs across populations.²⁰

We conduct a mega-analysis using whole-genome methods which entails pooling all cohorts to estimate genetic relatedness not only within, but also across populations. We utilize models based on GREML estimation¹⁰ using primary data from seven pooled sampling populations. This allows us to estimate the average common SNP-based heritability (h²_SNP) between and within environments. We subsequently apply gene-environment interaction models, adding a within population matrix to estimate the average SNP-based heritability within populations in our data and decompose the variance explanation of common SNPs within and between sampling populations and birth cohorts.^10,21 If SNP-based heritability is significantly higher within than across environments, we conclude that this is evidence for hidden heritability due to heterogeneity across the sample population or cohort. We applied a G×P model when stratifying by sampling populations, a G×C model when stratifying by birth cohorts born before or after the strong fertility postponement during 20^th century (see Material and Methods), and the G×P×C model when stratifying by both (see Material and Methods for details). We define the various genetic variance components of the models explicitly, and will refer to $h_{\text{SNP}}^2$ as the sum of all genetic effects relative to the phenotypic variance within the respective model specification. We quantify the hidden heritability due to heterogeneity as the discrepancy between $h_{\text{SNP}}^2$ from the baseline model and $h_{\text{SNP}}^2$ from the interaction models.

Our approach allows us to decompose average heritability levels across historical cohorts and countries into a genetic component that is either ‘universal’ across all environments or ‘environmentally specific’, enabling a test of whether the same genes are explaining variance in the phenotype to the same extent in different geographical (country) and historical (birth cohort) environments. To test for alternative explanations for heterogeneity across sampling populations, such as genotyping error, we conduct a series of simulation studies to evaluate the role of gene-environment interaction in contrast to alternative explanations (for details and results see Discussion and Material and Methods). A recent study used bivariate GREML models to investigate genetic heterogeneity in height and BMI between two populations in the US and Europe, providing evidence for homogeneity in both phenotypes.²² We expect negligible gene-environment interaction for these anthropometric traits and compare findings for these homogeneous phenotypes to those from behavioural phenotypes (education, human reproductive behavior) using the same modeling framework.

Results

SNP-based heritability across model specifications by phenotypes

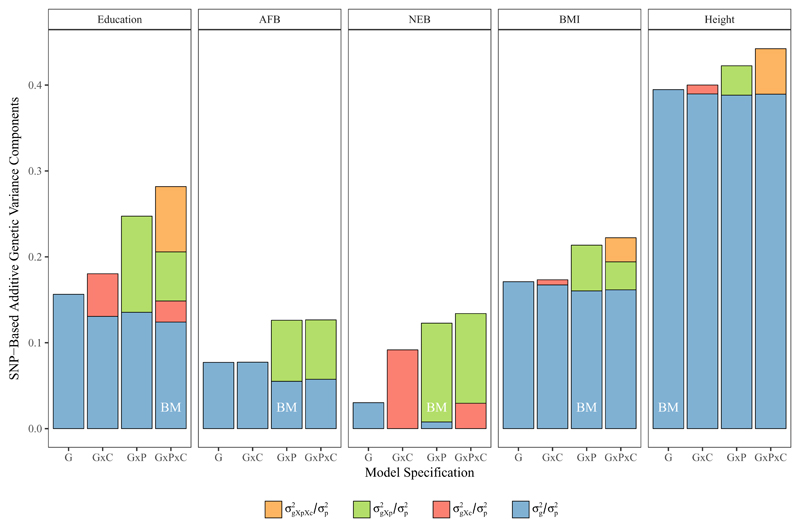
When we ignore environmental differences, h²_SNP in the standard GREML model (G) is significant for all phenotypes, but at different levels (Figure 1 and Supplementary Tables 1-5 for full model estimates). For height, h²_SNP is estimated as 0.40 (SE 0.01), meaning that 40% of the variance in height can be attributed to common additive genetic effects. h²_SNP is smaller for BMI (0.17 SE 0.01) and years of education (0.16 SE 0.01) and low for both reproductive behavior outcomes, NEB (0.03 SE 0.01) and AFB (0.08 0.02).

Figure 1. Stacked Bar Charts of average between $({\mathit{\sigma }}_{\mathit{g}}^{\mathbf{2}})$ and within $({\sigma }_{\mathit{g}\mathit{X}\mathit{p}}^{\mathbf{2}},{\sigma }_{\mathit{g}\mathit{X}\mathit{c}}^2{\sigma }_{\mathit{g}\mathit{X}\mathit{p}\mathit{X}\mathit{c}}^{\mathbf{2}})$ variance explanation by common SNPs estimated for Height, BMI, education, age at first birth (AFB) and number of children (NEB) in four model specifications (G, G×P, G×C, G×P×C).

The best model (BM in white, in chart) is based on likelihood ratio tests comparing the full model with one constraining the respective variance component to 0; see Supplementary Table 6. ${\sigma }_g^2/{\sigma }_P^2$ = proportion of observed variance in the outcome associated with genetic variance across all environments, ${\sigma }_{gXp}^2/{\sigma }_P^2$ = proportion of observed variance in the outcomes associated with additional genetic variance within populations, ${\sigma }_{gXc}^2/{\sigma }_P^2$ = proportion of observed variance associated with additional genetic variance within demographic birth cohorts, ${\sigma }_{gXpXc}^2/{\sigma }_P^2$ = proportion of observed variance associated with additional genetic variance within populations and demographic birth cohorts. Models specifications G, G×P, G×C, G×P×C refer to the model specifications including the respective variance components as well as those of lower order – see Material and Methods. For detailed results see Supplementary Table 1-5.

More importantly, however, for our question, h²_SNP in all phenotypes increases if we include stratified GRMs in addition to the baseline GRM (e.g., yielding the G×C model when stratifying by birth cohorts, the G×P model when stratifying by sampling populations, and the G×P×C model when stratifying by both). Particularly for the complex behavioral outcomes of education and reproductive behavior, the increase is substantial. For education, h²_SNP increases by 80% (up to 0.28 SE 0.03) in the G×P×C model compared to the standard GREML model (G). For AFB, the increase is 60% (0.13 SE 0.04) and for NEB it is as high as 342% (0.13 SE 0.03). In contrast, the increase in the full G×P×C model was considerably smaller at 12% (0.44 SE 0.03) for height and 30% (0.22 SE 0.03) for BMI.

Best model by phenotype

Based on likelihood ratio tests, we identified the best fitting while parsimonious model (in Figure 4 marked as BM; for full results see Supplementary Table 6). For height, the best fitting model includes no gene-environment interaction and therefore corroborates previous findings from the literature. ³⁶

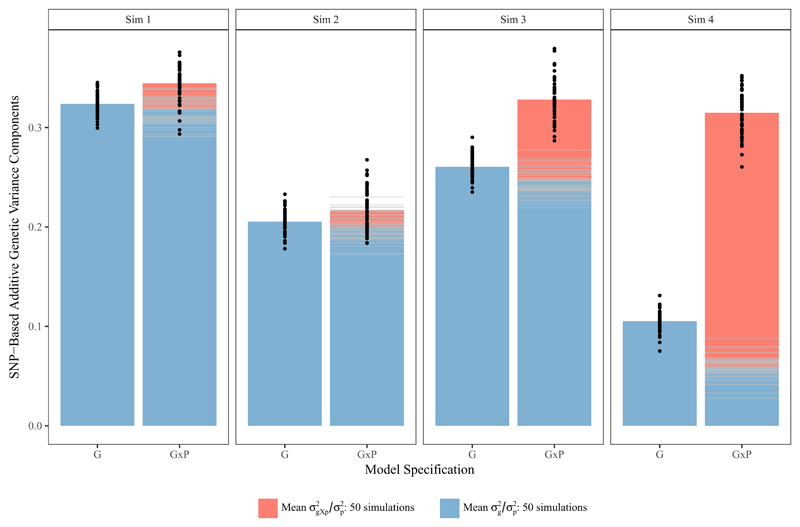
Figure 4. Stacked Bar Charts of average between $({\mathit{\sigma }}_{\mathit{g}}^{\mathbf{2}})$ and within $({\mathit{\sigma }}_{\mathit{g}\mathit{X}\mathit{p}}^{\mathbf{2}})$ variance explanation by common SNPs estimated across 50 simulated phenotypes in two model specifications (standard GREML model and the gene-environment interaction model by study population (G×P) and for four simulated phenotypes.

Sim 1 with homogeneous SNP-based heritability 0.5 without gene-environment interaction, Sim 2 heterogeneous SNP-based heritability between 0.25-0.625 without gene environment interaction, Sim 3 with homogeneous SNP-based heritability 0.5 with gene-environment interaction (genetic correlation of 0.8 across populations) and Sim 4 with homogeneous SNP-based heritability 0.5 with gene-environment interaction (genetic correlation of 0.5 across populations). Individual model estimates are represented by black dots, individual ${\sigma }_g^2$ components in the G×P models in gray stripes.

For BMI, and the reproductive phenotypes of AFB and NEB, the G×P specification shows the best model fit. This indicates significant heterogeneity interaction across sampling populations, while there is no evidence for heterogeneity by birth cohort. For BMI, additive SNP variance effective between and within populations (i.e., the blue column that assumes it is effective across the defined environments or ‘universal’ respectively; ${\sigma }_{\mathbf{\text{G}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2$), 16% of the variance in the phenotype and an additional 5% can be explained on average within populations (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2,$ green column). For AFB, around 6% of the variance can be explained by universal genetic effects while 7% are environmentally specific, and for NEB only 1% of the variance can be explained between populations, with 12% within them. Finally, for education, the best-fitting model (G×P×C) implies that both sampling population and birth cohort moderate genetic effects from the whole genome and that there are genetic effects unique to sampling populations within the defined birth cohorts. In contrast to reproductive behavior, however, 12% of the overall variance can still be explained by additive common genetic effects even between populations. Additionally, there is 2% variance explained within birth cohorts (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{C}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2,$ red column), 6% within populations and 8% which is unique within populations and birth cohorts (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{C}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2,$ orange column).

Quantifying ‘universal effects’ and ‘hidden heritability’ due to heterogeneity

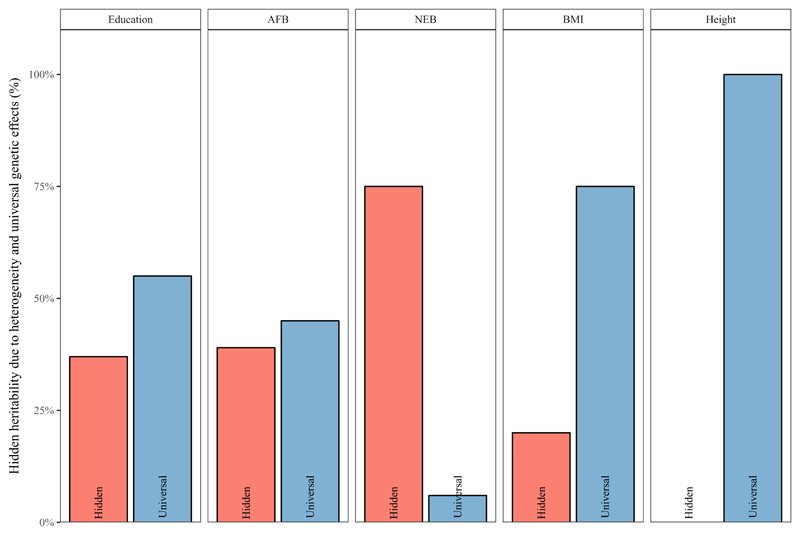
Figure 2 visualizes: (i) the ‘universal effects’ or ratio for genetic variance captured by the normal GRM in the best fitting model (i.e., blue column, ${\sigma }_{\mathbf{\text{G}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2$ in the model with the best fit) and the total $h_{\text{SNP}}^2$ (i.e., across all genetic components in the best fitting model). It also shows (ii) in red the ‘hidden heritability’ due to heterogeneity (i.e., the differences in total $h_{\text{SNP}}^2$ between the best fitting model and the baseline model, divided by the total $h_{\text{SNP}}^2$ of the best fitting model) for all phenotypes.

Figure 2. Bar Charts of average % of hidden heritability due to heterogeneity (% of h²_SNP of the best fitting model which is not captured in standard GREML models) and of universal genetic effects (% of h²_SNP of the best fitting model which is effectively identical across the defined environments).

The Figure illustrates hidden heritability due to heterogeneity particularly for the complex phenotypes we are most interested in, namely: education and the reproductive outcomes of AFB and NEB. For education, only 55% of $h_{\text{SNP}}^2$ in the best fitting model is ‘universal’ or effectively both within and between environments. A standard GREML model (G) would only capture around 63% of $h_{\text{SNP}}^2$ in the best fitting model resulting in 37% hidden heritability. For reproductive behavior, this becomes even stronger. For NEB only 6% of $h_{\text{SNP}}^2$ of $h_{\text{SNP}}^2$ of the best fitting model is universal, with 75% hidden in the baseline model. For AFB, 45% of $h_{\text{SNP}}^2$ is universal with around 40% of the $h_{\text{SNP}}^2$ hidden in the baseline model. For height, in contrast, we see that the $h_{\text{SNP}}^2$ in the best fitting model is effectively between environments and we find no evidence for hidden heritability. For BMI, around 75% of $h_{\text{SNP}}^2$ in the best fitting model is effectively between and within environments (i.e., universal). The standard GREML model (G) for BMI thus captures 80% of $h_{\text{SNP}}^2$ from the best fitting model with 20% hidden heritability.

Discussion

Using whole-genome data from seven populations, we demonstrate heterogeneity in genetic effects across populations and birth cohorts for educational attainment and human reproductive behavior in a mega-analysis framework. Our findings imply substantial ‘hidden heritability’ due to heterogeneity for educational attainment (37%) and reproductive behavior (40% for AFB and 75% for NEB) in the cohorts under study. Comparative analysis with anthropometric traits (height and BMI) corroborates previous findings from whole-genome methods of a more homogeneous genetic architecture of these phenotypes across environments (while for BMI GWA studies also find evidence for gene-environment interaction across birth cohorts in the HRS ^38,39).

Our findings indicate that the lower predictive power of polygenic scores from large GWA studies compared to SNP-based heritability on single or very few populations partly reflects the fact that genetic effects are (to some extent) not universal but rather specific to data sources for these complex traits. Estimates are well in line with the 36-38% loss in polygenic score R² across data sets reported for education.⁴⁰ They demonstrate therefore that the reference SNP-based heritability for the predictive power of polygenic scores obtained from the GWAS meta-analyses amongst several populations is smaller than SNP-based heritability obtained from single populations. While the need for statistical power often still necessitates large-scale GWAS meta-analysis combining multiple and diverse data sources, our findings also suggests that large homogeneous data sources such as the UK Biobank with around 500,000 genotyped individuals may trigger genetic discovery for behavioral outcomes. Drawing conclusions or making predictions out of one discovery sample alone, however, may be inaccurate, since SNPs may have different effects in different samples, or the phenotype may reflect different behavioral aspects.

Complementary simulation studies corroborate the interpretation that our findings are mainly driven by gene-environment interaction in contrast to heterogeneity in residual environmental variance – including measurement error – or genetic heterogeneity (e.g., genotyping platform, genetic architecture, imputation quality) across the data sources we pooled (see Material and Methods). When applying our models to simulated phenotypes without gene-environment interaction but rather to different levels of heritability due to varying residual variance, we find no systematic inflation of the G×P component in our models. Furthermore, we estimated both models including and excluding the causal 5000 SNPs our simulations have been based on. When causal SNPs are removed, estimates are based on correlated SNPs, which are in linkage disequilibrium (LD). To the extent that the structure in the genetic data we use is heterogeneous across populations for above reasons, we can expect that our models interpret it as heterogeneous genetic effects resulting in hidden heritability. However, results in- and excluding causal SNPs are nearly identical, so that we cannot expect heterogeneity drive our findings. However, in the total absence of gene-environment interaction, estimates show a slight inflation in the G×P model (5%) (see Material and Methods for all simulation studies). First, the substantial findings of hidden heritability between 40–75% for behavioral phenotypes largely exceeds this potential inflation, corresponding with simulations of a genetic correlation between 0.5–0.8 across populations for the behavioral phenotypes. Second, we conducted permutation analyses, generating a random gene-environment interaction, not stratifying by population or birth cohorts. Here we found no inflation for age at first birth by a randomly generated matrix included in the models (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2$ 0.000001, SE 0.03, p-value 0.50), nor for number of children ever born (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2$ 0.003, SE 0.02, p-value 0.43) nor education (${\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2$ 0.000001, SE 0.02, p-value 0.50; not listed). It remains vital to conclude that although the estimates of hidden heritability provided in our study are in a single design – in contrast to comparing GWAS and whole-genome methods – estimates do not represent generalizable values of hidden heritability for these traits. The estimates might be slightly inflated and also dependent on the number of cohorts combined for a study as well as the respective level of heterogeneity across them.

Contrary to our expectations, we did not find any evidence for gene-environment interaction across birth cohorts for human reproductive behavior. This is particularly surprising since across time there have been substantial environmental changes such as the introduction of effective contraception, social norms around the timing of childbearing and educational expansion – all factors which strongly modify reproductive behavior. ¹⁹ In contrast, we find cohort specific genetic effects on educational attainment. This contributes to solving the puzzle of missing heritability in educational attainment, since twin studies with higher heritability estimates are also conducted within homogeneous birth cohorts.

Our findings expose the challenges in detecting genetic variants associated with human reproductive behavior or other complex phenotypes in GWAS meta-analyses of multiple cohorts. First, SNP-based heritability within populations is comparably small and second, we find limited evidence that genetic effects underlying reproductive behavior in one country predicts the underlying behavior in another. Our findings likely reflect the interrelated behavioral nature of reproduction and education, which appears to be more sensitive to cultural and societal heterogeneity than for example anthropometric traits such as height or BMI. It has also been shown that pleiotropic genes affecting age at first birth and schizophrenia have different effects across populations.⁴¹ Recently, social scientists have made considerable efforts to integrate molecular genetics into their research.^7,8,12 When considering the highly socially- and biologically-related phenotype of reproductive behavior outcomes, environmental factors are critical in understanding how genetic factors are modified in relation to fecundity and infertility.

Finally, our study also has several important limitations. First, it is possible that heterogeneity in the phenotypic measures influences the patterns we observed. While we find no evidence that our models interpret changing relative environmental contributions to trait variation as gene-environment interaction, we cannot rule out the possibility that the trait definitions differ across environments. We consider this a minor issue for reproductive behavior. While measures are not perfectly harmonized across birth cohorts (for e.g., some questionnaires for example explicitly ask for number of still-births and others do not), in LifeLines and TwinsUK, we compared the live birth measures with number of children ever born and, as expected, given the low mortality rate in both populations, less than 0.2% of the children had not reached reproductive age. Moreover, the correlation between number of children ever born and number of children reaching reproductive age was 0.98. We therefore do not expect a large bias due to the exclusion of stillbirths in some countries (for details see Supplementary Note 1). Nevertheless, we cannot reject the possibility that heterogeneity in the measure of education remains even after homogenizing it with the standard ISCED scale. In this case, we would argue that large parts of the gene-environment interaction pattern we observe for education are due to interaction within populations by birth cohorts where we hypothetically have homogeneous measures. Furthermore, different cross-national definitions of education represent a case of gene-environment interaction. Finally, our statistical findings of heterogeneity are of major importance in shaping our expectations about the ability to locate genetic loci associated with education in GWAS meta-analyses despite their causal mechanisms.

Second, notwithstanding the fact that our simulation studies show no inflation of hidden heritability due to differences in the genetic structure across populations, it is plausible that empirical phenotypes are heterogeneous in reference to rare genetic variants which are not considered in our models and not present in our data. This is an issue demanding further consideration in future research. We are suitably cautious that part of the hidden heritability in our models might be driven by rare, population-specific variants. Previous studies of height and BMI show that rare variants explain a significant part of phenotypic variance,¹⁵ while our models show the least heterogeneity across populations for these phenotypes.

Third, the models we apply average within environmental effects across populations. An optimal study design would be a multivariate genetic modeling approach, which estimates SNP-based heritability for each population and the genetic correlations across them. This approach, however, is feasible for traits with strong or moderate heritability such as height and BMI,²² but lack statistical power²⁸ for phenotypes with small SNP-based heritability such as reproductive behavior¹¹ in the current samples. The models we propose allow us to investigate and compare gene-environment interaction across a range of phenotypes. Multivariate models may become feasible in the future with larger homogeneous data sources, and will also enable us to disentangle shared genetic effects across these phenotypes. ^8,42,43

Finally, in the current modeling approach, we cannot include childless individuals in the modeling of AFB, and future research in quantitative genetics may aim to integrate censored information in their modeling approaches, as is standard in demographic research (for further discussion see 11,44,45).

In conclusion, our study uncovers challenges for investigations into the genetic architecture of human reproductive behavior and education and suggests that gene-environment interaction is the main driver of heterogeneity across populations. These challenges, thus, can be overcome by interdisciplinary work between both geneticists and social scientists using ever-larger datasets, with combined information and substantive knowledge of complex phenotypes and environmental conditions. ^46,47

Material & Methods

Data

We pooled a series of large datasets consisting of unrelated genotyped men and women (individuals with a >0.05 relatedness as estimated using common SNP markers were removed) from six countries and seven sampling populations in the US (HRS (N=8,146), ARIC (N=6,633)), the Netherlands (LifeLines (N=6,021)), Sweden (STR/SALT (N=6,040)), Australia (QIMR (N=1,167)), Estonia (EGCUT (N=3,722)); and the UK (TwinsUK N=3,333)), for a total sample size of N=35,062 (see Supplementary Note 1 for further details).

We used genotype data from all cohorts, imputed to the 1000 genome panel. We then selected HapMap3 SNPs with an imputation score larger than 0.6, excluded SNPs with a missing rate greater than 5%, a lower minor allele frequency than 1% and those which failed the Hardy-Weinberg equilibrium test for a threshold of 10⁻⁶. We subsequently applied these criteria again after merging each dataset. We utilized 847,278 SNPs in analyses. The software PLINK²³ was used for quality control and merging.

Phenotypes

The phenotypes under study are education, human reproductive behavior (number of children ever born (NEB) and age at first birth (AFB)), height, and BMI. We received measures of height and BMI from all cohorts in centimeters and kg/m² respectively or already Z-transformed by sex and birth cohort. For education and human reproductive behavior, we received the phenotypes which cohorts have used in the respective large-scale GWAS meta-analyses, or constructed them based on raw data and Z-transformed the phenotypes for sex and birth cohorts by dataset.^7,24

The number of years of education was constructed based on educational categories with the typical years of education in the countries following the standard ISCED scale.^7,12 The number of children ever born (NEB) measures number of children a woman has given birth to or a man has fathered. This measure was available in all cohorts, although in ARIC and TwinsUK, only available for women. Information on age at first birth (AFB) was available for all cohorts except for ARIC and HRS. We focus only on individuals who reached the end of their reproductive period of 45 for women and 50 for men (for more details see Supplementary Note 2). Reproductive phenotypes are frequently recorded, virtually immune to measurement error and used as key parameters for demographic forecasting.²⁵

GREML Models

We first describe the baseline GREML model, which assumes the absence of gene-environment interactions. We then extend this model to a GCI-GREML model ^10,21 including genetic relatedness matrices where we stratify data by environments, setting pairwise relatedness for individuals in different environments to zero.¹⁰ Doing so allows us to test whether the pairwise genetic relatedness is a better predictor of pairwise phenotypic similarity if both individuals live in the same environment, and thus test for gene-environment interaction. We define the various genetic variance components of the models explicitly, and will refer to $h_{\text{SNP}}^2$ as the sum of all genetic effects relative to the phenotypic variance within the respective model specification.

Baseline model (GREML)

The genetic component underlying a trait is commonly quantified in terms of SNP-based heritability as the proportion of the additive genetic variance explained by common SNPs across the genome over the overall phenotypic variance $({\sigma }_{\mathbf{\text{Y}}}^2)$ of the trait: ⁹

$$h_{\mathit{\text{SNP}}}^2=\frac{{\sigma }_{\mathbf{\text{G}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}$$

The phenotypic variance is the sum of additive genetic and environmental variance, i.e. ${\sigma }_{\mathbf{\text{Y}}}^2={\sigma }_{\mathbf{\text{G}}}^2+{\sigma }_{\mathbf{\text{E}}}^2,$ where ${\sigma }_{\mathbf{\text{G}}}^2$ is the additive genetic variance explained by all common SNPs across the genome and ${\sigma }_{\mathbf{\text{E}}}^2$ is residual variance. The methods we applied have been detailed elsewhere.^9,10,26–28 Briefly, we applied a linear mixed model:

$$\mathbf{\text{y}}=\mathbf{\text{X}}\mathbf{\beta }+\mathbf{\text{g}}+\mathbf{\text{e}}$$

where y is an N×1 vector of dependent variables, N is the sample size, β is a vector for fixed effects of the M covariates in N×M matrix X (including the intercept and potential confounders such as birth year), g is the N×1 vector with each of its elements being the total genetic effect of all common SNPs for an individual, and e is an N×1 vector of residuals. We have $\mathbf{\text{g}}\sim N\left(0,\mathbf{\text{A}}{\sigma }_{\mathbf{\text{G}}}^2\right)\text{and}\text{e}\sim N\left(0,\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2\right).$ Hence, the variance matrix V of the observed phenotypes is:

$$\mathbf{\text{V}}=\mathbf{\text{A}}{\sigma }_{\mathbf{\text{G}}}^2+\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2,$$

To estimate the GRM, 847,278 HapMap3 SNPs were used to capture common genetic variation in the human genome. ²⁹ For each individual (j and k), the corresponding element of the GRM is defined as:

$$A_{jk}=\frac{1}{K}{\displaystyle \sum _{i=1}^K\frac{(x_{ij}-2{\mathit{p}}_i)(x_{ik}-2{\mathit{p}}_i)}{2{\mathit{p}}_i(1-{\mathit{p}}_i)}},$$

where x_ij denotes the number of copies of the reference allele for the i^th SNP for the j^th individual and p_i the frequency of the reference allele and K the number of SNPs. If two individuals had a genetic relatedness greater than 0.05, one was excluded from the analyses to avoid bias due to confounding by shared environment amongst close relatives. GCTA was used for the construction of the GRM and GREML analyses. ¹⁰

In the baseline model we apply this approach to the pooled data sources without environmental strata. Hence, the baseline model creates a reference point for SNP-based heritability in the mega-analysis.

Gene × sampling population (G×P) GCI-GREML model

In the case where genetic effects are heterogeneous across sampling populations, SNP-based heritability estimates obtained from the baseline model will be deflated when sampling populations are pooled. We therefore apply a gene × sampling population model (G×P) to simultaneously estimate within and between variance explanations of common SNPs (see also ^10,21 for GCI-GREML models).

The G×P model jointly estimates global genetic effects for the outcome variables effective between and within samples $({\sigma }_{\mathbf{\text{G}}}^2)$ and the averaged additional genetic effects within sampling populations $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2)$:

$$\mathbf{\text{V}}=\mathbf{\text{A}}{\sigma }_{\mathbf{\text{G}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2+\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2$$

where A is the genetic relatedness matrix and A_G×P is a matrix only with values for pairs of individuals within Populations 1–7:

$$\mathbf{\text{A}}=\left[\begin{array}{l}{A}_{\mathit{p}1\mathit{p}1}{A}_{\mathit{p}2\mathit{p}1}{A}_{\mathit{p}3\mathit{p}1}{A}_{\mathit{p}4\mathit{p}1}{A}_{\mathit{p}5\mathit{p}1}{A}_{\mathit{p}6\mathit{p}1}{A}_{\mathit{p}7\mathit{p}1}\hfill \\ A_{\mathit{p}1\mathit{p}2}{A}_{\mathit{p}2\mathit{p}2}{A}_{\mathit{p}3\mathit{p}2}{A}_{\mathit{p}4\mathit{p}2}{A}_{\mathit{p}5\mathit{p}2}{A}_{6\mathit{p}2\mathit{p}}{A}_{\mathit{p}7\mathit{p}2}\hfill \\ A_{\mathit{p}1\mathit{p}3}{A}_{\mathit{p}2\mathit{p}3}{A}_{\mathit{p}3\mathit{p}3}{A}_{\mathit{p}4\mathit{p}3}{A}_{\mathit{p}5\mathit{p}3}{A}_{\mathit{p}6\mathit{p}3}{A}_{\mathit{p}7\mathit{p}3}\hfill \\ A_{\mathit{p}1\mathit{p}4}{A}_{\mathit{p}2\mathit{p}4}{A}_{\mathit{p}3\mathit{p}4}{A}_{\mathit{p}4\mathit{p}4}{A}_{\mathit{p}5\mathit{p}4}{A}_{\mathit{p}6\mathit{p}4}{A}_{\mathit{p}7\mathit{p}4}\hfill \\ A_{\mathit{p}1\mathit{p}5}{A}_{\mathit{p}2\mathit{p}5}{A}_{\mathit{p}3\mathit{p}5}{A}_{\mathit{p}4\mathit{p}5}{A}_{\mathit{p}5\mathit{p}5}{A}_{\mathit{p}6\mathit{p}5}{A}_{\mathit{p}7\mathit{p}5}\hfill \\ A_{\mathit{p}1\mathit{p}6}{A}_{\mathit{p}2\mathit{p}6}{A}_{\mathit{p}3\mathit{p}6}{A}_{\mathit{p}4\mathit{p}6}{A}_{\mathit{p}5\mathit{p}6}{A}_{\mathit{p}6\mathit{p}6}{A}_{\mathit{p}7\mathit{p}6}\hfill \\ A_{\mathit{p}1\mathit{p}7}{A}_{\mathit{p}2\mathit{p}7}{A}_{\mathit{p}3\mathit{p}7}{A}_{\mathit{p}4\mathit{p}7}{A}_{\mathit{p}5\mathit{p}7}{A}_{\mathit{p}6\mathit{p}7}{A}_{\mathit{p}7\mathit{p}7}\hfill \end{array}\right]$$

$${\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}}=\left[\begin{array}{ccccccc}{A}_{\mathit{p}1\mathit{p}1}& 0& 0& 0& 0& 0& 0\\ 0& A_{\mathit{p}2\mathit{p}2}& 0& 0& 0& 0& 0\\ 0& 0& A_{\mathit{p}3\mathit{p}3}& 0& 0& 0& 0\\ 0& 0& 0& A_{\mathit{p}4\mathit{p}4}& 0& 0& 0\\ 0& 0& 0& 0& A_{\mathit{p}5\mathit{p}5}& 0& 0\\ 0& 0& 0& 0& 0& A_{\mathit{p}6\mathit{p}6}& 0\\ 0& 0& 0& 0& 0& 0& A_{\mathit{p}7\mathit{p}7}\end{array}\right]$$

The sum of both variance components $\text{(}{\sigma }_{\mathbf{\text{G}}}^2+{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2)$ are therefore expected to correspond with the results of a meta-analysis of the sample-specific $h_{\text{SNP}}^2$ of sufficient sample size. We quantify the hidden heritability due to heterogeneity as the discrepancy between $h_{\text{SNP}}^2=\frac{{\sigma }_{\mathbf{\text{G}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}$ from the baseline model and $h_{\text{SNP}}^2=\frac{{\sigma }_{\mathbf{\text{G}}}^2+{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}$ from the G×P model.

Gene × demographic birth cohort (G×C) GCI-GREML model

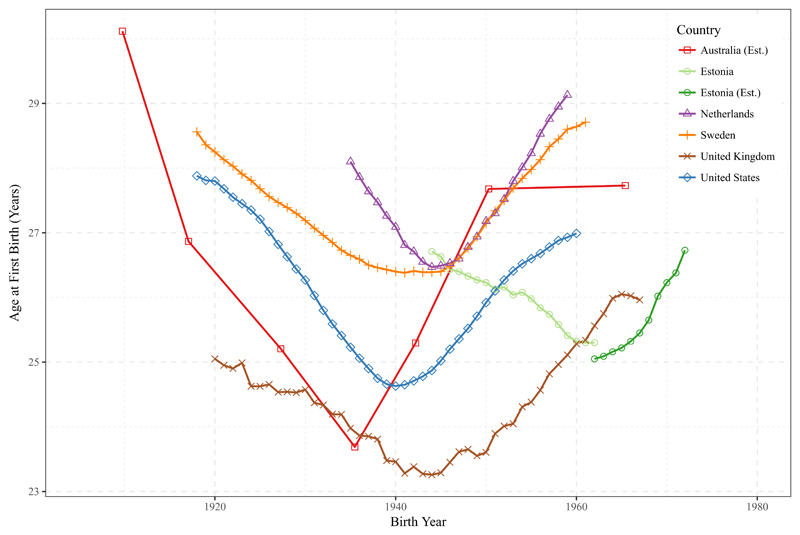
We are likewise interested in gene-environment interaction across birth cohorts. Fertility behavior and educational attainment have dramatically changed during the 20^th century.^19,30 Figure 3 shows the trends in age at first birth (AFB) during the 20^th century for the countries in our study (see Supplementary Note 3 for details on the data sources). We see the well-established U-shaped pattern of a falling AFB in the first half of the 20^th century followed by an upturn in the trend of AFB towards older ages. This widespread fertility postponement¹⁹ – referred to as the Second Demographic Transition ³¹ – was related to the spread of effective contraception, a drop in the NEB, changes in the economic need for children and female educational expansion.^19,32

Figure 3. Trends in mean age at first birth of women indicating environmental changes across cohorts (1903-1970) from the US, UK, Sweden, the Netherlands, Estonia and Australia.

Trends in the mean age at first birth of women are based on aggregated data obtained from Human Fertility Database and the Human Fertility Collection (for details see Supplementary Note 3). For Estonia, from 1962 onwards, we used estimated age at first births based on women older than 40. For Australia, no official data was available and the trends have been estimated from the QIMR dataset, averaged for each decade.

Environmental changes occurred at different periods in each country, with Australia having the earliest onset of fertility postponement (1939) and Estonia having the latest due to post-socialist transitions (1962; see Supplementary Table 7 for all turning points and details). To test for gene-environment interaction, we grouped the birth cohorts into environmentally homogeneous conditions by those born before and after each country-specific fertility postponement turning point. To investigate the moderating effect of turning points, we follow the previous modeling strategy, but divide individuals into these turning point birth cohorts.

The G×C model is a joint model estimating the universal genetic effects for the traits effective between and within samples $({\sigma }_{\mathbf{\text{G}}}^2)$ and the averaged additional genetic effects within defined birth cohorts $\left({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{C}}}^2\right):$

$$\mathbf{\text{V}}=\mathbf{\text{A}}{\sigma }_{\mathbf{\text{G}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{C}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{C}}}^2+\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2$$

where A is the genetic relatedness matrix and A_G×C is a matrix only with values for pairs of individuals within the same demographic birth Cohorts c₁– c₂:

$${\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{C}}}=\left[\begin{array}{cc}{\mathbf{\text{A}}}_{c_1{c}_1}& \mathbf{0}\\ \mathbf{0}& {\mathbf{\text{A}}}_{c_2{c}_2}\end{array}\right]$$

Genes × Population × Demographic birth cohorts (G×P×C) GCI-GREML model

In the G×P×C model, we included both interaction terms mentioned above and an additional interaction term A_G×P×C which is equal to zero for all pairs of individuals living in different time periods or in different cohorts represented by:

$$\mathbf{\text{V}}=\mathbf{\text{A}}{\sigma }_{\mathbf{\text{G}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{C}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{C}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{C}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{C}}}^2+\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2$$

where A is the genetic relatedness matrix, A_G×P is a matrix only with non-zero values for pairs of individuals within populations from the G×P Model, A_G×C is a matrix only with non-zero values for pairs of individuals within the same demographic periods from the G×C Model, and A_G×P×C is a matrix only with values for pairs of individuals with both the same demographic periods and the same populations.

Control variables

All phenotypes have been Z-transformed by sampling population, birth year and sex. We furthermore added fixed effects for sex, birth year, sampling population (with reference category Lifelines, the Dutch dataset) and the first 20 principal components calculated from the GRM across all populations to account for population stratification.³³ For the interaction model with birth cohorts, we included an additional fixed effect for the respective birth cohort turning point. In the G×P×C model, we additionally controlled for the interactions between the respective sampling population and the birth cohort division.

Model-fitting approach

The variance components are estimated using GREML estimation. When comparing the respective model specifications, to determine the best-fitting model, we rely on a model-fitting approach that compares the full model with reduced models that constrain specific effects to be zero. Since the models are nested, we perform likelihood-ratio tests and prefer the more parsimonious models if there is no significant loss in model fit (where the test statistic is distributed as a mixture of chi-squared with a probability of 0.5 and 0 ¹⁰; p-values from these tests are provided in Supplementary Tables 1-5). ¹⁰ This strategy is also robust against the violation of the assumption of requiring a normal distribution of the dependent variable – as for example in the case of NEB (number of children ever born).³⁴

Simulation Study

We conducted a series of simulation studies to illustrate how our models interpret gene-environment interaction and to evaluate the role of potential alternative sources of heterogeneity in our data. All simulation studies are detailed in Supplementary Note 4 (for the theory behind them see 21). First, we were interested in how the model construes heterogeneity in heritability levels across populations. Since heritability is a ratio of the proportion of total phenotypic variance that is attributable to additive genetic effects, differences in the residual variance for example due to heterogeneous phenotypic measurement error can lead to different levels of heritability across populations, even though genetic effects are perfectly correlated. In contrast to twin studies, we are not interested in comparing levels of heritability across populations, but in the question of whether genes have the same effect on the phenotype across environments. We thus decompose the heritability in the pooled data into additive genetic variance, both within and between environments.

In simple terms, we simulated phenotypes without gene-environment interaction across sampling populations and with gene-environment interaction across sampling populations based on 5000 SNPs that were in approximate linkage equilibrium (pairwise r² between SNPs below 0.05) and repeated this across 50 replications. First, to test for a model without gene-environment interaction, we set $h_{\text{SNP}}^2$ of the trait to 0.50 and the genetic correlations across environments to 1 (Supplementary Note 4 Sim 1). Second, we repeated the simulations with varying residual phenotypic variance across populations ³⁵, resulting in simulated $h_{\text{SNP}}^2$ between 0.25–0.625, but still with a genetic correlation of 1 across populations (Supplementary Note 4 Sim 2). Third, to illustrate weak levels of gene-environment interaction, we simulated $h_{\text{SNP}}^2$ to be 0.50 and the genetic correlations of traits across populations to be 0.80 (Supplementary Note 4 Sim 3). Finally, to illustrate stronger gene-environment interaction, we simulated $h_{\text{SNP}}^2$ to 0.50 and the genetic correlations of traits across populations to 0.50 (Supplementary Note 4 Sim 4).

The stacked bars in Figure 4 depict the average estimates of the four types of simulations for the simulated 50 phenotypes for the baseline model and the G×P model (individual estimates are presented as black dots for the full model and stripes in the bars represent variance components). Examining the first model (Sim 1) assumed no gene-environment interaction by sampling populations and thus homogeneous heritability, $h_{\text{SNP}}^2$ as ${\sigma }_{\mathbf{\text{G}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2$ (blue bar) is estimated at 0.324 and therefore around three fifths of the simulated heritability of 0.50 since the GRM is based not only on quantitative trait loci. Central to our approach is that for the phenotypes with no G×P interaction, the variance explanation that is effective both within and between populations $({\sigma }_{\mathbf{\text{G}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2)$ is nearly identical to the baseline model (0.318). The gene-environment interaction term $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2)$ estimates a small additional explanation of variance within populations of on average 0.026, with the full model estimate of $h_{\text{SNP}}^2$ within populations at 0.344 $\left(=\frac{{\sigma }_{\mathbf{\text{G}}}^2+{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}\right).$ Importantly, the same holds if we simulate differences in $h_{\text{SNP}}^2$ across populations due to varying residual variance. Sim 2 in Figure 4 shows an average $h_{\text{SNP}}^2$ of 0.205 and the G×P interaction model estimates of ‘universal’ genetic variance $({\sigma }_{\mathbf{\text{G}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2)$ of 0.200, with a gene-environment interaction term $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2/{\sigma }_{\mathbf{\text{Y}}}^2)$ of 0.0217. We therefore conclude that the model does not interpret heterogeneity in heritability levels due to differences in the residual variance as gene-environment interaction.

Sim 3 and 4 in Figure 4 depict how gene-environment interaction across sampling populations affects model estimates in scenarios of cross population genetic correlations of 0.80 (weak) and 0.50 (strong) gene-environment interaction respectively, with the same population specific $h_{\text{SNP}}^2$ of 0.50 as in Sim 1. First, we observe that $h_{\text{SNPs}}^2$ in the baseline models are deflated in the pooled data $\left(\frac{{\sigma }_{\mathbf{\text{G}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}=0.261\text{and}0.105\right)$ and therefore only capture around four-fifths and one-third of the estimates in the absence of G×P. Second, when taking G×P into account, the full model estimate reaches the same level as the baseline model in the absence of G×P $\left(\frac{{\sigma }_{\mathbf{\text{G}}}^2+{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}=0.328\text{and}0.315\right)$ due to a larger fraction of genetic variance explained within populations $\left(\frac{{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}=0.082\text{and}0.256\right)$ and do not appear to be inflated whatsoever. Third, the genetic variance explained effectively within and between populations in the G×P model is even smaller than in the baseline model $\left(\frac{{\sigma }_{\mathbf{\text{G}}}^2}{{\sigma }_{\mathbf{\text{Y}}}^2}=0.246\text{and}0.059\right)$. Therefore, while in the case of a genetic correlation of 0.5 across populations, within population estimates of $h_{\text{SNP}}^2$ capture around one third of the overall heritability; the shared genetic variance explanation across populations would be only around 19% (=0.059/0.315) of this value.

Based on the findings from Sim 4 for example, we would expect that in the case of meta-analyses of population specific GWAS on the gene-environment interaction phenotypes, that genome-wide significant SNPs could explain only up to 10% of the variance while $h_{\text{SNP}}^2$ of within populations could explain on average 32%. Around 68% of $h_{\text{SNP}}^2$ ((1-10/32)*100) would therefore be ‘hidden’ in the mega-analysis due to heterogeneity and in this case due to gene-environment interaction.

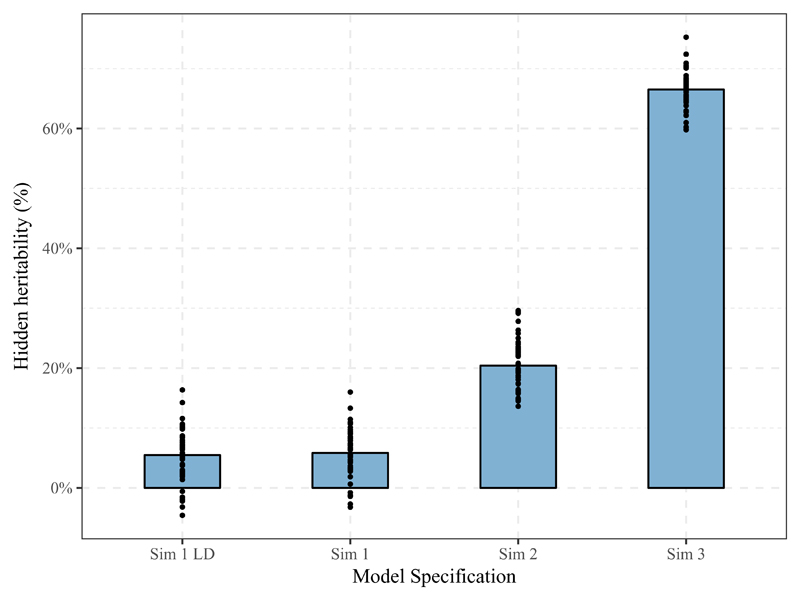
Figure 5 shows hidden heritability estimates for the simulations without gene-environment interaction (Sim 1) and with gene-environment interaction (Sim 3 and Sim 4). We were furthermore interested to what extent genetic heterogeneity across populations such as differences in genetic measurement, in linkage disequilibrium across sampling populations, or heterogeneous imputation quality across population can lead to observed heterogeneity or deflate $h_{\text{SNP}}^2$ in pooled data sources. To investigate this we removed the 5000 causal SNPs from the genetic data, which was the basis of how we simulated the phenotypes. We then re-estimated the GRM and repeated the analyses on Sim 1 of phenotypes without gene-environment interaction and homogeneous heritability across populations (depicted in Figure 5 as Sim 1 LD). If the causal SNPs are removed, estimates are based on correlated SNPs which are in linkage disequilibrium (LD). To the extent that the structure in the genetic data we use is heterogeneous across populations due to the aforementioned reasons, we can expect that our models interpret it as heterogeneous genetic effects resulting in hidden heritability.

Figure 5. Bar Charts of average % of hidden heritability due to heterogeneity (% of h²_SNP of the best fitting model which is not captured in standard GREML models) for Sim 1 including and excluding causal variants (Sim LD), for Sim 3 and 4. Individual estimates are represented by black dots.

In Figure 5, we see that hidden heritability is estimated to be around 68% for a genetic correlation of 0.50, around 20% for a genetic correlation of 0.80 and around 5% for the model without gene-environment interaction as well as a model based on SNPs in LD with the causal SNPs. This allows us to draw two conclusions. First, in the complete absence of gene-environment interaction (Sim 1), our models interpret, on average across 50 simulations, that 5% of the heritability in the G×P model is hidden in a standard model with a statistically significant G×P term in 10 simulation studies (10/50 = 20%; not listed) at the 5%-level. This is important to keep in mind when analyzing our phenotypes of interest. To evaluate phenotype specific model inflations, we conducted complementary permutation analyses generating a matrix with randomly stratified environments to see how estimates are inflated in the real data for specific phenotypes. This will be reported when discussing the findings. Second, we find no difference in inflation between the simulations including and excluding causal SNPs (Sim 1 LD and Sim 1). We conclude from this that heterogeneity in the genetic structure of the populations does not affect our interpretation of gene-environment interaction in comparison to the standard model. This is likely due to the fact that we only look at common SNPs and applied rigorous quality control. To investigate whether gene-environment interaction is present for education and human reproductive behavior, we applied the above models as well as G×C and G×P×C models to these phenotypes in seven sampling populations.

Sex differences

Previous whole-genome studies find no evidence for gene-sex interaction of common genetic effects on BMI, height³⁶ and also human reproductive behavior⁸ (note that a family based study shows evidence for sexual dimorphism in childlessness³⁷). We also tested for G x Sex interaction within sampling populations in our data, as:

$$\mathbf{\text{V}}={\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2+{\mathbf{\text{A}}}_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{sex}}}{\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{sex}}}^2+\mathbf{\text{I}}{\sigma }_{\mathbf{\text{E}}}^2$$

where A_G×P is the genetic relatedness matrix only with values for pairs of individuals within the same population and A_G×P×sex is a matrix with only values for pairs of individuals of the same sex and same sampling population.

Decomposing the genetic variance of all five phenotypes, height, BMI, education, number of children ever born (NEB) and age at first birth (AFB) into within population effects shared between sexes $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}}^2)$ and the averaged additional genetic effects within sexes $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{sex}}}^2)$, we find no evidence for sex-specific effects $({\sigma }_{\mathbf{\text{G}}\times \mathbf{\text{P}}\times \mathbf{\text{sex}}}^2)$ for education (p-value 0.49), AFB (p-value 0.5), NEB (p-value 0.41) or height (p-value 0.5). Only for BMI do we find evidence of around a 3% sex-specific variance explanation (p-value 0.046; for full results see Supplementary Table 8). Given that we focus on education and reproductive behavior, we applied all models to pooled data including both sexes, keeping in mind the findings for BMI.

Data availability

We utilize publicly available dbGaP data from the Atherosclerosis Risk in Communities (ARIC) Study (dbGaP phs000090.v1.p1), and Health and Retirement Study (HRS: dbGaP phs000428.v1.p1). Access to individual-level phenotypic, genetic data from the QIMR, EGCUT, STR/SALT, TwinsUK and the LifeLines Study is available with the obtainment of a research agreement (see also Supplementary Note 1).