Flow Cytometry using Brillouin Imaging and Sensing via Time-Resolved Optical (BISTRO) Measurements

Abstract

A novel concept of Brillouin Imaging and Sensing via Time-Resolved Optical (BISTRO) Measurements is introduced for flow cytometry applications. The system affords robust, maintenance-free and high-speed elasticity-sensitive measurements.

Mechanical properties of living cells are often directly related to the cell types and their conditions^1–3. Micropipette aspiration and atomic force microscopy (AFM) are the most commonly used techniques for measuring individual cell’s elasticity^4–6. Those elasticity measurements performed on individual cancer and healthy cells demonstrated a clear evidence of significant alteration of cell’s mechanical properties, which are likely associated with cytoskeleton reorganization.

However, both methods have very limited throughput, which is not sufficient to analyze millions of cells in a reasonable amount of time. There have been several substantial attempts to improve the throughput using microfluidic devices^7–11. However, non-invasive optical measurements would be preferable for both conducting basic studies on cell mechanics and utilizing cell elasticity as an indicator of cell phenotypes and conditions. In this report, we propose an alternative approach based on nonlinear Brillouin scattering. It is capable of measuring the elastic properties of simple fluids in a flow cytometry setup, and is expected to probe single cells in a flow-through manner in the future.

Brillouin scattering is an inelastic light scattering process which has been widely applied on studying acoustic phonons in the frequency range from several hundreds megahertz to several hundreds gigahertz where mechanical excitation are nearly impossible, and have become a powerful technique providing unique information on the samples’ viscoelastic properties^{12, 13}. Spontaneous Brillouin spectroscopy has been widely used in remote sensing^{14, 15}, material science^{16, 17}, and, more recently, is introduced into the field of biomedical applications^18–23. Brillouin spectroscopy, being an optical technique, provides a viable pathway to viscoelastic characterization without any external perturbation; its signal strength is fundamentally limited by the weak intensity of thermally excited phonons. Although spontaneous Brillouin scattering can be enhanced by nanostructures, the enhancement factor (< 10)²⁴, compared to Raman scattering (~ 10¹⁰)²⁵, is negligible. When extending spontaneous Brillouin spectroscopy to cellular/subcellular measurements, the throughput of the system is limited by its acquisition speed.

In this report, by incorporating the concept of Impulsive stimulated Brillouin scattering (ISBS^26–28), we report a Brillouin Imaging and Sensing system via Time-Resolved Optical (BISTRO) measurements, which significantly improves the acquisition speed of Brillouin spectroscopy. The ISBS concept is based on the optically generated phonons and the simultaneous optical heterodyne detection of these phonons using Bragg diffraction. Unlike the spontaneous Brillouin process, the phonons in ISBS are stimulated by an external pump laser. Therefore, the signal strength can be controlled, and is substantially stronger than the spontaneous Brillouin process. This technique has been successfully utilized in examining various bulk materials, including simple liquids^{29, 30}, glasses³¹, quasicrystals³², crystals^{33, 34} and thin films^35–37 and bulk biological materials³⁸. Recently, it has been extended to high-pressure environments^{32, 39, 40} and is used to characterize the sub-micron depth profile⁴¹ or surface textile⁴² of certain materials. However, in the previous instrumentation implementations, the distances between the two pump beam and the probe beam have to be precisely tuned, as the incident angle between the probe beam and the optically generated acoustic wave should strictly follow the Bragg condition^{27, 28, 43}. In this study, we introduced an external transmission grating to prepare the angle between the pump, the probe and the stimulated acoustic wave. In this way, the Bragg condition is automatically satisfied, and the optical setup maintenance is greatly simplified. As a proof of microscopic applications, we applied this setup to various simple liquids confined in quartz microchannels. Material-specific ISBS spectra showed a perfect correlation with their counterpart obtained from the spontaneous Brillouin process. The results proved the robustness of the setup. Moreover, the utilization of flow capillaries and dramatically improved signal strength enable its applications in the field of flow cytometry. The present report serves the purpose of introducing and validating our methodology for accurate assessment of Brillouin spectra of material flowing in microfluidic channels. The future research will involve flow cytometry studies of red blood cells (RBCs) and cancer cells.

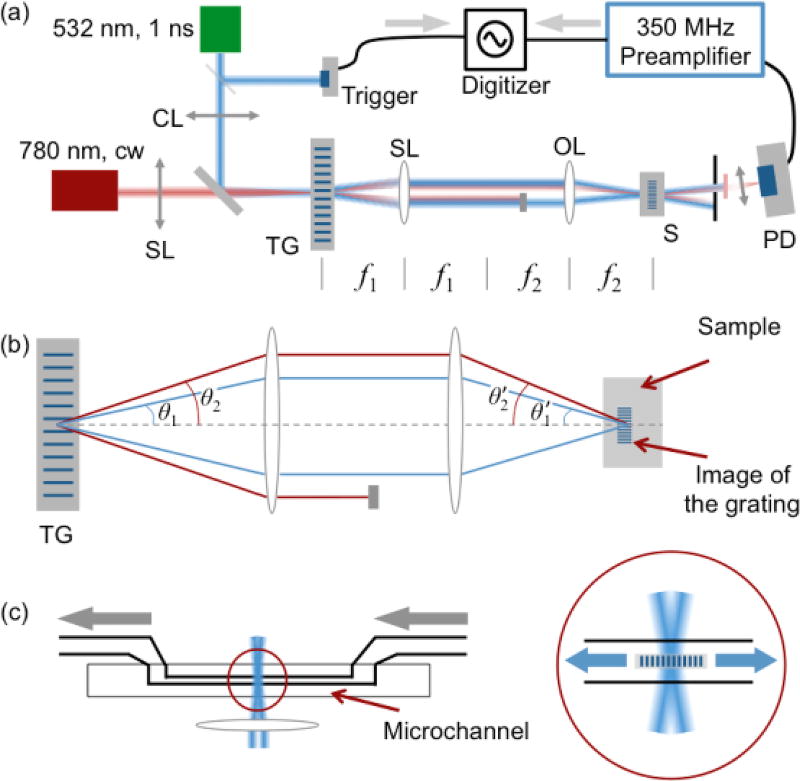
A schematic diagram of the experimental setup is illustrated in Fig. 1. Two laser sources were employed: a 532 nm nanosecond pulsed laser (pump source, IPG Photonics Inc., Model: GLPR-10) and a 780 nm cw diode laser (probe source, Newport Inc., TLB-6900). The pulse duration of the pump laser was 1 ns, and the energy per pulse – up to 16 µJ. The repetition rate was set as 20 kHz. The total pump power exerted on the sample was up to ~ 350 mW. The probe source was a single-frequency 780 nm diode laser. The emission power was ~ 5 mW. The pump and probe laser sources were combined by a dichroic mirror and sent to a transmission grating (Holo/Or Ltd., DS-006-Q-Y-A, 41.67 lines/mm). Prior to this, we inserted a cylindrical lens in the optical path of the pump laser. The focusing strip was on the transmission grating. Its orientation was perpendicular to the strip of the grating. The probe laser was focused at the center of the focusing stripe of the pump beam. After passing through the grating, both the pump and the probe were diffracted. We only utilized the +1^st and −1^st orders of the diffractions in this study. According to the grating resolution (d = 24 µm) and the optical wavelengths (λ = 532 nm), the diffraction angle can be calculated: sin θ = λ/d. The pump and the probe lasers were diffracted and propagate in different directions due to their distinct wavelengths. The laser beams were then sent to a 4f system, which was formed by a spherical lens (f₁ = 15 mm) and an objective lens (10× Olympus Plan Achromat Objective Lens, N.A. = 0.25, working distance = 10.6 mm). The front and back focal lengths of the objective lens were not specified by the manufacturer, and these two values may not be identical to a typical thick lens. Without loss of generality, we assume the objective lens works as a simple lens (focal length = f₂) in the following discussions. The +1^st and −1^st orders of the diffracted pump laser beams would intersect at the focusing point of the objective lens, and form an interference fringe that defined the local strength of the electrical field^{26, 27, 44}. According to the angular magnification of the system, the intersect angle (in air) could be calculated: $\text{sin }{\theta \prime }_1=\frac{f_2}{f_1}\text{sin }{\theta }_1$. Here, f₁ and f₂ are focal lengths of the two lenses used in the 4f system (shown in Fig. 1a). In the region of the interference fringe, the distance between local maxima of the electrical field is $d\prime =\frac{\lambda }{2\text{ sin }{\theta \prime }_1}=\left(\frac{f_2}{f_1}\right)d$. Here, λ is the wavelength of the pump laser. d′ remains the same among the samples with different refractive indices, as the pumping laser’s wavelength and the intersection angle would change accordingly. In view of the 4f system, the interference fringe is the image of the transmission grating. The lateral magnification factor of this image is $\frac{f_2}{f_1}$, in agreement with geometric optics. Depending on the absorptivity of the sample, the local density variation in the sample was induced via two distinct mechanisms: the photostriction effect and the photothermal effect⁴⁵. The former effect is brought by the correlation between the local electric field strength and the molecular density and generates a traveling sound wave, i.e., stimulated phonons^{26, 46}. Light absorption also results in density fluctuations in an absorptive sample, which contributes stimulated phonons as well as a static thermal grating⁴⁵. In this study, we selected transparent liquids (at 532 nm) instead of absorptive ones so that photostriction effect would dominate the phonon generation process.

Fig. 1.

(a) The basic optical setup for BISTRO measurements. CL: cylindrical lens; SL: spherical lens; TG: transmission grating; OL: objective lens; S: sample; f₁ & f₂: focal lengths for the spherical lens and the objective lens in the 4f system; (b) The geometric relationship between the objective lens and the micro-fluid channel; (c) The close-up illustration of the focal point. Gray arrows: the liquid flow; Blue arrows: the propagation direction of the stimulated acoustic wave.

Once formed, the stimulated acoustic wave would propagate along opposite directions within the scattering plane (Fig. 1b and c). Therefore, in the central region, a standing acoustic wave would be created immediately after the excitation of the pump, and quickly dissipate in the sample. The wavelength of the stimulated phonon (Λ) follows the spacing of the interference fringe: $\mathrm{\Lambda }=d\prime =\frac{\lambda }{2\text{ sin }{\theta \prime }_1}$. In this particular study, we focused on the application of flow cytometry. We pump various simple liquids to a microchannel (Translume Inc, Model: YSF-100250-L8-500-250-500, illustrated in Fig. 1c). The microchannel was adjusted so that it overlapped with the focusing stripe of the pump laser. Therefore, an acoustic grating could be generated inside of the microchannel.

On the other hand, the probe laser is focused by the objective lens and transmits through the region possessing the stimulated phonons. The incident angle of the probe beam can be calculated: $\text{sin }{\theta \prime }_2=(f_1/f_2)\frac{{\lambda }_2}{\mathrm{d}}=\frac{{\lambda }_2}{{\lambda }_1\text{sin }{\theta \prime }_1}=\frac{{\lambda }_2}{2\mathrm{d}\prime }$. According to this expression, the Bragg condition is automatically satisfied⁴³. In this way, the probe beam would be diffracted by the stimulated phonons in the focusing region. Due to the propagation of the phonons, standing acoustic wave is formed. Therefore, the power of the diffracted probe beam would oscillate. The oscillation frequency would be twice the frequency of the stimulated acoustic wave. The diffracted probe beam was captured by a fast photodiode detector (ThorLabs, Inc.; APD210, 1GHz bandwidth), and then digitized by an oscilloscope (Rigol, Model: DS 6202, 600 MHz bandwidth). We also inserted a DC blocker and a high-frequency preamplifier (Stanford Research Systems, Model: SRS445A, up to 625× amplification) to enhance the detection capability of the system. A fast Fourier transform was performed using the oscilloscope, enabling real-time monitoring of the oscillation frequency of the standing acoustic wave. By combining the frequency with the acoustic wavelength (calculated from the 4f system composited by the optical lenses), we were able to calculate the speed of sound within the sample. Other physical parameters, including longitudinal modulus and viscosity, could be retrieved after that.

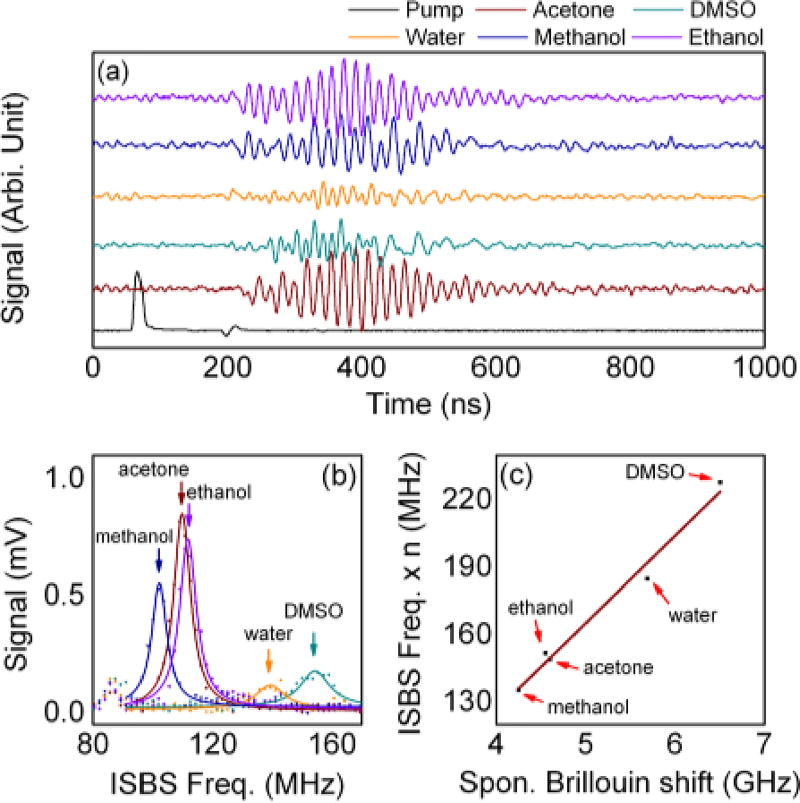
To prove the principle of the optical instrumentation, we pumped various simple liquids into the microchannel, then collected and analyzed the temporal profile of the diffracted probe laser. The results are presented in Fig. 2. Fig. 2(a) illustrates the temporal relationship between the pump and the output probe beams. The temporal profile of the incident pump pulse was recorded by the trigger detector shown in Fig. 1(a). All other signals were received by the photodiode detector. Experimental conditions were identical throughout except for the flowing liquids. Intensity oscillations in the output probe beam can be monitored following the excitation of the pump laser. The oscillation frequencies and amplitudes were found to be dependent on the flowing liquid, as expected. When taking the data, we averaged 1024 measurements for each sample. Considering the repetition rate of the pulsed laser (20 kHz), the integration time for one measurement is about 50 ms. Due to the limited vertical resolution limit of the oscilloscope (8-bit), the quality of the signal was insufficient for accurate analysis. By taking advantage of commercially available high-speed, 12–16 bit resolution signal digitizers, better signal quality can be obtained.

Fig. 2.

(a) The temporal relationship between the pump and the output probe intensities; (b) The results of the FFT analysis of the ISBS signal; (c) Correlation between the spontaneous Brillouin shifts and the ISBS frequency. The data for spontaneous Brillouin shift are taken from Boyd¹³.

The results of the FFT analysis of the output probe signals are displayed in Fig. 2(b) (magnitude only). Multiple peaks, including environmental noises, could be identified in the FFT spectra; however, we are interested in the sample-specific peaks only. For liquids with known sound speed, we can calculate the wavelength of the stimulated phonons with the assistance of the ISBS frequency. For example, the ISBS frequency for methanol was 102.058 MHz. Considering the sound speed of methanol is 1100.50 m/s⁴⁷, the wavelength of the stimulated phonon is 21.57 µm. The similar stimulated acoustic wavelength can be found in other liquids. For example, by combining the ISBS frequency (139.288 MHz) and the sound speed (1482.00 m/s) for water, the acoustic wavelength was determined as 21.28 µm. According to these results, the lateral magnification factor of the 4f system can be determined as 0.90, and the equivalent focal length of the objective lens is f₂ = 13.49 mm. When testing unknown liquids, based on their ISBS frequency, we were able to calculate the sound speed (V) as well as the longitudinal modulus (ρV²; ρ: mass density).

Fig. 2(c) shows a comparison between the ISBS frequency and the spontaneous Brillouin shift. Note that the ISBS frequency is proportional to the sample’s sound speed, while spontaneous Brillouin shift is proportional to the product of the sample’s refractive index and the sound speed. Therefore, when plotting this figure, we multiplied ISBS frequencies by the corresponding refractive indices of each sample. The spontaneous Brillouin shift data are taken from Boyd¹³ (excitation wavelength: 694 nm). A linear correlation between the ISBS and spontaneous Brillouin spectra is clearly evident, indicating that the measured ISBS signal originated from the ultrasonic phonons within the sample. Our recent study shows that the Brillouin shift different between different RBC types is ~ 400 MHz⁴⁸. According the correlation shown in Fig. 2(c), the corresponding ISBS frequency difference would be ~ 12 MHz, which can be readily resolved using our current signal acquisition setup.

In this study, we demonstrated that the concept of Brillouin Imaging and Sensing via Time-Resolved Optical (BISTRO) measurements could be employed as a tool for assessing local viscoelasticity. The sample was excited using a nanosecond pulsed laser, and an acoustic transmission grating was created inside the sample via photostriction effect. In this way, a series of stimulated phonons would be formed and start to propagate immediately after its formation. By taking advantage of a cw probe laser, the propagation of the stimulated phonons could be monitored in the temporal domain. As a result, the sample’s sound speed and associated mechanical properties can be retrieved from these measurements. The integration time for a single measurement takes about 50 ms, 20 times faster than spontaneous Brillouin acquisitions for the same signal-to-noise ratio (SNR).

Recent advances in atomic force microscopy (AFM) and optical tweezers have revealed the elasticity difference between healthy and diseased cells. For example, with the help of AFM, Cross et al. proved that, in microscopic scale, cancerous cells taken from lung, breast, and pancreas cancer patients are considerably softer than their benign counterparts¹. Using optical tweezers, the similar elasticity differences can also be monitored between healthy and diseased red blood cells (sickle cell disease)⁴⁹. However, all current detections are based on individual cells. The efficiencies of these techniques fundamentally impede their clinical applicability. Therefore, with the limited amount of samples (e.g., circulating tumor cells, CTCs⁵⁰), the elasticity of the cells cannot be statistically studied. As a high throughput elasticity-specific probing technique, our current BISTRO flow cytometry setup is capable of distinguishing cells possessing with distinct mechanical properties and is expected to be applied in cell sorting and disease diagnosis. It is capable of accurately assessing of Brillouin spectra of material flowing in microfluidic channels. The future study will involve RBCs and cancer cells.

The system can be further improved in, at least, two ways. Firstly, by lowering the wavelength of the simulated phonons, the spatial resolution can be improved. In our current system, the wavelength was longer than 20 µm, which set the lower limit of the system’s spatial resolution. The theoretical expression of the acoustic wavelength can be written as: $\mathrm{\Lambda }=\left(\frac{f_2}{f_1}\right)d$. Therefore, in order to obtain shorter wavelength, we may either decrease the focal length ratio between the two lenses (f₂/f₁), or elevate the line density of the transmission grating.

Secondly, the system’s signal quality can be improved by upgrading the pump laser and the signal acquisition devices. In this particular study, the signal quality and SNR are both less than 10 for certain samples (e.g., water and DMSO). By taking advantage of picosecond pulsed lasers, we keep the same pump energy while enhancing the strength of the stimulated acoustic wave. Moreover, a pump source with a longer wavelength (e.g., 800 – 1100 nm) can further elevate the damaging threshold of the sample. Once an NIR pump source is adopted, the SNR of the system could be further enhanced with higher pump power⁵¹. Meanwhile, the currently used preamplifier may also contaminate the signal quality. Signal digitizers with higher bit resolution could remove the necessity of the multi-stage preamplifiers, and, therefore, enhance the signal quality.

Conclusions

In summary, we demonstrated that the nonlinear impulsive stimulated Brillouin spectroscopy could be applied as a tool for probing samples’ viscoelasticity. This result enables investigators to probe the mechanical properties of the samples in a cell specific flow cytometry setup.