Adaptive testing for association between two random vectors in moderate to high dimensions

Abstract

Testing for association between two random vectors is a common and important task in many fields, however, existing tests, such as Escoufier’s RV test, are suitable only for low-dimensional data, not for high-dimensional data. In moderate to high dimensions, it is necessary to consider sparse signals, which are often expected with only a few, but not many, variables associated with each other. We generalize the RV test to moderate to high dimensions. The key idea is to data-adaptively weight each variable pair based on its empirical association. As the consequence, the proposed test is adaptive, alleviating the effects of noise accumulation in high-dimensional data, and thus maintaining the power for both dense and sparse alternative hypotheses. We show the connections between the proposed test with several existing tests, such as a generalized estimating equationsG-based adaptive test, multivariate kernel machine regression, and kernel distance methods. Furthermore, we modify the proposed adaptive test so that it can be powerful for non-linear or non-monotonic associations. We use both real data and simulated data to demonstrate the advantages and usefulness of the proposed new test. The new test is freely available in R package aSPC at https://github.com/jasonzyx/aSPC.

1 Introduction

To investigate genetic control of gene expression, it is common and useful to conduct association analysis between single nucleotide polymorphisms (SNPs) and gene expression (i.e. mRNA or transcript) levels, also known as eQTL analysis. This often involves massive univariate testing. For example, Colantuoni et al. (2011) examined 30,176 expression probes and 625,439 SNPs, leading to 1.89 × 10¹⁰ (19 billion) possible SNP-gene associations. After the conservative Bonferroni adjustment, only 1,628 individual associations surpassed the genome-wide significance level. However, when they conducted a global test for possible association between all SNPs and all transcripts, no association was detected. They noted: “This dramatic lack of association between genetic distance and transcriptome distance across our sample is a surprising result that requires further interrogation. It is possible that no association is found because most of the genetic polymorphisms measured do not impact on gene expression.” We agree with Colantuoni et al. (2011) on the possible reason for the lack of a global association in striking contrast to the presence of some individual associations: it is due to the lack of power of a global test for high-dimensional data with only sparse signals. Furthermore, the authors also commented on that, surprisingly, no association was found even for smaller subsets of the SNPs and genes. We note that their used method was Mantel’s (1967) test, which was originally proposed for low-dimensional data and may have only limited power for moderate- to high-dimensional data as to be confirmed. Nevertheless, this example pinpoints the importance of conducting global association testing with high-dimensional data, given that most of the existing tests were almost exclusively developed for low-dimensional data for historical reasons, as reviewed in Josse and Holmes (2014).

Some commonly used tests for association between two random vectors include the RV test (Escoufier, 1970), the Mantel test (Mantel, 1967) and the distance covariance (dCov) test (Székely, Rizzo and Bakirov, 2007). The RV test is based on the RV coefficient as a multivariate generalization of Pearson’s correlation coefficient. It is perhaps the most popular one in many fields, especially in ecology. The Mantel test aims to detect a possible correlation between two distance matrices among the subjects based on the two random vectors respectively; it is noted that the Mantel test was used by Colantuoni et al. (2011). The dCov test has only become popular recently due to its attracting property of being consistent in detecting any possible associations, including non-linear and non-monotonic relationships. A common problem with the above tests is their treating all the variables in the two random vectors equally a priori, which is perhaps reasonable for low-dimensional data, but not for moderate- to high-dimensional data: as for the SNP-gene expression data of Colantuoni et al. (2011), most of the SNPs do not have regulatory function; even for those regulatory ones, their targets are likely only a few, not most, of the genes. That is, for high-dimensional data, we expect that many or even most (e.g. SNP-gene) pairs are not associated, which is ignored by the above existing tests, leading to their noise accumulations and thus substantial power loss as to be confirmed in later numerical studies. Hence, to boost power, it is important to conduct variable selection or variable weighting. With weak associations, it is difficult for accurate variable selection, so we take a variable weighting approach. In our approach, we use the data to adaptively determine a weight for each pair of the variables: if a pair is more likely to be associated, we assign a higher weight to it. This will effectively down-weight many of those non-associated pairs, alleviating the effects of noise accumulation hindering most existing tests for high-dimensional data. Our adaptive test can be regarded as a generalization of the RV test to high-dimensional data, as to be shown later.

We note that the above tests aim to tackle the same problem as SNP-set- or gene-based association testing for multiple traits or longitudinal traits in genetics (e.g., Maity, Sullivan and Tzeng, 2012; He et al., 2015; Fan et al., 2016; Wang, Lee, Zhu, Redline and Lin, 2013;, Wang et al., 2015; Wang, Xu, Zhang, Wu and Wang, 2017; Kim, Zhang and Pan, 2016 and references therein), but the two lines of research seem to be largely non-overlapping; it is also our goal here to bridge the gap between the two lines of research. In particular, our proposed test is related to another adaptive test, called adaptive sum of powered score test based on generalized estimating equations (GEE-aSPU), originally designed in genetics for testing for multi-trait and multi-SNP associations in low to moderate dimensions (Kim et al., 2016), but we will also show some computational advantages of the proposed test over GEE-aSPU. It is also connected with kernel machine regression and kernel distance methods (Hua and Ghosh, 2015). Furthermore, due to the simplicity of our proposed test, it can be also extended to detect non-linear or even non-monotonic associations by borrowing the idea from the dCov test, though our test is much more powerful than the dCov test for sparse signals in moderate- to high-dimensions.

The rest of the article is organized as follows. In section 2 we will briefly review the RV test, which serves to motivate our proposed aSPC test. We then outline the connections of the aSPC test to some existing tests before presenting its several generalizations. Section 3 applies the new and some existing tests to an SNP-gene expression dataset drawn from the Alzheimer’s Disease Neuroimaging Initiative (ADNI), highlighting some advantages of the new tests over some existing ones. In section 4 more simulation results are shown to support the power and flexibility of the aSPC test. We end with a summary of the main conclusions in section 5.

2 Methods

Our goal is to test for association between two random vectors x_p×1 and y_q×1 in p and q dimensions respectively. We have n iid observations on x-y pair as stored in two matrices X_n×p and Y_n×q, respectively; each row of the two matrices corresponds to an observed x-y pair. Denote X_·l as the lth (l = 1, …, p) column of matrix X and Y_․m as the mth (m = 1 … q) column of Y. It is assumed throughout that each column of the two matrices is centered at mean 0 with a unit variance. We will use X and Y to test for association between x and y; with some abuse of notation, we also call it association between X and Y.

2.1 Review: the RV test

For the purpose of comparison, we first briefly review the RV test, largely following Josse and Holmes (2014). The two cross-product matrices of X and Y are W_X = XX^T and W_Y = YY^T, both of which are of size n × n. To measure their proximity, the Hilbert-Schmidt inner product between matrices W_X and W_Y can be used:

$$<W_X,W_Y>=\mathit{\text{tr}}({\mathit{\text{XX}}}^T{\mathit{\text{YY}}}^T)={(n-1)}^2\sum _{l=1}^p\sum _{m=1}^q{\text{Cov}}_n^2(X_{․l},Y_{․m}),$$ (1)

where Cov_n(X_·l, Y_․m) is the sample covariance between columns X_·l and Y_․m. The RV coefficient, a correlation coefficient proposed by Escoufier (1973) for two random vectors, is computed by normalizing the Hilbert-Schmidt inner product by the matrix norms:

$$\text{RV}(X,Y)=\frac{<W_X,W_Y>}{\Vert W_X\Vert \Vert W_Y\Vert }=\frac{\text{tr}({\mathit{\text{XX}}}^T{\mathit{\text{YY}}}^T)}{\sqrt{\text{tr}{({\mathit{\text{XX}}}^T)}^2\text{tr}{({\mathit{\text{YY}}}^T)}^2}},$$ (2)

which accounts for possibly different scales of x and y. The population RV coefficient is $\rho (\mathit{x},\mathit{y})=\text{tr}({\sum }_{\mathit{\text{xy}}}{\sum }_{\mathit{\text{yx}}})/\sqrt{\text{tr}({\sum }_{\mathit{\text{xx}}}^2)\text{tr}({\sum }_{\mathit{\text{yy}}}^2)}$, where Σ_xy is the population covariance between x and y. Our goal is to test H₀ : ρ(x, y) = 0.

If each column of X and of Y is standardized to have a zero mean and a unit variance, as always assumed here, the RV coefficient can be simplified as:

$$\text{RV}(X,Y)=\frac{\text{tr}({\mathit{\text{XX}}}^T{\mathit{\text{YY}}}^T)}{{(n-1)}^2\mathit{\text{pq}}}=\frac{{\sum }_{l=1}^p{\sum }_{m=1}^q{\text{corr}}_n^2(X_{․l},Y_{․m})}{\mathit{\text{pq}}}\propto \sum _{l=1}^p\sum _{m=1}^q{\text{corr}}_n^2(X_{․l},Y_{․m}),$$ (3)

where corr_n(X_·l, Y_․m) is the sample Pearson correlation coefficient between columns X_·l and Y_․m.

A permutation method can be used to calculate the P-value. Specifically, for each permutation b = 1, …, B, we permute the rows of matrix X (or Y), then calculate the corresponding RV coefficient RV^(b); the P -value is calculated as the sample proportion $[{\sum }_{n=1}^{B}I(\mathit{\text{RV}}\le {\mathit{\text{RV}}}^{(b)})+1]/(B+1)$.

2.2 New method: an adaptive sum of powered correlation (aSPC) test

To generalize the RV coefficient as reformulated in equation (3), we propose a family of so-called sum of powered correlation (SPC) tests:

$$\text{SPC}(\gamma )=\sum _{l=1}^p\sum _{m=1}^q{\text{corr}}_n^{\gamma }(X_{․l},Y_{․m})$$ (4)

for a set of integers γ ≥ 1. Each term ${\text{corr}}_n^{\gamma }(X_{․l},Y_{․m})$ in equation (4) can be re-written as ${\text{corr}}_n^{\gamma }(X_{․l},Y_{․m})=w_{\mathit{\text{lm}}}{\text{corr}}_n(X_{․l},Y_{․m})$, where $w_{\mathit{\text{lm}}}={\text{corr}}_n^{\gamma -1}(X_{․l},Y_{․m})$ is regarded as a weight for corr_n(X_․l, Y_․m). Therefore, a larger |corr_n(X_․l, Y_․m)| will yield higher weight |w_lm|, which will help improve power with sparse alternatives that are common for moderate- to high-dimensional data. Specifically, when γ = 1, all corr_n(X_․l, Y_․m)’s will be assigned an equal weight 1, which will be beneficial for dense alternatives (i.e. if all or most of the columns of the two matrices X and Y are associated) with the same association direction; however, when γ ≥ 2, the larger the γ, the higher weights would be assigned to those larger corr_n(X_․l, Y_․m)’s, more and more favoring sparse alternatives (i.e. when only few of the columns of X and Y, as indicated by those larger corr_n(X_․l, Y_․m)’s, are truly associated with each other); an even integer γ would give a test robust to varying association directions while an odd γ would not. In the extreme case of a sparse alternative with only one or few associated column-pairs between X and Y, for an even integer γ → ∞, we have

$$\text{SPC}(\gamma )\propto {(\sum _{l=1}^p\sum _{m=1}^q{\text{corr}}_n^{\gamma }(X_{․l},Y_{․m}))}^{1/\gamma }\to \underset{j}{\text{max}}|{\text{corr}}_n(X_{․l},Y_{․m})|=\text{SPC}(\infty ),$$ (5)

which we can see largely eliminates the effects of non-associated pairs and thus is expected to be more powerful for more sparse alternatives. We emphasize that, with large p and q in moderate to high dimensions, noise accumulation is a severe problem for sparse alternatives, which explains power loss of many non-adaptive tests like the RV test, as to be shown later.

In summary, depending on the type of a true alternative hypothesis to be tested, i.e. dense or sparse, a small or a large γ would yield higher power for the SPU(γ) test. In practice, because it is unknown what is the true alternative and thus which γ value would yield high power, we develop an adaptive SPC (aSPC) test to combine the evidence across the SPC tests:

$$\text{aSPC}=\underset{\gamma \in \mathrm{\Gamma }}{\text{min }}{P}_{\text{SPC}(\gamma )}$$ (6)

where P_SPC(γ) is the P-value of the SPC(γ) test, and Γ contains a set of candidate values for γ. In general, Γ = {1, 2, …, γ_u, ∞} with 1 < γ_u < ∞ can be used; larger p and q require a larger γ_u; a practical guideline on the choice of γ_u is that SPC(γ_u) gives results similar to SPC(∞). We used Γ = {1, …, 8, ∞} throughout this paper for its good performance based on our limited experience.

A permutation method can be used to obtain the P-values of all the SPC and aSPC tests in a single loop (or layer) of permutations. Briefly, B copies of the null statistic SPC(γ)^(b) for each γ ∈ Γ and b = 1, …, B can be calculated by permuting the rows of matrices X (or Y) B times. The P-value of each SPC(γ) is calculated as $P_{\text{SPC}(\gamma )}=[{\sum }_{b=1}^{B}I(|\text{SPC}{(\gamma )}^{(b)}|\ge |\text{SPC}(\gamma )|)+1]/(B+1)$. Furthermore, based on the same B copies of the null statistics, we calculate the P-value for the aSPU test as $P_{\text{aSPC}}=[{\sum }_{b=1}^{B}I({\text{aSPC}}^{(b)}\le \text{aSPC})+1]/(B+1)$ with ${\text{aSPC}}^{(b)}={\text{min}}_{\gamma \in \mathrm{\Gamma }}{p}_{\gamma }^{(b)}$ and $p_{\gamma }^{(b_1)}=[{\sum }_{b\ne b_1}I{(|\text{SPC}{(\gamma )}^{(b)}|\ge |\text{SPC}(\gamma )|)}^{(b_1)}+1]/B$.

2.3 Connections with some existing tests

We start by establishing a relationship between the aSPC test (with the Pearson correlation coefficient) and an existing test called GEE-aSPU, which was proposed by Kim et al. (2016) for multiple trait-multiple SNP associations. We first review the GEE-aSPU test before pointing out its connection to the aSPC test.

First we need some notations. Denote X_i· = (x_i1, …, x_ip) and Y_i· = (y_i1, …, y_iq)^T as ith row in matrices X and transpose of ith row in Y for i = 1, …, n, respectively; denote X_i = I ⊗ X_i·, where I is a q × q identity matrix, and ⊗ represents the Kronecker product.

Suppose we treat each column Y_·m for m = 1, …, q in Y_n×q as a response, each column X_·l for l = 1, …, p in X_n×p as a covariate or predictor of interest; recall that Y_·m and X_·l has been standardized to have zero mean and unit variance. We can then test if there is any association between the columns of X and those of Y with a marginal generalized linear model

$$g(E(Y_{i·}|X_i))=X_i\beta ,$$ (7)

where g(․) is a canonical link function, and β is a pq-dimensional vector of unknown parameters of interest. We aim to test the null hypothesis H₀ : β = 0. Denote Ȳ as the mean vector of columns of Y, which is a zero vector of length q. With a canonical link function and a working independence model in GEE (Liang and Zeger, 1986), the generalized score vector for β is

$$U=\frac{1}{n-1}\sum _{i=1}^n{X}_i^T(Y_{i·}-\overline{Y})=\frac{1}{n-1}\sum _{i=1}^n{X}_i^T{Y}_{i·}.$$ (8)

It is easy to verify U = (U₁₁, …, U_p1, …, U_1q, …, U_pq)^T with $U_{\mathit{\text{lm}}}=X_{·l}^T{Y}_{·m}/(n-1)={\text{corr}}_n(X_{·l},Y_{·m})$. That is, each element U_lm measures the association between columns X_·l and Y_·m. The GEE-SPU test statistic is defined by

$$\text{SPU}({\gamma }_1,{\gamma }_2)=\sum _{m=1}^q{\left[{\left(\sum _{l=1}^p{U}_{\mathit{\text{lm}}}^{{\gamma }_1}\right)}^{\frac{1}{{\gamma }_1}}\right]}^{{\gamma }_2}=\sum _{m=1}^q{\left[{(\sum _{l=1}^p{\text{corr}}_n^{{\gamma }_1}(X_{·l},Y_{·m}))}^{\frac{1}{{\gamma }_1}}\right]}^{{\gamma }_2}.$$ (9)

Denote Γ₁ and Γ₂ are two sets of positive integers. The GEE-aSPU test statistic is then defined as the minimum p-value of SPU(γ₁, γ₂)’ tests for all γ₁ ∈ Γ₁ and γ₂ ∈ Γ₂:

$$\text{aSPU}=\underset{{\gamma }_1,{\gamma }_2}{\text{min}}{p}_{{\gamma }_1,{\gamma }_2}$$ (10)

Here we observe a close connection between the SPC test and the GEE-SPU test: if γ₁ = γ₂ = γ, we have SPU(γ, γ) = SPC(γ). The difference between the aSPC and aSPU tests is that the latter searches for two optimal (γ₁, γ₂) in a two-dimensional space (i.e. over Γ₁ × Γ₂), while aSPC searches over only a one-dimensional space (i.e. Γ); the GEE-aSPU test reduces to aSPC if we impose γ₁ = γ₂ = γ.

Due to the currently inefficient implementation of the GEE-aSPU test (in its general regression framework) in R package GEE-aSPU, it cannot be applied to high-dimensional data: it requires a large memory space for its inefficient storage of the design matrix with dimension np × pq (or nq × pq) if Y (or X) is treated as the response. As an example, the GEE-aSPU test will need about a 40GB memory space if p = q = 300 and sample size n = 200, not yet available on many computers. In contrast, due to its simplicity, the aSPC test is applicable to high-dimensional data.

Finally, we comment on that the SPC(2) test is also closely related to several other tests, further illustrating the potential power of the aSPC test. First, since the dCov test and the Hilbert-Schmidt independence criterion (HSIC) test are equivalent (Sejdinovic, Sriperumbudur, Gretton and Fukumizu, 2013), Hua and Ghosh (2015) called them kernel distance covariance method (KDC); they further established the equivalence of KDC and multivariate kernel machine regression (KMR) test (Maity et al., 2012) (if the same kernels are used in the two). On the other hand, Kim et al. (2016) pointed out that GEE-SPU(2,2) is similar to multivariate KMR with a linear kernel; the two are exactly the same if the true correlation matrix is used as the working correlation structure in GEE for the former, which in general does not hold (unless the columns of Y are independent), because the working independence model is used in GEE-SPU tests. Now, by the equivalence between SPC(2) and GEE-aSPU(2,2) and by the above results, we see the close similarity between SPC(2) and other tests. Using the weighting argument motivating the development of other SPC(γ) tests with γ > 2, we expect that the other tests (i.e. dCov, HSIC and KMR with linear kernels) may lose power with sparse association patterns, which will be confirmed in our later simulations.

2.4 Extensions

So far we define the SPC test with the Pearson correlation coefficients between the columns of the two matrices. Here we generalize the SPC and thus aSPC tests with several other dependence measures and with covariates.

2.4.1 Fisher’s transformation

We may take Fisher’s z-transformation on the sample Pearson correlation coefficient r_lm = corr_n(X_․l, Y_․m) before plugging into equation (4). The reason is to account for heterogeneous variances of the sample correlations for an alternative hypothesis; as to be shown next, the variance of a sample correlation increases monotonically as the absolute value of the true correlation decreases (under the normality assumption). Specifically, the sample correlation r_lm = corr_n(X_․l, Y_․m) is replaced by $z_{\mathit{\text{lm}}}=\frac{1}{2}\text{ln}((1+r_{\mathit{\text{lm}}})/(1-r_{\mathit{\text{lm}}}))$ in equation (4). Under the normality assumption (on each pair of the columns of X and Y), z_lm is approximately normally distributed with mean $\frac{1}{2}\text{ln}((1+{\rho }_{\mathit{\text{lm}}})/(1-{\rho }_{\mathit{\text{lm}}}))$ and a constant variance 1/(n − 3), where ρ_lm is the population Pearson correlation coefficient.

Given that $z_{\mathit{\text{lm}}}\dot{~}N(\frac{1}{2}\text{ln}((1+{\rho }_{\mathit{\text{lm}}})/(1-{\rho }_{\mathit{\text{lm}}})),1/(n-3))$, it is not hard to find the approximate distribution of the sample Pearson correlation coefficient is $r_{\mathit{\text{lm}}}\dot{~}N({\rho }_{\mathit{\text{lm}}},{(1-{\rho }_{\mathit{\text{lm}}}^2)}^2/(n-3))$; the variance ${(1-{\rho }_{\mathit{\text{lm}}}^2)}^2/(n-3)$ is obtained by the delta method and clearly confirms the monotonicity mentioned above. In particular, since the variance is largest for no correlations, not taking Fisher’s transformation or not stabilizing the variance may lead to loss of power, especially for high-dimensional data, for which sparse alternatives are expected with many non-associated pairs.

Whenever needed, to distinguish using Fisher’s z-transformed Pearson correlation coefficients from using other dependence measures for the SPC and aSPC tests, we will use SPC.P and aSPC.P to refer to the former:

$$\text{SPC.P}(\gamma )=\sum _{l=1}^p\sum _{m=1}^q{z}_{\mathit{\text{lm}}}^{\gamma },$$ (11)

and the aSPC.P test is similarly defined as before.

2.4.2 The aSPC test with Spearman’s correlation

More generally, the sample Pearson correlation coefficient term r_lm = corr_n(X_․l, Y_․m) in equation (4) can be replaced by a different dependence measure. For example, we can use Spearman’s (1904) rank correlation coefficient, which is effective for monotonic relationships, in contrast to only linear relationships by Pearson’s coefficient. The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the ranked variables. Specifically, X_·l and Y_·m (l = 1, …, p and m = 1, …, q) are converted to the rank score vectors rank(X_·l) and rank(Y_·m) (e.g. rank score = 1 for the smallest value in X_·l (or Y_·m) and rank score = n for the largest value in X_·l or (Y_·m)). The sample Spearman correlation coefficient is calculated as

$$r_{\mathit{\text{lm}}}(\text{Spearman})=\frac{{\text{Cov}}_n(\text{rank}(X_{·l}),\text{rank}(Y_{·m}))}{\sqrt{{\text{Cov}}_n(\text{rank}(X_{·l}),\text{rank}(X_{·l})){\text{Cov}}_n(\text{rank}(Y_{·m}),\text{rank}(Y_{·m}))}},$$ (12)

where Cov_n(u, υ) is a sample covariance between vectors u_n×1 and υ_n×1. Then the SPC statistic with Spearman’s rank correlation coefficient is defined as:

$$T_{\text{SPC.Sp}(\gamma )}=\sum _{l=1}^p\sum _{m=1}^q{r}_{\mathit{\text{lm}}}^{\gamma }(\text{Spearman}),$$ (13)

and aSPC.Sp is defined similarly as before.

2.4.3 The aSPC test with the distance correlation

Another extension is to replace each sample Pearson correlation coefficient in equation (4) by a corresponding distance correlation coefficient (dCor), which is derived based on the distance covariance (dCov) (Szykely et al., 2007) and is consistent in detecting any dependency, not only the linear ones (detectable by Pearson’s) or monotonic ones (by Spearman’s); for example, in the presence of non-linear (and non-monotonic) dependency, use of dCor is expected to be more powerful, as to be confirmed in our later simulations. We first review the usual dCov test and then modify the SPC test with the distance correlations.

The standard dCov test utilizes all columns in X and Y to calculate the pairwise distance before computing the sample distance covariance:

$$a_{\mathit{\text{ij}}}={\Vert X_{i·}-X_{j·}\Vert }^t,b_{\mathit{\text{ij}}}={\Vert Y_{i·}-Y_{j·}\Vert }^t,$$ (14)

where ‖ · ‖ denotes the Euclidean distance/norm; X_i· and Y_i· denote the ith row of X and Y respectively (i = 1, …, n); t ∈ (0, 2] and t = 1 corresponds to the Euclidean norm, which was used in our data analysis throughout unless specified otherwise. The pairwise distances are doubly centered:

$$A_{\mathit{\text{ij}}}=a_{\mathit{\text{ij}}}-{\overline{a}}_{i·}-{\overline{a}}_{·j}+{\overline{a}}_{··},B_{\mathit{\text{ij}}}=b_{\mathit{\text{ij}}}-{\overline{b}}_{i·}-{\overline{b}}_{·j}+{\overline{b}}_{··},$$ (15)

where ā_i·, ā_·j ā‥ are the ith row mean, the jth column mean and the grand mean of matrix [a_ij]; b̄_i·, b̄_·j and b̄‥ are similar defined for matrix [b_ij]. Then the squared sample distance covariance of X and Y is defined as:

$${\text{dCov}}_n^2(X,Y)=\frac{1}{n^2}\sum _{i,j=1}^n{A}_{\mathit{\text{ij}}}{B}_{\mathit{\text{ij}}}.$$ (16)

A permutation method can be used to calculate the P-value. The null statistics $T_{\text{dCov}}^{(b)}=\frac{1}{n^2}{\sum }_{i,j=1}^n{A}_{\mathit{\text{ij}}}^{(b)}{B}_{\mathit{\text{ij}}}^{(b)}$ can be calculated based on each permuted sample X^(b) and Y^(b), where X^(b) (or Y^(b)) is generated by permuting the rows of X (or Y). The P-value is calculated as $P_{\text{dCov}}=({\sum }_b^{B}I({\text{dCov}}^{(b)}\ge \text{dCov})+1)/(B+1)$ based on B permutations.

In the standard dCov test, all columns of X and Y are used to calculate the pairwise distances; that is, each variable (or dimension) is treated equally a priori, which may not be a good idea for high-dimensional data for the abundance of sparse alternatives. In contrast, in our SPC test, each column/variable of X and Y is treated differently according to the magnitudes of their estimated pairwise associations. Specifically, similar to the standard dCov test, first we define all pairwise distances among the observations based on the ith and jth elements of X_·l and Y_·m as

$$a_{\mathit{\text{ij}}(l)}={\Vert X_{\mathit{\text{il}}}-X_{\mathit{\text{jl}}}\Vert }^t,b_{\mathit{\text{ij}}(m)}={\Vert Y_{\mathit{\text{im}}}-Y_{\mathit{\text{jm}}}\Vert }^t,$$ (17)

which computes the n × n distance matrices (a_ij(l)) and (b_ij(m)) for i = 1, …, n, j = 1, …, n, l = 1, …, p and m = 1, …, q. Denote ā_i·(l), ā_·j(l)and ā_‥(l) as the ith row mean, the jth column mean and the grand mean of [a_ij(l)]; similarly, denote b̄_i·(m), b̄_·j(m) and b̄_‥(m) for [b_ij(m)]. The elements a_ij(l) and b_ij(m) are then doubly centered as:

$$A_{\mathit{\text{ij}}(l)}=a_{\mathit{\text{ij}}(l)}-{\overline{a}}_{i·(l)}-{\overline{a}}_{·j(l)}+{\overline{a}}_{··(l)},B_{\mathit{\text{ij}}(m)}=b_{\mathit{\text{ij}}(m)}-{\overline{b}}_{i·(m)}-{\overline{b}}_{·j(m)}+{\overline{b}}_{··(m)},$$ (18)

then the squared sample distance covariance is defined as:

$${\text{dCov}}_n^2(X_{·l},Y_{·m})=\frac{1}{n^2}\sum _{i,j=1}^n{A}_{\mathit{\text{ij}}(l)}{B}_{\mathit{\text{ij}}(m)}.$$ (19)

The sample distance correlation (dCor) between X_·l and Y_·m is then defined as

$${\text{dCor}}_n(X_{·l},Y_{·m})=\frac{{\text{dCov}}_n(X_{·l},Y_{·m})}{\sqrt{{\text{dCov}}_n(X_{·l},X_{·l}){\text{dCov}}_n(Y_{·m},Y_{·m})}}.$$ (20)

The SPC.dCor test statistic is defined as:

$$\text{SPC.dCor}(\gamma )=\sum _{l=1}^p\sum _{m=1}^q{\text{dCor}}_n^{\gamma }(X_{·l},Y_{·m})$$ (21)

and the aSPC.dCor is similarly defined as before.

As to be shown later in simulations, the aSPC.dCor test was much more powerful than the standard distance covariance (dCov) test for sparse alternatives in even only moderate dimensions, presumably because the former’s weighting on the pairwise dCor’s alleviates the harmful effects of noise accumulations in the latter.

2.4.4 The aSPC test with covariates

The aSPC test can be applied to situations with covariates. We only need to first regress X and/or Y on the covariates, then use the residuals to construct the SPC tests. We will illustrate such an application in the example section.

2.5 Software

The asymptotic- and permutation-based RV tests are available as functions coeffRV() and RV.rtest() in R packages FactoMineR and ade4, respectively. The permutation-based Mantel test, dCov test and GEE-aSPU test are in functions mantel(), dcov.test(), GEEaSPUset() in R packages vegan, energy and GEEaSPU, respectively. We implemented various versions of the new SPC and aSPC tests in an R package aSPC, which is available on github (and CRAN).

3 Simulations

3.1 Simulation I: linear associations

To further investigate the operating characteristics of the proposed tests, we compare their power performance with several existing tests. We first consider an ideal situation with a linear association between two sets of normal variates.

To generate a simulated dataset, two matrices X_n×p and Y_n×p were simulated with n = 500. First, for each X and Y, p (= 25, 45 or 65) independent columns were simulated from a standard multivariate normal distribution. Second, a matrix Z_n×10 with ten columns were simulated from a multivariate normal distribution with mean 0 and a compound symmetry covariance matrix (with all diagonal elements equal to 1 and all off-diagonal elements equal to 0.1); for power comparisons, we added the first 5 columns of Z to X and the last 5 columns of Z to Y.

We applied the aSPC.P, aSPC.Sp, aSPC.dCor, RV, Mantel and dCov tests to each simulated dataset, and and compared their empirical Type I error and power estimates. The Mantel and dCov tests were conducted with the Euclidean distance. We set B = 1000 for any permutation-based tests. To save computing time, the empirical Type I error rates and power of aSPC.dCor were based on 1,000 replicates while for all other tests, they were based on 10,000 replicates.

As shown in Table 1, first, the Type I error rates were in general well controlled for each test. Second, among all the tests, GEE-aSPU was most powerful, followed by aSPC.P. Note that, due to the linear association, aSPC.P is expected to be more powerful than aSPC.Sp (and aSPC.dCor). Third, SPC.P(2) gave the results essentially the same as both the asymptotic and permutation-based RV tests, as expected. Fourth, due to the presence many independent columns in the two matrices X and Y, a SPC.P test with a larger and finite γ (e.g. γ = 6) was more powerful than that with a small γ ≤ 4; their power difference increased with the number of independent columns. Fifth, aSPC.dCor gave much higher power than dCov test, due to that SPC.dCor(γ) with larger γ reduced the effects of noise accumulation with independent columns. Moreover, we note the extremely low power of the Mantel test, followed by MANOVA.

Table 1.

Simulation I: empirical Type I error and power rates when the number of independent columns (denoted as “No. ind”) is 25, 45, and 65 respectively. “RV.asy” and “RV.perm” stand for the asymptotic and permutation-based RV tests, respectively

No.Ind		SPC.P(γ)									aSPC.P	aSPC.Sp	aSPC.dCor	RV.asy	RV.perm	Mantel	dCov	GEE-aSPU	MANOVA
		γ = 1	2	3	4	5	6	7	8	Inf
25	Type I	0.047	0.053	0.049	0.050	0.050	0.051	0.052	0.053	0.054	0.046	0.049	0.049	0.053	0.055	0.050	0.052	0.055	0.046
	Power	0.417	0.844	0.886	0.932	0.917	0.908	0.879	0.852	0.589	0.933	0.893	0.828	0.840	0.838	0.098	0.819	0.955	0.378
45	Type I	0.055	0.052	0.052	0.052	0.052	0.053	0.050	0.050	0.048	0.052	0.049	0.050	0.052	0.051	0.050	0.053	0.061	0.045
	Power	0.196	0.538	0.587	0.753	0.732	0.759	0.710	0.700	0.425	0.749	0.674	0.587	0.539	0.538	0.074	0.522	0.832	0.174
65	Type I	0.056	0.055	0.050	0.052	0.054	0.050	0.050	0.051	0.049	0.050	0.050	0.047	0.056	0.055	0.052	0.054	0.057	0.041
	Power	0.118	0.352	0.371	0.581	0.558	0.627	0.576	0.578	0.328	0.594	0.506	0.450	0.355	0.354	0.072	0.345	0.702	0.110

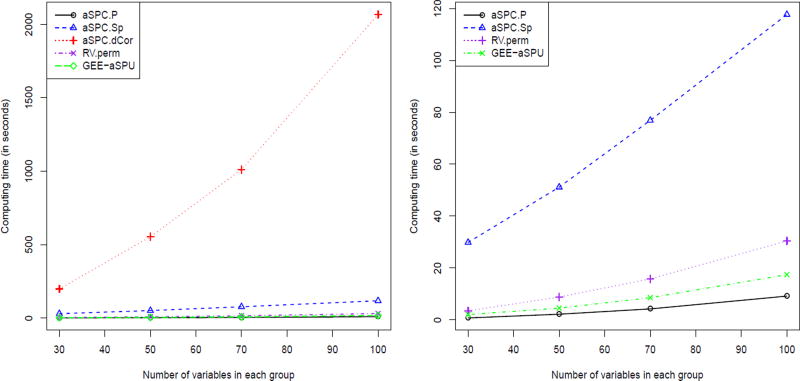
To assess the computing time and feasibility for the permutation-based RV, GEE-aSPU and aSPC tests, we changed the number of columns in X and Y to 30, 50, 70 and 100 respectively, and with a sample size n = 200. We then calculated the computing time with a permutation number B = 1 × 10³. Note that, for example, for p = q = 300, GEE-aSPU needs to construct a large design matrix with dimension 60, 000 × 90, 000, requiring about 40GB of memory. The computing time was based on one processor (Intel Haswell E5-2680v3 with 2.5GB of memory on Unix system) from a cluster at the Minnesota Supercomputing Institute (MSI).

As shown in Figure 1, first, our implementation of aSPC.P completely in R was even faster than the RV.perm test, which was surprising given that aSPC.P involved conducting SPC.P(γ) for γ = 1, …, 8, ∞ and RV.perm is equivalent to SPC.P(2). Second, aSPC.dCor was more computing-intensive than other tests; for data matrices X_n×p and Y_n×q, aSPC.dCor required calculating pairwise distance covariances pq times based on p + q distance matrices, even if we used more memory space to save the distance matrices in our current implementation in R.

Figure 1.

The computing time of the permutation-based RV, GEE-aSPU, aSPC.P, aSPC.Sp and aSPC.dCor tests. The left panel shows the computing time of aSPC.dCor test as compared to that of all the other tests, while the right panel is a zoom-in for all the tests except aSPC.dCor

3.2 Simulation II: non-linear associations

Now we consider a more challenging case with a non-linear and non-monotonic association. Our simulation set-up was similar to that of Székely et al. (2007).

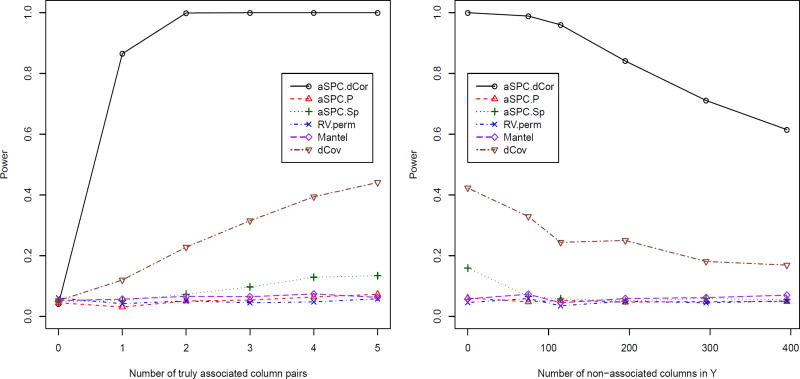
Data matrix X_n×5 was simulated from a multivariate standard normal distribution. To calculate the empirical type I error rates, for each replicate a matrix Y_n×5 was simulated from a multivariate standard normal distribution. For power, Y_n×p was generated such that each of the first p₀ (p₀ = 1, 2, 3, 4 or 5) columns $Y_{\mathit{\text{ij}}}=\mathit{\text{log}}(X_{\mathit{\text{ij}}}^2)$ for j = 1, …, p₀ and i = 1 …n; when p₀ ≤ 4, each of the other columns of Y_n×p was independently and identically simulated from a standard normal distribution. We were interested in how the empirical power changed as the number of non-linearly associated column pairs (p₀) between X and Y varied from 1 to 5. Six tests were applied, including aSPC.dCor, aSPC.Sp, aSPC.P, permutation-based RV test, the Mantel test with the Euclidean distance and Pearson correlation, and dCov. One thousand datasets were simulated to calculate the empirical type I error and power. We used B = 1000 for any permutation-based tests. The simulation results are summarized in the left panel of Figure 2 with sample size n = 40.

Figure 2.

Simulation II results. The left panel: when the number of columns in X and Y are 5, the empirical type I error and power curves of the tests as the number of truly non-linearly associated column pairs between X and Y ranges from 0 (type I error) to 5. Right panel: when the number of non-linearly associated column pairs in X and Y is fixed at 5, the power curves of the tests as more and more non-associated columns are added to Y. The nominal significance level is 0.05

First, the type I error rates were well controlled for all tests. Second, our aSPC.dCor test gave much higher power than the usual dCov test. For example, with only one truly associated pair, the power of aSPC.dCor was 86.5%, much higher than 12.0% of the dCov test. Third, due to the underlying non-monotonic true associations, as expected, none of the RV, aSPC.P, aSPC.Sp and Mantel tests performed well.

To further explore the performance of the tests with increasingly sparse associations, in addition to the above set-up with p₀ = 5, we added 75, 115, 195, 295 or 395 independent columns to matrix Y, each of which was simulated from a standard normal distribution. The power curves are shown in the right panel of Figure 2. It is clear that the power of aSPC.dCor remained significantly higher than that of the dCov test, whereas all other tests had no power.

4 Real data application

4.1 ADNI data

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California-San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

4.2 Testing for SNP-gene expression associations

To understand gene regulation, it is important to detect genetic variants like single nucleotide polymorphisms (SNPs) that are associated with gene expression (i.e. transcript) levels, called eQTL (Minas, Curry and Montana, 2013). Due to the relatively small sample size and a severe penalty on multiple testing for a large number of SNP-gene pairs, it is often low-powered to detect many associations at the individual pair level. As an alternative, we may first test the association between a set of SNPs and a set of the genes.

The ADNI genotype data consist of 757 subjects from ADNI-1, two hundred and thirty six of whom also have genome-wide gene expression data based on the whole blood. A pathway for Alzheimer’s disease (hsa05010, http://www.genome.jp/dbget-bin/www_bget?hsa05010) was downloaded from Kyoto Encyclopedia of Genes and Genomes (KEGG) website (Kanehisa, Sato, Kawashima, Furumichi and Tanabe, 2016). Since the ADNI-1 genotype data are based on the human genome version hg18, we used the hg18 gene coordinate file downloaded from the PLINK website (http://pngu.mgh.harvard.edu/~purcell/plink/) to identify the starting base pair (bp) and ending bp for each gene. We then extracted two sets of the SNPs for the genes in the AD pathway. In the first, the SNPs within each gene were selected, including possibly both protein coding and regulatory SNPs; in the second, to focus on only regulatory SNPs, only the SNPs within the upstream 20kb of a gene’s starting bp or within the downstream 20kb of its ending bp were selected. Since the results were similar, we will discuss only the first dataset.

To account for possible effects of age and gender on gene expression, we used a linear regression model to regress each gene’s expression level on the two covariates, then used the residuals as the gene’s adjusted expression levels in the subsequent analysis. In the end, there were 441 probes corresponding to 151 genes, and 2,483 SNPs (after excluding those with a minor allele frequency less than 0.05) in the first dataset.

To demonstrate the effects of association patterns, especially the signal sparsity levels, on the testing results, we screened the SNP-gene pairs using each pair’s P-value for their marginal association, which was based on a simple linear regression of each gene’s adjusted expression level on each SNP in the set. The expression level of each gene was calculated as the average of its corresponding probes for those genes with more than one probe. We used various threshold values to select subsets of the SNP-gene pairs, with a marginal P-value smaller than a given threshold. Then we pooled the SNPs and the probes in the genes surviving such a screening into a SNP set and a probe set respectively, then tested their associations using various methods. For any permutation-based test, we used a permutation number B = 1 × 10⁴ (unless specified otherwise). As the dimensions of the probes and the SNPs were high (i.e. in hundreds to thousands), it would be infeasible to run the GEE-aSPU test as it required a too large memory space. The results are summarized in Table 2.

Table 2.

The analysis results for the ADNI data. p and q denote the numbers of SNPs and of probes surviving the P-value cut-off based on the corresponding univariate SNP-gene expression associations

Cut- off	(p, q)	SPC.P(γ)					aSPC.P	RV.asy	RV.perm	Mantel	dCov	aSPC.Sp	aSPC.dCor
		γ = 1	2	3	4	5–8, ∞
1	(2483, 382)	5.85e-02	3.68e-02	2.87e-01	3.00e-04	1.00e-04	8.00e-04	6.89e-02	7.17e-02	8.69e-02	5.61e-02	9.00e-04	5.00e-04
0.9	(2274, 380)	3.63e-02	4.50e-02	2.16e-01	5.00e-04	1.00e-04	8.00e-04	6.47e-02	6.37e-02	9.76e-02	4.99e-02	8.00e-04	5.00e-04
0.8	(2069, 371)	2.29e-02	2.09e-02	2.22e-01	1.00e-04	1.00e-04	8.00e-04	3.87e-02	3.86e-02	7.40e-02	2.62e-02	8.00e-04	5.00e-04
0.7	(1871, 357)	3.26e-02	8.60e-03	2.39e-01	1.00e-04	1.00e-04	7.00e-04	2.01e-02	2.05e-02	5.81e-02	1.27e-02	8.00e-04	5.00e-04
0.6	(1647, 353)	1.39e-02	4.40e-03	1.74e-01	1.00e-04	1.00e-04	9.00e-04	9.22e-03	8.90e-03	4.71e-02	6.50e-03	7.00e-04	6.00e-04
0.5	(1435, 351)	1.62e-02	2.90e-03	2.80e-01	1.00e-04	1.00e-04	6.00e-04	6.69e-03	7.70e-03	5.96e-02	3.10e-03	6.00e-04	6.00e-04
0.4	(1228, 340)	1.99e-02	8.00e-04	2.54e-01	1.00e-04	1.00e-04	9.00e-04	1.91e-03	2.30e-03	1.49e-02	1.60e-03	9.00e-04	4.00e-04
0.3	(999, 306)	5.95e-02	1.20e-03	4.62e-01	1.00e-04	1.00e-04	8.00e-04	1.48e-03	1.50e-03	7.30e-03	9.00e-04	8.00e-04	1.00e-04
0.2	(756, 286)	7.54e-02	6.00e-04	5.93e-01	1.00e-04	1.00e-04	7.00e-04	6.07e-04	2.00e-04	2.00e-03	4.00e-04	9.00e-04	4.00e-04
0.1	(485, 245)	2.93e-01	1.00e-04	3.34e-01	1.00e-04	1.00e-04	7.00e-04	8.29e-05	3.00e-04	4.00e-04	2.00e-04	8.00e-04	4.00e-04

We have the following observations. First, when we included all the SNPs and the probes (with a P-value threshold 1), the aSPC tests (i.e. aSPC.P, aSPC.Sp, and aSPC.dCor) all gave significant P-values; in contrast, none of the other tests, including the RV test, the Mantel test and dCov test, gave any significant P-value less than the nominal level 0.05. Second, most strikingly, regardless of the dimensions (p, q) with various threshold values, the aSPC tests consistently gave small and significant P-values (e.g. < 0.001), showing their robustness to the varying association patterns (e.g. signal sparsity levels); in contrast, as fewer and fewer, but more significant, SNPs and probes were included, other global tests gradually gave more and more significant P-values, suggesting their loss of power in the presence of sparse signals due to their none-adaptiveness. Third, among the SPC tests, those SPC.P(γ) tests with larger γ (e.g. γ > = 4) gave more significant P-values than those with smaller γ (e.g. γ < 4), indicating sparse signals as expected (i.e. most SNP-probe pairs were not associated).

5 Discussion

We have proposed an adaptive and powerful association test called aSPC for two moderate- to high-dimensional random vectors. It has been shown to be more powerful in a a variety of simulations than several commonly used tests. In an application to a real genotype-gene expression dataset, under various moderately high dimensions for the SNPs and genes, the proposed test robustly and consistently gave more significant P-values than other existing tests, which appeared to lose power dramatically for larger sets of the SNPs and genes. The proposed aSPC test can be regarded as a generalization of the standard RV test from low-dimensional data to moderate- to high-dimensional data with the incorporation of data-adaptive weighting on each variable pair. The main idea is that, for moderate- to high-dimensional data, often there will be many variable pairs that are not associated; treating these null pairs equally as other truly associated pairs will simply accumulate noises, leading to substantial power loss as in most other existing tests like the RV test. Hence, this main idea is related to the GEE-aSPU test in genetics. Indeed the aSPC test (more precisely, the version denoted aSPC.P with Pearson’s correlation) is a special case of the GEE-aSPU test. However, due to its simplicity, the aSPC.P test has some computational advantage over the GEE-aSPU test, which in its currently implementation is not applicable to high-dimensional data. More importantly, the aSPC.P test can be easily extended by replacing the Pearson correlation coefficient with other coefficient, which may be more suitable for other non-linear associations. For example, if the distance correlation is used as in aSPC.dCor, it can detect non-monotonic associations. Compared to the usual dCov (or dCor) test, again due to its adaptiveness, the aSPC.dCor test is much more powerful for less dense or sparse signals for high-dimensional data, as shown in our simulations.

In the current implementation of the new tests, we have resorted to permutations to calculate their P-values, which seems feasible and satisfactory in many applications. However, it would be interesting to establish their asymptotics as both p and q diverge with n (Xu et al., 2016), which may be challenging due to the dependencies among the individual correlation coefficients in each SPC test statistic. Nevertheless, an asymptotic theory will be useful in facilitating speedy P-value calculations, especially for a high significance level.

The various versions of the aSPC test are implemented in R package aSPC, freely available on CRAN or at https://github.com/jasonzyx/aSPC.