The dock-and-coalesce mechanism for the association of a WASP disordered region with the Cdc42 GTPase

Abstract

Intrinsically disordered proteins (IDPs) play key roles in signaling and regulation. Many IDPs undergo folding upon binding to their targets. We have proposed that coupled folding and binding of IDPs generally follow a dock-and-coalesce mechanism, whereby a segment of the IDP, through diffusion, docks to its cognate subsite and, subsequently, the remaining segments coalesce around their subsites. Here, by a combination of experiment and computation, we determined the precise form of dock-and-coalesce operating in the association between the intrinsically disordered GTPase binding domain (GBD) of the Wiskott-Aldrich Syndrome protein (WASP) and the Cdc42 GTPase. The association rate constants (k_a) were measured by stopped-flow fluorescence under various solvent conditions. k_a reached 10⁷ M⁻¹s⁻¹ at physiological ionic strength and had a strong salt dependence, suggesting that an electrostatically enhanced, diffusion-controlled docking step may be rate-limiting. Our computation, based on the transient-complex theory, identified the N-terminal basic region of the GBD as the docking segment. However, several other changes in solvent conditions provided strong evidence that the coalescing step also contributed to determining the magnitude of k_a. Addition of glucose and trifluoroethanol and an increase in temperature all produced experimental k_a values much higher than expected from the effects on the docking rate alone. Conversely, addition of urea led to k_a values much lower than expected if only the docking rate was affected. These results all pointed to k_a being approximately two thirds of the docking rate constant under physiological solvent conditions.

Graphical Abstract

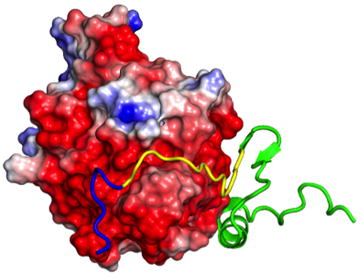
The binding of a WASP disordered region (ribbon representation) to the Cdc42 GTPase (surface representation) follows a dock-and-coalesce mechanism. In the first step, the basic rich segment (blue) of WASP docks to its cognate subsite on Cdc42 by diffusion, accelerated by electrostatic attraction. In the subsequent step, the remaining segments (yellow and green) of WASP coalesce around their respective subsites.

Introduction

Intrinsically disordered proteins (IDPs) and intrinsically disordered regions (IDRs) of proteins are widely involved in signaling, regulation, and other cellular functions. IDPs/IDRs often bind to structured targets, where they form highly extended structures [1–4] that are stabilized more by intermolecular than by intramolecular interactions. These structural and functional features are illustrated well by the complex formation between the intrinsically disordered GTPase binding domain (GBD) in the Wiskott–Aldrich Syndrome protein (WASP) and Cdc42 (a Rho GTPase) (Fig. 1). Because of the typical transient nature of the complexes formed during signaling and regulation by IDPs/IDRs with their cellular targets, both the rate constants and the mechanisms of the binding and unbinding processes can potentially be crucial for the cellular functions [5]. Yet, our knowledge on these important properties is far from complete. The aim of the present study was to dissect the physical factors that control the mechanism and rate constant for the binding of the WASP GBD to Cdc42.

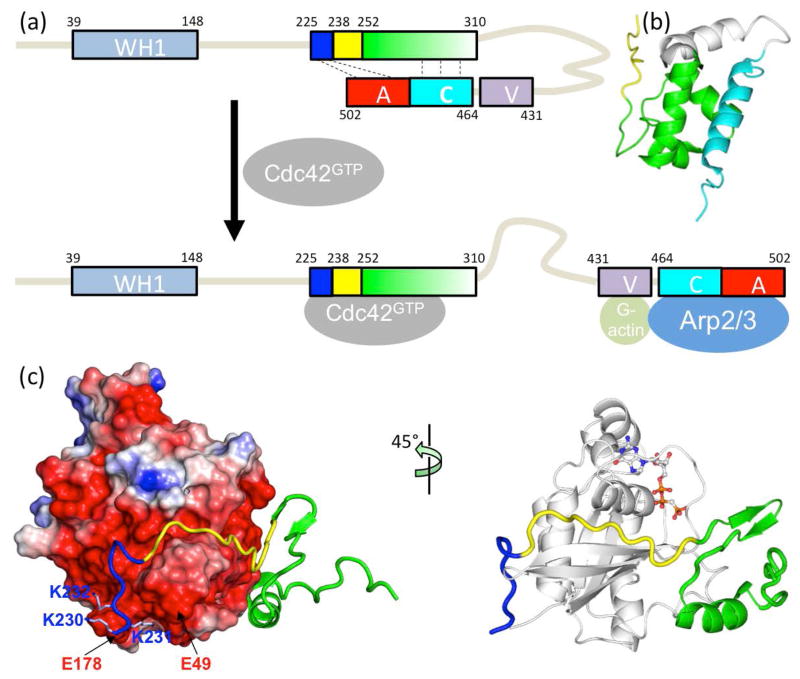
Fig. 1.

Structure and function of the intrinsically disordered GTPase binding domain (GBD) in the Wiskott-Aldrich Syndrome protein (WASP). (a) Domain organization of WASP and intramolecular and intermolecular interactions of the GBD, comprising a basic region (blue box), a Cdc42/Rac1 interactive binding motif (CRIB; yellow box), and a downstream sequence (green box). Cdc42 can dislodge from the GBD the VCA domain (V: verprolin-homology region; C: cofilin-homology region; and A: acidic region), allowing the latter to interact with G-actin and Arp2/3. (b) Autoinhibiting interaction between the GBD (green) and the C helix (cyan); structure from Protein Data Bank (PDB) entry 1EJ5. (c) Extended structure and intermolecular interaction of the WASP GBD on the surface of Cdc42 (PDB entry 1CEE). The left panel highlights the acidic Cdc42 surface interacting with the WASP BR; the right panel displays a bound nucleotide to indicate the position of the fluorophore used for monitoring binding kinetics.

Characterizing IDP binding kinetics presents significant challenges to both experimental and computational approaches. Experimental approaches, in particular stopped-flow spectroscopy, can easily determine binding rate constants, but face difficulty in producing atomic-level information on intermediates that is crucial for determining binding mechanisms. Nevertheless, by using point mutations, deletion constructs, and tailored NMR experiments, and by varying solvent conditions, valuable insight has been gained on the binding processes of a number of IDPs [6–15]. These studies generally support the notion that the structures of IDPs bound to their targets accrue sequentially on the latters’ surfaces [4]. Computational studies have sometimes employed simplified representations of proteins and often relied on the structure of the native complex for guidance [16–23]. These studies can provide qualitative descriptions of binding mechanisms but typically lack the capability of making quantitative predictions on binding rate constants, though there have been continued developments on the latter front [24, 25]. Again, sequential binding models are usually implicated.

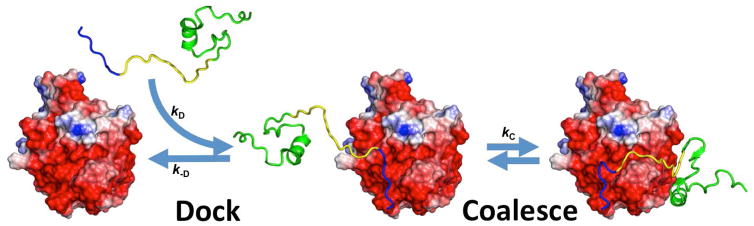
Guided in part by the observation that IDPs form highly extended structures on target surfaces, we proposed that their binding mechanisms are expected to involve some form of dock-and-coalesce, whereby one segment of an IDP first docks to its subsite on the target surface and the remaining segments subsequently coalesce around their respective subsites (Fig. 2) [26]. If, along a specific dock-and-coalesce pathway, the rate constants for the docking step and its reverse process, i.e., the undocking step, are k_D and k_−D, respectively, and the rate constant for the subsequent coalescing step is k_C, then the overall association rate constant along that pathway is

Fig. 2.

The dock-and-coalesce mechanism for the binding of an intrinsically disordered protein to a structured target. In the docking step, a segment (blue) docks to its cognate subsite to form a docked complex. The docking rate can be significantly accelerated by long-range electrostatic attraction between the docking segment and the target surface. Note that an extended charge surface (red) of the target may contribute to the electrostatic attraction. In the subsequent coalescing step, additional segments (yellow and green), guided by local interactions with the target surface, form native structures within their own subsites.

$$k_{\mathrm{a}}=\frac{k_{\mathrm{D}}{k}_{\mathrm{C}}}{k_{-\mathrm{D}}+k_{\mathrm{C}}}=\frac{k_{\mathrm{D}}}{1+k_{-\mathrm{D}}/k_{\mathrm{C}}}$$ (1)

Eq 1 is derived under the assumption that the docked complex accumulates only to a negligible extent, which is valid for WASP-Cdc42 binding since stopped-flow experiments did not detect any intermediate. As noted previously [27], the docking segment approaches its subsite on the target surface by translational/rotational diffusion, and simultaneously undergoes rapid conformational exchange to reach a kinetic intermediate, referred to as a docked complex, where the docking segment is natively bound but the remaining segment(s) of the IDP are still loose. The docking step likely is rate-limited by the diffusional approach, and the rate in turn can be sped up enormously by long-range electrostatic attraction of the target protein [28–30]. This rate constant can be calculated by our TransComp method (http://pipe.sc.fsu.edu/transcomp/) [26], according to

$$k_{\mathrm{D}}=k_{\mathrm{D}0}{e}^{-\mathrm{\Delta }{G}_{\text{el}}^{\ast }/k_{\mathrm{B}}T}$$ (2)

Here k_D0 is the basal rate constant, i.e., the value of k_D when long-range electrostatic interactions are turned off, and the Boltzmann factor of the electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$, calculated at the rim (a substate known as the transient complex) of the bound-state energy well, captures the electrostatic contribution.

In the subsequent coalescing step, the remaining segments evolve toward their native conformations, with energy barriers affected by secondary structure propensities [11, 14] and lowered by favorable interactions with surface residues of the target protein [13, 19]. These local interactions are difficult to treat realistically on timescales relevant for modeling k_C, and hence no reliable methods for k_C calculations exist. However, according to eq 1, k_a ≤ k_D, so the rate constant for the docking step provides an upper bound for the overall association rate constant of a given dock-and-coalesce pathway. In addition, although the binding can proceed along multiple pathways, each starting with the docking of some initial segment of the IDP and ending with the structural coalescence of some final segment on the target surface, it is quite possible that a single pathway has a k_a much higher than any alternative pathway, and hence becomes dominant [4]. The most likely dominant pathway is the one where the docking step is rate-enhanced by electrostatic attraction and close to being rate-limiting for the overall k_a of that pathway. By applying the TransComp method to different segments of an IDP, we can identify the docking segment of the dominant pathway and predict the rate constant of the docking step, thereby providing an upper bound for the rate constant of the overall binding process. This approach has yielded rate constants in good agreement with experimental results for a number of IDPs [4, 26, 27, 31, 32].

The 502-residue WASP comprises a WASP-homology-1 (WH1) domain, the GBD (residues 238–277) containing a basic region (BR; residues 225–237) and a CRIB motif (residues 238–251), and a VCA domain (Fig. 1). Unbound WASP is autoinhibited, with the VCA domain trapped through intramolecular binding with the GBD (Fig. 1a and b) [33]. Upon binding GTP-loaded Cdc42, the GBD engages in intermolecular interactions [34], thereby releasing the VCA domain for interacting with Arp2/3 (Fig. 1a and c). In this way, WASP activates Arp2/3 for nucleation of actin polymerization [33, 35–40]. The WASP GBD undergoes a disorder-to-order transition upon binding Cdc42, whereby the BR and CRIB adopt extended conformations while downstream residues of the GBD form a compact subdomain comprising a β hairpin and an α-helix (Fig. 1c) [34]. Three basic residues (K₂₃₀KK₂₃₂) in the BR interact with acidic residues, including Glu49 and Glu178, in Cdc42, while the CRIB is accommodated in a groove of Cdc42. Stopped-flow data of Hemsath et al. [8] showed fast association (k_a exceeding 10⁷ M⁻¹s⁻¹) at low salt concentrations and a strong decrease in k_a at high salt concentrations. In addition, mutations of the aforementioned basic and acidic residues resulted in significant decreases in k_a, leading Hemsath et al. to propose that the BR is the initial recognition site for Cdc42. Our TransComp calculations confirmed that the BR is the docking segment, and the calculated effects of salt concentration and charge mutations on the docking rate constant reproduced well the corresponding experimental results on the overall association rate constant [27].

In order to find direct evidence either for the possibility that the docking step is rate-limiting for the binding of the WASP GBD to Cdc42 or for the alternative that the coalescing step also contributes to determining the overall association rate constant, here we carried out stopped-flow measurements under a variety of solvent conditions. These include salt concentration, glucose, trifluoroethanol (TFE), temperature, and urea. These factors differentially affect the docking and coalescing steps, thus providing handles for dissecting the two kinetic steps. With the help of TransComp calculations for the docking rate constants under different solvent conditions, we were indeed able to tease out the relative importance of the docking and coalescing steps in the binding process.

Results and discussion

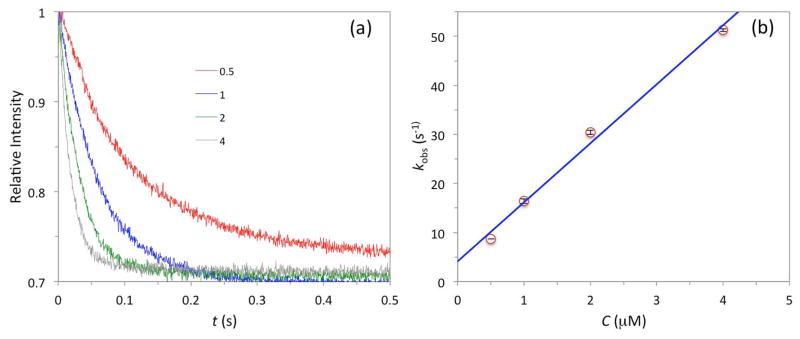
The binding kinetics of a WASP GBD construct, comprising residues G₁₅₄DR…SRG_322, and Cdc42 (residues M₁QT…LEP₁₇₉) was monitored on a stopped-flow spectrometer, using a nonhydrolyzable GTP analogue, mantGppNHp, as the fluorophore. The “standard” solvent conditions for the measurements were 50 mM sodium phosphate buffer (pH 7.0) with 5 mM MgCl₂ and 1 mM DTT at 25 °C. Under these conditions, the changes in fluorescence intensity upon mixing mantGppNHp-loaded Cdc42 with excess WASP GBD are shown in Fig. 3a. Each curve fitted well to a single exponential, and the observed pseudo-first order rate had the expected linear dependence on the WASP GBD concentration [C] (Fig. 3b):

$$k_{\text{obs}}=k_{\mathrm{a}}[C]+k_{\mathrm{d}}$$ (3)

Fig. 3.

Stopped-flow data for the binding of WASP GBD with Cdc42. The solvent conditions were 50 mM sodium phosphate buffer (pH 7.0) with 5 mM MgCl₂ and 1 mM DTT at 25 °C. The mantGppNHp-loaded Cdc42 concentration was kept at 0.05 μM. (a) Time-dependent fluorescence intensity traces for single measurements at four WASP GBD concentrations (shown, in units of μM). (b) Linear dependence of k_obs on WASP GBD concentration. Error bars, representing standard deviations of three independent measurements, fall within the symbols.

The values of k_a and k_d, at (12.0 ± 0.8) × 10⁶ M⁻¹s⁻¹ and (4.1 ± 1.7) s⁻¹, respectively, are in good agreement with previous measurements of Hemsath et al. [8] under similar conditions.

Salt dependence confirms significant electrostatic rate enhancement

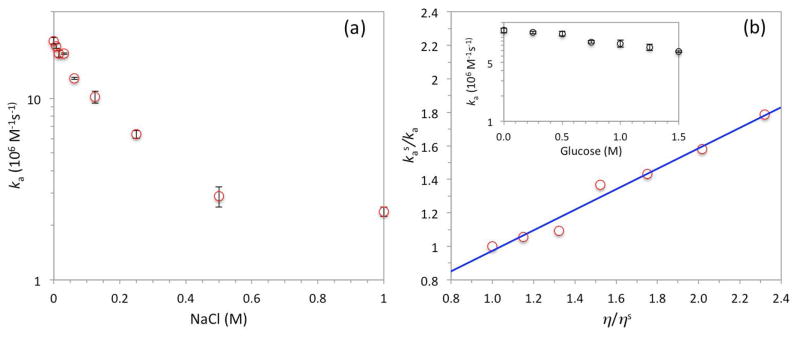
Both Hemsath et al.’s experimental results [8] and our previous TransComp calculations [27] have indicated a significant electrostatic contribution, mediated by the WASP BR, to the overall association rate constant. Here we confirmed this electrostatic rate enhancement by measuring the association rate constant over a range of NaCl concentrations. To accentuate the salt effect, we reduced the concentrations of the sodium phosphate buffer (pH 7.0) and MgCl₂ to 10 mM and 1 mM, respectively. As 1 M NaCl was added, k_a decreased by 10-fold, from (20.7 ± 0.9) × 10⁶ M⁻¹s⁻¹ to (2.4 ± 0.1) × 10⁶ M⁻¹s⁻¹ (Fig. 4a). Furthermore, the strong salt dependence was totally abolished when three basic residues (K₂₃₀KK₂₃₂) in the BR were neutralized by mutation to alanines. These results reinforce the conclusion that electrostatic attraction during the docking of the BR is a major rate-determining factor for the binding of the WASP GBD to Cdc42.

Fig. 4.

Effects of salt and glucose on the association rate constants. (a) Decrease in k_a with increasing NaCl concentration. Here the sodium phosphate and MgCl₂ concentrations were reduced to 10 and 1 mM, respectively. (b) Change in k_a by addition of glucose into the standard solvent conditions. The raw data (inset) are plotted as a relation between the inverse of k_a and the solvent viscosity; the line is a fit with a slope of 0.61 and an intercept of 0.36. Error bars represent fitting errors when data for k_obs from three independent measurements at each of four WASP GBD concentrations were fit to eq 3.

In fact, diffusion-controlled protein association steps that are accelerated by electrostatic attraction usually have strong salt dependences for the forward rates and weak salt dependences for the reverse rates, and these characteristic disparate salt effects are explained by the close proximity between the transient complex and the native complex [41]. Assuming that the same trends apply to the docking step of the present problem, the undocking rate k_−D should have a weak dependence on salt concentration. Further, our previous TransComp calculations [27] have found very little electrostatic attraction mediated by the coalescing segments of the WASP GBD, so k_C should also have a weak dependence on salt concentration. The strong salt dependence of the rate constant for the binding of the WASP GBD to Cdc42 can thus be attributed mostly to salt screening of the electrostatic attraction during BR docking but, on its own, does not necessarily lead to the further conclusion that the docking step is rate-limiting. However, a comparison between the measured k_a of (12.0 ± 0.8) × 10⁶ M⁻¹s⁻¹ under the standard solvent conditions and the calculated k_D values of 33 × 10⁶ and 17 × 10⁶ M⁻¹s⁻¹ at ionic strengths of 95 and 145 mM, respectively [27], does suggest that the docking step is largely rate-limiting, i.e., k_C at least surpasses k_−D but could be much greater. If k_C were significantly less than k_−D, k_a would have to be much less than k_D (see eq 1), rather than have the same order of magnitude.

Glucose dependence suggests a partial rate-limiting role for the docking step

To assess the extent to which the docking step is rate-limiting, we measured k_a in the presence of up to 1.5 M glucose (Fig. 4b inset). At 1.5 M glucose, k_a decreased by nearly 2-fold, from (12.0 ± 0.8) × 10⁶ M⁻¹s⁻¹ to (6.7 ± 0.2) × 10⁶ M⁻¹s⁻¹. Glucose is a viscogen and increases the solvent viscosity by 2.3-fold at 1.5 M [42], or approximately according to

$$\eta ={\eta }^{\mathrm{s}}{e}^{0.56[\text{Glucose}]}$$ (4)

where (also hereafter) a subscript “s” is used for denoting properties under the standard solvent conditions, i.e., in the absence of glucose. The nearly inverse proportional relation between k_a and η can be explained if k_a is rate-limited by k_D, which under diffusion control is proportional to the protein translational diffusion constant (D) and hence inversely proportional to the solvent viscosity [43].

In Fig. 4b we display the relation between k_a^s/k_a and η/η^s [44]. As just explained, if the docking step were completely rate-limiting, k_a^s/k_a would have a linear dependence on η/η^s,

$$k_{\mathrm{a}}^{\mathrm{s}}/k_{\mathrm{a}}=\eta /{\eta }^{\mathrm{s}}$$ (5)

with a slope of 1 and an intercept of 0. Instead the experimental data are best fitted to the linear function (with R² = 0.98)

$$k_{\mathrm{a}}^{\mathrm{s}}/k_{\mathrm{a}}=0.61\eta /{\eta }^{\mathrm{s}}+0.36$$ (6)

To explain this result, let us examine how glucose may affect k_−D and k_C. Increased solvent viscosity should slow down k_−D as much as it does k_D, so both k_D and k_−D are expected to follow the form in eq 5. Increased solvent viscosity may also slow down k_C to the same extent, because the coalescing step also involves translational motion of IDP segments in the viscous solvent. So if increased viscosity is all the effect exerted by glucose, k_C should also follow the form in eq 5. Then one recovers precisely eq 5 for the overall association rate constant k_a. However, in addition to being a viscogen, glucose is a structural stabilizer. In protein folding studies, the latter effect is known to accelerate the folding rate by lowering the free energy barrier [45]. Applying Kramers’ theory for diffusive barrier crossing to protein folding, one can account for both the viscogenic and stabilizing effects. The coalescing step is in essence protein folding, so we can adapt those results to obtain

$$k_{\mathrm{C}}/k_{\mathrm{C}}^{\mathrm{s}}=({\eta }^{\mathrm{s}}/\eta )e^{m_{\mathrm{G}}[\text{Glucose}]}={(\eta /{\eta }^{\mathrm{s}})}^{\alpha }$$ (7)

where m_G is a coefficient measuring the decrease in free energy barrier by increasing glucose concentration, and α = m_G/0.59 − 1. Then we obtain

$$k_{\mathrm{a}}^{\mathrm{s}}/k_{\mathrm{a}}=\frac{1}{1+k_{-\mathrm{D}}^{\mathrm{s}}/k_{\mathrm{C}}^{\mathrm{s}}}(\eta /{\eta }^{\mathrm{s}})+\frac{k_{-\mathrm{D}}^{\mathrm{s}}/k_{\mathrm{C}}^{\mathrm{s}}}{1+k_{-\mathrm{D}}^{\mathrm{s}}/k_{\mathrm{C}}^{\mathrm{s}}}{(\eta /{\eta }^{\mathrm{s}})}^{-\alpha }$$ (8)

If α = 0, then eq 8, with $k_{\mathrm{C}}^{\mathrm{s}}/k_{-\mathrm{D}}^{\mathrm{s}}$ at 1.6, reduces to eq 6. If α = 1 (the value found for protein L refolding [45]), then eq 8 fits the experimental data well (R² = 0.97) with $k_{\mathrm{C}}^{\mathrm{s}}/k_{-\mathrm{D}}^{\mathrm{s}}$ at 2.6.

In short, the glucose dependence of k_a suggests that the docking step is partially rate-limiting for the overall association process, with k_C/k_−D around 2, so that k_a is approximately two thirds of k_D under the standard solvent conditions. This implies that $k_{\mathrm{D}}^{\mathrm{s}}$ is approximately 18 × 10⁶ M⁻¹s⁻¹.

TFE dependence corroborates a contributing role for the coalescing step

The implication of a contributing role for the coalescing step by the data in the presence of glucose is based on the observation that the effect of glucose on k_a is weaker than expected for k_D alone. Still, the overall association rate decreased with increasing glucose concentration. The argument for the contribution of k_C to determining the magnitude of k_a would be stronger if an additive could increase k_a by significantly accelerating the coalescing step without adversely affecting the docking step. TFE might suit this purpose well. At 5–10% (v/v), TFE induced a marked increase in helical content for a WASP GBD construct as indicated by circular dichroism (CD) spectra, and the NMR spectra of this construct at 5% TFE were sufficiently dispersed to allow for the determination of a tertiary structure [33]. These findings suggest that TFE may significantly accelerate the coalescing step. On the other hand, 10% TFE only increased the solvent viscosity by approximately 25% [46].

We measured the CD spectra of our GBD construct to confirm that both 5% and 10% TFE resulting in almost doubling of the molar ellipticity at 222 nm (an indicator of helical content). Higher TFE levels were not studied because they led to significant changes in the CD spectrum of unbound Cdc42. The associate rate constants increased from (12 ± 0.8) × 10⁶ M⁻¹s⁻¹ under the standard conditions to (17.5 ± 1.0) × 10⁶ M⁻¹s⁻¹ at 5% TFE and (16.3 ± 1.4) × 10⁶ M⁻¹s⁻¹ at 10% TFE. Because there is no apparent reason for an increase in k_D by TFE, the obvious explanation for the increase in k_a is that TFE increased k_C, thus bringing k_a closer to k_D (i.e., making the overall association more rate-limited by the docking step) than in the standard conditions. Indeed, the observed k_a values at 5% and 10% TFE are very close to the inferred $k_{\mathrm{D}}^{\mathrm{s}}$ at 18 × 10⁶ M⁻¹s⁻¹.

Temperature effect on k_a is stronger than expected for k_D

Temperature provides another handle for separating the docking and coalescing steps. First of all, temperature affects the protein translational diffusion constant D. The Stokes-Einstein relation states that D ∝ T/η, and η in turn decreases with increasing temperature. We measured the association rate constants over the temperature range of 10 to 40 °C (Fig. 5a inset). k_a increased by 4.1-fold over this temperature range, but the increase is greater than expected from the effect of temperature on D, as a plot of k_a/k_a^s versus T/η clearly shows (Fig. 5a, symbols and black dash). According to eq 2, temperature can affect the docking rate constant k_D not only through D but also through the Boltzmann factor $e^{-\mathrm{\Delta }{G}_{\text{el}}^{\ast }/k_{\mathrm{B}}T}$. As temperature increases, the solvent dielectric constant decreases and hence the electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$ increases in magnitude. However, the latter increase is partly offset when $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$ is divided by k_BT in calculating the Boltzmann factor. Consequently, taking the electrostatic enhancement of k_D into consideration only produced a slight improvement in explaining the observed temperature dependence of k_a (Fig. 5a, blue curve).

Fig. 5.

Effects of temperature and urea on the association rate constants. (a) Increase in k_a with increasing temperature. The raw data (inset) are plotted as the dependence of k_a on T/η to show that the effects of temperature are more than only to influence the protein translational diffusion constant (black dash labeled “Diffu”). Further account of the effect on the solvent dielectric constant in calculating k_D (blue curve labeled “Diffu+Dielec”) only slightly narrows the discrepancy, but the data are explained well when the effect of temperature on facilitating barrier crossing in the coalescing step (green curve labeled “Diffu+Dielec+Barri”) is taken into consideration. (b) Decrease in k_a by the addition of urea. The blue curve accounts for the effects of urea on the solvent viscosity and dielectric constant, whereas the green curve further assumes that urea decreases the free energy barrier in the coalescing step. Error bars represent fitting errors when data for k_obs from three independent measurements at each of four WASP GBD concentrations were fit to eq 3.

The remaining temperature effect on k_a again points to the docking step as being only partially rate-limiting. If the coalescing step is a (diffusive) barrier crossing reaction as we modeled above in explaining glucose effects, then a rise in temperature will accelerate k_C. Consequently the overall association process will be more rate-limited by the docking step and k_a will become closer to k_D at high temperatures than at low temperatures. Qualitatively, these trends lead to the desired stronger temperature dependence for k_a than for k_D. Continuing the assumption that solvent viscosity affects k_C and k_−D to the same extent, we can write the temperature dependence of k_C/k_−D as

$$k_{\mathrm{C}}/k_{-\mathrm{D}}=(k_{\mathrm{C}}^{\mathrm{s}}/k_{-\mathrm{D}}^{\mathrm{s}})e^{-\mathrm{\Delta }{G}^{\ne }(1/k_{\mathrm{B}}T-1/k_{\mathrm{B}}{T}^{\mathrm{s}})}$$ (9)

where ΔG^≠ is the energy barrier of the coalescing step (assumed to be independent of temperature). Keeping $k_{\mathrm{C}}^{\mathrm{s}}/k_{-\mathrm{D}}^{\mathrm{s}}$ at 2 as suggested by the data on glucose effects, we can quantitatively explain the temperature dependence of k_a with an energy barrier of 7.8 kcal/mol for the coalescing step (Fig. 5a, green curve).

Urea dependence of k_a further supports a role for the coalescing step

The addition of glucose and TFE and the rise in temperature all serve to speed up the coalescing step. Their implication for a contributing role of the coalescing step rests on the observation that these changes in solvent conditions produced k_a values that were greater than expected if their effects were restricted to k_D alone. To provide additional support for the conclusion that the coalescing step contributes to the magnitude of k_a, we studied urea as an additive that would significantly slow down k_C with only a minimal effect on k_D. Our expectation was that the overall association process would become much less rate-limited by the docking step and a wide gap would emerge between observed k_a and calculated k_D.

The data for the effects of urea are shown in Fig. 5b. The concentration of urea was limited to 2 M to avoid any significant effect on the conformation of Cdc42 (as confirmed by CD spectroscopy). Urea at 2 M reduced k_a by 3.4-fold. To account for the effects on k_D, we note that urea has minor effects on the solvent viscosity (10% increase at 2 M urea [47]) and the solvent dielectric constant (7% increase at 2 M urea [48]). These effects together led to a modest 24% decrease in k_D (Fig. 5b, blue curve). The large gap between the observed k_a and calculated k_D at 2 M indeed supports a significant contribution of k_C to determining the magnitude of k_a.

Similar to our modeling for the stabilizing effect of glucose (eq 7), we assume that urea increases the free energy barrier of the coalescing step, leading to

$$k_{\mathrm{C}}/k_{-\mathrm{D}}=(k_{\mathrm{C}}^{\mathrm{s}}/k_{-\mathrm{D}}^{\mathrm{s}})e^{-m_{\mathrm{U}}[\text{Urea}]}$$ (10)

where m_U is the increase in free energy barrier by a unit increase in urea concentration. (Any effect of urea on solvent viscosity is assumed to influence k_C and k_−D to the same extent.) The data can be fitted well by eq 10 along with the aforementioned weak decrease in k_D, when m_U is set to 1.1 M⁻¹ (Fig. 5b, green curve). The latter is within the typical range of values for protein refolding in the presence of urea [49].

In contrast to the abolishment of salt effects on k_a by the BR K₂₃₀KK₂₃₂ to AAA mutation, the urea dependence of k_a was not just retained but accentuated. Urea at 2 M reduced the k_a of the mutant by approximately 9-fold. The stronger urea effect is precisely what is anticipated from our dissection of the docking and coalescing steps: the mutation (by increasing k_−D) makes the docking step less rate-limiting, so the urea effect on the coalescing step has a greater impact on the overall association rate constant.

Concluding remarks

In the present study, we have combined experiment and computation to determine the precise form of dock-and-coalesce operating in the association between the intrinsically disordered WASP GBD and the Cdc42 GTPase. Previous experimental and computational studies [8, 27] have focused on the docking step. Here, by changing solvent conditions in a variety of ways, we have assessed the extent to which the docking step is rate-limiting to the overall association process and the contribution of the coalescing step to determining the magnitude of the association rate constant. Together, these results support the conclusion that k_a is approximately two thirds of the docking rate constant under physiological solvent conditions.

The docking and coalescing steps have distinct rate-determining factors. The docking rate constants can be significantly enhanced by long-range electrostatic attraction, as found here as well as for a number of other IDPs [6, 12, 20, 22, 31, 32], reminiscent of the situation for the association rate constants of structured proteins [26, 28–30]. On the other hand, the coalescing rate constants are dictated by the free energy barriers, which in turn are determined by secondary structure propensities of the coalescing segments [11, 14] and their short-range intermolecular interactions with the target surface [13, 19]. It is fortunate that these factors can be selectively perturbed by changing solvent conditions. In particular, salts can weaken long-range electrostatic attraction, whereas TFE and urea can decrease and increase, respectively, the free energy barriers of the coalescing step. This fact has been exploited in previous experimental studies [12]. Here the analysis of the various effects brought by the changed solvent conditions, aided by TransComp calculations, allowed us to quantitatively tease out the relative importance of the docking and coalescing steps in the binding process. This approach should have general applicability.

Structured proteins usually form most of their intermolecular interactions all at once during association. High affinity there usually is achieved through a dense collection of intermolecular interactions, which could lead to very low dissociation rates. In contrast, IDPs usually form their intermolecular interactions sequentially, and not having to breaking these interactions all at once during dissociation ensures that the dissociation rates are sufficiently high for purposes of signaling and regulation [5]. Specifically, the dock-and-coalesce mechanism allows IDPs to code electrostatic complementarity into the docking segment to gain binding speed and use additional interactions formed by the coalescing segments to reinforce binding affinity.

Materials and methods

Protein preparation

The two proteins were prepared largely following published protocols [8]. Human Cdc42 (residues 1–179; accession number nm_001791) was cloned into pDEST527 vector and expressed in Rosetta Escherichia coli cells in a His-tagged form. Purification started with Ni²⁺-affinity chromatography (Ni-CAM HC, Sigma), followed by cleavage of the His tag with TEV protease, and ended with size-exclusion chromatography (Sepharose-100, GE Healthcare).

Human WASP GBD (residues 154–322; u19927) was cloned into pGEX expression vector and expressed as a glutathione S-transferase (GST) fusion protein in Rosetta E. coli cells. Purification started with Glutathione Sepharose 4 Fast Flow (GE Healthcare). Then thrombin cleavage of the GST-tag was followed by heat treatment (80 °C) for 30 min to induce aggregation of proteins other than WASP GBD. After centrifugation, the supernatant containing WASP GBD was finally run through a size-exclusion column (Sepharose-100, GE Healthcare).

Cdc42 labeling with mantGppNHp (2′,3′-O-N-methylanthraniloyl-GppNHp; Jena Bioscience) was prepared by degrading prebound nucleotides by Antarctic Phosphatase (New England Biolabs) [50]. Unbound nucleotides were removed on a disposable PD-10 Desalting Column (GE Healthcare). 1.5-fold molar excess of mantGppNHp was then added; any unbound nucleotides were again removed on the desalting column.

Stopped-flow spectroscopy

Binding kinetics was monitored on a stopped-flow apparatus (Applied Photophysics, model SX20). The fluorescence of mantGppNHp (loaded on Cdc42) was excited at 366 nm and detected with a cut-off filter below 395 nm. The standard solvent conditions were 50 mM phosphate buffer (pH 7.0) with 5 mM MgCl₂ and 1 mM DTT at 25°C. The mantGppNHp-loaded Cdc42 concentration remained at 0.05 μM, while the WASP GBD concentrations varied from 0.5 to 4 μM. Binding curves were individually fitted to a single exponential using the GraFit program (Erithacus Software). k_obs values were typically determined in three or more independent measurements.

TransComp calculations

Calculations of the docking rate constant k_D were as described previously [27], using the TransComp method, which is available as a web server (http://pipe.sc.fsu.edu/transcomp/) with default setting for the standard solvent conditions. In cases where changes in solvent conditions led to changes in the solvent dielectric constant, the latter values were used in calculating the electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$. Changes in solvent viscosity were accounted for by scaling the calculated k_D by η^s/η.

Abbreviations

BR

basic rich

GBD

GTPase binding domain

GST

glutathione S-transferase

IDP

intrinsically disordered proteins

IDR

intrinsically disordered region

PDB

protein data bank

TFE

trifluoroethanol

WASP

Wiskott-Aldrich Syndrome protein

WH1

WASP-homology-1