How can we really improve screening methods for AD prevention trials?

This edition of Alzheimer's & Dementia: Translational Research & Clinical Interventions includes an important article from Lutz et al. on the potential advantages of a novel genetics-based risk algorithm (GRBA) for selection of participants in Alzheimer's disease (AD) prevention trials [1]. The GRBA, described previously [2], has been used to identify subjects for the well-known TOMMORROW trial of pioglitazone for prevention of symptomatic AD dementia or MCI due to AD.

Efficient screening methods are of paramount importance for AD prevention trials. Studies such as TOMMORROW require years of follow-up, and they cost scores of millions of dollars. These costs accrue in part from the screening methods themselves, but they relate much more strongly to the trials' size and the duration of labor-intensive follow-up needed to identify sufficient “events” for adequate statistical power.

Certainly, the GBRA described here must be among the lower cost methods of screening. Relying as it does only on age and genetic markers available from peripheral blood, it should have clear cost advantages when compared against more elaborate or invasive screening techniques such as amyloid-PET scanning or CSF biomarker assays. Not surprisingly, therefore, Lutz et al. compare their GBRA with some of the latter, more ambitious methods. But the more salient portion of their argument relates to the comparison of the GBRA with similarly low cost and minimally invasive methods relying on age and peripheral blood markers.

Given that the GRBA is relatively inexpensive per candidate screened, how does it perform otherwise? Two factors determine its efficiency. First is the number of persons who must be screened to provide the needed number of “events”. Second is the efficiency of the method in rejecting persons who will not “convert” from cognitively normal to symptomatic disease states. Such “false-positives” are costly, as they must be followed laboriously >5 years for incident symptoms.

Consideration of test efficiency requires recognition, first, that only a certain proportion of any population will develop symptoms. This proportion is commonly referred to as the base rate of the population. Importantly, it can vary from one population to another, but it does not depend in any way on screening results. Whatever the base rate, an important function of the screening test is to identify the highest proportion of those candidates who will become symptomatic (the sensitivity of the test). More crucially, however (see below), the test should minimize the proportion of false-positives it identifies for trial enrollment. That proportion is, in fact, the complement of the test's specificity or proportion of “nonconverters” who are identified correctly as test negative.

Unlike other metrics such as the risk ratio associated with test positivity, the overall proportion of converters and nonconverters who are correctly identified or the positive and negative predictive values (PPV, NPV) in the test population, sensitivity and specificity are performance characteristics of the test exclusively. All other metrics depend in some way on the characteristics of the sample being screened. This latter shortcoming becomes important when comparing the performance of two or more test algorithms across multiple population samples. An important strength of the Lutz article is its direct comparison of the sensitivity and specificity of their GBRA with other algorithms based on age and APOE ε4 carriage alone, in its Fig. 4.

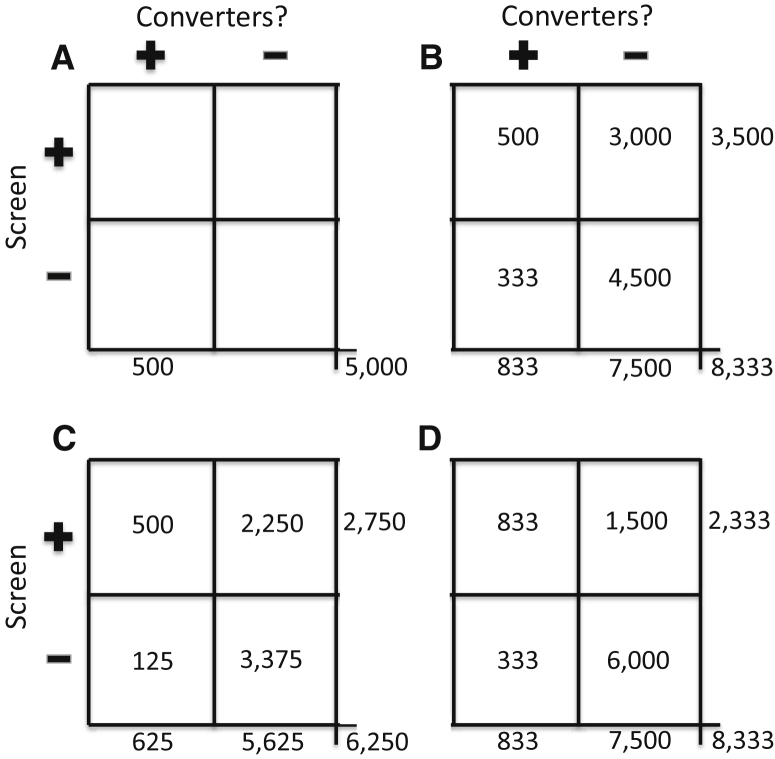
All screening tests generate two types of error—false-negatives (resulting from limitations in sensitivity) and false-positives (reflecting imperfect specificity). A cardinal principle, to be demonstrated below, is that false-positives raise trial costs much more than false-negatives. Fig. 1 is meant to illustrate this point. Panel A shows results obtained with no screening test except that participants must be old enough that 10% of them will develop symptoms over the coming 5 years (i.e., the base rate here, as elsewhere in the figure, is 10%). In this example, and throughout Fig. 1, under the null hypothesis of no treatment effects, the trial must observe 500 “events” over 5 years for adequate statistical power. In panel A, the 10% base rate implies that, without some method of enrichment, we would need a trial cohort of some 5000 persons. There are no costs for screening (other than for establishing basic eligibility requirements), but one may estimate that the all-in costs of the labor-intensive follow-up of these participants will be $10,000 per year (probably a conservative figure). Therefore, once eligible participants have been recruited, the trial will cost $10,000/participant/year × 5000 participants × 5 years or $250 million.

Fig. 1.

Four hypothetical applications of screening methods when selecting participants for an AD/MCI prevention trial in a population with base rate of 10% who will develop symptoms over 5 years of follow-up. (A) shows results with no screening test. (B) represents results expected with a screening test that provides 60% sensitivity and 60% specificity in identification of those who will “convert” during the 5-year trial interval. (C) indicates a degree of improvement expected if sensitivity of the prior method can be improved to 80% with no change in specificity. (D) shows the results expected when specificity is improved to 80% but sensitivity is 60%, as in (B). Implications for the costs of the trial are substantial (see text).

To avoid such enormous costs, one can use a screening test to enrich the trial cohort for those who will become symptomatic. Panel B shows results expected from a relatively good screening test that achieves sensitivity and specificity of 60% (i.e., a 40% false-positive rate). The screening test might cost $1000 per participant screened (an assumption to be used throughout this discussion). The test's sensitivity of 60% determines that one must screen 833 (500/60%) individuals to identify the needed 500 “events” in the trial. But we can identify these persons only after the fact. Because the 5-year base rate is still 10%, we need to screen 8333 persons in all to find these 833 “true” converters. Among the 7500 (8333 − 833) nonconverters to be screened, however, the false positive rate of 40% means the trial will identify (and thus enroll) 3000 other persons who are screen positive. Without knowing it, the trial enrolls these along with the 500 “true” screen-positives (3500 in all) and follows them for 5 years. Total screening costs are 8333 × $1000 per screen or $8.3 million. But to follow the cohort and count outcomes will cost 3500 participants × $10,000 per participant per year × 5 years, or $175 million. Total costs of the trial are therefore $183.3 million, representing a savings of $66.7 million (27%) compared to panel A.

One can try to improve on this result by increasing either the sensitivity or the specificity of the screening test. Which approach holds the potential for greater savings? Panel C shows results expected when one improves the sensitivity to 80%, whereas specificity is unchanged at 60%. Because of the improved sensitivity, one needs now to screen only 625 “true” converters to find the needed 500 trial “events.” Because the base rate has not changed, one must screen 6250 individuals in all, including not only the 625 but also 5625 nonconverters. Among the 5625 nonconverters screened, the false-positive rate is still 40%, so the trial will identify and enroll 2250 false-positives. Total trial enrollment will therefore be 500 + 2250 = 2750. Costs for follow-up observations will be 2750 × $10,000 per participant per year × 5 years = $137.5 million. Screening costs are 6250 × $1000 = $6.25 million, so total costs will be $143.75 million. The savings of an additional $40 million demonstrate clearly that costs can be reduced by screening methods with improved sensitivity.

But how does this benefit compare with an alternate method that improves specificity by a nominally identical amount (to 80%), while holding sensitivity at 60%? Panel D provides the answer. Once again, the test's sensitivity of 60% means one must screen 833 “true” converters to find the trial's 500 required “events.” The base rate (unchanged) then implies that one must screen 8333 people in all, of whom 7500 will be nonconverters. Of the 7500, the new false-positive rate of 20% means that the trial will now identify and enroll only 1500 false positives. Total enrollment will therefore be 1500 + 833 = 2333. Screening costs are back to $8.3 million, but follow-up costs will now be 2333 × $10,000 × 5 = $116.65 million. With total costs of $125 million, the improved-specificity screener has saved $58.3 million, or an $18.75 million improvement over the higher sensitivity method.

The lessons from these examples seem clear enough. Because the costs of follow-up in AD prevention trials far exceed the costs of screening, specificity trumps sensitivity in this application. The advantages of nominally identical improvements in sensitivity versus specificity are not equal.

One further example makes this point emphatically. The forthcoming API-Novartis trial of two different anti-amyloid strategies (NCT02565511) is slated to enroll some 1300 persons, all of whom will be homozygous for the APOE ε4 allele. Stated otherwise, the “screening test” here will be whether the candidate has genotype ε4/ε4. If yes, the person is to be randomized to drug or placebo; if no, then not. In fact, many studies have established that, depending on their age, APOE ε4 homozygotes are at 10–15-fold higher risk of incident AD dementia than others in the population [3]. It is also evident that (depending on age) as many as 60% of them will develop symptoms over an interval of 5 years (i.e., the positive-predictive value of the test may be 60%) [4]. But that does not mean that the sensitivity of APOE ε4/ε4 as a screening criterion in an AD prevention trial is high. APOE ε4 homozygotes constitute only 2.3% of most populations when (depending on age) the trial population will probably have a base rate similar to the above-assumed 10% who will develop symptoms over the next 5 years. The sensitivity of this screening test is therefore no more than 15% (remember, not all test-positive individuals will develop symptoms; perhaps 40% will become false-positives.) Importantly, though, the overall false-positive rate in the test population using the ε4 homozygote screening criterion is only 1%–2% (principally because 97.7% of the population will be test-negative and therefore cannot be false-positives).

Applying the API-Novartis screening techniques to the previous set of assumptions, this trial would need to screen 35,000 persons to identify 800 “screen-positives” who, in turn might yield the 500 needed “events”. For present purposes, one may again assume that each participant screened costs $1000. If so, the trial's screening costs might amount to $35 million. If one estimates as before that the follow-up costs for each trial enrollee are $10,000 per year, one can see that the costs for follow-up of eligible subjects will be $10,000 per subject-year × 800 subjects × 5 years, or $40 million. Total cost would be this sum plus $35 million for screening, or $75 million, that is, <two-thirds that of the improved-specificity example above.

What can all this tell us about the work of Lutz and colleagues? These authors, having developed their GBRA in an ADRC data set, attempted to validate its utility versus other methods in the well-known Alzheimer's Disease Neuroimaging Initiative (ADNI-1) sample. The GBRA features a combination of APOE genotype, age, and determination of allelic isoform of the polymorphic translocase of outer mitochondrial membrane 40 homolog (TOMM40) rs10524523 variable length poly-T repeat (TOMM40′523). Lutz et al. compare the utility of the GBRA and other screening algorithms including, notably, a combination of age and APOE genotype alone. Fig. 3 of their article compares the sensitivity and false-positive rate (1 − specificity) of the GBRA with the other screening methods in both the ADRC and the ADNI cohorts. Notwithstanding their assertion that the GBRA yields impressive PPV and NPV, Fig. 3 is difficult to interpret, as the various screening algorithms give results that are in very different regions of the receiver operating characteristic (ROC) curves for the two samples. ROC analyses are useful for observing the “trade-off” between sensitivity and specificity achieved by a screening method as the test cut-off is altered, or as the characteristics of the population may change. A clearer presentation of the relative performance of the GBRA in the two samples is shown in Fig. 4 of the article. Fig. 4A suggests a modest improvement for the GBRA versus age and APOE alone in the Bryan ADRC cohort. However, Fig. 4B shows this same comparison in the validation ADNI cohort. The authors do not analyze the areas under the curve (AUC) for the two methods (the usual way in which competing screening algorithms can be compared). It seems unlikely, however, that there is any meaningful difference in the AUC for the two curves in Fig 4B.

To this observer, the “bottom line” from all this is that the paramount criterion for efficiency in prevention trials is choice of a screening method that emphasizes specificity. As Fig. 3 of the Lutz article suggests, there is almost invariably a trade-off between sensitivity and specificity as one modifies a screening test. As the API-Novartis example shows, in this trade-off concern for specificity should prevail, even if this means accepting a sensitivity that appears mediocre. As a generalization, this principle appears to outweigh by far any advantage generated by improved test technology.