Abstract
Purpose:
To compare the accuracy of four different intraocular lens (IOL) power calculation formulas for eyes with mean keratometry values greater than 46 diopters (D).
Methods:
Forty five eyes from 45 patients who were candidates for senile cataract surgery with mean keratometry values greater than 46 D were included. Calculation of the IOL power was performed by the Lenstar. The implanted IOL in all cases was Acrysof SA60AT. The average absolute value of the differences between the actual and predicted spherical equivalent (SE) of the postoperative refractive error (mean absolute error: MAE) was calculated using 4 formulas (Haigis, Holladay 1, Hoffer Q, and SRK/T) with optical IOL constants from the User Group for Laser Interference Biometry constants.
Results:
The MAE was smallest in the SRK/T formula (0.39 D ± 0.35) followed by those of the Holladay 1 (0.44 D ± 0.32), Haigis (0.45 D ± 0.35) and Hoffer Q (0.5 D ± 0.38) formulas. However, there was no statistically significant difference between the MAE among different formulas. The SRK/T formula predicted more eyes within ± 0.5 D of the SE (77.8%) compared to other formulas.
Conclusion:
In eyes with steep corneas, there were no statistically significant differences among the accuracies of the four common IOL power calculation formulas.
Keywords: Intraocular Lens Power Calculation Formulas, Haigis, Hoffer Q, Holladay 1, SRK/T, Steep Cornea
INTRODUCTION
With improvement in the instruments and techniques used for cataract surgery, the most challenging subject in patient satisfaction is post-surgical refractive outcomes. Although new optical biometry systems have improved intraocular lens (IOL) power calculation results by accurate and reliable axial length (AL) and keratometry measurements,[1] the effective lens position (ELP) is still a matter of debate. Different generations of IOL power calculation formulas utilize different parameters for the prediction of the IOL position within the eye. Third-generation formulas are the most popular theoretical formulas, which predict the IOL position by the AL and keratometry. The Haigis, Olsen and Holladay 2 formulas utilize 2, 5 and 7 parameters for the prediction of the IOL position, respectively.[2,3,4] As the amount of keratometry is one of two cardinal factors in the calculation of the IOL power, and as most IOL power calculation formulas consider keratometry magnitudes for the prediction of ELP, we conducted this study to elucidate which formula is most accurate in eyes with steep keratometry. The superiority of different formulas for different amounts of AL has been shown in many studies,[5,6,7] but the accuracy of IOL power calculation formulas in steep keratometry has not been evaluated according to our best knowledge. Therefore, the purpose of the current study was to compare the accuracy of four common IOL power calculation formulas in steep corneas.
METHODS
The present study was a prospective comparative study, which included 45 eyes from 45 patients with senile cataracts and a mean keratometry greater than 46D who were candidates of phacoemulsification with IOL implantation from February 2014 to July 2015. The exclusion criteria were as follows: patients with a history of previous intraocular and/or corneal surgery, pre-existing ocular diseases including keratoconus or corneal scar, corneal astigmatism more than 0.75D, complicated cataract surgery including anterior or posterior capsular tear, combined surgical procedures, postoperative best-corrected visual acuity (BCVA) less than 20/40, and patients with follow-ups of less than 1 month. Topography was performed to rule out suspected keratoconus and keratoconus in all cases. Data collection included preoperative and postoperative examinations and refractive data. Additionally, age, sex, laterality, axial length, anterior chamber depth, and average corneal power were recorded. IOL power was calculated by the Lenastar 900 (Haag-Streit AG, Koeniz, Switzerland) using the Haigis, Holladay 1, Hoffer Q and SRK/T formulas with optimized IOL constants for the Haag-StreitLenstar 900 from the User Group for Laser Interference Biometry (ULIB). All patients underwent uneventful phacoemulsification cataract surgery by one experienced surgeon (AF) with a standard stop & chop technique with a sutureless 2.8 mm temporal incision under topical anesthesia. At the end of surgery, an AcrySof IOL (SA60AT, Alcon, Fort Worth, TX) was implanted in the capsular bag in all cases. The power of IOL measured by each formula that yielded a postoperative refraction nearest to emmetropia, erring on the side of myopia, was selected. The mean of four measurements was considered for IOL power selection.
Patients were examined one day, 1 week and 1 month after surgery. Postoperative refraction at least one month after the surgery was measured using an autorefractometer (RMA 7000, Tokyo, Japan) and converted to the spherical equivalent. For each patient, the prediction error was calculated, which is the difference in diopter between the achieved and predicted refractive outcomes in a particular patient. The mean numerical error (MNE) and the mean absolute error (MAE) were defined as the arithmetic mean of the prediction errors and the mean of the magnitude of the prediction errors, respectively. The MNE, MAE and the percentage of the eyes within ±0.5D, ±1.0D and ±2.0D of the SE were calculated for each formula.
Statistical Analysis
To assess the normal distribution of data, we used the Kolmogorov–Smirnov test and Q–Q plot. To describe the data, we used frequency (percent), mean, standard deviation, range and 95% confidence interval (95% CI) for each of the 4 formulas. To compare the MAE and the MNE values among the 4 formulas, we used a repeated measure ANOVA. The Bonferroni method was used to adjust for the multiple comparisons. P values less than 0.05 were considered statistically significant. All statistical analyses were conducted using SPSS software (IBM Corp. Released 2016. IBM SPSS Statistics for Windows, Version 24.0. Armonk, NY: IBM Corp.).
RESULTS
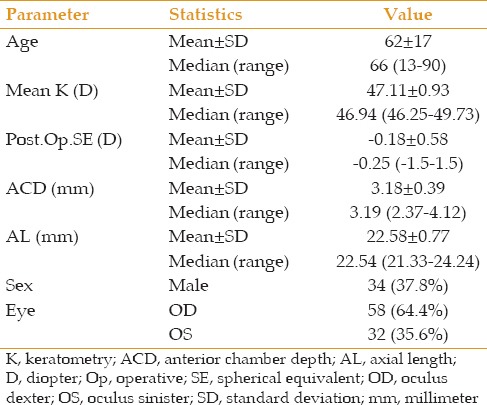
A total of 45 eyes from 45 patients with a mean keratometry greater than 46D who underwent phacoemulsification and IOL implantation were included in the present study. Table 1 summarizes the demographic and preoperative biometric ocular parameters of the patients.
Table 1.
Demographic and biometric parameters
The overall performances of the 4 formulas are presented in the Table 2. The MAE ranged from 0.39D to 0.5D, which was the smallest in the SRK/T formula (0.39D ± 0.35), followed by those of the Holladay 1 (0.44D ± 0.32), Haigis (0.45D ± 0.35) and Hoffer Q (0.5D ± 0.38) formulas. This study found no statistically significant differences between the MAE among different IOL calculation formulas compared to the Haigis formula (P > 0.05). The MNE values ranged from -0.06D to 0.36D. There was a positive MNE (hyperopic trend) with all formulas except the SRK/T formula, which was close to zero. Although the SRK/T formula showed the most accurate MNE and MAE, we did not find any statistically significant differences in MNE and MAE between the SRK/T and Haigis formulas (P = 0.25).
Table 2.
MAE & MNE and the percentages of the eyes within ±0.5D, ±1D and ±2D of the target refraction by 4 different formulas in all eyes
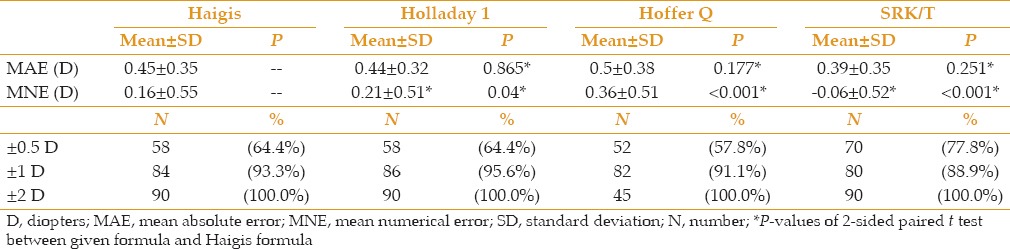
The SRK/T formula yielded the highest percentages of the eyes within ± 0.5D of the target refraction (77.8%) followed by those in the Holladay 1 and Haigis (64.4%), and Hoffer Q (57.8%) formulas. All formulas predicted 100% of the eyes within ± 2D of the target refraction [Table 2].
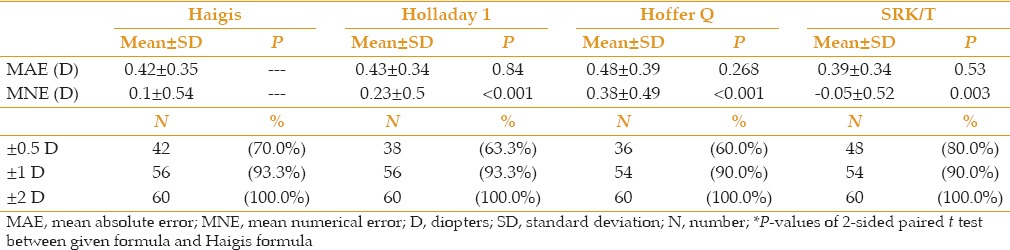
To clarify the role of the anterior chamber depth (ACD) on the results, the eyes were divided into two groups: the first group with an ACD less than 3 mm and the second group with AC depth equal and/or greater than 3 mm, and the analyses were repeated. We found no statistically significant differences in the MAE and MNE among the 4 different formulas for the two groups [Tables 3 and 4].
Table 3.
MAE & MNE and the percentages of the eyes within ±0.5D, ±1D and ±2D of the target refraction by 4 different formulas in eyes with ACD <3mm
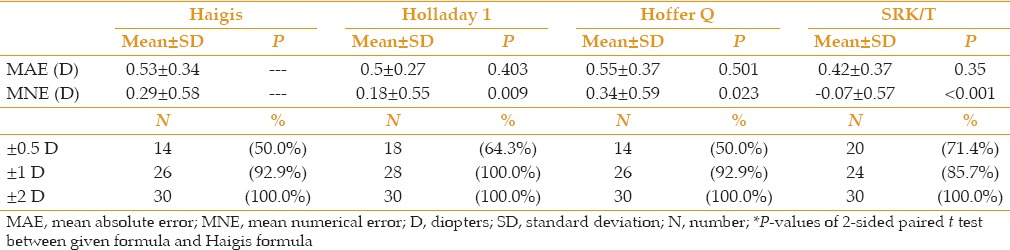
Table 4.
MAE & MNE and the percentages of the eyes within ±0.5D, ±1D and ±2D of the target refraction by 4 different formulas in eyes with ACD≥3mm
DISCUSSION
In the current study, we compared the accuracy of four widely used IOL power calculation formulas, namely Haigis, Holladay 1, Hoffer Q, and SRK/T formulas, in eyes with steep corneas. According to this study, there were no statistically significant differences between the accuracy of the aforementioned formulas; however, the percentage of the eyes within ±0.5D of the target refraction was higher in IOL power selection based on the SRK/T formula.
The MAE is often used as an indicator for the IOL formula prediction accuracy, although it does not show a resulting direction (myopic or hyperopic). In the present study, the small standard deviation of the MAE for all formulas highlights that the accuracy of the prediction was very good for all included eyes. None of the formulas showed significant differences in the MAE compared with that of the Haigis formula. The SRK/T formula predicted the greatest percentage of the eyes that fell within ± 0.5D of the target refraction (78%), which was the same as the results of the study by Shread et al (78.7%).[8] The MNE is the mean of the differences between the achievedand predicted SE, with consideration for the direction (negative or positive). Based on the MNE, a low hyperopic outcome was found with all formulas except the SRK/T. However, the differences were not statistically significant between the SRK/T and Haigis formulas.
The third-generation formulas, including the SRK/T, Hoffer Q and Holladay 1, utilize two biometric parameters (AL, keratometry) for the prediction of theELP and one constant for the optimization of the results. In contrast, the Haigis formula, which is a fourth-generation formula, utilizes AL and preoperative ACD to predict the ELP and has 3 constants [a0+ (a1× ACD) +(a2 × AL)] for the optimization of results. Therefore, rather than using a single number, the Haigis formula recommends the IOL power optimization based on three variables. According to the keratometry by reflection-based systems, the anterior corneal curvature is extrapolated from the corneal radius and translated into the corneal power using a keratometric index that is based on the presumed fixed correlation between the anterior and posterior corneal radii. All third-generation IOL power formulas (SRK/T, Holladay 1, Hoffer Q) required corneal power to predict the ELP. When using the true corneal power, the corneal radii and keratometric index are required, and in cases when we do not have access to the posterior corneal radius, using a variable keratometric index that is dependent on the radius of the anterior corneal surface has been proposed.[9,10] The Haigis formula utilizes the corneal radius to prevent problems related to the keratometric index.
There are many studies comparing the performance of various formulas in different patient groups. Moschos et al concluded that the Haigis formula provides more accurate results concerning the postoperative target of refraction in the eyes with an axial length less than 22 mm.[11] Roh et al reported that the IOL power calculation using the Haigis, Hoffer Q, SRK/T and SRK II formulas showed relatively good postoperative IOL power prediction in short eyes with axial length less than 22 mm, but the Haigis formula showed the best results.[12] According to Bang et al, the Haigis formula was found to be the most accurate in predicting postoperative refractive error in long eyes, the SRK/T formula was the second most accurate.[13] Eom et al found that the Haigis formula was significantly more accurate than the Hoffer Q formula in short eyes with an ACD less than 2.40 mm. They concluded that the predicted ELP by the Hoffer Q formula was deeper than the actual ELP, and the predicted refractions based on the ACD (the Haigis formula) were more accurate than fixed predicted refractions without considering the ACD (the Hoffer Q formula) in eyes with a short AL and shallow ACD.[14] However, the superiority of the Haigis formula in eyes with steep corneas has not been established in the current study, and only a trend toward better results with the SRK/T was observed in this series. Unexpectedly, we found that the Haigis formula came in third place with regards to both MAE and MNE accuracy.
Because the third-generation formulas use the keratometry magnitude to determine the ELP, there is an assumption that a high keratometry value corresponds to a deeper anterior chamber and an IOL position that is more posterior and thus higher in power. In cases with high keratometry and low preoperative ACD (less than 3 mm in the current study), this assumption may be incorrect, and this discrepancy can lead to the IOL power overestimation. Fourth-generation formulas such as Haigis should theoretically do quite well in eyes with steep corneas because they incorporate the measured preoperative ACD in the calculation and use the anterior corneal radius instead of corneal power. According to the above theory, we divided the eyes into two groups based on the ACD: lower than 3 mm and equal and/or greater than 3 mm. Unexpectedly, in the eyes with the shallow anterior chamber, we did not find higher accuracy of the Haigis formulas compared with third-generation formulas. In the eyes where the ACD was less than 3 mm, the number of the eyes within +/- 0.5D of the target refraction was highest in the SRK/T and Holladay 1 formulas (71.4% and 64.3%, respectively). In cases where the ACD was higher than 3 mm, the SRK/T and Holladay 1 formulas were superior in accuracy (not statistically significant) and the number of eyes within +/- 0.5D were higher in these two formulas compared with the other formulas (80% and 63.3%, respectively). This result may be due to the inaccuracy of the constants of the Haigis formula for the eyes with steep corneas. Adjustment of the constants of the Haigis formula may improve the results of this formula. However, the personalization of these constants requires input of at least 200 eyes.
The limitation of this study was the small number of cases. Further studies involving more eyes with steep corneas are warranted to further assess the accuracy of variable formulas for these subgroups.
In conclusion, the IOL power calculation using Lenstar showed relatively good postoperative IOL power prediction in steep corneas with Haigis, Holladay 1, Hoffer Q and SRK/T formulas. However, the SRK/T formula showed the best results.
Financial Support and Sponsorship
Nil.
Conflicts of Interest
There are no conflicts of interest.
Acknowledgements
The authors would like to acknowledge the contribution of their statisticians, Mehdi Yaseri, PhD and Bahareh Kheiri, MS (Ophthalmic Research Center, Shahid Beheshti University of Medical Sciences, Tehran, Iran).
REFERENCES
- 1.Sahin A, Hamrah P. Clinically relevant biometry. Curr Opin Ophthalmol. 2012;23:47–53. doi: 10.1097/ICU.0b013e32834cd63e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee AC, Qazi MA, Pepose JS. Biometry and intraocular lens power calculation. Curr Opin Ophthalmol. 2008;19:13–17. doi: 10.1097/ICU.0b013e3282f1c5ad. [DOI] [PubMed] [Google Scholar]
- 3.Olsen T. Prediction of the effective postoperative (intraocular lens) anterior chamber depth. J Cataract Refract Surg. 2006;32:419–424. doi: 10.1016/j.jcrs.2005.12.139. [DOI] [PubMed] [Google Scholar]
- 4.Haigis W. Challenges and approaches in modern biometry and IOL calculation. Saudi J Ophthalmol. 2012;26:7–12. doi: 10.1016/j.sjopt.2011.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.MacLaren RE, Natkunarajah M, Riaz Y, Bourne RR, Restori M, Allan BD. Biometry and formula accuracy with intraocular lenses used for cataract surgery in extreme hyperopia. Am J Ophthalmol. 2007;143:920–931. doi: 10.1016/j.ajo.2007.02.043. [DOI] [PubMed] [Google Scholar]
- 6.Wang JK, Hu CY, Chang SW. Intraocular lens power calculation using the IOLMaster and various formulas in eyes with long axial length. J Cataract Refract Surg. 2008;34:262–267. doi: 10.1016/j.jcrs.2007.10.017. [DOI] [PubMed] [Google Scholar]
- 7.Abulafia A, Barrett GD, Rotenberg M, Levy A, Koch DD, Wang L, et al. Intraocular lens power calculation for eyes with an axial length greater than 26.0 mm: Comparison of formulas and methods. J Cataract Refract Surg. 2015;41:548–556. doi: 10.1016/j.jcrs.2014.06.033. [DOI] [PubMed] [Google Scholar]
- 8.Sheard RM, Smith GT, Cooke DL. Improving the prediction accuracy of the SRK/T formula: TheT2 formula. J Cataract Refract Surg. 2010;36:1829–1834. doi: 10.1016/j.jcrs.2010.05.031. [DOI] [PubMed] [Google Scholar]
- 9.Piñero DP, Camps VJ, Mateo V, Ruiz-Fortes P. Clinical validation of an algorithm to correct the error in the keratometric estimation of corneal power in normal eyes. J Cataract Refract Surg. 2012;38:1333–1338. doi: 10.1016/j.jcrs.2012.03.026. [DOI] [PubMed] [Google Scholar]
- 10.Camps VJ, Piñero DP, de Fez D, Mateo V. Minimizing the IOL Power Error Induced by Keratometric Power. Optom Vis Sci. 2013;90:639–649. doi: 10.1097/OPX.0b013e3182972f50. [DOI] [PubMed] [Google Scholar]
- 11.Moschos MM, Chatziralli IP, Koutsandrea C. Intraocular lens power calculation in eyes with short axial length. Indian J Ophthalmol. 2014;62:692–694. doi: 10.4103/0301-4738.129791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Roh YR, Lee SM, Han YK, Kim MK, Wee R, Lee JH. Intraocular lens power calculation using IOLMaster and various formulas in short eyes. Korean J Ophthalmol. 2011;25:151–155. doi: 10.3341/kjo.2011.25.3.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bang S, Edell E, Yu Q, Pratzer K, Stark W. Accuracy of intraocular lens calculations using the IOLMaster in eyes with long axial length and a comparison of various formulas. Ophthalmology. 2011;118:503–506. doi: 10.1016/j.ophtha.2010.07.008. [DOI] [PubMed] [Google Scholar]
- 14.Eom Y, Kang SY, Song JS, Kim YY, Kim HM. Comparison of Hoffer Q and Haigis formulae for intraocular lens power calculation according to the anterior chamber depth in short eyes. Am J Ophthalmol. 2014;157:819–824. doi: 10.1016/j.ajo.2013.12.017. [DOI] [PubMed] [Google Scholar]


