PaCER - A fully automated method for electrode trajectory and contact reconstruction in deep brain stimulation

Abstract

Deep brain stimulation (DBS) is a neurosurgical intervention where electrodes are permanently implanted into the brain in order to modulate pathologic neural activity. The post-operative reconstruction of the DBS electrodes is important for an efficient stimulation parameter tuning. A major limitation of existing approaches for electrode reconstruction from post-operative imaging that prevents the clinical routine use is that they are manual or semi-automatic, and thus both time-consuming and subjective. Moreover, the existing methods rely on a simplified model of a straight line electrode trajectory, rather than the more realistic curved trajectory. The main contribution of this paper is that for the first time we present a highly accurate and fully automated method for electrode reconstruction that considers curved trajectories. The robustness of our proposed method is demonstrated using a multi-center clinical dataset consisting of N = 44 electrodes. In all cases the electrode trajectories were successfully identified and reconstructed. In addition, the accuracy is demonstrated quantitatively using a high-accuracy phantom with known ground truth. In the phantom experiment, the method could detect individual electrode contacts with high accuracy and the trajectory reconstruction reached an error level below 100 μm (0.046 ± 0.025 mm). An implementation of the method is made publicly available such that it can directly be used by researchers or clinicians. This constitutes an important step towards future integration of lead reconstruction into standard clinical care.

Highlights

• •A fully automated method for DBS electrode localization
• •Reconstruction of complete electrode trajectories including bending by brain shift
• •Automatic detection of individual contacts in high-resolution CT data
• •Very high accuracy shown using custom phantom and robustness shown on clinical data
• •Publicly available toolbox for convenient use

1. Introduction

Deep brain stimulation (DBS) in the subthalamic nucleus (STN) is an effective and widely-implemented treatment option for patients with advanced stage Parkinson's Disease Deuschl et al., 2006b, Schuepbach et al., 2013. Treatment outcome is directly related to precise electrode placement within the STN Wodarg et al., 2012, Welter et al., 2014. In addition, both short- and long-term neuropsychiatric side effects have been linked to sub-optimal electrode placement and unwanted spread of stimulation to neighboring structures Castrioto et al., 2014, Witt et al., 2013. DBS is a long-established and effective treatment for related movement disorders such as Dystonia (Vidailhet et al., 2005) and Essential Tremor Hubble et al., 1996, Schuurman et al., 2000. More recently it has been explored as a treatment option for a number of neuropsychiatric disorders such as OCD and severe depression (Hariz et al., 2013).

After DBS surgery and electrode fixation, clinicians will attempt to optimize treatment effects by altering stimulation parameters and consequently the electrical field generated (McIntyre et al., 2004). This optimization process relies on time-consuming and, for the patients, tiring clinical testing of individual electrode contacts to establish thresholds for treatment benefit and stimulation-induced side effects Deuschl et al., 2006, Krack et al., 2002, Volkmann et al., 2002. Information on final electrode position in relation to the target structures is routinely acquired as part of standard clinical protocols using pre-operative MRI and post-operative CT or MRI. However, despite the availability of these pre- and post-operative measures, they are rarely considered in combination. Combining these could be used to systematically inform post-operative stimulation programming (see for example, Paek et al., 2011). This would require tools that are clinically accessible to analyze precise electrode localization with patient-specific anatomy.

Previous studies have demonstrated that electrode artifacts seen in post-operative CT scans can in principle be used to accurately localize the electrode contact zone. This has been shown in both phantom (Hemm et al., 2009) and clinical data Hebb and Miller, 2010, Hebb and Poliakov, 2009. Several studies examining the impact of intra-operative brain shift have introduced lead extraction algorithms to facilitate automated reconstruction of electrode trajectories Lalys et al., 2014, Chen et al., 2014, Husch et al., 2015 or estimation of contact coordinates using CT scans (D’Haese et al., 2010). Another study (Hebb and Miller, 2010) demonstrated that algorithm-driven estimation provided more reliable electrode contact localization than manual expert (surgeon) estimation.

1.1. Motivation

Recently, several toolboxes have been described to facilitate DBS lead localization (DBSmapping (da Silva et al., 2015), PyDBS (D’Albis et al., 2015), DBSproc (Lauro et al., 2016), LeadDBS (Horn and Kühn, 2015)). Only DBSproc and LeadDBS are currently publicly available. While both provide researchers with a range of supplementary tools for image registration, stimulation modeling, structural connectivity-analysis and more, they also require a high level of technical expertise to setup and use. Both require image registration steps to align post-operative electrode imaging with other modalities. This limits their broad implementation and potential clinical use.

The MATLAB™-based LeadDBS is arguably the most established toolbox providing a semi-automatic framework for electrode localization based on automatic pre-processing and a manual refinement step. LeadDBS is employing a pure linear trajectory model, which is well suited to model the contact region of an electrode, but unavoidably induces large off-trajectory errors for the proximal electrode parts. The linear model is not suited for analysis of electrode bending, which might be interesting for further improvement of neurosurgical procedures with respect to brain shift. No quantitative accuracy analysis is available with any tool.

1.2. PaCER

The aim of this work was to introduce a fully automatic algorithm addressing the drawbacks of currently available software. Thus the focus was to accurately reconstruct the full electrode trajectory (including potential non-linear bending) as well as single contact positions from post-operative CT scans. Key aims were robustness and convenient application using standard clinical CT scans without a need for manual intervention. The system should be fully self-contained and require no secondary co-registered imaging modalities or atlases. However, the results of the electrode reconstruction should be easy to integrate with such modalities, enabling visualization with atlas structures as well as with segmentations of a patient's individual brain structures. To facilitate further analysis, an easy integration with existing toolboxes should be a focus point.

Given these goals, the method is referred to as Precise and Convenient Electrode Reconstruction for Deep Brain Stimulation (PaCER) throughout this paper. A MATLAB based reference implementation of PaCER is provided as free download. For standalone use, the reference implementation includes essential visualization aids (multi-planar image view, segmentation and atlas structure visualization) and a simplified volume of tissue activated model. The reconstruction results outputted by PaCER are implemented using object orientated programming. The electrode objects encapsulate appropriate visualization methods, accordingly, PaCER results could be immediately and easily integrated in any MATLAB based software. The method is evaluated on clinical datasets from two different DBS centers. This evaluation uses three different electrode types from two vendors. Accuracy is quantitatively validated using a high-accuracy 3D phantom with electrodes implanted at precisely known locations.

2. Methods

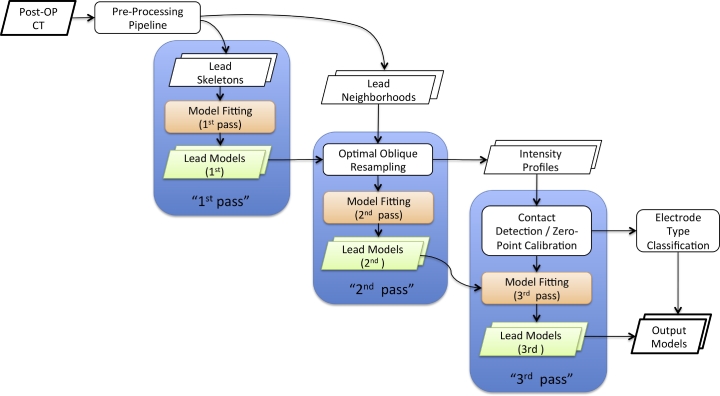
Fig. 1 provides an overview of PaCER's workflow. It is organized into tasks that follow a repetitive scheme of three model fitting iterations.

Fig. 1.

Flowchart of PaCER electrode reconstruction. PaCER is organized in a pre-processing and three model fitting passes. The 1st pass fits a polynomial model to a set of lead skeleton points gained from the image pre-processing pipeline. The 2nd pass is a refinement stage where the 1st pass output is used together with the lead neighborhoods applying optimal oblique re-sampling. Thus the 2nd pass yields an improved model as well as intensity profiles of the electrodes. In the 3rd pass the intensity profiles are used for contact detection and zero-point calibration. Subsequently the model is refitted again to accurately reflect the detected zero-point.

2.1. Pre-processing pipeline

The first step of the workflow is the application of an automatic image pre-processing stage. In summary, this pre-processing is based on detecting metal components within the image dataset. All operations are constrained to the brain area using a brain mask derived directly from the CT data. To yield robust results, the brain mask is relaxed to a convex hull of the brain, which is sufficient for the intended task of restricting the search area. Thus, the algorithm is self contained and can operate on individual CT datasets, requiring no other co-registered image modalities. The output of this pre-processing is a point cloud that models the center-line of each lead within the image. In this initial stage the lead skeletons are determined following an axial slice processing flow. Additionally, location and intensity values of the neighborhood voxels of the center-line can be extracted. A more detailed description of the pre-processing pipeline can be found in Husch et al. (2015).

2.2. 1st pass model fitting

A parameterized polynomial is fitted to skeleton points of leads detected in the pre-processing stage. The concept of polynomial fitting is similar to the algorithm presented in Lalys et al. (2014). The result is a parameterized polynomial electrode model

$$F:[0,1]\to {\mathbb{R}}^3\text{where}F\text{is a polynomial}.$$ (1)

This electrode model is referred to as first pass model, as it serves as an initial estimate for the subsequent processing steps. The polynomial F is efficiently represented by its coefficient matrix.

2.3. Enabling precise length measurements

By representing the electrode trajectory as a parameterized polynomial it enables a precise analytic treatment and allows exact length measurements along the trajectory. The arc length, i.e. the length (in millimeters, as the world coordinate system is defined in millimeters) travelled along the curve between two parameter points a and b is given as a mapping arclength_F : [0,1] × [0,1] →ℝ with

$${\text{arclength}}_F(a,b)={\int }_a^b\parallel F^{\prime }(\tau ){\parallel }_{2}d\tau ,$$ (2)

where F′ : [0,1] →ℝ³ is the derivative of the model polynomial F. The inverse of this integral, i.e. finding the integration bound b for a given arc length l is difficult to compute in the general case potentially involving polynomials F of very high order. However, as arclength_F is always monotonic in b for a given a, |l −arclength_F(a,b)| is quasi-convex and features a single minimum. Thus b can reliably be computed by finding arg minb|l −arclength_F(a,b)| using numerical methods with arbitrary precision and very low computational cost. Consequently ${\text{arclength}}_F^{-1}:{\mathbb{R}}^3\to [0,1]$ is defined as

$${\text{arclength}}_F^{-1}(l)=\underset{b}{\arg \min }|l-{\text{arclength}}_F(0,b)|$$ (3)

for the inverse arc length measured from the origin. Eq. (3) enables the convenient re-parameterization of any polynomial model F in the sense of F_R : ℝ →ℝ³ where

$$F_R(l)=F\left({\text{arclength}}_F^{-1}(l)\right).$$ (4)

2.4. Optimal oblique re-sampling and 2nd pass model fitting

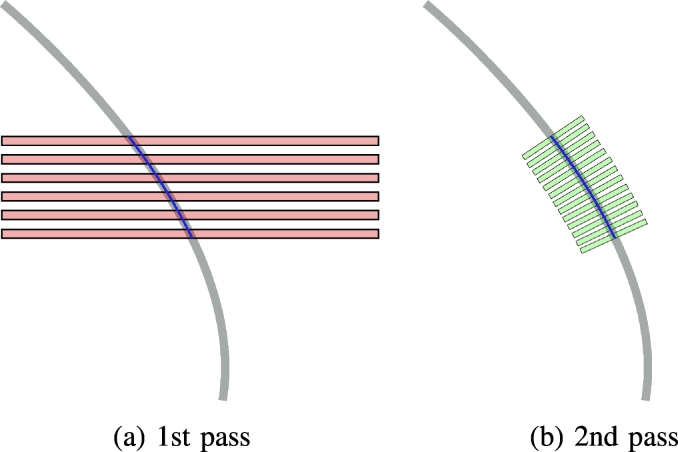
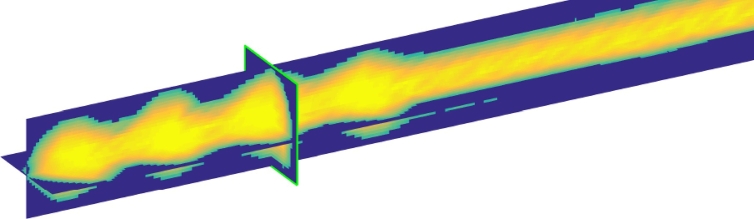
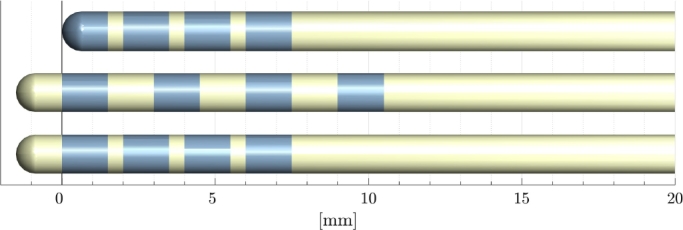
Using the previously determined first pass polynomial and the re-parameterization with respect to arc length F_R, the lead neighborhood can be reassessed using oblique slices re-sampled perpendicular to the local electrode trajectory. This procedure is referred to as optimal oblique re-sampling (OOR), as it defines oblique slices optimally tilted with respect to the initial trajectory guess. By using OOR an even higher precision can be achieved for trajectory center-line reconstruction. In addition, it facilitates detailed analysis of signal intensities at each location along the electrode path, enabling automatic contact localization. A 2D-sketch1 of the concept is shown in Fig. 2. The re-sampling could technically be carried out using arbitrary slice thicknesses, but given common electrode geometries an in plane resolution of 0.1 mm and a slice thickness of 0.025 mm was chosen for the reference implementation. Data generated by OOR re-sampling of a Medtronic 3387 electrode from a clinical dataset is shown using three planes in Fig. 3. The contact region of the quadripolar electrode shows four clearly distinct areas in the OOR data, reflecting the contact regions.

Fig. 2.

Principle of optimal oblique re-sampling: (a): Axial CT slices (red) are evaluated in the pre-processing yielding a first electrode skeleton model (blue) of the underlying trajectory (gray) for the 1st pass, (b): using the analytic model from the 1st pass, oblique slices parallel to the normals of the model (green) are evaluated in the 2nd pass (Slice spacing and selected electrode part only for illustrative purposes).

Fig. 3.

Optimal oblique re-sampled (OOR) data stacked and displayed as a three plane MPR view cutting through the volume.

Finally, the parameterized polynomial is refitted to the re-sampled data, establishing the 2nd pass model. The center-line pointcloud of the OOR data is detected using the intensity weighted mean position of the artifact in each slice as skeleton point, i.e. $p=\frac{\sum Pv}{\sum v}$ where $P\subset {\mathbb{R}}^3$ is the set of in plane points and $v\subset \mathbb{R}$ the corresponding set of intensity values. The accuracy of the lead skeleton is expected to be below the voxel size as partial volume effects are taken into account by the intensity weighting. The efficacy of applying the intensity weighted mean for sub-voxel accuracy detection of symmetrical structures in CT data was previously demonstrated (Grunert et al., 1999). This result was found applicable to any type of electrode featuring a symmetric contact region, including those with segmented contacts arranged symmetrically (e.g. Boston Scientific Vercise Directional Lead). However, for these electrodes the challenge remains of accurately identifying the rotation of individual segments.

2.5. 1D intensity profiles and contact detection

An intensity profile of the electrode trajectory is generated by integrating the intensity values in the individual OOR planes in the form of a projection of the plane values to a scalar quantity.

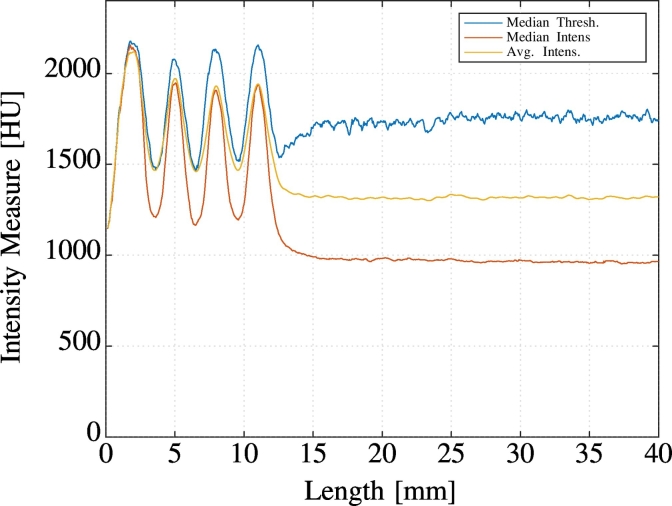
Fig. 4 shows an example of intensity profiles for a Medtronic 3387 electrode comparing different operators to project the OOR data to 1D (average, median, median after threshold).

Fig. 4.

1D intensity profiles of a Medtronic 3387 Electrode scanned post-operatively at 0.7 mm slice thickness created using different operators (average, median, and median after thresholding). Note the four prominent signal peaks indicating the locations of the electrode contacts and compare with Fig. 3.

The transformation of the 3D trajectory into the 1D intensity profile allows a straightforward and precise discrimination of contact locations. Furthermore, this provides very good signal-to-noise-ratio (SNR) due to the projection of information which leads to a noise cancellation. A mapping between points on the 1D profile and 3D points on the trajectory is established by using the polynomial electrode model and Eq. (3). Thus all operations carried out on the generated 1D signal can immediately be transformed into 3D positions. Due to the excellent SNR the median intensity was selected as projection operator to be used in PaCER. It is combined with a subsequent zero-phase shift filtering in 1D to further stabilize the signal.

For the contact detection it was hypothesized that each of the signal peaks corresponds to the center-of-gravity of one of the electrode contacts. This hypothesis is widespread in the literature, e.g. it is applied to the semi-automatic cross-correlation based contact detection method with manual refinement suggested before (e.g. Horn and Kühn, 2015). However, the 1D transformation introduced in this section has the potential for much easier, more robust and efficient implementation. Furthermore, it allows straightforward manual verification.

2.5.1. Zero-point calibration

The definition of the zero-point of the parameter space, as the base of all length measurements along a trajectory, is in principle arbitrary. Given the different electrode designs of various vendors, i.e. some with a non-metal tip and others where the first contact2 forms the tip, the point-of-origin is defined as the distal edge of the first electrode contact, see Fig. 5. A final refitting is performed after detection of the contacts. This step generates the 3rd pass model, which is calibrated to the defined zero-point. This calibration enables us to establish precise 3D point to point correspondences between longitudinal scans of electrodes. Thus it facilitates accurate analysis of electrode drift over time (e.g. by brain shift).

Fig. 5.

Definition of zero-point/origin of electrode space visualized for different electrode types. The origin is defined as the distal edge of the most distal electrode contact.

2.5.2. Automatic electrode type classification

The 1D intensity profiles provide a straightforward approach to determine the electrode type using a comparison with template intensity profiles. However, an even simpler approach relying on only the modal values, i.e. the location of the peaks of the intensity profiles, proved very robust and correctly classified the electrode type in 100% of the tested datasets, consisting of N = 44 electrodes including Medtronic 3389, Medtronic 3387 and Boston Scientific Vercise Directional Leads. The set of ring-contact distances (plus additional intensity peaks expected by the X-Ray opaque marker in case of the Boston Scientific electrode) for the three electrode types was used as template for this approach. The most probable electrode type was determined by calculating the Euclidian distance d = ∥p −s_i∥₂ between the vector of the detected peak distances p and the vector of distances given by the electrode specification s_i. Subsequently, the type with the lowest norm was selected as the most probable.

2.6. Reference implementation

A reference implementation of the described methods has been created using MATLAB. The input CT data is expected in NiFti-file format (http://nifti.nimh.nih.gov). Object oriented programming was used to model entities representing outputs. Thus, the resulting electrode reconstructions are capsuled in self contained electrode objects including appropriate visualization methods.

Based on this design it is possible to rapidly integrate the PaCER algorithm into other MATLAB toolboxes, as the provided electrode objects encapsulate all necessary functionality for instant use.

To facilitate convenient stand-alone evaluation of PaCER results, an interactive MPR view, visualizing underlying image data in orthogonal planes is included. Furthermore, a simple monopolar volume of tissue activated model based on work by Madler and Coenen (2012) as well as a software class to visualize segmented brain structures is provided with PaCER. All objects support automatic plot updating on the change of parameters. The PaCER toolbox is released as a free download.

2.7. Phantom validation

An imaging phantom was fabricated to evaluate the accuracy of the trajectory reconstruction as well as the contact detection. Initially a pilot phantom was produced using 3D printing, subsequently a very high accuracy version was created by turning of an acrylic glass cube using computer-aided-manufacturing (CAM), see Fig. 6. The translucent acrylic glass version allows visual inspection of the electrode while implanted in the phantom. Both phantoms were equipped with seven titanium balls (diameter 6~mm) that define a reference coordinate frame and act as fiducial markers. Ball shaped fiducials can be detected with sub-voxel accuracy, i.e. an accuracy much higher than the slice thickness of a CT scan (Grunert et al., 1999). Thus, the reference coordinate frame of the phantom could be detected with very high precision (mean fiducial registration error 0.0806 ± 0.041 mm) and the electrode trajectories reconstructed from CT data using PaCER could thus be compared to the known ground truth of the phantom blueprint with very small measurement errors. Two electrodes segments of approximately 8 cm length were implanted into the phantom, one following a straight line trajectory, the other following a well defined curve. The electrodes were placed from the side using notches of 8 cm length turned into the phantom, thus ruling out any compressing stress to the tip area due to the insertion. Furthermore, this design ensures that the electrodes are placed within a well defined plane (at the bottom of the notch) within the phantom.

Fig. 6.

Acrylic glass phantom holding two electrodes (one curved, one straight-line) equipped with titanium reference balls for accurate registration.

3. Results

3.1. Phantom experiment

The high accuracy phantom was CT scanned using a high resolution CT sequence (0.5 mm slice thickness, J30s kernel, Siemens Somatom Definition Flash) as typically used for post-operative electrode assessment. The results for trajectory reconstruction and contact detection are discussed in the following.

3.1.1. Trajectory reconstruction

For the trajectory reconstruction, a mean error between detected trajectory and model ground truth of 0.039 ± 0.015 mm was found for the curved 3387 electrode.

For the 3389 electrode following a linear trajectory, the off-trajectory detection error was 0.052 ± 0.030 mm. There was no statistical difference between the straight or curved electrode trajectory. Therefore, the results could be combined and the overall detection error for the phantom experiment computed to 0.046 ± 0.025 mm.

3.1.2. Individual contact detection

Surprisingly ‘large’ errors (above 200 μm) were found when comparing the detected contact positions to those expected based on the lead specifications from the electrode vendor. The results indicated that the contact spacing of the electrodes was slightly but significantly diverging from the specification, i.e. the detection accuracy of PaCER is good enough to detect such slight changes on high-resolution data. To verify this hypothesis we took photogrammetry pictures of the two electrodes implanted in the glass phantom. A camera was set up with the camera plane parallel to the planes where the electrodes were placed within the phantom. The electrode contacts were arranged in the center of the image plane to limit optical distortion (see Fig. 7a and b).

Fig. 7.

Photogrammetry picture of the 3387 and 3389 electrode within the phantom. Note the slightly non-uniform contact spacings.

The orthographic photos produced in this way allow precise distance measurements using standard image processing software. Reference measurements were made of a distance known with very high precision (the width of the CAM produced holding notches) facilitating the conversion between image pixels and millimeters. After this calibration precise measurements within the images could be made and act as ground truth reference for further analysis (Fig. 8).

Fig. 8.

(a) Photogrammetry picture of the 3387 electrode within the phantom; (b) overlayed with the CT based 3D reconstruction using the presented algorithm. Note the visually perfect accuracy of trajectory as well as contact detection.

For the curved electrode of type Medtronic 3387 we found ground truth contact spacings of 1.396 mm, 1.615 mm and 1.656 mm in contrast to the specified value of 1.5 mm. PaCER's contact detection applied on 0.5 mm slice thickness CT imaging reported contact spacings of 1.350 mm, 1.6836 mm and 1.631 mm. The mean absolute error for the 3387 electrode contacts was 0.047 ± 0.022 mm. For the 3389 electrode the ground truth contact spacing was 0.574 mm, 0.530 mm and 0.433 mm. The contact spacings reported by the algorithm were 0.817 mm, 0.539 mm and 0.360 mm. The mean absolute error computed to 0.108 ± 0.121 mm.

3.2. Evaluation on clinical data

Clinical data is challenged by unknown ground-truth and does not allow quantitative evaluations. A fully automated reconstruction algorithm needs to be robust across clinical datasets with varying image quality and resolution. Therefore, PaCER was qualitatively evaluated using post-operative CT scans from DBS procedures with a total of N = 44 implanted electrodes. The datasets involved CT scans generated using three different CT machines and included three different electrode types (Medtronic 3387 and 3389, Boston Scientific Vercise directional lead). Across all datasets, the automatic trajectory reconstruction was successful. Detection of individual electrode contacts was possible in all scans with a slice thickness lower than 1 mm (25 cases). In all cases the correct electrode type was classified automatically. In the remaining 19 cases, only low resolution CT scans with a slice thickness between 1 mm and 3 mm were available. For such lower resolution data PaCER implements an automatic fallback to a ‘contact area’-based detection strategy. In this, the algorithm detects the entire contact area in the intensity profiles and places the electrode contacts within that area based on the electrode specifications. With this strategy, a reliable contact placement was possible in all cases.

3.3. Influence of imaging resolution

In order to quantitatively assess the influence of different imaging resolutions, which is in CT imaging mostly governed by the slice thickness, a re-sampling study was carried out.

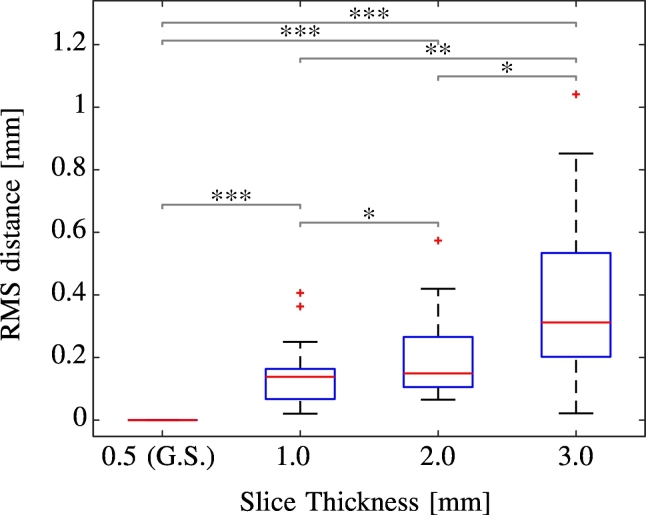
For 20 electrodes (Medtronic 3389) electrode trajectories and single contact locations where reconstructed from high quality data acquired with 0.5 mm slice thickness. This dataset served as gold-standard. Subsequently the CT images were linearly re-sampled to 1 mm, 2 mm and 3 mm slice thickness. The PaCER reconstruction was repeated for each slice thickness level. Even at the 1 mm level, the SNR was found to be too poor to facilitate individual contact detection in several cases, which is in-line with the results on low resolution clinical data. As a fallback, the method in this cases detects the entire contact area and places the electrode contacts within that area based on the electrode's specification. The root mean squared distance between the gold-standard electrode contact locations and the respective resolution levels locations was calculated for each electrode.

Fig. 9 summarizes the results. The average RMS error between gold-standard and the 1 mm resampling was 0.142 mm, for 2 mm thickness it was 0.203 mm and for 3 mm it was 0.405 mm. All differences are statistically significant (paired Wilcoxon-Signed-Rank Test). The results indicate that contact reconstruction for electrodes with 0.5 mm contact spacing is already significantly worse at a scan resolution of 1.0 mm compared to 0.5 mm. At the 3 mm level, the detection error exceeds the size of the spacing between two consecutive contacts (0.5 mm) in a large number of cases.

Fig. 9.

Influence of different slice thicknesses on contact localization in clinical data for Medtronic 3389 electrodes. RMS errors between the four contacts of 20 electrodes for three different resolution levels compared to a 0.5 mm scan used as gold-standard, * indicates p < 0.05, ** indicates p < 0.01, *** indicate p < 0.001 (paired Wilcoxon-Signed-Rank Test).

3.4. Application potentials and use-cases

In this section, use-cases enabled by PaCER are discussed using illustrative example datasets. All examples and visualizations can be easily reproduced using the reference implementation available for download.

3.4.1. Use-Case A: Curved and longitudinal trajectory analysis

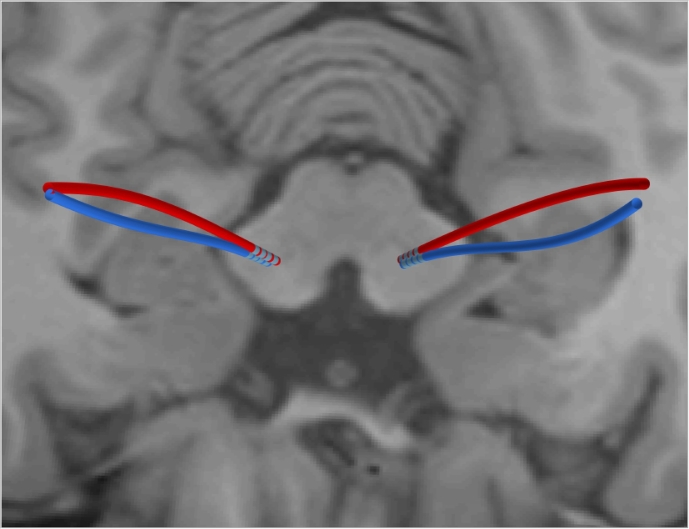
The reconstruction of the curved shape of an electrode enables longitudinal analysis of trajectory behavior, e.g. in the context of brain shift. This is a field of study that is not possible with algorithms imposing a straight line model. An example is demonstrated in Fig. 10.

Fig. 10.

Electrode reconstruction from co-registered CT data one day after surgery (red) and one year later (blue). Co-registered T1 MRI displayed in background. Note the non-linear bending of the trajectories due to brain shift respectively inverse brain shift.

Using contact detection based zero-point calibration and Eqs. (2) and (3), a point correspondence between distinct points on trajectories at different time points can be established. This enables precise 3D drift measurements of points on the electrode over time. This might create a novel source of information for brain tissue mechanics models and help improve future neurosurgical procedures.

3.4.2. Use-Case B: Analysis of plan deviations

Detailed analysis of the (non-linear) electrode trajectory relative to the original plan is useful for post-operative assessment and potential improvement of future electrode implantation procedures. Ideally, planning data is imported in digital format from the planning station using the untouched reference coordinate system of the planning system (Husch et al., 2015). This avoids bias introduced when using manually defined coordinate systems (like the AC/PC-System).

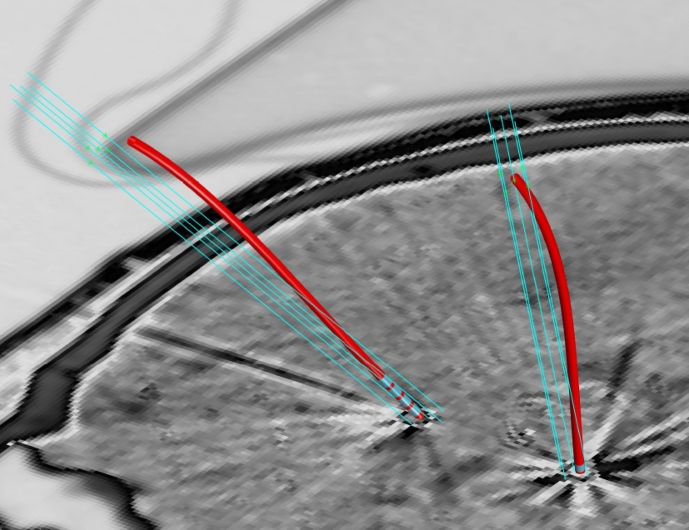
An example is shown in Fig. 11 where the PaCER reconstructed electrodes are displayed together with the pre-planned targeting and micro electrode recording tracks. The electrode reconstructions are based on post-operative CT one day after surgery at which point brain shift had not yet resolved.

Fig. 11.

Planned micro electrode recording trajectories (light blue) and final electrode outcome revealed by PaCER (red) one day after surgery with brain shift still present.

The example demonstrates a good accuracy in the target area with significant (brain shift induced) deviations in upper brain areas. Gaining more knowledge about plan outcome relations might facilitate improved surgical methods e.g. to safely avoid potential risk inducing structures adjacent to the surgical plan.

3.4.3. Use-Case C: Streamlining clinical DBS programming

A potential avenue for streamlining DBS programming is to use a reliable electrode reconstruction together with a co-registered 3D model of the target structure, a goal that is shared by most publications in the field. As PaCER is independent of any sort of atlas or other co-registered modalities, it seems promising to use individual segmentations of target structures of a particular patient, e.g. by co-registration of T2 or SWI and post-operative CT Data instead of only relying on atlas data. Using such a strategy only intra-subject registrations are used, avoiding potentially error prone inter-subject registrations when applying atlases. However, the use of atlas data is easily achieved with PaCER if desired. To further aid efficient programming the Madler and Coenen VTA approximation might prove helpful. Fig. 12 shows an example of a case where electrode reconstruction together with manual segmentation from T2 data could help in optimizing the programming.

Fig. 12.

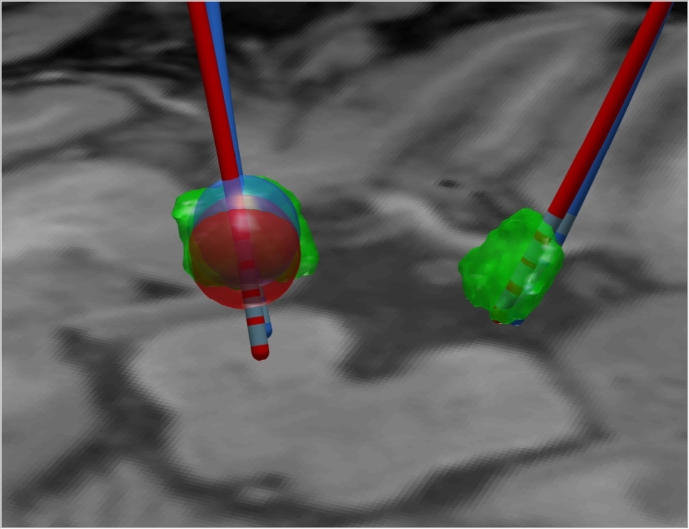
Co-registered electrode reconstruction one day after surgery (red) and one year later (blue) together with manually segmented STN structures from T2 imaging (green). Electrode reconstruction reveals that DBS programming of the left electrode should assess the most proximal contact. Mädler/Coenen VTA estimates are indicated as blue repetitively red spheres. Note the upwards displacement of the later reconstruction.

Note the apparent difference in the STN part covered by VTA models (both: impedance=800Ω, voltage=3.6 V) of the electrode immediately post surgery vs. one year later.

3.4.4. Use-Case D: Reconstruction in different spaces

As already pointed out, PaCER is independent of a specific coordinate system. Thus it is easily possible to apply PaCER for electrode reconstruction in native (subject) space, as well as in any image space where the CT data have been transformed too. Fig. 13 shows an example of a PaCER reconstruction after registration of the CT image to the high-resolution 7T deep-brain atlas by Wang et al. (2016).

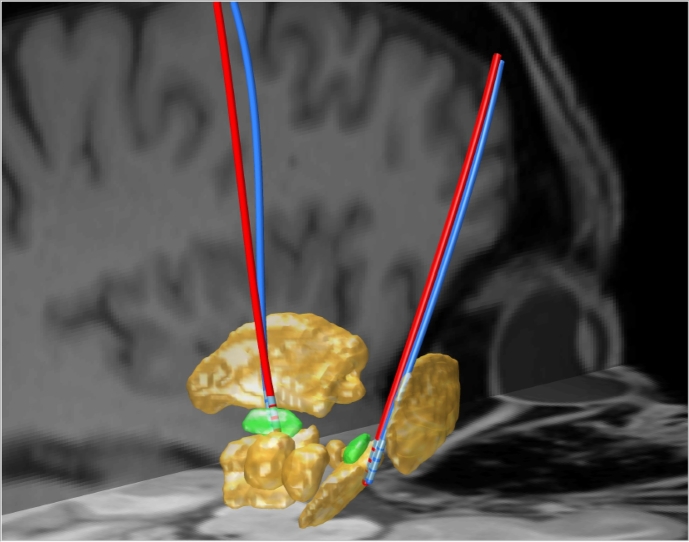
Fig. 13.

Electrode reconstructions carried out in atlas space (high-resolution deep-brain atlas). The electrodes are displayed with the subcortical structures from the atlas. STNs highlighted in green.

The displayed electrodes were reconstructed after transforming the post-operative CT data to atlas space, as this is a standard method. However, due to the re-sampling of the original image to the atlas template the signal to noise ratio declines. A technically more reasonable approach enabled by PaCER is to carry out all electrode reconstructions in native post-op image space and subsequently apply transformations to the reconstructed electrode objects. This is easily possible due to the representation of the electrode trajectory by a polynomial coefficient matrix. With this method no re-sampling of images is involved and the original SNR is fully preserved.

3.4.5. Use-Case E: Integration with other software

The component oriented software architecture of PaCER enables the convenient integration with other software toolboxes by providing reusable objects. As such, PaCER could be integrated as electrode reconstruction algorithm within existing image-analysis software. Another option is to integrate data generated with dedicated state-of-the-art tools back into the PaCER MATLAB environment. One such example is the processing of diffusion MRI data and streamline tractography. Fig. 14 provides an example of combining streamlines generated using the MRtrix3 software package (http://www.mrtrix.org) together with PaCER electrode reconstruction. The cortico-spinal-tract fibers in this illustration are delineated using a probabilistic tractography framework based on constrained spherical deconvolution (Tournier et al., 2004) and high angular resolution diffusion imaging data. Recent studies have demonstrated the clear potential for refining and individualizing both pre-operative planning Coenen et al., 2014, Petersen et al., 2017 and post-operative stimulation management by using tractography to delineate relevant white matter pathways Gunalan et al., 2017, Mahlknecht et al., 2017 or connectivity sweet spots Plantinga et al., 2016, Akram et al., 2017, Horn et al., 2017.

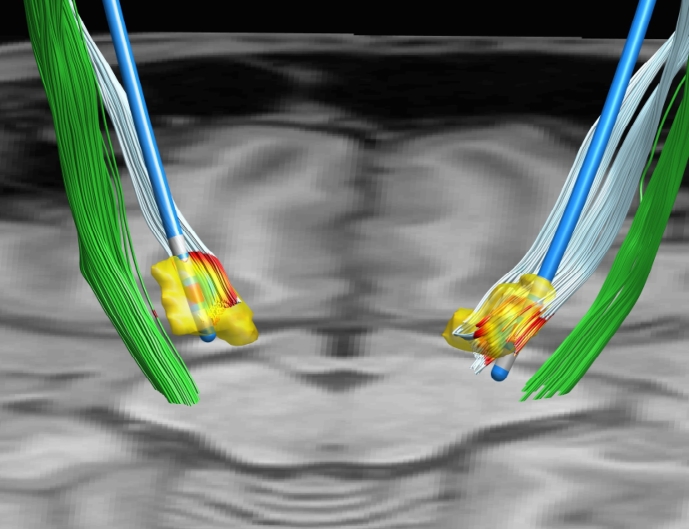
Fig. 14.

PaCER electrode reconstruction and VTA approximation. Instead of displaying the VTA as a sphere (cf. Fig. 10), it is visualized as a colormap projected onto hyper-direct-pathway and cortico-spinal-tract fibers imported from MRtrix. Manually segmented STN is shown in yellow.

Within PaCER, the imported tractography data are coupled with the existing VTA approximation, coloring parts of the tract overlapped by the VTA. The automatic plot update feature of PaCER is fully retained (cf. supplementary video).

4. Discussion

In this study, we have introduced a novel algorithm for high accuracy reconstruction of DBS leads using post-operative CT scans. The method is fully automatic and retains curved trajectories. The algorithm was validated using scans of a custom made high-accuracy phantom and evaluated using multi-center clinical datasets with varying resolution.

4.1. Accuracy in phantom experiment

The average trajectory reconstruction error was found to be below 100 μm in high-accuracy phantom experiments, which is remarkable compared to the typical electrode diameter of 1270 μm. The accuracy found in the phantom experiment showed no significant difference in reconstruction accuracy for curved vs linear trajectories. Thus PaCER is expected to be fully able to accurately recover electrode bending. Only a few studies have previously examined the impact of brain shift on electrode trajectories inducing curved trajectories (cf. Lalys et al., 2014) and none of these have made analysis-tools openly available.

Analysis of the contact detection accuracy demonstrates that electrodes with wider contact spacing (e.g. Medronic 3387) provide better SNR for individual contact detection. Conversely if electrodes with narrow spacing are used (e.g. Medtronic 3389) then CT imaging with thinnest possible slice thickness should be recommended for robust contact detection. To accommodate different scanning protocols and electrodes used in different centers the PaCER user can easily switch between contact definition based on individual detection or a (potentially less accurate but more robust) contact region based approach.

4.2. Robustness in clinical data

PaCER provided excellent results in all clinical CT scans with a slice thickness lower or equal to 1 mm and successfully reconstructed full trajectories including individual contacts in 100% of this cases.

To study the behavior on larger slice thickness, additional scans with larger slice thickness were evaluated. The trajectory reconstruction was found to be reliable even in 3 mm slices. However, the individual contact detection is not robustly usable in this case and therefore only a simplified method based on detection of the center of the contact region in the intensity profile is available. This might limit accuracy. Re-sampling experiments indicate that at 3 mm slices a contact detection bias in the range of 0.5 mm along the trajectory should be expected. However, this is still a remarkable accuracy given the extreme slice thickness of 3 mm compared to the electrode diameter of 1.27 mm respectively the contact spacing of 0.5 mm or 1.5 mm.

4.3. Limitations

Limitations and future areas of work are discussed in the following.

4.3.1. CT data

The presented algorithm is until now limited to CT data. CT provides decent geometric accuracy, great electrode contrast, is widely available at low cost and currently the standard in post-operative DBS care in many centers. Furthermore, the CT intensity range is standardized using Hounsfield Units, allowing easy translation to different scanners and centers. However, some centers rely on MRI for post-operative assessment primarily due to the advantage of avoiding X-ray exposure. MRI also has significant drawbacks such as lower resolution and weaker contrast despite higher acquisition times. This is further complicated by the restrictions on usable scanning protocol when the patient has electrodes implanted. The general concept of the PaCER algorithm might be applicable to MRI data too, however measures would have to be taken to deal with the inferior SNR. At this point it is not clear if a reconstruction of electrode contacts would be possible from MRI with high accuracy if contact spacings are small.

The first stage of PaCER is based on axial CT slices, where all subsequent operations are independent of slice flow. Thus CT slices tilted out of the axial plane by more than approximately 45 ° might require manual intervention by correcting orientation or change the expected slice flow of the first stage. No such extremely tilted case was present in the test dataset.

4.3.2. Hyper-parameters

The only relevant hyper-parameter of PaCER is the degree of the polynomial fitted to the electrode. A degree of d = 1 corresponds to a straight line model. It is clear that a straight line model is not appropriate to capture electrode bending (cf. Fig. 10). However, there is no clear answer yet which degree is the most appropriate as the choice of degree imposes a classical bias/variance trade off between fitting accuracy and noise removal. Based on results in phantom measurements and variance analysis of clinical data, the reference implementation of PaCER is currently using a degree of d = 8 in all stages until stage three. This degree was suggested as an optimal theoretical bias/variance trade off by evaluating the Akaike-Information-Criterion (AIC). In the final (3rd) stage, the electrode is refitted using only degree d = 3, which induces a smoothing and noise canceling effect that provided superior accuracy in the phantom study. It has to be taken into account that the model polynomial is independent in its x,y,z components. Thus the flexibility in 3D space, formed by superposition of all three components, is relatively large even with such a low degree.

4.3.3. The signal peak to contact center relation hypothesis

The contact detection is based on the hypothesis that the peaks of the 1D intensity profiles coincide with the center-of-gravity of the electrode contacts. While the projection to 1D space is a new robust method introduced in this paper, the hypothesis of a coincidence between location of strong signal and contact center location is common in the literature (cf. D’Haese et al., 2010, Hebb and Miller, 2010, Horn and Kühn, 2015, Lauro et al., 2016. However, it should be noted that neighboring contacts might influence the signal of adjacent contacts. This effect grows increasingly important for smaller contact spacings or lower imaging resolution. Phantom experiments suggest a different detection accuracy for Medtronic 3387 electrodes vs. Medtronic 3389 electrodes. These electrode types are technically identical except for the larger contact spacings of the 3387 electrode. The results thus support an extended hypothesis that contact location and peak intensity are homologous if and only if the contact spacing is large enough with respect to the imaging resolution. As a rule of thumb, a CT slice thickness smaller than the contact spacings seems reasonable if a precise localization of individual contacts is desired. However, for clinical practice a detection accuracy in the range of a contact spacing (e.g. 0.5 mm) might be acceptable. In this case, a pure detection of the ‘ contact region’ and a fitting of electrode contacts as specified by the electrode type (neglecting tolerances) to this region might by sufficient. The results presented in Section 3.3 indicate that a slice thickness as large as two millimeters might be sufficient to reach this level of accuracy in most cases.

4.4. Segmented contacts

The PaCER algorithm can identify contacts areas in DBS electrodes with symmetric contact segments such as the Vercise Cartesia™ segmented lead from Boston Scientific. However, it is not designed to identify the rotation of the individual segments. Very recently, methods for accurately identifying rotation of the lead segments using fluoroscopic techniques (Reinacher et al., 2017) have been proposed. Combining such an approach with the presented algorithm for trajectory and symmetric contact detection is straightforward.

5. Conclusion

To the best of our knowledge this is the first report of a DBS electrode localization algorithm that is a) fully automatic b) retains the (non-linearly curved) shape of an electrode across the whole in-brain trajectory c) is applicable to native space data utilizing the optimal SNR and d) enables precise length-measurements along the curved trajectory, thus allowing longitudinal drift analysis of electrodes.

Given high-resolution data, the contact detection appears accurate enough to even reveal slight tolerances of an actual electrode for certain electrode types. Prior publications in the field have relied purely on general vendor specifications. Furthermore, this is the only algorithm that has been validated by rigorous phantom measurements to allow ground truth comparisons. The phantom experiments indicate unprecedented accuracy. The PaCER reference implementation (http://adhusch.github.io/PaCER/) is self contained and enables stand-alone use as well as easy integration in fully automated image processing work-flows or existing MATLAB toolboxes by providing reusable objects. In summary, the presented work should constitute a crucial step towards future integration of lead reconstruction into standard clinical care.