Capture, Learning, and Classification of Upper Extremity Movement Primitives in Healthy Controls and Stroke Patients

Abstract

There currently exist no practical tools to identify functional movements in the upper extremities (UEs). This absence has limited the precise therapeutic dosing of patients recovering from stroke. In this proof-of-principle study, we aimed to develop an accurate approach for classifying UE functional movement primitives, which comprise functional movements. Data were generated from inertial measurement units (IMUs) placed on upper body segments of older healthy individuals and chronic stroke patients. Subjects performed activities commonly trained during rehabilitation after stroke. Data processing involved the use of a sliding window to obtain statistical descriptors, and resulting features were processed by a Hidden Markov Model (HMM). The likelihoods of the states, resulting from the HMM, were segmented by a second sliding window and their averages were calculated. The final predictions were mapped to human functional movement primitives using a Logistic Regression algorithm. Algorithm performance was assessed with a leave-one-out analysis, which determined its sensitivity, specificity, and positive and negative predictive values for all classified primitives. In healthy control and stroke participants, our approach identified functional movement primitives embedded in training activities with, on average, 80% precision. This approach may support functional movement dosing in stroke rehabilitation.

I. INTRODUCTION

In the next 15 years, the incidence of stroke is expected to surpass 1 million US adults annually, with stroke-related costs expected to skyrocket to $240 billion [1][2]. Two-thirds of stroke survivors have significant upper extremity (UE) impairment, limiting autonomy and performance of activities of daily living [3]. The cornerstone of treatment for UE impairment is rehabilitation training, with a focus on training functional movements. Functional movements consist of a reach to, grasp/touch of, action on, and release of a target object [4]. From research in animal models of stroke, a high number of functional movements in the weak limb is needed to induce neuroplasticity and behavioral improvement [5][6]. In humans, however, little has been done to relate the number of UE functional movements (i.e. dose) to recovery after stroke, with the exception of a recent trial in chronic stroke [7]. Without knowing the training doses required to potentiate recovery in humans, therapists must rely on intuited amounts of training, with uncertain ramifications on recovery [8].

In order to establish an optimal training dose, it is necessary to identify what and how much is being practiced, in a rehabilitation environment. Time spent in therapy sessions, the main metric used in most rehabilitation studies, is an inadequate surrogate for the number of functional movements trained–if they are even trained [4]. Hand-tallying of observed movements, as recently employed [7], is laborious, time-intensive, and impractical for clinical implementation. Motion capture with vision-based and optical technologies suffers from occlusion, noisy visual backgrounds, a need for multiple viewpoints, and restricted work volumes, limiting their application in a busy rehabilitation setting.

Sensor-based technologies use wearable sensors to generate data about movement, and can overcome the practical challenges of motion capture in the rehabilitation environment. Some groups have effectively used accelerometers to quantify movement, particularly if the movement is fairly invariant and has limited degrees of freedom, like gait [9]. For more complex movements made in various planes and with multiple degrees of freedom, like those of the UE, accelerometers have insufficient data dimensionality for movement identification [10]. Functional, non-functional, and passive movements all register as “activity” and are afforded equal weight, despite their different effects on neuroplasticity and recovery.

A potential solution for functional movement capture is the application of inertial measurement units (IMUs), wearable sensors consisting of an accelerometer, gyroscope, and magnetometer. IMUs wirelessly transmit their data over a considerable distance, obviating the need for a specialized motion capture set-up. Importantly, IMUs capture 3D motion with high spatial and temporal precision. Thus, an IMU-based system is ideal for capturing UE movement in a busy rehabilitation environment. Like all other forms of motion capture, IMU data alone do not identify movements. Rather, specialized analysis must be applied to the data stream to detect functional movement primitives, discussed below.

II. RELATED WORK

The technological advancement of robust, powerful and ubiquitous sensor technologies has allowed for a better understanding, modeling, and classification of human activity recognition (HAR). Sensors such as networks of cameras in the environment [11] and accelerometers [12] have been used for tracking and discrimination among certain types of physical activities.

These activities include walking, running, stair climbing, feeding, and self-hygiene [13][14][15][16][17][18]. Other groups have focused on monitoring general activities of older adults [19][20] and stroke patients [18]. In work by Lemmens and colleagues, activity recognition was successfully accomplished in 30 healthy participants and 1 stroke patient performing drinking, eating, and hair-brushing activities while wearing IMUs attached to the moving UE. Of note, activities are comprised of various functional movements, and differ inter-individually by the types and sequences of functional movements used to accomplish the activity. Because of this variability, identification at the level of activity is challenging, and dosing by activity would be expected to have variable therapeutic effects. Hence, the aim of this study was to learn and classify movement primitives, the discrete motions that comprise a single functional movement. Like phonemes, movement primitives can be strung together in various combinations to make a functional movement (analogous to a word), which in turn are strung together to make an activity (analogous to a sentence) [21]. For example, a string of reach-manipulation-retraction primitives could constitute a functional movement for closing a button, within the activity of dressing. We focused on primitives for three reasons: (1) because primitives are clinically non-divisible and fairly invariant, inter-individual identification is improved, (2) because some stroke patients may be unable to complete a full functional movement, primitives can provide a more nuanced picture of performance, and (3) because motor control and learning are believed to be neurally mediated at the level of primitives, they may enable us to more precisely track neural reorganization after stroke [22].

Algorithms such as Support Vector Machines (SVM) [23], K-Nearest Neighbor (KNN), Decision Trees and Naïve Bayes [24] have been previously employed to perform HAR; however, studies have demonstrated that non-statistically exchangeable data are more successfully modeled using Hidden Markov Models (HMM) [25]. Sequential Deep Learning has also been used for the classification of human activities [26]. Although this algorithm demonstrated improved HAR performance compared to other methods, the model was trained in a fully supervised way. In contrast, the methodology provided in this paper performs the learning and classification of human movement primitives in a semi-supervised setting, allowing for use of new unlabeled data for future model training while utilizing the previously labeled data for correlation to human movement primitives.

III. APPROACH

A. Sensor Data Acquisition

Data were collected from 10 healthy older individuals and 6 chronic stroke subjects during a single visit. We used healthy subjects to develop and train the analysis approach and to test its performance. We then tested the performance of the unaltered approach in stroke subjects. All testing was performed in an inpatient rehabilitation gym. Subject demographics are shown in the (Table I), and did not significantly differ between groups. UE motor impairment in the weak arm was assessed with the UE Fugl-Meyer (FM) scale, where a higher score (maximum 66) connotes less impairment [27].

TABLE I.

Demographics

	Healthy Control	Stroke Patients
N	10	6
Age* (years)	67.1 (55.1–83.5)	61.7 (46.5–71.0)
Gender (Male:Female)	5M: 5F	4M: 2F
Race (Black:White:Asian)	2B: 6W: 1A	2B: 3W: 1A
Arm Dominance (Right:Left)	10R: 0L	5R: 1L
Impairment*(FM)	–	52.8 (45–62)
Time since stroke*(years)	–	12.0 (2.0–37.1)

^*Age, impairment and time since stroke are given in mean(range)

Xsens MVN Inertial Measurement Units MTX 2-4A7G6 (Xsens Technologies, Netherlands) were used to track motion in the upper body. Each sensor records 3D linear and angular accelerations at a sampling rate of 240 Hz. 11 IMU sensors were placed on the following body segments: head, sternum, pelvis, bilateral scapulae, arm, forearm, and hand (Figure 3). However, at this stage, data were only used from the right side (7 sensors), which was also the weak side of stroke patients. Because the system is wired on the body, subjects wore a tight fitting long-sleeved shirt over the sensors to avoid snagging the wires. IMU data were transmitted wirelessly to a data receiver and stored on a PC for offline analysis. Software recalibration was performed every 5–10 minutes to offset gyroscopic drift. Single-camera videography synchronously recorded motion at 30 Hz.

Fig. 3.

Feeding activity

A sample of representative activities was chosen from those typically performed during rehabilitation therapy. To determine whether differences in arm/forearm configuration affected primitive detection, objects of various weights, shapes, and sizes were used. To train the algorithm to detect movement primitives in a natural volume of space [28], targets were placed at various horizontal and vertical locations. Each activity was repeated 5 times per object and location. Subjects were positioned at a consistent distance from the workspace, and were instructed to move at a comfortable speed. Healthy controls performed all activities; stroke patients performed the radial activities only because of time limitations. The activities were as follows:

Radial Activity: the subject interacted with an object in a horizontal array of targets on a table top (Figure 1). Objects were a roll of toilet paper and an empty tin can (light can), which prompted a pronated or neutral forearm orientation, respectively, during reach and transport. Subjects reached to grasp the object at the center, transported it to one of the targets [1, 2, 3, 4, 5, 6, 7, 8], and released the object and retracted the arm back to a resting position. They then reached to the object at the target, transported it back to the center, and retracted the arm to rest. These movement primitives were repeated for all 8 targets.

Fig. 1.

Radial activity

Shelf Activity: the subject interacted with an object in a vertical array of targets on shelves (Figure 2). Objects were a roll of toilet paper, a full can of beans (heavy can), a light can, a box of dish detergent, and a small book. Pronated forearm reaching and transport were prompted by the toilet paper and book, whereas a neutral forearm orientation was prompted by the other objects. Subjects transported an object from a “0” target to a “1” or “2” target within the same column (i.e., A0 to A1 or A2 only), using the same sequences of reach, transport, retract, and rest as in the radial activity. These movement primitives were repeated for all 6 targets [A1, A2, B1, B2, C1, C2].

Fig. 2.

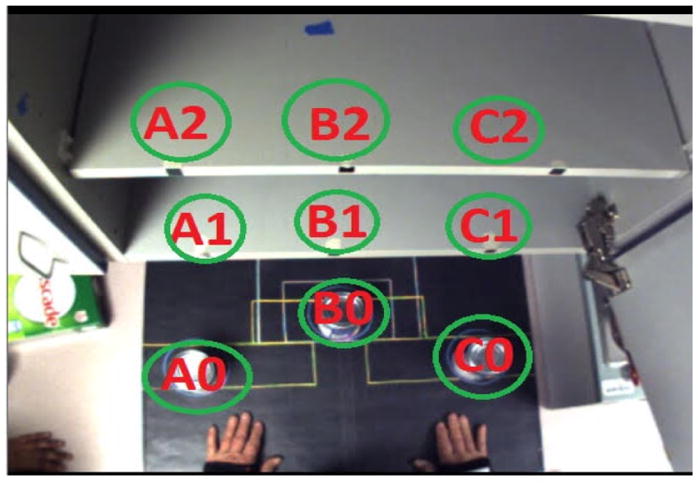
Shelf activity

Feeding Activity: the subject interacted with objects positioned on a table (Figure 3). Objects were a slice of bread in a plastic zippered bag, an individual-sized butter container, a plastic fork and knife, and a paper plate affixed to the table. This activity required the subject to retrieve the bread from the bag, to open the container and butter the bread, to cut the bread into quarters, and to bring a section of the bread to the mouth with the fork. While having an overall sequence of steps, this activity allowed subjects to accomplish the task with a more unstructured order of movement primitives. Although this activity is bimanual, we focused on movement primitives in the right arm, in keeping with the other activities.

Data labeling

Using the MVN software, the video data were used to label components of functional movement primitives in the IMU data. These “true” labels were generated to train the algorithm, and to determine the accuracy of algorithm-recognized patterns. Labels consisted of the start and finish of movement primitives. All activities contained these primitives: rest, reach-to-grasp, and release-to-retract. Each activity had additional movement primitives acting on a target object: transport, manipulation, stabilization, and their subtypes. These movement primitive subtypes include cyclic manipulation (repeatedly engaging a target with the small amplitude distal motions, e.g., buttering the bread), stabilization-transport (holding an object still by working across its surface, e.g. successively pinning down the bread with a fork during cutting), and stabilization-manipulation (holding an object steady but making distal adjustments throughout, e.g., orienting the butter container towards the knife). When used, tools acted as extensions of the hand, and we labeled the primitive performed with the tool on the target object.

B. Feature Extraction

The IMU software generated, per sensor, 3D linear accelerometer, 3D rate gyroscope and 3D magnetometer data. In order to extract the relevant features from the data, a sliding window was implemented to segment the data [29]. The sliding window divided the whole dataset into a temporal segment of a given size and step. The size represented the number of time-frames needed to characterize the sensor data; the steps provided the overlapping number of time-frames [30]. With larger window sizes, short-duration primitives may be lost; with smaller windows sizes, motions’ noise is more likely to be included.

For complex activities, other studies have found that the best trade-off between accuracy of classification and speed of processing is to use a sliding window with an interval of 1–2 seconds [29][16]. However, these studies segmented and classified activities, not movements or their primitives. Taking into consideration these previous studies [29] and through cross-validation, a window of 0.25 seconds and with a step size of 0.004 seconds empirically showed the best classification performance.

While performing the segmentation, one method to characterize the signal is to calculate statistical descriptors [31]. The statistical descriptors, calculated on each of the dimensions of the sliding window, were: mean, variance, min, max, and root mean square (RMS). The mean μ over a signal removes random spikes or noise (both mechanical and electrical), smoothing the overall dataset. The variance σ² extracts the variability of the signal, and represents the stability of the segmented signal. The minimum and the maximum represent the range of the energy of the motion [32], and provide specific information about tasks that produce similar range signal but exert a higher or lower energy. In addition, because the signal also contains negative values, the RMS enables signal characteristics when the average would not suffice. To summarize, using the 7 sensors (head, sternum, pelvis, bilateral scapulae, arm, forearm, and hand), 5 vectors (linear and angular acceleration, linear and angular velocity, position) each represented by 3 dimensions, orientation (represented by 4 dimensions) and 5 statistical descriptors, the final dimensionality of the data set is 665. By decomposing this dataset through the use of statistical descriptors, the resulting processed data provide more descriptive information of the motion.

C. Hidden Markov Model

A HMM is a temporal probabilistic model whose system is a Markov process with hidden or latent states [33]. A Markov process is a stochastic model based on the Markov property. This property indicates that the belief state distribution at any given time t is only based on the state at time t − n where n ≥ 1. Given a time series of observed sensor data, the model will use techniques from probability theory to infer the posterior probability of the hidden states that generated those observations.

Notation

The HMM is defined by the following components:

• T = length of the activities

• N = number of states in the model

• X = X₁, X₂, …, X_n = set of possible states

• A = state transition probability distribution

• B = observation probability distribution

• π = initial state distribution

• O = O₁, O₂, …, O_T = observation sequence of processed data points

The length of the observation sequence T represent the duration, in time-frames, of the activities. Using cross-correlation, N=25 performed best for modeling the dataset without overfitting. The observation O_t is represented by a Gaussian distribution, with unknown parameters, conditioned on the state X_t at time t. The matrix $A=\overrightarrow{a_{ij}}$ is N × N with a_ij = P (state x_j at t + 1 | state q_i at t) and A is row stochastic. The matrix B = b_j(X) is characterized by the mean μ and variance α of the data in state K such that b_j(K) = P (observation k at t| state q_j at t). The HMM model is denoted by λ = (A, B, π) [34].

Problems

There are three fundamental problems that can be solved by implementing a HMM [33]:

• Given an observation sequence O = O₁, …, O_T, find the model λ = (A, B, π) that maximizes the probability of actually seeing the observations O. In other words, train the model to get the best results based on the observation. 3 HMMs are created and trained based on the shelf, radial and feeding tasks. This problem is solved by implementing the Baum-Welch (Expectation Maximization) algorithm to calculate the transition matrix A, mean μ, variance σ and prior distribution π for each of the models.

• Given a model λ = (A, B, π) and an observation sequence O = O₁, …, O_T, choose a corresponding state sequence X = x₁, x₂, …, x_n that best explains the observations or uncover the sequence of states (hidden parts). Implementing the Viterbi algorithm, for each time frame, the probability of the states is calculated. These states, however, do not correlate to human movement primitives; therefore, a Logistic Regression algorithm is implemented to map the set of states likelihood to the actual movement primitive, which will be explained in the next session.

• Given a model λ = (A, B, π) and an observation sequence O = O₁, …, O_T, compute P (O|λ), the probability of the observation sequence, given the model. After the training phase, the likelihood for each of the testing dataset is calculated. The HMM with the greatest likelihood is used to classify the data.

D. Logistic Regression Implementation

The HMM calculates the likelihood of each state s ∈ [1, 25] per time frame. Because the HMM was trained using 25 states and there were 4 possible movement primitives for the shelf and radial tasks (e.g., resting, reaching, transporting and retraction) and 9 possible movement primitives for the feeding task (e.g., resting, reaching, transporting, retraction, stabilization, stabilization-transport, manipulation, stabilization-manipulation and cyclic-manipulation), a HMM’s state does not correspond to a specific primitive. For instance, the “reaching” movement primitive might be represented by the set of states s_k where k ∈ [6, 12], but “transporting” could be represented by the sequence of states s_j where j ∈ [1, 8]. As a result, because a set of the same states could be used in the representation of two or more movement primitives, the prediction of the HMM cannot be interpreted as the actual human movement primitive. A Logistic Regression algorithm was thus used to match those state likelihoods to actual human movement primitives.

Sliding Window: a second sliding window is used on the likelihood of the states predicted by the HMM. Through cross-validation, a window size of 0.5 seconds and step size of 0.04 seconds empirically showed the best movement primitive classification. The average of the likelihood of states is calculated per segment. Each averaged segmentation is mapped to a labeled primitive during the training phase. The resulting training dataset is used to train the Logistic Regression algorithm in order to match each time frame to a true movement primitive name (as identified by video analysis).

Implementation

The Logistic Regression optimization function is:

$$Pr(X)=\frac{e^{{\beta }^{T}X}}{1+e^{{\beta }^{T}X}}$$

Where, β is the coefficient or vector parameters. In order to estimate these coefficients, Maximum Likelihood Estimation [35] is performed in the function. Ideally, the goal of the estimator is to estimate β₀, β₁, …, β_k such that the predicted probability Pr(X) of labels from the HMM correspond as closely as possible to the true labels a human understands. The Logistic Regression algorithm was implemented without alterations. The algorithm was trained using the HMM’s predictions on the training data and the labeled information. As a result, the Logistic Regression algorithm provides an actual movement primitive per time frame when implemented on the testing data.

E. Performance Measurement

In order to inspect the real-world relevance of the algorithm predictions, a comparison between the predictions and the true movement primitive labels was performed. We calculated the number of true positives (TP; algorithm and label matched in identifying a movement primitive), true negatives (TN, algorithm and label matched in not identifying a movement primitive), false positives (FP, algorithm identified a movement primitive that did not occur), and false negatives (FN, algorithm did not identify a movement primitive that did occur).

From these, we estimated the following performance metrics: sensitivity, specificity, and positive and negative predictive values (PPV, NPV). PPV and NPV adjust for the prevalence of different movement primitives in the activities.

Sensitivity or Recall: given a subject made a particular movement primitive, how often did the algorithm correctly identify that primitive, e.g. when the true primitive label was “reach”, how often did the algorithm predict “reach”: Sensitivity = TP=(TP + FN).

Specificity: given a subject did not make a particular movement primitive, how often did the algorithm correctly not identify that primitive, e.g., when the true label was not “reach”, how often did the algorithm not predict “reach”: Specificity = TN=(TN + FP).

Positive Predictive Value (PPV): given the algorithm identified a particular movement primitive, how often did the subject truly make that movement primitive, e.g., when the algorithm predicted “reach”, how often was it correct: PPV = TP=(TP + FP).

Negative Predicted Value (NPV): given the algorithm did not identify a particular movement primitive, did the subject truly not make that primitive, e.g., when the algorithm did not predict “reach”, how often was it correct: NPV = TN=(TN + FN).

IV. RESULTS

Results of healthy subjects: the algorithm was trained on 9 of the subjects and was tested on each of the remaining subjects (i.e,. leave-one-out cross-validation). Performance metrics were calculated for all movement primitives, and the averages from the 10 subjects are provided for each activity in (Tables II – IX):

TABLE II.

Radial Can

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.87	0.97	0.77	0.97
Reach	0.81	0.95	0.87	0.93
Transport	0.88	0.90	0.80	0.94
Retract	0.83	0.95	0.86	0.93

TABLE IX.

Feeding

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.54	0.97	0.42	0.98
Reach	0.29	0.97	0.48	0.93
TP1	0.68	0.67	0.49	0.81
ST2	0.90	0.98	0.81	0.96
MN3	0.59	0.92	0.60	0.92
ST-TP	0.89	0.96	0.86	0.95
ST-MN	0.49	0.95	0.67	0.94
Cyclic-MN	0.93	0.96	0.82	0.91
Retract	0.77	1.00	0.87	0.97

HMM-Logistic Regression. Where

¹Transport,

²Stabilization and

³Manipulation.

Benchmark of success: To evaluate whether our approach was successful, performance metrics for all movement primitives of healthy controls were obtained with HMM-Logistic Regression (LR) and averaged across activities, excluding feeding (Table X).

TABLE X.

HMM-LR (all tasks except feeding)

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.86	0.97	0.80	0.97
Reach	0.77	0.94	0.81	0.93
Transport	0.86	0.86	0.79	0.91
Retract	0.78	0.94	0.81	0.92
Overall Perf.1	0.82	0.93	0.80	0.93

In order to provide a benchmark for success, the same metrics were obtained with only a Logistic Regression algorithm:

These results demonstrate the superior performance of the HMM-LR approach. This semi-supervised approach takes into consideration the non-statistically exchangeable characteristics of the data, which other methods, such as the Logistic Regression, do not.

Results of stroke patients: the trained algorithm was tested on each of the 6 stroke patients. The same performance metrics were calculated for all movement primitives and are shown in (Tables XII – XIII).

TABLE XII.

Radial Can

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.76	0.98	0.73	0.97
Reach	0.72	0.92	0.82	0.88
Transport	0.85	0.79	0.66	0.93
Retract	0.72	0.94	0.85	0.88

TABLE XIII.

Radial Toilet Paper

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.76	0.98	0.89	0.99
Reach	0.80	0.96	0.91	0.91
Transport	0.59	0.82	0.58	0.95
Retract	0.83	0.96	0.90	0.92

Average performance metrics for activities performed by stroke patients are shown below:

V. CONCLUSIONS

Movement recognition is a challenging task. However, the approach demonstrated here robustly captured upper extremity motion using wearable IMUs, and classified functional movement primitives using HMMs, with precision generally around 80% for control patients and 79% for stroke patients. Previous work in healthy controls and a stroke patient used IMUs and 2D convolution to recognize drinking, eating, and hair-brushing, but at the level of activities and not their component movements [18].

The present approach was developed to maximize ecological and content validity: motion was captured in a rehabilitation gym, and the algorithm was optimized for datasets generated by activities normally practiced, with objects commonly used, during rehabilitation training. The unadjusted algorithm performed well in chronic stroke patients making horizontal functional movement primitives.

Importantly, the algorithm continued to perform robustly regardless of the objects used. Because data about hand shape and grasp aperture are not captured by the IMU system, we assessed whether arm configuration (particularly forearm and hand position) would differentially affect algorithm performance. Despite different configurations, the algorithm detected functional reaches and transports in healthy subjects with 81% and 79% precision, respectively, with ranges of 70–87% (excluding feeding). Similarly, object weight did not appear to affect precision. These performance metrics suggest the generalizability of the algorithm to multiple testing conditions.

The use of HMM and Logistic Regression, as presented, generalized with high precision to other movement primitives performed by the same subject, as well as to the same primitives performed by other subjects. However, this approach does have some limitations: functional movement primitives were not detected with 100% precision, particularly in the activity of feeding. It is possible that parameters of the movement primitive may affect detection, for example, the amplitude or extent of reach. Thus the primitive nomenclature itself may require refinement to enable a more successful classification. Clearly, a higher level of algorithm performance in unconstrained activities is desired before clinical implementation.

In addition, there was no drop-off in algorithm performance when it was applied to stroke data. This good performance may speak to the robustness of the algorithm, or to the relative normality of the movement primitives, as all the patients were mildly impaired. Additional testing is needed within the full spectrum of motor impairment to determine if the approach is sufficiently robust for all stroke patients, or if titration to impairment level is required.

In conclusion, we used a combination of IMU-based motion capture, data pre-processing with a sliding window, and an HMM algorithm for pattern recognition to successfully identify functional UE movement primitives in healthy individuals and stroke patients. This proof-of-principle study suggests that our approach may be an appropriate means in rehabilitating stroke patients to identify functional movement primitives, which can be tallied to provide training dose. While other quantitative methods exist, their execution is laborious or their outputs are insufficiently granular, limiting clinical applicability. With our approach, motion data can be obtained innocuously and primitives identified robustly, making it a pragmatic choice for the quantitative dose-response trials so sorely needed in early stroke. With refinement, our approach could be expected to vertically advance neurorehabilitation research.

TABLE III.

Radial Toilet Paper

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.88	0.98	0.82	0.97
Reach	0.85	0.95	0.87	0.94
Transport	0.87	0.92	0.81	0.94
Retract	0.86	0.95	0.88	0.94

TABLE IV.

Light can

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.89	0.97	0.80	0.96
Reach	0.73	0.92	0.74	0.92
Transport	0.79	0.85	0.74	0.88
Retract	0.73	0.90	0.74	0.90

TABLE V.

Heavy can

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.88	0.98	0.78	0.98
Reach	0.80	0.94	0.80	0.94
Transport	0.86	0.89	0.84	0.92
Retract	0.80	0.94	0.83	0.92

TABLE VI.

Toilet Paper

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.83	0.98	0.77	0.97
Reach	0.82	0.93	0.82	0.93
Transport	0.84	0.90	0.80	0.91
Retract	0.82	0.94	0.84	0.93

TABLE VII.

Detergent

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.81	0.97	0.77	0.96
Reach	0.76	0.97	0.84	0.94
Transport	0.93	0.84	0.85	0.92
Retract	0.74	0.96	0.81	0.94

TABLE VIII.

Book

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.83	0.97	0.88	0.96
Reach	0.64	0.95	0.73	0.90
Transport	0.87	0.73	0.70	0.89
Retract	0.67	0.94	0.75	0.92

TABLE XI.

Logistic Regression (all tasks except feeding)

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.80	0.96	0.79	0.95
Reach	0.78	0.90	0.77	0.90
Transport	0.63	0.75	0.71	0.79
Retract	0.79	0.91	0.73	0.89
Overall Perf.1	0.75	0.88	0.75	0.88

TABLE XIV.

Performance in Stroke

Primitive	Sensitivity	Specificity	PPV	NPV
Rest	0.76	0.98	0.81	0.98
Reach	0.76	0.94	0.86	0.89
Transport	0.72	0.81	0.62	0.94
Retract	0.78	0.95	0.87	0.90
Overall Perf.1	0.75	0.92	0.79	0.93

¹The overall performance represents the average of these performance metrics across primitives.